圖

0.PTA得分截圖

1.本周學習總結（6分）

1.1 圖的存儲結構

圖主要分為無向圖、有向圖和網。存儲方式主要是鄰接矩陣和鄰接表。

1.1.1 鄰接矩陣

帶/無權圖：如果圖的邊的長度不完全相同，則圖為帶權圖。有/無向圖：如果給圖的每條邊規定一個方向，那么得到的圖稱為有向圖。在有向圖中，與一個節點相關聯的邊有出邊和入邊之分，而與一個有向邊關聯的兩個點也有始點和終點之分。相反，邊沒有方向的圖稱為無向圖。
有/無向圖：如果給圖的每條邊規定一個方向，那么得到的圖稱為有向圖。在有向圖中，與一個節點相關聯的邊有出邊和入邊之分，而與一個有向邊關聯的兩個點也有始點和終點之分。相反，邊沒有方向的圖稱為無向圖。

無向圖的鄰接矩陣

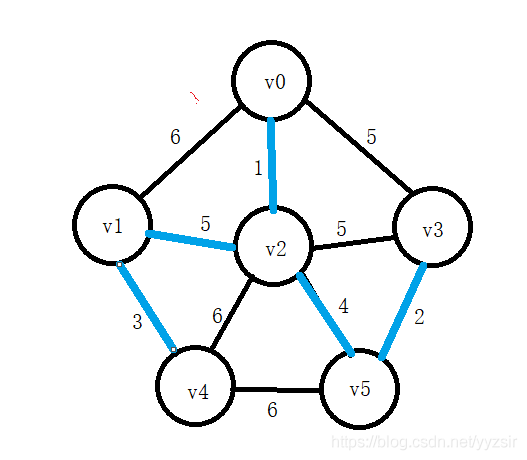
圖的頂點數為n，邊數為m
. 無向圖的鄰接矩陣
. 利用一個一維數組V[n-1]存儲頂點下標
. 利用一個二維數組A[n][n],其中A[i][j]中存放的是頂點i到頂點j的距離
. 若i=j則距離為0（鄰接矩陣的對焦新為0）
. 若i與j之間不存在邊，則設為∞（后文代碼中設為0）,否則設為邊長
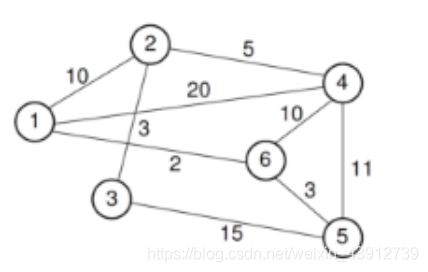
該圖可以得到如下的鄰接矩陣，v1->v2為2，因此A[0][1]=2.A[1][0]=2,V2與V3之間沒有邊，A[1][2]=A[2][1]=∞其余頂點同理。有向圖的同理。
鄰接矩陣的結構體定義

#define MAX  20   //邊和頂點的最大數量 
typedef char ElemType;
typedef struct Graph{
    int vexNum;  //頂點數
    int arcNum;  //邊的數量 
    ElemType vexs[MAX];       //頂點信息 
    int arcs[MAX][MAX];    //邊的信息 
}Graph,*myGraph;

建圖函數

void createGraph(myGraph &G)
{
    G=(Graph*)malloc(sizeof(Graph));  //結構體的指針要初始化
     
    int i,j,k;
    int vexNum,arcNum;
    char v1,v2;    //邊的兩個頂點 
    printf("請輸入頂點的數量:");
    scanf("%d",&G->vexNum);
    printf("請輸入邊的數量:");
    scanf("%d",&G->arcNum);
    
    printf("請依次將頂點數據輸入進來\n");
    for(i=0;i<G->vexNum;i++)
    {   
        getchar();
        scanf("%c",&G->vexs[i]); 
    }
    
    for(i=0;i<G->vexNum;i++)
    {
        for(j=0;j<G->vexNum;j++)
        {
            G->arcs[i][j]=0;//初始化矩陣 
        }
    }
    
    printf("請依次將邊輸入進來\n");
    for(i=0;i<G->arcNum;i++)
    {
        getchar();
        scanf("%c%c",&v1,&v2);
        j=getLocate(G,v1);
        k=getLocate(G,v2);
        G->arcs[j][k]=1;
        G->arcs[k][j]=1;
    }
}

1.1.2 鄰接表

. 頂點表也就是個結構體數組，是存放頂點的結構，頂點表中有data元素，存放頂點信息 firstarc是一個邊結構體表指針，存放鄰接點的信息。
. 邊表也是一個結構體，內有adivex元素，存放鄰接點的下標，weight存放頂點與鄰接點之間線的權重，next是邊表結構體指針，存放該頂點的下一個鄰接點，next就是負責將頂點的鄰接點連起來。
*鄰接表的結構體定義

typedef struct ANode //邊結點；
{
    int adjvex;//該邊的終點編號；
    struct ANode* nextarc;//指向下一條邊的指針；
    INfoType info;//保存該邊的權值等信息；
}ArcNode;
typedef struct Vnode //頭結點
{
    int data;//頂點；
    ArcNode* firstarc;//指向第一個鄰接點；
}VNode;
typedef struct
{
    VNode adjlist[MAX];//鄰接表；
    int n, e;//n:頂點數  e:邊數
}AdjGraph;

建圖函數

無向圖

void CreateAdj(AdjGraph*& G, int n, int e)
{
	ArcNode* p;
	int i, j, a, b;
	G = new AdjGraph;
	/*鄰接表初始化*/
	for (i = 0;i <= n;i++)
	{
		G->adjlist[i].firstarc = NULL;
	}
	/*建立鄰接表*/
	for (i = 0;i < e;i++)
	{
                //無向圖，a，b有邊互連
		cin >> a >> b;
		p = new ArcNode;
		p->adjvex = a;
		p->nextarc = G->adjlist[b].firstarc;
		G->adjlist[b].firstarc = p;
		p = new ArcNode;
		p->adjvex = b;
		p->nextarc = G->adjlist[a].firstarc;
		G->adjlist[a].firstarc = p;
	}
	G->n = n;G->e = e;
}

有向圖

void CreateAdj(AdjGraph*& G, int n, int e)
{
	ArcNode* p;
	int i, j, a, b;
	G = new AdjGraph;
	/*鄰接表初始化*/
	for (i = 0;i <= n;i++)
	{
		G->adjlist[i].firstarc = NULL;
	}
	/*建立鄰接表*/
	for (i = 0;i < e;i++)
	{
                //有向圖，僅一邊連接
		cin >> a >> b;
		p = new ArcNode;
		p->adjvex = b;
		p->nextarc = G->adjlist[a].firstarc;
		G->adjlist[a].firstarc = p;
	}
	G->n = n;G->e = e;
}

1.1.3 鄰接矩陣和鄰接表表示圖的區別

鄰接矩陣：圖的鄰接矩陣存儲方式是用兩個數組來表示圖。一個一維數組存儲圖中頂點信息，一個二維數組（鄰接矩陣）存儲圖中的邊或弧的信息。
鄰接表：鄰接矩陣是不錯的一種圖存儲結構，但是，對于邊數相對頂點較少的圖，這種結構存在對存儲空間的極大浪費。因此，找到一種數組與鏈表相結合的存儲方法稱為鄰接表。
鄰接表的處理方法是這樣的：
（1). 圖中頂點用一個一維數組存儲，當然，頂點也可以用單鏈表來存儲，不過，數組可以較容易的讀取頂點的信息，更加方便。
（2). 圖中每個頂點vi的所有鄰接點構成一個線性表，由于鄰接點的個數不定，所以，用單鏈表存儲，無向圖稱為頂點vi的邊表，有向圖則稱為頂點vi作為弧尾的出邊表。
區別
對于一個具有n個頂點e條邊的無向圖，它的鄰接表表示有n個頂點表結點2e個邊表結點；
對于一個具有n個頂點e條邊的有向圖，它的鄰接表表示有n個頂點表結點e個邊表結點；
如果圖中邊的數目遠遠小于n2稱作稀疏圖，這是用鄰接表表示比用鄰接矩陣表示節省空間;
如果圖中邊的數目接近于n2,對于無向圖接近于n*(n-1)稱作稠密圖,考慮到鄰接表中要附加鏈域，采用鄰接矩陣表示法為宜。

1.2 圖遍歷

1.2.1 深度優先遍歷

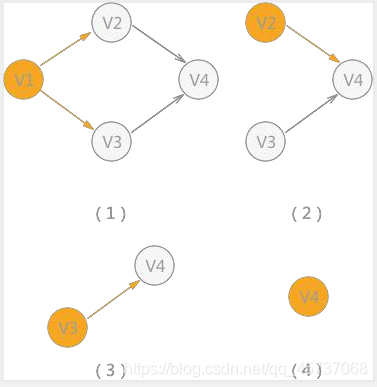
深度遍歷就是圖遍歷的一種，深度遍歷是一直遍歷為遍歷過的鄰邊，如果遇到鄰邊都是已遍歷過的就要回溯尋找為遍歷過的頂點，知道全部頂點都遍歷過，所以我們深度遍歷用的是遞歸的方法。

深度優先遍歷圖的方法是，從圖中某頂點v出發：
??a. 訪問頂點v；
??b. 依次從v的未被訪問的鄰接點出發，對圖進行深度優先遍歷；直至圖中和v有路徑相通的頂點都被訪問；
??c. 若此時圖中尚有頂點未被訪問，則從一個未被訪問的頂點出發，重新進行深度優先遍歷，直到圖中所有頂點均被訪問過為止。
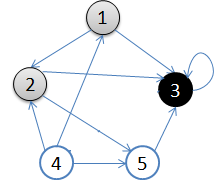
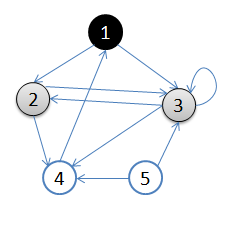
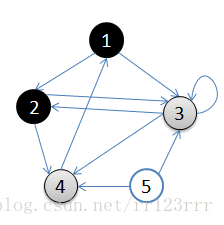
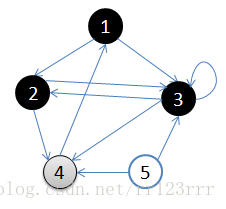
??用一副圖來表達這個流程如下：

從v = 頂點1開始出發，先訪問頂點1。

深度遍歷代碼
矩陣

void DFS(MGraph g, int v)//深度遍歷 
{
    int flag = 0;
    visited[v] = 1;
    for (int j = 0; j <g.n; j++)
    {
        if (visited[j] == 1)
        {
            flag++;
        }
    }
    if (flag == 1)
        cout << v;
    else
        cout << " " << v;
    for (int i = 0; i < g.n; i++)
    {
        if (g.edges[v][i] != 0 && visited[i] == 0)
        {
            DFS(g, i);
        }
    }
}

鏈表

void DFS(AdjGraph* G, int v)//v節點開始深度遍歷 
{
    int flag = 0;
    visited[v] = 1;
    for (int j = 1; j <= G->n; j++)
    {
        if (visited[j] == 1)
        {
            flag++;
        }
    }
    if (flag == 1)
        cout << v;
    else
        cout << " " << v;
    
    ArcNode* p;
    
    for (int i = 0; i < G->n; i++)
    {
        p = G->adjlist[v].firstarc;
        while (p)
        {
            if (visited[p->adjvex] == 0&&p!=NULL)
            {
                DFS(G, p->adjvex);
            }
            p = p->nextarc;
        }
    }
}

深度遍歷適用哪些問題的求解。（可百度搜索）

深度遍歷算法例題應用
1: 全排列問題
2: ABC+DEF=GHI問題
3: 二維數組尋找點到點的最短路徑
4: 求島嶼的面積
5: 求島嶼的個數
6: 地板的埔法有多少種
7: 二叉樹的深度遍歷
8: 圖的深度遍歷
9: 圖的最短路徑求解
10: 找子集等于某給定的數

1.2.2 廣度優先遍歷

廣度優先遍歷是按層來處理頂點，距離開始點最近的那些頂點首先被訪問，而最遠的那些頂點則最后被訪問.

初始狀態，從頂點1開始，隊列={1}
訪問1的鄰接頂點，1出隊變黑，2,3入隊，隊列={2,3,}
訪問2的鄰接頂點，2出隊，4入隊，隊列={3,4}
訪問3的鄰接頂點，3出隊，隊列={4}
訪問4的鄰接頂點，4出隊，隊列={ 空}
*廣度遍歷代碼
矩陣

void BFS(MGraph g, int v)//廣度遍歷 
{
    int front;
    queue<int>q;
    q.push(v);
    visited[v] = 1;
    cout << v;
    while (!q.empty())
    {
        front = q.front();
        q.pop();
        for (int i = 0; i < g.n; i++)
        {
            if (g.edges[front][i] == 1 && visited[i] == 0)
            {
                q.push(i);
                visited[i] = 1;
                cout << " " << i +;
            }
        }
    }

}

鏈表

void BFS(AdjGraph* G, int v) //v節點開始廣度遍歷  
{
    int i, j;
    int front;
    queue<int>q;
    ArcNode* p;
    q.push(v);
    visited[v] = 1;
    cout << v;
    while (!q.empty())
    {
        front = q.front();
        q.pop();
        p = G->adjlist[front].firstarc;
        do
        {
            if (p != NULL&&visited[p->adjvex]==0)
            {
                q.push(p->adjvex);
                visited[p->adjvex ] = 1;
                cout << " " << p->adjvex ;
            }
            p = p->nextarc;
        }while (p != NULL);
    }
}

廣度遍歷適用哪些問題的求解。

最短路徑;
最遠頂點

1.3 最小生成樹。

生成樹從前述的深度優先和廣度優先遍歷算法知，對于一個擁有n個頂點的無向連通圖，它的邊數一般都大于n－1。生成樹是指在連通圖中，由n個頂點和不構成回路的n－1條邊構成的樹。若由深度優先遍歷得到的生成樹稱為深度優先生成樹，則由廣度優先遍歷得到的生成樹稱為廣度優先生成樹。再進一步分析可知，對于滿足條件，連通圖的n個頂點和不構成回路的n－1條邊構成的生成樹有多棵，換言之，圖的生成樹不唯一。
最小生成樹對于帶權的圖，其生成樹的邊也帶權，在這些帶權的生成樹中必有一棵邊的權值之和最小的生成樹，這棵生成樹就是最小（代價）生成樹。

1.3.1 Prim算法求最小生成樹

基于上述圖結構求Prim算法生成的最小生成樹的邊序列

Prim算法思想：
假設G=（V，E）是連通無向網，T=（V，TE）是求得的G的最小生成樹中邊的集合，U是求得的G的最小生成樹所含的頂點集。初態時，任取一個頂點u加入U，使得U=｛u｝，TE=?。重復下述操作：找出U和V-U之間的一條最小權的邊（u，v），將v并入U，即U=U∪｛v｝，邊（u，v）并入集合TE，即TE=TE∪｛（u，v）｝。直到V=U為止。最后得到的T=（V，TE）就是G的一棵最小生成樹。也就是說，用Prim求最小生成樹是從一個頂點開始，每次加入一條最小權的邊和對應的頂點，逐漸擴張生成的。
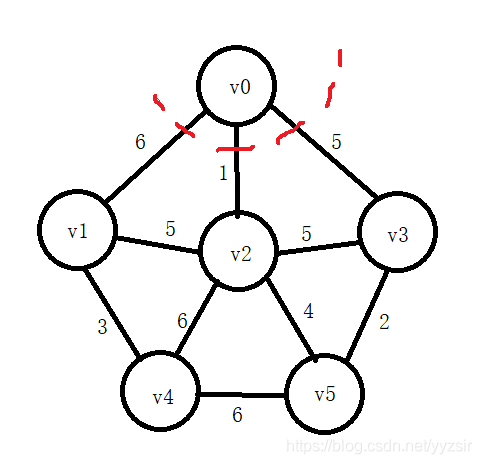
1). 初始化U=｛v0｝，TE=?

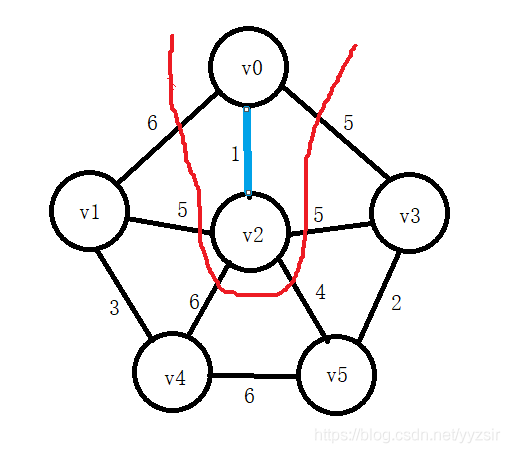
2). U=｛v0，v2｝，TE=｛（v0，v2）｝

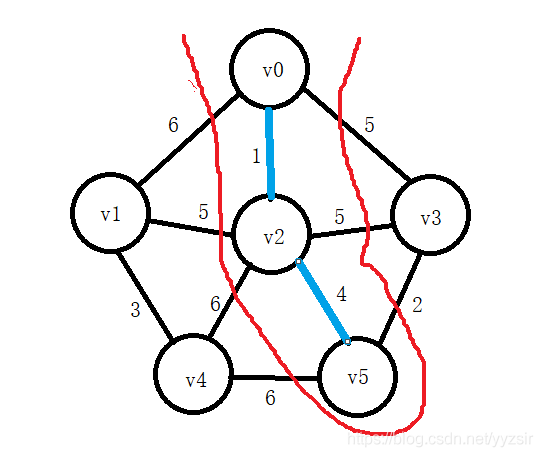
3). U=｛v0，v2，v5｝，TE=｛（v0，v2），（v2，v5）｝

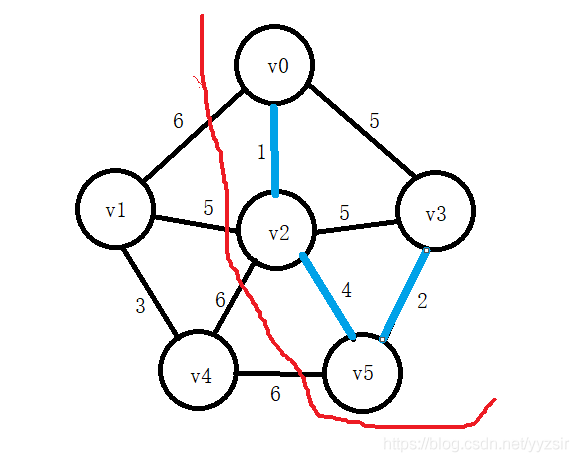
4). U=｛v0，v2，v5，v3｝，TE=｛（v0，v2），（v2，v5），（v5，v3）｝

5). U=｛v0，v2，v5，v3，v1｝，TE=｛（v0，v2），（v2，v5），（v5，v3），（v2，v1）｝

6). U=｛v0，v2，v5，v3，v1，v4｝，TE=｛（v0，v2），（v2，v5），（v5，v3），（v2，v1），（v2，v4）｝

實現Prim算法的2個輔助數組是什么？其作用是什么？Prim算法代碼。

一個是lowcost[]:存放候選邊，每個頂點到u中最小邊;
另一個是closet[]:U中頂點的鄰邊頂點
代碼：

#define INF 32767
//INF表示oo
void Prim(MGraph g, int v)
{
    int lowcost[MAXV], min, closest[MAXV], i, j, k;
    for (i = 0; i < g.n; i++)//給lowcost[]和lclosest[]置初
    {
        lowcost[i] = g.edges[v][i; closest[i] = v;
    }
    for (i = 1; i < g.n; i++)
        //找出(n - 1)個頂點
    {
        min = INF;
        for (j = 0; j < g.n; j++)//在(V - U)中我出離U最近的項點k
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j]; k = j; //k記錄最近頂點的編號
                printf("邊(%d,%d)權為:%d\n", closest[k], k, min);
                lowocost[k] = 0;// 記已經加入U
                for (j = 0; j < g.n; j++)
                    //修改數組lowcost和closest
                    if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j])
                    {
                        lowcost[j] = g.edges[k][j];
                        {
                            closest[j] = k;
                        }
                    }
            }
    }

時間復雜度為O(n^2).

1.3.2 Kruskal算法求解最小生成樹

Kruskal算法用到的數據結構有：
1. 邊頂點與權值存儲結構
2. 并查集
Kruskal算法的步驟包括：

對所有權值進行從小到大排序（這里對邊排序時還需要記錄邊的索引，這樣以邊的權值排完序后只改變了權值的索引位置）
然后每次選取最小的權值，如果和已有點集構成環則跳過，否則加到該點集中。最終有所有的點集構成的樹就是最佳的

代碼

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

//并查集實現最小生成樹
vector<int> u, v, weights, w_r, father;
int mycmp(int i, int j)
{
    return weights[i] < weights[j];
}
int find(int x)
{
    return father[x] == x ? x : father[x] = find(father[x]);
}
void kruskal_test()
{
    int n;
    cin >> n;
    vector<vector<int> > A(n, vector<int>(n));
    for(int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            cin >> A[i][j];
        }
    }

    int edges = 0;
    // 共計n*(n - 1)/2條邊
    for (int i = 0; i < n - 1; ++i) {
        for (int j = i + 1; j < n; ++j) {
            u.push_back(i);
            v.push_back(j);
            weights.push_back(A[i][j]);
            w_r.push_back(edges++);
        }
    }
    for (int i = 0; i < n; ++i) {
        father.push_back(i);    // 記錄n個節點的根節點，初始化為各自本身
    }

    sort(w_r.begin(), w_r.end(), mycmp); //以weight的大小來對索引值進行排序

    int min_tree = 0, cnt = 0;
    for (int i = 0; i < edges; ++i) {
        int e = w_r[i];    //e代表排序后的權值的索引
        int x = find(u[e]), y = find(v[e]);
        //x不等于y表示u[e]和v[e]兩個節點沒有公共根節點，可以合并
        if (x != y) {
            min_tree += weights[e];
            father[x] = y;
            ++cnt;
        }
    }
    if (cnt < n - 1) min_tree = 0;
    cout << min_tree << endl;
}

int main(void)
{

    kruskal_test();

    return 0;
}

1.4 最短路徑

1.4.1 Dijkstra算法求解最短路徑

算法特點：
迪科斯徹算法使用了廣度優先搜索解決賦權有向圖或者無向圖的單源最短路徑問題，算法最終得到一個最短路徑樹。該算法常用于路由算法或者作為其他圖算法的一個子模塊。
算法的思路
Dijkstra算法采用的是一種貪心的策略，聲明一個數組dis來保存源點到各個頂點的最短距離和一個保存已經找到了最短路徑的頂點的集合：T，初始時，原點 s 的路徑權重被賦為 0 （dis[s] = 0）。若對于頂點 s 存在能直接到達的邊（s,m），則把dis[m]設為w（s, m）,同時把所有其他（s不能直接到達的）頂點的路徑長度設為無窮大。初始時，集合T只有頂點s。
然后，從dis數組選擇最小值，則該值就是源點s到該值對應的頂點的最短路徑，并且把該點加入到T中，OK，此時完成一個頂點，
然后，我們需要看看新加入的頂點是否可以到達其他頂點并且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短，如果是，那么就替換這些頂點在dis中的值。
然后，又從dis中找出最小值，重復上述動作，直到T中包含了圖的所有頂點。

Dijkstra算法需要哪些輔助數據結構

dis[] path[]

Dijkstra算法的時間復雜度，使用什么圖結構，為什么

Dijkstra算法最簡單的實現方法是用一個鏈表或者數組來存儲所有頂點的集合Q,所以搜索Q中最小元素的運算(Extract-Min(Q))只需要線性搜索Q中的所有元素。算法的運行時間是O(n2)。
對于邊數少于n2稀疏圖來說，我們可以用鄰接表來更有效的實現Dijkstra算法。同時需要將一個二叉堆或者斐波納契堆用作優先隊列來尋找最小的頂點(Extract-Min)。當用到二叉堆的時候，算法所需的時間為O((m+n)log n).

1.4.2 Floyd算法求解最短路徑

Floyd算法解決什么問題？
Floyd算法需要哪些輔助數據結構
Floyd算法優勢，舉例說明。
最短路徑算法還有其他算法，可以自行百度搜索，并和教材算法比較。

1.5 拓撲排序

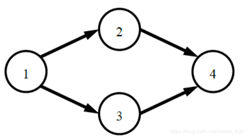
拓撲排序指的是將有向無環圖（又稱“DAG”圖）中的頂點按照圖中指定的先后順序進行排序。

對有向無環圖進行拓撲排序，只需要遵循兩個原則：

在圖中選擇一個沒有前驅的頂點 V；
從圖中刪除頂點 V 和所有以該頂點為尾的弧
上面左圖拓撲排序如下：

結構體

typedef struct//表頭節點類型
{
    vertex data;//頂點信息
    int count; // 存放頂點入度
    ArcNode* firstarc;//指向第一條弧

}VNode;

偽代碼：

遍歷鄰接表
   把每個頂點的入度算出來
遍歷圖頂點
   度為0，入棧st
    while (st不為空)
    {
        出棧v，訪問
            遍歷v的所有鄰接點
        {
            所有鄰接點的度 - 1；
            鄰接點的度若為0，進棧st
        }
    }

1.6 關鍵路徑

什么叫AOE-網？

在現代化管理中，人們常用有向圖來描述和分析一項工程的計劃和實施過程，一個工程常被分為多個小的子工程，這些子工程被稱為活動（Activity)，在帶權有向圖中若以頂點表示事件，有向邊表示活動，邊上的權值表示該活動持續的時間，這樣的圖簡稱為AOE網

AOE網的性質：
⑴ 只有在某頂點所代表的事件發生后，從該頂點出發的各活動才能開始；
⑵ 只有在進入某頂點的各活動都結束，該頂點所代表的事件才能發生。

什么是關鍵路徑概念？

在AOE網中，從始點到終點具有最大路徑長度（該路徑上的各個活動所持續的時間之和）的路徑稱為關鍵路徑。

什么是關鍵活動？

鍵路徑上的活動稱為關鍵活動。關鍵活動：e[i]=l[i]的活動
　　由于AOE網中的某些活動能夠同時進行，故完成整個工程所必須花費的時間應該為始點到終點的最大路徑長度。關鍵路徑長度是整個工程所需的最短工期。

代碼實現

Status TopologicalOrder(ALGraph G, Stack &T)
{
    // 有向網G采用鄰接表存儲結構，求各頂點事件的最早發生時間ve(全局變量)。
    // T為拓撲序列定點棧，S為零入度頂點棧。
    // 若G無回路，則用棧T返回G的一個拓撲序列，且函數值為OK，否則為ERROR。
    Stack S;
    intcount=0,k;
    charindegree[40];
    ArcNode *p;
    InitStack(S);
    FindInDegree(G, indegree); // 對各頂點求入度indegree[0..vernum-1]
    for(int j=0; j<G.vexnum; ++j)     // 建零入度頂點棧S
        if(indegree[j]==0)
            Push(S, j); // 入度為0者進棧
    InitStack(T);//建拓撲序列頂點棧T
    count = 0; 
    for(inti=0; i<G.vexnum; i++)
        ve[i] = 0; // 初始化
    while(!StackEmpty(S))
    {
        Pop(S, j);  Push(T, j);  ++count;      // j號頂點入T棧并計數
        for(p=G.vertices[j].firstarc;  p;  p=p->nextarc)
        {
            k = p->adjvex;           // 對j號頂點的每個鄰接點的入度減1
            if(--indegree[k] == 0) Push(S, k);   // 若入度減為0，則入棧
            if(ve[j]+p->info > ve[k])  ve[k] = ve[j]+p->info;
        }//for  *(p->info)=dut(<j,k>)
    }
    if(count<G.vexnum)
        returnERROR;  // 該有向網有回路
    else
        returnOK;
}

2.PTA實驗作業（4分）

2.1 六度空間（2分）

2.1.1 偽代碼（貼代碼，本題0分）

定義一個結構體來存放節點編號和深度遍歷是節點所在的層次
typedef struct Element { 
    VertexType v;        /* 結點編號 */
    int Layer;           /* BFS的層次 */
} QElementType;

    從第一個節點作為開始·標記為已訪問過
    將開始節點存放到結構體中并將層數記為0
    將其帶有節點信息的結構體入隊
    while (當隊中非空時 )
        取隊頭元素為qe并出隊
        for 從該點的第一條邊開始 to 沒有邊截止
            若edge->Adjv是v的尚未訪問的鄰接頂點,將其記為六度以內的頂點并將層數加1
             如果該節點的層數小于6
                將其入隊
             恢復qe的層數
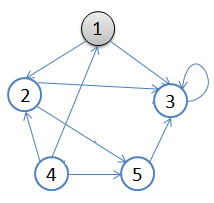
    計算符合“六度空間”理論的結點占結點總數的百分比。

2.1.2 提交列表

2.1.3 本題知識點

圖的廣度搜索原理解析類似二叉樹的層序遍歷
(1). 從所需要的頂點進入圖（類似利用此頂點為樹的根結點，構建一棵樹）
(2). 根結點入隊列
(3). 尋找與此頂點相連的所有頂點并放入隊列中（圖的臨接矩陣中，儲存的是每個頂點間的邊的關系，而且無向圖的臨接矩陣一定為對稱矩陣）
(4). 當頂點所在行遍歷結束，取出隊列的下一個頂點，重復。直至遍歷所有的頂點
實現動態分配二維數組注意：
(1). 動態分配必須按照順序分配
(2). 同時數組釋放內存的時候要按照先后順序釋放
(3). 否則會出現野指針
(4). 內存泄漏導致程序崩潰

2.2 村村通或通信網絡設計或旅游規劃（2分）

2.2.1 偽代碼

本題運用prime算法解決 
int edges[MAXV][MAXV]; 	
int n,e;  //圖結構 
void prime()
	定義lowcost[MAXV]數組表示某個頂點當前最低花費，并在確定該頂點的closest后將其賦值為0 
	定義closest[MAXV]數組表示某頂點最低花費情況下的前一個頂點 
	定義min存儲最小值 
	for i = 1 to n
		lowcost[i] = edges[1][i];
		closest[i] = 1;   初始化最低花費和最近頂點 
	end for
	for i = 1 to n
		min = INF (INF為無限大，其值自定義一個較大的數)
	 	for j = 1 to n
		若 lowcost[j] != 0&&lowcost[j] < min
			min = lowcost[j]
			k = j
		end for
	 end for
	 令k = j即令k 等于 離i最近的那個頂點
	 lowcost[k] = 0表示該頂點已被訪問
	 for j = 1 to n 加入k后尋找新的最低花費 
	 	if(edges[k][j] != 0&&edges[k][j] < lowcost[j]) 
	 		lowcost[j] = edges[k][j];
			closest[j] = k
	 end for;
	 for i = 0 to n
	 	累加各個最低花費并且輸出
		若出現某個頂點的最低距離為INF，表示無法暢通輸出 -1

2.2.2 提交列表

2.2.3 本題知識點

prime算法解決

posted on 2021-05-23 22:41 長安& 閱讀(106) 評論(0) 收藏舉報

刷新頁面返回頂部

楊佳琴

圖