給定一個非負整數數組，你最初位于數組的第一個位置。

數組中的每個元素代表你在該位置可以跳躍的最大長度。

你的目標是使用最少的跳躍次數到達數組的最后一個位置。

示例:

輸入: [2,3,1,1,4]
輸出: 2
解釋: 跳到最后一個位置的最小跳躍數是 2。
從下標為 0 跳到下標為 1 的位置，跳 1 步，然后跳 3 步到達數組的最后一個位置。

說明:

假設你總是可以到達數組的最后一個位置。

思路：這道題是一道典型貪心算法，通過局部最優來達到最優解

方法一：反向查找出發位置

class Solution {
public:
    int jump(vector<int>& nums) {
        int position = nums.length - 1;
        int steps = 0;
        while (position > 0) {
            for (int i = 0; i < position; i++) {
                if (i + nums[i] >= position) {
                    position = i;
                    steps++;
                    break;
                }
            }
        }
        return steps;
    }
};
//時間復雜度是 O（n^2)，效率并不是很高但容易理解

方法二：正向查找可到達的最大位置

方法一雖然直觀，但是時間復雜度比較高，有沒有辦法降低時間復雜度呢？

如果我們「貪心」地進行正向查找，每次找到可到達的最遠位置，就可以在線性時間內得到最少的跳躍次數。

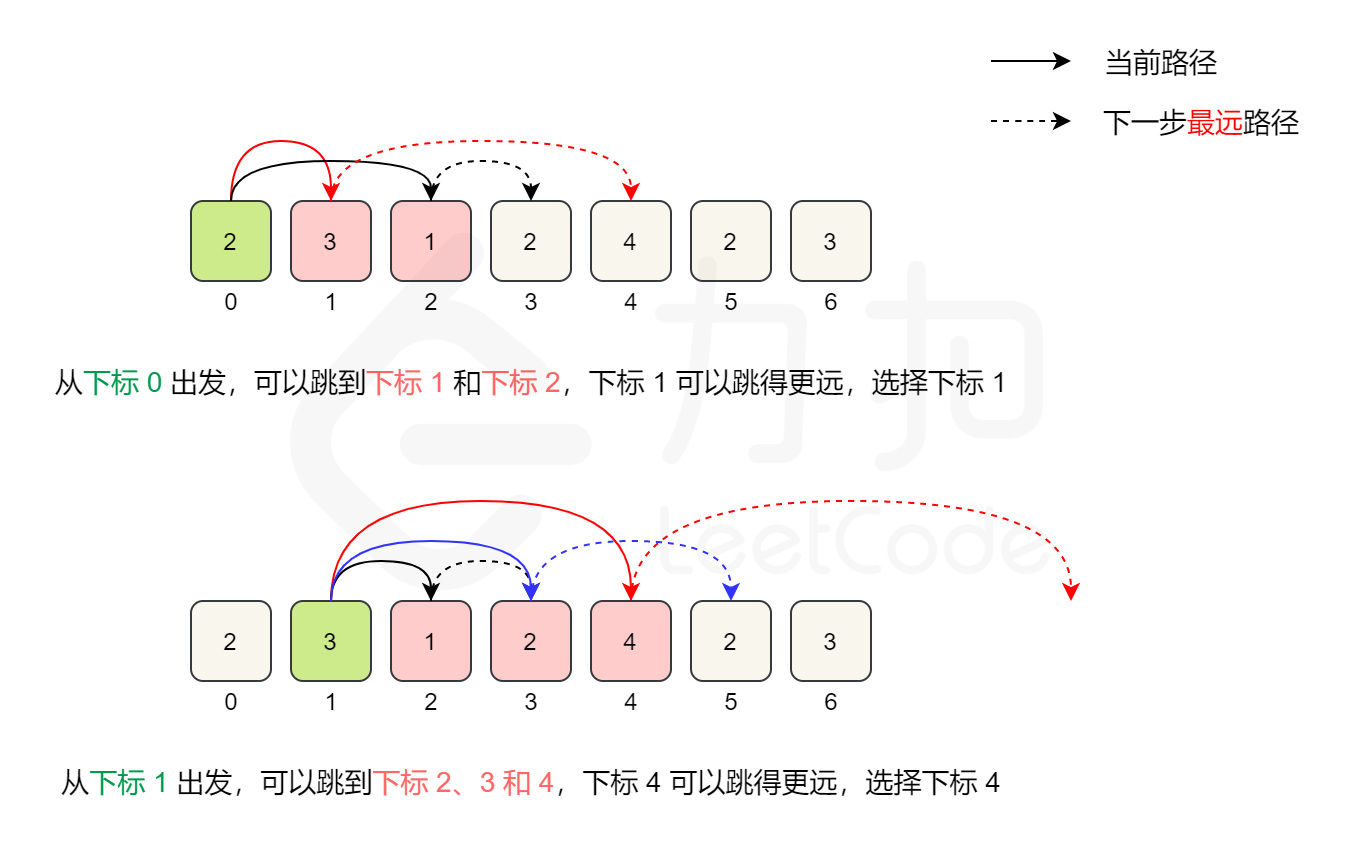
例如，對于數組 [2,3,1,2,4,2,3]，初始位置是下標 0，從下標 0 出發，最遠可到達下標 2。下標 0 可到達的位置中，下標 1 的值是 3，從下標 1 出發可以達到更遠的位置，因此第一步到達下標 1。

從下標 1 出發，最遠可到達下標 4。下標 1 可到達的位置中，下標 4 的值是 4 ，從下標 4 出發可以達到更遠的位置，因此第二步到達下標 4。

在具體的實現中，我們維護當前能夠到達的最大下標位置，記為邊界。我們從左到右遍歷數組，到達邊界時，更新邊界并將跳躍次數增加 1。

在遍歷數組時，我們不訪問最后一個元素，這是因為在訪問最后一個元素之前，我們的邊界一定大于等于最后一個位置，否則就無法跳到最后一個位置了。如果訪問最后一個元素，在邊界正好為最后一個位置的情況下，我們會增加一次「不必要的跳躍次數」，因此我們不必訪問最后一個元素。

class Solution {
public:
    int jump(vector<int>& nums) {
        int maxPos = 0, n = nums.size(), end = 0, step = 0;
        for (int i = 0; i < n - 1; ++i) {
            if (maxPos >= i) {
                maxPos = max(maxPos, i + nums[i]);
                if (i == end) {
                    end = maxPos;
                    ++step;
                }
            }
        }
        return step;
    }
};
//時間復雜度：O（n）