計(jì)算機(jī)組成原理—運(yùn)算方式
計(jì)算機(jī)組成原理—中央處理器(1)
四、計(jì)算機(jī)的運(yùn)行方式
1.有符號(hào)數(shù)和無(wú)符號(hào)數(shù)
計(jì)算機(jī)的數(shù)均存在寄存器中,通常稱寄存器的位數(shù)為機(jī)器字長(zhǎng)
1.1無(wú)符號(hào)數(shù)
沒(méi)有表示符號(hào)的數(shù),每一位均可存放數(shù)值。eg:若機(jī)器字長(zhǎng)16位,則可表示無(wú)符號(hào)數(shù)的范圍為0-65535(2^16 - 1)
1.2有符號(hào)數(shù)
符號(hào)的“+”、“-”用“0”和“1”來(lái)表示。0=>正;1=>負(fù)
真值:帶有正負(fù)的二進(jìn)制數(shù)字表達(dá)
機(jī)器數(shù):真值的機(jī)器表示
計(jì)算碼值。前提:已知真值
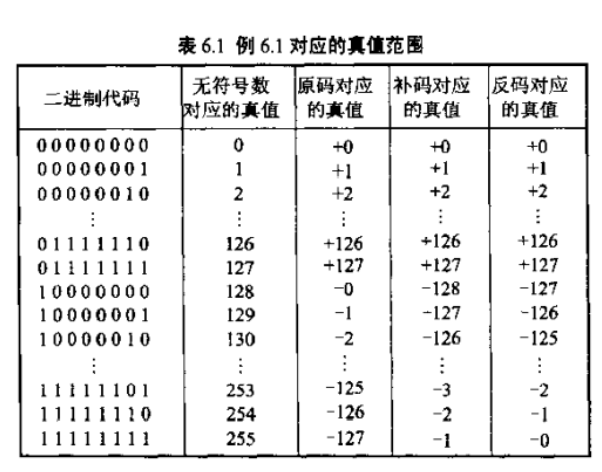
| 原碼 | 反碼 | 補(bǔ)碼 | |
|---|---|---|---|
| 正數(shù)整數(shù) | 0,真值 | 同原碼 | 同原碼 |
| 正數(shù)小數(shù) | 0.小數(shù)后真值 | 同原碼 | 同原碼 |
| 負(fù)數(shù)整數(shù) | 1,去負(fù)號(hào)真值 | 首位不變,后位取反 | 首位不變,最后1位加1 |
| 負(fù)數(shù)小數(shù) | 1.小數(shù)后無(wú)負(fù)號(hào)真值 | 首位不變,后位取反 | 首位不變,最后1位加1 |
以8進(jìn)制為例,不同碼對(duì)應(yīng)的真值范圍
- 移碼
已知真值,求其移碼
移碼 = 真值 + 2^n(真值位數(shù)) 最高位為正負(fù)位
注:二進(jìn)制的加減法
2.數(shù)的定點(diǎn)、浮點(diǎn)表示
2.1定點(diǎn)表示
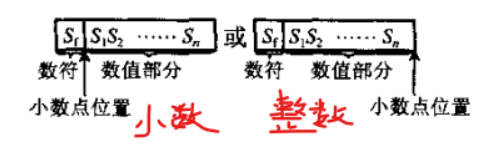
2.2浮點(diǎn)表示
N = S * r^j
S:是尾數(shù)(可正可負(fù),首位非零)
j:為階數(shù)(可正可負(fù))
r:為基數(shù)(2、4、8、16進(jìn)制)
eg:N = 11.0101 =>0.110101 * 2^10(二進(jìn)制)
2.2.1此為浮點(diǎn)位的表示形式

2.2.2 定點(diǎn)數(shù)和浮點(diǎn)數(shù)的比較
| 定點(diǎn)數(shù) | 浮點(diǎn)數(shù) | |
|---|---|---|
| 范圍 | 小 | 大 |
| 精度 | 低 | 高 |
| 運(yùn)算步驟 | 少 | 多 |
| 溢出判斷 | 本身判斷 | 規(guī)格化階數(shù)判斷 |
3.定點(diǎn)運(yùn)算
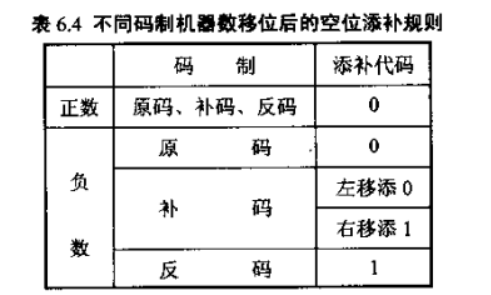
3.1移位
小數(shù)點(diǎn)不動(dòng),左移,絕對(duì)值增大;反之減小
- 移位規(guī)則
符號(hào)位不變 +
3.2加減運(yùn)算
全部換成補(bǔ)碼進(jìn)行 +運(yùn)算
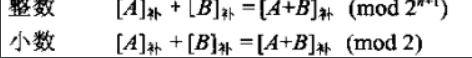
注:超出的位丟掉,所得的結(jié)果為補(bǔ)碼(要還原)
- 溢出判斷
一個(gè)符號(hào)位:正正 ->負(fù)或是負(fù)負(fù)->正為溢出;若有進(jìn)位,則與原操作 數(shù)符號(hào)對(duì)比,相同,未溢出,反之,溢出
兩個(gè)符號(hào)位:10/01為溢出,最高位為正真的符號(hào)位
4.浮點(diǎn)四則運(yùn)算
4.1加減運(yùn)算
- 對(duì)階(小階向大階對(duì)齊)
先寫出要運(yùn)算的數(shù)的計(jì)算機(jī)補(bǔ)碼表示

再求階差
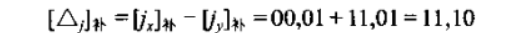
結(jié)果為負(fù)且等于(注意結(jié)果是補(bǔ)碼)-2,說(shuō)明y的階大于x的階,x->y對(duì)齊:尾數(shù)向右移動(dòng)兩位,x的階要增大2
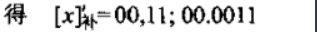
- 尾數(shù)求和
直接相加即可

- 規(guī)格化
左規(guī):將結(jié)果00.0xxx => 00.1xxx
? 將結(jié)果11.1xxx => 11.0xxx
? 尾數(shù)向左移動(dòng),階數(shù)減小
右規(guī):將結(jié)果01.xxx ->00.1xxx
? 將結(jié)果10.xxx ->11.0xxx
? 尾數(shù)向右移動(dòng),階數(shù)減大

- 舍入
“0”舍“1”入,尾數(shù)右移時(shí),同”四舍五入“
”恒置1“法,尾數(shù)右移時(shí),最右位恒為1
- 溢出判斷
根據(jù)階碼來(lái)判斷



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)