C++紅黑樹的實現

最近閑來無事，一直沒有研究過紅黑樹,B樹，B+樹之類的，打算自己用C語言實現一下它們。

紅黑樹的性質定義:

節點只能是黑色或者紅色。
根節點必須是黑色。
每個葉子節點是黑色節點（稱之為NIL節點，又被稱為黑哨兵）；可以理解為紅黑樹中每個節點都有兩個子節點，除了黑色的空節點。
每個紅色節點的兩個子節點都是黑色（或者說從每個葉子節點到根的所有路徑上不能有兩個連續的紅色節點）。
從任一節點到它所能到達的葉子節點的所有簡單路徑都包含相同數目的黑色節點。

上面就是紅黑樹的定義了，光有定義并不能幫助我們更好去理解紅黑樹。因此我在網上找了一些資料，發現一顆紅黑樹可以等價于一顆234樹，紅黑樹就是234樹的一種實現方式。而一顆234樹可以對應多顆紅黑樹。

234樹與紅黑樹的對應關系

舉個例子

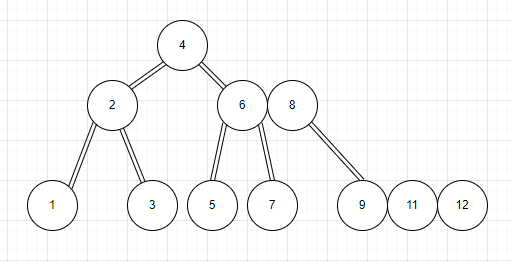
這是一顆234樹，我們現在將他轉化成一顆紅黑樹

紅黑樹1

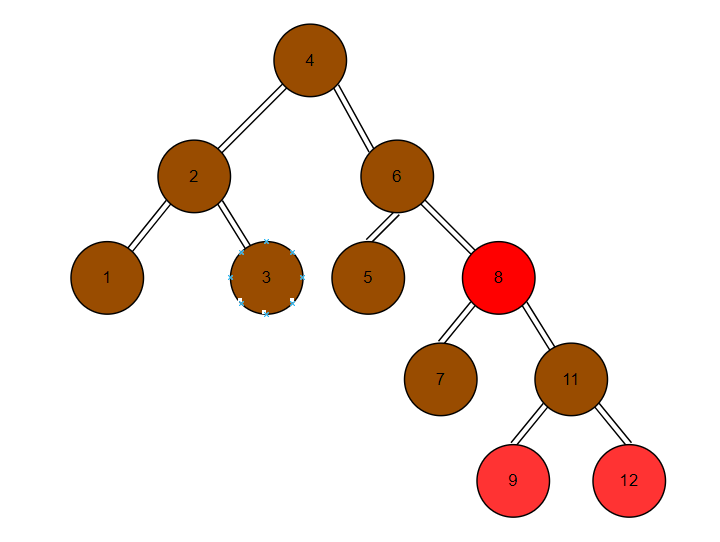
紅黑樹2

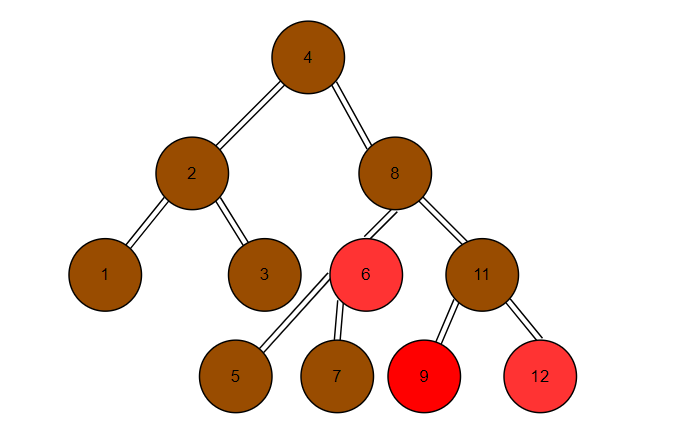
由此我們可以知道，一顆234樹可以對應多個紅黑樹，而一顆紅黑樹只有對應的一顆234樹。

這里我們說一下234樹的特點

每個節點每個節點有1、2或3個key，分別稱為2（孩子）節點，3（孩子）節點，4（孩子）節點。
所有葉子節點到根節點的長度一致（也就是說葉子節點都在同一層）。
每個節點的key從左到右保持了從小到大的順序，兩個key之間的子樹中所有的key一定大于它的父節點的左key，小于父節點的右key

因此我們可以得到這樣的對應關系

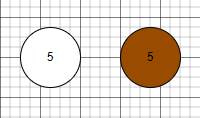
2節點對應紅黑樹上的一個黑色節點
3節點對應紅黑樹上兩種狀態，上黑下紅
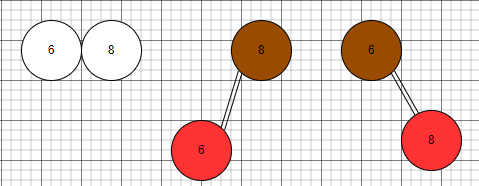
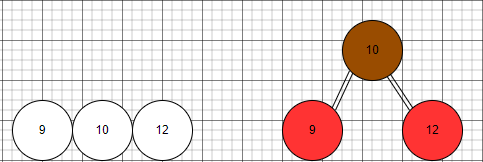
4節點對應紅黑樹上，上黑下兩紅
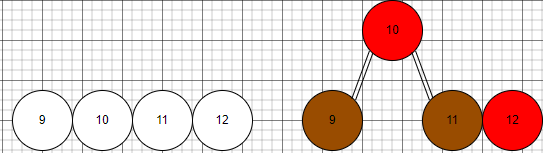
裂變狀態下（中間狀態，本身是4節點，現在又插入一個節點），上紅下兩黑

紅黑樹的旋轉

現在我們大概知道了234樹和紅黑樹轉換關系，接下來就是我們如何去理解旋轉的問題。
需要理解旋轉，我們就必須去理解，AVL樹的一些概念
avl樹對子樹的高度有一種要求:對于每個節點來說，這個節點的左右子樹的高度最多差1
為了保持AVL樹的平衡，就產生了旋轉的概念，那我們為什么不使用AVL樹來實現MAP那？我自己理解因為旋轉的次數太多，可能會程序的運行效率吧。紅黑樹就是一種近似平衡，不會產生那么多次的旋轉，效率會更高一點。

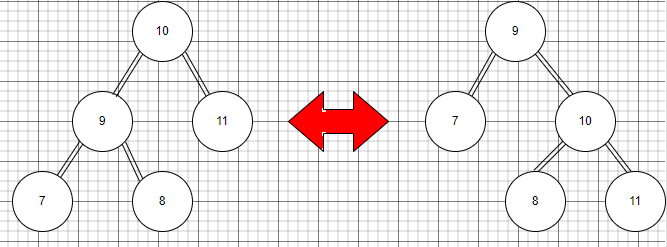
如圖所示，這就是左旋和右旋的轉換示意圖。
這里我們就把對應的紅黑樹的定義的代碼貼出來

結構體的定義

#define RED 0
#define BLACK 1
typedef struct _RBTREE_NODE
{
    int key;
    void* value;
    struct _RBTREE_NODE* right;
    struct _RBTREE_NODE* left;
    struct _RBTREE_NODE* parent;
    unsigned char color;
}RBTREE_NODE,*PRBTREE_NODE;

typedef struct _RBTREE
{
    struct _RBTREE_NODE* root;
    struct _RBTREE_NODE* nil;
}RBTREE,*PRBTREE;

這里是根據我們的示意圖寫出來旋轉的代碼

旋轉的代碼(包括左旋和右旋)

//左旋
void rbtree_left_rotate(PRBTREE  T,PRBTREE_NODE x)
{
    //右子樹
    PRBTREE_NODE y = x->right;
    x->right = y->left;
    if (y->left!=T->nil)
    {
        y->left->parent = x;
    }
    y->parent = x->parent;
    if (x->parent==T->nil)
    {
        T->root = y;
    }
    else if (x == x->parent->left)
    {
        x->parent->left = y;
    }
    else
    {
        x->parent->right = y;
    }

    y->left = x;
    x->parent = y;

}
//右旋
void rbtree_right_rotate(PRBTREE T, PRBTREE_NODE y)
{
    //右子樹
    PRBTREE_NODE x = y->left;
    y->left = x->right;
    if (x->right != T->nil)
    {
        x->right->parent = y;
    }
   x->parent = y->parent;
    if (y->parent == T->nil)
    {
        T->root = x;
    }
    else if (y == y->parent->right)
    {
        y->parent->right = x;
    }
    else
    {
        y->parent->left = x;
    }

    x->right = y;
    y->parent = x;

}

紅黑樹的插入

現在我們就來進行紅黑樹的最難的兩個部分的研究與學習，為了更好的理解紅黑樹插入的過程，我來先演示一下1-10的234樹插入的過程，我們借助234樹的插入，讓我們去了解紅黑樹的插入，這樣更便于我們去理解。
首先是1-3的插入

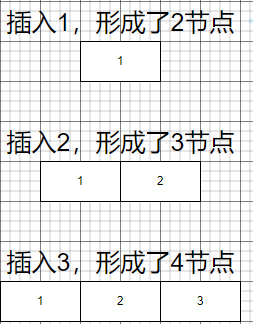
從4開始的插入操作，就會開始影響我們234樹的節點定義，需要開始進行調整。
插入4節點

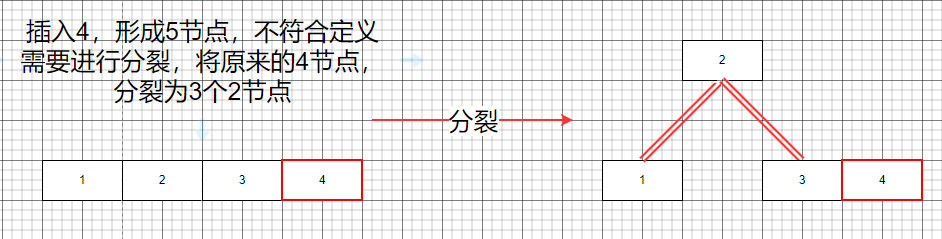
插入5節點

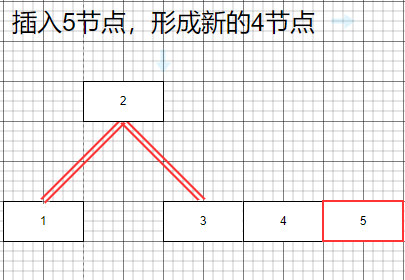
插入6節點

插入7節點

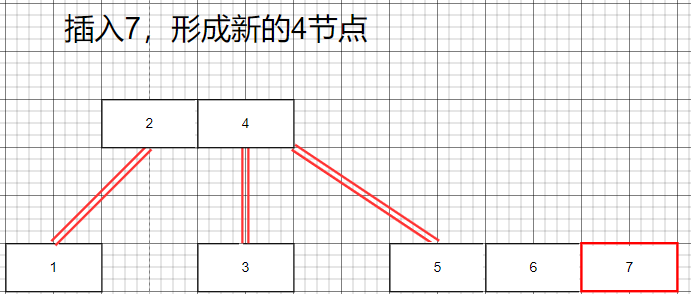
插入8節點

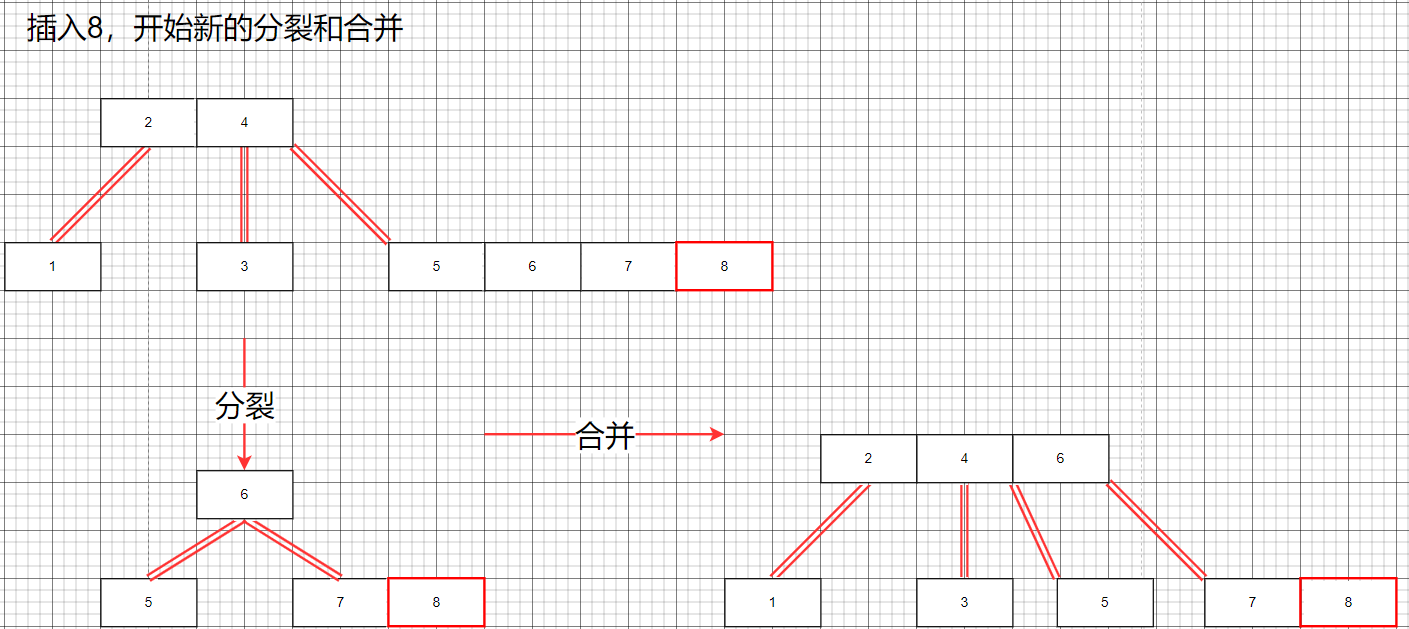
插入9節點

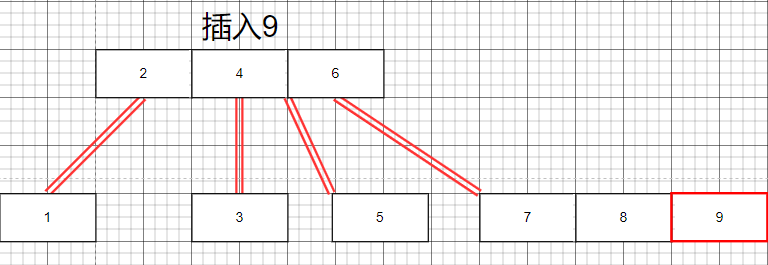
插入10節點

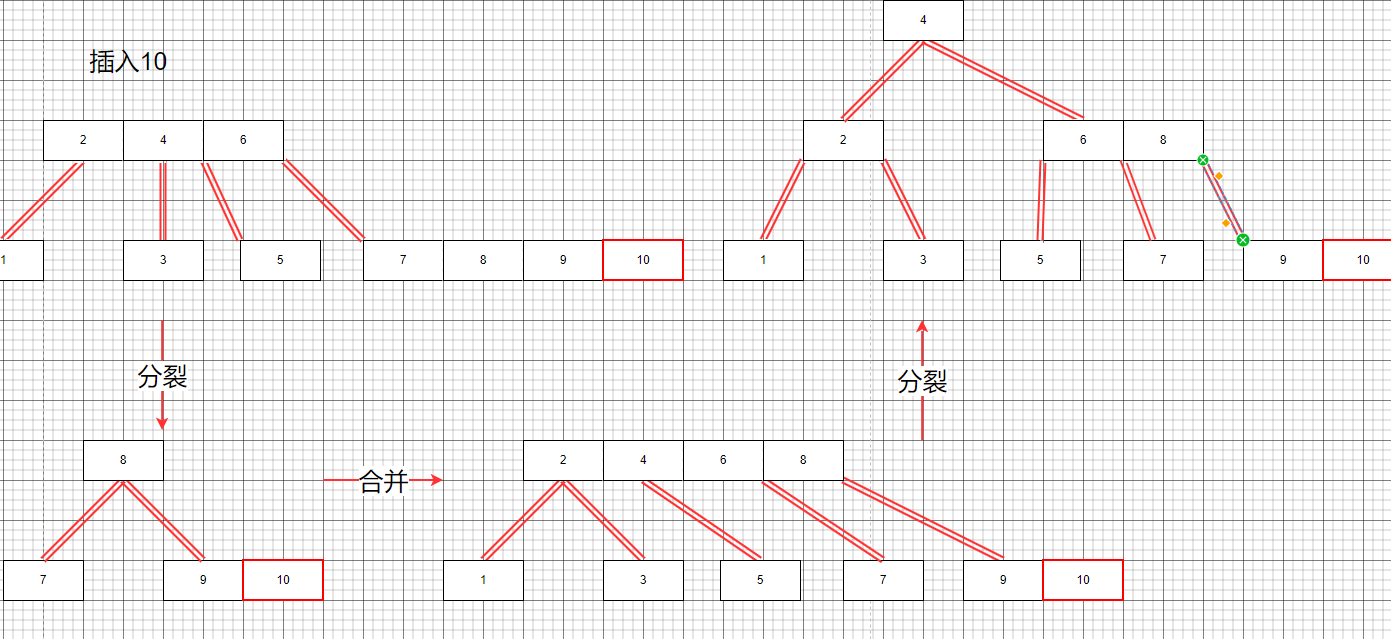
到這里，我們演示了一下1-10的234樹的插入的過程。
由于234樹與紅黑樹是等價的。
我們總結一下234樹插入的規律。

插入都是向最下層插入的
將2節點升級成3節點，或者將3節點升級成4節點。
向4節點插入元素后，需要將中間元素作為新的父節點，原結點變成兩個2節點，再把元素插入2節點中，如果父節點也是4節點，則遞歸向上層進行分裂，至到根結點后將樹高加1；

我們通過234樹的插入規律應用到紅黑樹的插入規律:

新插入的節點顏色為紅色，這樣才可能不會對紅黑樹的高度產生影響。(為什么插入的節點默認是紅色的)
2節點對應紅黑樹中的單個黑色結點，插入時直接成功（2節點升級為3節點）。
3節點對應紅黑樹中的黑+紅子樹，插入后將其修復成紅+黑+紅子樹（對應3節點的圖形）；
4節點對應紅黑樹中的紅+黑+紅子樹，插入后將其修復成紅色祖父+黑色父叔+紅色孩子子樹，然后再把祖父節點當成新插入的紅色節點遞歸向上層修復，直至修復成功或遇到root結點；

在這里我們針對幾種插入的情況進行分析:
首先是二節點插入一個新的元素變成3節點

其次就是3節點變成一個4節點，這里我們討論了幾種情況方便我們編寫代碼。

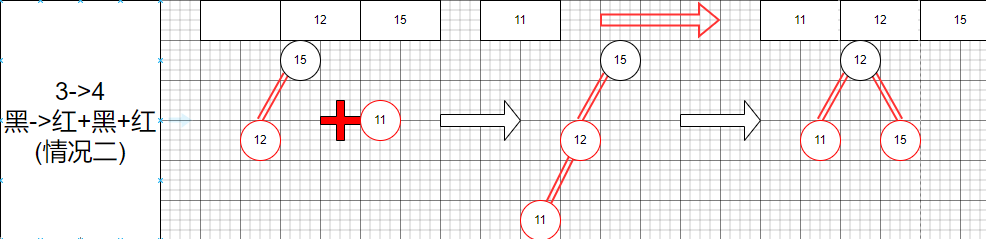
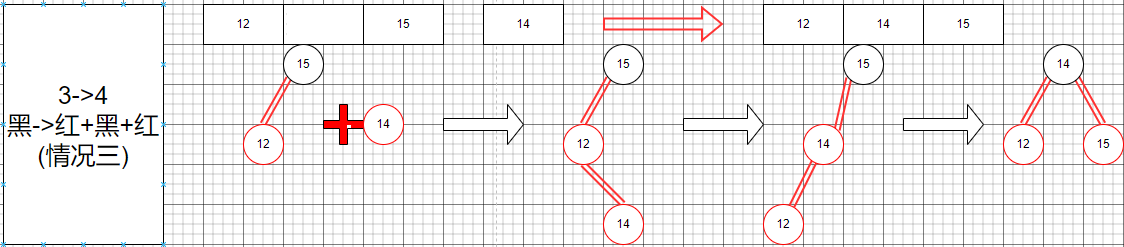
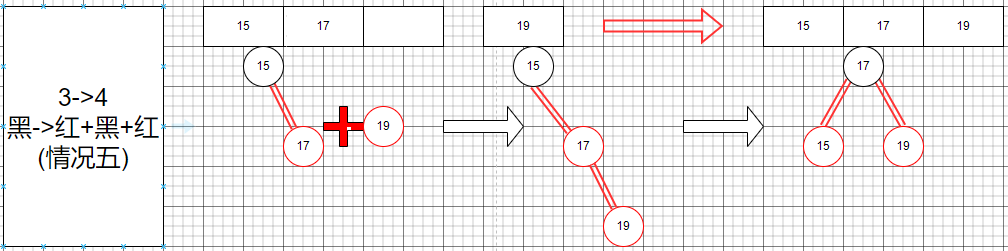
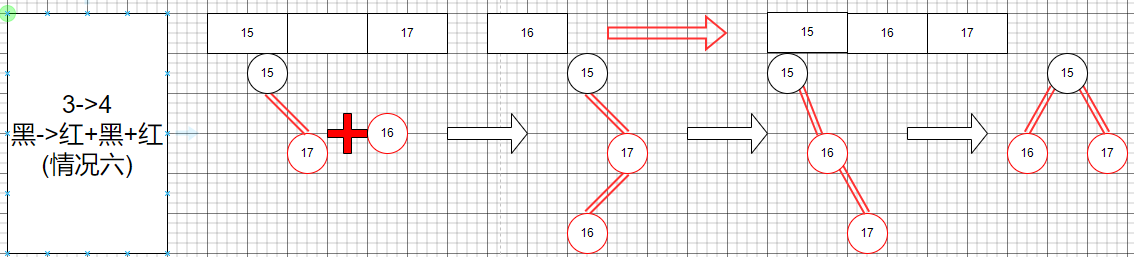
這些就是從3節點編程一個4節點的情況，我們列舉出來了所有可能的情況。
最后就是4節點插入元素進行裂變的過程的處理

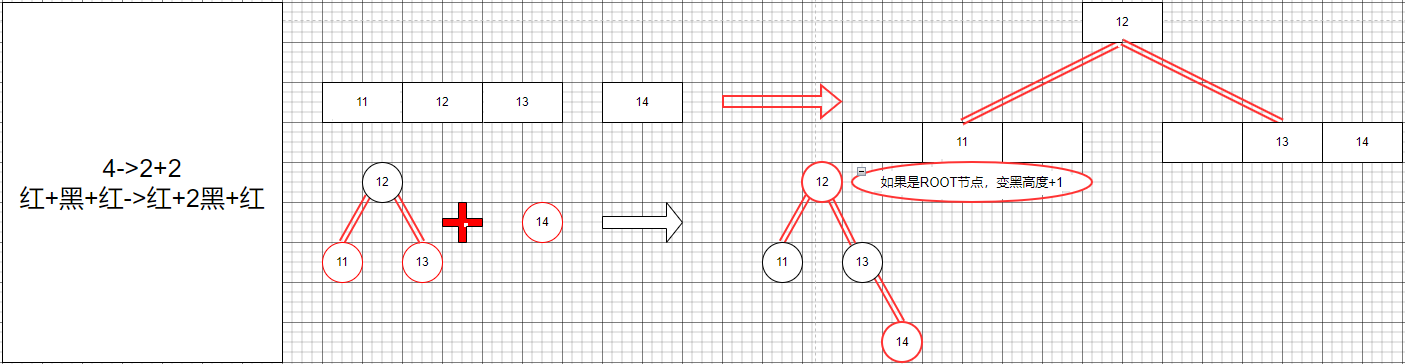
以上就是對插入情況的總結，我們來完成對應的紅黑樹的插入的代碼的實現。
我們首先就是正常的進行二叉樹的插入，然后再插入后在對紅黑樹進行修改處理。

正常的二叉樹的插入

void rbtree_insert(PRBTREE T, PRBTREE_NODE node)
{
    PRBTREE_NODE x = T->root;
    PRBTREE_NODE y = T->nil;
    while (x!=T->nil)
    {
        y = x;
        if (node->key<x->key)
        {
            x = x->left;
        }
        else if (node->key > x->key)
        {
            x = x->right;
        }
        else {
            return;
        }
    }
    if (y==T->nil)
    {
        T->root = node;
    }
    else
    {
        if (y->key > node->key)
        {
            y->left = node;
        }
        else
        {
            y->right = node;
        }
    }
    node->parent = y;
    node->left = T->nil;
    node->right = T->nil;
    node->color = RED;
    rbtree_insert(T,node);
}

然后就是我們根據特殊的情況，進行二叉樹的插入后的修復。

插入后調整

void rbtree_insert_fixup(PRBTREE T, PRBTREE_NODE node)
{
    //node == Red
    while (node->parent->color==RED)
    {
        if (node->parent==node->parent->parent->left)
        {
            //叔叔節點
            //4->2+2
            PRBTREE_NODE y = node->parent->parent->right;
            if (y->color==RED)
            {

                node->parent->color = BLACK;
                y->color = BLACK;
                node->parent->parent->color = RED;
                node = node->parent->parent; //z --> RED
            }
            else
            { //y=BLACK
                if (node==node->parent->right)
                {
                    //    15
                    //    /
                    //   12    
                    //     \
                    //     14
                    node = node->parent;
                    rbtree_left_rotate(T, node);
                    
                }
                    //   15 
                    //   /
                    //  14
                    //   /
                    //  12
                     
                node->parent->color = BLACK;
                node->parent->parent->color = RED;                
                rbtree_right_rotate(T, node->parent->parent);
                
            }
        }
        else
        {

        
            PRBTREE_NODE y = node->parent->parent->left;
            if (y->color == RED)
            {      
                //叔叔節點
                //4->2+2
                node->parent->color = BLACK;
                y->color = BLACK;
                node->parent->parent->color = RED;
            }
            else
            {
              
                if (node==node->parent->left)
                {

                    //    15
                    //      \
                    //      17
                    //      /
                    //    16
                    node = node->parent;
                    rbtree_right_rotate(T, node);
                }
                    //    15
                    //     \
                    //     16
                    //      \
                    //      17
                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                rbtree_left_rotate(T, node->parent->parent);
            }
            
        }
    }

}

二叉樹的刪除

現在我們到了紅黑樹最難理解的部分，就是紅黑樹的刪除操作，我們首先需要了解一下234樹的刪除，再去對比紅黑樹的刪除，幫助我們更好的去理解紅黑樹的刪除。
這里我們忽略了二叉樹刪除的時候會尋找前驅和后驅節點的查找。默認已經理解了這個概念，不然文章就太長了。（如果看的人多，可以留下評論，我再把這部分內容補上。）

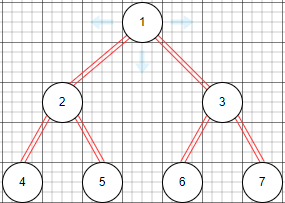
前驅節點：當前節點左子樹的最右節點（例如1節點的前驅節點為5），若無左子樹，則：當前節點是其父節點的右子樹(5節點的前驅節點為2).

后繼節點：當前節點右子樹的最左節點(1節點的后繼節點為6)，若無右子樹，則：當前節點為其父節點的左子樹(6節點的后繼節點為3).

查找前驅或者后繼節點

PRBTREE_NODE rbtree_min(PRBTREE T, PRBTREE_NODE x) {
    while (x->left != T->nil) {
        x = x->left;
    }
    return x;
}

PRBTREE_NODE rbtree_max(PRBTREE T, PRBTREE_NODE x) {
    while (x->right != T->nil) {
        x = x->right;
    }
    return x;
}

PRBTREE_NODE rbtree_successor(PRBTREE T, PRBTREE_NODE x) {
    

    if (x->right != T->nil) {
        return rbtree_min(T, x->right);
    }
    PRBTREE_NODE y = x->parent;
    while ((y != T->nil) && (x == y->right)) {
        x = y;
        y = y->parent;
    }
    return y;
}

PRBTREE_NODE rbtree_predecessor(PRBTREE T, PRBTREE_NODE x) {


    if (x->right != T->nil) {
        return rbtree_max(T, x->left);
    }
    PRBTREE_NODE y = x->parent;
    while ((y != T->nil) && (x == y->left)) {
        x = y;
        y = y->parent;
    }
    return y;
}

234樹的刪除，我們這里也是分幾種情況去討論的，看我們的圖把
比較復雜的地方，是2節點刪除的問題，一般非2節點的刪除，并不會有什么太大的影響。
非二節點的刪除
3節點的刪除

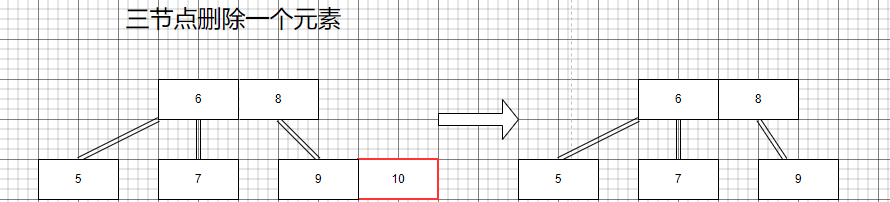
4節點的刪除

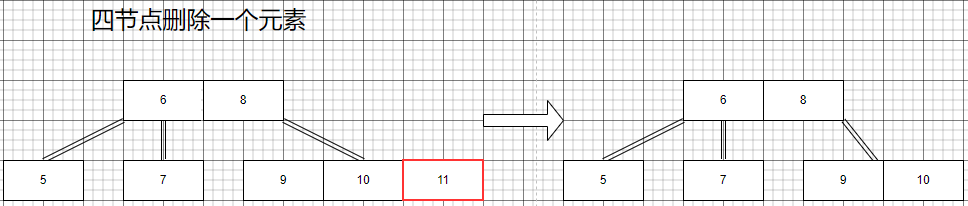
現在就是二節點刪除的一些情況了，我們這里來討論一下
對于2節點的刪除，需要轉換為3、4節點中節點的刪除
父節點為非2節點，兄弟節點為2節點

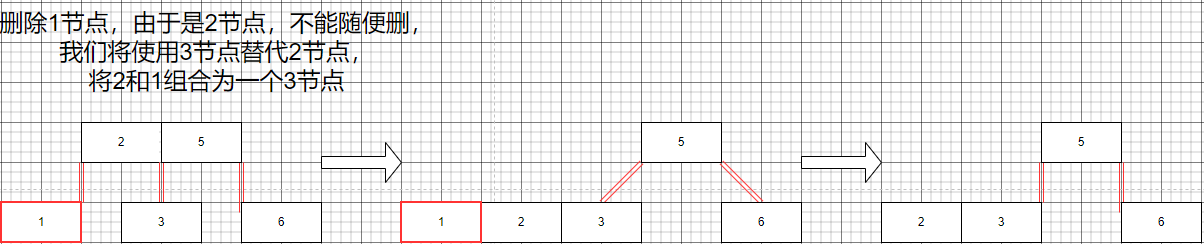
父節點為非2節點，兄弟節點為非2節點

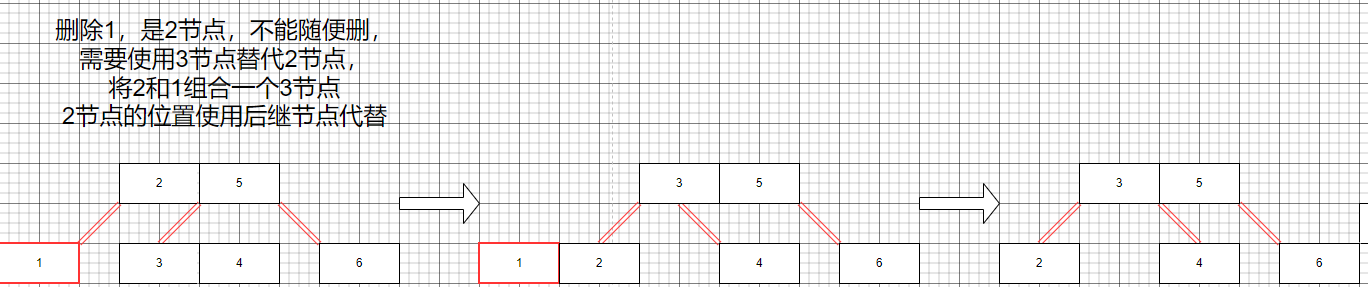
父節點為2節點，兄弟節點非2節點

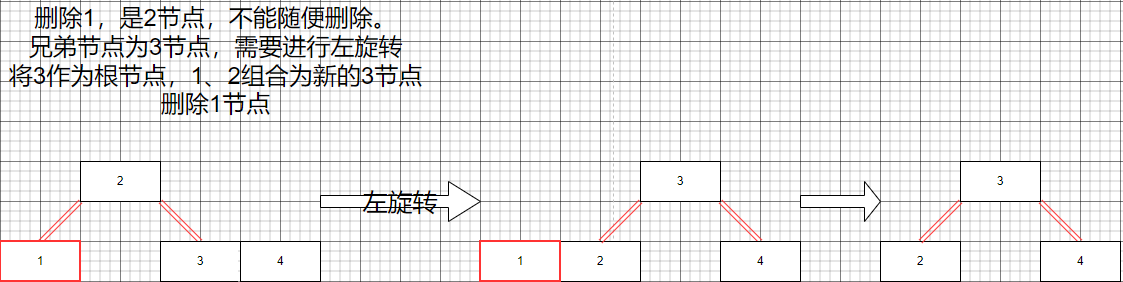
父節點為2節點，兄弟節點2節點

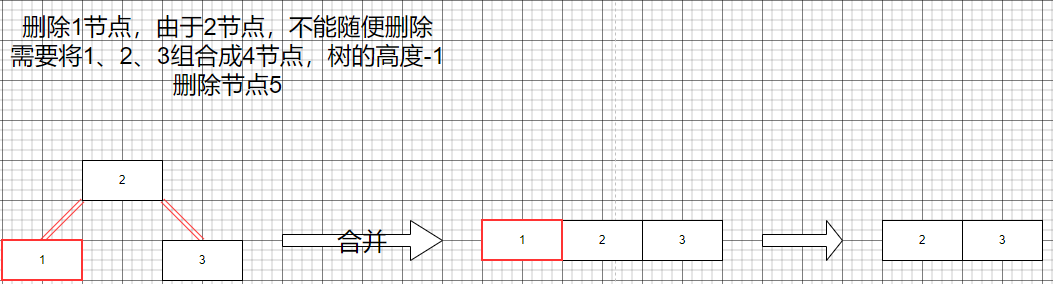
這里就是234樹刪除節點的幾種情況，我們應該如何的處理，如圖所示。
我們大概的總結一下

查找最近的葉子結點中的元素替代被刪除元素，刪除替代元素后，從替代元素所處葉子結點開始處理；
降低節點：4-結點變3-結點，3-結點變2-結點；
2-結點中只有一個元素，所以借兄弟結點中的元素來補充刪除后的造成的空結點；
當兄弟結點中也沒有多個元素可以補充時，嘗試將父結點降低，失敗時向上遞歸，至到子樹降元成功或到Root結點樹高減1

將這些規則對應到紅黑樹中即：

查找離當前結點最近的葉子結點作為替代結點（左子樹的最右結點或右子樹的最左結點都能保證替換后保證二叉查找樹的結點的排序性質，葉子結點的替代結點是自身）替換掉被刪除結點，從替代的葉子結點向上遞歸修復；
替代結點顏色為紅色（對應 2-3-4樹中 4-結點或 3-結點）時刪除子結點直接成功；
替代結點為黑色（對應 2-3-4樹中 2-結點）時，意味著替代結點所在的子樹會降一層，需要依次檢驗以下三項，以恢復子樹高度：
兄弟結點的子結點中有紅色結點（兄弟結點對應 3-結點或 4-結點）能夠“借用”，旋轉過來后修正顏色；
父結點是紅色結點（父結點對應 3-結點或 4-結點，可以降元）時，將父結點變黑色，自身和兄弟結點變紅色后刪除；
父結點和兄弟結點都是黑色時，將子樹降一層后把父結點當作替代結點遞歸向上處理.

我們需要先正常刪除我們的二叉樹節點，然后在刪除的節點為黑色節點的時候，進行調整，如果刪除的是紅色節點，不會影響紅黑樹的平衡，不需要平衡。

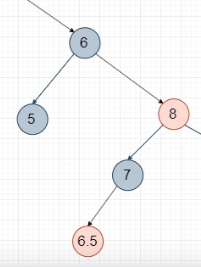
判斷是紅色節點的情況，5的兄弟節點應該是7，不是8.

紅黑樹的調整刪除的代碼

void rbtree_delete_fixup(PRBTREE T, PRBTREE_NODE x)
{
    //如果 X不是根節點，同時X的顏色是黑色
    while ((x != T->root) && (x->color == BLACK)) {
        //如果刪除的節點是左節點，同時是234樹的2節點
        if (x == x->parent->left) {
            //情況2:如果兄弟節點有子節點，就借用
            PRBTREE_NODE w = x->parent->right;
            //這里判斷是否是紅色節點，如果是紅色節點，說明不是真正的兄弟節點，需要進行左旋
            if (w->color == RED) {
                w->color = BLACK;
                x->parent->color = RED;

                rbtree_left_rotate(T, x->parent);
                w = x->parent->right;
            }
            //情況3如果兄弟節點沒有孩子節點，（通過自損，避免樹的不平衡）
            if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
                w->color = RED;
                x = x->parent;
            }
            else {
                //情況2 的第1種小情況，如果兄弟節點是3節點，需要通過2次旋轉(借1個節點）
                //右孩子為空的情況
                //          6(R)                6(R)
                //           /  \                 /  \
                //         5(B)  7(B)（W） ==>   5(B) 6.5(b)
                //               /                    \
                //              6.5(R)                 7(r)
                if (w->right->color == BLACK) {
                    w->left->color = BLACK;
                    w->color = RED;
                    rbtree_right_rotate(T, w);
                    w = x->parent->right;
                }
                //情況2 的第2種小情況，如果兄弟節點是4節點，需要通過1次旋轉(借2個節點，避免了1次旋轉)                
                w->color = x->parent->color;
                x->parent->color = BLACK;
                w->right->color = BLACK;
                rbtree_left_rotate(T, x->parent);
                //停止循環的條件
                x = T->root;
            }

        }
        //相反的情況不做討論
        else {

            PRBTREE_NODE w = x->parent->left;
            if (w->color == RED) {
                w->color = BLACK;
                x->parent->color = RED;
                rbtree_right_rotate(T, x->parent);
                w = x->parent->left;
            }

            if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
                w->color = RED;
                x = x->parent;
            }
            else {

                if (w->left->color == BLACK) {
                    w->right->color = BLACK;
                    w->color = RED;
                    rbtree_left_rotate(T, w);
                    w = x->parent->left;
                }

                w->color = x->parent->color;
                x->parent->color = BLACK;
                w->left->color = BLACK;
                rbtree_right_rotate(T, x->parent);

                x = T->root;
            }

        }
    }
    //如果是替代節點是紅色，直接染黑

    x->color = BLACK;
}

紅黑樹的刪除代碼

PRBTREE_NODE rbtree_delete( PRBTREE T,PRBTREE_NODE node)
{
    PRBTREE_NODE y = T->nil;
    PRBTREE_NODE x = T->nil;
    if ((node->left==T->nil)||(node->right==T->nil))
    {
        // 要刪除的node 為15
        // 15       15 y
        // /   或    \ 
        //14          16 x
        //這種就是再刪除有孩子節點的節點
        y = node;
    }else
    {
	    //要刪除的node為15
        //             15 y
        //            /  \
        //           14  16 x
        //它的左右節點都不為空
        //要找到它的后驅節點
        y = rbtree_successor(T, node);

    }
    //如果它的孩子不為空，需要用孩子來替換它，這里就是再獲取它的孩子節點
    if (y->left!=T->nil)
    {
        x = y->left;
    }else if(y->right!=T->nil)
    {
        x = y->right;
    }
    //3.4節點可以直接刪除
    //設置孩子節點的父親為被刪除節點的父親
    x->parent = y->parent;
    if (y->parent==T->nil)
    {
        //如果是根節點的情況
        //三節點
        // 15

        //四節點
        //    16
        //     /
        //    14
        T->root = x;
    }else if(y==y->parent->left)
    {
        //如果是那種拐彎的樹
	    //類似這種情況
        //          4                                4
        //        /   \         刪除4的時候,y=5     /   \       
        //       2     6                          2     6     
        //      / \   / \                        / \   / \
        //     1   3 5  8           刪除后      1   3  nil 8    
        //              / \                              / \
        //             7  10                            7   10
        //                / \                              / \
        //                9 11                             9 11
        y->parent->left = x;
    }else
    {
        y->parent->right = x;
    }

    if (y!=node)
    {
        node->key = y->key;
        node->value = y->value;
    }
    //這里紅色節點并不需要去處理，需要處理的僅有刪除的節點的顏色為黑色的時候。
    if (y->color==BLACK)
    {
        rbtree_delete_fixup(T, x);
    }


}

推薦一個零聲學院免費教程，個人覺得老師講得不錯，
分享給大家：[Linux，Nginx，ZeroMQ，MySQL，Redis，
fastdfs，MongoDB，ZK，流媒體，CDN，P2P，K8S，Docker，
TCP/IP，協程，DPDK等技術內容，點擊立即學習:
服務器
 音視頻
 dpdk
Linux內核

posted @ 2022-08-03 12:42 飄雨的河閱讀(221) 評論(0) 收藏舉報

刷新頁面返回頂部

飄雨的河

一個自己學習記錄的學習樂園