基礎排序算法(五)直接插入排序
一 直接插入排序
直接插入排序是一種非常直觀且基礎的排序算法,其核心思想類似于我們整理撲克牌。
1.1 特性總結
插入排序特性總結
| 特性 | 說明 |
|---|---|
| 核心思想 | 將待排序序列視為一個有序表和一個無序表。每次從無序表中取出第一個元素,將其插入到有序表中的正確位置,直到無序表為空 |
| 時間復雜度 | 最好情況 O(n):序列已有序 最壞情況 O(n2):序列完全逆序 平均情況 O(n2) |
| 空間復雜度 | O(1)。是原地排序算法,只需要常數級別的額外空間 |
| 穩定性 | 穩定。在比較時,只有當待插入元素小于前一個元素時才移動,相等時不移動,因此相等元素的相對順序保持不變 |
| 主要優勢 | 實現簡單;對于小規模或基本有序的數據效率很高;穩定;原地排序 |
| 主要劣勢 | 對于大規模隨機數據,效率較低(O(n2)) |
1.2 算法原理
直接插入排序的運作過程非常直觀,下圖以數組 [5, 2, 4, 6, 1, 3]為例,展示了其排序過程:
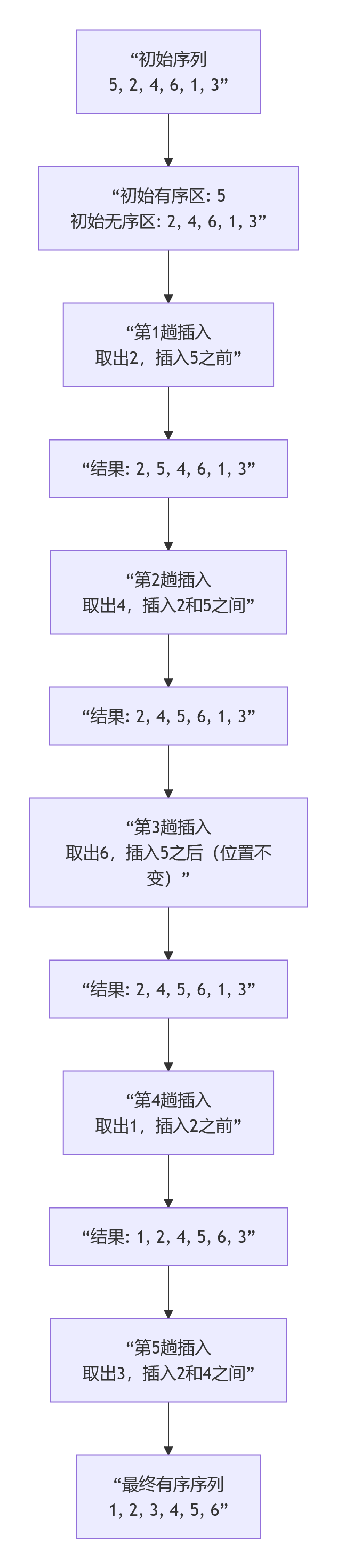
- 初始狀態??:將序列的第一個元素(例如5)視為一個已排序的有序區。其余元素(2, 4, 6, 1, 3)構成無序區。
- ??遍歷與插入??:從無序區取出第一個元素(例如2),將其與有序區的元素??從后向前??依次比較。
- ??移動元素??:在有序區中,所有比待插入元素大的元素都向后移動一個位置,為待插入元素騰出空間。
- ??插入元素??:將待插入元素放入騰出的空位。
- ??重復??:重復步驟2-4,直到無序區為空,整個序列變為有序。
1.3 復雜度分析
1.3.1 時間復雜度分析??:
- ??最好情況 O(n)??:當輸入序列已經是有序時,內層循環每次只比較一次就會發現待插入元素已在正確位置,因此需要進行 n-1 次比較,0次移動。這是最高效的情況。
- ??最壞情況 O(n2)??:當輸入序列完全逆序時,每次插入都需要與有序區中的所有元素比較并移動。總的比較和移動次數都與 n(n-1)/2 成正比,即 O(n2)。
- ??平均情況 O(n2)??:對于隨機排列的序列,平均每次插入需要移動有序區的一半元素,因此平均時間復雜度也為 O(n2)。
1.3.2 ?空間復雜度 O(1) 的由來??:
- 排序過程是在原數組上進行的,只需要固定數量的額外臨時變量(如用于暫存待插入元素的 key或 temp,以及循環索引 i, j),不隨待排序數據規模 n 的增大而增加額外空間。
1.4 使用場景
直接插入排序在以下特定場景中表現出色:
- ??小規模數據排序??:當待排序元素數量很少(例如 n < 50)時,其實現簡單的優勢凸顯,雖然時間復雜度是O(n2),但常數因子很小,實際效率可能比一些更復雜的O(n log n)算法更高。
- ??數據基本有序??:如果序列已經大部分有序,需要進行的比較和移動操作會大幅減少,效率很高。
- ??作為高級算法的子過程??:在一些復雜的排序算法中,如??快速排序??或??歸并排序??,當遞歸分解到小規模子序列時,常會切換使用插入排序來優化整體性能。
- ??鏈式存儲結構??:該算法可以很好地應用于鏈表排序,因為插入操作在鏈表中只需要修改指針,無需像在順序表中那樣大量移動元素
1.5 代碼實現
1.5.1 c語言實現
#include <stdio.h>
// 直接插入排序函數
// 參數: arr - 待排序數組指針, n - 數組長度
void insertionSort(int arr[], int n) {
int i, j, key;
// 從第二個元素開始遍歷(下標1到n-1),因為第一個元素視為已排序
for (i = 1; i < n; i++) {
key = arr[i]; // 取出當前待插入的元素(無序區的第一個元素)
j = i - 1; // j指向有序區的最后一個元素
// 在有序區中從后向前掃描,尋找key的正確插入位置
// 同時將比key大的元素向后移動一位,為key騰出空間
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j]; // 將大于key的元素后移
j--; // 指針前移,繼續比較
}
// 跳出循環時,j+1的位置就是key應該插入的位置
arr[j + 1] = key; // 將key插入到正確位置
}
}
// 打印數組函數,用于測試
void printArray(int arr[], int n) {
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
// 主函數,測試排序算法
int main() {
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]); // 計算數組長度
printf("排序前的數組: \n");
printArray(arr, n);
insertionSort(arr, n);
printf("排序后的數組: \n");
printArray(arr, n);
return 0;
}
1.5.2 ?代碼關鍵點解釋
- ?外層循環 (for i from 1 to n-1)??:從第二個元素開始,因為第一個元素自然構成初始有序區。
- ??內層循環 (while j >= 0 and arr[j] > key)??:這是算法的核心。它從有序區的末尾開始,將每個大于 key的元素向后移動一個位置,直到找到 key應該插入的位置(即找到第一個小于或等于 key的元素后面)。
- ??插入操作 (arr[j + 1] = key)??:在找到的正確位置插入待排序元素。
- ??穩定性??:內層循環的條件是 arr[j] > key,而不是 >=。這意味著當遇到相等的元素時,循環停止,key會插入到相等元素的后面,從而保證了排序的穩定性。
1.6 常用算法比較
排序算法全面比較
| 算法 | 平均時間復雜度 | 最好情況 | 最壞情況 | 空間復雜度 | 穩定性 | 主要特點與適用場景 |
|---|---|---|---|---|---|---|
| 直接插入排序 | O(n2) | O(n)(已有序) | O(n2)(逆序) | O(1) | 穩定 | 小規模或基本有序數據;實現簡單;穩定 |
| 冒泡排序 | O(n2) | O(n)(已有序,可優化) | O(n2) | O(1) | 穩定 | 實現簡單,但交換操作頻繁,通常效率低于插入排序 |
| 簡單選擇排序 | O(n2) | O(n2) | O(n2) | O(1) | 不穩定 | 交換次數少(最多n-1次),但比較次數固定為O(n2)。當元素移動成本高時可能有優勢 |
| 快速排序 | O(n log n) | O(n log n) | O(n2)(如已有序) | O(log n) | 不穩定 | 大規模隨機數據平均性能最佳;但最壞情況性能差,且不穩定 |
| 歸并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 穩定 | 性能穩定,穩定的O(n log n)排序,但需要O(n)額外空間,適合外部排序和對穩定性有高要求的場景 |
1.7 總結
直接插入排序是一種概念簡單、編碼容易的??穩定??排序算法,其??原地排序??的特性使其空間效率高(O(1))。它的性能??強烈依賴于輸入數據的初始狀態??:對于??小規模數據??或??基本有序的序列??,其效率非常高,甚至優于一些更復雜的算法;但對于??大規模隨機數據??,其O(n2)的時間復雜度是主要瓶頸。
它的核心價值在于??教學演示??、作為??更復雜算法(如希爾排序、快速排序混合使用)的組成部分??,以及在特定應用場景(如小數據量、近乎有序、鏈表排序)下的實際應用。
posted on 2025-10-31 14:18 weiwei2021 閱讀(9) 評論(0) 收藏 舉報


 浙公網安備 33010602011771號
浙公網安備 33010602011771號