海量用戶積分排名算法探討
問題
某海量用戶網站,用戶擁有積分,積分可能會在使用過程中隨時更新。現在要為該網站設計一種算法,在每次用戶登錄時顯示其當前積分排名。用戶最大規模為2億;積分為非負整數,且小于100萬。
PS: 據說這是迅雷的一道面試題,不過問題本身具有很強的真實性,所以本文打算按照真實場景來考慮,而不局限于面試題的理想環境。
存儲結構
首先,我們用一張用戶積分表user_score來保存用戶的積分信息。
表結構:
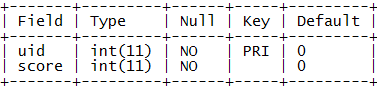
示例數據:
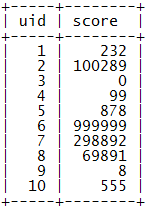
下面的算法會基于這個基本的表結構來進行。
算法1:簡單SQL查詢
首先,我們很容易想到用一條簡單的SQL語句查詢出積分大于該用戶積分的用戶數量:
select 1 + count(t2.uid) as rank
from user_score t1, user_score t2
where t1.uid = @uid and t2.score > t1.score
對于4號用戶我們可以得到下面的結果:

算法特點
優點:簡單,利用了SQL的功能,不需要復雜的查詢邏輯,也不引入額外的存儲結構,對小規模或性能要求不高的應用不失為一種良好的解決方案。
缺點:需要對user_score表進行全表掃描,還需要考慮到查詢的同時若有積分更新會對表造成鎖定,在海量數據規模和高并發的應用中,性能是無法接受的。
算法2:均勻分區設計
在許多應用中緩存是解決性能問題的重要途徑,我們自然會想能不能把用戶排名用Memcached緩存下來呢?不過再一想發現緩存似乎幫不上什么忙,因為用戶排名是一個全局性的統計性指標,而并非用戶的私有屬性,其他用戶的積分變化可能會馬上影響到本用戶的排名。然而,真實的應用中積分的變化其實也是有一定規律的,通常一個用戶的積分不會突然暴增暴減,一般用戶總是要在低分區混跡很長一段時間才會慢慢升入高分區,也就是說用戶積分的分布總體說來是有區段的,我們進一步注意到高分區用戶積分的細微變化其實對低分段用戶的排名影響不大。于是,我們可以想到按積分區段進行統計的方法,引入一張分區積分表score_range:
表結構:

數據示例:
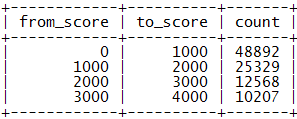
表示[from_score, to_score)區間有count個用戶。若我們按每1000分劃分一個區間則有[0, 1000), [1000, 2000), …, [999000, 1000000)這1000個區間,以后對用戶積分的更新要相應地更新score_range表的區間值。在分區積分表的輔助下查詢積分為s的用戶的排名,可以首先確定其所屬區間,把高于s的積分區間的count值累加,然后再查詢出該用戶在本區間內的排名,二者相加即可獲得用戶的排名。
乍一看,這個方法貌似通過區間聚合減少了查詢計算量,實則不然。最大的問題在于如何查詢用戶在本區間內的排名呢?如果是在算法1中的SQL中加上積分條件:
select 1 + count(t2.uid) as rank
from user_score t1, user_score t2
where t1.uid = @uid and t2.score > t1.score and t2.score < @to_score
在理想情況下,由于把t2.score的范圍限制在了1000以內,如果對score字段建立索引,我們期望本條SQL語句將通過索引大大減少掃描的user_score表的行數。不過真實情況并非如此,t2.score的范圍在1000以內并不意味著該區間內的用戶數也是1000,因為這里有積分相同的情況存在!二八定律告訴我們,前20%的低分區往往集中了80%的用戶,這就是說對于大量低分區用戶進行區間內排名查詢的性能遠不及對少數的高分區用戶,所以在一般情況下這種分區方法不會帶來實質性的性能提升。
算法特點
優點:注意到了積分區間的存在,并通過預先聚合消除查詢的全表掃描。
缺點:積分非均勻分布的特點使得性能提升并不理想。
算法3:樹形分區設計
均勻分區查詢算法的失敗是由于積分分布的非均勻性,那么我們自然就會想,能不能按二八定律,把score_range表設計為非均勻區間呢?比如,把低分區劃密集一點,10分一個區間,然后逐漸變成100分,1000分,10000分 … 當然,這不失為一種方法,不過這種分法有一定的隨意性,不容易把握好,而且整個系統的積分分布會隨著使用而逐漸發生變化,最初的較好的分區方法可能會變得不適應未來的情況了。我們希望找到一種分區方法,既可以適應積分非均勻性,又可以適應系統積分分布的變化,這就是樹形分區。
我們可以把[0, 1,000,000)作為一級區間;再把一級區間分為兩個2級區間[0, 500,000), [500,000, 1,000,000),然后把二級區間二分為4個3級區間[0, 250,000), [250,000, 500,000), [500,000, 750,000), [750,000, 1,000,000),依此類推,最終我們會得到1,000,000個21級區間[0,1), [1,2) … [999,999, 1,000,000)。這實際上是把區間組織成了一種平衡二叉樹結構,根結點代表一級區間,每個非葉子結點有兩個子結點,左子結點代表低分區間,右子結點代表高分區間。樹形分區結構需要在更新時保持一種不變量(Invariant):非葉子結點的count值總是等于其左右子結點的count值之和。
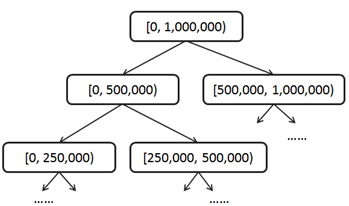
以后,每次用戶積分有變化所需要更新的區間數量和積分變化量有關系,積分變化越小更新的區間層次越低。總體上,每次所需要更新的區間數量是用戶積分變量的log(n)級別的,也就是說如果用戶積分一次變化在百萬級,更新區間的數量在二十這個級別。在這種樹形分區積分表的輔助下查詢積分為s的用戶排名,實際上是一個在區間樹上由上至下、由粗到細一步步明確s所在位置的過程。比如,對于積分499,000,我們用一個初值為0的排名變量來做累加;首先,它屬于1級區間的左子樹[0, 500,000),那么該用戶排名應該在右子樹[500,000, 1,000,000)的用戶數count之后,我們把該count值累加到該用戶排名變量,進入下一級區間;其次,它屬于3級區間的[250,000, 500,000),這是2級區間的右子樹,所以不用累加count到排名變量,直接進入下一級區間;再次,它屬于4級區間的…;直到最后我們把用戶積分精確定位在21級區間[499,000, 499,001),整個累加過程完成,得出排名!
雖然,本算法的更新和查詢都涉及到若干個操作,但如果我們為區間的from_score和to_score建立索引,這些操作都是基于鍵的查詢和更新,不會產生表掃描,因此效率更高。另外,本算法并不依賴于關系數據模型和SQL運算,可以輕易地改造為NoSQL等其他存儲方式,而基于鍵的操作也很容易引入緩存機制進一步優化性能。進一步,我們可以估算一下樹形區間的數目大約為2,000,000,考慮每個結點的大小,整個結構只占用幾十M空間。所以,我們完全可以在內存建立區間樹結構,并通過user_score表在O(n)的時間內初始化區間樹,然后排名的查詢和更新操作都可以在內存進行。一般來講,同樣的算法,從數據庫到內存算法的性能提升常常可以達到10^5以上;因此,本算法可以達到非常高的性能。
算法特點
優點:結構穩定,不受積分分布影響;每次查詢或更新的復雜度為積分最大值的O(log(n))級別,且與用戶規模無關,可以應對海量規模;不依賴于SQL,容易改造為NoSQL或內存數據結構。
缺點:算法相對更復雜。
算法4:積分排名數組
算法3雖然性能較高,達到了積分變化的O(log(n))的復雜度,但是實現上比較復雜。另外,O(log(n))的復雜度只在n特別大的時候才顯出它的優勢,而實際應用中積分的變化情況往往不會太大,這時和O(n)的算法相比往往沒有明顯的優勢,甚至可能更慢。
考慮到這一情況,仔細觀察一下積分變化對排名的具體影響,可以發現某用戶的積分從s變為s+n,積分小于s或者大于等于s+n的其他用戶排名實際上并不會受到影響,只有積分在[s,s+n)區間內的用戶排名會下降1位。我們可以用于一個大小為1,000,000的數組表示積分和排名的對應關系,其中rank[s]表示積分s所對應的排名。初始化時,rank數組可以由user_score表在O(n)的復雜度內計算而來。用戶排名的查詢和更新基于這個數組來進行。查詢積分s所對應的排名直接返回rank[s]即可,復雜度為O(1);當用戶積分從s變為s+n,只需要把rank[s]到rank[s+n-1]這n個元素的值增加1即可,復雜度為O(n)。
算法特點
優點:積分排名數組比區間樹更簡單,易于實現;排名查詢復雜度為O(1);排名更新復雜度O(n),在積分變化不大的情況下非常高效。
缺點:當n比較大時,需要更新大量元素,效率不如算法3。
總結
上面介紹了用戶積分排名的幾種算法,算法1簡單易于理解和實現,適用于小規模和低并發應用;算法3引入了更復雜的樹形分區結構,但是O(log(n))的復雜度性能優越,可以應用于海量規模和高并發;算法4采用簡單的排名數組,易于實現,在積分變化不大的情況下性能不亞于算法3。本問題是一個開放性的問題,相信一定還有其他優秀的算法和解決方案,歡迎探討!

 浙公網安備 33010602011771號
浙公網安備 33010602011771號