數(shù)論中

數(shù)論中
- 前言
一些定理

數(shù)論中

前言

疊甲：本文的許多定義并不是最官方嚴(yán)謹(jǐn)?shù)模瞧鋵嵤潜举|(zhì)相同的，不過更偏實用一點。有部分內(nèi)容我并沒有寫代碼驗證過，可能有錯，希望發(fā)現(xiàn)問題的大佬能及時指出。歡迎轉(zhuǎn)載。但如果是全文轉(zhuǎn)載，請附上原文鏈接。因為博客園與本地的渲染有細微差別，可能會導(dǎo)致有少量格式錯誤，但應(yīng)該不會影響閱讀，也歡迎大佬指出。

這不是給數(shù)論初學(xué)者寫的博客！這是作者在整理各種數(shù)論知識的邊邊角角梳理出來的文章，不保證內(nèi)容按照難度遞增，而是按照邏輯順序排列的，相關(guān)聯(lián)的知識點會放在一起。文章分為前、中、后和配套題目與題解四個部分，分成四偏文章的原因是，放在一起會導(dǎo)致非常卡，猜測是因為文章太大了，每個部分之間有著藕斷絲連的關(guān)系，前三部分是知識點，有著互相依賴的邏輯關(guān)系（但是保證不會有自己證明自己的情況出現(xiàn)），第四篇是具體的題目，對提分來說更加重要。建議配合食用。

本文很多內(nèi)容是我之前寫的博客復(fù)制過來，修繕了一下，個人感覺比之前寫的更本質(zhì)，更清晰一點，還有不少內(nèi)容是我這次整理新學(xué)的知識。四篇文章總源碼超過 100 KB，我認為整理的還是比較全面了，沒有涉及到的內(nèi)容，大概率在數(shù)論練習(xí)題里的后記里面提及。

合集鏈接：數(shù)論上，數(shù)論中，數(shù)論下，數(shù)論練習(xí)題。

一些定理

歐幾里得算法全家桶

也稱為輾轉(zhuǎn)相除算法。

基礎(chǔ)款

易得：$\gcd(a, b) = \gcd(a ? b, b)$。

多減幾次得：$\gcd(a, b) = \gcd(a \bmod b, b)$

對于邊界 $a = 0$，此時的 $b$ 即是最大公約數(shù)。

這個復(fù)雜度基于取模運算的性質(zhì)：進行取模運算，要么值不變，要么值至少減半。于是遞歸次數(shù)是 $O(\log n)$ 的。

可以直接使用 c++ 自帶的 __gcd 函數(shù)。

inline int gcd(int a, int b) {return !b ? a : gcd(b, a%b);}

有一個非常神秘的小常數(shù)非遞歸版本，其實是等價的。

inline ll gcd(ll a, ll b) { while(b) b ^=a ^=b ^=a %=b; return a;}

裴蜀定理

這個是拓歐的前置知識。

內(nèi)容：$\gcd(a,b)$ 是用 $a$ 和 $b$ 能線性組合出的最小的正整數(shù)。這里線性組合是指給 $a$ 和 $b$ 乘上一個系數(shù)后加起來。

~~很好感性理解吧~~。對于任意線性組合，一定可以提取出一個 $\gcd(a,b)$ 這個因子出來，這說明 $a$ 和 $b$ 的線性組合一定是 $\gcd(a,b)$ 的正整數(shù)倍。還可以思考一下 $a$ 和 $b$ 的最小線性組合還有什么性質(zhì)。

設(shè) $d$ 為 $a,b$ 的線性組合中最小的一個，設(shè) $d = ma + nb$，$a = dq + r(0 \leq r < d)$

$\therefore r = a - dq = a - q(ma + nb) = (1 - qm)a - qnb$

$\therefore r$ 也是 $a, b$ 的線性組合。

$\because 0 \leq r < d$ 且 $d$ 為 $a, b$ 的線性組合中最小的一個。

$\therefore r = 0$

$\therefore d \mid a$，同理可得 $d \mid b$ 。這說明最小線性組合同時是 $a,b$ 的因子，而剛才我又說明了任何線性組合都是 $\gcd(a,b)$ 的倍數(shù)，所以 $a,b$ 的最小線性組合的值就是 $\gcd(a,b)$.

推論：對于方程 $ax+by=c$ ，當(dāng) $c$ 不是 $\gcd(a,b)$ 的倍數(shù)時，無 $x,y$ 整數(shù)解。（這個只用證明的前半段即可得到）

拓展版

此算法可用于解不定方程，用處廣泛，可以求非質(zhì)數(shù)意義下的逆元，合并同余方程（埋下伏筆）等。

不定方程：$ax + by = c$ ( $$a,b,c$$ 均為整數(shù)，求 $$x,y$$ 的合法整數(shù)解）

核心思路：在剛才求 $\gcd$ 的算法的末狀態(tài)時，求出一組合法的 $x_末,y_末$，又因為有個天才腦洞大開發(fā)現(xiàn)可以順著 $\gcd$ 遞歸回去，于是可以求出一組 $x,y$ 的特解，再找通解的表達。

具體做法：

當(dāng) $c$ 不是 $\gcd(a,b)$ 的倍數(shù)，時無 $x,y$ 整數(shù)解。（裴蜀定理）

否則：$ax + by = k \times gcd$，兩邊同時除 k，可先求出 $x/k，y/k$ 的值。

觀察 $\gcd$ 的末狀態(tài)：$a = \gcd,b = 0$。此時只要取 $x_末 = 1, y_末=任意數(shù)$ ，等式是成立的。

普通版 $\gcd$ 的轉(zhuǎn)移方法是：$ax + by = \gcd = bx' + (a - {\lfloor a / b \rfloor} b) y'$; ( $\gcd$ 的遞歸轉(zhuǎn)移)

整理一下：$y = x' - {\lfloor a / b \rfloor} * y', x = y'$

遞歸回去可得一組 $x/k,y/k$ 的整數(shù)解，再乘上 $k$ 就是一組 $x,y$ 的特解。

接下來就是求通解：

假設(shè)求出來的特解是 ${x2,y2}$ ，我們要通過這組特解求出另外一組解 ${x1,y1}$.

首先，不管是特解還是通解，肯定滿足不定方程

\[\begin{aligned} ax_1 + by_1 &= c\\ ax_2 + by_2 &= c\\ \therefore a(x_1 - x_2) &= b(y_2 - y_1) \end{aligned} \]

兩邊同除 $\gcd(a,b)$，得 $a'(x_1 - x_2) = b'(y_2 - y_1)$，此時 $a'$ 與 $b'$ 互質(zhì)

\[\therefore(x_1 - x_2) = k * b', (y_2 - y_1) = k * a' \]

整理一下：$x_1 = k * b' + x_2,y_1 = y_2 - k * a'$ ($k$ 為任意, $x_2,y_2$ 為特解，$x_1,y_1$ 為通解)

代碼：

void exgcd(ll a, ll b){
	if(b == 0) {
		x = 1, y = 0, gcd = a;
		return ;
	}
	exgcd(b, a % b);
	tmp = x, x = y, y = tmp - (a/b) * y;
}

用 $exgcd$ 求逆元：$ax = 1 (\bmod p) => ax = 1 + pk => ax - pk = 1$，然后解不定方程。

練習(xí) 1 ：解 $n$ 元一次不定方程 $\sum a_ix_i = c$ 。

首先還是用裴蜀定理判掉無解。可以一個一個地做 exgcd ，然后合并。復(fù)雜度：不知道。

練習(xí) 2 ：還是線性組合 $ax + by = c$ ，保證 $\gcd(a,b)=1$ ，不過這次要求 $x,y$ 都大于等于 0，然后我們反其道而行之，求最大的不可以得到的 c （困難，可以跳過）

問題主要在于 $x,y$ 非負，考慮先手玩一下小數(shù)據(jù)。

手玩發(fā)現(xiàn)答案應(yīng)該是 $ab-a-b$ 這個神秘的東西。

找一下可以被表示出來的 c 的必要條件。

$ax + by = c$ ，對于這個方程可以直接使用 exgcd 找到一個 x 和 y 的特解。

回憶一下，x，y 的通解分別是 $x=x_0+kb,y=y_0-ka$。

這說明我們可以找到一個 $x \in [0,b-1]$ 。改寫不定方程有 $y = \frac{n - ax}b$ 。

$x \le b-1$ ，這時候 $y \ge \frac{n-ab+a}b$。剛才不是猜了個結(jié)論嗎？試試帶入 $n > ab - a- b$ ，可以得到 $y > -1$。

關(guān)鍵的來了，因為 y 是非負整數(shù)，所以 y 至少是 0。這里可能有同學(xué)會感到不解，考慮 x 不是每次都該取 b - 1，如果 n 比較小，x 也比較小。

先在相當(dāng)于證明了 n 最大是 $ab -a -b+1$ ，只需要證明 $ab-a-b$ 不能被 $a,b$ 用非負數(shù)線性組合出來即可。

假設(shè)有 $ax+by=ab-a-b$

整理可得 $\dfrac{a(x+1)+b(y+1)}a=b$。

發(fā)現(xiàn)等式成立的一個必要條件是 $\frac {b(y+1)}a$ 是整數(shù)，由于 $\gcd(a,b) = 1$，可得 $a\mid (y+1)$。

同理可得 $b\mid (x + 1)$.

不妨設(shè) $(y+1)=k_1a, (x+1)=k_2b$，帶入最初的式子化簡可得：$k_1+k_2=1$ ，但是由于 $x,y$ 非負，可得 $k_1\ge1,k_2\ge1$ ，假設(shè)不成立，故得證。

還有生成函數(shù)做法，這等價于計算使得 $[x^n]\dfrac 1{(1-x^a)(1-x^b)} = 0$ 成立的最大的 $n$ 是多少。

還有一個結(jié)論是，不可被表示出的 c 的數(shù)量是 $\frac{(a-1)(b-1)}2$ 。詳見。

這玩意還有幾何意義，甚至還可以使用類歐求解！詳見

拓歐最大的缺點在于，解方程是通過特定的算法流程來實現(xiàn)的，不是一個顯性的式子，不利于后續(xù)的推導(dǎo)。拓歐只是一個用于解方程的工具罷了。

類似版

這里指的是類歐。

給定 $n, a, b, c$ ，分別求

\[\sum_{i=0}^{n}\left\lfloor \frac{ai+b}{c} \right\rfloor\,,\ \sum_{i=0}^{n}{\left\lfloor \frac{ai+b}{c} \right\rfloor}^2\,,\ \sum_{i=0}^{n}i\left\lfloor \frac{ai+b}{c} \right\rfloor \]

先求第一個，后面兩個的思路類似于第一個。為了方便，我們定義：

\[f(a,b,c,n)=\sum_{i=0}^{n}\left\lfloor \frac{ai+b}{c} \right\rfloor\ \]

整體思路：如果 $a>c$ 或 $b>c$，把 $f(a,b,c,n)$ 轉(zhuǎn)換成 $f(a\bmod c,b\bmod c,c,n)$；否則轉(zhuǎn)化成類似于 $f(c,c-b-1,a,m)$ 的形式。

具體做法：

對于 $a\ge c$ 或 $b\ge c$ 時：

\[\begin{aligned} f(a,b,c,n)&=\sum_{i=0}^n\left\lfloor \frac{ai+b}{c} \right\rfloor\\ &=\sum_{i=0}^n\left\lfloor \frac{\left(\left\lfloor\frac{a}{c}\right\rfloor c+a\bmod c\right)i+\left(\left\lfloor\frac{b}{c}\right\rfloor c+b\bmod c\right)}{c}\right\rfloor\text{這一步是關(guān)鍵}\\ &=\frac{n(n+1)}{2}\left\lfloor\frac{a}{c}\right\rfloor+(n+1)\left\lfloor\frac{b}{c}\right\rfloor+ \sum_{i=0}^n\left\lfloor\frac{\left(a\bmod c\right)i+\left(b\bmod c\right)}{c} \right\rfloor\\ &=\frac{n(n+1)}{2}\left\lfloor\frac{a}{c}\right\rfloor +(n+1)\left\lfloor\frac{b}{c}\right\rfloor+f(a\bmod c,b\bmod c,c,n) \end{aligned} \]

對于 $a,b < c$，

\[\begin{aligned} f(a,b,c,n) &= \sum^n_{i=0}\sum^{\left\lfloor \frac{ai+b}{c} \right\rfloor-1}_{j=0} 1\\ &=\sum^{\left\lfloor \frac{an+b}{c} \right\rfloor-1}_{j=0}\sum^n_{i=0}[j \le \left\lfloor \frac{ai+b}{c} \right\rfloor - 1] \end{aligned} \]

轉(zhuǎn)化右邊的式子：

\[\begin{aligned} j\le\left\lfloor \frac{ai+b}{c} \right\rfloor -1 &\iff j+1\leq \left\lfloor \frac{ai+b}{c} \right\rfloor \iff j+1\leq \frac{ai+b}{c}\\ &\iff jc+c\le ai+b \iff jc+c-b-1< ai\\ &\iff \left\lfloor\frac{jc+c-b-1}{a}\right\rfloor< i \end{aligned} \]

為了方便表示，令 $m=\left\lfloor \frac{an+b}{c} \right\rfloor$，則

\[\begin{aligned}f(a,b,c,n)&=\sum_{j=0}^{m-1}\sum_{i=0}^n\left[i>\left\lfloor\frac{jc+c-b-1}{a}\right\rfloor \right]\\&=\sum_{j=0}^{m-1}(n-\left\lfloor\frac{jc+c-b-1}{a}\right\rfloor)\\&=nm-f\left(c,c-b-1,a,m-1\right)\end{aligned} \]

遞歸即可。$O(n\log n)$

對于

\[g(a,b,c,n) = \sum_{i=0}^{n}i{\left\lfloor \frac{ai+b}{c} \right\rfloor}\\ h(a,b,c,n) = \sum_{i=0}^{n}{\left\lfloor \frac{ai+b}{c} \right\rfloor}^2 \]

同樣的做法，可以得到：

對于 $ a\ge c$ 或 $b\ge c$

\[g(a,b,c,n) =g(a\bmod c,b\bmod c,c,n)+\left\lfloor\frac{a}{c}\right\rfloor\frac{n(n+1)(2n+1)}{6}+\left\lfloor\frac{b}{c}\right\rfloor\frac{n(n+1)}{2}\\ \]

\[\begin{aligned} h(a,b,c,n) &=\frac{n(n+1)(2n+1)}{6}\left\lfloor\dfrac{a}{c}\right\rfloor^2+(n+1)\left\lfloor\frac{b}{c}\right\rfloor^2+n(n+1)\left\lfloor\dfrac{a}{c}\right\rfloor\left\lfloor\frac{b}{c}\right\rfloor\\ &\ \ \ \ +2\left\lfloor\dfrac{a}{c}\right\rfloor g(a\bmod c,b\bmod c,c,n)+2\left\lfloor\dfrac{b}{c}\right\rfloor f(a\bmod c,b\bmod c,c,n)\\ &\ \ \ \ +h(a\bmod c,b\bmod c,c,n) \end{aligned} \]

否則：

\[g(a,b,c,n) = \frac{1}{2}[mn(n+1)-h(c,c-b-1,a,m-1)-f(c,c-b-1,a,m-1)]\\ h(a,b,c,n) = m(m+1)n-2f(c,c-b-1,a,m-1)-2g(c,c-b-1,a,m-1)-f(a,b,c,n) \]

其中 $m=\left\lfloor \frac{an+b}{c} \right\rfloor$.

與普通版的共同點在于都運用了取模運算的性質(zhì)：進行取模運算，要么值不變，要么值至少減半。類歐主要不用用于處理一個有取整的求和式，但是又不能整除分塊的式子。

吐槽一下：這玩意寫起來是真史，要是不給我公式要我手推出來寫代碼，不知道得調(diào)到什么時候。

萬能版

其實是類歐的拓展版。我簡單了解了下，目前理解還不夠深刻，而且沒有寫代碼，只能簡單口糊一下，見諒。

首先看一下類歐這個式子有什么實際含義。

假設(shè)有一條直線 $y=\dfrac{ax+b}{c}$。

那么第一象限中滿足 $x\le n$ 的那段直線，下方的整點數(shù)為：

\[\sum_{i=0}^{n}\left\lfloor \frac{ai+b}{c} \right\rfloor \]

在坐標(biāo)系中，如果這個直線遇到一條橫線，就記錄下一個 U ；如果遇到一個豎線，就記錄下一個 R ，如果同時遇到橫線和豎線（穿過一個整點），就先記錄 U 再記錄 R 。最后會形成一個由 U 和 R 構(gòu)成的操作串。例如對于直線 $y=\dfrac{7x+2}3$，其操作序列是：UUURUURUURUUURU.

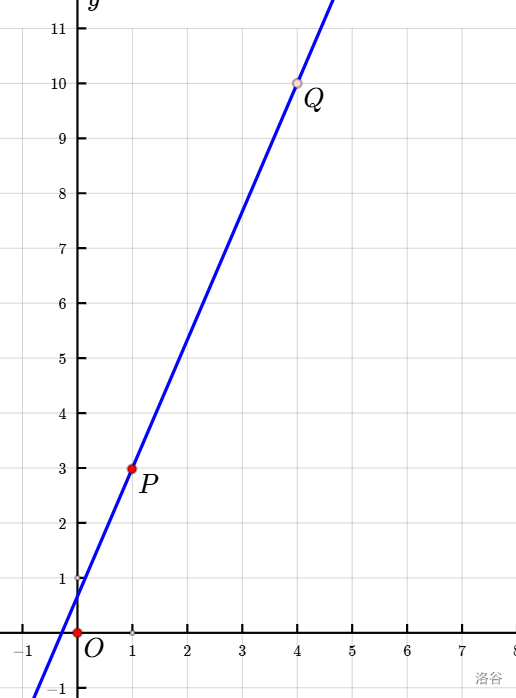
這里可以把 U 和 R 寫成矩陣的形式，表示對答案的影響，然后用向量 $\begin{bmatrix} \sum y\\ y\\1\end{bmatrix}$ 一路掃過去，就可以得到答案。（注意，U 和 R 要有結(jié)合律才能使用萬歐）

考慮要合并一些 U R 矩形來降低復(fù)雜度。

設(shè)原問題的答案為 $f(a,b,c,n,U,R)$，U 和 R 就是當(dāng)前的操作矩陣是什么，因為在進行矩形合并以后，U 和 R 可能會變，所以要記錄這兩維。

$a\ge c$

則每個 R 前面都有 $a/c$ 個 U，可以直接合并掉，問題轉(zhuǎn)化為 $f(a\bmod c,b,c,n,U,U^{a/c}R)$.

$a< c$

根據(jù)歐幾里得算法的套路，是時候該交換 $a$ 和 $c$ ，然后就變成第一類問題了。

改寫直線解析式，用 y 來表示 x，有 $x=\dfrac{cy-b}a$ 。

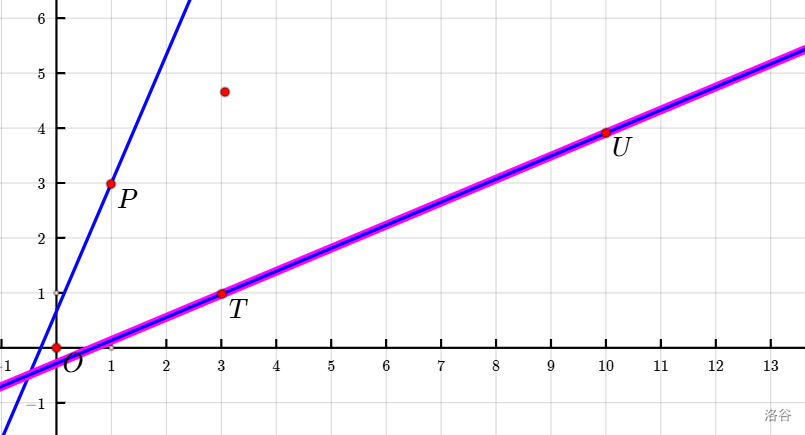
但是直接這樣子會導(dǎo)致原本是 UR 的操作變成了 RU，于是發(fā)揚人類智慧，我們可以直接把直線向左平移一點點（只要平移的幅度小，就不會改變直線下點的數(shù)量），這樣就變成了：

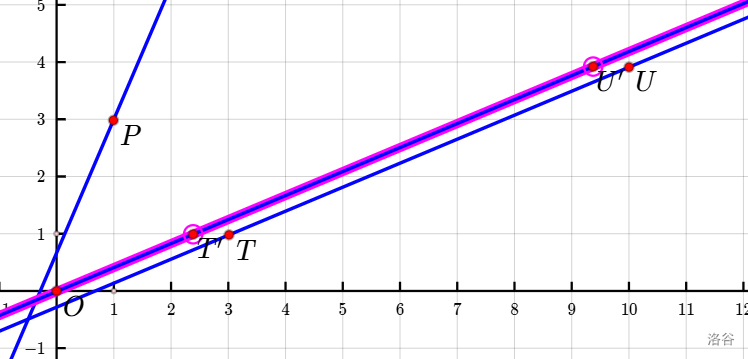
問題就變成了 $f(c,c-b-1,a,cnt_u,R,U)$，然后還會有一些多余的邊界細節(jié)的矩形操作，我暫時沒太想清楚。

賀來的代碼：

Matrix solve (ll p, ll q, ll r, ll l, Matrix a, Matrix b) {
	if (!l) {return Matrix();}
	if (p>=q) {return solve(p % q, q, r, l, a, qpow(a, p / q) * b);}
	ll m = div(l, p, r, q);
	if (!m) {return qpow(b,l);}
	ll cnt = l - div(q, m, - r - 1, p);
	return qpow(b, (q - r - 1) / p) * a * solve(q, p, (q - r - 1) % p, m - 1, b, a) * qpow(b, cnt);
}

萬歐的優(yōu)勢在于每次只用考慮如何計算合并矩形操作的貢獻，不用重新推式子。代碼里就是重載一下矩陣乘法的運算。

中國剩余定理及其拓展（CRT）

處理問題：同余方程，合并同余式

\[\begin{aligned} x &\equiv y_1\pmod {p_1}\\ x &\equiv y_2\pmod {p_2}\\ &…………\\ x &\equiv y_n\pmod {p_n}\\ \end{aligned} \]

使用條件：所有 $p$ 互質(zhì)
核心思路：硬湊
算法流程

令 $M = \prod p,m_i = M / p_i,m^{-1}_i = m_i^{\varphi(p_i)-1}\bmod p_i$.

可以湊出來 $x = \sum_{i=1}^n y_i \times m_i \times m^{-1}_i + K\times M$ ( $K$ 是任意數(shù)，因為 $x$ 有無數(shù)個)

現(xiàn)在要證明這個湊出來的式子滿足上面每一個同余方程。

對于任意 p ，最后一項都是 0。前面第 i 個式子，因為有所有 $p$ 互質(zhì)這個條件，所以除了第 i 項，每一項里面的 $m_i$ 都含有 $p_i$ 這個因子，模一下就沒了，只有和式里面的第 i 項可以幸存，而 $m_i^{-1}$ 其實就相當(dāng)于逆元，與 $m_i$ 一乘就變成 1 了，于是諾大一個式子就只剩下 $x \equiv y_i\pmod {p_i}$ ，這就是我們想要的。

理解 CRT 要對逆元有深刻的理解。

一般來說，在 p 都是質(zhì)數(shù)的時候，使用 CRT 比較方便。CRT 相比 exCRT 還有一個優(yōu)勢是，它直接給出了一個公式，可能可以在后續(xù)的推到中進一步化簡。（？）

很多題目需要合并同余式，所以 CRT 會被大量運用。

拓展版（exCRT）

個人認為 exCRT 比 CRT 自然得多

對 p 沒有任何限制。但是此時不一定有解。

例如：

\[\left\{\begin{matrix} x\equiv2 \bmod 4\\ x\equiv3 \bmod 6 \end{matrix}\right. \]

你要是算出一組解來 ~~我請你抽煙~~。exCRT 還具有檢驗方程是否有解的能力。

考慮只要能一個一個地去合并方程，就可以搞出答案。

考慮合并這兩個方程：

\[\left\{\begin{matrix} x\equiv r_1 \bmod m_1\\ x\equiv r_2 \bmod m_2 \end{matrix}\right. \]

\[\left\{\begin{matrix} x = r_1 + k_1 * m_1\\ x = r_2 + k_2 * m_2 \end{matrix}\right. \]

上下相減：

\[k_1 * m_1 - k_2 * m_2 = r_2 - r_1 \]

如果 $r_2 - r_1$ 不是 $\gcd(m_1,m_2)$ 的倍數(shù)，則無解（裴蜀定理），否則用 exgcd 解方程即可得到 $k_1,k_2$,可以搞出一個 $x_0$ ，通解是 $x = x_0 + k*lcm(m_1,m_2)$，所以合并出來的方程就是 $x\equiv x_0 \bmod lcm(m_1,m_2)$.

寫代碼小心爆 long long。

這啟示我們，可以把一個同余式當(dāng)成一個不定方程

模板：P4777 【模板】擴展中國剩余定理（EXCRT） - 洛谷。

例題：[P4621 COCI 2012/2013 #6] BAKTERIJE - 洛谷。這是個大糞題。

威爾遜定理及逆定理

用處不是很大？不過這個思想很有趣。

甚至只是七級考點，noip 可以考...

內(nèi)容

如果 $p$ 是質(zhì)數(shù)，一定有：

\[(p-1)! \equiv -1 \pmod p \]

或者說，把 $p$ 的完全剩余系里面，除了 0 的所有數(shù)乘起來等于 $-1$。

主要思想：發(fā)現(xiàn)很多數(shù)和它們的逆元一乘就沒了，有用的數(shù)不多

首先發(fā)現(xiàn)，如果有 $p$ 是質(zhì)數(shù)，可得 $(a^{p-2})^{p-2}\bmod p \equiv a^{(p-2)(p-2)\bmod p-1 }\equiv a^{-1\times -1}\equiv a$ 。這說明 $a$ 與 $a^{p-2}$ 形成一一對應(yīng)的關(guān)系，又因為對于所有非零數(shù)都有 $a\times a^{p-2}\equiv1$，在計算階乘的時候可以把 $a$ 和 $a^{p-2}$ 這兩項扣掉。但是如果 $a\equiv a^{p-2}$，就不能把這兩個數(shù)同時扣掉。這時候，我們只需要計算 $[1,p)$ 之間，到底是那些數(shù)滿足 $a\equiv a^{p-2}$，然后只累乘這些數(shù)即可。

這些數(shù)肯定滿足 $x^2\equiv 1\pmod p$ （怎么又是這個經(jīng)典式子？），滿足這個式子的只有 $1$ 和 $-1$ ，然后 $1\times -1 = -1$ ，所以 $(p-1)!\equiv -1\pmod p$?。

注意，根據(jù)原根那一塊的知識，一個數(shù) $a$ 有 $\varphi(p)\over \delta(a)$ 個“逆元”，所以如果那那逆元去論證，而不用 $a^{p-2}$ 來論證，則不嚴(yán)謹(jǐn)

逆定理

對于 $n\ge2$，如果滿足 $(n-1)!\equiv -1\pmod n$ ，則 $n$ 是質(zhì)數(shù)。（這好像是我看到的唯一一個可以證明一個數(shù)是質(zhì)數(shù)的非定義的定理，看來我還是太孤陋寡聞了）

假設(shè) $n$ 是合數(shù)，那么有些數(shù)根本就沒有逆元，$(n-1)! \equiv -1 \pmod n$ 就可能不成立。現(xiàn)在要證明它一定不成立。

可以換個思路。

考慮反證法，假設(shè) $n$ 是一個合數(shù)，且 $(n - 1)! \equiv -1 \pmod n$。

因為 $n$ 是合數(shù)，找到 $n$ 的一個在 $(1,n)$ 之間的因子 $d$。

因為 $(n - 1)! \equiv -1 \pmod n$，然后同余式轉(zhuǎn)整除式，有 $n\mid (n - 1)! + 1$。

又有 $d\mid n$ ，容易得到 $d\mid(n-1)!+1$ 。

但是，由于 $(n-1)!$ 里面肯定有一項是 $d$ ，所以 $d\mid (n-1)!$。

這表示 $d$ 是 $(n-1)!+1$ 和 $(n-1)!$ 的公因數(shù)，但是 $(n-1)!+1$ 和 $(n-1)!$ 的最大公因數(shù)顯然是 $1$，于是 $d$ 只能是 $1$。

與假設(shè)矛盾，證完了。

例題1

給定一個正整數(shù) $d$，滿足 $d\le 2.5\times 10^5$，問是否存在一個正整數(shù) $n$ ，滿足 $n\le 2.5\times 10^5$ 且 $d$ 是 $n!+1$ 的次小約數(shù)，如果存在請給出任意一個合法的 $n$；否則報告無解。

先考慮打表如何求一個數(shù)的次小約數(shù)，這是問題突破的關(guān)鍵。

發(fā)現(xiàn)最小約數(shù)就是分解了質(zhì)因數(shù)后，最小的質(zhì)數(shù)。

所以如果 $d$ 是合數(shù)，就不可能是一個數(shù)的次小約數(shù)，就直接 G 了。

考慮 $d$ 是質(zhì)數(shù)的時候怎么做。

根據(jù)威爾遜定理，有 $(d-1)!\equiv-1\pmod d$。

轉(zhuǎn)整除式，有 $(d-1)!+1\mid d$，于是 $d-1$ 就是合法的 $n$，游戲結(jié)束。

加強版，但是打表基礎(chǔ)練習(xí)題，很有趣，但是過于神秘，壓表 Trick，認為沒有必要講，題解在這里。

拉格朗日定理（沒有用，不需要講）

沒有用的新定理又增加了。

設(shè) $p$ 為素數(shù)，對于模 $p$ 意義下的整系數(shù)多項式

\[f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0\;(p\nmid a_n) \]

的同余方程 $f(x)\equiv 0\pmod p$ 在模 $p$ 意義下至多有 $n$ 個不同解。

證明：對 $n$ 使用歸納法。當(dāng) $n=0$ 時，由于 $p\nmid a_0$，故 $f(x)\equiv 0\pmod p$ 無解，定理對 $n=0$ 的多項式 $f(x)$ 都成立。

若命題對于 $\deg f<n$ 的 $f$ 都成立，由反證法，假設(shè)存在一個滿足題目條件的 $f$ 在模 $p$ 意義下有著至少 $n+1$ 個不同的解 $x_0,x_1,\cdots,x_{n}$。

可設(shè) $f(x)-f(x_0)=(x-x_0)g(x)$，則 $g(x)$ 在模 $p$ 意義下是一個至多 $n-1$ 次的多項式。現(xiàn)在由 $x_0,x_1,\cdots,x_n$ 都是 $f(x)\equiv 0\pmod p$ 的解，知對 $1\leq i\leq n$，都有

\[(x_i-x_0)g(x_i)\equiv f(x_i)-f(x_0)\equiv 0\pmod p \]
而 $x_i \not\equiv x_0 \pmod p$，故 $g(x_i)\equiv 0\pmod p$，從而 $g(x)\equiv 0\pmod p$ 有至少 $n$ 個根，與歸納假設(shè)矛盾。

所以，命題對 $n$ 次多項式也成立，定理獲證。

補充：關(guān)于拉格朗日定理的證明中，由于 $f(x_i)=0$，故 $f(x)-f(x_i)$ 就是 $f(x)$，不影響閱讀。

posted @ 2025-10-09 12:14 花子の水晶植輪daisuki 閱讀(11) 評論(0) 收藏舉報

刷新頁面返回頂部

water-flower

數(shù)論中

數(shù)論中

前言

一些定理

歐幾里得算法全家桶

中國剩余定理及其拓展（CRT）

威爾遜定理及逆定理

拉格朗日定理（沒有用，不需要講）

公告