特殊的數

前言：

我之前是對每個特殊的數都各開一個博客的，但是這些數用生成函數的視角下看，似乎有一些關系，感覺分開寫就太雜了，于是我把這些特殊的數整合到了一起。

卡特蘭數

定義

$Catalan$ 數列 $H_n$ 是以下問題的方案數：

有一個大小為 $n × n$ 的方格圖，左下角為 $(0, 0)$ 右上角為 $(n, n)$，從左下角開始每次都只能向右或者向上走一單位，不走到對角線 $y = x$ 上方（但可以觸碰）的情況下到達右上角有多少可能的路徑？
在圓上選擇 $2n$ 個點，將這些點成對連接起來使得所得到的 $n$ 條線段不相交的方法數？
一個棧的進棧序列為 $1, 2, 3, · · · , n$ 有多少個不同的出棧序列？
$n$ 個結點可構造多少個不同的二叉樹？
$n$ 對括號能組成的括號序列數？
......

這些問題的方案數可以證明是相等的。我們先以第一個命題來具體研究 $Catalan$ 數

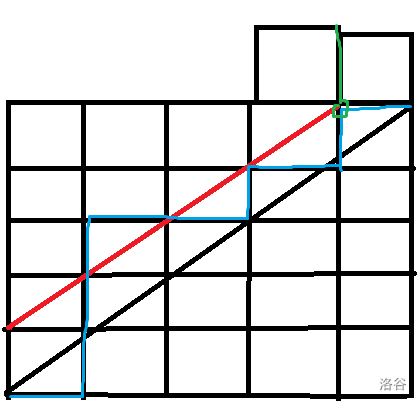
圖片有點抽象還請各位海涵一下。

我們從（1，1）走到（n，n）的方案數可以遞推來求。

設我們第一次接觸到對角線時的橫坐標為i，前面的方案數可看為從（2，1）走到（i，i-1）的方案數，后面的方案數可看為從（i，i）走到（n,n）的方案數。

對 $i$ 求和有：$H_n = \sum^{n}_{i=1}H_{i-1}H_{n-i}$，這就是卡特蘭數的遞推式。初值為 $H_0 = 1$。

我們還可以看為總方案數減去超過對角線（觸碰到紅線）的方案數。

我們對最后一次觸碰到紅線后的部分進行翻轉，則原來的每一條不合法路徑（如藍色）就一一對應了一條終點為（n-1，n+1）的路徑(如綠色)。

所以卡特蘭數的組合意義是 $H_n = {2n \choose n} - {2n \choose n-1}$。

綜上：

\[H_n = \begin{cases} \sum_{i = 0}^{n - 1} H_iH_{n - i - 1} & (n\geq2) \\ 1 & (n = 0,1) \end{cases}\\ H_n = \binom{2n}{n}-\binom{2n}{n - 1} \]

再看卡特蘭數的第二個和第四個定義，可以發現它們的遞推式與該遞推式相同。對于第三個和第五個定義，可以認為就是在走網格，并且橫向步數不超過縱向步數。

生成函數：$\dfrac{H(x)-1}x =H^2(x) \Rightarrow H(x)=\dfrac{1-\sqrt{1-4x}}{2x}$

可以推導出 $\sum_n\dbinom {2n}n x^n = \sqrt{(1-4x)}$.

通項公式：$H_n = \dfrac{\binom{2n}{n}}{n + 1}$。這個使用遞推公式的生成函數搞出來的，證明比較麻煩，這里不再贅述。你也可以把該式子帶入組合意義中來驗證其正確性。

遞推式2：$H_n = \dfrac{H_{n - 1}(4n - 2)}{n + 1}$ ，這個可以直接帶入驗證。

因為上課講的例題都沒怎么聽懂，這里就不放題了。

斯特林數

第二類斯特林數

定義 :

$n \brace m$ 表示將n個有標號數放在m個非空無標號集合的方案數（注：斯特林數寫作大括號）

遞推式：

\[{n \brace m} = {n - 1 \brace m - 1} + m \times{n - 1 \brace m} \]

其組合意義是：把最后一個數單開一列 ${n - 1 \brace m - 1}$ 加上把最后一個數放入 $m$ 個集合中的其中一個 $m \times{n - 1 \brace m}$

遞推邊界：${n\brace n} = {n \brace 1} = 1(n \ge 0) $， ${n \brace 0} = [n = 0]$

還有其他一些特值: $\ \begin{array}{l} \left\{\begin{matrix}n\\2\end{matrix}\right\}=2^{n - 1}-1(n>0), \left\{\begin{matrix}n\\n - 1\end{matrix}\right\}=\binom{n}{2} \end{array} $

通項公式：

\[{n \brace m} = \sum_{i=0}^m\frac{i^n\cdot(-1)^{m-i}}{(m-i)!i!} \]

證明：設將 n 個有標號物品放到 k 個有標號盒子（允許空盒子）的方案數為 $G_k$；將 n 個有標號物品放到 k 個有標號盒子（不允許空盒子）的方案數為 $F_k$

\[\therefore G_k = k^n, G_k = \sum^k_{i=0} \binom ki F_i \]

第二個式子表示從 n 個盒子選 i 個必須放物品，然后對 i 求和。

然后二項式反演，得到：

\[F_k = \sum^k_{i=0}(-1)^{k-i}\binom kiG_i = \sum^k_{i=0}(-1)^{k-i}\binom ki k^n \]

因為 $F$ 的物品有標號，所以 :

\[{F_k\over n!} = {n \brace k} \]

帶回去就得到：

\[{n \brace m} = \sum_{i=0}^m\frac{i^n\cdot(-1)^{m-i}}{(m-i)!i!} \]

例題 P5162 WD與積木 - 洛谷

題意 : 把$1...n$分割成若干個集合,集合之間有順序,問所有不同的分割方法之中,集合個數的期望。

相當于求 $\dfrac{\sum_i{n\brace i}i!i}{\sum_i{n\brace i}i!}$ .

對于分母：

\[\begin{aligned}&\sum_{n\geq 0}\frac{x^n}{n!}\sum_{i=0}^n\begin{Bmatrix}n\\i\end{Bmatrix}i!\\=&\sum_{i\geq 0}i!\sum_{n\geq 0}\frac{x^n}{n!}\begin{Bmatrix}n\\i\end{Bmatrix}\\=&\sum_{i\geq 0}\sum_{n\geq 0}\frac{x^n}{n!}\sum_{k=0}^i(-1)^k\binom{i}{k}(i-k)^n\\=&\sum_{i\geq 0}\sum_{k=0}^i(-1)^{i-k}\binom{i}{k}\sum_{n\geq 0}\frac{(kx)^n}{n!}\\=&\sum_{i\geq 0}\sum_{k=0}^i(-1)^{i-k}\binom{i}{k}(e^x)^k\\=&\sum_{i\geq 0}(e^x-1)^i\\=&\frac{1}{2-e^x}\end{aligned} \]

對于分子：

\[\begin{aligned}&\ \ \sum_{n\geq 0}\frac{x^n}{n!}\sum_i{n\brace i}i!i \\&=\sum_{i\geq 0}i(e^x-1)^i\\ &=\sum_{i\geq 0}\sum_{j=1}^i(e^x-1)^i\\ &=\sum_{j=1}^n\sum_{i}(e^x-1)^{i+j}\\ &=\sum_{j=1}^n(e^x-1)^{j}\sum_{i}(e^x-1)^{i}\\ &=\frac{1}{2-e^x}\sum_{j=1}^n(e^x-1)^{j}\\ &=\frac{1-e^x}{(2-e^x)}\sum_{j=0}^n(e^x-1)^{j}\\ &=\frac{1-e^x}{(2-e^x)^2}\\ \end{aligned} \]

分子分母取 n 次項系數后相除即可。

第一類斯特林數

定義：

$n \brack m$：表示將 n 個元素排成 m 個輪換的方案數。也即所有 n! 個排列中，構成的置換有 m 個無標號環的排列數。

遞推式：

\[{n\brack m} = {n-1\brack m-1} + (n-1){n-1\brack m} \]

其組合意義是：考慮最后一個元素，可以加入任意一個輪換并且可以插入任意一個位置，相當于可以任選一個數，插在其后面 $(n-1){n-1\brack m}$，也可以新開一個輪換 ${n-1\brack m-1}$。

遞推邊界以及特殊值：

\[{n\brack 0} = [n = 0], {n \brack n} = 1\\ {n\brack 1} = (n-1)!, {n\brack n-1} = {n \choose 2} \]

兩種斯特林數的大小關系：

由定義和遞推式容易看出：${n \brace m} \le {n \brack m}$。當 m 等于 n，n-1，0 時等號成立。

定理

我們知道一個有 n 個元素的排列和一個 n 個元素的置換一一對應，于是對所有置換中的輪換個數求和，我們有:

\[\sum_{k = 0}^{n}\begin{bmatrix}n\\k\end{bmatrix}=n! \]

斯特林數與三種冪(很重要！)

先復習一下上升冪，下降冪：

下降冪

$n^{\underline{m}}=n(n - 1)(n - 2)\cdots(n - m + 1)$

上升冪

$n^{\overline{m}}=n(n + 1)(n + 2)\cdots(n + m - 1)$

上升下降冪與普通冪的轉換

注意到，上升冪和下降冪本質上也是多項式，所以一個多項式也可以用上升冪和下降冪來表示。

他們的關系如下：

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}}=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}\binom{x}{k}k!\\ x^{\overline n} = \sum^n_{k=0}{n\brack k}x^k \]

可以簡記為第二類斯特林數對應下降冪，第一類斯特林數對應上升冪

因為下降冪的組合意義比上升冪更好，所以更常用第一個式子來轉換普通冪

對于第一個式子，考慮組合意義證明：

$x^n$ 表示 x 個有標號盒子放 n 個有標號球的方案數，盒子可以為空。

現在枚舉非空盒子數 i，先從 x 個盒子里面選 i 個盒子，$\dbinom xi$，

然后發現第二類斯特林數的定義是把 n 個球放入 i 個無標號盒子的方案數，

注意到這里的盒子是有標號的，所以 ${n\brace i}i!$ 就是有標號球放到有標號盒子的數量，所以：(個人感覺這里和第二類斯特林的通項公式證明幾乎一致)

\[x^n = \sum_i^n {n\brace i}\dbinom xi i!= \sum_i^n {n\brace i}x^\underline i \]

當然也可以使用數學歸納法證明第一個式子：

首先觀察到：$x^{\underline{k + 1}}=x^{\underline{k}}(x - k)\Longrightarrow x\cdot x^{\underline{k}}=x^{\underline{k + 1}}+kx^{\underline{k}}$。

那么：

\[\begin{align*} x\cdot x^{n - 1}&=x\cdot\sum_{k = 0}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}x^{\underline{k}}\\ &=\sum_{k = 0}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}x^{\underline{k+1}}+\sum_{k = 0}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}kx^{\underline{k}}\\ &=\sum_{k = 1}^{n}\left\{\begin{matrix}n - 1\\k - 1\end{matrix}\right\}x^{\underline{k}}+\sum_{k = 1}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}kx^{\underline{k}}\\ &=\sum_{k = 1}^{n}\left(k\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}+\left\{\begin{matrix}n - 1\\k - 1\end{matrix}\right\}\right)x^{\underline{k}}\\ &=\sum_{k = 1}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}} \end{align*} \]

第二個式子也可以用數學歸納法證明：

不過這次的觀察是 : $(x+n-1) \cdot x^{k}=x^{k+1}+(n-1) x^{k}$

\[\begin{aligned} x^{\overline n} & =(x+n-1) x^{\overline{n-1}} \\ & =(x+n-1) \sum_{k=0}^{n-1}\left[\begin{array}{c} n-1 \\ k \end{array}\right] x^{k} \\ & =\sum_{k=0}^{n-1}(n-1)\left[\begin{array}{c} n-1 \\ k \end{array}\right] x^{k}+\sum_{k=1}^{n}\left[\begin{array}{l} n-1 \\ k-1 \end{array}\right] x^{k} \\ & =\sum_{k=0}^{n}\left[\begin{array}{l} n \\ k \end{array}\right] x^{k} \end{aligned} \]

觀察到，注意到上升冪和下降冪的多項式展開后，系數是有交錯的符號，比如：

\[\begin{align*} x^{\underline{4}}&=x(x - 1)(x - 2)(x - 3)=x^{4}-6x^{3}+11x^{2}-6x\\ x^{\overline{4}}&=x(x + 1)(x + 2)(x + 3)=x^{4}+6x^{3}+11x^{2}+6x \end{align*} \]

形式化的表示為：

\[\begin{aligned} & x^{\overline{n}}=\sum_{k = 0}^{n}\left[\begin{array}{l}n\\k\end{array}\right]x^{k}\\ & x^{\overline{n}}=\sum_{k = 0}^{n}(-1)^{n-k}\left[\begin{array}{l}n\\k\end{array}\right]x^{k} \end{aligned} \]

由

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}} \]

和

\[x^{\underline{n}}=(-1)^{n}(-x)^{\overline{n}} \]

得到：

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}(-1)^k(- x)^{\overline{k}} \]

用 $-x$ 替換 $x$，然后合并 $-1$ 的系數后易得：

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}(-1)^{n-k}x^{\overline{k}} \]

推論 : $\sum\limits_{i=0}^ni^k=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{n+1}{j+1}$ (設$0^0=1$)

左邊 $=\sum\limits_{i=0}^n\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{i}{j}$

$=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\sum\limits_{i=0}^n\dbinom{i}{j}$

$=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{n+1}{j+1}$

反轉公式

由上總結，我們能感受到兩類斯特林數密不可分的關系，接下來我們就來探究它們的關系。

我們把普通冪轉上升冪再轉普通冪得：

\[x^n=\sum^n_{j=0}\sum_{k = j}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j}x^j \]

把 $\sum_{k = j}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j}$ 作為 $x^j$的系數，只有 $j = n$ 時右邊的系數為1，其余的系數為0。

所以得到第一個反轉公式：

\[\sum_{k = j}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j} = [j = n] \]

\[\because \left\{\begin{matrix}n\\n\end{matrix}\right\}{n\brack n} = 1\\ \therefore \sum_{k = j}^{n-1}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j} = 0 \]

同理我們把普通冪轉下降冪再轉普通冪得：

\[\sum_{k=m}^{n}\left[\begin{array}{l}n\\k\end{array}\right]\left\{\begin{array}{l}k\\m\end{array}\right\}(-1)^{n - k}=[m = n] \]

\[\sum_{k=m}^{n}\left\{\begin{array}{l}n\\k\end{array}\right\}\left[\begin{array}{l}k\\m\end{array}\right](-1)^{n - k}=[m = n] \]

斯特林反轉

\[f(n)=\sum_{k = 0}^{n}\left\{\begin{array}{l}n\\k\end{array}\right\}g(k)\Longleftrightarrow g(n)=\sum_{k = 0}^{n}(-1)^{n - k}\left[\begin{array}{l}n\\k\end{array}\right]f(k)\\ f(m)=\sum_{k = m}^{n}\left\{\begin{array}{l}k\\m\end{array}\right\}g(k)\Longleftrightarrow g(m)=\sum_{k = m}^{n}(-1)^{k - m}\left[\begin{array}{l}k\\m\end{array}\right]f(k) \]

帶入用反轉公式可以驗證。

總結一下：

上升下降冪的互相轉換： $n^{\overline{m}}=(n + m - 1)^{\underline{m}}$ 和 $x^{\underline{n}}=(-1)^{n}(-x)^{\overline{n}}$

普通冪轉下降冪：$x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}}$

下降冪轉普通冪（由斯特林反演得）：$x^{\underline n} = \sum^n_{k=0}(-1)^{n-k}{n\brack k}x^k$

上升冪轉普通冪：$x^{\overline n} = \sum^n_{k=0}{n\brack k}x^k$

普通冪轉上升冪（由斯特林反演得）：$x^n=\sum_{k = 0}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\overline{k}}$

斯特林數與生成函數

第一類斯特林數的二元生成函數：

這里盒子無標號，數字有標號，所以是 x 的 EGF，y 的 OGF。

\[S1(x,y)=\sum\limits_{i=0}\sum\limits_{j=0}\begin{bmatrix}i\\j \end{bmatrix}\dfrac{x^iy^j}{i!}=(1-x)^{-y} \]

證明：

主要思路是先得到只有一個置換環時的的生成函數，然后用 exp 的驚天組合意義得到 y 行的生成函數。

一個環排列的 EGF 為 $F(x)=\sum\limits_{i=0}\begin{bmatrix}i\\1 \end{bmatrix}\dfrac{x^i}{i!}=\sum\limits_{i=1}\dfrac{x^i}{i}=-\ln(1-x)$ 。

現在要把圓排列組合成置換，由于用 $y$ 的次數來記錄環的個數，因為現在之統計單個環，只有 $y = 1$ 時有系數，所以單個環排列的生成函數變為 $yF(x)$。

根據 exp 的組合意義，置換的生成函數即為 $\exp\big(yF(x)\big)=\exp\big(-y\ln(1-x)\big)=(1-x)^{-y}$。

第一類斯特林一行的生成函數

也就是固定上指標，求下指標的生成函數。所以要取 $n![x^n]$ ，得到的是關于盒子的 OGF：

\[\begin{aligned} &n![x^n](1-x)^{-y}\\ =&n![x^n]\sum_i(-x)^{i}\binom {-y}i 廣義二項式定理\\ =&n!(-1)^{n}\dfrac{(-y)^\underline n}{n!}\\ =&(-1)^{n}{(-y)^\underline n}\\ =&{y^\overline n}\\ \end{aligned} \]

這相當于證明了之前我們用數學歸納法湊出來的式子：$x^\overline n=\sum {n\brack i}x^i$，上升冪轉普通冪。

如果要求 $y^\overline n$ 的系數，可以使用分治 FFT $O(n\log^2n)$，也可以使用多項式平移 $O(n\log n)$. 詳見這里

第一類斯特林一列的生成函數

也就是盒子（置換環）數固定，小球數不定的方案數，得到的時關于球的 EGF。這里要提取 $y^n$ 項系數，而 y 在指數上，所以可以轉化成 exp 的形式

\[\begin{aligned} &[y^n](1-x)^{-y}\\ =&[y^n]\exp(yF(x))\\ =&[y^n]\sum\dfrac{y^iF^i(x)}{i!}\\ =&\dfrac{(-\ln(1-x))^n}{n!}\\ \end{aligned} \]

第二類斯特林數的二元生成函數

小球有標號，用 EGF，盒子無標號，用 OGF。

\[\begin{aligned} &S2(x,y)\\ =&\sum_i\sum_j{i\brace j}\dfrac{x^iy^j}{i!}\\ =&\exp(y(e^x-1))\\ \end{aligned} \]

推導：只有一個無標號非空盒子方案的生成函數：$\sum_{i=1} \dfrac{x^i}{i!} = e^x-1$.

然后因為 y 是盒子數，一個盒子的時候是 $y(e^x-1)$ ，又根據 exp 驚天組合意義，得到最終的答案：

\[\exp(y(e^x-1)) \]

補充

高階差分與第二類斯特林數有奇妙的性質：

\[\left.\Delta^{m}x^{n}\right|_{x = 0}=m!\begin{Bmatrix}n\\m\end{Bmatrix} \]

伯努利數

我們可用有限積分求自然數下降冪的和，結果發現自然數普通冪的和我們居然還不會求？

我們定義 S：

\[S_m(n)=\sum_{i=0}^{n-1}i^m \]

可以發現這可以表示為 $m + 1$ 次的多項式，可以拉差出它的系數，發現它的系數似乎很有規律。

假設 $B(x) = \dfrac x{e^x - 1}$，用 $B_i$ 表示 $i![x^i]B(x)$ 則有：

\[S_m(n) = \frac 1{m + 1} \sum_i^m \binom{m+1}iB_i n^{m+1-i} \]

序列 B 就是伯努利數，然后 $B(x)$ 被稱為伯努利數的 EGF。

推論：$\sum_i^m \dbinom{m+1}iB_i =[m = 0]$.其實就是帶入 $n = 1$ 即可得到。不過沒有用。

小小變化一下式子還可以得到：

\[\sum_{i = 0} ^{n-1}i^k=k!\sum_{i=0}^k\dfrac{B_{k-i}n^{i+1}}{{(k-i)!}(i+1)!} \]

給一個生成函數的證明：

為了方便使用生成函數，定義 $F_n(x) = \sum\limits_{i}(\sum\limits_c^{n-1}c^i)\dfrac{x^i}{i!}$，則有 $S_m(n)=m![x^m]F_n(x) = \sum\limits_{i=0}^{n-1} i^m$，繼續推導 $F$ 的式子：

\[\begin{aligned} F_n(x) =& \sum_{i}\sum_c^{n-1}\dfrac{c^ix^i}{i!}\\ =& \sum_c^{n-1}\sum_{i}\dfrac{(cx)^i}{i!}\\ =& \sum_c^{n-1}e^{cx}\\ =& \frac{e^{nx} - 1}{e^{x}-1}\\ \end{aligned} \]

其實如果只求自然數冪的和的話到這一步就可以了，但是為了裝逼證明前面那個式子的正確性，還可以繼續推導：

令 $B(x) = \dfrac x{e^x-1},G(x)=\dfrac {e^{nx}-1}x$，則 $F_n(x)=B(x)G(x)$.

\[\begin{aligned} G(x) &=\dfrac {e^{nx}-1}x\\ &= \frac 1x\sum_{i=1}\frac{n^ix^i}{i!}\\ &= \sum_{i=0}\frac{n^{i+1}x^i}{(i+1)!}\\ \end{aligned} \]

所以有：

\[\sum_{i = 0} ^{n-1}i^k=k![x^k]B(x)G(x)=k!\sum_{i=0}^k\dfrac{B[k-i]n^{i+1}}{(i+1)!} \]

這里的 $B[k-i]$ 表示 $x^{k-i}B(x)$.

這玩意最大的用處就是 k 很小 n 很大的時候可以把求和上界從 n 變成 k，還有一個用是把枚舉上界從 n - 1 改為 k + 1，方便推式子。不過話說這玩意如果只求一個數的話可以直接拉差，如果要求多個數的話可以多項式多點求值。綜上所述，學這玩意大概率八輩子都用不到。

總結：自然數 k 次方和問題 $f_k(n)=\sum_{i=0}^{n-1}i^k$

當 k 足夠小（比如 1，2，3，4 這種小常數）的時候，可以暴力把普通冪拆成下降冪，然后用有限積分做。例如 $x^2=x^\underline 2 + x^\underline 1$.

如果 k 不能當成常數，但是 n 遠大于 k 時，那么可以推一下式子得到 $f_k(n)=\sum_{j=0}^k\dfrac{k\brace j}{j+1}n^\underline{j+1}$，可以花 $O(k\log k)$ 的時間預處理出一行的斯特林數，然后 $O(k)$ 地得到一個 $f_k(n)$，聰明一點的會發現上式可以當成 n 的 k + 1 次多項式，可以拉差出 f 的第 n 項。還更快。

如果需要求出多個甚至每一個 k 時的答案，可以考慮用伯努利數，或者直接莽一個多項式多點求值，不過前者是但 log，后者是雙 log

小推一下式子可以得到 f 在 k 上的 EGF 是 $\dfrac{e^{nx} - 1}{e^{x}-1}$，取 $k![x^k]$ 即可得到答案。

如果 k 固定，對不同的 n 求這個東西，那么顯然有 $f_k(n)=f_k(n-1)+(n-1)^k$，如果 n 連續并且從 0 開始，直接遞推就可以了，如果 n 連續但是不從 0 開始，可以先拉差出第一項。如果 n 不連續應該可以多項式多點求值，不過我沒試過，理論可行。

歐拉數

~~這個更是沒用~~

定義 $\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle$ 為有 $k$ 個升高的，長度為 $n$ 的排列的個數。其中“升高”定義為讓 $p_i<p_{i+1}$ 成立的 $(p_i,p_{i+1})$。

遞推式：

\[\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle=(k+1)\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle+(n-k)\left\langle\begin{matrix}n-1\\k-1\end{matrix}\right\rangle \]

解釋：不妨從小到大地插入數字。考慮最后插入的數，如果插到一個升高的中間，原本的升高沒了，但是又多一個升高，總個數還是不變 $k\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle$。如果插入到最開始的位置，升高肯定不變 $\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle$。因為最后插入的數字最大，所以插入到其他地方一定升高加 1 $(n-k)\left\langle\begin{matrix}n-1\\k-1\end{matrix}\right\rangle$。加起來就是原式。

推導歐拉數·行的生成函數

這里有個模板題：P5825 排列計數 - 洛谷。

設 $g(k)$ 表示長度為 n 的排列恰好 k 個升高的方案數，也就是答案 $\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle$ ，$f(k)$ 表示長度為 n 欽定 $k$ 個升高的方案數，容易得到：

\[g(k) = \sum_{i=k}^n(-1)^{i-k}\binom ikf(i) \]

考慮這么搞 f。

我們把連續的上升叫做一個 "段"，現在相當于求欽定了 $n-i$ 個段的方案數。

先考慮只有一個段，個數到方案的函數是 $P(n)= [n\neq 0]$.思考該用 OGF 還是 EGF。

如果有兩個段，那么方案數 $P'(n)=\sum \dbinom niP(i)P(n-i)$，這里要乘上一個分配數的方案 $\dbinom ni$ ，所以其組合意義是 EGF。

容易得到 P 的 EGF 是 $e^x-1$，那么 k 個段的 EGF 就是 $(e^x-1)^k$，然后再取 n 次項系數得到：

\[f(n-k)=n![x^n](e^x-1)^k \]

（注意：歐拉數沒有要求內部是連續的，所以有一個選數的過程，肯定會乘上一個歸并的系數，要用 EGF，而之前的 queue2 要求內部連續，這里的組合意義是有序拼接，所以只用在最后乘上一個外部排列方案數，用 OGF。）

然后帶入 g 得到：

\[\begin{aligned} g(k) &= \sum_{i=k}^n(-1)^{i-k}\binom ikn![x^n](e^x-1)^{n-i}\\ &= \sum_{i=k}^n(-1)^{i-k}\binom ikn![x^n]\sum_j^{n-i}\binom {n-i}je^{jx}(-1)^{n-i-j}\\ &= \sum_{i=k}^n(-1)^{i-k}\binom ik\sum_j^{n-i}\binom {n-i}jj^{n}(-1)^{n-i-j}\\ &= \sum_j^{n-k}(-1)^{n-k-j}j^{n}\sum_{i=max(k,j)}^n\binom ik\binom {n-i}j\\ &= \sum_j^{n-k}(-1)^{n-k-j}j^{n}\binom {n+1}{k+j+1}\\ \end{aligned} \]

最后一步范德蒙德卷積的范圍可以仔細推一下，可以發現在后面表達式在 $i< max(k,j)$ 時，值都是零。

把組合數拆了，然后設 $f(j)=j^n,g(k+j)=(-1)^{n-k-j}\dbinom {n+1}{k+j+1}$，然后做差卷積就行了。

歐拉數還滿足如下恒等式 :

\[x^n=\sum\limits_{k=0}^n\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle\dbinom{x+k}{n} \]

歐拉數的二元生成函數為：

\[E(x,y)=\sum\limits_{n=0}\sum\limits_{m=0}\left\langle\begin{matrix}n \\ m\end{matrix}\right\rangle\dfrac{x^ny^m}{n!}=\dfrac{1-y}{e^{x(y-1)}-y} \]

分拆數

模板題鏈接

定義：記 $P_n$ 為將 n 拆分成若干個若干無序正整數的和的方案數。

如 $3$ 可以拆分成 $1+1+1$ 或 $1+2$ （和 $2+1$ 視為同種方案）或 $3$。于是 $P_3=3$。

可以發現，分拆數本質上是所有種類的質量的物品都有的完全背包方案數，于是按照背包套路能寫出它的 OGF:

\[P(x)=\prod_{k = 1} \sum_{i = 0}x^{ik} = \prod_{k=1}\frac{1}{1-x^k} \]

然后 ln，exp：

\[\exp(\sum_{k=1}\ln\frac{1}{1-x^k}) = \exp \sum_{k=1}\sum_{i=1}\frac {x^{ki}}i \]

發現后面暴力求解的復雜度是調和級數，再套一個 exp 板子即可。

五邊形數定理

用處1. 在沒有 ntt 模數時，而且你有懶得寫 mtt 時，但是你要求分拆數時，并且時間有比較充裕夠根號的復雜度時，而且時間又不太充裕不能暴力時用。

用處2. 在每個數的使用次數有統一上界時用。例如上界為 k 時有： $$P(x)=\prod_{k=1}\sum_{i=0}^{K-1}x=\prod_{k=1}\dfrac{1-x^{kK}}{1-xk}$$。

對于剛才式子分母的展開后發現：

\[\prod_{i=1} (1-x^i) = 1-x-x^2+x^5+x^7-x^{12}-x^{15}+\cdots \]

然后合理猜測發現：

\[\prod_{i=1}(1-x^i)=1 + \sum_{i=1}(-1)^ix^{i(3i\pm 1)/2} \]

證明過于鬼畜，我不會。然后上面的等式叫做五邊形數定理，名字來于 x 的次數為五邊形套娃后合法點數構成的遞推式拓展到整數后的數列。、

Ferrers 圖（又稱楊表）

在分拆數的基礎上，要求拆分出來的數不超過 m 個。

有一個非常人類智慧的做法，就是對于每個正確的方案，用柱狀圖來表示，例如：

拆分 $1+1+2+4+5$ 的 Ferrers 圖如下所示：

\[\begin{aligned} &5 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &4 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &2 : \blacksquare\ \blacksquare\\ &1 : \blacksquare\\ &1 : \blacksquare\\ \end{aligned} \]

然后豎著看這個圖（也就是把原來的一列當成一排）：

\[\begin{aligned} & 5\ \ 3\ \ \ 2 \ \ 2\ \ 1 \\ &\blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &\blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &\blacksquare\ \blacksquare\\ &\blacksquare\\ &\blacksquare\\ \end{aligned} \]

然后非常神奇的事情發生了！你發現驚奇地問題變成統計每個數都小于 m，但是不限制拆分的數的個數時的方案數！而且仔細想一下發現這甚至是意義對應的的！然后就可以快樂地轉化問題了。

這只是做一個改了一下上界的分拆數，外重循環的上界是 m ，即：$\exp \sum_{k=1}^m\sum_{i=1}\frac {x^{ki}}i$ 復雜度顯然還是 $O(n\log n)$.

神秘結論：對于 $n$ 的分拆，各個分拆方案中出現至少 $k$ 次的數的個數和，等于所有方案中 $k$ 出現的總次數。證不來，根本證不來！

posted @ 2025-09-02 19:52 花子の水晶植輪daisuki 閱讀(23) 評論(0) 收藏舉報

刷新頁面返回頂部

water-flower

特殊的數

特殊的數

卡特蘭數

定義

斯特林數

第二類斯特林數

定義 :

遞推式：

通項公式：

第一類斯特林數

定義：

遞推式：

遞推邊界以及特殊值：

兩種斯特林數的大小關系：

定理

斯特林數與三種冪(很重要！)

下降冪

上升冪

相關結論

上升下降冪與普通冪的轉換

反轉公式

斯特林反轉

總結一下：

斯特林數與生成函數

補充

伯努利數

歐拉數

推導歐拉數·行的生成函數

分拆數

五邊形數定理

Ferrers 圖（又稱楊表）

公告