之前項目有聚類的一些需求，現(xiàn)大致對一些聚類算法總結(jié)下：

    聚類是對一系列事物根據(jù)其潛在特征按照某種度量函數(shù)歸納成一個個簇的動作，使得簇內(nèi)數(shù)據(jù)間的相似度盡可能大，不同簇的數(shù)據(jù)相似度盡可能小。

    通常聚類流程如下：數(shù)據(jù)獲取-數(shù)據(jù)預(yù)處理-模型選型-模型聚類調(diào)參-輸出結(jié)果。其中數(shù)據(jù)預(yù)處理、模型選型是流程中較為重要部分。數(shù)據(jù)預(yù)處理將雜亂無章的數(shù)據(jù)處理為具備某些共同點的特征，從而模型能更好地擬合數(shù)據(jù)，很經(jīng)典的一句話：特征處理決定模型的上限。模型選型需要根據(jù)業(yè)務(wù)的具體需求及數(shù)據(jù)特性結(jié)合各聚類模型的特點進(jìn)行選擇。由于數(shù)據(jù)預(yù)處理需要根據(jù)具體數(shù)據(jù)及具體業(yè)務(wù)進(jìn)行處理，本文僅介紹下各類聚類算法：

 

一、基于劃分的聚類算法

K-means

經(jīng)典K-means算法流程：
1. 隨機(jī)地選擇k個對象，每個對象初始地代表了一個簇的中心；
2. 對剩余的每個對象，根據(jù)其與各簇中心的距離，將它賦給最近的簇；
3. 重新計算每個簇的平均值，更新為新的簇中心；
4. 不斷重復(fù)2、3，直到準(zhǔn)則函數(shù)收斂

 

優(yōu)點：

K-means算法簡單快速；

當(dāng)簇較為密集，呈現(xiàn)球狀或團(tuán)狀時能有比較好的效果

缺點：

對K值敏感，聚類結(jié)果會受到K值很大的影響

對噪聲點敏感，如當(dāng)數(shù)據(jù)中只有2個簇，此時添加一個噪聲點，則極大可能會導(dǎo)致噪聲點分為一個簇，數(shù)據(jù)中的2個簇分為一個簇

只能聚凸的數(shù)據(jù)集

 

二、基于層次的聚類算法

該類主要有自下而上和自上而下兩種思想。

以自下而上流程為例：

1. 將每個對象看作一類，計算兩兩之間的最小距離；

2. 將距離最小的兩個類合并成一個新類；

3. 重新計算新類與所有類之間的距離；

4. 重復(fù)2、3，直到所有類最后合并成一類

 

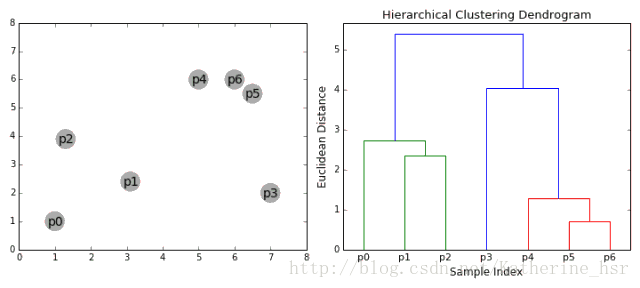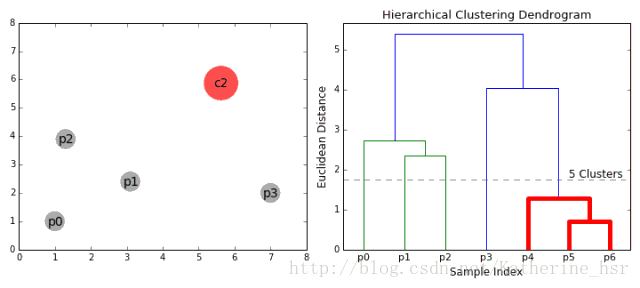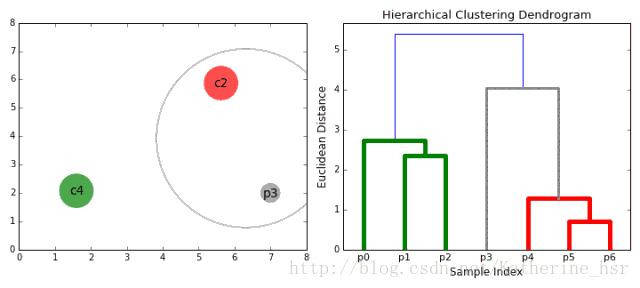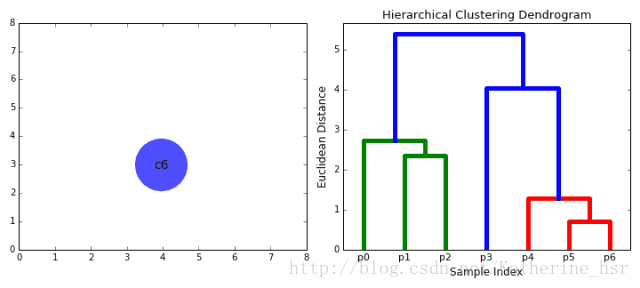
優(yōu)點：

不需提前設(shè)置K值

可以發(fā)現(xiàn)層次關(guān)系

缺點：

計算復(fù)雜度高

奇異值有較大影響

 

三、基于密度的聚類算法

例如DBSCAN

DBSCAN 算法是一種基于密度的聚類算法：

　　1.聚類的時候不需要預(yù)先指定簇的個數(shù)

　　2.最終的簇的個數(shù)不確定

DBSCAN算法將數(shù)據(jù)點分為三類：

　　1.核心點：在半徑Eps內(nèi)含有超過MinPts數(shù)目的點。

　　2.邊界點：在半徑Eps內(nèi)點的數(shù)量小于MinPts,但是落在核心點的鄰域內(nèi)的點。

　　3.噪音點：既不是核心點也不是邊界點的點。

DBSCAN流程：

1.將所有點標(biāo)記為核心點、邊界點或噪聲點；

2.刪除噪聲點；

3.為距離在Eps之內(nèi)的所有核心點之間賦予一條邊；

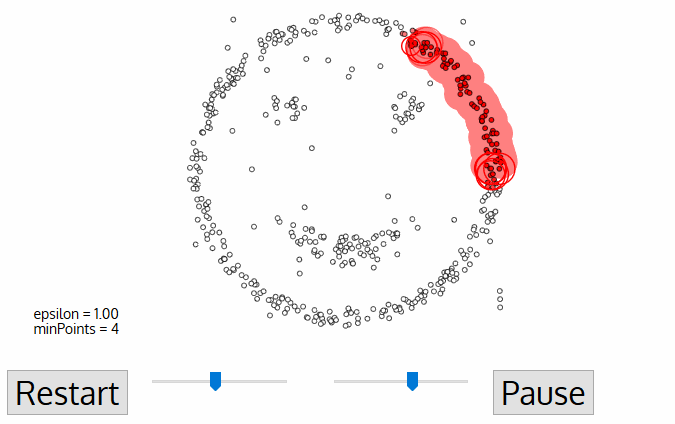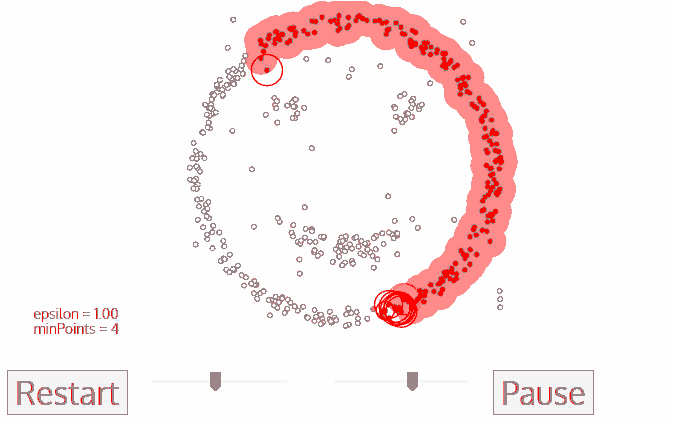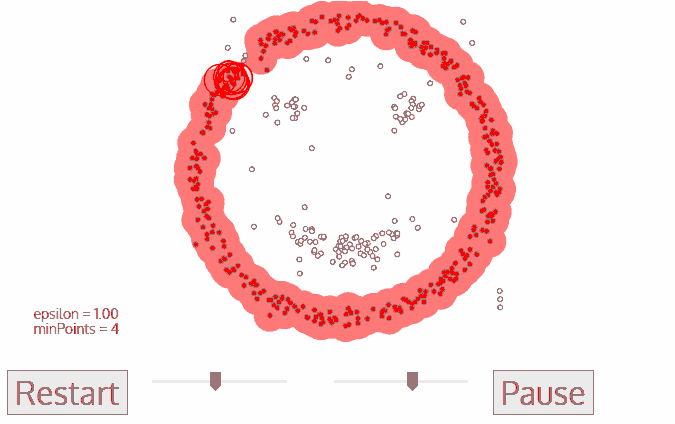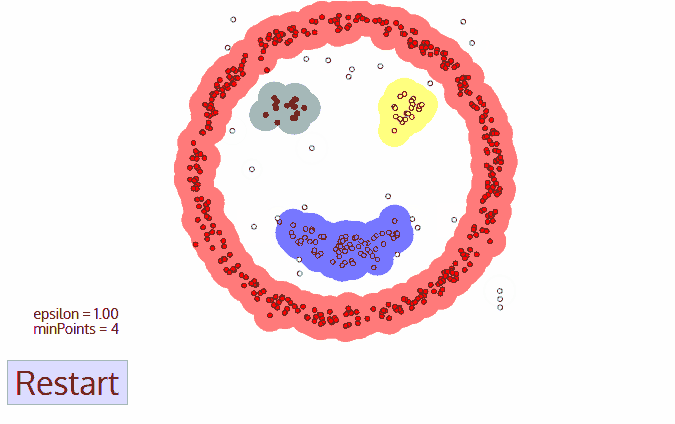
4.每組連通的核心點形成一個簇；

5.將每個邊界點指派到一個與之關(guān)聯(lián)的核心點的簇中（哪一個核心點的半徑范圍之內(nèi)）。

 

優(yōu)點：

自適應(yīng)的聚類，不需提前設(shè)置K值

對噪聲不敏感

能發(fā)現(xiàn)任意形狀的簇

缺點：

對兩個參數(shù)圈的半徑、閾值敏感

數(shù)據(jù)集越大，花費時間越長

 

四、基于滑動窗口的聚類算法

例如均值聚類漂移

均值聚類漂移算法流程：

     1.我們從一個以 C 點（隨機(jī)選擇）為中心，以半徑 r 為核心的圓形滑動窗口開始。均值漂移是一種爬山算法，它包括在每一步中迭代地向更高密度區(qū)域移動，直到收斂。

     2.在每次迭代中，滑動窗口通過將中心點移向窗口內(nèi)點的均值來移向更高密度區(qū)域。滑動窗口內(nèi)的密度與其內(nèi)部點的數(shù)量成正比。自然地，通過向窗口內(nèi)點的均值移動，它會逐漸移向點密度更高的區(qū)域。

     3.我們繼續(xù)按照均值移動滑動窗口直到?jīng)]有方向在核內(nèi)可以容納更多的點。

     4.步驟 1 到 3 的過程是通過許多滑動窗口完成的，直到所有的點位于一個窗口內(nèi)。當(dāng)多個滑動窗口重疊時，保留包含最多點的窗口。然后根據(jù)數(shù)據(jù)點所在的滑動窗口進(jìn)行聚類

 

 

 

優(yōu)點：

不需提前設(shè)置K值

可以處理任意形狀的簇類

 

缺點：

窗口半徑有可能是不重要的

對于較大的特征空間，計算量較大