題意

有 \(K\) 種顏色的球，第 \(i\) 種顏色的球有 \(A_i\) 個。另外給定一個集合 \(B\)，里面有 \(M\) 個數 \(B_1,B_2,\cdots,B_M\)。

現在要把球堆成若干堆，要求：

• 每堆不能有重復顏色；
• 每堆的大小是 \(B_1,B_2,\cdots,B_M\) 中的一個數。

請你最小化堆數，并輸出方案。

題解

設最終有 \(n\) 堆，高度為 \(H_1,H_2,\cdots,H_n\)。交換堆的順序肯定是沒有影響的，為了方便，對于下文（包括后文移動完之后），我們不妨設 \(H\) 不增。

考慮如何判定這樣一個序列合法。這也是我們得出答案序列后，求顏色方案的方法。

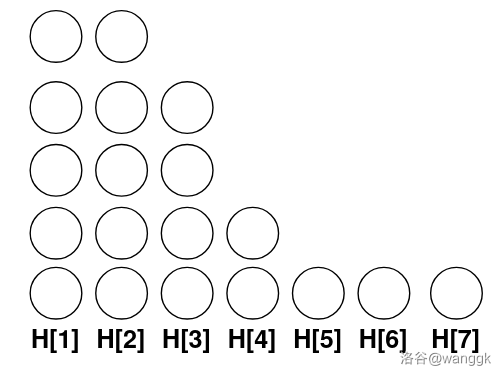
我們要求每一堆沒有相同顏色，那么按照出現次數從大到小加入顏色。

對于每種顏色，從左往右，將離目標高度 \(H_i\) 最遠的堆疊高一層。因為是優先疊那些最拖后腿的堆，這樣的貪心是最優的。如果高度序列可能被達到，那么該最終狀態合法。

因為我們是貪心地向上疊（先消耗出現次數多的顏色，先消耗比較高的堆，最可能合法），所以我們發現，對于一個合法局面，把前面堆的元素移到后面，也一定是合法的，如下圖。

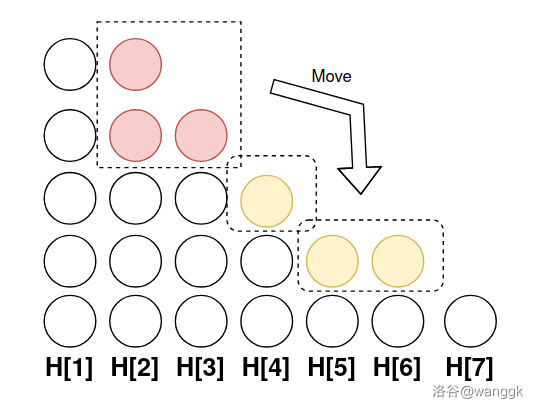
這是很好理解的，因為“拖后腿”的堆變矮了，顏色不重復的限制就變松了。

于是我們只需要限制最緊（找到前面的堆最多）的合法狀態，再統計不超過這個的局面數量，就可以了。這個非常簡單，只需要所有顏色都放一個前綴：

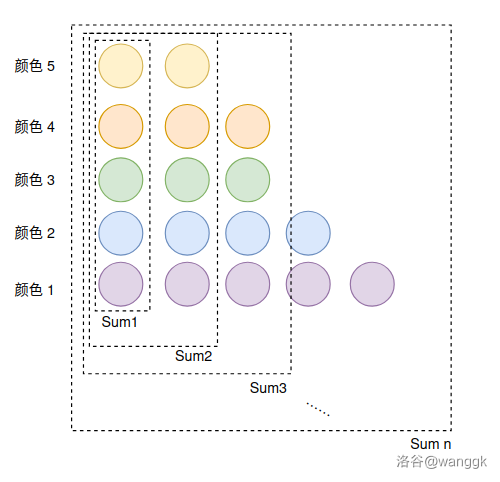
我們得到了盡可能最靠前放的序列，記其前綴和為 \(Sum\)（如圖），合法序列 \(H_n\) 一定滿足：

• 單調不增排序后，\(\forall i \in [1,n],\sum_{j \leq i} \leq Sum_i\)

最小堆數看起來不是很好轉移，那就設計一個可行性 DP：設 \(f_{i,j,k}\) 表示，考慮完了前 \(i\) 大的高度，用了 \(j\) 堆，目前前綴和為 \(k\)，是否可行。轉移有兩種，繼承前一層 \(i-1\) 的值，和在本層中拿一個（相當于完全背包）：

括號內表示轉移條件，另外我們已經將 \(B\) 降序排序，即 \(B_1 > B_2> \cdots > B_n\)。

同時由于前綴和不超過 \(k\)，則 \(j \leq \frac{k}{B_i}\)，所以 \(j\) 是 \(\log\) 級別的，再用 bitset 優化可行性 DP（優化完全背包的部分），復雜度就降到了 \(O(\frac{n^2 \log n}{w})\)，就可以通過了。

代碼

看起來挺可讀的。

#include<bits/stdc++.h>
#define For(i,il,ir) for(int i=(il);i<=(ir);++i)
#define Rof(i,ir,il) for(int i=(ir);i>=(il);--i)
using namespace std;
typedef pair<int,int> pii;
const int maxn=15005;

int n,m,V;
int a[maxn],b[maxn],sum[maxn];

bitset<maxn> pw[maxn];
vector<bitset<maxn> > f[maxn];

void prework()
{
    scanf("%d",&n);
    For(i,1,n){
        scanf("%d",&a[i]); V+=a[i];
        For(j,1,a[i]) sum[j]++;
    }
    pw[0].set(0);
    For(i,1,V){
        sum[i]+=sum[i-1];
        pw[i]=pw[i-1]<<1,pw[i].set(0);
    }
    scanf("%d",&m);
    For(i,1,m) scanf("%d",&b[i]);
    reverse(b+1,b+1+m);
}

int res[maxn];
vector<int> sol[maxn];
void dfs(int i,int j,int k){
    if(!i||!j||!k) return;
    if(k>=b[i] && f[i][j-1][k-b[i]]) res[j]=b[i],dfs(i,j-1,k-b[i]);
    else dfs(i-1,j,k);
}
signed main()
{
    prework();
    bitset<maxn> tmp; tmp.set(0);
    f[0].push_back(tmp),b[0]=V+1;
    For(i,1,m) For(j,0,V/b[i])
    {
        bitset<maxn> dp;
        if(j) dp|=(f[i][j-1]<<b[i]);
        if(b[i-1]*j<=V) dp|=f[i-1][j];
        dp&=pw[sum[j]];
        f[i].push_back(dp);
    }
    
    int ans=-1;
    For(j,0,V/b[m]) if(f[m][j][V]){ ans=j; break; }
    printf("%d\n",ans);
    if(ans==-1) return 0;
    else dfs(m,ans,V);

    priority_queue<pii> q,q2;
    For(i,1,n) q.push(make_pair(a[i],i));
    For(i,1,ans)
    {
        printf("%d ",res[i]);
        while(res[i]--){
            pii x=q.top(); q.pop();
            printf("%d ",x.second);
            if(--x.first); q2.push(x);
        }printf("\n");
        while(!q2.empty()) q.push(q2.top()),q2.pop();
    }
    return 0;
}