對稱二叉樹
- 標簽:二叉樹遞歸、對稱性判斷
題目描述
給你一個二叉樹的根節點 root , 檢查它是否軸對稱。
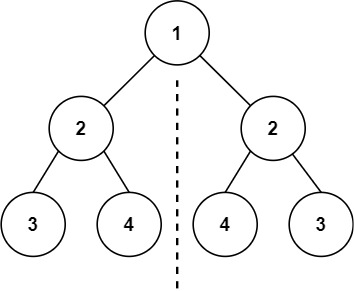
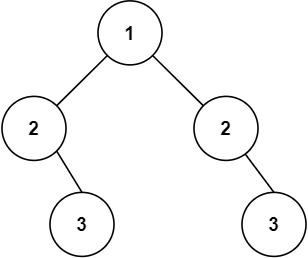
示例 1:
輸入:root = [1,2,2,3,4,4,3] 輸出:true 示例 2:
輸入:root = [1,2,2,null,3,null,3] 輸出:false
提示:
樹中節點數目在范圍 [1, 1000] 內
-100 <= Node.val <= 100進階:你可以運用遞歸和迭代兩種方法解決這個問題嗎?
原題: LeetCode 101
思路及實現
方式一:遞歸(推薦)
思路
乍一看無從下手,但用遞歸其實很好解決。
根據題目的描述,鏡像對稱,就是左右兩邊相等,也就是左子樹和右子樹是相當的。
注意這句話,左子樹和右子相等,也就是說要遞歸的比較左子樹和右子樹。
我們將根節點的左子樹記做 left,右子樹記做 right。比較 left 是否等于 right,不等的話直接返回就可以了。
如果相當,比較 left 的左節點和 right 的右節點,再比較 left 的右節點和 right 的左節點
比如看下面這兩個子樹(他們分別是根節點的左子樹和右子樹),能觀察到這么一個規律:
左子樹 2 的左孩子 == 右子樹 2 的右孩子
左子樹 2 的右孩子 == 右子樹 2 的左孩子
根據上面信息可以總結出遞歸函數的兩個終止條件:
- left 和 right 不等,或者 left 和 right 都為空
- 遞歸的比較 left,left 和 right.right,遞歸比較
left,right 和 right.left
代碼實現
Java版本
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true; // 如果根節點為null,即空樹,視為對稱二叉樹,返回true
}
return isMirror(root.left, root.right); // 調用isMirror方法判斷左子樹和右子樹是否對稱
}
private boolean isMirror(TreeNode left, TreeNode right) {
if (left == null && right == null) {
return true; // 如果左子樹和右子樹都為null,也視為對稱,返回true
}
if (left == null || right == null) {
return false; // 如果左子樹和右子樹只有一個為null,視為不對稱,返回false
}
return left.val == right.val && isMirror(left.left, right.right) && isMirror(left.right, right.left);
// 如果左子樹和右子樹的值相等,且同時滿足左子樹的左子樹和右子樹的右子樹對稱,
// 以及左子樹的右子樹和右子樹的左子樹對稱,則視為對稱,返回true;否則,返回false
}
}
說明:
isSymmetric方法是該函數的入口,接收一個二叉樹的根節點作為參數。首先判斷根節點是否為null,如果是,即空樹,視為對稱二叉樹,返回true。否則,調用isMirror 方法來判斷左子樹和右子樹是否對稱。isMirror方法是遞歸判斷左右子樹是否對稱的函數。首先判斷左子樹和右子樹是否都為null,如果是,即均為空樹,視為對稱,返回true。然后判斷左子樹和右子樹中只有一個為null的情況,即一個為空樹一個不為空樹,視為不對稱,返回false。最后,判斷左子樹的值和右子樹的值是否相等,并且同時遞歸判斷左子樹的左子樹和右子樹的右子樹是否對稱,以及遞歸判斷左子樹的右子樹和右子樹的左子樹是否對稱。只有全部滿足才視為對稱,返回true;否則,返回false。
C語言版本
#include <stdbool.h>
/*struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
*/
bool isMirror(struct TreeNode *left, struct TreeNode *right);
bool isSymmetric(struct TreeNode *root) {
if (root == NULL) {
return true; // 如果根節點為NULL,即空樹,視為對稱二叉樹,返回true
}
return isMirror(root->left, root->right); // 調用isMirror函數判斷左子樹和右子樹是否對稱
}
bool isMirror(struct TreeNode *left, struct TreeNode *right) {
if (left == NULL && right == NULL) {
return true; // 如果左子樹和右子樹都為NULL,也視為對稱,返回true
}
if (left == NULL || right == NULL) {
return false; // 如果左子樹和右子樹只有一個為NULL,視為不對稱,返回false
}
return (left->val == right->val) && isMirror(left->left, right->right) && isMirror(left->right, right->left);
// 如果左子樹和右子樹的值相等,并且同時滿足左子樹的左子樹和右子樹的右子樹對稱,
// 以及左子樹的右子樹和右子樹的左子樹對稱,則視為對稱,返回true;否則,返回false
}
Python3版本
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if root is None:
return True # 如果根節點為空,返回True,空樹被認為是對稱的
return self.isMirror(root.left, root.right)
def isMirror(self, left: TreeNode, right: TreeNode) -> bool:
if left is None and right is None:
return True # 如果左子樹和右子樹都為空,認為是對稱的
if left is None or right is None:
return False # 如果左子樹和右子樹只有一個為空,不對稱
return left.val == right.val and self.isMirror(left.left, right.right) and self.isMirror(left.right, right.left)
# 比較左子樹的左子樹和右子樹的右子樹,以及左子樹的右子樹和右子樹的左子樹,滿足條件才認為是對稱的
# 假設定義了TreeNode類,包含val、left和right屬性
class TreeNode:
def __init__(self, val: int = 0, left: TreeNode = None, right: TreeNode = None):
self.val = val
self.left = left
self.right = right
說明:代碼中使用了 TreeNode 類來定義樹節點,包含 val、left 和 right 屬性。其中 val 存儲節點的值,left 和
right 存儲左子樹和右子樹的引用。
復雜度分析
- 時間復雜度:O(n),其中 n 表示樹的節點數。
- 空間復雜度:O(n),遞歸調用的棧空間最多為樹的高度。
方式二:隊列(迭代)
思路
回想下遞歸的實現:
當兩個子樹的根節點相等時,就比較:
左子樹的 left 和 右子樹的 right,這個比較是用遞歸實現的。
現在我們改用隊列來實現,思路如下:
首先從隊列中拿出兩個節點(left 和 right)比較:
將 left 的 left 節點和 right 的 right 節點放入隊列
將 left 的 right 節點和 right 的 left 節點放入隊列
代碼實現
Java版本
//leetcode submit region begin(Prohibit modification and deletion)
import java.util.LinkedList;
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return false; // 根節點為空,不算對稱
}
if (root.left == null && root.right == null) {
return true; // 左右子樹都為空,算對稱
}
LinkedList<TreeNode> queue = new LinkedList(); // 使用隊列來保存待比較的節點
queue.add(root.left);
queue.add(root.right);
while (queue.size() > 0) {
TreeNode left = queue.removeFirst();
TreeNode right = queue.removeFirst();
// 只要兩個節點都為空,繼續循環;兩者有一個為空,返回false
if (left == null && right == null) {
continue;
}
if (left == null || right == null) {
return false;
}
// 判斷兩個節點的值是否相等
if (left.val != right.val) {
return false;
}
// 將左節點的左子節點和右節點的右子節點放入隊列
queue.add(left.left);
queue.add(right.right);
// 將左節點的右子節點和右節點的左子節點放入隊列
queue.add(left.right);
queue.add(right.left);
}
return true;
}
}
//leetcode submit region end(Prohibit modification and deletion)
說明:
這段代碼使用迭代方法判斷二叉樹是否對稱。在 isSymmetric 方法中,首先判斷根節點是否為空,如果為空,返回 false,表示不對稱。然后,如果根節點的左右子樹都為空,返回 true,表示對稱(只有一個元素的case)。
接下來,創建一個隊列 queue,并將根節點的左子節點和右子節點加入隊列。然后進入循環,每次從隊列中取出兩個節點進行比較。在比較過程中,只要兩個節點均為空,繼續循環;如果只有一個節點為空,返回
false,表示不對稱。然后,比較兩個節點的值是否相等,如果不相等,返回 false。將左節點的左子節點和右節點的右子節點放入隊列,用于后續比較。同時,將左節點的右子節點和右節點的左子節點放入隊列,也用于后續比較。
當隊列為空時,表示所有節點都已比較完畢,沒有發現不對稱的情況,返回 true,表示對稱。
這段代碼使用了迭代方法,利用隊列存儲待比較的節點,逐層按順序比較,避免了遞歸方法的額外棧空間開銷。
C語言版本
// leetcode submit region begin(Prohibit modification and deletion)
#include <stdbool.h>
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
bool isSymmetric(struct TreeNode* root) {
if (root == NULL) {
return false; // 根節點為空,不算對稱
}
struct TreeNode* queue[10000]; // 使用隊列來保存待比較的節點
int front = 0, rear = 0;
queue[rear++] = root->left;
queue[rear++] = root->right;
while (rear != front) {
struct TreeNode* left = queue[front++];
struct TreeNode* right = queue[front++];
// 只要兩個節點都為空,繼續循環;兩者有一個為空,返回false
if (left == NULL && right == NULL) {
continue;
}
if (left == NULL || right == NULL) {
return false;
}
// 判斷兩個節點的值是否相等
if (left->val != right->val) {
return false;
}
// 將左節點的左子節點和右節點的右子節點放入隊列
queue[rear++] = left->left;
queue[rear++] = right->right;
// 將左節點的右子節點和右節點的左子節點放入隊列
queue[rear++] = left->right;
queue[rear++] = right->left;
}
return true;
}
//leetcode submit region end(Prohibit modification and deletion)
說明:
這段代碼使用C語言實現了迭代方法來判斷二叉樹是否對稱。在 isSymmetric 函數中,首先判斷根節點是否為空,如果為空,返回 false,表示不對稱。
創建一個隊列 queue,使用數組來保存待比較的節點。使用 front 和 rear 變量分別表示隊首和隊尾的索引。
將根節點的左子節點和右子節點依次加入隊列 queue。
然后進入循環,每次從隊列中取出兩個節點進行比較。
在比較過程中,只要兩個節點均為空,繼續循環;如果只有一個節點為空,返回
false,表示不對稱。然后,比較兩個節點的值是否相等,如果不相等,返回 false。將左節點的左子節點和右節點的右子節點放入隊列,用于后續比較。同時,將左節點的右子節點和右節點的左子節點放入隊列,也用于后續比較。
當隊列為空時,表示所有節點都已比較完畢,沒有發現不對稱的情況,返回 true,表示對稱。
這段代碼使用了迭代方法,利用數組隊列方式存儲待比較的節點,逐個按序比較,避免了遞歸方法的額外棧空間開銷。
Python3版本
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if root is None:
return False # 根節點為空,不算對稱
queue = []
queue.append(root.left)
queue.append(root.right)
while queue:
left = queue.pop(0)
right = queue.pop(0)
if left is None and right is None:
continue # 只要兩個節點都為空,繼續循環
if left is None or right is None:
return False # 兩者有一個為空,返回False,不對稱
if left.val != right.val:
return False # 節點值不相等,不對稱
queue.append(left.left) # 左節點的左子節點入隊列
queue.append(right.right) # 右節點的右子節點入隊列
queue.append(left.right) # 左節點的右子節點入隊列
queue.append(right.left) # 右節點的左子節點入隊列
return True # 隊列為空,所有節點比較完畢,對稱
說明:(基礎說明可查看java或者c的實現)
在函數參數的類型注解中,使用了 TreeNode 類型來標注 root 參數的類型。
使用了 is 運算符來判斷節點是否為 None。is 運算符比較的是對象的身份標識,用于判斷對象是否是同一個對象。這里用它來判斷節點是否為None。
使用了列表 queue 來實現隊列的功能,通過 append() 方法將節點加入隊列的尾部,通過 pop(0)
方法來從隊列的頭部取出節點。Python的列表可以很方便地實現隊列的功能。
復雜度分析
- 時間復雜度:O(n),其中 n 表示樹的節點數。在最壞情況下,需要遍歷樹的所有節點。
- 空間復雜度:O(n),最壞情況下,隊列中需要存儲樹的一層節點,所以空間復雜度與樹的高度有關。在最壞情況下,樹的高度為 n/2,因此空間復雜度為 O(n)。
綜合來看,這個算法的時間復雜度和空間復雜度都是 O(n),其中 n 表示樹的節點數。算法的性能隨著節點數的增加而線性增長。
總結
| 方法 | 優點 | 缺點 | 時間復雜度 | 空間復雜度 |
|---|---|---|---|---|
| 遞歸法 | - 直觀易懂 - 代碼相對簡潔 | - 可能導致函數調用棧溢出的風險 - 需要額外的空間來存儲函數調用棧 | O(n) | O(n) |
| 隊列法 | - 不會導致函數調用棧溢出的風險 - 無需遞歸,代碼較為直觀 - 靈活的節點入隊和出隊順序 | - 需要手動維護隊列數據結構和追蹤節點的層次 - 需要額外的空間來存儲隊列和節點的信息 | O(n) | O(m) |
相似題目
| 題目 | 描述 | 難度 |
|---|---|---|
| LeetCode 100 | 判斷兩個二叉樹是否相同 | Easy |
| LeetCode 226 | 反轉二叉樹 | Easy |
| LeetCode 104 | 計算二叉樹的最大深度 | Easy |
| LeetCode 110 | 判斷二叉樹是否平衡 | Easy |
| LeetCode 222 | 統計完全二叉樹的節點個數 | Medium |
| LeetCode 124 | 計算二叉樹中的最大路徑和 | Hard |
| LeetCode 199 | 返回二叉樹從右側看的節點值列表 | Medium |
| LeetCode 116 | 填充二叉樹的每個節點的下一個右側節點指針 | Medium |
| LeetCode 112 | 判斷二叉樹是否存在從根節點到葉子節點的路徑和等于給定目標值 | Easy |
| LeetCode 257 | 返回二叉樹所有從根節點到葉子節點的路徑 | Easy |





 浙公網安備 33010602011771號
浙公網安備 33010602011771號