難是真的難，也值得好好整理一下。

首先，一個圖的dfs生成樹有一個性質：不含橫插邊。

所以在本題中，因為原圖是一棵樹，所以一個點 \(u\) 周圍的邊在生成樹上一定在一條鏈上（首尾相連）。

那么，設 \(d_i\) 為 \(i\) 的度數，則對于一個點周圍的邊，一共有 \(d_i!\) 中排列方式。如果確定鏈的起點，則有 \((d_i-1)!\) 種情況。

（如下圖的紅色邊）

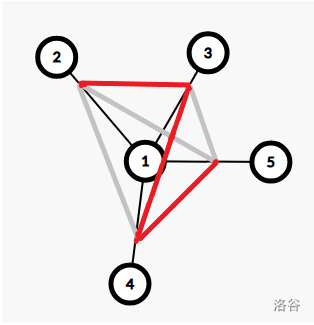
所以對于 \(k=1\) 的情況下，答案就是 \(\Pi_{i=1}^n (d_i-1)!\)。因為每一個鏈的起點是定的。

我們稱用來生成這棵dfs樹的關鍵邊為 生成樹的根。

現在的問題在于，我們可能會重復計算一棵生成樹多次。

所以現在我們需要考慮一棵生成樹可能會被那些關鍵邊給計算。

考慮下面這個圖，這是以邊 \((5,8)\) 構成的生成樹。

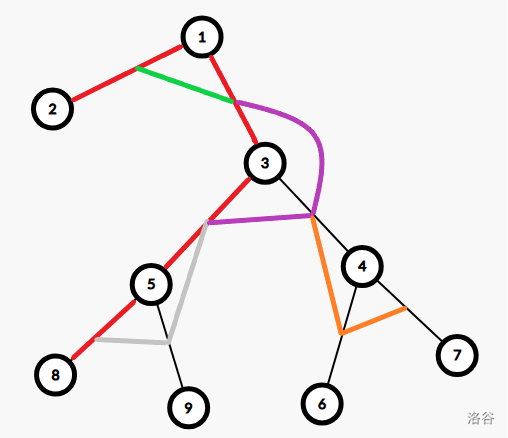
其中灰色、粉紅、橙色、綠色分別為點 \(5、3、4、1\) 相鄰的邊構成的鏈。其他的點因為度數為 \(1\) ，所以我們暫時不管他們。

因為一個點周圍的邊要構成一條鏈，所以 \((3,4)、(4,7)\) 就不能作為這棵生成樹的根。因為從他們出發，點 \(3\) 的鏈就不是鏈了。

所以發現，上圖的紅色邊就是可以作為這棵生成樹根的邊。

所以可以發現，能作為同一棵生成樹的根的邊，是原樹中一個葉子節點到另一個葉子節點之間的路徑上的邊。并且與生成樹建立起雙射，就是一條這樣的路徑只對應一棵生成樹，而一棵生成樹也只對應一條這樣的路徑。

為什么這棵生成樹一定存在這樣一個路徑可以作為根呢？

就如上圖，我們是拿邊 \((5,8)\) 生成的。此時向 \(8\) 節點走，發現 \(8\) 節點構成的鏈的起點一定是 \((5,8)\)，而其終點 \((3,5)\) 則可以作為另一個根。于是就這樣不斷地從鏈的起點到鏈的終點，而鏈的終點又是下一個鏈的起點。這樣不斷遍歷，最終會到達一個葉子節點。

因為需要保證，從可能的根節點出發遍歷一棵樹，原本欽定為鏈的部分必須還是鏈。

那么只要我從一個根向兩邊跳，每一次都從鏈頂跳到鏈尾，這樣就可以找到一個路徑。

所以說，我們只需要統計有多少個 原樹中從一個葉子到另一個葉子之間的路徑使得這條路徑上至少有 \(k\) 條關鍵邊中的一條。

那么如何統計方案數？

我們會發現，對于一條路徑上可以作為根節點的邊的端點，其鏈的起點與終點都是定的，單個方案數為 \((d_i-2)!\)。所以方案數為 \(\Pi_{x在鏈上}(d_x-2)!\ \Pi_{x不在鏈上}(d_x-1)!\)。為了方便，我們把它改成 \(\Pi(d_i-1)!\ \Pi_{x在鏈上}(d_x-1)^{-1}\)。

這樣問題就變為：對于所有葉子到葉子的路徑，滿足其中至少一條邊為關建邊，路徑上所有點的權值乘積之和。這里讓一個點的點權為 \((d_x-1)^{-1}\)。

先把 \(n=2\) 判掉。然后對于 \(n>2\)，找一個度數 \(>1\) 的位置作為根方便后續dp。

所以考慮dp，設 \(dp_{u,0/1}\) 表示以 \(u\) 為根的子樹中，從 \(u\) 出發，不經過/經過關建邊的乘積之和。

那么進行分類討論，對于 \(v\in son_u\)。

• 若 \((u,v)\) 為關建邊

  則答案貢獻增加 \((dp_{u,0}+dp_{u,1})(dp_{v,0}+dp_{v,1})\)。

  然后讓 \(dp_{u,1}\gets dp_{v,1}+dp_{v,0}\)。

• 若 \((u,v)\) 不是關建邊

  則答案貢獻增加 \(dp_{v,1}(dp_{u,0}+dp_{i,1})+dp_{v,0}\times dp_{u,1}\)。

  然后 \(dp_{u,1}\gets dp_{v,1}\)，\(dp_{u,0}\gets dp_{v,0}\)。

然后輸出答案即可。時間復雜度 \(O(n)\)。為了方便，處理逆元我用的 \(O(n\log n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,mod=1e9+7;
#define int long long
int head[N],cnt,n,k,u[N],v[N],w[N];

int ru[N],fac[N],inv[N],mul;

int dp[N][2],ans;

struct edge
{
	int v,nxt,w;
}a[N<<1];
void add(int u,int v,int w)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void dfs(int u,int fa)
{
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==fa) continue;
		dfs(v,u);
		
		if(a[i].w) 
		{
			ans=(ans+(dp[v][0]+dp[v][1])*(dp[u][0]+dp[u][1])%mod)%mod;
			dp[u][1]=(dp[u][1]+inv[ru[u]-1]*(dp[v][0]+dp[v][1]))%mod;
		}
		else
		{
			ans=(ans+dp[v][1]*(dp[u][0]+dp[u][1])%mod+dp[v][0]*dp[u][1]%mod)%mod;
			dp[u][1]=(dp[u][1]+inv[ru[u]-1]*dp[v][1])%mod;
			dp[u][0]=(dp[u][0]+inv[ru[u]-1]*dp[v][0])%mod;
		}
	}
	if(ru[u]==1) dp[u][0]=inv[ru[u]-1];
}
void solve()
{
	n=read(),k=read();
	
	for(int i=1;i<=n;i++) head[i]=0,dp[i][0]=dp[i][1]=ru[i]=0;
	cnt=0;
	ans=0;
	mul=1;
	
	for(int i=1;i<n;i++) u[i]=read(),v[i]=read(),w[i]=0;
	for(int i=1;i<=k;i++) w[read()]=1;
	for(int i=1;i<n;i++)
	{
		ru[u[i]]++;
		ru[v[i]]++;
		add(u[i],v[i],w[i]),add(v[i],u[i],w[i]);
	}
	if(n==2)
	{
		printf("1\n");
		return;
	}
	
	int pos=0;
	for(int i=1;i<=n;i++) 
	{
		mul=mul*fac[ru[i]-1]%mod;
		if(ru[i]>1) pos=i;
	}
	dfs(pos,0);
	printf("%d\n",ans*mul%mod);
}
int qpow(int a,int b)
{
	int ans=1;
	while(b>0)
	{
		if(b&1) ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1; 
	}
	return ans;
}
signed main()
{
	fac[0]=1,inv[0]=1;
	for(int i=1;i<=1e5;i++) fac[i]=fac[i-1]*i%mod,inv[i]=qpow(i,mod-2);
	int ID=read(),T=read();
	while(T--) solve();
	return 0;
}