1. CF868F Yet Another Minimization Problem

難度：1.5

首先可以很快列出方程。設 \(dp_{j,i}\) 表示考慮將 \([1,i]\) 拆成 \(j\) 段的最小代價。設 \(w[i,j]\) 表示區間 \([i,j]\) 的代價。

則有轉移：

直接做是 \(O(n^2k)\)，考慮優化。

感覺不太能優化？感覺斜率優化、DS優化啥的都用不了。試一試決策單調性吧。

需要證明，對于任意 \(i,j\in[1,n],j\ge i+3\)：

發現很好證啊，按照定義直接拆開。要證上式，只要證：

兩邊一消。只要證：

真的顯然成立。

所以可以用決策單調性解決。

我們先把 \(j\) 這一維循環給甩到最外面。然后考慮從 \(j-1\to j\) 的轉移。設 \(k_i\) 為 \(i\) 的最優決策點。

我曾有一個疑問就是為什么不可以直接雙指針線性解決？既然已經有了決策單調性了，就維護一個指針指到當前決策點，然后往后掃，直到掃到被轉移點的最優決策點為止。然后發現沒法判斷是否是被轉移點的最優決策點，遂卒。

所以考慮用分治解決。對于區間 \([l,r]\) ，我們找到他的中間點 \(mid\) 并求出 \(k_{mid}\)，再分治下去。因為有決策單調性，所以有 \(k_{l-1}\le k_{mid}\le k_{r+1}\)，所以只用在這個范圍內枚舉即可。

然后如何求出 \(w[x,mid]\)，考慮用莫隊動態維護。發現左右端點的移動次數都是 \(O(n\log n)\)。

所以總時間復雜度 \(O(kn\log n)\)。

提交記錄

2. [IOI2000] 郵局

Easy版： [IOI 2000] 郵局（原始版）

Medium版： [IOI 2000] 郵局 加強版

Hard版： [IOI 2000] 郵局 加強版 加強版

難度：0/0.5/1.5

題意是一樣的，只是數據范圍有差異。

先看 Easy 版，設 \(dp_{j,i}\) 表示考慮了前 \(i\) 個村莊，建設了 \(j\) 個郵局的最小代價。

則有轉移：

而給出的數據是有序的，所以可以記錄 \(pre_i=\sum_{i=1}^n d_i\)。設 \(mid=\lfloor\frac{l+r}{2}\rfloor\)，則 \(w(l,r)=(mid-l+1)\times d_{mid}-(pre_{mid}-pre_{l-1})+(pre_r-pre_{mid})-d_{mid}\times (r-mid)\)。可以 \(O(1)\) 得到。

所以時間復雜度 \(O(n^2k)\)，其中 \(n\) 為村莊個數，\(k\) 為郵局個數。可以通過 Easy 版。

Easy版提交記錄

現在考慮優化。發現有 建恰好k個郵局 的條件，想到wqs二分，找一找凸性質。根據打表，答案函數是一個下凸函數。

所以考慮用wqs二分優化，check 函數里類似 Easy 版的轉移。時間復雜度 \(O(n^2\log k)\)。可以通過 Medium 版。

Medium版提交記錄 wqs二分優化

但還有另一種優化思路。重點在 \(w(l,r)\) 上。

這個東西滿不滿足四邊形不等式呢？

也就是對于 \(l,r\in[1,n],r>l+2\) ，滿足：

寫成差分形式，有：

分類討論區間長度奇偶性：

• 若 \(r-l+1\) 為奇數

  設 \(mid=\frac{(l+r)}{2}\)。

  則 \([l,r]\)、\([l,r-1]\)、\([l+1,r]\)、\([l+1,r-1]\) 的中位數都可以是 \(d_{mid}\)。

  所以有 \(w(l,r)-w(l,r-1)=w(l+1,r)-w(l+1,r-1)=d_r-d_{mid}\)。

• 若 \(r-l+1\) 為偶數

  設 \(mid=\frac{(l+r-1)}{2}\)。

  則 \([l,r]\)、\([l,r-1]\) 的中位數都可以是 \(d_{mid}\)。\([l+1,r]\)、\([l+1,r-1]\) 的中位數都可以是 \(d_{mid+1}\)。

  所以有 \(w(l,r)-w(l,r-1)=d_r-d_{mid},w(l+1,r)-w(l+1,r-1)=d_r-d_{mid+1}\)。

  因為 \(d_r-d_{mid}\ge d_r-d_{mid+1}\)，所以\(w(l,r)-w(l,r-1)\ge w(l+1,r)-w(l+1,r-1)\)。

綜上得證。

然后就有決策單調性。對于上述的二維轉移，則可以用分治處理。設 \(K_i\) 為 \(i\) 的最優決策點。對于一個區間，先算出 \(K_{mid}\)，再遞歸到左右子區間。

對于區間 \(i\in[l,r]\)，一定有 \(K_{l-1}\le K_i\le K_{r+1}\)。所以直接分治即可。（不用wqs二分）

時間復雜度 \(O(kn\log n)\)。

Medium版提交記錄 決策單調性優化

現在考慮 Hard 版。

其實發現 Medium 版的兩個方法可以合并的，然后時間復雜度就是對的。

但是有一個問題。就是在上文給出的分治求決策單調性優化需要滿足 轉移跟枚舉轉移順序無關。也就是說因為是一個二維dp，在處理 \(dp_{j,i}\) 的轉移時，我們已經直到 \(dp_{j-1,k}\) 的所有值了，也就跟轉移順序無關。

但是用wqs二分時，check函數里應該是一維dp。因為沒有個數限制了。

轉移式子（\(val\) 是wqs二分的值）：

如果還按分治的方法做，我們都不知道 \(dp_{K_i}\) ，怎么轉移到 \(dp_i\) 啊。

所以考慮用 二分答案+單調隊列 解決。

我們考慮動態維護更新數組 \(K\)。如一開始，我們讓 \(K=\{1,1,1,...\}\)，因為只能從 \(1\) 轉移。但更新 \(2\) 了以后，\(K\) 的某一個后綴會全部更新成 \(2\)，即 \(K=\{1,1,1,2,2,...,2\}\)，以此遞推。

所以考慮用單調棧維護順序出現的所有 \(K\) 值。然后記錄每一種 \(K\) 值出現的第一個位置。

然后更新時，就從隊尾開始，如果隊尾的 \(K\) 值的第一個位置 用新的 \(K\) 值轉移更優 就把隊尾刪去。一直刪，直到新的值更劣為止。然后再在 \([隊尾的 K 值出現的第一個位置,n]\) 中二分答案，找到第一個用新的 \(K\) 轉移更優的位置，記錄下來。將新的 \(K\) 值放在隊尾。

然后轉移到 \(i\)，就判斷隊首的后一個 \(K\) 值出現的第一個位置是否小于等于 \(i\)，如果小于等于就彈出隊首。然后拿新的隊首轉移。

這樣就可以做到 \(O(n\log n)\) 的check。

所以時間復雜度 \(O(n\log n\log V)\)。然后wqs二分上界為 \(0\)，下界取 \(-nV=-10^{12}\) 保險。

Hard版提交記錄 wqs二分+決策單調性優化，一遍過！

3. CF1031F Familiar Operations

難度：1

模擬賽沒改的題，擱置了一個月，還是改了。*2800，放在T4。

考場上糊了一堆貪心，然后假了。

欽定一個閾值 \(W\)，下面所有操作中的數都只討論 \(\le W\) 的情況。

因為因子個數只跟質因數的指數有關。因為 \(因數個數=\Pi (質因數指數+1)\)。所以我們對于一個數 \(w=p_1^{r_1}p_2^{r_2}...p_k^{r_k}\) 將 \(r_i\) 提出來，再從大到小排序，從而生成一個數組。

而發現生成的數組有很多是重復的，而相同的數組的因子個數又是相同的，所以可以直接去重。去重后，發現不同的數組個數很少。當 \(w\le 10^6\) 時，只有 \(289\) 個。反正就是很少。

那么現在可以進行乘一個質數或者除以一個質因子的操作就相當于在生成這個序列中的某一個位置 \(+1\) 或 \(-1\)，并且代價為 \(1\)。

那么可以考慮用圖論解決。因為加一和減一是可逆的，所以就只用考慮向減一后的數組建一條邊權為 \(1\) 的雙向邊即可。

而又想讓因子個數相同。那么可以建立一些點代表這因子個數。讓每一個數組被 代表它的因子個數的點 連一條邊權為 \(0\) 的單向邊。

再從每一個代表因子個數的點出發，跑單源最短路。

這樣對于每一次查詢 \((x,y)\)，就可以求出 \(x\) 生成的數組 \(a\) 和 \(y\) 生成的數組 \(b\)。然后枚舉代表因子個數的點 \(k\)，則答案為 \(\min dis_{k,a}+dis_{k,b}\)。

大體思路確定，現在考慮實現。

處理代表數組的點的方式有點類似與AT_arc057_d 全域木 的實現方式。先用dfs求出每一個不同的數組，然后處理出它的因子個數，存下來。

求這個數組時，為了使得直接判斷這個數組是否存在，即是否存在一個數 \(w\le W\) 使得 \(w\) 生成的數組是這個數組，我們只取前幾個質數，讓數組中的數從大到小依次成為從小到達的幾個質數的指數，如果這個乘積 \(\le W\) 則存在。

然后將每一個數組的因子個數預處理出來并離散化，并編上號，要與數組的點的編號不同。

然后就是數組與數組之間的邊了。為了方便，我們對于前幾個質數隨機一個值 \(hsh_i\)，則一個數組的哈希值為 \(\sum_{i=1}^k hsh_i\times r_i\)，這樣就可以讓數組與一個值之間建立雙射。

我們要讓數組內一個數減一，為了讓減一后該數組還是有序的，如果有一段相同的數，我們要減只減最后一個位置。找到哈希值為原數組哈希減去該位置的 \(hsh\) 值的數組點，連一條邊權為 \(1\) 的雙向邊。

然后就以每一個代表因子個數的點跑單源最短路。可以用01bfs或者Floyd。

那么對于查詢 \((x,y)\)，先將 \(x,y\) 分解質因數，然后將質因數指數從大到小排序，找到對應的數組點 \(a\) 和
\(b\)。然后枚舉因子個數的點 \(p\)，則答案為 \(\min dis_{p,a}+dis_{p,b}\)。

\(W\) 取 \(10^8\) 能保證正確性。此時因子個數有 \(190\) 種，數組有 \(803\) 種。

設 \(n\) 為不同數組個數，\(m\) 為不同因子個數。則時間復雜度 \(O(nm+tm\sqrt V)\)。

瓶頸在于分解質因數。改為線性篩分解質因數可以優化到 \(O(nm+tm\ln V)\)。

跑得非常快。是目前洛谷最優解&學校OJ最優解。

提交記錄

4. P2305 [NOI2014] 購票

難度：2.5

還是挺難的，搞了幾遍才搞懂。從除夕搞到初十，也是終于會了。

這里只介紹出棧序+線段樹套李超樹的做法。

首先，不要讀錯題了，注意是從根向葉子轉移，而不是從葉子向根轉移。

先列出 \(dp\) 式子。記 \(dis_u\) 為 \(u\) 到根的距離。則有：

改一下，則有：

然后發現這個式子可以斜率優化，用李超樹維護。

先考慮部分分吧。

性質1：構成鏈

考慮用線段樹套李超線段樹，對于 \(i\)，找到它最遠的祖先 \(j\) 使得 \(dis_i-dis_j\le l_i\)。然后從 \([i,j]\) 里轉移。

李超樹需動態開點。

時間復雜度 \(O(n\log ^2n)\)，空間復雜度 \(O(n\log n)\)。

性質2：不考慮 \(l_i\) 的限制

可以考慮可持久化李超樹，對于每一個節點的李超樹為其父親節點修改而成。最多只更改 $\log $ 個節點，所以可以做。

時間復雜度 \(O(n\log n)\)，空間復雜度 \(O(n\log n)\)。

正解

現在有 \(l_i\) 的限制，怎么做？可能會用到樹剖或者其它東西來處理。

這里就需要用出棧序了。

出棧序就是dfs中退出一個節點時將這個節點存入后形成的序列。

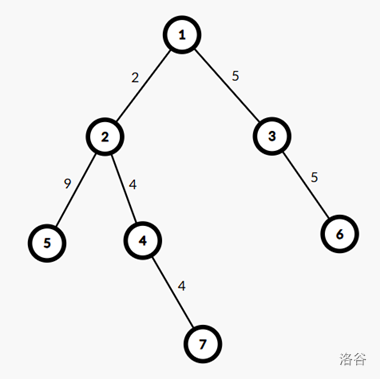
這是樣例1的圖。

我們以 \(1\to 2\to 5\to 4\to 7\to 3\to 6\) 的順序dfs。

那么它的出棧序為： \(5\ 7\ 4\ 2\ 6\ 3\ 1\)。記為 \(st\) 數組。并類似性質1的方式對該式構建線段樹套李超樹方便轉移。

現在我們要對 \(i\) 找到最遠且滿足要求的祖先 \(j\)。就如 \(i=5,j=1\)。

此時在出棧序中，\(st_1=5,st_7=1\)，我們取區間 \([1,7]\) ，但是中間有一些數并不在 \(5\) 到 \(1\) 的路徑上。這怎么辦？

我們發現，如果我們按上面dfs的順序去依次更新 \(dp\) 值，并在每一次更新完后插入對應位置的幾個李超樹，這樣并不會對答案造成影響。

因為所有不在這條路徑上的點都沒有被更新過。

所以根據此結論，我們可以先處理出出棧序，并按原先dfs的順序更新 \(dp\) 值。

更新 \(u\) 的值時，找到它最遠且距離 \(\le l_u\) 的祖先 \(fa\)，找到 \(u\) 和 \(fa\) 在出棧序中對應的位置，然后對該區間進行查詢更新 \(dp\) 值。更新完后又更新李超樹上的值。

時間復雜度 \(O(n\log^2n)\)，空間復雜度 \(O(n\log n)\)。

提交記錄

5. P3081 [USACO13MAR] Hill Walk G

難度：2

有點繞，腦袋一時半會兒沒想到。

首先不能直接李超線段樹，因為李超線段樹只能記錄最大值。而可能會出現這樣的情況：當前在 \((x1,y1,x2,y2)\) 這條線段上，但是存在一條 \((x3,y3,x4,y4)\) 滿足 \(y3>>y1\)，\(y4>>y2\)，\(x3\le x2<x4\)。也就是在這條線段的頭頂上。

顯然我們不能從第一條線段到第二條線段。所以不能直接找 \(x2\) 這個位置的最大值。

可以注意到第二條線段是不可達的，無論如何。所以考慮將不可達的線段都不加入李超線段樹。

如果可能能從 \((x1,y1,x2,y2)\) 到達 \((x1',y1',x2',y2')\)，那么必須有 \(x1'\le x2<x2'\)，且后者在 \(x=x2\) 的取值要 \(<y2\)。

而在不斷往后跳線段的過程中， \(x2\) 是遞增的。

所以考慮將所有線段按 \(x1\) 從小到大排序。對于 \(x1\le 當前x2\) 的線段判斷是否滿足上面的要求，如果滿足要求再加入李超樹中的 \([x1,x2-1]\)。

這樣就可以直接查在 \(x=x2\) 處的最大值了。

時間復雜度 \(O(n\log^2n)\)。但是線段之間不相交，所以可以改成線段樹，時間復雜度 \(O(n\log n)\)。

提交記錄

6. P4069 [SDOI2016] 游戲

難度：2

將 \((u,v)\) 的路徑拆成 \((u,lca)\) 和 \((lca,v)\)。

記錄 \(dis_u\) 為 \(u\) 到根的距離。

則對于 \((u,lca)\) 上的點 \(i\)，加入的直線為 \(a\times(dis_u-dis_i)+b=-a\times dis_i+(a\times dis_u+b)\)。斜率為 \(-a\)，截距為 \(a\times dis_u+b\)。

對于 \((lca,v)\) 上的點 \(i\)，加入的直線為 \(a\times(dis_u+dis_i-2dis_{lca})+b=a\times dis_i+a\times (dis_u-2dis_{lca})+b\)。斜率為 \(a\)，截距為 \(a\times (dis_u-2dis_{lca})+b\)。

現在考慮樹剖維護。我們只對一條鏈進行操作，而這條鏈上的 \(dis\) 值是單增的，所以可以離散化為李超樹的下標。

我們需要查詢區間最小函數值，所以記錄一個最小函數值，每一次修改都上傳一下即可。

因為李超樹是永久化標記，則對 \([L,R]\) 查詢時需注意對于區間 \([l,r]\) 滿足 \(l<L\) 或 \(r>R\) 時也要對它在 \(L\) 或 \(R\) 處的取值統計在內。因為查詢的可能不是一個整鏈。

時間復雜度查詢 \(O(n\log^2n)\)，修改 \(O(n\log^3n)\)。

提交記錄

7. CF1303G Sum of Prefix Sums

難度：0.9

樹上大量路徑處理問題，考慮點分治。

設有向路徑 \((k_1,k_m)\) 依次經過點 \(\{k_1,k_2,...,k_m\}\)，則權值為 \(\sum_{i=1}^m i\times w_{k_i}\)。

考慮經過分治中心 \(rt\) 的路徑。設 \(p\) 為 \(v\) 的祖先，且為 \(rt\) 的兒子，則可以將有向路徑 \((u,v)\) 拆成 \((u,rt)\) 和 \((p,v)\) 。

分治中，對于每一個節點處理出 \(pre_u\)，\(suf_u\)，\(sum_u\)。

設 \((u,rt)\) 經過 \(\{k_1,k_2,...,k_m\}\)，則有：

設 \(d_{u}\) 為 \(u\) 的深度（根為 \(rt\) 時），那么對于路徑 \((u,v)\) 的權值就為 \(pre_u+(d_u-d_{rt}+1)\times sum_v+suf_v\)。

如下圖。

考慮用 \(suf_v\) 去匹配之前的 \(u\) 從而找到最大的 \((u,v)\)。

發現上式的形式是一個直線的表達式，斜率為 \((d_u-d_{rt}+1)\)，截距為 \(pre_u\)。所以考慮用李超線段樹維護之前的 \(u\) 生成的直線，需要動態開點。然后找到 \(x=sum_v\) 處最大的直線，更新答案。

李超樹每一次分治用完要清空。

還有一些細節要注意：因為是有向路徑 \((u,v)\)，則每一次分治需要從前往后和從后往前進行兩次統計。然后還可能出現 \(u=rt\) 或 \(v=rt\) 的情況，需特判。

時間復雜度 \(O(n\log^2 n)\)，空間復雜度 \(O(n)\)。

提交記錄

8. P7114 [NOIP2020] 字符串匹配

難度：1.5

自己的思路是枚舉C，用KMP找出最短周期個數（AB最多能有多少個），然后對這個數找因數，再用樹狀數組求值。時間復雜度 \(O(nd(n)\log n)\)。只能拿 \(84\) 分。

正解的思路是枚舉循環節（AB）的長度 \(i\)。

用exKMP求出 \(z\) 函數，則（AB）最多的個數為 \(1+\lfloor\frac{z_{i+1}}{i}\rfloor\)。

而C的起點可以是任意一個循環節后的一個位置。

如 \(i=3\)，\(z_4=10\)。則循環周期為 \([1,3],[4,6],[7,9],[10,13]\)。那么C的起點可以是 \(4,7,10,14\)。

如果我們去枚舉C的起點，再逐個計算時，時間復雜度會達到 \(O(n^2)\)。

考慮挖掘限制函數 \(F(X)\) 的性質。\(F(X)\) 是串 \(X\) 中出現奇數次的字符的個數。而C的起點在向左移時，每一次相當于增加了一個循環節，而每增加兩個循環節，它的 \(F\) 值又會變回來。也就是說，循環節長度定了，\(F(C)\) 的值最多又只有兩個。

可以通過計算得到這兩個 \(F\) 值對應的位置個數。記 \(num=\lfloor\frac{z_{i+1}}{i}\rfloor\)。則與最靠右的C的起點的 \(F\) 值相同的點有 \(\lfloor\frac{num}{2}\rfloor+1\)，與另一個 \(F\) 值相同的點有 \(\lfloor\frac{num+1}{2}\rfloor\)。

直接用樹狀數組計算兩個 \(F\) 值得權值，并將系數乘上即可。

需要注意，C不能為空，如果最靠右的C的起點 \(>n\)，則需要刪掉最后一個循環節。讓 \(num\gets num-1\)，C起點位置 \(\gets\) C起點位置 \(-i\)。

時間復雜度 \(O(n\log n)\)。

提交記錄

9. P5563 [Celeste-B] No More Running

難度：0.5

zjk大佬&&學長 出的題，不過不是很難阿。

轉化一下題意，也就是對于 \(u\) ，求出 \(\max_{v=1}^n (w(u,v)\% mod)\)，其中 \(w(u,v)\) 為 \(u\) 到 \(v\) 的路徑邊權和。

大量的路徑問題，考慮點分治。

以 \(O(\log n)\) 的代價，將問題加上限制：經過根節點的路徑。

將 \((u,v)\) 拆成 \((u,rt)\) 和 \((v,rt)\)。

考慮如何快速合并路徑的問題。如何使得取模后的值最大？參考 P6105 [Ynoi2010] y-fast trie 進行分類討論。

設當前數為 \(a\)，想找一個 \(b\)，使得 \([(a+b)\% mod]\) 最大（\(0\le a,b<mod\)）。

• 欽定 \(a+b\ge mod\)，則答案為 \(a+b-mod\)。此時直接去找最大的 \(b\) 即可。
• 欽定 \(a+b<mod\)，則答案為 \(a+b\)。找 \(<mod-a\) 且最大的 \(b\) 即可。

所以對每一個點求出它到根的路徑權值和 \(\% mod\)，存入樹狀數組。這樣就可以直接查詢。

時間復雜度 \(O(n\log^2n)\)。

提交記錄

10. UVA12161 鐵人比賽 Ironman Race in Treeland

難度：0.7

沒有翻譯，要看英文題面。不過還是看得懂。也不算難。

題意：

一顆樹，每條邊有兩個權值 \(cost\) 和 \(len\)。現在要找一條路徑滿足 \(\sum cost \le m\) 且 \(len\) 最大。輸出最大的 \(len\)。

也是找路徑，考慮點分治。

將 \((u,v)\) 分成 \((u,rt)\) 和 \((v,rt)\)。

枚舉 \(v\) 處理出 \((v,rt)\) 的 \(cost\) 和 \(len\)。那么我們要在 \([0,m-cost]\) 的花銷范圍內找到最長的 \(len\)。

反過來想，以 \(len\) 為下標，開一顆線段樹。每一個位置維護最小的 \(cost\)。然后查詢時線段樹二分，如果右兒子存在 \(<m-cost\) 的值則向右走，否則向左走。

但是有個問題，這個 \(len\) 的范圍是 \(10^7\) 的，為了與當前點分治的連通塊大小 \(sz\) 有關，考慮每一次點分治后先處理出當前所有的 \(len\)，再離散化即可。

時間復雜度 \(O(n\log ^2n)\)。

提交記錄

11. P3714 [BJOI2017] 樹的難題

難度：0.99

自己切的，但感覺好妙啊。

維護顏色段權值，且找權值最大且邊數在 \([l,r]\) 的路徑。記 \(val_i\) 為顏色 \(i\) 的權值。

同樣考慮點分治。同樣將 \((u,v)\) 拆成 \((u,rt)\) 和 \((v,rt)\) 并考慮合并。

以下稱 \(u\) 到 \(rt\) 路徑上 一個端點為 \(rt\) 的邊 為 \(u\) 的頂邊。記 \(len_v\) 為 \(v\) 到 \(rt\) 的邊數。記路徑 \((u,v)\) 的權值為 \(w(u,v)\)。

但是二者的權值不能直接相加，因為可能出現兩個段合成一個段的情況，如下圖一，兩條橙色邊合并就會變成一個段。

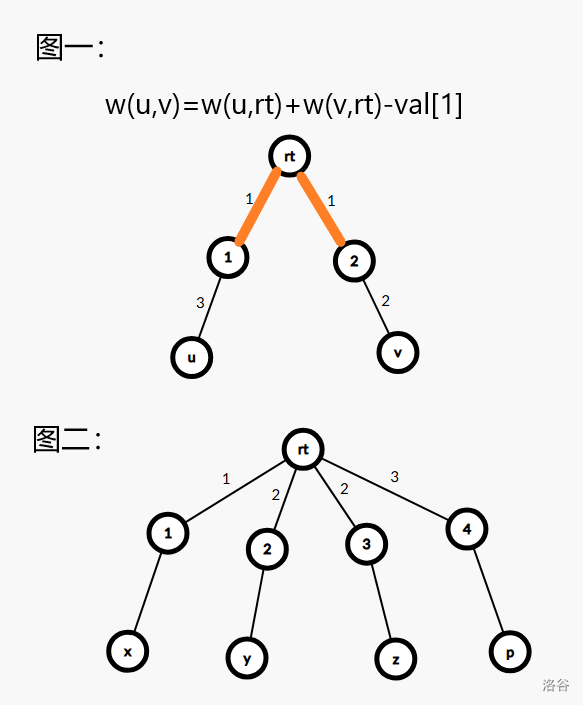
所以怎么做呢？

如圖二，在對 \(z\) 進行配對時，如果配對的是 \(x\) 則權值就為 \(w(x,rt)+w(z,rt)\)；但是如果配對的是 \(y\) 則權值就為 \(w(z,rt)+(y,rt)-val_2\)。二者權值計算方式有差異。

為了方便，我們用 vector 存圖，并按邊權排序，讓顏色相同的邊一起被遍歷。就如圖二給出的 \(rt\) 的連邊，從左到右即為遍歷順序。

這樣開兩顆線段樹 \(s1,s2\)， \(s1\) 用于存儲頂邊顏色與當前枚舉點的頂邊顏色不同的子樹的答案，\(s2\) 用于存儲頂邊顏色與當前相同的子樹的答案。

兩顆線段樹的下標 \(i\) 上放的都是 \(\max w(u,rt)\) 滿足 \(len_u=i\)。所以線段樹大小就是當前連通塊最大的深度，可以先處理出來。

這樣進行查詢時，設當前點為圖二的 \(z\)。則 \(s1\) 存的是子樹 \(1\) 的答案，\(s2\) 存的是子樹 \(2\) 的答案。

那么與 \(z\) 匹配的最大值就是

然后如果當前頂邊的顏色更變了，則需要將 \(s2\) 合并入 \(s1\) 并清空 \(s2\)。合并時，為保證時間復雜度，如果 \(s2\) 的一個兒子的最大值 \(=-inf\)，則直接 return，不管它。

那么這樣的時間復雜度是多少呢？大約是 \(O(sz\log sz)\)，因為是 \(\sum{每顆子樹大小}\times \log sz\)。

而查詢又是 \(O(sz\log sz)\)。

所以總時間復雜度 \(O(n\log^2n)\)。

提交記錄

12. P11364 [NOIP2024] 樹上查詢

難度：2

考場上，自己得到了一個偏了的結論，就一直往這邊想，結果沒有去找其他性質。

首先一個顯然的性質就是

可以用虛樹的方式證明。然后我竟然沒看出來？

然后就可以預處理出 \(dep[\operatorname{lca}(i,i+1)]\) 的值。

現在我們對于 \(dep[\operatorname{lca}(i,i+1)]\) 處理出極長區間 \([x_i,y_i,v_i]\)，代表區間 \(dep[\operatorname{lca}[x_i,y_i]]=v_i=dep[\operatorname{lca}(i,i+1)]\)。有點類似一條線段。

這個東西用單調棧從前往后和從后往前掃一遍就可以處理。

那么查詢 \([l,r,k]\) 時實際上就是找到合法且 \(v_i\) 最小的線段。

那么怎么找合法線段？進行分類討論：

• 滿足 \(r \le y_i\) 且 \(x_i\le r-k+1\)

  則可以將線段對 \(y_i\) 進行排序，將詢問對 \(r\) 進行排序。用線段樹維護 \(x_i\) 在 \([1,r-k+1]\) 的最小 \(v_i\) 即可。

• 滿足 \(l+k-1\le y_i<r\) 且 \(y_i-x_i+1\ge k\)

  則可以將線段對 \(y_i-x_i+1\) 進行排序，將詢問對 \(k\) 進行排序。用線段樹維護 \(y_i\) 在 \([l+k-1,r-1]\) 的最小 \(v_i\) 即可。

實際上就是掃描線。

然后就做完了，挺簡單的，碼量也不是特別大。時間復雜度 \(O(n\log n)\)。

提交記錄

13. P7215 [JOISC 2020] 首都

難度：2

好像有一種樹剖+線段樹優化建圖+縮點的做法。

就是枚舉一種顏色 \(i\)，如果顏色為 \(i\) 的兩個點之間的路徑會經過顏色 \(j\) 的點，則讓 \(i\) 向 \(j\) 連邊。

這個部分需要用樹鏈剖分+線段樹優化建圖解決。

然后跑強連通分量縮點。則答案就是出度為 \(0\) 且大小最小的強連通分量的大小。時間復雜度 \(O(n\log^2n)\)。

不過不夠優雅。

我們從鏈的性質入手，發現可以進行分治。考慮必須取中間這個位置時的最小代價。然后再分治到左右兩邊，再進行分治。

現在放在樹上也一樣，考慮用點分治。欽定必須選分治中心 \(u\)。先處理出該分治連通塊內每個點的父親。開一個隊列維護要取的顏色，將 \(col_u\) 放入隊列。

然后每一次從隊列里取出一種顏色，將它的所有點判斷是否都在該分治連通塊內，如果不在則直接退出，因為在之前的分治已經處理過了，不優。

然后將該顏色的所有點判斷它父親的顏色是否不一樣且沒被放入隊列過，如果沒有就放入隊列。

一直這樣知道隊列為空。則代價為隊列里出現過的顏色數 \(-1\)。

然后取 \(\min\) 即可。

時間復雜度 \(O(n\log n)\)。

提交記錄

14. P6326 Shopping

難度：2

好題。

首先，我們最后購買東西的商店一定構成一個連通塊。考慮用點分治查詢連通塊。

現在有分治中心 \(rt\)。將 \(rt\) 定為新樹根，則問題轉化為樹上依賴性多重背包。

多重背包可以用二進制拆分解決。將 \(d\) 個物品拆成 \(b+\sum_{i=0}^k 2^i\) 這 \(k+1\) 個物品，\(b<2^{k+1}\)。然后進行dp，可以做到 \(O(m\log d)\) 的時間復雜度的插入物品。

但是樹上背包進行合并時的時間復雜度為 \(O(m^2)\) 每次，無法接受。所以需要將合并操作轉化為插入操作。

考慮對這棵樹記錄dfs序，在dfs序上dp。設 \(dp_{i,j}\) 表示從后往前考慮到dfs序中下標為i，總體積為 \(j\) 時的最大價值。

對于節點 \(u\)，如果取 \(u\) 的物品，就由 \(dp_{dfn_u+1}\) 轉移。如果不取 \(u\) 的物品，則從dfs序中“刪去”這個子樹，由 \(dp_{dfn_u+sz_u}\) 轉移。這樣就可以只用插入而不用合并操作了。

然后就可以做到 \(O(nm\log d\log n)\)。可以通過。

提交記錄

15. P5071 [Ynoi Easy Round 2015] 此時此刻的光輝

難度：2

lxl 的題還是有難度的。

正常來說，這道題感覺可以用莫隊搞，因為序列區間查詢且不帶修。

但是發現單次修改是 \(O(w(n))\) 的，為 \(a_i\) 的質因子個數，也就是接近 \(O(\ln n)\)。那么總的時間復雜度是 \(O(n\sqrt n\ln n)\)，還要取模，顯然過不去。

如何優化？

從值域入手，\(a_i\le 10^9\)。

所以考慮，對于 \(\le 1000\) 的質因子，有 \(168\) 個，我們直接暴力判斷，統計答案。這樣是 \(168(n+q)\) 的運算次數。

為了加速，將乘法取模改成除法。就是這么寫（不然會被卡常）：

int mul(int a,int b,int m)
{
	ull c=(ull)a*b-(ull)((long double)a/m*b+0.5L)*m;
	if(c<(ull)m) return c;
	return c+m;
}

那么對于 \(a_i\)，我們就可以將它所有 \(\le 1000\) 的質因子除去了。現在剩下的 \(a_i\) 只有三種可能：

1. \(a_i\) 為質數。
2. \(a_i\) 為兩個 \(>1000\) 且不同的質數相乘。
3. \(a_i\) 為某個 \(>1000\) 的質數的平方。

但是，它們的質因子個數都 \(\le 2\)。

那么此時就可以上莫隊了。

需要先用 Miller_rabin 算法判斷是否為質數，再用Pollard-Rho 算法求出所有質因子。為了避免用哈希表，我們將 \(a_i\) 的質因子離散化存下。

因為值域只有 \(10^9\)，所以 Miller-rabin 可以只用取 \(\{2,7,61\}\) 三個底數。此處時間復雜度為 \(O(n(V^{\frac 14}+\log n))\)。

然后莫隊就直接做了，但是有幾個注意事項：

1. 由于是乘積，當我們乘上一個 \(0\) 時，操作是無法逆向回來的。所以需要隨時保證動態區間的長度為正數。

   判斷 \(qr<l\) 時就先動左端點，否則就先動右端點。

2. 為了減小常數以通過題目，先將 \([1,n]\) 的逆元預處理出。

   然后在每一次從一個詢問挪到下一個詢問時，開一個桶記錄下被修改出現次數的元素，這樣就可以在區間挪動完畢后統一修改，而不用每一次挪動都更改而浪費大量時間。

然后就可以過了，時間復雜度 \(O(n(\sqrt n+V^{\frac 14}+\log n))\)。有點卡常，開 C++11 會更快。

提交記錄

16. P11675 [USACO25JAN] Photo Op G

難度：2

\(X\) 到 \(Y\) 的路徑一定可以拆成 \((X,x'),(x',y'),(y',Y)\)。

賽場上想的是，對于每一個 \(x\)，維護它可以到的 \([y_l,y_r]\)。想用吉司機線段樹去搞。但是沒想好怎么快速統答案，而且時間復雜度也不對，多了個 \(O(\log n)\)。

其實，維護 \([y_l,y_r]\) 可以用樹狀數組的。

對于邊 \((x_i,y_i)\)，將 \(x\in[1,x_i-1]\) 的上界定為 \(\min(y_r,y_i)\)。將 \(x\in[x_i+1,10^6]\) 的下界定為 \(\max(y_l,y_i)\)。維護上界就用樹狀數組維護后綴最小值，維護下界就用樹狀數組維護前綴最大值即可。

接下來需要從查詢答案入手。

對于 \(x\) 的可選區間 \([y_l,y_r]\)。

• 當 \(y_l>Y\) 時，此時選 \(y_l\) 最優，權值為 \(|y_l-Y|+|x-X|+\lfloor\sqrt{y_l^2+x^2}\rfloor\)。
• 當 \(y_r<Y\) 時，此時選 \(y_r\) 最優，權值為 \(|y_r-Y|+|x-X|+\lfloor\sqrt{y_r^2+x^2}\rfloor\)。
• 當 \(y_l\le Y\le y_r\) 時，此時選 \(Y\) 最優，權值為 \(|x-X|+\lfloor\sqrt{Y^2+x^2}\rfloor\)。

現在再畫出圖來，并計算出每一個 \(x\) 的 \([y_l,y_r]\)。

我們可以發現，\(x\) 的上下界都是非嚴格單增的。所以可以把可以從中間穿過的部分視為連通塊。（如下圖黃色部分，圖來自 @dahuiji 的題解）

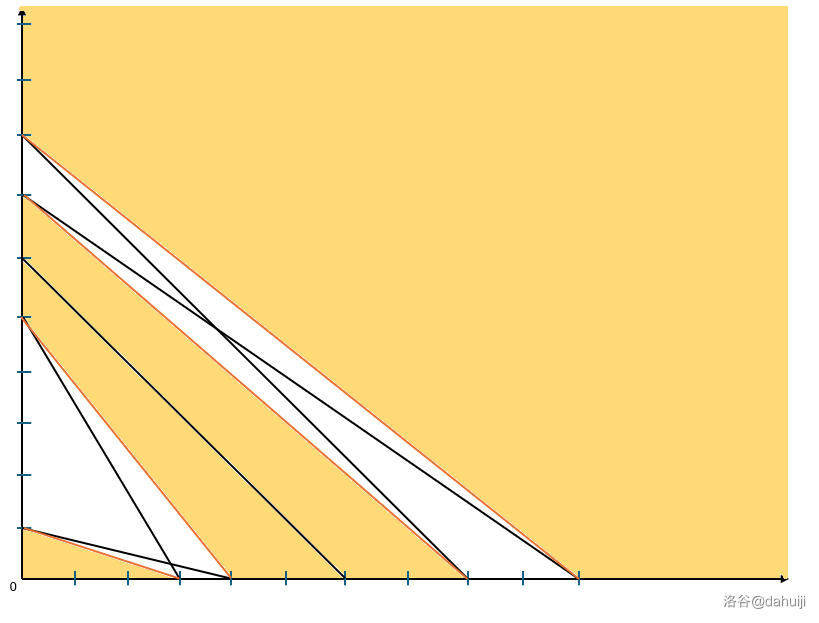
我們可以把所有 \(y_r<y_l\) 的 \(x\) 給刪去。

那么可能最優的 \(x'\) 就是 \(X\) 左邊（\(\le X\)）第一個仍存在的 \(x\) 和 \(X\) 右邊（\(>X\)）第一個仍存在的 \(x\)。可以根據單調性證明。分別代入 \([y_l,y_r]\) 求值。

但是可能還不夠優，就是當左邊的 \(x\) 和右邊的 \(x\) 的下界都 \(>Y\) 或上界都 \(<Y\) 時，此時可能存在另一個 \(x\) 使得選出的 \([y_l,y_r]\) 不同。

也就是當左邊的 \(x\) 和右邊的 \(x\) 的下界都 \(>Y\) 時，可能存在一個 \(x\) 的上界 \(<Y\) 或者包括 \(Y\)，此時可能選新的 \(x\) 會更優。

所以同樣，我們對于每一個 \(y\)，需要預處理出可選區間 \([x_l,x_r]\)。然后將 \(x_l>x_r\) 的 \(y\) 刪去。再將 \(Y\) 左邊（\(\le Y\)）第一個仍存在的 \(y\) 和 \(Y\) 右邊（\(>Y\)）第一個仍存在的 \(y\) 代入求值。

則答案就是上述四個值的最小值。

我們需要將 \(y_l>y_r\) 的 \(x\) 刪去，需要支持刪除。所以考慮用 set 維護。

時間復雜度 \(O(n\log n)\)。

提交記錄

17. P11673 [USACO25JAN] Median Heap G

難度：1

感覺中位數的題做法都差不多啊。

類似于AGC006D的做法，我們將 \(<m\) 的數定為 \(0\)，將\(\ge m\) 的數定為 \(1\)。

因為本題要求于 \(m\) 相等，所以改一下，我們讓 \(=m\) 的數為 \(1\)，\(>m\) 的數為 \(2\)。

然后初始化所有數都是 \(2\)。那么可以跑一個dp。

設 \(dp_{u,0/1/2}\) 表示讓 \(u\) 節點上傳 \(0/1/2\) 的最小代價。

然后傻傻的我還去枚舉每一種狀態，再討論。碼量和思維難度大，而且還容易寫錯。雖然最后寫對了，錯的地方不在這。但是有更簡便的寫法。

首先，對于葉子節點，我們設給它賦的值為 \(w_u\)。則對于 \(i\neq w_u\)，則初始化 \(dp_{u,i}=c_u\)，讓 \(dp_{u,w_u}=0\)。

然后轉移就可以枚舉左兒子的上傳值 \(i\)，右兒子的上傳值 \(j\) 和自己的值 \(k\)，再算出 \(i,j,k\) 的中位數更新。

int med(int i,int j,int k)//求中位數 
{
	return i+j+k-max({i,j,k})-min({i,j,k});
}
for(int i=0;i<3;i++)
{
	for(int j=0;j<3;j++)
	{
		for(int k=0;k<3;k++)
		{
			int mid=med(i,j,k);
			dp[u][mid]=min(dp[u][mid],dp[u<<1][i]+dp[u<<1|1][j]+w[u][k]);
		}
	}
}

然后將詢問離線下來，并按權值從小到大排序。將樹中的點按從小到大排序。

然后對于一次詢問 \(m\)，用指針維護，將 \(<m\) 的點的 \(w\) 值賦值為 \(0\)，將 \(=m\) 的點的值賦值為 \(1\)。

然后將所有 \(=m\) 的詢問計算完后，將所有賦值為 \(1\) 的節點賦值為 \(0\)。

因為樹高只有 \(O(\log n)\)。所以時間復雜度是 \(O(n+q\log n)\)。

提交記錄

18. P11676 [USACO25JAN] DFS Order P

難度：1

我們可以從dfs生成樹的方向去考慮。

我們發現，對于一棵dfs生成樹，如果 \(u\) 和 \(v\) 之間不是祖先關系則 \((u,v)\) 之間不能有連邊。否則可以有連邊。

現在回到題目。先考慮原圖沒有邊的情況。

因為要求dfs序為 \(\{1,2,...,n\}\)，所以考慮倒著dp。

設 \(dp_{i,j}\) 表示使得存在一棵dfs序為 \(\{i,i+1,...,j-1,j\}\) 的生成樹的最小代價。

現在枚舉點 \(i\)。考慮將后面的幾棵dfs生成樹合并起來，讓這些生成樹的根成為 \(i\) 的兒子。

首先初始化 \(dp_{i,i}=0\)。因為我可以讓 \(i\) 節點成為生成樹的葉子。

然后先考慮合并第一棵生成樹。為了滿足要求，則它的樹根一定是 \(i+1\)。

所以枚舉 \(k\) 表示這棵生成樹的dfs序為 \([i+1,k]\)，然后合并成一棵 \([i,k]\) 的生成樹，代價為 \(a_{i,i+1}\)。

所以有轉移 \(dp_{i,k}=\min_{k=i+1}^n dp_{i+1,k}+a_{i,i+1}\)。

但是還可能繼續合并，則下一棵合并的樹根為 \(k+1\)，然后又可以類似上述轉移。

所以總的dp轉移式子為：

時間復雜度 \(O(n^3)\)。

現在考慮有原邊的情況。先考慮將所有原邊刪去，代價和 \(sum=\sum {-a_{i,j}}\times [a_{i,j}<0]\)。那么現在加這一條邊的權值就是 \(a_{i,j}\)，也就相當于還原了這一條邊。

因為上文說了，dfs生成樹當 \(u,v\) 之間有祖先關系時，二者是可以在原圖上有連邊的。

所以將 \([i,j-1]\) 和 \([j,k]\) 合并起來時，可以從 \(i\) 向 \([j,k]\) 的點連邊。那么這中間先前就有的邊就可以還原。因為必須連 \((i,j)\)，所以只考慮 \(i\) 到 \([j+1,k]\) 的連邊中原本存在于原圖的邊的權值和。

用前綴和處理即可。

時間復雜度 \(O(n^3)\)。

提交記錄

19. P7834 [ONTAK2010] Peaks 加強版

難度：1

首先對于從 \(u\) 開始，通過 \(\le x\) 的路徑可以到達的點，考慮類似 [NOI2018] 歸程 的做法。

用Kruskal重構樹 將整個圖變成一個有 \(2n-1\) 個點的二叉樹。

現在我們要對這個樹的每一個點處理它這棵子樹葉子的第 \(k\) 大值。

我當時腦抽，想了個樹上啟發式合并+主席樹的做法，時空復雜度 \(O(n\log^2n)\)。然后加強版的 128MB 空間限制給我打醒了。

其實因為只用維護葉子，所以考慮用dfs序將所有葉子排序，這樣的話，一個點對應的子樹葉子就是一個連續的區間了。然后就可以用主席樹在序列上處理。

時間復雜度 \(O(q\log n)\)。

提交記錄

20. P2839 [國家集訓隊] middle

難度：2

設原序列為 \(A\)，排完序后為 \(A'\)。

感覺可以二分，因為是求中位數。將 \(<mid\) 的位置賦值為 \(-1\)，將 \(\ge mid\) 的位置賦值為 \(1\)。

然后對于一個區間 \([l,r]\)，當它的和 \(\ge 0\) 時就向上二分，否則就向下二分。

現在問題是如何在 \(O(\log n)\) 的時間內求出一個區間的和。

我們將題目給的區間 \(\{a,b,c,d\}\) 分成 \([a,b-1]、[b,c]、[c+1,d]\)。那么對于區間 \([b,c]\) 就是直接求和即可。對于區間 \([a,b-1]\) 就是求最大后綴。對于區間 \([c+1,d]\) 就是求最大前綴。

因為最終二分停下的值一定是序列中存在的一個值。所以考慮將原序列排序后，按下標，在 \([1,n]\) 中二分，每一次 \(mid\) 取 \(A'_i\)。這樣就可以保證二分的 \(mid\) 只有 \(n\) 個。

所以對這 \(n\) 個，每一個開一棵線段樹，維護最大前后綴以及和。將 \(\ge A'_i\) 的位置賦值為 \(1\)，將 \(<A'_i\) 的位置賦值為 \(-1\)。

但是 \(A'_i\) 和 \(A'_{i+1}\) 最后賦值出來的數組最多只有一個位置不同。所以考慮用主席樹去優化這一過程。

時間復雜度 \(O(n\log n+q\log^2n)\)，空間復雜度 \(O(n\log n)\)。

21. P7424 [THUPC 2017] 天天愛射擊

難度：0.5

可以對于每一個木板，二分它什么時候會被打掉。這里可以用主席樹去維護這個前綴和。

時間復雜度 \(O(n\log^2n)\)，因為主席樹的常數導致TLE。平均需要 3.0s，而實現只有 1.0s。

考慮用整體二分。對于每一次 \(\text{solve}(st,en,l,r)\)，表示考慮第 \(l\sim r\) 次射擊，對于 \(st\sim en\) 的木板是否被擊碎。

注意，這里的木板下標是會隨著二分而更改的。

設 \(l_i\) 和 \(r_i\) 為第 \(i\) 塊木板的左右位置，\(k_i\) 為耐久。

將第 \(l\sim mid\) 次射擊存入樹狀數組。然后枚舉木板，如果 \([l_i,r_i]\) 的被射擊次數 \(\ge k_i\)，則將 \(i\) 歸為左邊；否則讓 $k_i\gets k_i-[l_i,r_i]被射擊次數 $，然后歸為右邊。

時間復雜度 \(O(n\log^2n)\)。但因為其優秀的常數，使得它能在平均300ms 跑過。