大O復(fù)雜度表示法

　　大 O 時(shí)間復(fù)雜度實(shí)際上并不具體表示代碼真正的執(zhí)行時(shí)間，而是表示代碼執(zhí)行時(shí)間隨數(shù)據(jù)規(guī)模增長(zhǎng)的變化趨勢(shì)，
　　所以，也叫作漸進(jìn)時(shí)間復(fù)雜度（asymptotic time complexity），簡(jiǎn)稱時(shí)間復(fù)雜度。

時(shí)間復(fù)雜度分析

　　1. 只關(guān)注循環(huán)執(zhí)行次數(shù)最多的一段代碼　　

　　　　大 O 這種復(fù)雜度表示方法只是表示一種變化趨勢(shì)。我們通常會(huì)忽略掉公式中的常量、低階、系數(shù)，只需要記錄一個(gè)最大階的量級(jí)就可以了。

　　　　所以，我們?cè)诜治鲆粋€(gè)算法、一段代碼的時(shí)間復(fù)雜度的時(shí)候，也只關(guān)注循環(huán)執(zhí)行次數(shù)最多的那一段代碼就可以了。

　　2. 加法法則：總復(fù)雜度等于量級(jí)最大的那段代碼的復(fù)雜度　

　　　　總的時(shí)間復(fù)雜度就等于量級(jí)最大的那段代碼的時(shí)間復(fù)雜度。

　　　　比如說(shuō)，如果初步分析出復(fù)雜度為O(n+2n+n^2),那么它的總時(shí)間復(fù)雜度為O(n^2)。

　　　　那我們將這個(gè)規(guī)律抽象成公式就是：如果 T1(n)=O(f(n))，T2(n)=O(g(n))；

　　　　那么 T(n) = T1(n)+T2(n) = max(O(f(n)), O(g(n))) = O(max(f(n), g(n))).

　　3. 乘法法則：嵌套代碼的復(fù)雜度等于嵌套內(nèi)外代碼復(fù)雜度的乘積

　　　　落實(shí)到具體的代碼上，我們可以把乘法法則看成是嵌套循環(huán)，我舉個(gè)例子給你解釋一下。

int cal(int n) {
   int ret = 0; 
   int i = 1;
   for (; i < n; ++i) {
     ret = ret + f(i);
   } 
 } 
 
 int f(int n) {
  int sum = 0;
  int i = 1;
  for (; i < n; ++i) {
    sum = sum + i;
  } 
  return sum;
 }

　　　　T1(n) = O(n)。T2(n) = O(n)。

　　　　整個(gè) cal() 函數(shù)的時(shí)間復(fù)雜度就是，T(n) = T1(n) * T2(n) = O(n*n) = O(n2)。

幾種常見(jiàn)時(shí)間復(fù)雜度實(shí)例分析

對(duì)于剛羅列的復(fù)雜度量級(jí)，我們可以粗略地分為兩類，多項(xiàng)式量級(jí)和非多項(xiàng)式量級(jí)。其中，非多項(xiàng)式量級(jí)只有兩個(gè)：O(2^n)和O(n!)。

當(dāng)數(shù)據(jù)規(guī)模 n 越來(lái)越大時(shí)，非多項(xiàng)式量級(jí)算法的執(zhí)行時(shí)間會(huì)急劇增加，求解問(wèn)題的執(zhí)行時(shí)間會(huì)無(wú)限增長(zhǎng)。所以，非多項(xiàng)式時(shí)間復(fù)雜度的算法其實(shí)是非常低效的算法。

因此，關(guān)于 NP 時(shí)間復(fù)雜度我就不展開(kāi)講了。我們主要來(lái)看幾種常見(jiàn)的多項(xiàng)式時(shí)間復(fù)雜度。

1. O(1)

　　稍微總結(jié)一下，只要代碼的執(zhí)行時(shí)間不隨 n 的增大而增長(zhǎng)，這樣代碼的時(shí)間復(fù)雜度我們都記作 O(1)。

　　或者說(shuō)，一般情況下，只要算法中不存在循環(huán)語(yǔ)句、遞歸語(yǔ)句，即使有成千上萬(wàn)行的代碼，其時(shí)間復(fù)雜度也是Ο(1)。

 int i = 8;
 int j = 6;
 int sum = i + j;

2. O(logn)、O(nlogn)

　　以2為底

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

　　　以3為底

 i=1;
 while (i <= n)  {
   i = i * 3;
 }

　　實(shí)際上，不管是以 2 為底、以 3 為底，還是以 10 為底，我們可以把所有對(duì)數(shù)階的時(shí)間復(fù)雜度都記為 O(logn)。　　

　　因?yàn)椋趯?duì)數(shù)階時(shí)間復(fù)雜度的表示方法里，我們忽略對(duì)數(shù)的“底”，統(tǒng)一表示為 O(logn)。

　　如果你理解了我前面講的 O(logn)，那 O(nlogn) 就很容易理解了。還記得我們剛講的乘法法則嗎？

　　如果一段代碼的時(shí)間復(fù)雜度是 O(logn)，我們循環(huán)執(zhí)行 n 遍，時(shí)間復(fù)雜度就是 O(nlogn) 了。

　　而且，O(nlogn) 也是一種非常常見(jiàn)的算法時(shí)間復(fù)雜度。比如，歸并排序、快速排序的時(shí)間復(fù)雜度都是 O(nlogn)。

3. O(m+n)、O(m*n)

我們?cè)賮?lái)講一種跟前面都不一樣的時(shí)間復(fù)雜度，代碼的復(fù)雜度由兩個(gè)數(shù)據(jù)的規(guī)模來(lái)決定。代碼如下：

 1 int cal(int m, int n) {
 2   int sum_1 = 0;
 3   int i = 1;
 4   for (; i < m; ++i) {
 5     sum_1 = sum_1 + i;
 6   }
 7 
 8   int sum_2 = 0;
 9   int j = 1;
10   for (; j < n; ++j) {
11     sum_2 = sum_2 + j;
12   }
13 
14   return sum_1 + sum_2;
15 }

　　從代碼中可以看出，m 和 n 是表示兩個(gè)數(shù)據(jù)規(guī)模。我們無(wú)法事先評(píng)估 m 和 n 誰(shuí)的量級(jí)大，所以我們?cè)诒硎緩?fù)雜度的時(shí)候，就不能簡(jiǎn)單地利用加法法則，省略掉其中一個(gè)。所以，上面代碼的時(shí)間復(fù)雜度就是 O(m+n)。

　　針對(duì)這種情況，原來(lái)的加法法則就不正確了，我們需要將加法規(guī)則改為：T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法則繼續(xù)有效：T1(m)*T2(n) = O(f(m) * f(n))。 

空間復(fù)雜度分析

前面我講過(guò)，時(shí)間復(fù)雜度的全稱是漸進(jìn)時(shí)間復(fù)雜度，表示算法的執(zhí)行時(shí)間與數(shù)據(jù)規(guī)模之間的增長(zhǎng)關(guān)系。

類比一下，空間復(fù)雜度（asymptotic space complexity)，全稱就是漸進(jìn)空間復(fù)雜度，表示算法的存儲(chǔ)空間與數(shù)據(jù)規(guī)模之間的增長(zhǎng)關(guān)系。

具體例子如下：

 1 void print(int n) {
 2   int i = 0;
 3   int[] a = new int[n];
 4   for (i; i <n; ++i) {
 5     a[i] = i * i;
 6   }
 7 
 8   for (i = n-1; i >= 0; --i) {
 9     print out a[i]
10   }
11 }

　　跟時(shí)間復(fù)雜度分析一樣，我們可以看到，第 2 行代碼中，我們申請(qǐng)了一個(gè)空間存儲(chǔ)變量 i，但是它是常量階的，跟數(shù)據(jù)規(guī)模 n 沒(méi)有關(guān)系，所以我們可以忽略。

　　第 3 行申請(qǐng)了一個(gè)大小為 n 的 int 類型數(shù)組，除此之外，剩下的代碼都沒(méi)有占用更多的空間，所以整段代碼的空間復(fù)雜度就是 O(n)。

　　我們常見(jiàn)的空間復(fù)雜度就是 O(1)、O(n)、O(n^2)，像 O(logn)、O(nlogn)這樣的對(duì)數(shù)階復(fù)雜度平時(shí)都用不到。

　　而且，空間復(fù)雜度分析比時(shí)間復(fù)雜度分析要簡(jiǎn)單很多。所以，對(duì)于空間復(fù)雜度，掌握剛我說(shuō)的這些內(nèi)容已經(jīng)足夠了。

內(nèi)容小結(jié)

　　復(fù)雜度也叫漸進(jìn)復(fù)雜度，包括時(shí)間復(fù)雜度和空間復(fù)雜度，用來(lái)分析算法執(zhí)行效率與數(shù)據(jù)規(guī)模之間的增長(zhǎng)關(guān)系，可以粗略地表示，越高階復(fù)雜度的算法，執(zhí)行效率越低。

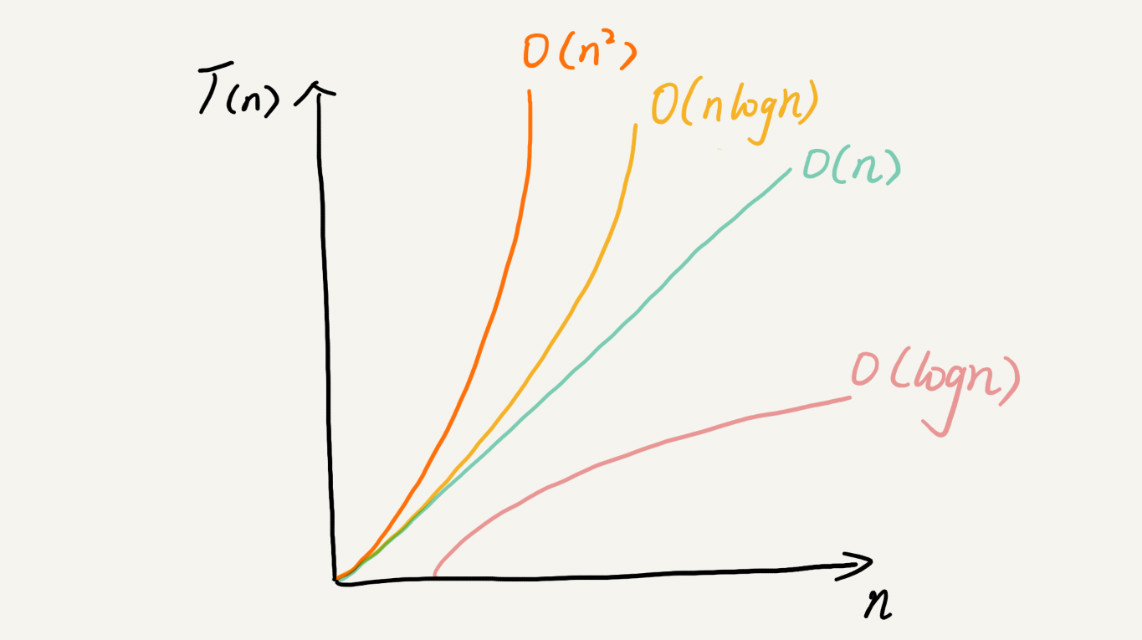
　　常見(jiàn)的復(fù)雜度并不多，從低階到高階有：O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)。之后你就會(huì)發(fā)現(xiàn)幾乎所有的數(shù)據(jù)結(jié)構(gòu)和算法的復(fù)雜度都跑不出這幾個(gè)。