2025.8.18校隊題單分享+總結
T1
P10804 [CEOI 2024] 玩具謎題
題目描述
CEOI 2024 的命題人 Ben 從科學委員會收到了一份禮物——一個玩具。這個玩具是個謎題,可以想象成一個 \(H\) 行 \(W\) 列的網格,上面放著一個金屬物體。這個金屬物體由兩部分組成:一個橫向的 \(1\) 行 \(K\) 列的部分和一個縱向的 \(L\) 行 \(1\) 列的部分,這兩部分松散地連接在一起。它們都不能旋轉,但可以在網格內水平或垂直滑動,只要它們始終重疊在一個方格上。
網格里還有一些障礙物。金屬物體的任何部分都不能穿過障礙物,更糟糕的是,它們也不能(即使部分)移出網格。Ben 的任務是將金屬物體從指定起始位置移動到(可能不同的)目標位置,使得兩部分重疊在指定的目標方格上。
然而,Ben 玩這個玩具已經有一段時間了,還沒有解開謎題。事實上,他開始懷疑組織者在捉弄他,給了他一個無解的謎題。因此,他向你求助,想知道這個謎題是否有解。
輸入格式
輸入的第一行包含四個空格分隔的整數 \(W, H, K, L\),分別表示謎題的寬度、高度、橫向部分的寬度和縱向部分的高度。第二行包含四個整數 \(x_h, y_h, x_v, y_v\),表示橫向部分最左上角方格的坐標和縱向部分最左上角方格的坐標。
行從上到下編號為 \(0\) 到 \(H-1\),列從左到右編號為 \(0\) 到 \(W-1\)。\(x\) 坐標表示列號,\(y\) 坐標表示行號。
接下來的 \(H\) 行每行包含 \(W\) 個字符,表示網格。字符 . 表示空方格,字符 X 表示障礙物,字符 * 表示目標方格。
保證金屬物體的初始位置合法,即兩部分重疊在一個方格上,并且兩部分不與障礙物重疊也不超出網格。
只有一個目標方格,即玩具中只有一個字符 *,它可能與金屬物體的初始位置重疊。
輸出格式
如果可以將金屬物體移動到目標方格,則輸出一行 YES,否則輸出 NO。
輸入輸出樣例 #1
輸入 #1
4 3 2 2
0 1 0 0
.X.*
....
...X
輸出 #1
YES
輸入輸出樣例 #2
輸入 #2
2 3 2 3
0 1 0 0
.X
.*
.X
輸出 #2
NO
說明/提示
樣例解釋 1
初始狀態如下:
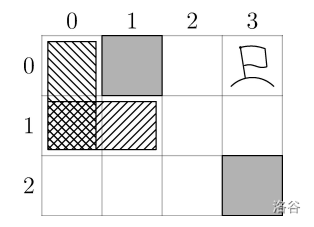
我們可以先將縱向部分向下移動一格,然后盡可能地交替移動橫向和縱向部分,直到無法繼續。接著,我們可以將縱向部分向上并向右移動,到達目標方格,最后將橫向部分向上移動,也到達目標方格。
樣例解釋 2
無法移動縱向部分而不碰到障礙物,因此永遠無法到達目標方格。
對于所有輸入數據,滿足:
- \(2 \leq W, H \leq 1\,500\)
- \(2 \leq K \leq W, 2 \leq L \leq H\)
- \(0 \leq x_h \leq W - K, 0 \leq y_h \leq H - 1\)
- \(0 \leq x_v \leq W - 1, 0 \leq y_v \leq H - L\)
詳細子任務附加限制及分值如下表所示。
| 子任務 | 附加限制 | 分值 |
|---|---|---|
| \(1\) | \(W, H \le 50\) | \(14\) |
| \(2\) | \(W, H \le 90\) | \(21\) |
| \(3\) | \(W, H \le 300, K, L \le 10\) | \(9\) |
| \(4\) | \(W, H \le 360\) | \(29\) |
| \(5\) | 無附加限制 | \(27\) |
先暴力,狀態是橫著的和豎著的的左上角坐標,如題面所示,但是這樣的時間復雜度是 \(O(H^2M^2)\)
通過枚舉焦點減少狀態量,交點的移動其實就可以判斷出橫豎的移動,交點左右動就是豎著的左右動,交點上下移動就是橫著的上下動,再加上前綴后綴預處理,時間復雜度就降成了 \(O(H \times M)\) ;
給一個代碼:
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N = 1510;
int n, m, K, L;
int sx, sy, tx, ty;
int Dx[4] = {-1, 0, 1, 0};
int Dy[4] = {0, 1, 0, -1};
struct Node1
{
int l, r;
};
struct Node2
{
Node1 X, Y;
};
char edge[N][N];
Node2 f[N][N];
bool st[N][N];
bool bfs()
{
queue<pair<int, int>> q;
q.push({sx, sy});
st[sx][sy] = true;
while(q.size())
{
pair<int, int> tmp = q.front();
q.pop();
int x = tmp.x, y = tmp.y;
if(x == tx && y == ty) return true;
for(int i = 0 ; i < 4 ; i ++ )
{
int dx = x + Dx[i], dy = y + Dy[i];
if((dx >= 1 && dx <= n && dy >= 1 && dy <= m && edge[dx][dy] != 'X' && !st[dx][dy]) == false) continue;
if(dy == y && (min(f[dx][dy].X.r, f[x][y].X.r) - max(f[dx][dy].X.l, f[x][y].X.l) + 1 >= K))
{
q.push({dx, dy});
st[dx][dy] = true;
}else if(dx == x && (min(f[x][y].Y.r, f[dx][dy].Y.r) - max(f[dx][dy].Y.l, f[x][y].Y.l) + 1 >= L))
{
q.push({dx, dy});
st[dx][dy] = true;
}
}
}
return false;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> m >> n >> K >> L;
int tmp = 0;
cin >> tmp >> sx >> sy >> tmp;
sx ++ ;
sy ++ ;
for(int i = 0 ; i <= n + 1 ; i ++ )
for(int j = 0 ; j <= m + 1 ; j ++ )
{
if(i >= 1 && i <= n && j >= 1 && j <= m) cin >> edge[i][j];
else edge[i][j] = 'X';
if(edge[i][j] == '*') tx = i, ty = j;
}
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = 1 ; j <= m ; j ++ )
if(edge[i][j] != 'X')
f[i][j].X.l = (edge[i][j - 1] == 'X' ? j : f[i][j - 1].X.l);
for(int j = m ; j >= 1 ; j -- )
if(edge[i][j] != 'X')
f[i][j].X.r = (edge[i][j + 1] == 'X' ? j : f[i][j + 1].X.r);
}
for(int j = 1 ; j <= m ; j ++ )
{
for(int i = 1 ; i <= n ; i ++ )
if(edge[i][j] != 'X')
f[i][j].Y.l = (edge[i - 1][j] == 'X' ? i : f[i - 1][j].Y.l);
for(int i = n ; i >= 1 ; i -- )
if(edge[i][j] != 'X')
f[i][j].Y.r = (edge[i + 1][j] == 'X' ? i : f[i + 1][j].Y.r);
}
if(bfs()) cout << "YES";
else cout << "NO";
return 0;
}
T2
P6803 [CEOI 2020] 星際迷航
題目背景
原時空限制:0.2s,32m
題目描述
星際聯邦由 \(N\) 顆行星組成,分別編號為 \(1 \sim N\)。一些行星間由星際通道相連。通過這些星際通道,飛船可以在短時間內往返于各星球之間。整個星際聯邦中恰好有 \(N-1\) 條星際通道,并且通過這些星際通道,任意兩顆行星之間均能相互抵達。
除了我們所處的宇宙之外,還有 \(D\) 個平行宇宙,這些平行宇宙是我們的宇宙的完全復刻,它們的行星,星際通道都和我們的完全相同。我們將這些平行宇宙編號為 \(1 \sim D\)(我們的宇宙編號為 \(0\)),記第 \(i\) 個宇宙的第 \(x\) 顆行星為 \(P_{x}^i\)。通過星門,我們可以在這些平行宇宙間穿梭。\(\forall i \in [0,D)\),我們將選擇一個 \(A_i\) 和一個 \(B_i\)(要求 \(1 \leq A_i,B_i \leq N\)),在 \(P_{A_i}^i\) 和 \(P_{B_i}^{i+1}\) 之間搭建一個單向(只能從 \(P_{A_i}^i\) 前往 \(P_{B_i}^{i+1}\))星門。
當所有的星門都準備就緒后,聯邦星艦 Batthyány 號將會開始它的處女航,它目前正環繞著 \(P_1^0\) 行星。ágnes 艦長準備和 Gábor 中尉玩這樣一個游戲:兩個人交替選擇星艦接下來前往的目的地,要求該目的地可以通過星際通道或星門直接抵達。他們希望每次前往的星球都是之前未抵達過的。即,如果星艦抵達了 \(P_{x}^i\),他們將不再經過這個星球(但是可以抵達 \(x\) 在其他平行宇宙中的相應星球)。由 ágnes 艦長作為先手開始游戲,Gábor 中尉作為后手,當一位玩家在他的回合中,不能選擇一個合法的目的地時,他就輸掉了游戲。
艦長和中尉都是絕對聰明的,他們知道所有星際通道和星門的排布方案,并且他們每次都按照最優方案行動。你需要求出,有多少種布置星門的方案,使得作為先手的 ágnes 艦長必勝?兩種布置星門的方案是不同的,當且僅當存在一個整數 \(i\),使得 \(A_i\) 或 \(B_i\) 不同。
輸入格式
第一行兩個整數 \(N,D\),分別代表星際聯邦擁有的行星數和平行宇宙的數量。
接下來 \(N-1\) 行,每行兩個整數 \(u,v\),表示 \(\forall i \in [0,D]\),\(P_u^i,P_v^i\) 之間有星際通道相連。
輸出格式
輸出能使艦長必勝的星門布置方案數對 \(10^9+7\) 取模的結果。
輸入輸出樣例 #1
輸入 #1
3 1
1 2
2 3
輸出 #1
4
說明/提示
樣例解釋
共有 \(3 \times 3=9\) 種本質不同的布置星門的方案,下面列出四種艦長必勝的情況。
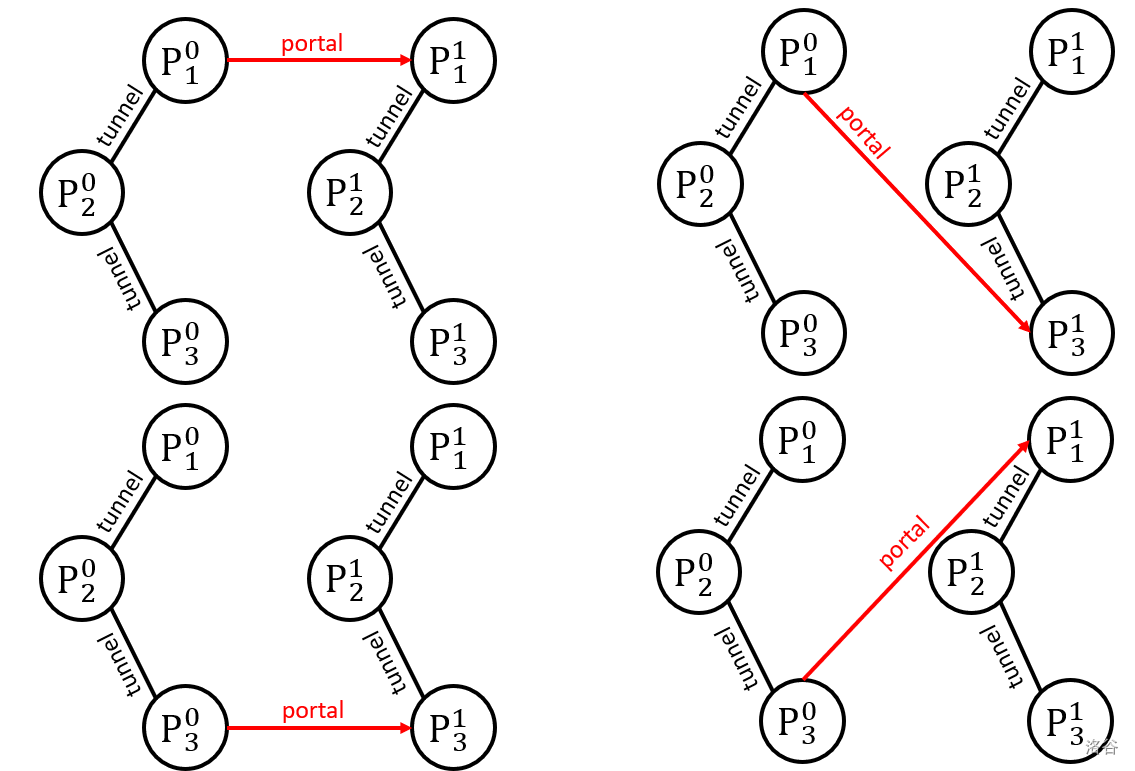
子任務
所有數據均滿足:\(1 \leq N \leq 10^5\),\(1 \leq D \leq 10^{18}\),\(1 \leq u,v \leq N\)。
各子任務的約束條件如下:
| 子任務編號 | 分值 | 約束 |
|---|---|---|
| \(1\) | \(0\) | 樣例 |
| \(2\) | \(7\) | \(N=2\) |
| \(3\) | \(8\) | \(N \leq 100\),\(D=1\) |
| \(4\) | \(15\) | \(N \leq 1000\),\(D=1\) |
| \(5\) | \(15\) | \(D=1\) |
| \(6\) | \(20\) | \(N \leq 1000\),\(D \leq 10^5\) |
| \(7\) | \(20\) | \(D \leq 10^5\) |
| \(8\) | \(15\) | 無特殊約束 |



 浙公網安備 33010602011771號
浙公網安備 33010602011771號