2025.8.15校隊題單分享+總結

T1

Cow at Large G

題目描述

最后，Bessie 被迫去了一個遠方的農場。這個農場包含 \(N\) 個谷倉（\(2 \le N \le 10^5\)）和 \(N-1\) 條連接兩個谷倉的雙向隧道，所以每兩個谷倉之間都有唯一的路徑。每個只與一條隧道相連的谷倉都是農場的出口。當早晨來臨的時候，Bessie 將在某個谷倉露面，然后試圖到達一個出口。

但當 Bessie 露面的時候，她的位置就會暴露。一些農民在那時將從不同的出口谷倉出發嘗試抓住 Bessie。農民和 Bessie 的移動速度相同（在每個單位時間內，每個農民都可以從一個谷倉移動到相鄰的一個谷倉，同時 Bessie 也可以這么做）。農民們和 Bessie 總是知道對方在哪里。如果在任意時刻，某個農民和 Bessie 處于同一個谷倉或在穿過同一個隧道，農民就可以抓住 Bessie。反過來，如果 Bessie 在農民們抓住她之前到達一個出口谷倉，Bessie 就可以逃走。

Bessie 不確定她成功的機會，這取決于被雇傭的農民的數量。給定 Bessie 露面的谷倉K，幫助 Bessie 確定為了抓住她所需要的農民的最小數量。假定農民們會自己選擇最佳的方案來安排他們出發的出口谷倉。

輸入格式

輸入的第一行包含 \(N\) 和 \(K\)。接下來的 \(N - 1\) 行，每行有兩個整數（在 \(1\sim N\) 范圍內）描述連接兩個谷倉的一條隧道。

輸出格式

輸出為了確保抓住 Bessie 所需的農民的最小數量。

輸入輸出樣例 #1

輸入 #1

輸出 #1

先模擬一下樣例:

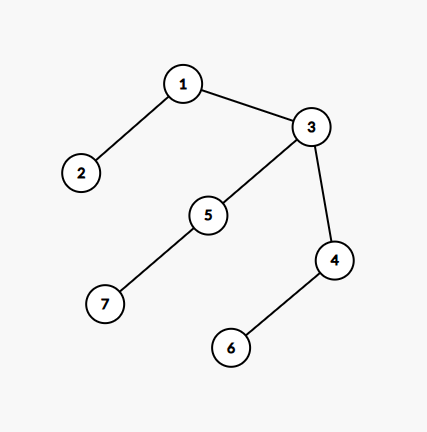
我們在葉子節點上放三個農民，分別在 \(2\), \(6\), \(7\) 上，剛開始是這樣的：

接著因為 \(2\) 號點上有農民，所以 \(Bessie\) 只能去 \(3\), 最后：

\(Bessie\) 被困死了，綜上三個村民是可行的，我們也可以證明兩個村民是不行的，詳見其他題解區，我們怎么正向的去做這道題呢，我們的村民一定是從葉子走到根的(這里的樹是以 \(k\) 為根的）這樣子能縮包圍圈，所以一定可行，那我們一定可以有更優解，具體考慮從葉子節點不斷標記，直到遇到 \(Bessie\), 接下來 \(Bessie\) 走到的被標記的點的個數就是能困住他的需要的最少的農民個數，這個東西就感性理解就好，主要是我自己也不太會證，這個打標記的做法有很多種，我用的是遍歷兩次，第一次記錄父節點，第二次暴力往上推就好了，其他的題解還給了下面兩種方法：

在第一遍遍歷的時候用一個棧記錄路徑，每次找到葉子節點就在棧頂的位置 \(\times 0.5\) 處的節點做標記。
在第一遍遍歷的時候記錄一個 \(down\) 數組表示離這里最近的葉子節點的距離。在第二遍遍歷的時候，如果當前的深度 ≥ 當前節點的 \(down\) 值，就算遇到了標記。

給一個代碼：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;
const int M = N << 1;

int n, k;
int p[N], deep[N] = {-1}, ans;
bool vis[N], st[N];
int h[N], e[M], ne[M], idx;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs1(int u, int fa)
{
	vis[u] = 1;
	p[u] = fa;
	deep[u] = deep[fa] + 1;
	for(int i = h[u] ; i != -1 ; i = ne[i])
	{
	    int j = e[i];
	    if(j == fa) continue;
		vis[u] = 0;
		dfs1(j, u);
	}
}

void dfs2(int u, int fa)
{
	if(st[u])
	{
		ans ++ ;
		return;
	}
	for(int i = h[u] ; i != -1 ; i = ne[i])
	{
	    int j = e[i];
	    if(j == fa) continue;
		dfs2(j, u);
	}
}

int main()
{
	cin >> n >> k;
	p[k] = 0;
	memset(h, -1, sizeof h);
	for(int i = 1 ; i < n ; i ++ )
	{
	    int a, b;
		cin >> a >> b;
		add(a, b);
		add(b, a);
	}
	dfs1(k, 0);
	for(int i = 1 ; i <= n ; i ++ )
		if(vis[i])
		{
			int tmp = i;
			for(int j = 1 ; j <= deep[i] / 2 ; j ++ ) tmp = p[tmp];
			st[tmp] = 1;
		}
	dfs2 (k, 0);
	cout << ans;
	return 0;
}

T2

P9017 [USACO23JAN] Lights Off G

題目描述

給定正整數 \(N\)，和兩個長為 \(N\) 的 \(01\) 序列 \(a\) 和 \(b\)。定義一次操作為：

將 \(b\) 序列中的一個值翻轉（即 \(0\) 變成 \(1\)，\(1\) 變成 \(0\)，下同）。
對于 \(b\) 序列中每個值為 \(1\) 的位置，將 \(a\) 序列中對應位置的值翻轉。
將 \(b\) 序列向右循環移位 \(1\) 位。即若當前 \(b\) 序列為 \(b_1b_2\cdots b_{n}\)，則接下來變為 \(b_{n}b_1b_2\cdots b_{n-1}\)。

有 \(T\) 次詢問，對每一次詢問，你需要回答出至少需要幾次操作，才能使 \(a\) 序列中每一個位置的值都變為 \(0\)。

輸入格式

第一行為兩個正整數 \(T,N\;(1\leq T\leq 2\times10^5,2\leq N\leq 20)\)。

接下來 \(T\) 行，每行為兩個長為 \(N\) 的 \(01\) 序列 \(a\) 和 \(b\)，表示一組詢問。

輸出格式

共 \(T\) 行，每行一個正整數，表示最少的操作次數。

輸入輸出樣例 #1

輸入 #1

輸出 #1

輸入輸出樣例 #2

輸入 #2

1 10
1100010000 1000011000

輸出 #2

若某一答案為 \(k\)，我們可以先把 \(b\) 中每個 \(1\) 可以改變的 \(k\) 個位置反轉，然后第 \(i\) 次操作就只改變了它后的 \(k?i+1\) 位的狀態。所以問題轉化為給一個二進制串，問是否能 \(k\) 次操作給他變成全零。用狀壓 DP \(O(n^2 \times 2^n)\) 預處理，之后對于每一組詢問枚舉判斷就好了，總時間復雜度 \(O(T \times n^2 + n^2 \times 2^n)\)。

代碼

#include <bits/stdc++.h>

#define int long long

using namespace std;

int T, n;
int g[45][22], mask[22];
bool f[45][1 << 21];
string s, t;

int calc(int s, int t)
{
    if(s == 0) return 0;
    for(int i = 1 ; i <= 2 * n ; i ++ )
    {
        int vis = s;
        for(int j = 0 ; j < n ; j ++ )
            if(t & (1 << j))
                vis = vis ^ g[i][j];
        if(f[i][vis]) return i;
    }
}

signed main() 
{
    f[0][0] = 1;
    cin >> T >> n;
    for (int i = 0 ; i <= n ; i ++ ) mask[i] = 1 << i;
    int N = 1 << n;
    for(int k = 0 ; k < n ; k ++ )
        for(int i = 1; i <= 2 * n ; i ++ )
            for(int j = 0; j < i ; j ++ ) 
                g[i][k] ^= mask[(k + j) % n];
    for(int i = 1 ; i <= 2 * n ; i ++ ) 
        for(int j = 0 ; j < N ; j ++ ) 
        {
            if(!f[i - 1][j]) continue;
            for(int k = 0 ; k < n ; k ++ )
            {
                int vis = j;
                vis ^= g[i][k];
                f[i][vis] = 1;
            }
        }
    while (T --)
    {
        cin >> s >> t;
        int S = 0, T = 0;
        for(int i = 0 ; i < n ; i ++ )
        {
            if (s[i] == '1') S ^= (1 << i);
            if (t[i] == '1') T ^= (1 << i);
        }
        cout << calc(S, T) << endl;
    }
    return 0;
}

T3

P9016 [USACO23JAN] Find and Replace G

題目描述

你有一個字符串 \(S\)，最開始里面只有一個字符 \(\text{a}\)，之后你要對這個字符串進行若干次操作，每次將其中每一個字符 \(c\) 替換成某個字符串 \(s\)（例如對于字符串 \(\text{ball}\)，將其中的 \(\text{l}\) 替換為 \(\text{na}\) 后將會變為 \(\text{banana}\)）。現在給定 \(l,r\)，你需要輸出 \(S_{l\ldots r}\)（也就是 \(S\) 的第 \(l\) 個字符到第 \(r\) 個字符對應的子串）是什么。

輸入格式

第一行三個整數，分別表示 \(l,r\) 和操作次數。

輸出格式

一行，表示對應的子串。

輸入輸出樣例 #1

輸入 #1

3 8 4
a ab
a bc
c de
b bbb

輸出 #1

bdebbb

說明/提示

\(l,r\le\min(\left | S \right |,10^{18})\)；

\(r-l+1\le2\times10^5\)；

\(\sum\left | s \right | \le 2\times 10^5\)。

所有的字符串都只包含小寫字母 \(\text{a}-\text{z}\)。

其中對于測試點 \(2-7\)，滿足：

\(r-l+1\le2000\)，\(\sum\left | s \right | \le 2000\)。

設 \(f_{i,j}\) 為第 \(i\) 時間，以字符 \(j\) 展開之后的字符，然后暴力展開，考慮一下優化：

首先就是記憶化
小于 \(l\) 跳過
大于 \(r\) 直接輸出，程序結束

這樣就做完啦，簡單粗暴，比別人的都簡單~~

給個代碼：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 2e5 + 110;
const int K = 30;

int n;
int L, R;
int e[N][K], p[N][K];
int size_[N][K];
string s[N];

void build() 
{
    for(int r = 0 ; r < K ; r ++ ) e[n + 1][r] = n + 1, size_[n + 1][r] = 1, p[n + 1][r] = n + r + 1;
    for(int i = n ; i >= 1 ; i -- ) 
    {
        for(int r = 0 ; r < K ; r ++ ) 
        {
            if(e[i][r] == 0) p[i][r] = n + r + 1, e[i][r] = i + 1;
            for(char& ch : s[p[i][r]]) size_[i][r] = min((int)1e18, size_[i][r] + size_[e[i][r]][ch - 'a']);
        }
    }
}
int now = 0;
char ans[N], *tmp = ans;

void print(int r) 
{
    *tmp++ = r + 'a';
    if(++now >= R) cout << ans << endl, exit(0);
}

char *st[N][K], *ed[N][K];

void dfs(int u, int r)
{
    if(now + size_[u][r] < L)
    {
        now += size_[u][r];
        return;
    }
    if(st[u][r]) 
    {
        for(char* p = st[u][r] ; p != ed[u][r] ; p ++ ) print(*p - 'a');
        return;
    }
    if(now >= L) st[u][r] = tmp;
    if(u == n + 1) print(r);
    else for(char& ch : s[p[u][r]]) dfs(e[u][r], ch - 'a');
    ed[u][r] = tmp;
}

signed main() 
{
    cin >> L >> R >> n;
    for(int i = 1 ; i <= n ; i ++ )
    {
        char ch;
        cin >> ch >> s[i];
        e[i][ch - 'a'] = i + 1;
        p[i][ch - 'a'] = i;
    }
    for(int i = n + 1 ; i <= n + 26 ; i ++ ) s[i] = i - n - 1 + 'a';
    build();
    dfs(1, 0);
    cout << ans;
    return 0;
}

P11843 [USACO25FEB] The Best Subsequence G

題目描述

Farmer John 有一個長為 \(N\) 的位串（\(1 \leq N \leq 10^9\)），初始時全部為零。

他將首先按順序對字符串執行 \(M\) 次更新（\(1 \leq M \leq 2 \cdot 10^5\)）。每次更新會翻轉從 \(l\) 到 \(r\) 的每個字符。具體地說，翻轉一個字符會將其從 \(0\) 變為 \(1\)，或反之。

然后，他會進行 \(Q\) 次查詢（\(1 \leq Q \leq 2 \cdot 10^5\)）。對于每個查詢，他要求你輸出由從 \(l\) 到 \(r\) 的子串中的字符組成的長為 \(k\) 的字典序最大子序列。如果你的答案是一個位串 \(s_1s_2 \dots s_k\)，則輸出 \(\sum_{i=0}^{k-1} 2^i \cdot s_{k-i}\)（即將其解釋為二進制數時的值）模 \(10^9+7\) 的余數。

一個字符串的子序列是可以從中通過刪除一些或不刪除字符而不改變余下字符的順序得到的字符串。

我們知道，字符串 \(A\) 的字典序大于長度相等的字符串 \(B\)，當且僅當在第一個 \(A_i \neq B_i\) 的位置 \(i\) 上（如果存在），我們有 \(A_i > B_i\)。

輸入格式

輸入的第一行包含 \(N\)，\(M\) 和 \(Q\)。

以下 \(M\) 行，每行包含兩個整數 \(l\) 和 \(r\)（\(1 \leq l \leq r \leq N\)），為每次更新的端點。

以下 \(Q\) 行，每行包含三個整數 \(l\)，\(r\) 和 \(k\)（\(1 \leq l \leq r \leq N\)，\(1 \leq k \leq r - l + 1\)），為每個查詢的端點和子序列的長度。

輸出格式

輸出 \(Q\) 行。第 \(i\) 行包含第 \(i\) 個查詢的答案。

輸入輸出樣例 #1

輸入 #1

輸出 #1

輸入輸出樣例 #2

輸入 #2

9 1 1
7 9
1 8 8

輸出 #2

輸入輸出樣例 #3

輸入 #3

30 1 1
1 30
1 30 30

輸出 #3

73741816

說明/提示

樣例 1 解釋：

在執行 \(M\) 次操作后，位串為 \(10101\)。

對于第一個查詢，長度為 \(5\) 的子序列僅有一個，\(10101\)，其解釋為 \(1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 21\)。

對于第二個查詢，長度為 \(4\) 的不同的子序列有 \(5\) 個：\(0101\)，\(1101\)，\(1001\)，\(1011\)，\(1010\)。字典序最大的子序列為 \(1101\)，其解釋為 \(1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1\cdot 2^0 = 13\)。

對于第三個查詢，字典序最大的序列是 \(111\)，其解釋為 \(7\)。

樣例 3 解釋：

確保輸出答案對 \(10^9+7\) 取模。

測試點 \(4\)：\(N \leq 10, Q \leq 1000\)。
測試點 \(5\)：\(M \leq 10\)。
測試點 \(6\sim 7\)：\(N, Q \leq 1000\)。
測試點 \(8\sim 12\)：\(N \leq 2 \cdot 10^5\)。
測試點 \(13\sim 20\)：沒有額外限制。

先離線用類似差分處理，得到極長 \(0\) 與極長 \(1\) 。一個貪心：先加盡可能多的 \(1\)，如果沒有 \(1\) 了，那就從右往左找 \(0\) 加，可以證明這是最優的。考慮最后的答案形成一個結構：一個 \(1\) 塊后綴，數個 \(1\) 整塊，一個 \(0\) 塊前綴，由 \(0\) 整塊與 \(1\) 整塊構成的一個大塊，一個 \(0\) 塊或 \(1\) 塊后綴。先判 \(l,r\) 在同一塊的情況。按塊做 \(1\) 數量前綴和，處理 \(1\) 數量超過 \(k\) 的情況。按塊做后綴轉十進制的結果，可以求任意塊間的二進制串的值。按塊做 \(0\) 數量后綴和，用二分找到 \(0\) 塊前綴所在塊編號，注意當 \(r\) 位于 \(0\) 塊時有細節。根據這個編號就可以求出由 \(0\) 整塊與 \(1\) 整塊構成的大塊的值。把答案拼一起即可，時間復雜度 \(O((m+q) \times log_n)\)。

代碼如下：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 5e5 + 10;
const int p = 1e9 + 7;

int n, m, q, k;
int L[N], w[N], c[N];
int s[N], tmp1[N], tmp2[N];

int qmi(int a, int k)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        a = a * a % p;
        k >>= 1;
    }
    return res;
}

int work1(int l, int r)
{
    if (l > r) return 0;
    return (s[l] - s[r + 1] + p) % p * qmi(qmi(2, n - L[r + 1] + 1), p - 2) % p;
}

int work2(int l, int r) 
{
    return (l > r) ? 0 : (tmp1[r] - tmp1[l - 1]); 
}

int query(int l, int r, int x)
{
    int idl, idr;
    idl = upper_bound(L + 1, L + 1 + k, l) - L - 1, idr = upper_bound(L + 1, L + 1 + k, r) - L - 1;
    if (idl == idr) return w[idl] * (qmi(2, x) - 1 + p) % p;
    int b1 = 0, b4 = 0, s1, idz, sufz = tmp2[k - (idr + 1) + 1];
    if (w[idl]) b1 = L[idl + 1] - l;
    if (w[idr]) b4 = r - L[idr] + 1;
    s1 = b1 + b4 + work2(idl + 1, idr - 1);
    if (s1 >= x) return (qmi(2, x) - 1 + p) % p;
    if (w[idr] == 0) sufz += L[idr + 1] - r - 1;
    idz = lower_bound(tmp2 + 1, tmp2 + 1 + k, x - s1 + sufz) - tmp2;
    idz = k - idz + 1;
    b1 = b1 + work2(idl + 1, idz - 1);
    return ((qmi(2, b1) - 1 + p) % p * qmi(2, x - b1) % p + work1(idz + 1, idr - 1) * qmi(2, r - L[idr] + 1) % p + qmi(2, b4) - 1 + p) % p;
}

signed main() 
{
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> m >> q;
    for (int i = 1 ; i <= m ; i ++ )
    {
        int l, r;
        cin >> l >> r;
        c[2 * i - 1] = l;
        c[2 * i] = r + 1;
    }
    sort(c + 1, c + 1 + 2 * m);
    k ++ ;
    for (int i = 1, cnt = 1, cv = 0; i <= 2 * m; i++) 
    {
        cv ^= 1;
        if ((c[i] != c[i + 1] || i == 2 * m) && c[i] <= n && cv != w[k]) 
        {
            k ++ ;
            L[k] = c[i];
            w[k] = cv;
        }
    }
    if (k >= 2 && L[2] != 1) L[1] = 1;

    L[k + 1] = n + 1;
    for(int i = k ; i >= 1 ; i -- ) 
    {
        tmp2[i] = tmp2[i + 1];
        s[i] = s[i + 1];
        if (w[i]) s[i] = (s[i + 1] + (qmi(2, L[i + 1] - L[i]) - 1 + p) % p * qmi(2, n - L[i + 1] + 1) % p) % p;
        else tmp2[i] += L[i + 1] - L[i];
    }
    reverse(tmp2 + 1, tmp2 + 1 + k);
    for(int i = 1 ; i <= k ; i ++ ) 
    {
        tmp1[i] = tmp1[i - 1];
        if (w[i])
            tmp1[i] += L[i + 1] - L[i];
    }
    for (int i = 1, l, r, k1; i <= q; i++) cin >> l >> r >> k1, cout << query(l, r, k1) << endl;
    return 0;
}

T6

P12029 [USACO25OPEN] Election Queries G

題目描述

農夫約翰有 \(N\) 頭（\(2 \leq N \leq 2 \cdot 10^5\)）編號從 \(1\) 到 \(N\) 的奶牛。農場正在舉行選舉，將選出兩頭新的領頭牛。初始時，已知第 \(i\) 頭奶牛會投票給第 \(a_i\) 頭奶牛（\(1 \leq a_i \leq N\)）。

選舉過程如下：

農夫約翰任意選擇一個非空真子集 \(S\)（即至少包含一頭牛但不包含所有牛）。
在 \(S\) 集合中，得票數最多的候選牛將被選為第一頭領頭牛 \(x\)。
在剩余奶牛組成的集合中，得票數最多的候選牛將被選為第二頭領頭牛 \(y\)。
定義兩頭領頭牛的差異度為 \(|x - y|\)。若無法選出兩頭不同的領頭牛，則差異度為 \(0\)。

由于奶牛們經常改變主意，農夫約翰需要進行 \(Q\) 次（\(1 \leq Q \leq 10^5\)）查詢。每次查詢會修改一頭奶牛的投票對象，你需要回答當前狀態下可能獲得的最大差異度。

輸入格式

第一行包含 \(N\) 和 \(Q\)。

第二行包含初始投票數組 \(a_1, a_2, \ldots, a_N\)。

接下來 \(Q\) 行，每行兩個整數 \(i\) 和 \(x\)，表示將 \(a_i\) 修改為 \(x\)。

輸出格式

輸出 \(Q\) 行，第 \(i\) 行表示前 \(i\) 次查詢后的最大可能差異度。

輸入輸出樣例 #1

輸入 #1

輸出 #1

4
3
2

輸入輸出樣例 #2

輸入 #2

8 5
8 1 4 2 5 4 2 3
7 4
8 4
4 1
5 8
8 4

輸出 #2

說明/提示

樣例一解釋：

第一次查詢后，\(a = [1,2,4,4,5]\)。選擇 \(S = \{1,3\}\) 時：

\(S\) 中：牛 \(1\) 得 \(1\) 票，牛 \(4\) 得 \(1\) 票 \(\to\) 可選擇牛 \(1\) 或牛 \(4\) 作為第一頭領頭牛。
剩余牛中：牛 \(2,4,5\) 各得 \(1\) 票 \(\to\) 可選擇牛 \(2,4,5\) 作為第二頭領頭牛。

最大差異度為 \(|1-5| = 4\)。

第二次查詢后，\(a = [2,2,4,4,5]\)。選擇 \(S = \{4,5\}\) 時：

\(S\) 中：牛 \(4\) 得 \(1\) 票，牛 \(5\) 得 \(1\) 票。
剩余牛中：牛 \(2\) 得 \(2\) 票。

最大差異度為 \(|5-2| = 3\)。

測試點 \(3\sim4\)：\(N,Q \leq 100\)。
測試點 \(5\sim7\)：\(N,Q \leq 3000\)。
測試點 \(8\sim15\)：無額外限制。

令奶牛 \(x\) 的得票數為 \(c_x\)，記 \(mx=max{c_1...c_n}\) 。顯然兩頭奶牛 x,y 能當選的充要條件為 \(mx \le c_x + c_y\)。考慮一種 \(O(n^2)\) 做法：對于每種 \(c\) 的值 \(v\)，找出最小和最大的 \(i\) 滿足 \(c_i = v\)，枚舉其中一個出現次數 \(c_x\) ，找出 \(c_x\) 對應的最小的 \(x_{min}\) ，使用雙指針找出 \(c_y ≥mx?c_x\) 中的 \(y_max\) ，將所有情況取最大值即為答案。需要用到的值都可以用 set 維護。
構造 \(c_i = i\) 即可。由于 \(sum_{c_i} = n\)，所以 \(c_i\) 的值只有本質不同的 \(O(\sqrt{n})\) 種。
于是對于上面的暴力做法，如果只考慮至少對應著一個 \(x\) 的 \(c_x\) ，時間復雜度就是 \(O(n\sqrt{n})\) 的。

#include <bits/stdc++.h>

using namespace std;

int n, q;

int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> q;
    vector<int> a(n), c(n);
    for(auto &i : a)
    {
        cin >> i;
        i -- ;
        c[i] ++ ;
    }
    vector<set<int>> s(n + 1);
    set<int> v;
    for(int i : a) s[c[i]].insert(i), v.insert(c[i]);
    while(q -- ) 
    {
        int p, x, r = 0;
        cin >> p >> x;
        p -- ;
        x -- ;
        s[c[a[p]]].erase(a[p]);
        s[c[x]].erase(x);
        if(s[c[a[p]]].size() == 0) v.erase(c[a[p]]);
        if(s[c[x]].size() == 0) v.erase(c[x]);
        c[a[p]] -- ;
        s[c[a[p]]].insert(a[p]);
        c[x] ++ ;
        s[c[x]].insert(x);
        v.insert(c[a[p]]), v.insert(c[x]), a[p] = x;
        vector<int> e(v.begin(), v.end());
        for (int i = 0, p = e.size() - 1, mx = 0 ; i < e.size() ; i ++ )
            if(e[i]) 
            {
                while(p >= 0 && e[p] && e[p] + e[i] >= e.back())
                {
                    mx = max(mx, *prev(s[e[p]].end()));
                    p -- ;
                }
                r = max(r, mx - *s[e[i]].begin());
            } 
        cout << r << endl;
    }
    return 0;
}

posted @ 2025-08-15 10:00 tony0530 閱讀(17) 評論(0) 收藏舉報

刷新頁面返回頂部

tony0530 的小窩

歡迎常來！

2025.8.15校隊題單分享+總結

T1

Cow at Large G

題目描述

輸入格式

輸出格式

輸入輸出樣例 #1

輸入 #1

輸出 #1

T2

P9017 [USACO23JAN] Lights Off G

題目描述

輸入格式

輸出格式

輸入輸出樣例 #1

輸入 #1

輸出 #1

輸入輸出樣例 #2

輸入 #2

輸出 #2

代碼

T3

P9016 [USACO23JAN] Find and Replace G

題目描述

輸入格式

輸出格式

輸入輸出樣例 #1

輸入 #1

輸出 #1

說明/提示

P11843 [USACO25FEB] The Best Subsequence G

題目描述

輸入格式

輸出格式

輸入輸出樣例 #1

輸入 #1

輸出 #1

輸入輸出樣例 #2

輸入 #2

輸出 #2

輸入輸出樣例 #3

輸入 #3

輸出 #3

說明/提示

P12029 [USACO25OPEN] Election Queries G

題目描述

輸入格式

輸出格式

輸入輸出樣例 #1

輸入 #1

輸出 #1

輸入輸出樣例 #2

輸入 #2

輸出 #2

說明/提示

公告