2025.8.13校隊(duì)題單分享+總結(jié)

那個(gè)隨筆寫不下了，先暫時(shí)放這

T1

由于電信技術(shù)的發(fā)展，人人都可以通過手機(jī)互相聯(lián)系。

有一位電信大佬最近想生產(chǎn)一大批手機(jī)，然而從生產(chǎn)線上一臺(tái)一臺(tái)地生產(chǎn)實(shí)在太慢了，于是他想出了一個(gè)辦法 —— 讓手機(jī)自我復(fù)制。
于是他給手機(jī)加上了一個(gè)內(nèi)置的函數(shù) fork()。手機(jī)的程序如果調(diào)用這個(gè)函數(shù)，那么手機(jī)會(huì)生產(chǎn)出一臺(tái)完全一模一樣的手機(jī)（包括程序運(yùn)行狀態(tài)），并且自己這臺(tái)的函數(shù)返回值為 \(1\) ，新手機(jī)的函數(shù)返回值為 \(0\) ，然后兩臺(tái)手機(jī)都繼續(xù)執(zhí)行程序。（請(qǐng)注意黑體字內(nèi)容）

初始時(shí)，只有一臺(tái)手機(jī)。接著，大佬讓手機(jī)計(jì)算形如這樣的表達(dá)式：

fork() <op> fork() <op> ... <op> fork()

其中是二元運(yùn)算符，為 && 或者 || 中的一種。例如：

fork() && fork() || fork() && fork() && fork() || fork()

兩個(gè)運(yùn)算都是左結(jié)合的，且 && 的優(yōu)先級(jí)比 || 高，所以上面的那個(gè)表達(dá)式相當(dāng)于：

((fork() && fork()) || ((fork() && fork()) && fork())) || fork()

對(duì)于表達(dá)式 \(a\) && \(b\)，手機(jī)會(huì)先計(jì)算 a 的值，如果為 \(0\) 那么不計(jì)算 \(b\) 的值（因?yàn)楹苤匾哉f兩遍，請(qǐng)注意這里不計(jì)算 \(b\) 的值），該表達(dá)式值為 \(0\)；否則計(jì)算 \(b\) 的值并將其值作為該表達(dá)式的值。

對(duì)于表達(dá)式 \(a\) || \(b\)，手機(jī)會(huì)先計(jì)算 \(a\) 的值，如果為 \(1\) 那么不計(jì)算 \(b\) 的值（因?yàn)楹苤匾哉f兩遍，請(qǐng)注意這里不計(jì)算 \(b\) 的值），該表達(dá)式值為 \(1\)；否則計(jì)算 \(b\) 的值并將其值作為該表達(dá)式的值。

表達(dá)式計(jì)算完成后，大佬制造出了數(shù)量驚人的手機(jī)，人類終于叩開了指數(shù)級(jí)工業(yè)制造的大門。

一萬萬年后，一位考古學(xué)家調(diào)查了此次事件。他得到了大佬讓手機(jī)計(jì)算的表達(dá)式。他想知道大佬當(dāng)年究竟制造出了多少臺(tái)手機(jī)。（包括初始的那臺(tái)手機(jī)）

你可以參照樣例解釋來更好地理解題意。

輸入格式
第一行一個(gè)正整數(shù) \(n\)，表示表達(dá)式中的 \(fork()\) 的數(shù)量。

接下來一行 \(n?1\) 個(gè)用空格隔開的字符串，每個(gè)字符串為 "&&” 或者 “||”，依次表示表達(dá)式中對(duì)應(yīng)位置的運(yùn)算符。

輸出格式
一行，一個(gè)整數(shù)表示制造出的手機(jī)的數(shù)量，你只用輸出答案對(duì) \(998244353\) 取模后的結(jié)果。

樣例一

input

2
&&

output

explanation

共生產(chǎn) \(3\) 臺(tái)手機(jī)，過程如下：

第 \(1\) 臺(tái)手機(jī)開始計(jì)算 \(fork()\) && \(fork()\)。
第 \(1\) 臺(tái)手機(jī)開始計(jì)算 \(fork()\)，產(chǎn)生了第 \(2\) 臺(tái)手機(jī)。
第 \(1\) 臺(tái)和第 \(2\) 臺(tái)的 \(fork()\) 計(jì)算完成，第 \(1\) 臺(tái)返回 \(1\)，第 \(2\) 臺(tái)返回 \(0\) 。
第 \(1\) 臺(tái)手機(jī)由于 \(fork()\) 返回值為 \(1\)，開始計(jì)算 \(fork()\) && \(fork()\) 右邊的 \(fork()\)，產(chǎn)生了第 \(3\) 臺(tái)手機(jī)。
第 \(2\) 臺(tái)手機(jī)由于 \(fork()\) 返回值為 \(0\) ，于是 \(fork()\) && \(fork()\) 值為 \(0\)（跳過右邊的 \(fork\) 的計(jì)算），程序結(jié)束。
第 \(1\) 臺(tái)和第 \(3\) 臺(tái)的 \(fork()\) 計(jì)算完成，第 \(1\) 臺(tái)返回 \(1\)，第 \(3\) 臺(tái)返回 \(0\)。
第 \(1\) 臺(tái)手機(jī)由于 \(fork()\) 返回值為 \(1\)，于是 \(fork()\) && \(fork()\) 值為 \(1\)，程序結(jié)束。
第 \(3\) 臺(tái)手機(jī)由于 \(fork()\) 返回值為 \(0\)，于是 \(fork()\) && \(fork()\) 值為 \(0\)，程序結(jié)束。

樣例二
input

6
&& || && && ||

output

限制與約定: \(n \le 10^5\)

題解

因?yàn)?&& 的優(yōu)先級(jí)高于 || 就將 || 作為分割線，每一塊 && 依次處理。
觀察題目，如果是 && 那么前面是 \(0\) 就停止，如果是 || 那么前面是 1 就停止
只有當(dāng)手機(jī)返回值為1時(shí)才能造出手機(jī)。而且在當(dāng)前這塊中復(fù)制出的手機(jī)，在下一塊中才能造出其他的手機(jī)。
所以就引導(dǎo)出了答案等于塊長的前綴乘加在一起。

接下來就是最簡單的實(shí)現(xiàn)了：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 1e5 + 10;
const int mod = 998244353;

int n;
string str;
int cont[N], cnt = 0, idx = 0;

signed main()
{
    cin >> n;
    cnt = 1;
    for(int i = 1 ; i < n ; i ++ )
    {
        cin >> str;
        if(str[0] == '|') cont[ ++ idx] = cnt, cnt = 1;
        else cnt ++ ;
    }
    cont[ ++ idx] = cnt;
    int now = 1, ans = 1;
    for(int i = 1 ; i <= idx ; i ++ )
    {
        now = (now * cont[i]) % mod;
        ans = (ans + now) % mod;
    }
    cout << ans;
    return 0;
}

T2

關(guān)羽喜歡下象棋！

不過這次，他下膩了傳統(tǒng)象棋，并叫來了你做他的對(duì)手。你們將在一張 \(100\) 行 \(100\) 列的象棋棋盤格點(diǎn)上對(duì)弈。關(guān)羽一身傲骨，給你了一輛大幅加強(qiáng)的車，自己則操縱一個(gè)小過河卒東躲西藏。具體規(guī)則如下：

卒初始在第 \(x_1\) 行第 \(y_1\) 列的格點(diǎn)上，車初始在第 \(x_2\) 行第 \(y_2\) 列的格點(diǎn)上。
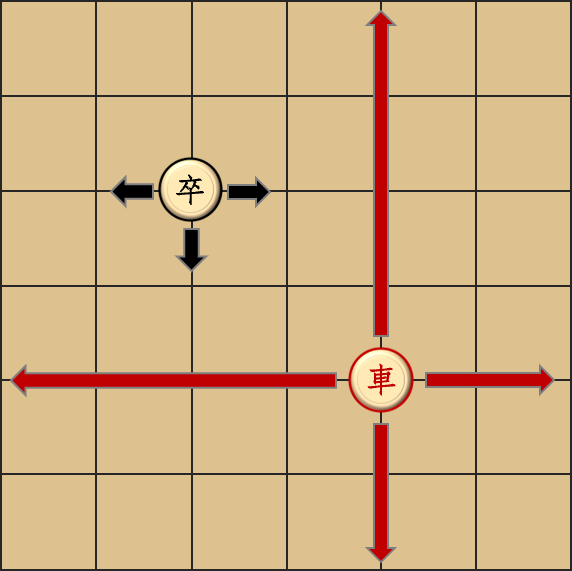
卒每次可以在左、右、下三種移動(dòng)方向中選擇一種，然后移動(dòng)一格（但是不能往上）。即，若記第 \(x\) 行第 \(y\) 列的格點(diǎn)為 \((x,y)\)，則卒可以從 \((x,y)\) 移動(dòng)到 \((x+1,y),(x,y+1),(x,y?1)\)。
車可以向左向右移動(dòng)多格，也可以向上向下移動(dòng)多格，也可以不動(dòng)。即，車可以從 \(x,y\) 移動(dòng)到 \((x,y′)(x,y′) 或(x′,y)(x′,y)\)，其中 \(1 \le x′,y′ \le 100\)
卒和車均不可以走到棋盤外。
這輛車經(jīng)過現(xiàn)代科技改造，會(huì)沿路散發(fā)毒氣，車經(jīng)過的格點(diǎn)都會(huì)被毒霧覆蓋，卒不能停留。例如，如果車從 \((x,y)\) 向右移動(dòng)到 \((x,y′)（y′>y)\)，則 \((x,y),(x,y+1),…,(x,y′)\) 都會(huì)帶毒。其余三種移動(dòng)方向類似。
這輛車不可被摧毀，即卒不能吃車，也不能移動(dòng)到車占據(jù)的位置。

b913a8ae2d7da20bbb9005066404a0fe

聰明的你發(fā)現(xiàn)你可以因此吊打武神關(guān)羽！于是你非常好奇，你最快幾步可以擊敗關(guān)羽。這個(gè)特殊的象棋分為若干回合，每回合是這樣進(jìn)行的：

你操控車移動(dòng)一次，也可以選擇不動(dòng)。
如果車吃掉了卒（即車占據(jù)了卒所在位置），游戲結(jié)束。
卒移動(dòng)一步。當(dāng)且僅當(dāng)卒沒有可移動(dòng)方向時(shí)，卒才可以選擇不動(dòng)（即左、右、下三個(gè)方向均為車、毒氣、棋盤邊界中的一種）。例如，如果進(jìn)行到某一輪前，\((1,2)\) 有毒霧，且該回合車從 \((2,2)\) 移動(dòng)到 \((2,1)\)，那么卒無可移動(dòng)方向，故卒該輪不進(jìn)行移動(dòng)。

d9154141b645a860a0f53b3a0d4c4d8a

游戲總回合數(shù)定義為車決策的次數(shù)。

當(dāng)然武神也很聰明，他希望游戲回合數(shù)盡可能多，而你希望游戲回合數(shù)盡可能少，并且你們都足夠聰明。你想提前知道，游戲?qū)?huì)進(jìn)行幾回合？

樣例一
input

output

explanation

對(duì)于第一組數(shù)據(jù)，車可以選擇停在原地，而輪到卒的時(shí)候卒必須移動(dòng)。無論向下還是向右，都會(huì)立馬被車吃掉。

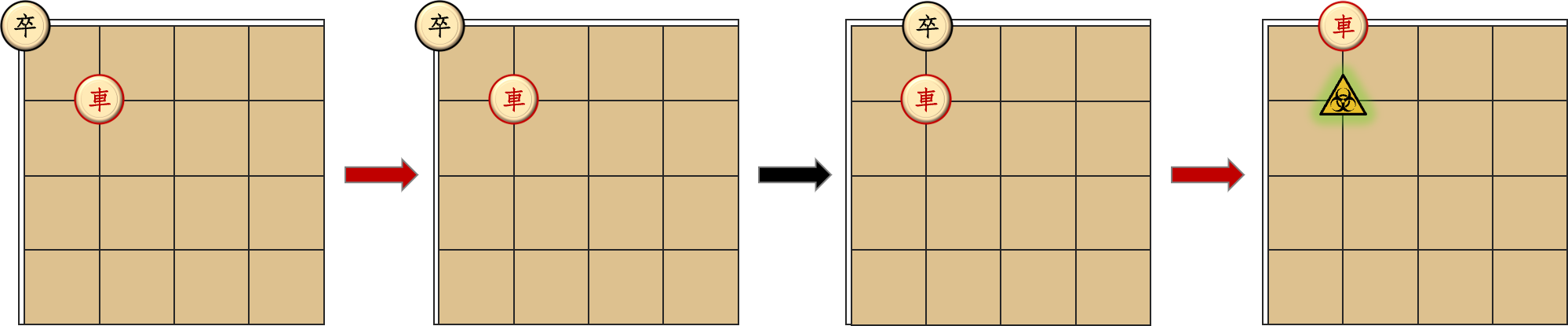
448ccc346d97c7a69bf821df5262b69b

注意這里只畫了棋盤左上角。

對(duì)于第二組數(shù)據(jù)，車可以先在卒下方灑出一行毒霧，然后再走到卒所在的第一行，即可必殺。

415f69d3261cae3257ab584e45d884ff

對(duì)于第三組數(shù)據(jù)，車移動(dòng)到 \((100,3)\)，即可下一輪必殺。

對(duì)于第四組數(shù)據(jù)，答案是 \(3\)，這是為什么呢？

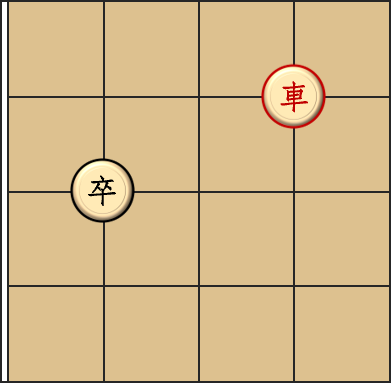
1065882f70fb27054ac70cf83fe6ee69

一道很有意思的題，我們要先控制一下，答案的最大值，我們可以考慮怎樣關(guān)羽必輸？觀察到關(guān)羽不能往后走，所以只要把關(guān)羽的前一行弄滿
毒氣，這樣就把關(guān)羽鎖在了一行里，最后直接走到關(guān)羽的那一行就好了，那最少要多少步呢？

事實(shí)證明，最多只要四步就能完成，接下來就只要爆搜亦或者分類討論就好了，我寫的是分類討論 :

#include <bits/stdc++.h>

#define int long long

using namespace std;


int T;

signed main()
{
    cin >> T;
    while(T -- )
    {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        if(a == c || b == d) cout << 1 << endl;
        else 
        {
            if(b > d) b = 100 - b + 1, d = 100 - d + 1;
            if(a == 100) cout << 2 << endl;
            else if(b == 1)
            {
                if(c == a + 1 || d == 2) cout << 2 << endl;
                else cout << 3 << endl;
            }else if(b == 2)
            {
                if(c == a + 1 || d == 3) cout << 3 << endl;
                else if(c <= a && d == 4) cout << 3 << endl;
                else{
                    if(c == a + 1) cout << 3 << endl;
                    else if(a == 99) cout << 3 << endl;
                    else cout << 4 << endl;
                }
            }else{
                if(c == a + 1) cout << 3 << endl;
                else if(a == 99) cout << 3 << endl;
                else cout << 4 << endl;
            }
        }
    }
    return 0;
}

T3

新年的毒瘤

辭舊迎新之際，喜羊羊正在打理羊村的綠化帶，然后他發(fā)現(xiàn)了一棵長著毒瘤的樹。

這個(gè)長著毒瘤的樹可以用 \(n\) 個(gè)結(jié)點(diǎn) \(m\) 條無向邊的無向圖表示。這個(gè)圖中有一些結(jié)點(diǎn)被稱作是毒瘤結(jié)點(diǎn)，即刪掉這個(gè)結(jié)點(diǎn)和與之相鄰的邊之后，這個(gè)圖會(huì)變?yōu)橐豢脴洹湟布礋o簡單環(huán)的無向連通圖。

現(xiàn)在給你這個(gè)無向圖，喜羊羊請(qǐng)你幫他求出所有毒瘤結(jié)點(diǎn)。

輸入格式
第一行兩個(gè)正整數(shù) \(n\), \(m\)，表示有 \(n\) 個(gè)點(diǎn) \(m\) 條邊。保證 \(2 \le n\)

接下來 \(m\) 行，每行兩個(gè)整數(shù) \(v,u\)，表示 \(v\) 和 \(u\) 之間有一條無向邊。\(1 \le v,u \le n\)。保證沒有重邊和自環(huán)。

input

output

3
4 5 6

首先呢，是一棵樹，那么得聯(lián)通，所以呢我們刪掉的這個(gè)點(diǎn)一定不能是割點(diǎn)，這直接用點(diǎn)雙來求割點(diǎn)就好了，其次呢，就是不能有環(huán)，也就是刪完之后得剩 \(n-2\) 條邊，就直接判斷就好了。很簡單，給一個(gè)丑陋的代碼：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 1e5 + 10;
const int M = 2e5 + 10;

int n, m;
vector<int> edge[N];
int dfn[N], low[N], timestamp;
bool st[N];

void tarjan(int u, int fa)
{
    dfn[u] = low[u] = ++ timestamp;
    int son_cnt = 0;
	for (int i = 0 ; i < edge[u].size() ; i ++ ) 
	{
		int j = edge[u][i];
        if (!dfn[j])
        {
            son_cnt ++ ;
            tarjan(j, u);
            low[u] = min(low[u], low[j]);
            if(low[j] >= dfn[u]) st[u] = true;
        }else if (dfn[j] < dfn[u] && j != fa) low[u] = min(low[u], dfn[j]);
    }
	if (fa < 0 && son_cnt == 1) st[u] = 0;
}

signed main()
{
    cin >> n >> m;
	for(int i = 0 ; i < m ; i ++ )
	{
	    int a, b;
	    cin >> a >> b;
	    a -- ;
	    b -- ;
		edge[a].push_back(b);
		edge[b].push_back(a);
	}
	tarjan(0, -1);
	vector<int> ans;
	for(int i = 0 ; i < n ; i ++ )
		if(st[i] == false && m - edge[i].size() == n - 2)
			ans.push_back(i + 1);
    sort(ans.begin(), ans.end());
    cout << ans.size() << endl;
    for(int i = 0 ; i < ans.size() ; i ++ ) cout << ans[i] << " ";
    return 0;
}

T4

票數(shù)統(tǒng)計(jì)

妹滋滋是一個(gè)善于編程的女孩子。

但是某一天，她一不小心把 UOJ 后臺(tái)的票數(shù)統(tǒng)計(jì)程序?qū)戝e(cuò)了。

本來嘛在這種根本沒有什么用的功能上出了 bug 也沒有什么大關(guān)系，但是又有某一天，UOJ 突然就開始搞全民公投了。

這可怎么辦呢？如果這個(gè)消息讓別人知道的話自己肯定會(huì)被查表，更不要說讓所有用戶重新來投一次票了。

作為一個(gè)要強(qiáng)的女孩子，妹滋滋決定自力更生。

通過一些奧妙重重的方式，妹滋滋知道了一些關(guān)于這次全民公投的信息。

這次全民公投一共有 \(n\) 位用戶排隊(duì)參加，編號(hào)為 \(1\) 到 \(n\)。每一位用戶要么投了通過，要么投了不通過。
有 \(m\) 個(gè)二元組 \((x_i,y_i)\)，每個(gè)二元組給出這樣一個(gè)信息： “前 \(x_i\) 位用戶中，恰好 \(y_i\) 位投了通過” 和 “后 \(y_i\) 位用戶中，恰好有 \(x_i\) 位投了通過” 這兩句話中，至少有一句是成立的。

作為分析的第一步，她想要知道有多少種投票情況是滿足她所得到的信息的。當(dāng)然，可能所有投票情況都不滿足條件。

解法：考慮組合數(shù)

當(dāng) \(x>y\) 時(shí)條件為前綴限制，\(x<y\) 時(shí)條件為后綴限制。
既有前綴限制，又有后綴限制的情況下，我們枚舉總共1的個(gè)數(shù)，把后綴限制轉(zhuǎn)化為前綴限制。
如果所有限制均有 \(x \not= y\) 則可以直接使用組合數(shù)計(jì)算。預(yù)處理組合數(shù)，單次計(jì)算的時(shí)間復(fù)雜度是 \(O(n)\) 的。

當(dāng)有 \(x=y\) 時(shí)，顯然只需要考慮所有 \(x = y\) 限制中 \(x\) 最大的限制即可，總方案數(shù)為滿足前綴+滿足后綴-滿足前綴和后綴。時(shí)間復(fù)雜度 \(O(n^2)\)。

代碼就不給了

T5

T5很簡單，就不總結(jié)了，最然當(dāng)時(shí)其他同學(xué)沒有分享的時(shí)候還不會(huì)，但是是腦抽沒想到，真的沒啥好總結(jié)的

posted @ 2025-08-13 10:01 tony0530 閱讀(21) 評(píng)論(0) 收藏舉報(bào)

刷新頁面返回頂部

tony0530 的小窩

歡迎常來！

2025.8.13校隊(duì)題單分享+總結(jié)

公告