簡單多項式
前言:本文按照筆者自身理解撰寫,力求通透易懂,如有不嚴謹處請多擔待,有問題歡迎反饋。
復數:
我們都知道 \(x ^ 2 = 1\) 的解是:\(x_1 = 1,x_2 = -1\) 那么方程 \(x ^ 4 = 1\) 的解是什么呢?
首先一個 \(N\) 次方程如果有 \(N\) 個解,所以這里應該有四個解。
因為 \(x ^ 4 = (x ^ 2) ^ 2\) 所以 \(x ^ 2 = 1\) 或 \(x ^ 2 = -1\) 這時我們會發現 \(x = \sqrt{-1}\) 我們稱這樣的 \(x\) 叫做 \(i\),同理 \(i\) 也滿足 \(i ^ 2 = -1\)。
這里引入復數:對于任意的數,都可以表示成 \(a + bi\) 這里 \(a,b\in R\) 并且實數是完全被復數包含在內的。
我們知道,對于任意實數 \(x\in R\) 其在數軸上都能被唯一地表示出來。那么對于復數,我們應該用什么樣的坐標系,才能讓他們都能被唯一地表示出來呢?
考慮每個 \(a + bi\) 我們將其常數項和 \(i\) 的系數組成一個二元組,發現對于每種二元組都能唯一地對應一個復數,或者說,每個這樣的二元組都和其對應的復數組成雙射關系,那么我們就可以把它們放到二維坐標系中。
一些概念:
- 我們把復數 \(a + bi\) 對應的坐標 \((a,b)\) 所在的坐標系中的橫軸表示實軸,縱軸表示虛軸。
- 如果我們把原點 \(O\) 和一個復數 \(a + bi\) 對應的坐標 \((a,b)\) 連邊,那么這條邊的長度就稱作這個復數的模長。
- 如果我們把原點 \(O\) 和一個復數 \(a + bi\) 對應的坐標 \((a,b)\) 連邊,那么這條邊和實軸的正方向所夾的角稱作幅角。
由于每個復數所對應的二元組在二維坐標系中,我們可以將它和向量的知識聯系在一起。
復數運算:
- 加法運算,設我們有兩個復數 \(a + bi\) 和 \(c + di\) 那么運算法則就是對應位置(即:常數相加,\(i\) 的系數相加)相加,也就是 \(a + bi + c + di \rightarrow a + c + bi + di \rightarrow a + c + (b + d)i\)
- 減法運算,其實就是加法運算的逆,可以把 \(a + bi - (c + di)\rightarrow a + bi + (-c - di)\) 即 \(a + bi - (c + di) \rightarrow a - c + (b - d)i\)
- 乘法運算,其實就是 \((a + bi)\times (c + di) \rightarrow ac + bdi^2 + bci + adi\) 因為 \(i ^ 2 = -1\),所以原式就是:\((a + bi)\times (c + di) \rightarrow ac - bd + (bc + ad)i\)
- 除法運算,其實就是 \(\frac{a + bi}{c + di}\) 可以分子分母同乘 \(c - di\) 從而分子變成平方差,即 \(\frac{a + bi}{c + di} \times \frac{c - di}{c - di} \rightarrow \frac{ac - adi + bci -bdi^2}{c ^ 2 - d^2i^2}\rightarrow \frac{ac + bd + (bc - ad) i}{c ^ 2 + d ^ 2}\)
- 復數的共軛:實部相同,虛部相反(根據實軸對稱)。
- 復數相乘的時候模長相乘,幅角相加。
單位圓:
和三角函數一樣,就是以 \(O\) 為圓心,半徑為一個單位長度的圓。
比如這樣:

不難發現,單位圓上的每一個點模長都是 \(1\)
為了方便書寫,我們下文稱 \(|x|\) 為 \(x\) 的模長。
快速傅里葉變換思想:
引理: 一個 \(N\) 次多項式可以由 \(N + 1\) 個 \(x\) 互不相同的點值唯一確定出來,比如一次函數需要兩個點,二次函數需要三個點。
一些符號的說明: 設當前有兩個多項式 \(f,g\),我們稱 \(fg\) 表示多項式 \(f\) 和 \(g\) 相乘,即,若 \(h = fg\) 則 \(h_i = \sum_{j + k = i} f_j\times g_k\),定義 \(deg_f\) 表示多項式 \(f\) 次數。
首先暴力做法就是對于 \(0\leq i\leq deg_f,0\leq j\leq deg_g, h_{i + j}\rightarrow h_{i + j} + f_i\times g_j\)
時間復雜度是 \(O(n^2)\) 的。
我們設多項式 \(f(x) = a_0 + a_1x + a_2x^2 + ... a_nx^n\) 中系數為 \(<a_0,a_1,....a_n>\) 我們發現直接對系數進行合并是難以優化的,但是如果轉成點值呢?假設我們已經把 \(f,g\) 分別轉成點值序列 \(A\) 和 \(B\) 那么點值相乘是 \(O(n)\) 的,即 \(C = A\times B,\forall i\in [0,\max(deg_f,deg_g)],C_i = A_i\times B_i\) 最后我們只需要再進行一次多項式轉點值的逆,也就是點值轉多項式就好了,所以我們把重點放到了如何知道一個多項式 \(f\) 求出 \(deg_f + 1\) 個點的點值序列。
離散傅里葉變換 DFT
既然我們打算要把一個多項式 \(f\) 轉成一個點值序列 \(A\) 那么我們就需要任意找 \(deg_f + deg_g + 1\) 個點分別帶入兩個多項式,因為 \(|fg| = |f| + |g| - 1\) 而 \(|f| = deg_f + 1\) 其中 \(|f|\) 表示多項式 \(f\) 有多少個冪, \(0\) 次冪也算冪。
但是想法是好的,顯示是很殘酷的,因為多項式多點求值需要使用 \(FFT\) 實現,但是我們研究的是 \(FFT\) 肯定是不能這樣的,因此我們應該找一些特殊點。
偉大的傅里葉告訴我們,要從單位根上來考慮這個問題。
具體的,我們把單位圓均分成 \(N\) 份,比如 \(N = 8\) 的時候圖長這樣:
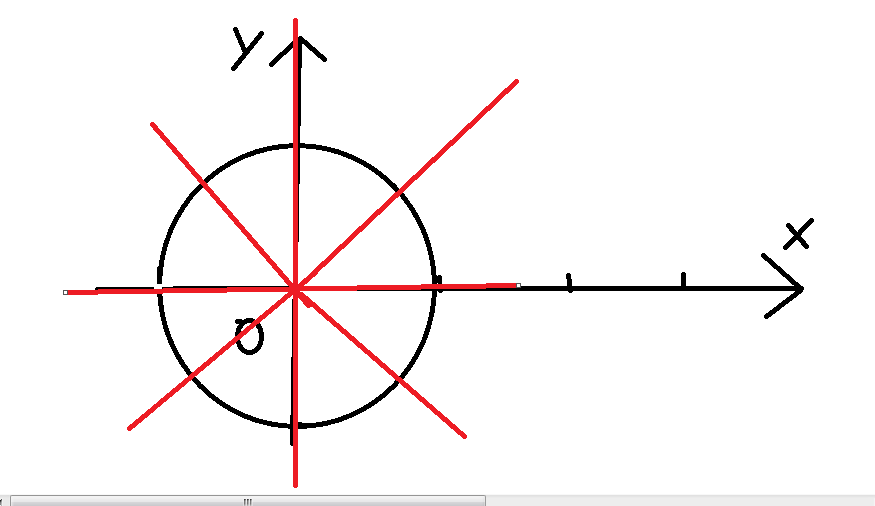
我們發現,這 \(N\) 個根也是 \(x ^ N = 1\) 的解,后文稱作單位根,我們設實軸上的邊為 \(\omega_{n}^0\) 然后逆時針的過程中第一個遇到的紅線就是 \(\omega_{n}^1\) 同理,第 \(i\) 個遇到的紅線就是 \(\omega_{n}^i\) 容易發現,由于我們有 \(n\) 個單位根,所以也就是有 \(\omega_{n}^0 .... \omega_{n}^{n - 1}\) 下面我們重點來討論一下這些單位根的性質。
單位根性質:
- \(\omega_n^{0,1.....n - 1}\) 并不是幾個獨立的點,而是代表一個集合,因為如果在某一個點,它逆時針再走 \(2\pi\) 步仍然可以到這個點,由此也能推出單位圓中的周期性 \(T = 2\pi\) 或者說 \(w_n^i = w_n^{i\bmod n},i\in Z\)
- \(\omega_n^j \times \omega_n^i = \omega_n^{i + j}\) 這個就是剛剛復數運算中的復數相乘,幅角相加。
- \((\omega_n^i)^j = \omega_n^{ij}\) 這個其實就是 \(j\) 個 \(w_n^i\) 相乘和 \(2\) 一樣的分析。
- \(\omega_{2n}^{2i} = \omega_n^i\) 類比分蛋糕的時候,就是原來是分了 \(2n\) 塊然后選了 \(2i\) 塊,現在是分了 \(n\) 塊,選了 \(i\) 塊,不難發現是一樣的,注意:這里的“分”指的是均分。
- 如果 \(n\) 是偶數,那么 \(\omega_n^i = -\omega_n^{i + \frac{n}{2}}\) 因為 \(n\) 是偶數,所以 \(w_n^{\frac{n}{2}}\) 就相當于逆時針走了 \(180\) 度,自然就是變成了原來中心對稱的位置了。
準備好了嗎,即將開始最重要的部分!
考慮當前有個 \(n\) 次多項式 \(f(x) = a_0 + a_1x + a_2x^2 + ... a_nx^n\) 并且這里 \(n - 1\) 是偶數。
我們把他按照奇偶性分開:
令 \(g(x) = a_0 + a_2x^2 + a_4x^4 + ... a_{n - 2}x^{n - 2}\)
令 \(h(x) = a_1x + a_3x^3 + a_5x^5 + ... a_{n - 1}x^{n - 1}\)
顯然 \(f(x) = g(x) + h(x)\) 這里 + 是按位相加。
再變:
\(g(x)\rightarrow a_0 + a_2x + a_4x^2 + a_{n - 2}x^{\frac{n}{2} - 1}\)
\(h(x)\rightarrow a_1 + a_3x + a_5x^2 + a_{n - 1}x^{\frac{n}{2} - 1}\)
所以現在 \(f(x) = g(x ^ 2) + xh(x ^ 2)\),我們就可以帶值找找規律了。
設當前帶入 \(\omega_n^k,k < \frac{n}{2}\) 分兩種情況帶入:
- 帶入 \(\omega_{n}^k\) 此時 \(f(\omega_{n}^k) = g((\omega_{n}^k)^2) + \omega_{n}^kh((\omega_{n}^k)^2)\)
- \(f(\omega_{n}^k) = g((\omega_{n}^k)^2) + \omega_{n}^kh((\omega_{n}^k)^2)\rightarrow f(\omega_{n}^k) = g(\omega_{n}^{2k}) + \omega_{n}^kh(\omega_{n}^{2k})\rightarrow f(\omega_{n}^k) = g(\omega_{\frac{n}{2}}^k) + \omega_{n}^kh(\omega_{\frac{n}{2}}^k)\)。
- 由此得出來了,對于 \(k < \frac{n}{2}\),\(f(\omega_n^k)\) 的點值就是 \(g(\omega_{\frac{n}{2}}^k) + \omega_n^kh(\omega_{\frac{n}{2}} ^ k)\) 也就是說,而 \(g,h\) 都是子問題,且范圍縮小了一倍,所以我們每次把原問題的范圍分成兩半來分別解決然后合并,這是典型的分治,總的層數是 \(O(\log n)\) 級別的。
- 帶入 \(\omega_{n}^{k + \frac{n}{2}}\) 此時 \(f(\omega_{n}^{k + \frac{n}{2}}) = g((\omega_{n}^{k + \frac{n}{2}}) ^ 2) + \omega_n^{k + \frac{n}{2}}h((\omega_n^{k + \frac{n}{2}}) ^ 2)\)
- 因為 \((\omega_{n}^j)^k = \omega_n^{jk}\),原式得:\(f(\omega_{n}^{k + \frac{n}{2}}) = g(\omega_{n}^{2k + n}) + \omega_n^{k + \frac{n}{2}}h(\omega_n^{2k + n})\)
- 因為 \(\omega_n^j = \omega_n^{j\bmod n}\),原式得:\(f(\omega_{n}^{k + \frac{n}{2}}) = g(\omega_{n}^{2k}) + \omega_n^{k + \frac{n}{2}}h(\omega_n^{2k})\)
- 因為 \(\omega_{2n}^{2j} = \omega_n^j\),原式得:\(f(\omega_n^{k + \frac{n}{2}}) = g(\omega_{\frac{n}{2}} ^ k) + \omega_n^{k + \frac{n}{2}} h(\omega_{\frac{n}{2}}^k)\)
- 這里為了方便,可以根據 \(\omega_n^{k + \frac{n}{2}} = -\omega_n^k\),原式得:\(f(\omega_n^{k + \frac{n}{2}}) = g(\omega_{\frac{n}{2}} ^ k) - \omega_n^{k} h(\omega_{\frac{n}{2}}^k)\)
因此我們就得到了關于計算 \(f(\omega_n^i)\) 的式子,也就是每次把原序列折半分成奇數偶數兩半,然后分別計算子問題的 \(f(\omega_n^i)\) 最后合并,不難發現我們轉換后的式子恰好滿足 \(n\rightarrow \frac{n}{2}\) 且 \(k < \frac{n}{2}\) 所以成功劃分成了子問題!
這里有些細節:
如果遞歸到某一層, \(n = 1\) 那么直接 return,這個是因為遞歸到 \(n = 1\) 的時候是計算 \(f(w_1^0)\) 由于 \(w_1 ^ 0\) 其實就是 \(1 + 0i = 1\) 所以 $f(w_1 ^ 0) = $ 分治到 \(i\) 時 \(i\) 的系數,所以可以直接分治的時候記錄系數,然后把系數當做 \(f(w_1 ^ 0)\) 來計算。
時間復雜度不難發現是 \(T(n) = 2T(\frac{n}{2}) + O(n) = O(n\log n)\)
離散逆傅里葉變換 IDFT
假設我們已經進行了一次正變換 DFT,得到的 \(N\) 個點值是序列 \(\{y\},\forall i\in[1,|y|]\) 對于 \(y_i = f(\omega_n^i)\) 設原來的函數是 \(f(x) = a0 + a1x + a2x ^ 2 + a3x ^ 3 + ... a_{n - 1} x ^ {n - 1}\) 我們現在來構造一個新的多項式 \(A\) 滿足:
\(A(x) = \sum_{0\leq i< n} y_ix^i\)
我們再設 \(b\) 序列,其中 \(b_i = \omega_n^{-i}\) 那么我們來看看把 \(\{b\}\) 序列帶入 \(A(x)\) 看看會產生什么樣的點值序列。
\(A(b_k) = \sum_{i = 0}^{n - 1} y_i{b_k}^i\)
因為 \(y_i = f(\omega_n ^ i) = \sum_{j = 0}^{n - 1} a_j({\omega_n ^ i}) ^ j\)
所以原式得:\(A(b_k) = \sum_{i = 0}^{n - 1} {b_k} ^ i \sum_{j = 0}^{ n- 1} a_j(\omega_n^{i})^j\)
因為: \((\omega_n^i)^j = \omega_n ^ {ij}\)
所以原式得:\(A(b_k) = \sum_{i = 0}^{n - 1} {b_k} ^ i \sum_{j = 0}^{ n- 1} a_j\omega_n^{ij}\)
因為 \(b_k = \omega_n^{-k}\)
所以原式得:\(A(b_k) = \sum_{i = 0}^{n - 1} {\omega_n^{-k}} ^ i \sum_{j = 0}^{ n- 1} a_j\omega_n^{ij}\rightarrow \sum_{i = 0}^{n - 1} {\omega_n^{-ik}} \sum_{j = 0}^{ n- 1} a_j\omega_n^{ij}\)
交換求和:
\(A(b_k) = \sum_{i = 0}^{n - 1} \sum_{j = 0}^{ n- 1} {\omega_n^{-ik}}a_j\omega_n^{ij}\)
因為:\(\omega_n^i\omega_n^j = \omega_n^{i + j}\)
所以原式得:\(A(b_k) = \sum_{i = 0}^{n - 1} \sum_{j = 0}^{ n- 1} a_j\omega_n^{ij}\omega_n^{-ik}\rightarrow \sum_{i = 0}^{n - 1} \sum_{j = 0}^{ n- 1} a_j\omega_n^{i(j - k)}\)
因為 \((\omega_n^i)^j = \omega_n^{ij}\)
所以原式得:\(A(b_k) = \sum_{i = 0}^{n - 1} \sum_{j = 0}^{ n- 1} a_j(\omega_n^{j -k}) ^ i\)
交換求和得:
\(A(b_k) = \sum_{j = 0}^{n - 1} a_j\sum_{i = 0}^{n - 1} (\omega_n^{j - k})^i\)
此時記 \(S(\omega_n^a) = \sum_{i = 0}^{n - 1} (\omega_n^{a}) ^ i\)
- 如果 \(a \bmod n = 0\) 那么顯然 \(\omega_n^a = 1\) 所以 \(\sum_{i = 0}^{n - 1}(\omega_n^a) ^ i = n \times 1 = n\)
- 否則考慮相鄰兩項作差:
- 等式兩邊同乘 \(\omega_n^a\)
- 原式得:\(\omega_n ^ a S(\omega_n^a)=\sum_{i = 1}^{n}(\omega_n^{a}) ^ i\)
- 兩者作差得:\(\omega_n^aS(\omega_n^a) - S(\omega_n ^ a) = \sum_{i = 1}^n (\omega_n^a)^i - \sum_{i = 0}^{n - 1}(\omega_n^a)^i\)
- 左邊提取公因式得:\((\omega_n^a - 1)S(\omega_n^a)= \sum_{i = 1}^n (\omega_n^a)^i - \sum_{i = 0}^{n - 1}(\omega_n^a)^i\)
- 由于 \(a\bmod n\ne 0\) 所以 \(\omega_n^a\ne 1\) 所以 \((\omega_n^a - 1)\ne 0\) 所以可以等式兩邊同時除以 \((\omega_n^a - 1)\)
- 因此,原式得:\(S(\omega_n^a) = \frac{\sum_{i = 1}^n (\omega_n^a)^i - \sum_{i = 0}^{n - 1}(\omega_n^a)^i}{\omega_n^a - 1}\)
- 不難發現 \(\sum_{i = 1}^n (\omega_n^a)^i - \sum_{i = 0}^{n - 1}(\omega_n^a)^i = (\omega_n^a)^n - (\omega_n^a)^0\)
- 前者可以寫成 \((\omega_n^n)^a = (\omega_n^0)^n = 1\) 后者是 \(0\) 次方也是 \(1\)
- 所以可以得到對于 \(a\bmod n \ne 0\) 的所有 \(a\) 滿足 \(S(\omega_n^a) = 0\)
所以最后可以歸納成:對于 \(a < n\) 的所有 \(\omega_n^a\) 滿足:也就是說
$ S\left(\omega_n^a\right)=
\begin{cases}
n,&a=0\
0,&a\neq 0
\end{cases}
$
好的,現在我們把這個公式帶到 \(A(b_k) = \sum_{j = 0}^{n - 1} a_j\sum_{i = 0}^{n - 1} (\omega_n^{j - k})^i\)
原式得:\(\sum_{j = 0}^{n - 1} a_j S(\omega_n^{j - k})\)
顯然這個式子,只有在 \(j = k\) 的時候有值,且值為 \(n\) 所以這個式子的值就是 \(na_k\)
也就是說,給定點 \(b_i = \omega_n ^ {-i}\) 它的點值序列表示就是 \(\{(b_0,a_0n),(b_1,a_1n),....,(b_{n - 1},a_{n - 1}n)\}\)
所以我們就得到了如何在求出 \(f,g\) 的點值序列后如何還原出來新的多項式的系數,當然,因為最后還原出來的點值是 \(a_in\) 所以要除以 \(n\)。
不難發現,我們這個過程和 DFT 幾乎一模一樣,無非就是將 \(n\) 個單位根 \(\omega_n^i\rightarrow \omega_n^{-i}\) 這兩個式子是關于實軸(x軸)對稱的,所以只需要把縱坐標乘上一個 \(-1\) 即可。
但是我們發現直接寫分治,我們空間復雜度應該也是 \(O(n \log n)\) 的,因為需要對每個點開一個 \(O(len)\) 級別的數組,所以要引進一種空間上的優化:蝶形優化。
蝶形優化
對于當前分治區間 \([l_i,r_i]\) 設當前長度是 \(n_i = r_i - l_i + 1\)
我們要計算 \(f(\omega_{n_i}^{0,1,...n_i - 1})\) 需要 \(g(\omega_{\frac{n_i}{2}} ^ {0,1,2,...\frac{n_i}{2} - 1})\) 和 \(h(\omega_{\frac{n_i}{2}} ^ {0,1,2,...\frac{n_i}{2} - 1})\)
我們可以在遞歸開始前,就把 \(g,h\) 給放到 \(f\) 的第 \([0 , \frac{n_i}{2} - 1]\) 的位置和 \([\frac{n_i}{2},n_i - 1]\) 的位置上,這個位置是個指針,此時修改 \(g\) 和 \(h\) 也會在對應的 \(f\) 上進行修改,(類似長剖一樣)所以在我們更新 \(f\) 的時候不能直接拿 \(g\) 和 \(h\) 來改 \(f\) 而是新開一個輔助數組 \(G\) 最后再把 \(G\) 賦值給 \(f\) 不然直接改 \(f\) 的值,對應的 \(g\) 和 \(h\) 的值也會進行修改,就不對了。這樣空間就被優化成 \(O(n)\) 級別了。
最后,一些實現上的小細節:
- 我們發現當 \(n = 1\) 的時候 \(\omega_n^{n - 1} = 1\) 的,所以可以直接把一開始的點值放進去,因為此時點值的 \(f\) 值就是自己不會變。所以一開始的時候,就直接輸入 \(A,B\) 的實部就可以了。
- 一定要注意,\(f(i) = a + bi\) 中 \(a + bi\) 中的 \((a,b)\) 是個整體,代表一個復數,而不是當 \(x = a\) 的時候對應的值是 \(b\)。
- 分治的時候,一定不要直接修改 \(f\) 的值,因為使用蝶形優化后,\(g\) 和 \(h\) 和 \(f\) 公用一個數組。
- 因為我們剛才說的,每次分治的時候都需要能均分奇偶數,所以要求所有大于 \(1\) 的分治區間長度是 \(2\) 的倍數,自然想到構造一個 \(2 ^ k\) 的數列,如果一開始不夠就補 \(0\) 即可,然后找到最大的 \(k\) 滿足 \(2^k \ge n + m + 1\)
- 由于我們是進行的實數運算,會有精度問題,所以最后要輸出四舍五入后的值。
代碼:
#include <iostream>
#include <cmath>
#include <algorithm>
constexpr double Pi = acos(-1);
constexpr int N = 4e6 + 5;
#define int long long
struct complex{
double x,y;
inline complex operator + (const complex & a){
return {a.x + x,a.y + y};
}
inline complex operator - (const complex & a){
return {x - a.x,y - a.y};
}
inline complex operator * (const complex & a){
// (x + yi) * (a.x + a.yi)
// a.x * x + xa.yi + a.xyi + a.yi*yi
// a.x * x + xa.yi + a.xyi - a.y*y
return {a.x * x - a.y * y,x * a.y + a.x * y};
}
}A[N],B[N],g[N];
int n , m;
inline void fft(complex * f,int len,int rev){
if(len == 1) return;
for(int i = 0; i < len; ++ i){
g[i] = f[i];
}
complex * ls = f,* rs = f + len / 2;
for(int i = 0; i < len / 2; ++ i){
ls[i] = g[i << 1];
rs[i] = g[i << 1 | 1];
}
fft(ls,len / 2,rev);
fft(rs,len / 2,rev);
complex w = {cos(2 * Pi / len),sin(2 * Pi / len) * 1.0 * rev},now;
now.x = 1;now.y = 0;
for(int i = 0; i < len / 2; ++ i){
g[i] = ls[i] + now * rs[i];
g[i + len / 2] = ls[i] - now * rs[i];
now = now * w;
}
for(int i = 0; i < len; ++ i){
f[i] = g[i];
}
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m;
for(int i = 0; i <= n; ++ i){
std::cin >> A[i].x;
}
for(int i = 0; i <= m; ++ i){
std::cin >> B[i].x;
}
int len = 1;
for(int k = n + m; len <= k; len <<= 1);
fft(A,len,1);
fft(B,len,1);
for(int i = 0; i <= len; ++ i){
A[i] = A[i] * B[i];
}
fft(A,len,-1);
for(int i = 0; i <= n + m; ++ i){
std::cout << (int)(A[i].x / len + 0.5) << ' ';
}
return 0;
}
下面介紹迭代法實現快速傅立葉變換
我們發現,其實 $0 $ 到 \(n - 1\) 的最后位置是已經確定好的了,比如 \(n = 8\) 序列 \(\{0,1,2,3,4,5,6,7\}\) 分治的過程如下:
原序列: \(\{0,1,2,3,4,5,6,7\}\)
一次變換: \(\{0,2,4,6\},\{1,3,5,7\}\)
二次變換: \(\{0,4\},\{2,6\},\{1,5\},\{3,7\}\)
三次變換: \(\{0\},\{4\},\{2\},\{6\},\{1\},\{5\},\{3\},\{7\}\)
最后序列: \(\{0,4,2,6,1,5,3,7\}\)
我們發現了什么規律,沒錯,如果設 \(2^M = n + 1\) 那么設如果二進制一共 \(M\) 位,也就是 \([0,n - 1]\) 都表示成 \(M\) 位多項式,如果位數不夠就前面補 \(0\),那么最終的位置就是 \(i\) 二進制下取反再轉成十進制表示的位置,我們把這樣的操作叫位逆序置換。
- 如何求解位逆序置換:
- 顯然有一個 \(O(n\log n)\) 的做法,對每個數暴力分解二進制然后翻轉,單個數時間復雜度是 \(O(\log n)\) 的,總的就是 \(O(n\log n)\)。
- 但是其實可以 \(O(n)\) 從小到大地求出位逆序置換。
- 我們稱位逆序置換后的數組為 \(R\)
- 首先 \(R_0 = 0\)
- 假設我們已經知道了 \(R(\lfloor \frac{n}{2}\rfloor)\) 我們能否求出 \(R(n)\) 呢?我們發現,其實 \(R(n)\) 就是 \(R(\lfloor \frac{n}{2}\rfloor)\) 二進制下右移一下,但是這充分了嗎?
- 正確規律應該是,如果一個數右移了一位,且如果 \(x\) 末位是 \(1\) 那么就把最高位變成 \(1\),這里因為是右移,所以之前最高位一定是 \(0\),所以可以直接加上 \(2^{M - 1}\)
- 所以我們可以這樣計算一個 \(R(n)\),\(R(n) = \lfloor\frac{R(\lfloor\frac{n}{2}\rfloor)}{2}\rfloor\) 也就是
C++中的右移一位,然后判斷一下此時的 \(R(n)\) 末位是否是 \(1\),如果是 \(1\) 就讓 \(R(n)\rightarrow R(n) + 2 ^ {M - 1}\) - 使用
C++中的位運算可以讓單次操作復雜度降至 \(O(1)\) 總的時間復雜度為 \(O(n)\) - 值得注意的是,最后我們求出來了 \(R\) 數組,并且要 \(i\) 和 \(R\) 交換位置,實際上我們只需要在 \(i < R_i\) 的時候交換就可以了,不然在 \(R_i\) 再進行交換就相互抵消了(我的理解)。
所以我們可以直接把每個位置的最后位置求出來,然后迭代法合并結果即可,具體就是先從小到大枚舉當前分治 區間的長度(這里不是真的分治,是類比之前的分治做法),第二輪枚舉在這個區間長度的前提下所有滿足分治區間長度是當前枚舉區間長度的區間左端點,最后一維則是枚舉每個當前長度左端點的對應區間,復雜度也是 \(O(n\log n)\) 的,但是會比遞歸要快一些。
迭代版本代碼,其中 reverse 函數就是實現求解 \(R\) 的過程。
#include <iostream>
#include <cmath>
using ll = long long;
constexpr int N = 4e6 + 5;
constexpr double Pi = acos(-1);
class complex{
public:
double x,y;
complex operator + (const complex & a){
return (complex){
x + a.x,y + a.y
};
}
complex operator - (const complex & a){
return (complex){
x - a.x,y - a.y
};
}
complex operator * (const complex & a){
// (x + yi) * (a.x + a.yi)
// a.x * x + x * a.yi + a.x * yi + a.yi * yi
// i ^ 2 = - 1
// a.x * x - a.y * y + (a.y * x + a.x * y) i
return (complex){
a.x * x - a.y * y,a.y * x + a.x * y
};
}
}a[N],b[N];
int n,m,len = 1,R[N];
inline void reverse(complex f[],int len){
R[0] = 0;
for(int i = 1; i < len; ++ i){
R[i] = R[i >> 1] >> 1;
if(i & 1){
R[i] |= len >> 1;
}
}
for(int i = 0; i < len; ++ i){
if(i < R[i]){
std::swap(f[i],f[R[i]]);
}
}
}
inline void fft(complex f[],int len,int rev){
reverse(f,len);
for(int L = 2; L <= len; /*下標是 0 ~ n - 1 長度是 n*/ L <<= 1){
complex w_1 = {cos(2 * Pi / L),sin(2 * Pi / L) * rev};
for(int l = 0; l < len; l += L){
complex now = {1,0};
for(int i = l; i < l + L / 2; ++ i,now = now * w_1){
complex g = f[i],h = now * f[i + L / 2];
f[i] = g + h;
f[i + L / 2] = g - h;
}
}
}
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m;
for(int i = 0; i <= n; ++ i){
std::cin >> a[i].x ;
// 讀入實部
}
for(int i = 0; i <= m; ++ i){
std::cin >> b[i].x;
}
for(int k = n + m; len <= k; len <<= 1);
fft(a,len,1);
fft(b,len,1);
for(int i = 0; i <= len; ++ i){
a[i] = a[i] * b[i];
}
fft(a,len,-1);
for(int i = 0; i <= n + m; ++ i){
std::cout << (ll)(a[i].x * 1.0 / len + 0.5) << ' ';
}
return 0;
}
接下來講解另一種多項式乘法的方法:
快速數論變換(NTT)
我們先來回顧一下 FFT,FFT 利用了比較特殊,且有周期性的單位根 \(\omega_n^i\) 從而快速求出 \(n\) 個點值,但是 FFT 運用的是復數,運算多是浮點數運算,具有精度問題,那么有沒有一種算法,能有效規避這種精度而且具有和單位根一樣良好的性質呢?
答曰:有的兄弟,有的,沒錯這就是 NTT
首先我們需要知道 原根:
設一個質數 \(p\) 和一個數 \(a\),滿足 \(\gcd(a,p) = 1\),且存在 \(x\) 滿足 \(a^x \bmod p = 1\) 那么我們就稱 \(x\) 是,稱作 \(a\) 模 \(m\) 的階,記作 \(\delta_m(a)\) 或 \(\operatorname{ord}_m(a)\)
原根:
設 \(m \in \mathbf{N}^{*},
g\in \mathbf{Z}\) 若
\((g,m)=1\),且
\(\delta_m(g)=\varphi(m)\),則稱
\(g\) 為模
\(m\) 的原根。
即 \(g\) 滿足
\(\delta_m(g) = \left| \mathbf{Z}_m^* \right| = \varphi(m)\)
最重要的性質之一:
若一個數 \(m\) 有原根 \(g\),則 \(g,g^2,\ldots,g^{\varphi(m)}\) 構成模 \(m\) 的簡化剩余系。
特別地,當 \(m\) 是質數時,有 \(g^i\bmod m,0 < i < m\) 的結果兩兩不同,這也是 NTT 運用原根的核心部分。
現在我們來考慮把原根和單位根聯系起來:
- 周期性:
- 單位根 \(\omega\) 滿足 \(\omega_n^i = \omega_n^{i + n}\)
- 原根 \(g\) 滿足 \(g^i = g^{i + p - 1},p\) 是質數,這是因為費馬小定理 \(g^{i + p - 1} = g^i g^{p - 1}\),而 \(g^{p - 1} \mod p = 1\)
- 所以不難想到我們應該讓每 \(p - 1\) 作為一個周期,類比單位根,我們應該以 \(\frac{p - 1}{n}\) 作為 \(\omega_n^1\)
- 合法性(亂取的):
- 由于我們確定 \(n\) 次多項式需要 \(n + 1\) 個點值,且滿足橫坐標兩兩不同,而原根則滿足這一點,具體的,因為 \(1 < \frac{p - 1}{n}\) 且 \(n\times (\frac{p - 1}{n}) = p - 1 < p\) 所以自然滿足這 \(n\) 個單位根兩兩不同。
- 可逆性(亂取的):
- 注意到 FFT 的逆運算只需要把單位根變成關于實軸對稱點,也就是 \(\omega_n^i\rightarrow \omega_n^{-i}\) 其實說白了就是給做了個 \(-1\) 次方,因為 \(p\) 是質數,所以 NTT 中的 \(\omega_n^i\) 也是有模意義下的乘法逆元的,最后除以 \(n\) 也只需要乘上 \(n\) 的逆元即可。
那么此時 NTT 中的“單位根”就有和 FFT 中的復數單位根有著相同的作用了。
由于只需要實數(整數)的運算,時間效率明顯快了一些。
NTT 迭代版代碼:
#include <iostream>
using ll = long long;
constexpr int N = 4e6 + 5;
constexpr ll mod = 998244353;
ll a[N],b[N];
int R[N],n,m,len = 1;
inline void reverse(ll f[],int len){
R[0] = 0;
for(int i = 1; i < len; ++ i){
R[i] = R[i >> 1] >> 1;
if(i & 1) R[i] |= len >> 1;
}
for(int i = 0; i < len; ++ i){
if(i < R[i]){
std::swap(f[i],f[R[i]]);
}
}
}
inline ll ksm(ll x,int y){
ll ans = 1;
for(;y;y >>= 1,(x *= x) %= mod){
if(y & 1) (ans *= x) %= mod;
}
return ans;
}
inline void NTT(ll f[],int len,int rev){
reverse(f,len);
for(int L = 2; L <= len; L <<= 1){
ll w_1 = ksm(3,(mod - 1) / L);
if(rev == -1) w_1 = ksm(w_1,mod - 2);
for(int l = 0; l < len; l += L){
ll now = 1;
for(int i = l; i < l + L / 2; ++ i,(now *= w_1) %= mod){
ll g = f[i],h = f[i + L / 2] * now % mod;
f[i] = (g + h) % mod;
f[i + L / 2] = (g - h + mod) % mod;
}
}
}
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m;
for(int i = 0; i <= n; ++ i){
std::cin >> a[i];
}
for(int i = 0; i <= m; ++ i){
std::cin >> b[i];
}
for(int k = n + m; len <= k; len <<= 1);
NTT(a,len,1);
NTT(b,len,1);
for(int i = 0; i < len; ++ i){
(a[i] *= b[i]) %= mod;
}
NTT(a,len,-1);
ll inv = ksm(len,mod - 2);
for(int i = 0; i <= n + m; ++ i){
(a[i] *= inv) %= mod;
std::cout << a[i] << ' ';
}
return 0;
}
分治 FFT(CDQ + NTT)
前置只是:
CDQ 分治思想,快速數論變換(NTT)
題意描述:
給定序列 \(g_{1,...,n - 1}\) 求序列 \(f_{0,...,n - 1}\),其中 \(f_i = \sum_{j = 1} ^ i g_j f_{i - j}\)
首先,我們發現 \(f\) 的計算方式比較特殊,想計算 \(f_i\) 的時候,必須要知道 \(f_{0,...i - 1}\),那么不難想到我們可以類似 CDQ 分治那樣去做,就是先計算分治區間左邊一半的 \(f\),然后去更新右邊的 \(f\),再遞歸右邊,而 CDQ 分治正確的原因就是左邊的區間已經計算好了答案,不會存在左側沒計算完就更新右邊的情況。
設當前我們分治區間是 \([l,r]\),設中點是 \(mid\),我們現在應該計算 \(f_{l,...mid}\) 和 \(g\) 的前 \(mid - l + 1\) 項對 \([mid + 1,r]\) 的 \(f\) 的影響,我們發現,此時已經轉換成了對 \(f_{l,...mid}\) 和 \(g\) 的前 \(mid - l + 1\) 項做卷積,這里要認為 \(f_l\) 是第一個多項式的第一項的系數,然后這樣卷積后的第 \(i\) 項,實際上是 \(l + i\) 的位置,因為剛開始我們讓 \(f\) 往前移了 \(l\) 位,乘法的時候使用 NTT 即可。
根據主定理,時間復雜度是 \(T(n) = 2T(n / 2) + O(n\log n) = O(n\log ^ 2n)\),可以通過。
代碼:
#include <iostream>
using ll = long long;
constexpr int N = 4e5 + 5;
constexpr ll mod = 998244353;
int n,len = 0,R[N];
ll g[N],f[N],a[N],b[N];
inline ll ksm(ll x,ll y){
ll ans = 1;
for(;y;y >>= 1,(x *= x) %= mod){
if(y & 1){
(ans *= x) %= mod;
}
}
return ans;
}
inline void reverse(ll *f,int len){
R[0] = 0;
for(int i = 1; i < len; ++ i){
R[i] = R[i >> 1] >> 1;
if(i & 1){
R[i] |= len >> 1;
}
}
for(int i = 0; i < len; ++ i){
if(i < R[i]) std::swap(f[i],f[R[i]]);
}
}
inline void NTT(ll *f,int len,int rev){
reverse(f,len);
for(int L = 2; L <= len; L <<= 1){
ll w_1 = ksm(3,(mod - 1) / L);
if(rev == -1){
w_1 = ksm(w_1,mod - 2);
}
for(int l = 0; l < len; l += L){
ll w_now = 1;
for(int i = l; i < l + L / 2; ++ i){
ll g = f[i],h = w_now * f[i + L / 2] % mod;
f[i] = (g + h) % mod;
f[i + L / 2] = (g - h + mod) % mod;
(w_now *= w_1) %= mod;
}
}
}
if(rev == -1){
for(int i = 0; i < len; ++ i){
f[i] = f[i] * ksm(len,mod - 2) % mod;
}
}
}
inline void solve(int l,int r){
if(l == r){
if(!l) f[l] = 1;
return;
}
int mid = (l + r) >> 1;
solve(l,mid);
for(int i = l; i <= mid; ++ i){
a[i - l] = f[i];
}
for(int i = 1; i <= r - l + 1; ++ i){
b[i] = g[i];
}
len = 1;
for(;len <= r - l + 1; len <<= 1);
for(int i = mid - l + 1; i < len; ++ i){
a[i] = 0;
}
for(int i = r - l + 2; i < len; ++ i){
b[i] = 0;
}
NTT(a,len,1);NTT(b,len,1);
for(int i = 0; i < len; ++ i){
(a[i] *= b[i]) %= mod;
}
NTT(a,len,-1);
for(int i = mid + 1; i <= r; ++ i){
(f[i] += a[i - l]) %= mod;
}
solve(mid + 1,r);
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for(int i = 1; i < n; ++ i){
std::cin >> g[i];
}
solve(0,n - 1);
for(int i = 0; i < n; ++ i){
std::cout << f[i] << ' ';
}
return 0;
}
多項式求逆
前置知識:
快速數論變換(NTT),模意義下的乘法逆元。
題意描述:
給定 \(n - 1\) 次多項式 \(f(x) = \sum_{i = 0}^{n - 1} a_ix^i\),求一個 \(n - 1\) 次多項式 \(g\),滿足 \(f\times g \equiv 1 \pmod {x ^ n}\)
首先,一個 \(n\) 次多項式 \(f\),對 \(x ^ k\) 次方取模的結果如下:
- 若 \(k > n\) 那么取模后 \(f\) 不變。
- 否則 \(f\rightarrow \sum_{i = 0}^{k - 1} a_i x ^ k\) 也就是保留 \(f\) 的前 \(k\) 項。
那么由于本題是 \(n - 1\) 次多項式,而要求對 \(x ^ n\) 取模,所以等價于找到一個多項式 \(g\),滿足 \(g\) 只有常數項是 \(1\),其他項系數都是 \(0\)
考慮分治處理這個問題
首先不妨設 \(n = 2 ^ k,k\in N\)
下面分兩種情況:
- 當 \(n = 1\) 的時候,就是求解 \(f_0\times g_0\equiv 1\pmod {x ^ 1}\),顯然此時 \(g_0 = {f_0}^{-1}\),求 \(f_0\) 的逆元作為 \(g_0\) 即可。
- 當 \(n > 1\) 的時候:
- 假設我們已經求出來了 \(f\) 在模 \(x^{\frac{n}{2}}\) 的時候符合要求的 \(g\),記為 \(g'\)。
- 那么自然有 \(g'f \equiv 1\pmod{x ^ {\frac{n}{2}}}\)
- 即:\(g'f - 1\equiv 0\pmod{x ^ {\frac{n}{2}}}\)
- 由于 \(x\equiv 0\pmod{p}\) 那么有 \(x^2 \equiv 0\pmod {p ^ 2}\)
- 證明:因為 \(x\equiv 0\pmod{p}\) 所以 \(x\bmod p = 0\) 即,\(x = kp,k\in Z\),那么 \(x ^ 2 = k ^ 2p ^ 2 = (kp) ^ 2\),因為 \(k\in Z\) 所以 \(k ^ 2\in Z\),所以 \(x ^ 2\bmod p = 0\),所以 \(x ^ 2\equiv 0\pmod{p ^ 2}\)。
- 那么我們把左右兩邊同時平方,根據完全平方公式得:\((g'f) ^ 2 + 1 - 2g'f\equiv 0\pmod{x ^ n}\),即:\((g'f)^2 - 2g'f \equiv -1\pmod{x ^ n}\)
- 兩邊乘 \(-1\) 得:\(2g'f - (g'f) ^ 2\equiv 1\pmod{x ^ n}\)
- 設 \(gf\equiv 1\pmod{x ^ n}\)
- 那么聯立上方兩個式子,得到:\((g'f) ^ 2 - 2g'f\equiv gf\pmod{x ^ n}\)
- 兩邊同時除以 \(f\) 得:\(f{g'} ^ 2 - 2g'\equiv g\pmod{x ^ n}\),那么根據這個公式就可以求解 \(g\) 了。
由于我們計算模 \(x ^ n\) 的符合的 \(g\) 時只需要知道模 \(x ^ {\frac{n}{2}}\) 的符合的 \(g'\)
所以我們時間復雜度根據主定理是 \(T(n) = T(n / 2) + O(n\log n) = O(n\log n)\)
一個細節就是,遞歸的時候長度應該要設成 \(2 \times n\) 而不是 \(n\),因為 NTT 的時候需要二的冪次,而 \(f\) 是 \(n\) 項的,\(g'\) 是 \(\frac{n}{2}\) 項的,取二的整次冪就是 \(2\times n\)
思考:如果求一個 \(n - 1\) 次多項式 \(f(x)\) 此時不是對 \(x ^ n\) 取模,而是對 \(m < n\) 的 \(x ^ m\) 取模呢?
我們發現此時只有 \(f(x)\) 的前 \(m\) 項式有用的,所以直接等價于求解一個 \(m - 1\) 次多項式,對 \(x ^ m\) 取模了。
代碼:
#include <iostream>
constexpr int N = 4e5 + 5;
using ll = long long;
constexpr ll mod = 998244353;
ll ksm(ll x,ll y){
ll ans = 1;
while(y){
if(y & 1) (ans *= x) %= mod;
(x *= x) %= mod;
y >>= 1;
}
return ans;
}
ll inv(ll x){
return ksm(x,mod - 2);
}
int R[N * 2];
inline void reverse(ll f[],int n){
R[0] = 0;
for(int i = 1; i < n; ++ i){
R[i] = R[i >> 1] >> 1;
if(i & 1){
R[i] |= n >> 1;
}
}
for(int i = 0; i < n; ++ i){
if(i < R[i]){
std::swap(f[i],f[R[i]]);
}
}
}
inline void NTT(ll f[],int n,int rev){
reverse(f,n);
for(int L = 2; L <= n; L <<= 1){
ll w_1 = ksm(3,(mod - 1) / L);
if(rev == -1){
w_1 = inv(w_1);
}
for(int l = 0; l < n; l += L){
ll w_now = 1;
for(int i = l; i < l + L / 2; ++ i){
ll g = f[i],h = w_now * f[i + L / 2] % mod;
f[i] = (g + h) % mod;
f[i + L / 2] = (g - h + mod) % mod;
(w_now *= w_1) %= mod;
}
}
}
if(rev == -1){
ll inv_n = inv(n);
for(int i = 0; i < n; ++ i){
(f[i] *= inv_n) %= mod;
}
}
}
ll c[N],d[N];
inline void solve(ll a[],ll b[],int n){
if(n == 1){
b[0] = inv(a[0]);
return;
}
for(int i = 0; i <= n * 2; ++ i){
c[i] = d[i] = 0;
}
solve(a,c,n >> 1);
for(int i = 0; i < n; ++ i){
d[i] = a[i];
}
NTT(d,n << 1,1);NTT(c,n << 1,1);
for(int i = 0; i < n * 2; ++ i){
b[i] = (2 * c[i] - d[i] * c[i] % mod * c[i] % mod + mod) % mod;
}
NTT(b,n << 1,-1);
for(int i = 0; i < n; ++ i){
b[i + n] = 0;
}
}
int n,len = 0;
ll a[N],b[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for(int i = 0; i < n; ++ i){
std::cin >> a[i];
}
for(len = 1; len <= n; len <<= 1);
solve(a,b,len);
for(int i = 0; i < n; ++ i){
std::cout << b[i] << ' ';
}
return 0;
}
多項式除法
定義:
\(f = gq + r\)
其中,如果 \(f\) 是一個 \(n\) 次多項式,\(g\) 是 \(m\) 次多項式,那么 \(q\) 是 \(n - m\) 次多項式,\(h\) 是小于 \(m\) 次多項式
我們令 \(f' = rev(f)\) 即把 \(f\) 的系數翻轉,\(f'(x) = \sum_{i = 0}^n a_ix^{n - i}\),其實 \(f'(x) = f(\frac{1}{x})x ^ n\)
那么有 \(f(x) = g(x)q(x) + r(x)\)
把 \(\frac{1}{x}\) 帶入得到:\(f(\frac{1}{x}) = g(\frac{1}{x})q(\frac{1}{x}) + r(\frac{1}{x})\)
等式兩邊同時乘上 \(x ^ n\) 得到:\(f(\frac{1}{x})x^n = g(\frac{1}{x})x ^ mq(\frac{1}{x})x ^ {n - m} + r(\frac{1}{x})x ^ n\)
\(f' = g'q' + r'x^{n - m + 1}\),這里因為 \(deg_r < m\) 所以最大是 \(m - 1\),那么剩余的冪次就是 \(n - (m - 1) = n - m + 1\)
那么移項得:\(f' - g'q' = r'x^{n - m + 1}\)
注意到此時如果我們對等式兩邊同時對一個數 \(x\) 取模,等式兩邊是同余的,那么我們讓等式兩邊同時對 \(x ^ {n - m + 1}\) 取模,由于等式右邊最低次冪是 \(n - m + 1\) 所以等式右邊對 \(x ^ {n - m + 1}\) 取模后,右邊應該是 \(0\),所以 \(f' - g'q'\equiv 0\pmod{x ^ {n - m + 1}}\)
移項得:\(f'\equiv g'q'\pmod{x ^ {n - m + 1}}\)
同時除以 \(g'\) 得:
\(\frac{f'}{g'}\equiv q'\pmod{x ^ {n - m + 1}}\)
注意到 \(q'\) 的次數是 \(n - m\) 所以可以直接把 \(q'\) 的系數再翻轉回去求出 \(q\)
那么知道 \(q\),很容易也能求出 \(r\) 了,也就是 \(r = f - gq\)
時間復雜度是求逆元的復雜度為 \(O(n\log n)\)
代碼:
#include <iostream>
#include <algorithm>
#define int long long
constexpr int N = 6e5 + 5,mod = 998244353;
int n,m,f[N],g[N],rev_f[N],rev_g[N],inv_g[N],q[N],r[N];
inline int ksm(int x,int y){
int ans = 1;
for(;y; y >>= 1,(x *= x) %= mod){
if(y & 1) (ans *= x) %= mod;
}
return ans;
}
struct poly{
int R[N],c[N * 2],d[N * 2];
inline void reverse(int f[],int n){
R[0] = 0;
for(int i = 1; i < n; ++ i){
R[i] = R[i >> 1] >> 1;
if(i & 1){
R[i] |= n >> 1;
}
}
for(int i = 0; i < n; ++ i){
if(i < R[i]){
std::swap(f[i],f[R[i]]);
}
}
}
inline void NTT(int f[],int n,int rev){
reverse(f,n);
for(int L = 2; L <= n; L <<= 1){
int w_1 = ksm(3,(mod - 1) / L);
if(rev == -1) w_1 = ksm(w_1,mod - 2);
for(int l = 0; l < n; l += L){
int w_now = 1;
for(int i = l; i < l + L / 2; ++ i,(w_now *= w_1) %= mod){
int g = f[i],h = w_now * f[i + L / 2] % mod;
f[i] = (g + h) % mod;
f[i + L / 2] = (g - h + mod) % mod;
}
}
}
if(rev == -1){
int inv_n = ksm(n,mod - 2);
for(int i = 0; i < n; ++ i){
(f[i] *= inv_n) %= mod;
}
}
}
inline void inv(int a[],int b[],int len){
if(len == 1){
b[0] = ksm(a[0],mod - 2);
return;
}
for(int i = 0; i <= (len << 1); ++ i){
c[i] = d[i] = 0;
}
inv(a,c,(len + 1) >> 1);
for(int i = 0; i < len; ++ i){
d[i] = a[i];
}
NTT(c,len << 1,1);
NTT(d,len << 1,1);
for(int i = 0; i < (len << 1); ++ i){
b[i] = (c[i] * 2 % mod - c[i] * c[i] % mod * d[i] % mod + mod) % mod;
}
NTT(b,len << 1,-1);
for(int i = 0; i < len; ++ i){
b[i + len] = 0;
}
}
inline void Inv(int f[],int g[],int n){
int len = 1;
for(;len <= n; len <<= 1);
inv(f,g,len);
}
inline void mul(int f[],int g[],int n){
int len = 1;
for(;len <= n; len <<= 1);
NTT(f,len,1);
NTT(g,len,1);
for(int i = 0; i < len; ++ i){
(f[i] *= g[i]) %= mod;
}
NTT(f,len,-1);
}
}P;
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m;
for(int i = 0; i <= n; ++ i){
std::cin >> f[i];
rev_f[n - i] = f[i];
}
for(int i = 0; i <= m; ++ i){
std::cin >> g[i];
rev_g[m - i] = g[i];
}
for(int i = n - m + 1; i <= m; ++ i){
rev_g[i] = 0;
}
P.Inv(rev_g,inv_g,n - m + 1);
P.mul(rev_f,inv_g,(n << 1) + m);
for(int i = 0; i <= n - m; ++ i){
q[i] = rev_f[n - m - i];
std::cout << q[i] << ' ';
}
std::cout << '\n';
P.mul(g,q,n);
for(int i = 0; i < m; ++ i){
r[i] = (f[i] - g[i] + mod) % mod;
std::cout << r[i] << ' ';
}
return 0;
}
FWT 快速沃爾什變換
FWT 通常用于處理位運算的卷積運算,形如 \(C_i = \sum_{i = j + k} A_j . B_k\) 其中,\(.\) 分別代表 \(\mid,\text{\&},\oplus\) 也就是或,與和異或。
FWT 具有線性性,即 \(FWT(A + B) = FWT(A) + FWT(B)\),還有 \(FWT(\lambda A) = \lambda FWT(A)\)
下面來看這個題:
分別求:
\(C_i = \sum_{j\mid k = i} A_j B_k\\ C_i = \sum_{j\text{\&} k = i} A_j B_k\\ C_i = \sum_{j\oplus k = i} A_j B_k\)
我們分別來看看如何求解:
或(or)卷積:
類比 FFT 的方法,我們讓 \(A\rightarrow FWT_A,B\rightarrow FWT_B\),然后令 \(FWT_C = FWT_A\times FWT_B\),然后讓 \(FWT_C\rightarrow C\) 即可得到 \(C\)
對于或卷積,令 \({FWT_A}_i = \sum_{j\subseteq i} A_j\),同理設出 \(FWT_B\),下面證明 \(FWT_C = FWT_A\times FWT_B\)
證明:
\({FWT_C}_k = {FWT_A}_k \times {FWT_B}_k\)
- \({FWT_A}_k \times {FWT_B}_k = (\sum_{p\subseteq k} A_p)(\sum_{q\subseteq k } B _q)\)
- \(p\subseteq k,q\subseteq k\Leftrightarrow p\mid q\subseteq k\)
- \({FWT_A}_k \times {FWT_B}_k = (\sum_{p\subseteq k} A_p)(\sum_{q\subseteq k } B _q) = \sum_{p\mid q\subseteq k} A_p B_q = {FWT_C}_k\)
根據這個式子我們可以分治解決,設當前分治區間前一半是 \(A_0\),后一半是 \(A_1\),那么 \(FWT\) 當前區間等于 \(\text{merge}(FWT_{A_0},FWT_{A_0} + FWT_{A_1})\) 這里 + 是按位相加,merge 類似字符串拼接,把前后拼起來組成 \(FWT\) 序列。
說一下為啥,注意到對于 \(A_0\) 的第 \(i\) 個數,他對應的 \(A_1\) 的第 \(i\) 個數,在二進制表示下只是比 \(A_0\) 最高位多了一個 \(1\),所以 \(A_0\) 的第 \(i\) 個數也是 \(A_1\) 的第 \(i\) 個數的子集,也就是 \(A_0\subseteq A_1\) 所以要把 \(FWT_{A_0}\) 的貢獻也要加到 \(FWT_{A_1}\) 的對應位置上。
逆變換:
考慮如何根據 \(FWT_A\) 來還原 \(A\) 的值,注意到 \(\text{merge}\) 的時候是 \(\text{merge}(FWT_{A_0},FWT_{A_0} + FWT_{A_1})\),那么我們要還原就是把 \(A_1\) 的位置減去之前 \(FWT_{A_0}\) 的貢獻。
于是可以和 FFT 一樣去迭代計算即可,或卷積的代碼:
inline void FWT_or(int *f,int rev){
for(int L = 2; L <= (1 << n); L <<= 1){
for(int l = 0; l < (1 << n); l += L){
for(int i = l; i < l + L / 2; ++ i){
(f[i + L / 2] += f[i] * rev % mod) %= mod;
}
}
}
}
接下來講與卷積:
類比或卷積,我們設 \({FWT_A}_i = \sum_{i\subseteq j} A_j\),也就是 \(i\) 的超集的和。
下面證明 \({FWT_C}_k = {FWT_A}_k \times {FWT_B}_k\)
證明:
- \({FWT_A}_k\times {FWT_B}_k = (\sum_{k\subseteq p} A_p)(\sum_{k\subseteq q} B_q)\)
- \(k\subseteq p,k\subseteq q\Leftrightarrow k\subseteq p\text{\&} q\)
- 所以 \({FWT_A}_k\times {FWT_B}_k = (\sum_{k\subseteq p} A_p)(\sum_{k\subseteq q} B_q) = \sum_{k\subseteq p\text{\&} q} A_p B_q = {FWT_C}_k\)
那么類比剛剛的 \(\text{merge}\),得到現在的 \(\text{merge}\) 就是 \(FWT(A) = \text{merge}(FWT_{A_0} + FWT_{A_1},FWT_{A_1})\)
這個也很好解釋,就是對于 \(A_0\) 的第 \(i\) 個數,他和 \(A_1\) 的第 \(i\) 個數的唯一差別就是最高位沒有 \(1\)(這個同上面的或卷積),所以 \(A_1\) 的第 \(i\) 個數包含的超集 \(A_0\) 的第 \(i\) 個數也包含,所以有這個 \(\text{merge}\) 的過程。
與卷積的代碼:
inline void FWT_and(int *f,int rev){
for(int L = 2; L <= (1 << n); L <<= 1){
for(int l = 0; l < (1 << n); l += L){
for(int i = l; i < l + L / 2; ++ i){
(f[i] += f[i + L / 2] * rev % mod) %= mod;
}
}
}
}
異或卷積:
這個卷積是最難的也是最妙的,首先定義 \(x\circ y = popcount(x\text{\&} y)\bmod 2\),定義 \({FWT_A}_i = \sum_{j\circ i = 0} A_j - \sum_{k\circ i = 1} A_k\)
\(FWT[A]_i=\sum_{i\circ j=0}A_j-\sum_{i\circ j=1}A_j\)。我們來證一下
\(FWT[C] = FWT[A] \cdot FWT[B]\) 的正確性:
\(\begin{aligned} FWT[A]_iFWT[B]_i&=\left(\sum_{i\circ j=0}A_j \sum_{i\circ j=1}A_j\right)\left(\sum_{i\circ k=0}B_k-\sum_{i\circ k=1}B_k\right) \\ &=\left(\sum_{i\circ j=0}A_j\sum_{i\circ k=0}B_k+\sum_{i\circ j=1}A_j\sum_{i\circ k=1}B_k\right)-\left(\sum_{i\circ j=0}A_j\sum_{i\circ k=1}B_k+\sum_{i\circ j=1}A_j\sum_{i\circ k=0}B_k\right) \\ &=\sum_{(j\oplus k)\circ i=0}A_jB_k-\sum_{(j\oplus k)\circ i=1}A_jB_k \\ &=FWT[C]_i \end{aligned}\)
根據定義,易得 \(\text{merge}\) 為 \(FWT_A = \text{merge}(FWT_{A_0} + FWT_{A_1},FWT_{A_0} - FWT_{A_1})\),可以理解成左邊無論右邊什么最高位and 起來都是 \(0\),而 \(0\) 屬于正貢獻,所以加上右邊,右邊則相反。
逆變換:
\(IFWT[A'] = \text{merge}(\frac{IFWT[A_0'] + IFWT[A_1']}{2}, \frac{IFWT[A_0'] - IFWT[A_1']}{2})\)
逆變換的兩種解釋方法:根據 qyc 老師的原話,\(FWT\) 的異或卷積可以看作是每一位膜 \(z^2 - 1\) 的 \(FFT\) 的乘法原因就是把 \(0\) 看作 \(0\) 次項,而 \(1\) 看作一次項,那么這個多項式不斷乘 \(z^2\) 由于異或的性質兩兩抵消所以等于膜 \(z^2\) 的結果為 \(1\),所以就是對 \(z^2 - 1\) 取模。
還有一種是根據方程組來解釋,由于逆變換就是我們要把 \((a,b)\) 給還原出來 \((x,y)\),易得:\((x + y,x - y) = (a,b)\),易得 \((x,y)\) 的值,異或卷積代碼:
inline void FWT_xor(int *f,int rev){
for(int L = 2; L <= (1 << n); L <<= 1){
for(int l = 0; l < (1 << n); l += L){
for(int i = l; i < l + L / 2; ++ i){
int g = f[i] * rev % mod,h = f[i + L / 2] * rev % mod;
(f[i] = (g + h) % mod) %= mod;
(f[i + L / 2] = (g - h + mod) % mod) %= mod;
}
}
}
}
子集卷積
模版,求 \(f(i) = \sum_{j\mid k = i,j\text{\&} k = 0} a_j b_k\)
我們發現此時要求的是或是 \(i\) 但是不能相交,不難發現這個第一個限制很簡單就是 FWT 的板子,但是第二個有些困難,但是別忘了,我們可以在原來基礎上再加一個維度表示選的子集的集合大小,具體的,設 \(g(S,i) = \sum_{T\subseteq S} [popcount(T) = i] a_T\) 這個顯然可以預處理,然后我們設 \(f\) 是 \(g\) 和 \(h\) 乘起來的結果,那么我們可以讓 \(f(i,j) = \sum_{k = 0} ^ j g(i,k)\times h(i,j - k)\) 但是這樣的滿足條件的會有相交的嗎,我們發現他們相交不相交并沒有什么問題,但是如果他們相交,那么他們并起來的長度就不是 \(i\) 了,在 IFWT 的時候自然不會被計算進去,所以我們可以這樣算出來 \(f\),然后再對每個可能的長度 \(i\in [1,n]\) 都算一遍 IFWT,時間復雜度 \(O(n ^ 22 ^ n)\)
特別鳴謝 qyc 老師的教導,他解釋了為什么 \(|s| + |t| \rightarrow |s\mid t|\) 一定是正確的,首先我們有暴力對吧,首先做對 \(A,B\) 分別做 \(FWT\),這個時候一個暴力的想法是我們暴力枚舉兩狀態 \(S,T\),然后把 \({FWT_A}(S,i)\times {FWT_B}(T,j)\rightarrow {FWT_C}({S\mid T},i + j)\) 這樣盡管可能 \(popcount(S\mid T)\ne |S| + |T|\) 但是我們壓根不會考慮這種情況,因為我們最后都是取那些 \({IFWT_C}(S,popcount(S))\) 的取計算答案,所以那些不合法的點自然會被篩掉,根據 qyc 老師的話是,我們發現最后從 \({FWT_A}(S,i)\times {FWT_B}(T,j)\rightarrow {FWT_C}({S\mid T},i + j)\) 的過程其實內部就是或卷積,所以此時直接 IFWT 是不會算重的,還有一種我自己的角度考慮,IFWT 的或卷積實際上是高維差分,所以如果不合法會在之前合法的時候被差分掉,不是很嚴謹感性理解即可。
第二類斯特林數
形式如下,給定 \(N\) 個不同的球,把它們放到 \(M\) 個相同的集合,不能有空集,自然有 \(M \leq N\),求方案數,對 \(N\) 的每個 \(0\leq M\leq N\) 都算答案。
遞推式
\(\begin{Bmatrix}n\\ k\end{Bmatrix}=\begin{Bmatrix}n-1\\ k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\ k\end{Bmatrix}\)
邊界是
\(\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]\)。
感性證明法好,實際就是對于第 \(i\) 個球,要么單開一個,要么去之前分好的箱子里面,正確性顯然。
性質:
$\Large{m ^ n} = \Large{\sum_{i =0} ^ m} \begin{Bmatrix}n\ i\end{Bmatrix}\Large{\Large{\binom{n}{i}} i!} $ 這也是唯一的性質了,左邊相當于可以有空集,右邊相當于計算有多少種可能的。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號