進階線段樹

線段樹：

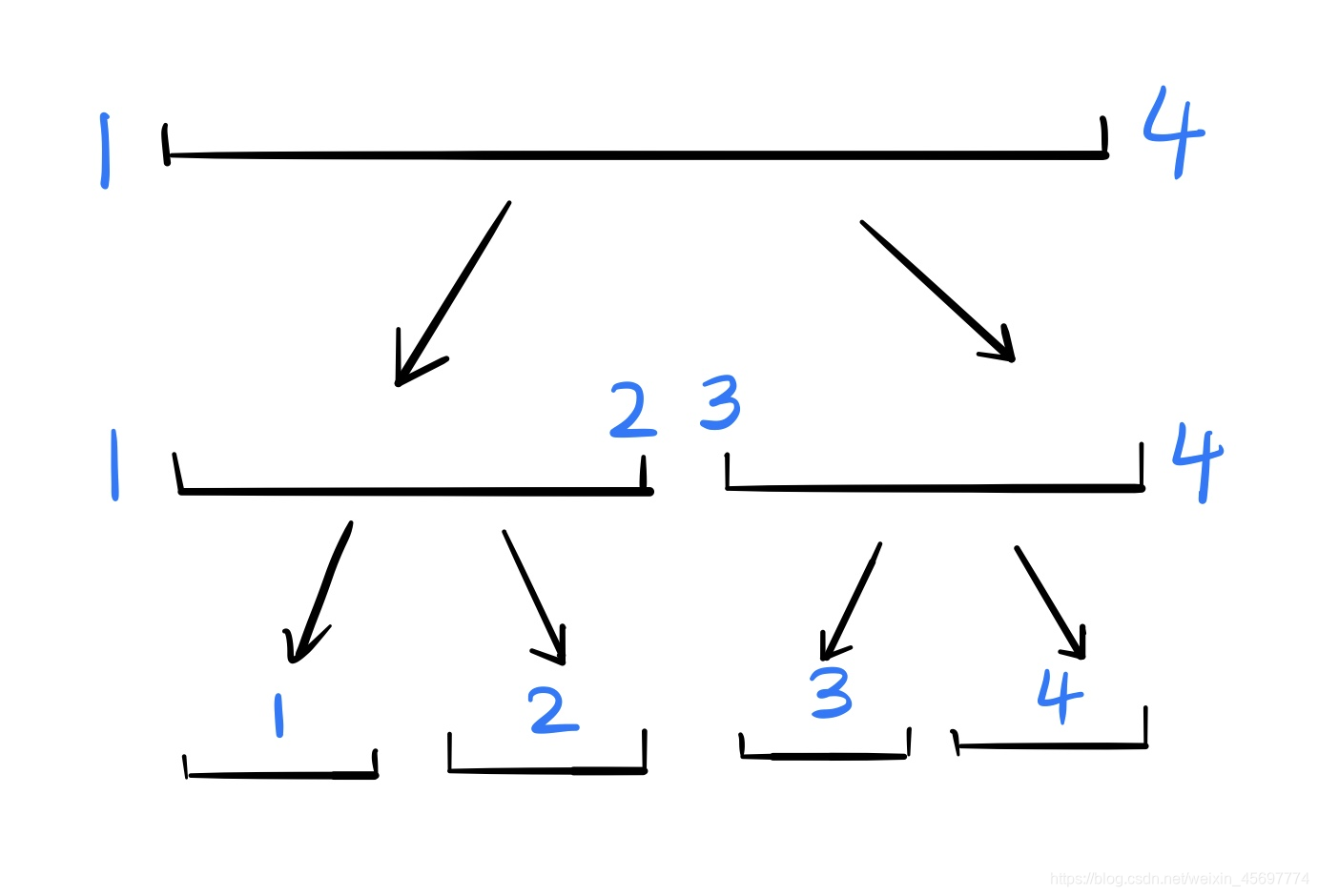
這是一個線段樹的例圖。

我們可以發現其實線段樹就是將幾個連續的小區間拼湊成一個個大區間的過程，從而實現查找時的優秀的復雜度。

引入-分塊基礎的思想：

其實如果你知道分塊的思想，那么你會更好理解線段樹的思想，分塊就是將一個序列分成 \(\sqrt N\) 個塊每個塊的塊長就是 \(N / \sqrt N = \sqrt N\) 每次維護一個區間的信息就會通過零塊暴力，整塊直接對這個塊做標記，其實這個標記和線段樹的懶標記是一樣的道理。只不過線段樹是一個樹形的結構。

線段樹的懶標記：

既然我們知道了線段樹的懶標記的大致的作用那么我們該如何去實現呢？
其實不難就是在查詢和修改時多了一些維護的東西。

常見的修改題型有以下幾種：

將區間 \([l,r]\) 的數加 \(k\) 。
將區間 \([l,r]\) 的數乘 \(k\) 。
將區間 \([l,r]\) 的數統一賦值為 \(k\) 。
將區間 \([l,r]\) 的數統一開平方。
將區間 \([l,r]\) 的值統一都取反(僅用于數組內所有數都為 0|1)

常見的查詢題型有以下幾種：

輸出 \(\Sigma_{i=l}^r a_i\)
輸出 \([l,r]\) 中的最大值。
輸出 \([l,r]\) 中的最小值。
輸出 \([l,r]\) 中的所有數的乘積。

今天我們主要圍繞這幾個方面進行講解

例題1

首先先看修改操作：

我們分析下這個對于區間 \([l,r]\) 的數加 \(k\)，用 t 數組表示總和，用 lz 數組表示懶標記。
那么對于 \(t_i\) 顯然表示 \(i\) 這顆子樹的總和， \(lz_i\) 表示 \(i\) 這顆子樹的加標記是多少。
1.修改時如果是當前的區間完全覆蓋線段樹某一個節點所對應的區間，那么就將這個節點的 \(t_i\) 所對應的區間的每一個數的值統一加上 \(k\) 具體的，將區間 \([l_i-r_i]\) 加上 \(k\) 因為這個區間的長度是 \(r_i-l_i+1\) 所以 \(t_i\) 的值應該加上 \((r_i-l_i+1) \times k\) 那么對于 \(lz\) 數組我們直接將他加上 \(k\) 即可表示這顆子樹統一被加上了 \(k\)。
2.如果是零塊，那么就將這個節點的信息傳到他的左右兒子節點，即 pushdown 函數，因為這樣可以方便零塊去繼續遞歸繼續修改。
由于線段樹為 \(\log_2 N\) 層，所有單次的時間復雜度會為 \(O(\log_2 N)\) 十分高效。
以上就是修改操作的核心。

再看查詢操作：

設查詢的區間為 \([l,r]\) 則如果遞歸到一個節點使得 \([l,r]\) 能完全覆蓋這個節點所對應的區間，那么就直接加上這個節點的信息，否則遞歸，知道能被 \([l,r]\) 的區間完全覆蓋。

查詢的細節：

查詢時應該查詢什么值呢？
肯定是查詢 \(t\) 數組的值，因為 \(t\) 數組代表這個子樹的和。
需要注意的時查詢時也需要將標記下傳。
查詢相對于修改就好理解了許多。

例題1-tag&pushdown部分的代碼：

void tag(int p,int l,int r,ll k){
	t[p]+=(r-l+1)*k;
	lz[p]+=k;
}
void pushdown(int p,int l,int r){
	int mid=(l+r)>>1;
	tag(ls(p),l,mid,lz[p]);
	tag(rs(p),mid+1,r,lz[p]);
	lz[p]=0;
}

因為前面已經講過如何修改了，所以這里不再復述。

例題2

修改部分：

根據數學知識我們知道 \((x+y)k = xk + yk\) 線段樹中也是基于這個原理對于區間乘法，如果我們的 \(t\) 數組的值為 \(x\)， \(lz\) 數組的值為 \(y\)
設區間總值為 \(sum\) 設乘標記為 \(z\) 則實際的區間總和應該為 \(sum\times z+y\) 如果將這個整體乘 \(k\) 則根據乘法分配律得 \((sum\times z+y)\times k = (sum\times k) \times (z\times k) + y \times k\) 也就是 \(sum,z,y\) 都相比于原來乘了一個 \(k\) 因為這個涉及到乘法所有乘標記清空的狀態應該是 1 而不是 0。
查詢自然和線段樹 1 相同，不再復述。

例題2-tag&pushdown 代碼：

void tag(int p,int l,int r,ll k,bool add){
	/*add表示是否為加法標記*/
	if(add){
		t[p].t=(t[p].t+(r-l+1)*k%m)%m;
		/*總和變化*/
		t[p].z1=(t[p].z1+k)%m;
		/*加法標記變化*/
	}else{
		t[p].t=t[p].t*k%m;
		/*總和變化*/
		t[p].z1=t[p].z1*k%m;
		t[p].z2=t[p].z2*k%m;
		/*加法標記與乘法標記都乘k*/
	}
}
void push_down(int p,int l,int r){
	int mid=(l+r)>>1;
	tag(ls(p),l,mid,t[p].z2,false);
	tag(rs(p),mid+1,r,t[p].z2,false);
	t[p].z2=1;
	/*下傳乘法標記*/
	tag(ls(p),l,mid,t[p].z1,true);
	tag(rs(p),mid+1,r,t[p].z1,true);
	t[p].z1=0;
	/*下傳加法標記*/
}

例題3

這道題涉及到區間賦值的問題。

設原來的子樹總和為 \(sum\) 需要賦值的數為 \(k\) 那么我們將 \(lz\) 的值清零即可因為統一賦值，再將賦值的標記變為 \(k\) 即可。其次我們將 \(sum\) 改為 \(k\times (r_i-l_i+1)\) 這里很好理解就是把 \(sum\) 設為要賦值的數乘區間的長度即可。
單本題讓我們維護區間最值，這個更簡單，直接將最值改為 \(k\) 即可。

例題3-tag&pushdown 代碼：

void tag(int p,int l,int r,ll k,int o){
	if(o==1){
		/*區間賦值*/
		t[p]=k;
		z1[p]=0;z2[p]=k;
	}else{
		/*區間加法*/
		t[p]+=k;
		z1[p]+=k;
	}
}
void push_down(int p,int l,int r){
	int mid=(l+r)>>1;
	if(z2[p]!=NONE){
		/*有區間賦值標記*/
		tag(ls(p),l,mid,z2[p],1);
		tag(rs(p),mid+1,r,z2[p],1);
		z2[p]=NONE;
	}
	if(z1[p]){
		/*有區間加法標記*/
		tag(ls(p),l,mid,z1[p],2);
		tag(rs(p),mid+1,r,z1[p],2);
		z1[p]=0;
	}
}

簡單提一下區間取反和區間開平方：

區間取反：

對于區間取反會有一個特點，0 變成 1 反之變成 0 所以統計答案的時候應該把 \(t_i = r_i-l_i+1-t_i\) 就是用總長度減去以前在長度，即為取反后的長度。

區間開方：

本題的操作是區間開方和區間查詢，但區間開方不能直接用 Lazy-Tag 實現。本題的關鍵是：一個數如果被開方7次，那么它一定會變為1，后面再怎么開方也還是1。于是我們可以記錄一個區間中是否有不為1的數，在修改時，如果都為1，直接跳過。

線段樹在其他算法中在組合應用：

樹鏈剖分算法：

樹鏈剖分是一個常見的線段樹與重鏈之間的組合的算法，他的思想是對于每一條鏈和一個子樹，它在線段樹上的標號總是連續的因此就可以用線段樹的相關知識去實現快速的加減求和。
樹鏈剖分中使用線段樹修改查詢部分的代碼：

inline void update1(int x,int y,int k){
	while(t[x].tot!=t[y].tot){
		if(t[t[x].tot].d<t[t[y].tot].d)swap(x,y);
		seg.upd(1,1,n,t[t[x].tot].id,t[x].id,k);
		x=t[t[x].tot].fa;
	}
	if(t[x].d>t[y].d)swap(x,y);
	seg.upd(1,1,n,t[x].id,t[y].id,k);
}
inline int query1(int x,int y){
	int ans=0;
	while(t[x].tot!=t[y].tot){
		if(t[t[x].tot ].d<t[t[y].tot ].d )swap(x,y);
		ans+=seg.que(1,1,n,t[t[x].tot].id,t[x].id)%mod;
		x=t[t[x].tot].fa;
	}
	if(t[x].d>t[y].d)swap(x,y);
	ans+=seg.que(1,1,n,t[x].id,t[y].id )%mod;
	return ans%mod;
}
inline void update2(int x,int k){
	seg.upd(1,1,n,t[x].id,t[x].id+t[x].sz-1,k);
}
inline int query2(int x){
	return seg.que(1,1,n,t[x].id,t[x].id+t[x].sz-1)%mod;
}