Efficient Construction of Approximate Call Graphs for JavaScript IDE Services

Introduction

文章提出了 a field-based flow analysis for constructing call graphs。Java 基于 class-hierarchy 的方法并不適用于 JavaScript：JavaScript 是動態類型的，使用基于 prototype 的面向對象機制而且具備“一等函數”的函數式性質。Flow-analysis 比如 Andersen 指針分析則不夠 scalable。這篇文章的主要貢獻在于：

• Field-based analysis：e.f 會在分析過程中被記錄為一個 f 結點，忽略 e，也就是說不能分析 f 是哪個對象的字段

• Only tracks function objects：只關注 callgraph 的構建

• Ignores dynamic property access：忽略動態字段的訪問（即使這會使得分析是 unsound 的）

Analysis Formulation

Flow graph 的構建基于 AST。

Intraprocedural Flow

過程內的 flow graph 有下面幾種結點：

\(\text{Exp}(\pi)\) 是 \(\pi\) 位置的表達式的值結點

\(\text{Var}(\pi)\) 是 \(\pi\) 位置定義的變量結點

\(\text{Prop}(f)\) 是名稱為 f 的字段結點，代碼中的實現如下：

function propVertex(nd) {
    var p;
    if(nd.type === 'Identifier')
      p = nd.name;
    else if(nd.type === 'Literal')
      p = nd.value + "";
    else
      throw new Error("invalid property vertex");

    return propVertices.get(p, { type: 'PropertyVertex',
                                 name: p,
                                 attr: { pp: function() { return 'Prop(' + p + ')'; } } });
  }

Literal 是用來處理數組訪問的標記，所有的數組訪問會被處理成名稱為 i 的 Property 結點。所有的 Property 結點被維護在 propVertices 下面。

\(\text{Fun}(\pi)\) 是 \(\pi\) 位置定義（包括函數表達式）的函數結點

定義一個函數 \(V\) 把位置為 \(\pi\) 的表達式 \(t^\pi\) 映射到 flow graph 上的結點：

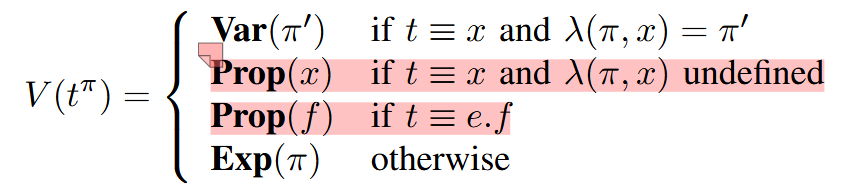
在代碼中的實現對應函數 vertexFor：

/* Return the flow graph vertex corresponding to a given AST node. */  
  function vertexFor(nd) {
    switch(nd.type) {
    case 'Identifier':
      // global variables use a property vertex, local variables a var vertex
      var decl = nd.attr.scope.get(nd.name);
      return decl && !decl.attr.scope.global ? varVertex(decl) : propVertex(nd);
    case 'ThisExpression':
      // 'this' is treated like a variable
      var decl = nd.attr.scope.get('this');
      return decl ? varVertex(decl) : exprVertex(nd);
    case 'MemberExpression':
      // ignore dynamic property accesses
      if(!nd.computed)
        return propVertex(nd.property);
      // FALL THROUGH
    default:
      return exprVertex(nd);
    }
  }

再觀察一下 varVertex 的實現可以發現代碼把有些結點保存在 AST 上結點的屬性下面（通過這種方式保證“唯一性”）：

// variable vertices are cached at the variable declarations
  function varVertex(nd) {
    if(nd.type !== 'Identifier')
      throw new Error("invalid variable vertex");
    
    return nd.attr.var_vertex
        || (nd.attr.var_vertex = {
             type: 'VarVertex',
             node: 'nd',
             attr: { pp: function() { return 'Var(' + nd.name + ', ' + astutil.ppPos(nd) + ')'; } }
           });
  }

Interprocedural Flow

為了處理過程間的流分析，添加下面幾種結點和規則：

在具體實現中，還添加了 nativeVertex 來維護 JS 標準對象上的函數（比如 Array.indexOf），會有一條邊從 nativeVertex 指向 PropVertex，同樣地，只維護字段名稱。

function addNativeFlowEdges(flow_graph) {
  	for(var native in nativeFlows) {
  		if(!nativeFlows.hasOwnProperty(native))
  			continue;
  		var target = nativeFlows[native];
  		flow_graph.addEdge(flowgraph.nativeVertex(native), flowgraph.propVertex({ type: 'Identifier',
  			                                                                      name: target }));
  	}
  	return flow_graph;
  }

nativeFlows = {
  "Array": "Array",
    "Array_isArray": "isArray",
    "Array_prototype_some": "some",
    "Array_prototype_indexOf": "indexOf",
    "Array_prototype_lastIndexOf": "lastIndexOf"
}

文章使用了兩種方法來具體地構造 callgraph：pessimistic 和 optimistic。在 pessimistic 方法中，只處理那些 one-shot calls 的函數對象的流動，比如：(function(...){...})(...)。之后，再按照上面提到過的 rules 處理過程內和過程間的流圖。剩下的逃逸函數和逃逸調用點被使用 UNKNOWN 進行建模（連接到返回值或者參數）。算法描述如下：

optimistic 的方法要求 \((C, E, U)\) 從 \((\emptyset, \emptyset, \emptyset)\) 開始迭代，重復 pessimistic 的規則（不再只處理 one-shot call）直到達到不動點為止。

An Example

對于上面的代碼，運行 pessimistic 的方法：

Evaluation

項目

在真實項目上運行了分析，框架有時是以壓縮形式出現的，在實際運行中被替換成非壓縮版本。使用 LOC，number of functions，number of calls 度量項目的大小。最后一行覆蓋率是對項目插樁后動態調用圖調用非框架函數的百分比，作者認為超過 60% 就算相當完整的。

Scalable

對于可擴展性，使用 UNIX 時間度量解析和分析的時間。Pessimistic 方法的效率最慢不到 9 秒，或許可以被使用到 IDE 中。

Precision

由于這里的方法是解決前人沒有解決的問題，所以沒辦法使用別的靜態分析方法當作一個 baseline，所以把結果和動態調用圖進行比較。

設D為動態調用圖中某個 callsite 對應的調用目標的集合，S為靜態分析確定的目標集合，那么精確度（即所有目標中“真實”調用目標的百分比） = \(\frac{|D \cap S|}{|S|}\)，召回率（即正確識別的真實目標的百分比） = \(\frac{|D \cap S|}{|D|}\)

不精確和精確度差異的來源：1. 兩個對象的同名屬性的函數；2. 回調函數

IDE

暫時不太關注

Summary and Threats to Validity

極端異常情況是對toString的調用，由于我們基于字段的方法，這些調用有超過100個被調用者。

大多數研究對象程序都使用了jQuery，只有兩個程序使用了其他框架。

準確性測量是相對于不完整的動態調用圖而言的，而不是相對于健全的靜態調用圖。因此，召回率應該被理解為一個上限（即，在更完整的調用圖上，召回率可能會更低），而精確度是一個下限（即，精確度可能會更高）。鑒于將健全的調用圖算法擴展到現實程序的困難性，動態調用圖是我們目前可以用來比較的最佳數據。此外，動態調用圖的相對較高的函數覆蓋率表明它們能夠代表整個程序。

Correlation Tracking for Points-To Analysis of JavaScript

Introduction

由于 JS 的動態特性，no field-sensitive 的方法會造成很大的不精確性，但是 field-sensitive 的方法會帶來極大的時間開銷，同時也無法很好的處理動態字段訪問的問題（訪問的字段必須在運行時計算出來），比如對于下面這個例子：

但是，注意到在一個讀-寫對中，讀和寫有時會操作不同對象上的同名字段，稱為 an obvious correlation，比如 x[p] = y[p]（或者說 t = x[p]; y[p] = t;）。這篇文章提出的方法就是捕獲這些在相同屬性上操作的讀-寫對，然后對于變量 p 的所有可能的取值分別的進行約束圖的構建（基于 Andersen）。在 WALA 上作為一個擴展實現了這個方法。這篇文章的方法不關注 eval 或者其他的動態生成的代碼，因此同樣是 unsound 的。

Field-Sensitive Points-To Analysis for JavaScript

一個 Field-sensitive 的 Andersen 指針分析如下：

前面幾條規則和 Java 中的指針分析類似。v = x.nextProp() 被用來建模 JS 中的 for-in 結構，JS 代碼經常使用 for-in 來遍歷對象中的每個屬性：

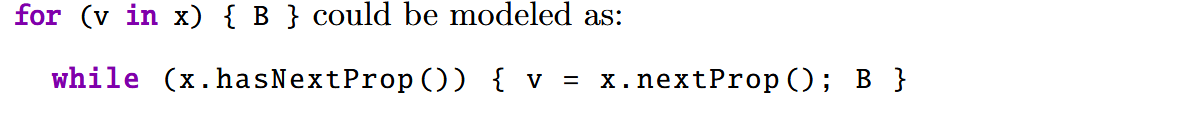
Andersen 指針分析可以被看作是約束圖上的一個傳遞閉包（DTC）的求解問題，最差時間復雜度是 \(O(n^3)\)，又因為 JS 允許向對象上動態的增減屬性，因此對象上的屬性的數量不能被簡單的建模成常數級別，所以 \(O(n^4)\)（太粗略了，暫時還不太理解為什么可以被看作一個 DTC 的求解，可以參考 SAS 2009 的一篇文章：https://manu.sridharan.net/files/sas2009.pdf）

對于上面的指針分析，容易出現不精確的結果，比如對于下面這個代碼：

按上面的規則，下面的推理是成立的：

原因來自于 prop 本質是在運行時被動態計算得到的，andersen 一方面沒有動態分析，另一方面沒有識別出 t = src[prop]; dest[prop] = t; 是對同名屬性進行讀寫，不可能出現這種“交叉”的情況（能不能理解成 andersen 沒有準確的捕捉所有的約束？）

Correlation Tracking

Example

Correlation tracking 主要分為兩個步驟：1. 從 JS 程序中識別上面形式的讀寫對；2. 把對于讀寫對的操作提取成一個匿名函數，prop 作為函數形參，使用上下文敏感技術實現前面提到的“對于變量 p 的所有可能的取值分別的進行約束圖的構建”。

Implementing Correlation Tracking

定義 read \(r\) 具備形式 o[p]，write \(w\) 具備形式 o'[p'] = e，如果 p 和 p' 具備相同的取值，那么認為 \(r\) 和 \(w\) 是 correlated 的。在具體實現中，“具備相同的取值”被定義為 p 和 p' 指向同一個局部變量 \(p\)，并且 \(p\) 沒有在 \(r\) 和 \(w\) 之間被重復定義。有時 \(r\) 和 \(p\) 會被傳入某個函數調用，我們做假設：所有的函數調用都會對對象上的字段做寫操作，那么 write \(w\) 也可以認為具備形式 fun(r, p, ...)

Function Extraction

一旦我們識別出屬性名 \(p\) 上的一次讀取 \(r\) 和一次寫入 \(w\) 之間的關聯，就把包含這兩個訪問的代碼片段提取到一個新函數中，并把 \(p\) 作為該函數的形參。如果不同關聯對所對應的抽取區域相互重疊，就將它們合并并提取為一個函數，該函數接收所有這些相關屬性名作為參數。某些代碼結構需要特殊處理。

Context Sensitivity

若函數 \(f\) 在某個動態屬性訪問中使用形參 \(p\) 作為屬性名，則對 \(f\) 進行上下文敏感分析，并為 \(p\) 的每一個具體取值創建一個獨立上下文。該策略可視作 field-sensitive 的變體，只是把區分上下文的基準從 this 換成了屬性名參數。

Evaluation

算法的實現基于 WALA。而且仍然存在不健全性：1. with；2. eval Function；3. 隱式類型轉換；4. 標準庫和 DOM 的模型不完整

在多個流行框架上評估了方法，對每個框架各收集了 6 個小型基準應用。多數框架大量使用反射（call apply），為了評估反射的影響，額外分別運行一次“建模 call/apply”和一次“不建模 call/apply”的分析，得到

• Baseline?：WALA 標準分析，不支持 call/apply
• Baseline+：WALA 標準分析，支持 call/apply
• Correlations?：啟用相關性追蹤，不支持 call/apply
• Correlations+：啟用相關性追蹤，支持 call/apply

實驗結果明確顯示，相關性追蹤顯著提升了面向一系列 JavaScript 框架的字段敏感指向分析的可擴展性與精度。