文法和語言的形式定義

終結符號 \(V_T\)、非終結符號 \(V_N\) 滿足 \(V_T \cap V_N = \emptyset\)

產生式 $\alpha \rightarrow \beta $， \(\alpha \in (V_T \cup V_N)^+, \beta \in (V_T \cap V_N)^*\)

文法 \(G[S] = (V_N, V_T, P, S)\)，\(P\) 是產生式的集合，\(S\) 是開始符號

• 0 型文法（短語結構文法） $\alpha \rightarrow \beta $， \(\alpha \in (V_T \cup V_N)^+, \beta \in (V_T \cap V_N)^*\)

• 1 型文法（上下文有關文法）$\alpha \rightarrow \beta $， \(\alpha \in (V_T \cup V_N)^+, \beta \in (V_T \cap V_N)^*, 1 \leq |\alpha| \leq |\beta|\)

• 2 型文法（上下文無關文法）$\alpha \rightarrow \beta $， \(\alpha \in V_N, \beta \in (V_T \cap V_N)^*, 1 \leq |\alpha| \leq |\beta|\)

• 3 型文法（正則文法）滿足右線性（非終結符號只能出現在產生式的最右側）或者左線性，即 \(A \rightarrow a | aB\) 或者 \(A \rightarrow a | Ba\)

一個只含有加法、乘法和括號的文法：

\(G[E] = (\{E, T, F\}, \{i, +, *, (, ) \}, P, E)\)

\(P = \{E \rightarrow E + T | T, T \rightarrow T * F | F, F \rightarrow (E) | i \}\)

推導的符號暫時定義為 \(\Rightarrow\)

句型：如果 \(G[E]\) 滿足 \(E \Rightarrow^* u\)，那么 \(u\) 就是文法 \(G[E]\) 的一個句型

句子：如果 \(G[E]\) 滿足 \(E \Rightarrow^* u\) 并且 \(u \in V_T^*\)，那么 \(u\) 就是文法 \(G[E]\) 的一個句子

淺顯的理解，句型等于所有在推導中可能出現的串，句子等于所有推導最后一步的串

語言：文法 \(G[E]\) 的語言是所有句子的集合，在描述時可以寫成 \(V_T^*\) 的形式

語法樹：滿足下面條件的樹

• 每個結點都用一個標記 \(l\) 表示，\(l \in V_N \cup V_T\)

• 樹根的標記是起始符號

• 非葉子節點的標記必然是非終結符號

• 父子關系必然和一條產生式規則相對應

最左(右)推導：如果在某個推導過程中的任何一步直接推導α?β中，都是對符號串α的最左(右)非終結符號進行替換，則稱其為最左（右）推導

如果產生式滿足 \(U \rightarrow xUy\)，那么為規則遞歸（直接遞歸）

如果產生式滿足 \(U \Rightarrow^* xUy\)，那么為間接遞歸，同樣地，可以定義左右遞歸

如果兩個文法產生的語言是相同的，則稱這兩個文法是等價文法

結合性體現在文法是左遞歸還是右遞歸，優先級則體現在出現在語法樹的位置

如果文法\(G\)的某個句子存在兩棵(包括兩棵)以上不同的語法樹(即有兩個不同的最左/最右推導)，則稱該文法是二義性文法

二義性問題是不可判定的

正向標記法可以推導出所有可達的非終結符號，反向標記法可以推導出所有可推導出終結符號串的非終結符號

有窮自動機

正則文法、正則表達式、有窮自動機相互等價

確定型有窮自動機 \(\text{DFA} = \{Q, \Sigma, t, q_0, F \}\), $t: Q \times \Sigma \rightarrow Q $

非確定型有窮自動機 \(\text{NFA} = \{Q, \Sigma, t, Q_0, F \}\), \(t: Q \times \Sigma^* \rightarrow 2^Q\)

被一個有窮自動機接受的符號串的集合稱為這個自動機的語言 \(L(\text{DFA})\)

如果兩個有窮自動機 \(A_1, A_2\) 滿足 \(L(A_1) = L(A_2)\)，那么它們是等價的

DFA 和 NFA 在表達能力上是等價的：

1. \(\text{DFA} \Rightarrow \text{NFA}\)：DFA 天然的是一種 NFA，顯然成立

2. \(\text{NFA} \Rightarrow \text{DFA}\)：

TBD

從證明過程中容易得出 NFA 向 DFA 轉換的方法：

定義 \(\epsilon\) 閉包：\(p' \in \epsilon -Closure(p)\) 當且僅當 \(p\) 通過若干條 \(\epsilon\) 的轉移邊后可以到達 \(p'\)

通過 \(\epsilon\) 閉包，可以把轉移函數 \(t\) 改寫成 \(t: 2^Q \times \Sigma \rightarrow 2^Q\)，并且只在必要的時刻引入狀態的集合

這樣構造出的 DFA 可以化簡。對于兩個狀態集合 \(P, Q\)，如果對于任意的符號 \(k \in \Sigma\)，都有 \(t(P, \Sigma) = t(Q, \Sigma) = R\)，那么它們可以合并；換言之，如果兩個狀態到達了不同的子集中，那么它們就應該從一個狀態集合中分離。

通過正則文法可以構造出一個DFA，使得二者能接受的符號串集合相同。同理，通過DFA可以構造出一個正則文法。

對于 \(U \rightarrow aW\)，可以構造狀態及其轉移邊 U --a--> W；對于 \(U \rightarrow Wa\)，可以構造 W --a--> U，反之亦然。

通過正則表達式也可以構造出一個等價的DFA。正則表達式有遞歸定義：\((e), e_1e_2, e_1|e_2, e^*\)。通過正則表達式直接構造DFA比較麻煩，可以先構造出對應的GNFA在轉換為等價DFA。

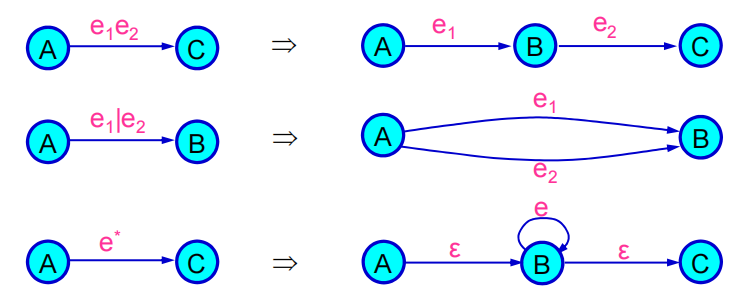
通過DFA構造出對應的正則表達式需要不斷地刪去狀態。可以以一個最小狀態機為例。TBD。

遞歸下降語法分析

構建一個語法分析器最方便的方法是遞歸下降。

自上而下語法分析

遞歸下降會遇到兩個問題：

1. 公共前綴：這需要預處理文法，提取不同的分支之間的公共前綴。

2. 左遞歸導致的無窮遞歸：因為一般寫出的遞歸下降方法是前序遍歷的，我們會先處理左子樹，如果有個左遞歸我們會不斷進入左子樹，不會接受任何的新字符。

公共前綴的處理比較簡單，左遞歸難處理一些：

1. 直接左遞歸：對于產生式 \(A \rightarrow A\alpha_1|A\alpha_2|...|\beta_1|\beta_2\)，引入新的符號 \(A'\) 使得串變為 \(A \rightarrow \beta_1A'|\beta_2A'|...\) \(A' \rightarrow \alpha_1A' | ...\)，容易證明它們等價

2. 間接左遞歸：通過代換把間接左遞歸轉換為直接左遞歸的形式

遞歸下降的其他問題是：

1. 不斷回溯效率太低

2. 代碼本身和文法深度耦合（雖然你可以構建一個通過文法自動構建解析程序的程序）

因此我們引入兩個新的集合防止我們做出錯誤的抉擇：

\(\text{FIRST}\) 集合：\(FIRST(A)\) 表示符號 \(A\) 可以推導出的所有串的首部終結符號的集合，這決定了通過某個符號我們進入哪一個解析程序

\(\text{FOLLOW}\) 集合：\(FOLLOW(A)\) 表示文法的所有句型中，可能緊跟著非終結符號 \(A\) 的所有終結符號的集合，這決定了我們是否結束當前的解析程序進入下一個解析程序

想法是好的，但是大家發現容易執行壞了：

1. 如果一個產生式的多個右部的 \(FIRST\) 集合相交，且無法通過提取公共前綴的方式解決，那么我們還是會進入錯誤的解析程序

2. 如果對于 \(U \rightarrow \alpha | \epsilon\)，\(FOLLOW(U)\) 和 \(FIRST(\alpha)\) 相交，那么我們就不知道是進入新的解析程序還是退出（大家給它起了個名字叫移入歸約沖突）

因此，不滿足上面兩個條件的文法被稱為 LL(1) 文法，可以使用這兩個集合改進解析方法

下面需要給這兩個“想法”下形式化定義：

后面又引入了一個集合 \(SELECT\) 用來統一判斷某個文法是否是 LL(1) 的，此外 \(SELECT\) 的元素還是一種“程序接下來要做什么”的標識

下面需要把上面的形式化想法轉化為實踐，考慮利用它們構建一個 LL(1) 分析算法。我們引入一個分析表把集合轉化成狀態與對應的動作，再引入符號棧和狀態棧保存狀態（下推自動機）：

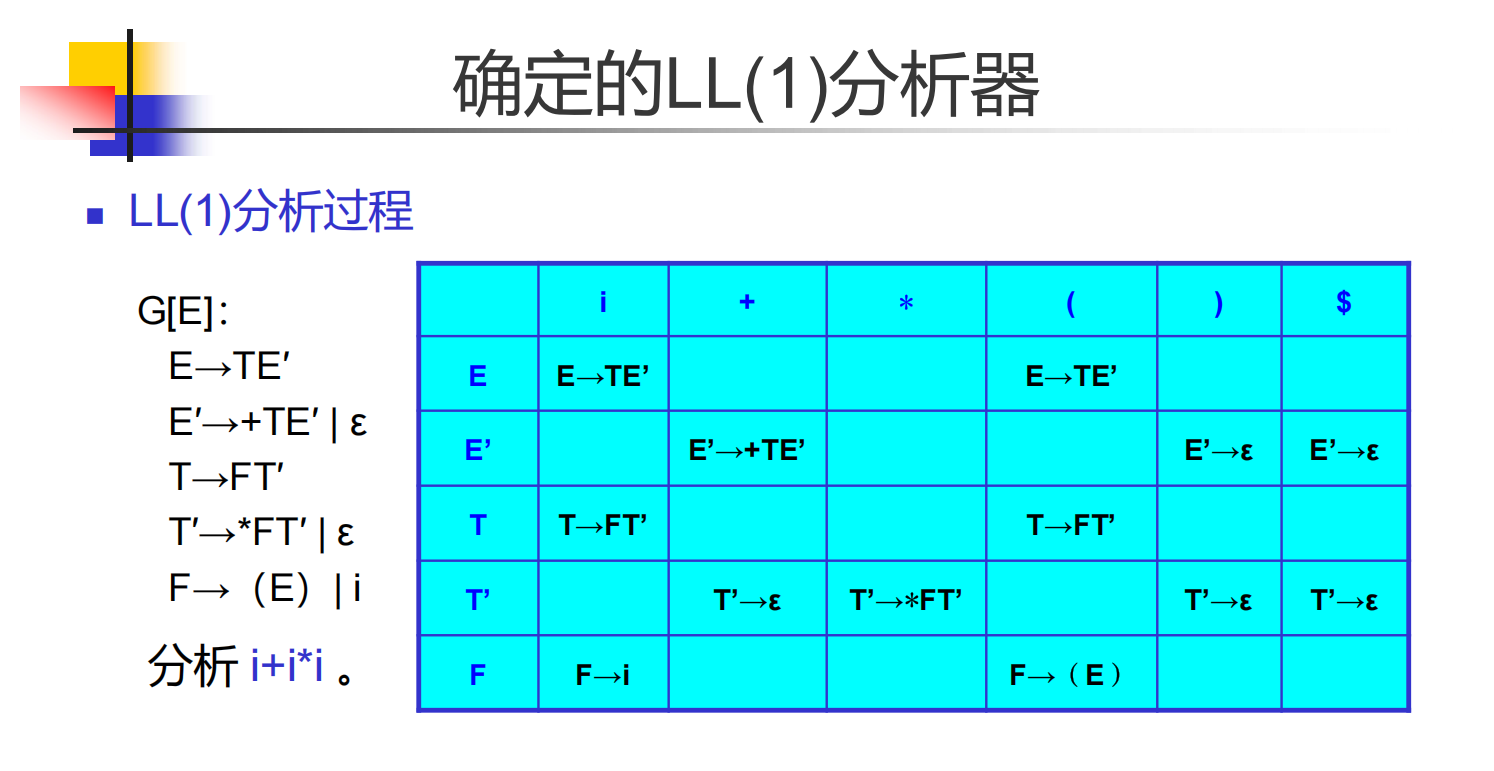
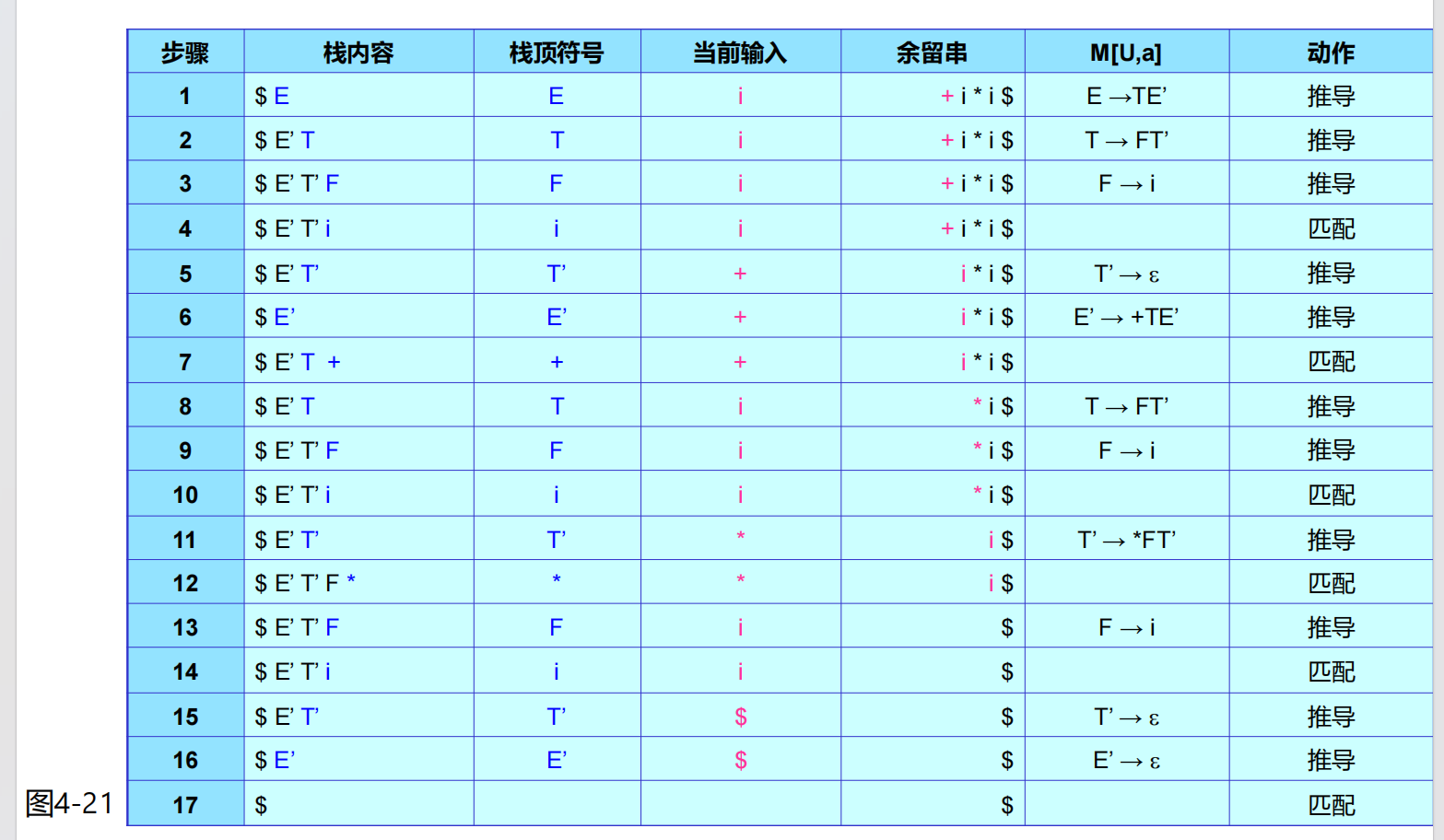
自下而上語法分析

相比于自上而下的語法分析，自下而上的語法分析不發源于遞歸下降的想法，而是自下而上的構建語法樹，不過一樣面臨“選擇”問題。選擇什么時候移入或歸約。

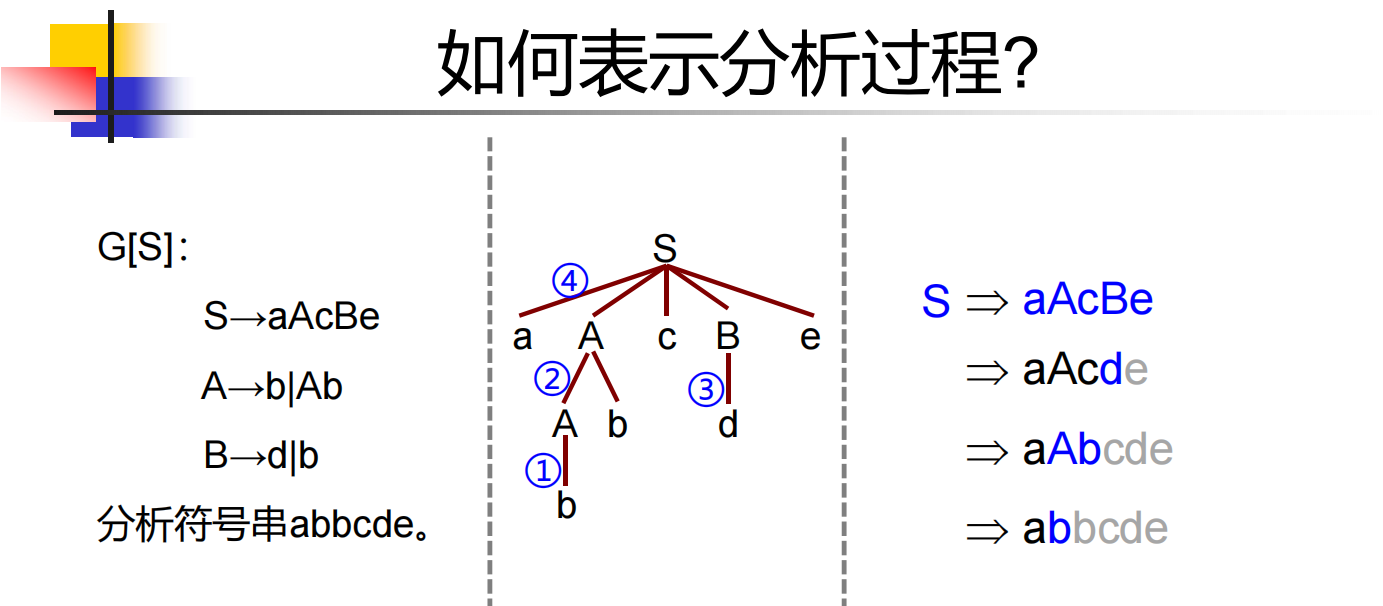
首先給出幾個定義：

• 短語：對于文法 \(G[E]\)和它的一個句型 \(xuy\)，如果有 \(E \rightarrow xUy\) 滿足 \(U \Rightarrow^* u\)，那么 \(u\) 就是一個短語。直觀的說，短語代表了那些能被規約的東西。

• 直接短語：對于文法 \(G[E]\)和它的一個句型 \(xuy\)，如果有 \(E \rightarrow xUy\) 滿足 \(U \Rightarrow u\)，那么 \(u\) 就是一個短語。直觀的說，短語代表了那些直接一步規約的東西。

• 句柄：句型的最左直接短語稱為句柄

從定義不難看出，不斷地對某個句型的句柄進行一次歸約，那么最終能歸約到開始符號

對于任意一個長度為 \(k\) 的句柄，它必須經歷 \(k\) 次移入和 \(1\) 次歸約，如果用一個狀態機去描述的話，一共有 \(k + 1\) 個狀態

又因為句柄是最左直接短語，不難看出某個句柄必然對應一個產生式的右部，產生式的數量和長度都是有限的，那么所有狀態的數量也是有限的。我們用一種記號描述狀態：

所有的這種被描述的狀態稱為 LR(0) 項（term）

顯然，只利用這些狀態以及狀態之間的轉移關系只能構建出一個 DFA，不能構建出一個 PDA，也無法進行語法分析。因此同樣地需要引入棧。這里還有一個常考的定義：

活前綴：活前綴包含了句柄識別到當前時刻的歷史，并逐步向后傳遞，最長的活前綴(可歸約前綴)包含了句柄完全被識別的整個歷史。

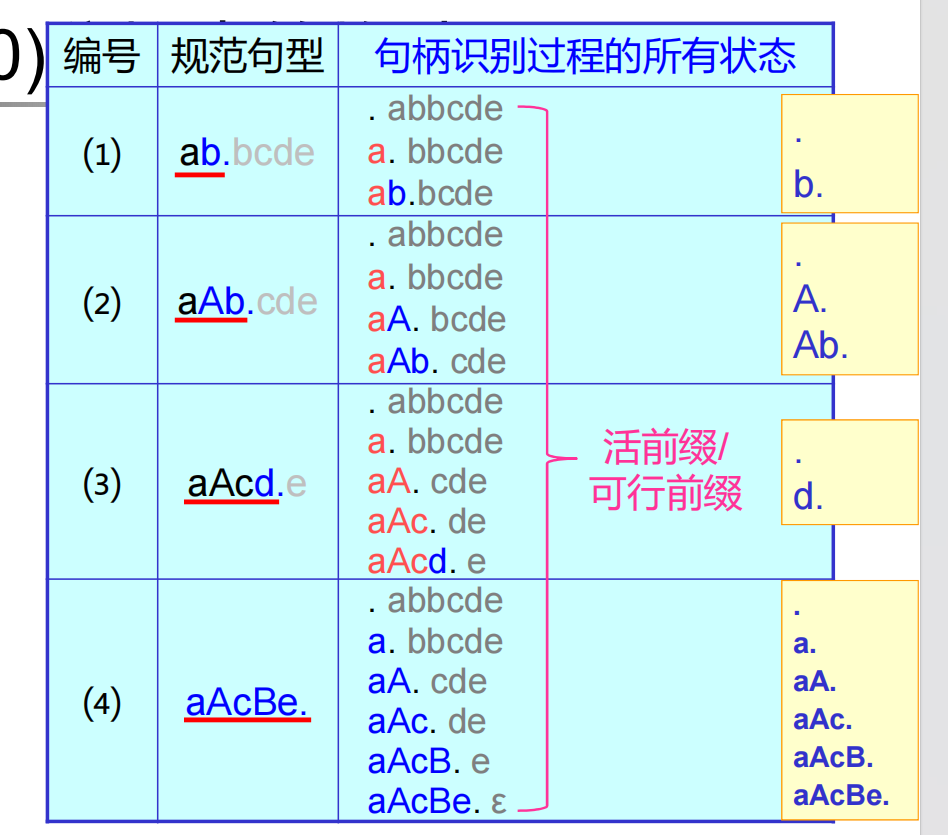
說人話，活前綴就是分析棧中可能出現的所有串

如果把每個 LR(0) 項都建成一個狀態，不僅內存的開銷很大，還因為有 \(\epsilon\) 邊的存在導致這實際上是一個 NFA，因此使用一個 \(\epsilon -CLOSURE\) 來合并 NFA 中的一些結點。

哎寫不動了

SLR 在 LR(0) 上做了一點小改進，避免了一些錯誤的歸約狀態（從而避免掉一些移入-歸約沖突）

LR(1) 在 SLR 上做了更好的改進，通過在狀態中引入一個符號，標識了在某些情況下的緊跟的終結符，增強了表達能力（可以理解成本來很泛泛的一個狀態添加了一個細節），規避掉了更多的歸約歸約沖突

LALR(1) 只是對 LR(1) 在存儲空間上的改進

語法制導翻譯

從理論上也不是很漂亮，從實踐上也不是很實用

可以為文法符號，引入一組屬性 \(attr_1, attr_2, ...\)，并定義程序的語義 \([[P]] = f(attr)\)，在這個過程中，隨著語法分析進行，每當使用一個產生式的時候就執行對應的語義動作

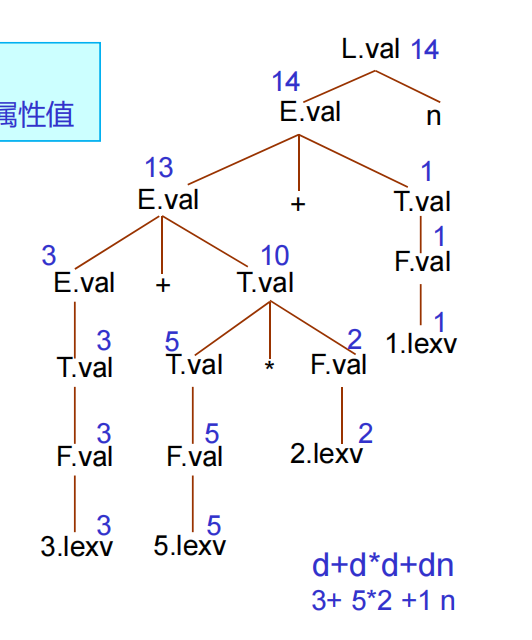
注釋語法樹：語法分析樹的各個節點上標記了相應的屬性值

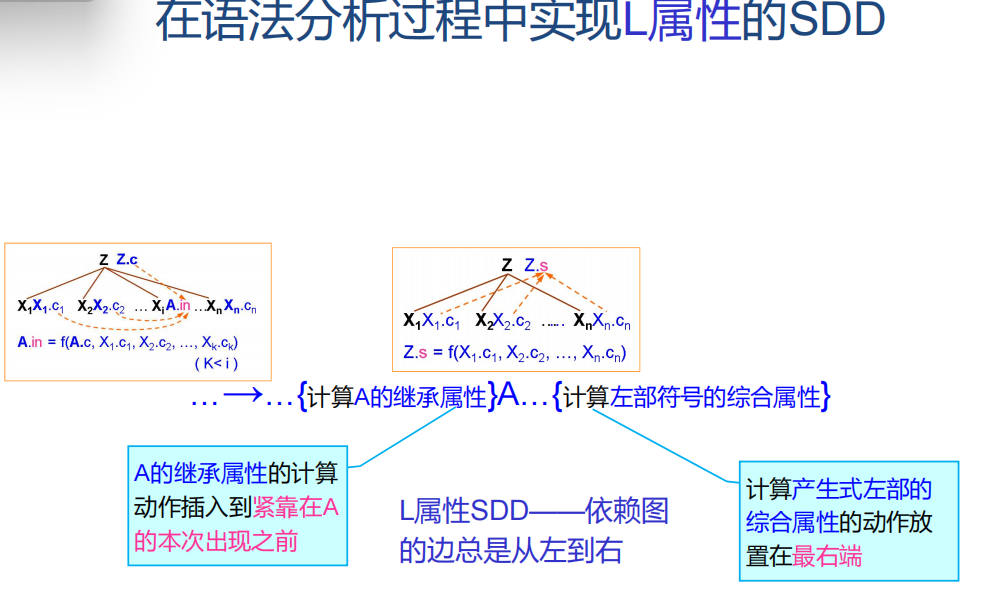
語法制導定義 SDD：定義與文法符號相關聯的屬性集，定義與產生式關聯的一組語義規則（程序片段），屬性文法是沒有副作用的 SDD

語法指導翻譯方案：將程序片段附加到文法各個產生式右部的合適位置，后綴SDT指所有程序片段都在產生式的最后進行

屬性本身可以被劃分為綜合屬性和繼承屬性：

綜合屬性：從子結點的屬性值計算得出的屬性

繼承屬性：從父結點或兄弟結點繼承的屬性值

中間代碼生成的核心在于處理文法、程序、中間代碼三種不同的順序關系。回填技術是處理這個問題的一個很好的算法。

怎么中間代碼不講 SSA 啊（

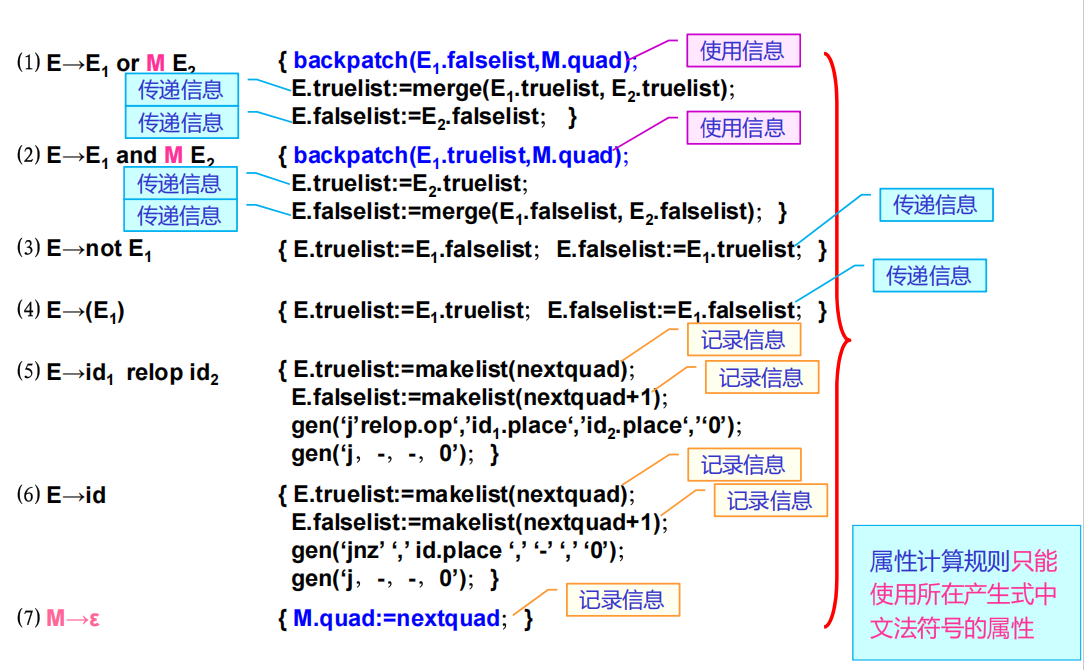
在涉及控制流語句的時候，我們會定義兩個鏈表 falselist 和 truelist，用來保存所有涉及跳轉的語句的真出口和假出口，這樣在回填時就無需再次向下遍歷整個語法樹，通過鏈表中的位置就可以訪問所有需要回填的位置

運行時刻環境

最近嵌套作用域原則：一個 Identifier 的作用域是個包含了這個 Identifier 的說明的最近的過程或函數

參數傳遞規則：

1. 傳地址：callee 接受到的是一個引用

2. 傳值：calle 接受到的是值本身

3. 傳結果：哎這個好抽象 被調用者的代碼中使用形式參數時，訪問的是形式參數的值單元，不修改實在參數；在結束調用返回時，修改實在參數

4. 傳名：常見在數組傳遞中 個人覺得和傳地址區別不大 被調用者數據區中需要一個單元存放實參地址計算程序的入口地址

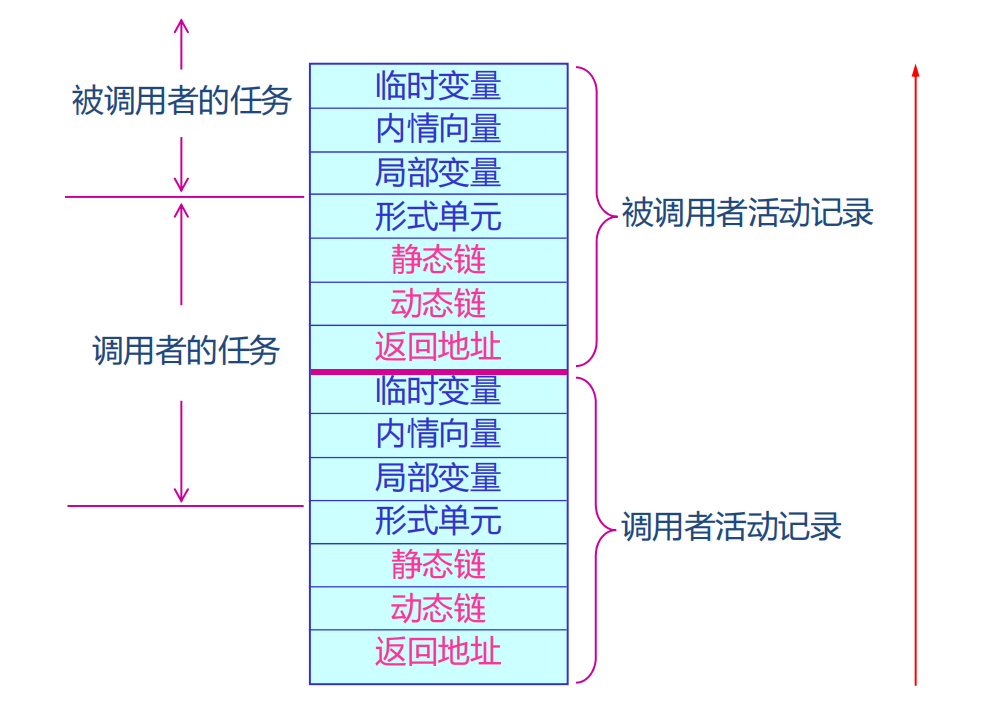
一個過程的數據區（也叫活動記錄）是一個在執行中會使用的連續數據塊，幾乎所有數據區的大小都可以在編譯期確定。這意味著在生成代碼時，可以確定申請多少的棧區大小，從而組織整個存儲空間。

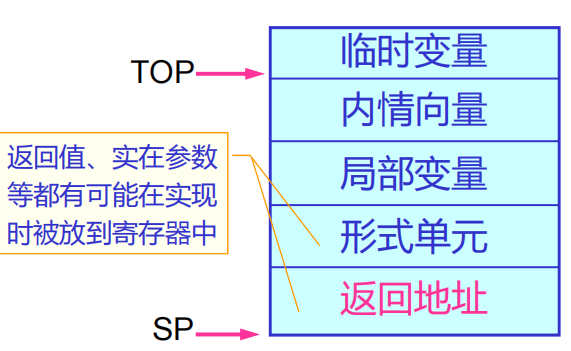
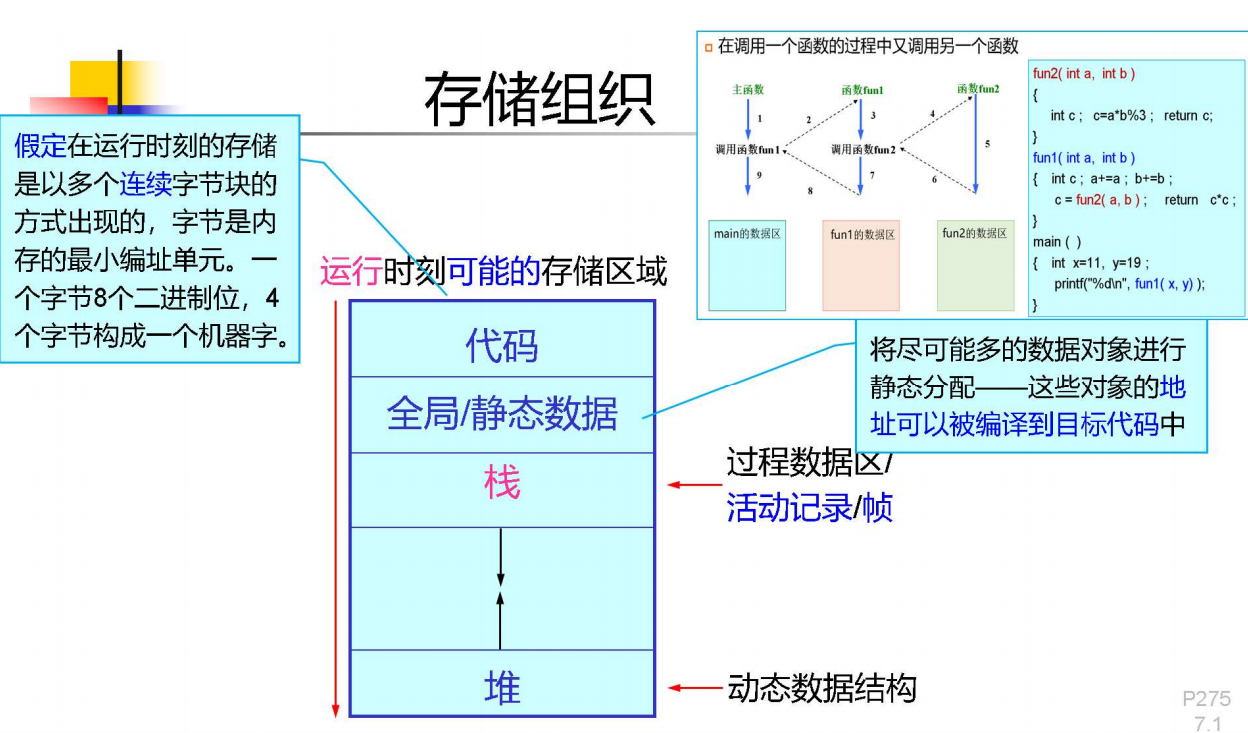
我們假定棧向高地址增長。

寫在考試前的總結

自動機理論與形式文法

1. 注意辨別自己構建的是 NFA 還是 DFA

2. 假設 DFA D 識別語言 L，如果要構造一個新的 DFA D' 識別語言 L 的補集，那么 D' 就是把 D 的接受狀態和非接受狀態翻轉

3. 在化簡某個 DFA 時，先觀察是否能劃分為接受狀態集和非接受狀態集，如果能，那么不斷地分割就可以得到最簡 DFA，否則肉眼觀察劃分吧

4. 題目中出現的 DFA 與正則表達式的對應，關注“連續的...”“以...為結尾”“以...開頭”這樣的特征

5. 題目中可能出現不止一個左遞歸

6. 對于 E -> E E | a 這種形式的文法，很容易構造其無二義性版本：E -> a E

7. 一個包含加法和乘法的文法：

Expr -> Expr + Term | Term
Term -> Term * Factor | Factor
Factor -> (Expr) | id

可以通過消除左遞歸的方式得到它的另一個版本：

Expr -> Term Expr'
Expr' -> + Term Expr' | epsilon
Term -> Factor Term'
Term' -> * Factor Term' | epsilon
Factor -> (Expr) | id

這兩個版本都很常用而且在龍書上出現過

自上而下的語法分析

1. 自上而下的語法分析發源于遞歸下降法，First 集和 Follow 集的發明可以節省遞歸下降法在某些情況下的非必要搜索回溯步驟：

比如

E -> A B C
A -> a | epsilon
B -> b | epsilon
C -> c | epsilon

input: bc

對于輸入串 bc，如果沒有 First 集輔助選擇，遞歸下降法就會錯誤的進入 A 對應的子程序，效率很低

為了更方便，大家干脆把所有的子程序進入的邏輯全都提取出來，搞成一張表，變成表格驅動的語法分析，用原輸入串上的一個移動的指針代表分析進度

First 集合之間的沖突可以通過提取公共前綴解決，First 集合和 Follow 集合之間的沖突則需要謹慎文法設計

2. LL(1) 分析表的構建：

• 對于產生式 A -> a, 如果終結符 s 在 FIRST(a) 中，那么在表中的對應位置填入這個產生式

• 對于產生式 A -> a, 如果 epsilon 在 FIRST(a) 中，那么對于 FOLLOW(a) 中的每個終結符，把產生式加入到它們對應的位置中

3. LL(1) 算法的執行：

三個部分，符號棧、輸入串、動作，符號棧的棧底放在右邊更合適，動作包括“推導”和“匹配”

自下而上的語法分析

1. 自下而上的語法分析來源于對句柄的認識，以及某個句柄必然出現在符號棧的頂端的這一推論

2. LR 比 LL 更加強大

3. 內核項：初始項以及點不在最左端的所有項

4. SLR 分析表的構建：

• 如果狀態 A 通過一個終結符號 s 達到狀態 B，那么在表中 ACTION 的對應位置填寫移入 s，如果狀態 A 通過一個非終結符號 E 到達狀態 B，在么在表中 GOTO 的對應位置填寫 B

• 如果狀態 A 里面有產生式 E -> e · 已經終結，那么對于 FOLLOW(E) 中的所有終結符號 s，在對應位置填寫歸約

• 如果 S' -> S · 在狀態中，那么 $ 置為 acc

5. LR(1) 項目集的構建：

• 從 S' -> S · , $ 開始，對于每個 A -> a · Bc, y，把 B -> · b, FIRST(cy) 加入狀態中

• 轉移邊不改變后面跟的符號

6. LR(1) 分析表的構建：把 FOLLOW(E) 改編成后面跟的符號，后面跟的符號對移入動作沒有貢獻

7. LALR 分析表的構建：在 LR(1) 項目集的基礎上，合并掉那些具有相同核心的集合，在分析表中體現為合并掉兩個狀態行

8. LR 語法分析算法的執行：

四個部分，狀態棧，符號棧，輸入串，動作，當執行一個歸約動作時，符號棧和狀態棧要彈出相同數量的元素，符號棧壓入被歸約的符號，狀態棧則壓入棧頂符號 GOTO 后的結果

語法制導翻譯