GPT-4o-mini 翻譯，經(jīng)個人審校。添加了一點筆記。

原文地址 Type Systems

Introduction

類型系統(tǒng)的基本目的是避免程序運行過程中出現(xiàn)運行錯誤。這個不夠正式的說法激勵了對類型系統(tǒng)的研究，但是還需要更進一步的澄清。這個說法的準確性首先依賴于一個相當微妙的問題，即什么構成運行錯誤，我們將對此進行詳細探討。即使這個問題得到解決，要程序運行中不發(fā)生錯誤仍然是一個復雜的特性。當這種特性在某個編程語言可以表達的所有程序中都成立時，我們稱該語言為類型安全的。實際上，為了避免對編程語言的類型安全性做出錯誤或模棱兩可的聲明，進行細致的分析是必不可少的。因此，類型系統(tǒng)的分類、描述和研究逐漸發(fā)展成為一門正式的學科。

為了形式化類型系統(tǒng)，要求給出精確的符號和定義，以及形式性質的詳細證明，以確保定義的合理性。有時，這一學科會變得相當抽象。但是應該始終銘記，核心動機是實用性的：這些抽象概念是出于實用要求而產生的，通常可以直接與具體的直覺相聯(lián)系。此外，形式化技術并不需要完全應用才能發(fā)揮其作用和影響。掌握類型系統(tǒng)的主要原則能夠幫助我們避免顯而易見或不易察覺的陷阱，同時還能在語言設計中激發(fā)可復用和解耦的特性。

當類型系統(tǒng)被正確設計時，它可以作為一種工具，用來評估編程語言定義中關鍵部分是否足夠完善。相反，非正式的語言描述往往無法清晰地定義語言中類型的結構，這會導致實現(xiàn)時出現(xiàn)模糊性。同一語言的不同編譯器可能會實現(xiàn)略有不同的類型系統(tǒng)。此外，有些語言的定義存在類型不安全的問題，即程序雖然通過了類型檢查（type checker），但運行時仍可能崩潰。理想情況下，形式化的類型系統(tǒng)應該成為所有類型化編程語言定義的一部分。這樣，類型檢查算法就可以根據(jù)明確的規(guī)范進行驗證，而整個語言也有可能被證明是類型安全的，從而避免潛在的問題。

在這一節(jié)中，我們會提出一套關于類型、執(zhí)行錯誤及相關概念的非正式術語。我們將討論類型系統(tǒng)的預期特性和優(yōu)勢，并回顧類型系統(tǒng)如何進行形式化定義。引言中使用的術語并非完全標準，這主要是由于來源不同而導致的標準術語存在不一致性。通常情況下，我們避免在描述運行時相關概念時使用“類型”和“類型化”這樣的詞匯。例如，我們用“動態(tài)檢查”替代“動態(tài)類型”，并避免使用諸如“強類型”這樣常見但含糊不清的術語。這些術語的定義將在“術語定義”部分中進行總結。

第2節(jié)中，我們解釋了描述類型系統(tǒng)時常用的符號表示法。我們回顧了判斷（judgments），即關于程序類型的形式化斷言；類型規(guī)則（type rules），即判斷之間的推理關系；以及推導（derivations），即基于類型規(guī)則進行的演繹過程。第3節(jié)中，我們回顧了一系列簡單類型，這些類型的類似概念可以在常見編程語言中找到，并詳細說明了它們的類型規(guī)則。第4節(jié)中，我們展示了一種簡單但完整的命令式語言的類型規(guī)則。第5節(jié)中，我們討論了一些高級類型構造的類型規(guī)則，包括多態(tài)性和數(shù)據(jù)抽象。第6節(jié)中，我們解釋了如何通過引入子類型概念來擴展類型系統(tǒng)。第7節(jié)是對一些我們未詳細討論的重要主題的簡要評論。第8節(jié)中，我們探討了類型推斷問題，并介紹了針對主要類型系統(tǒng)的類型推斷算法。最后，第9節(jié)總結了研究成果并展望了未來的發(fā)展方向。

note: 引言部分

Execution errors

程序運行錯誤（execution error）最明顯的表現(xiàn)是出現(xiàn)意外的軟件錯誤，例如非法指令錯誤或非法內存引用錯誤。然而，還有一些更為隱蔽的執(zhí)行錯誤會導致數(shù)據(jù)損壞，但不會立刻表現(xiàn)出明顯的癥狀。此外，還有一些軟件錯誤（例如除以零或解引用空指針）通常并不會被類型系統(tǒng)所檢查出來并防止其發(fā)生。最后，也存在一些缺乏類型系統(tǒng)的語言，但在這些語言中軟件錯誤并未發(fā)生。因此，我們需要謹慎地定義相關術語，從“什么是類型”這一問題開始。

Typed and untyped languages

程序變量在程序執(zhí)行期間可以取一系列的值，值域的上界稱為該變量的類型。例如，一個類型為布爾（Boolean）的變量 \(x\)，在程序的每次運行中都應該僅取布爾值。如果 \(x\) 的類型是布爾，那么布爾表達式 \(\text{not}(x)\) 在程序的每次運行中都具有合理的意義。能夠為變量賦予（非平凡）類型的語言稱為類型化語言（typed languages）。

note: 此處的上界我理解是在格上的上界，比如布爾型的 true 和 false 的上界應該是 {true, false}，是兩個取值的并集，也是二者在格上的最小上界，然后我們認為這個集合是“布爾型”這個名詞

不限制變量取值范圍的語言被稱為無類型語言（untyped languages）：它們沒有類型，或者等價地說，它們只有一個包含所有值的單一通用類型。在這些語言中，操作可能會被應用于不適當?shù)膮?shù)，其結果可能是一個固定的任意值、一個錯誤（fault）、一個異常（exception），或者一個未定義的效果（unspecified effect）。純 \(\lambda\)-演算（pure \(\lambda\)-calculus）是無類型語言的一個極端例子，其永遠不會發(fā)生錯誤：因為唯一的操作是函數(shù)應用，而由于所有值都是函數(shù)，所以該操作永遠不會失敗。

類型系統(tǒng)（type system）是類型化語言中的一個組成部分，用于追蹤變量的類型，以及通常情況下，程序中所有表達式的類型。類型系統(tǒng)被用來判斷程序是否表現(xiàn)良好（這一點將在后續(xù)討論）。只有符合類型系統(tǒng)的程序源代碼才應被視為類型化語言的真正程序；不符合類型系統(tǒng)的源代碼應在運行之前被拋棄掉。

一門語言之所以被稱為類型化語言，是因為它具有一個類型系統(tǒng)，而不論類型是否實際出現(xiàn)在程序的語法中。如果類型是語法的一部分，則稱為顯式類型化（explicitly typed）；否則稱為隱式類型化（implicitly typed）。目前沒有主流語言是純粹隱式類型化的，但諸如 ML 和 Haskell 等語言支持在大范圍的程序片段中省略類型信息；這些語言的類型系統(tǒng)會自動為這些程序片段分配類型。

Execution errors and safety

在程序執(zhí)行過程中，可以將錯誤分為兩種類型：一種是會導致計算立即停止的錯誤，另一種是暫時未被察覺（可能持續(xù)一段時間），最終導致程序出現(xiàn)不可預測行為的錯誤。前者稱為可捕獲錯誤（trapped errors），而后者稱為不可捕獲錯誤（untrapped errors）。

一個典型的不可捕獲錯誤的例子是對合法地址的不當訪問，例如在缺乏邊界檢查的情況下訪問數(shù)組末尾之后的數(shù)據(jù)。另一個可能長時間未被發(fā)現(xiàn)的不可捕獲錯誤是跳轉到錯誤的地址：該地址上的內存可能表示指令流，也可能不表示。相比之下，可捕獲錯誤的例子包括除以零和訪問非法地址：在許多計算機架構上，這些錯誤會導致計算立即停止。

如果一個程序不會導致不可捕獲錯誤（untrapped errors）的發(fā)生，則稱該程序是安全的（safe）。產生的所有程序均安全的語言被稱為安全語言（safe languages）。因此，安全語言排除了運行錯誤中最隱蔽的形式：那些可能暫時未被察覺的錯誤。無類型語言（untyped languages）可以通過運行時檢查來強制實現(xiàn)安全性，而類型化語言則可以通過靜態(tài)檢查來拒絕所有潛在不安全的程序。此外，類型化語言也可能結合運行時檢查和靜態(tài)檢查來實現(xiàn)安全性。

盡管安全性是程序的重要屬性，但很少有類型化語言僅關注消除不可捕獲錯誤。類型化語言通常還試圖排除大量的可捕獲錯誤（trapped errors），以及不可捕獲錯誤。接下來我們將討論這些問題。

note: 把類型化和安全/不安全看作獨立的部分，也就是說，暫時忘掉類型化

Execution errors and well-behaved programs

對于任意一種語言，我們將所有可能出現(xiàn)的執(zhí)行錯誤劃分出一個子集，稱為禁止錯誤（forbidden errors）。禁止錯誤應包括所有的不可捕獲錯誤（untrapped errors）以及可捕獲錯誤（trapped errors）的子集。如果一個程序片段不會導致任何禁止錯誤的發(fā)生，則稱該程序片段具有良好行為（good behavior），或者等價地稱其為行為良好（well behaved）。相反，若程序片段導致禁止錯誤的發(fā)生，則稱其具有不良行為（bad behavior），或者等價地稱其為行為不良（ill behaved）。特別地，一個行為良好的程序片段是安全的（safe）。如果某種語言的所有（合法）程序都具有良好行為，則稱該語言是強檢查的（strongly checked）。

因此，對于給定的類型系統(tǒng)，以下性質適用于強檢查語言：

• 不會發(fā)生不可捕獲錯誤（安全性保證）。
• 不會發(fā)生被指定為禁止錯誤的可捕獲錯誤。
• 其他可捕獲錯誤可能會發(fā)生，此時避免這些錯誤的責任由程序員自行承擔。

類型化語言可以通過靜態(tài)檢查（即編譯時檢查）來強制實現(xiàn)良好行為（包括安全性），從而防止不安全或行為不良的程序被執(zhí)行。這類語言被稱為靜態(tài)檢查語言（statically checked languages）。檢查過程稱為類型檢查（typechecking），執(zhí)行該檢查的算法稱為類型檢查器（typechecker）。通過類型檢查器的程序被稱為良類型的（well typed），否則被稱為類型不良（ill typed）。類型不良可能意味著程序實際上具有行為不良，也可能只是表示無法保證其行為良好。靜態(tài)檢查語言的典型例子包括 ML、Java 和 Pascal（需要注意的是，Pascal 存在一些不安全的特性）。

非類型化語言可以通過另一種方式來強制實現(xiàn)良好行為（包括安全性），即執(zhí)行足夠詳細的運行時檢查（run-time checks），以排除所有禁止錯誤。例如，這些語言可能會檢查所有數(shù)組邊界以及所有除法操作，并在禁止錯誤即將發(fā)生時生成可恢復的異常。這種語言中的檢查過程稱為動態(tài)檢查（dynamic checking）。LISP 是這種語言的一個典型例子。盡管這些語言既沒有靜態(tài)檢查，也沒有類型系統(tǒng)，它們仍然可以被稱為強檢查的（strongly checked）。

即使是靜態(tài)檢查的語言，通常也需要在運行時執(zhí)行某些測試以確保安全性。例如，數(shù)組邊界通常必須通過動態(tài)檢查來驗證。一個語言是靜態(tài)檢查的，并不意味著程序的執(zhí)行可以完全“盲目”進行。

一些語言利用其靜態(tài)類型結構來實現(xiàn)復雜的動態(tài)測試。例如，Simula67 的 INSPECT、Modula-3 的 TYPECASE 和 Java 的 instanceof 構造能夠根據(jù)對象的運行時類型進行區(qū)分。盡管如此，這些語言仍然（稍顯不準確地）被認為是靜態(tài)檢查的語言，部分原因是這些動態(tài)類型測試是基于靜態(tài)類型系統(tǒng)定義的。換句話說，用于類型相等的動態(tài)測試與類型檢查器在編譯時用于確定類型相等性的算法是兼容的。這種兼容性使得動態(tài)測試與靜態(tài)類型系統(tǒng)保持一致，從而支持靜態(tài)檢查語言的安全性和靈活性。

note: 區(qū)分可捕獲錯誤/不可捕獲錯誤和禁止錯誤/非禁止錯誤，區(qū)分安全/不安全和良好行為/不良行為，程序語言期望保證程序的良好行為

Lack of Safety

根據(jù)我們的定義，一個行為良好的程序是安全的。安全性是一種更基礎且更重要的屬性，甚至比良好行為更為重要。類型系統(tǒng)的主要目標是通過排除所有程序運行中的不可捕獲錯誤來確保語言的安全性。然而，大多數(shù)類型系統(tǒng)的設計目標是確保更廣泛的良好行為屬性，并隱含地保證安全性。因此，類型系統(tǒng)的聲明目標通常是通過區(qū)分類型正確的程序與類型錯誤的程序來確保所有程序的良好行為。

實際上，某些靜態(tài)檢查語言并不能完全確保安全性。這意味著，這些語言的禁止錯誤未涵蓋所有的不可捕獲錯誤。這些語言可以被委婉地稱為弱檢查語言，即某些不安全操作能夠被靜態(tài)檢測到，而某些則不能。屬于這一類的語言之間在其“弱檢查”程度上差異也很大。例如，Pascal 只有在使用未標記的變體類型和函數(shù)參數(shù)時才會變得不安全；而 C 則有許多不安全且被廣泛使用的特性，例如指針運算和類型轉換。有趣的是，C 程序員的“十誡”中前五條都是為了彌補 C 的弱檢查特性所帶來的問題。C++ 對 C 中的一些弱檢查問題進行了緩解，而 Java 更進一步解決了更多問題，這表明編程語言正在逐漸遠離弱檢查的趨勢。此外，Modula-3 支持不安全特性，但僅限于那些明確標記為“不安全”的模塊，并且禁止安全模塊導入不安全接。這種設計進一步強化了語言的安全性，同時允許在需要時使用不安全的功能。

大多數(shù)無類型語言出于必要性，實際上是完全安全的（例如，LISP）。否則，如果既沒有編譯時檢查也沒有運行時檢查來防止數(shù)據(jù)的損壞，那么編程將變得極其困難。相比之下，匯編語言屬于令人不快的無類型且不安全的語言。

note: 語言的安全與否是可以通過嚴格的設計解決的

Should languages be safe?

一些編程語言（如 C）由于性能方面的考慮，刻意設計得不夠安全：為了實現(xiàn)安全性所需的運行時檢查，有時被認為代價過高。即使是在進行廣泛靜態(tài)分析的語言中，安全性也有其成本：例如，數(shù)組邊界檢查這樣的測試通常無法在編譯時完全消除。

盡管如此，人們仍然進行了許多嘗試，設計出 C 的一個安全子集，并開發(fā)工具，通過引入各種（相對高成本的）運行時檢查來嘗試安全地執(zhí)行 C 程序。這些嘗試主要出于兩個原因：一是 C 被廣泛應用于對性能要求不高的場景，二是由不安全的 C 程序引發(fā)的安全問題。這些安全問題包括由于指針運算或缺乏數(shù)組邊界檢查而導致的緩沖區(qū)溢出和下溢，這些問題可能導致任意內存區(qū)域被覆蓋，并可能被利用來發(fā)動惡意攻擊。

安全性從多種衡量標準來看是具有成本效益的，而不僅僅是純粹的性能考量。安全性在發(fā)生執(zhí)行錯誤時能夠產生失敗終止行為（fail-stop behavior），從而縮短調試時間。安全性可以保證運行時結構的完整性，因此支持垃圾回收（garbage collection）。反過來，垃圾回收雖然犧牲了一定的性能，卻顯著減少了代碼規(guī)模和開發(fā)時間。此外，安全性已經(jīng)成為系統(tǒng)安全的必要基礎，尤其是對于那些需要加載并運行外部代碼的系統(tǒng)（如操作系統(tǒng)內核和網(wǎng)頁瀏覽器）。系統(tǒng)安全正日益成為程序開發(fā)和維護中最昂貴的方面之一，而安全性可以幫助降低這類成本。

因此，在選擇使用安全語言還是不安全語言時，最終可能需要在開發(fā)與維護時間和執(zhí)行時間之間進行權衡（trade-off）。盡管安全語言已經(jīng)存在了數(shù)十年，但直到最近由于安全問題的日益突出，它們才逐漸成為主流選擇。這種轉變主要是因為安全性已經(jīng)成為現(xiàn)代系統(tǒng)設計中不可忽視的關鍵需求。

Should languages be typed?

關于編程語言是否應該具有類型系統(tǒng)的問題仍然存在爭議。然而，對于代碼的生產而言，用無類型語言編寫的代碼在維護上毋庸置疑會極為困難。從可維護性的角度來看，即使是弱類型檢查的不安全語言，也優(yōu)于安全但無類型的語言（例如，C 相對于 LISP）。以下是從軟件工程角度出發(fā)，支持類型化語言的主要論點：

• 執(zhí)行的高效性：類型信息最初被引入編程中是為了改進代碼生成和數(shù)值計算的運行時效率，例如在 FORTRAN 中。在 ML 中，精確的類型信息消除了對指針解引用時進行空值檢查的需求。通常來說，在編譯時提供精確的類型信息，可以在運行時直接應用適當?shù)牟僮鳎鵁o需進行昂貴的測試。

• 小規(guī)模開發(fā)的高效性。當一個類型系統(tǒng)設計良好時，類型檢查可以捕獲大量常見的編程錯誤，從而避免冗長的調試過程。實際發(fā)生的錯誤也更容易調試，因為大類的其他錯誤已經(jīng)被排除。此外，有經(jīng)驗的程序員會采用一種編碼風格，使某些邏輯錯誤表現(xiàn)為類型檢查錯誤：他們將類型檢查器作為一種開發(fā)工具。（例如，當某個字段的不變量發(fā)生變化時，即使其類型保持不變，也通過更改字段名稱來觸發(fā)錯誤報告，從而定位其所有舊的使用位置。）

• 編譯的高效性。類型信息可以組織成程序模塊的接口，例如在 Modula-2 和 Ada 中。模塊可以彼此獨立編譯，每個模塊僅依賴于其他模塊的接口。這樣，大型系統(tǒng)的編譯效率得以提高，因為當接口保持穩(wěn)定時，對某個模塊的修改不會導致其他模塊重新編譯。

note: 類型信息可以幫助程序員確定模塊間的接口

• 大規(guī)模開發(fā)的高效性。接口和模塊在代碼開發(fā)中具有方法論上的優(yōu)勢。大型團隊的程序員可以協(xié)商要實現(xiàn)的接口，然后分別著手實現(xiàn)對應的代碼部分。代碼片段之間的依賴性被最小化，代碼可以在局部范圍內進行調整，而無需擔心對全局產生影響。（雖然這些優(yōu)勢也可以通過非正式的接口規(guī)范來實現(xiàn)，但實際上，類型檢查在驗證對規(guī)范的遵守方面提供了極大的幫助。）

• 注重安全的應用領域中開發(fā)和維護的高效性。盡管安全性對于消除諸如緩沖區(qū)溢出之類的安全漏洞是必要的，但類型系統(tǒng)對于消除其他災難性的安全漏洞同樣不可或缺。以下是一個典型的例子：如果存在任何途徑（無論多么復雜）可以將整數(shù)轉換為指針類型（或對象類型）的值，那么整個系統(tǒng)就會被攻破。如果這種轉換可能發(fā)生，攻擊者就能夠以任何類型查看數(shù)據(jù)，從而訪問系統(tǒng)中任意位置的數(shù)據(jù)，即使是在其他方面受到類型語言約束的情況下。此外，還有一種常見但不必要的技術，即將一個類型化的指針轉換為整數(shù)，再將其轉換為另一種類型的指針，這也可能導致類似問題。在維護成本和整體執(zhí)行效率方面，使用類型化語言是消除這些安全問題的最具成本效益的方法。然而，安全性是一個貫穿系統(tǒng)各個層次的問題：類型化語言提供了一個優(yōu)秀的基礎，但并不是完整的解決方案。

• 語言特性的高效性。類型構造能夠自然地以“正交”的方式組合。例如，在 Pascal 中，數(shù)組的數(shù)組可以用來建模二維數(shù)組；在 ML 中，具有單個參數(shù)（該參數(shù)是包含 \(n\) 個元素的元組）的過程，可以用來建模具有 \(n\) 個參數(shù)的過程。因此，類型系統(tǒng)促進了語言特性的可擴展性，從而降低編程語言的復雜性。

note: 這里的“正交”指一個新的特性能被很自然的添加到一個語言中，而無需做出特別的適配或調整

Expected properties of type systems

在本章中，我們假設編程語言應該既安全又類型化，因此應當采用類型系統(tǒng)。在研究類型系統(tǒng)時，我們不區(qū)分“可捕獲錯誤”和“不可捕獲錯誤”，也不區(qū)分安全性和良好行為：我們專注于良好行為，并將安全性視為一種隱含的屬性。

note: 良好行為的程序必定是安全的

類型，在編程語言中通常具有一些實際的特性，這些特性使它們區(qū)別于程序中的其他注解形式。一般來說，關于程序行為的注解可以從非正式的注釋到需要定理證明的形式化方法，跨度非常大。類型處于這一范圍的中間位置：它們比程序注釋更精確，但比形式化方法更容易實現(xiàn)和操作。

以下是對所有的類型系統(tǒng)的基本預期屬性：

• 類型系統(tǒng)應當是可判定驗證的（Decidably Verifiable）：類型系統(tǒng)需要提供一個算法（稱為類型檢查算法），用來確保程序是良好行為的。類型系統(tǒng)的目的不僅僅是表達程序員的意圖，還要在程序執(zhí)行之前主動捕獲可能的執(zhí)行錯誤。（任意的正式規(guī)范通常不具備這種特性，因其可能需要復雜的定理證明，甚至不可判定。）

note: 就是說類型檢查算法必須是可判定的

• 類型系統(tǒng)應當是透明的（Transparent）：程序員應該能夠輕松預測程序是否可以通過類型檢查。如果程序未能通過類型檢查，失敗的原因應該是顯而易見的。（自動定理證明通常不具備這種透明性，因為其失敗原因可能難以理解或追蹤。）

• 類型系統(tǒng)應當是可強制執(zhí)行的（Enforceable）：類型聲明應盡可能在靜態(tài)檢查階段驗證；對于無法靜態(tài)驗證的部分，應在運行時動態(tài)檢查。程序中的類型聲明與其關聯(lián)的代碼之間的一致性應當被例行驗證。（程序注釋和編程約定通常無法強制執(zhí)行這種一致性。）

How type systems are formalized

正如我們所討論的，類型系統(tǒng)用于定義“良好類型化”（well typing）的概念，而良好類型化本身是良好行為（隱含安全性）的一種靜態(tài)近似。安全性通過“失敗停止行為”（fail-stop behavior）來簡化調試過程，并通過保護運行時狀態(tài)來實現(xiàn)垃圾回收。良好類型化進一步通過在運行時之前捕獲執(zhí)行錯誤，促進了程序的開發(fā)過程。

但是，我們如何保證良好類型化的程序確實是良好行為的呢？也就是說，我們如何確保一種語言的類型規(guī)則不會意外地允許不良行為的程序通過檢查？

形式化的類型系統(tǒng)是對編程語言手冊中所描述的非形式化類型系統(tǒng)的數(shù)學刻畫。一旦類型系統(tǒng)被形式化，我們就可以嘗試證明一個類型正確性定理（type soundness theorem），該定理聲明良好類型化的程序具有良好行為。如果這樣的正確性定理成立，我們就稱這個類型系統(tǒng)是正確的（sound）。(一種類型化語言中所有程序的良好行為與其類型系統(tǒng)的正確性是同義的。)

為了形式化一個類型系統(tǒng)并證明其正確性，我們必須從本質上形式化整個語言。

形式化編程語言的第一步是描述其語法。對于大多數(shù)感興趣的語言，這歸結為描述類型和項的語法。類型表達程序的靜態(tài)知識，而項（語句、表達式和其他程序片段）表達算法行為。

下一步是定義語言的作用域規(guī)則，這些規(guī)則明確地將標識符的出現(xiàn)與其綁定位置（即標識符聲明的位置）關聯(lián)起來。類型化語言所需的作用域規(guī)則通常是靜態(tài)的，這意味著標識符的綁定位置必須在運行時之前確定。綁定位置通常可以僅通過語言的語法來確定，而無需進一步的分析；這種靜態(tài)作用域被稱為詞法作用域。缺乏這種靜態(tài)作用域則被稱為動態(tài)作用域。

作用域可以通過形式化地定義程序片段的自由變量集合來指定（這涉及明確變量如何通過聲明被綁定）。隨后可以定義與之相關的類型或項對自由變量的“替換”概念。

當這些內容確定后，就可以進一步定義語言的類型規(guī)則。這些規(guī)則描述了一種形式為 \(M : A\) 的“具有類型”關系，其中 \(M\) 是項，\(A\) 是類型。一些語言還需要定義類型之間的“子類型”關系，形式為 \(A <: B\)，以及類型等價關系，形式為 \(A = B\)。語言的類型規(guī)則的集合構成了它的類型系統(tǒng)。具有類型系統(tǒng)的語言被稱為類型化語言。

在正式化類型規(guī)則之前，必須引入另一個基礎成分，這個成分并未直接體現(xiàn)在語言的語法中：靜態(tài)類型環(huán)境。靜態(tài)類型環(huán)境用于記錄程序片段中自由變量的類型信息，在類型檢查過程中，它與編譯器的符號表緊密對應。類型規(guī)則總是相對于正在進行類型檢查的程序片段的靜態(tài)環(huán)境來制定的。例如，“具有類型”關系 \(M : A\) 是與一個靜態(tài)類型環(huán)境 \(\Gamma\) 相關聯(lián)的，這個環(huán)境包含關于 \(M\) 和 \(A\) 中自由變量的信息。完整的關系寫作 \(\Gamma \vdash M : A\)，表示在環(huán)境 \(\Gamma\) 中，項 \(M\) 的類型為 \(A\)。

類型系統(tǒng)的基本概念幾乎適用于所有編程范式（如函數(shù)式、命令式、并發(fā)式等）。具體的類型規(guī)則通常可以在不同的范式中保持不變。例如，關于函數(shù)的基本類型規(guī)則，無論語義是按名調用（call-by-name）還是按值調用（call-by-value），或者無論語言是函數(shù)式還是命令式，這些規(guī)則基本上都可以直接沿用。

在本章中，我們將獨立于語義來討論類型系統(tǒng)。然而，需要明確的是，最終類型系統(tǒng)必須與某種語義相關聯(lián)，并且健全性（soundness）必須在該語義下成立。健全性確保類型系統(tǒng)的靜態(tài)檢查與程序的動態(tài)行為之間的一致性。值得一提的是，結構化操作語義（structural operational semantics）是一種能夠統(tǒng)一處理多種編程范式的技術方法，與本章對類型系統(tǒng)的討論非常契合。結構化操作語義提供了一種系統(tǒng)化的方式來描述程序的動態(tài)行為，從而為類型系統(tǒng)的健全性證明提供了堅實的基礎。

Type equivalence

在大多數(shù)非平凡的類型系統(tǒng)中，通常需要定義一個類型等價關系（type equivalence），即判斷兩個類型表達式是否等價。這是定義編程語言時的一個重要問題：什么時候兩個獨立的類型表達式可以被認為是等價的？假設有兩個不同的類型名稱，它們分別被關聯(lián)到相同的類型：

\(type X = Bool\)
\(type Y = Bool\)

如果類型名稱 \(X\) 和 \(Y\) 因關聯(lián)到相同的類型而匹配，我們稱之為結構等價。如果它們因為類型名稱不同而無法匹配（而不考慮關聯(lián)的類型），我們稱之為按名稱等價。

在實際應用中，大多數(shù)編程語言都會混合使用結構等價和按名稱等價。純粹的結構等價可以通過類型規(guī)則輕松且精確地定義，而按名稱等價則更難明確定義，其通常具有算法化的特性。結構等價在需要存儲或通過網(wǎng)絡傳輸類型化數(shù)據(jù)時具有獨特的優(yōu)勢；相比之下，按名稱等價在處理分時或分空間開發(fā)和編譯的交互程序時較為困難。

在后續(xù)討論中，我們假設使用結構等價。

The language of type systems

一個類型系統(tǒng)獨立于具體的類型檢查算法來指定編程語言的類型規(guī)則。這類似于通過形式化文法描述編程語言的語法，而和具體的解析算法相獨立。

將類型系統(tǒng)與類型檢查算法分離既方便又有用：類型系統(tǒng)屬于語言定義的范疇，而算法則屬于編譯器的范疇。通過類型系統(tǒng)解釋語言的類型特性比通過特定編譯器使用的算法來解釋更為容易。此外，不同的編譯器可能會為同一個類型系統(tǒng)使用不同的類型檢查算法。

從技術上講，可以定義出只允許不可行的類型檢查算法，甚至完全沒有算法的類型系統(tǒng)。然而，通常來說類型系統(tǒng)的設計要允許有高效的類型檢查算法。

Judgments

類型系統(tǒng)通常通過一種特定的形式化方法來描述。我們現(xiàn)在介紹這種形式化方法。描述一個類型系統(tǒng)的過程始于對一組稱為判斷（judgments）的形式化表達的定義。

一個典型的判斷（Judgment）形式如下：

我們稱 \(\Gamma\) 蘊含 \(\mathcal{J}\)。這里的 \(\Gamma\) 是一個靜態(tài)類型環(huán)境；例如，它是一個有序的、包含不同變量及其類型的列表，形式為 \(\cdot, x_1 : A_1, \dots, x_n : A_n\)。空環(huán)境用 \(\cdot\) 表示，而 \(\Gamma\) 中聲明的變量集合（即 \(x_1, \dots, x_n\)）被記為 \(\text{dom}(\Gamma)\)，即 \(\Gamma\) 的域（domain）。斷言 \(\mathcal{J}\) 的形式在不同的判斷中可能有所不同，但 \(\mathcal{J}\) 中的所有自由變量都必須在 \(\Gamma\) 中聲明。

對于我們當前的目的，最重要的判斷是類型判斷（typing judgment）。它斷言一個項 (M) 在其自由變量的靜態(tài)類型環(huán)境下具有類型 (A)。類型判斷的形式為：

這里，\(\Gamma\) 是靜態(tài)類型環(huán)境，描述了 \(M\) 的自由變量及其類型。

還需要再加入其他的判斷形式；一個常見的形式是簡單地斷言一個環(huán)境是良構的（well-formed）：

這表示環(huán)境 \(\Gamma\) 是良構的，即其中的所有變量及其類型聲明都是有效的。任何給定的判斷都可以被視為有效（例如，\(\Gamma \vdash \text{true} : \text{Bool}\)）或無效（例如，\(\Gamma \vdash \text{true} : \text{Nat}\)）。有效性形式化地定義了程序類型正確的概念。有效判斷和無效判斷之間的區(qū)分可以通過多種方式表達。然而，一種高度結構化的方式已經(jīng)成為主流，用于描述有效判斷的集合。這種表達方式基于類型規(guī)則，它在陳述和證明關于類型系統(tǒng)的技術引理和定理時非常有用。此外，類型規(guī)則具有高度的模塊化：不同構造的規(guī)則可以單獨書寫（與單一的、整體化的類型檢查算法形成對比）。因此，類型規(guī)則相對來說更易于閱讀和理解。

Type rules

類型規(guī)則通過基于已知有效的其他判斷來斷言某些判斷的有效性。這個過程通常從一些顯然正確的判斷開始。例如：

這表明空環(huán)境是良構的。這種初始判斷為整個類型系統(tǒng)的推導過程提供了基礎。

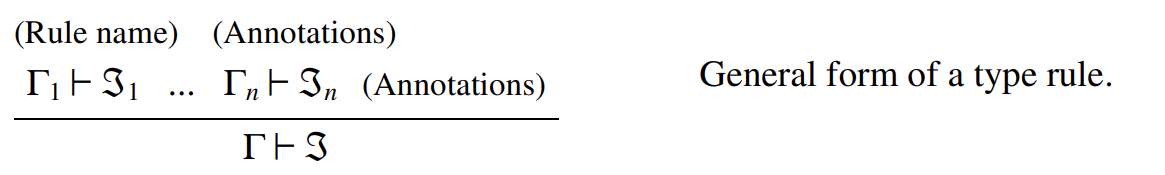
每條類型規(guī)則都以若干前提判斷（\(\Gamma_i \vdash \mathcal{J}_i\)）書寫在橫線的上方，并在橫線的下方給出一個單一的結論判斷（\(\Gamma \vdash \mathcal{J}\)）。當所有前提都滿足時，結論必須成立；前提的數(shù)量可以為零。每條規(guī)則都有一個名稱。（根據(jù)慣例，規(guī)則名稱的第一個單詞由結論判斷的類型決定。例如，名稱形式為“(Val ...)”的規(guī)則，其結論通常是一個值類型判斷。）在需要時，規(guī)則適用范圍的限制條件，以及規(guī)則中使用的縮寫，也會標注在規(guī)則名稱旁邊或前提的附近。

例如，以下兩條規(guī)則中的第一條表明，在任何良構的環(huán)境 \(\Gamma\) 中，任何數(shù)字都是類型為 \(\text{Nat}\) 的表達式。第二條規(guī)則表明，兩個表示自然數(shù)的表達式 \(M\) 和 \(N\) 可以組合成一個更大的表達式 \(M + N\)，該表達式同樣表示一個自然數(shù)。此外，\(M\) 和 \(N\) 所在的環(huán)境 \(\Gamma\)（用于聲明 \(M\) 和 \(N\) 中任意自由變量的類型）會延續(xù)到 \(M + N\)。

前面提到的基本規(guī)則表明，空環(huán)境在沒有任何假設的情況下是良構的。

一組類型規(guī)則被稱為一個（形式化的）類型系統(tǒng)。從技術上講，類型系統(tǒng)屬于形式化證明系統(tǒng)的通用框架：它是一組用于逐步推導的規(guī)則。在類型系統(tǒng)中，進行的推導與程序的類型判定相關。

Type derivations

在給定類型系統(tǒng)中的推導是一個由判斷組成的樹結構，樹的葉子（可能是多個前提）位于頂部，根（一個結論）位于底部。每個判斷通過類型系統(tǒng)中的某條規(guī)則從其直接上方的判斷推導而來。類型系統(tǒng)的一個基本要求是，必須能夠檢查一個推導是否被正確構造出來。這意味著我們需要能夠驗證每一步推導是否符合類型規(guī)則，以及整個推導樹是否遵循類型系統(tǒng)的結構和約束。這種檢查確保了類型系統(tǒng)的可靠性和一致性，從而保證程序的類型判定是正確的。

一個有效判斷是指可以通過在給定類型系統(tǒng)中正確構造推導樹而獲得的結論。換句話說，只有通過正確應用類型規(guī)則推導出的判斷才是有效的。例如，假設我們之前展示了三個類型規(guī)則，可以用它們來構造以下推導樹，證明 \(1 + 2 : \text{Nat}\) 是一個有效判斷。推導樹的每一步都顯示了應用的規(guī)則，具體如下：

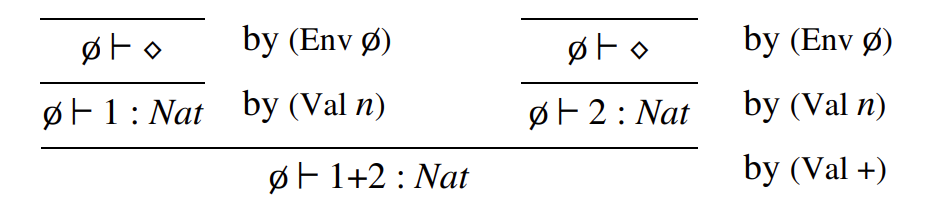
Well typing and type inference

在給定的類型系統(tǒng)中，如果存在某個類型 \(A\)，使得 \(\Gamma \vdash M : A\) 是一個有效判斷，那么術語 \(M\) 在環(huán)境 \(\Gamma\) 下是良類型的；也就是說，如果項 \(M\) 能夠被賦予某種類型，那么它就是良類型的。發(fā)現(xiàn)一個項的推導（進而發(fā)現(xiàn)其類型）的過程被稱為類型推斷問題。在由以下規(guī)則組成的簡單類型系統(tǒng)中： \(Env\) 環(huán)境規(guī)則 \(Val n\) 自然數(shù)值規(guī)則 \(Val +\) 加法規(guī)則，可以在空環(huán)境下（\(\Gamma = \emptyset\)）為術語 \(1 + 2\) 推斷出一個類型。根據(jù)之前的推導，這個類型是 \(\text{Nat}\)。

假設我們現(xiàn)在向類型系統(tǒng)中添加一個新的類型規(guī)則，其前提是 $\Gamma \vdash \Diamond $, 結論是 \(\Gamma \vdash \text{true} : \text{Bool}\)。在這個擴展后的類型系統(tǒng)中，我們無法為術語 \(1 + \text{true}\) 推斷出任何類型，因為沒有規(guī)則允許將一個自然數(shù)與一個布爾值相加。由于不存在任何推導可以支持 \(1 + \text{true}\)，我們稱 \(1 + \text{true}\) 不可類型化，或者說它是類型不良的（ill-typed），又或者說它存在類型錯誤（typing error）。

我們還可以進一步添加一個類型規(guī)則，其前提是 \(\Gamma \vdash M : \text{Nat}\) 和 \(\Gamma \vdash N : \text{Bool}\)，結論是 \(\Gamma \vdash M + N : \text{Nat}\)（例如，意圖將布爾值 \(\text{true}\) 解釋為 \(1\)）。在這樣的類型系統(tǒng)中，可以為術語 \(1 + \text{true}\) 推斷出一個類型，這樣它就會成為良類型的。

因此，給定項的類型推斷問題取決于所討論的類型系統(tǒng)。類型推斷算法的難易程度完全取決于具體的類型系統(tǒng)。對于某些類型系統(tǒng)，找到類型推斷算法可能非常容易，也可能極其困難，甚至根本無法找到。即使能夠找到，最優(yōu)算法可能非常高效，也可能慢得無法接受。類型系統(tǒng)通常以抽象的形式表達和設計，但它們的實用性卻依賴于是否能夠提供好的類型推斷算法。

顯式類型的過程式語言（例如 Pascal）的類型推斷問題相對容易解決；我們將在第 8 節(jié)中討論這一點。而對于隱式類型語言（例如 ML）的類型推斷問題則要微妙得多，我們在這里不作討論。盡管基本的算法已經(jīng)被很好地理解（文獻中有多種描述），并且被廣泛使用，但實踐中使用的算法版本較為復雜，目前仍在研究之中。

當涉及多態(tài)性時（在第 5 節(jié)中討論），類型推斷問題變得特別困難。對于 Ada、CLU 和 Standard ML 等語言中顯式類型的多態(tài)特性，其類型推斷問題在實踐中是可處理的。然而，這些問題通常通過算法解決，而不先描述相關的類型系統(tǒng)。最純粹且最通用的多態(tài)類型系統(tǒng)體現(xiàn)在第 5 節(jié)中討論的 λ 演算中。對于這種多態(tài) λ 演算的類型推斷算法相對簡單，我們將在第 8 節(jié)中介紹它。然而，解決方案的簡單性依賴于不切實際的極為冗長的類型注解。為了使這種通用多態(tài)性在實踐中可行，必須允許適當?shù)氖÷阅承╊愋托畔ⅰ＿@類類型推斷問題仍然是一個活躍的研究領域。

Type soundness

我們現(xiàn)在已經(jīng)建立了關于類型系統(tǒng)的所有一般概念，可以開始研究具體的類型系統(tǒng)。從第 3 節(jié)開始，我們將回顧一些非常強大但相對理論化的類型系統(tǒng)。這樣做的目的是，通過首先理解這些類型系統(tǒng)，編寫針對編程語言中各種復雜特性的類型規(guī)則也會更容易。

當我們深入研究類型規(guī)則時，應牢記一個合理的類型系統(tǒng)不僅僅是任意規(guī)則的集合。良好的類型設計旨在對應于程序行為的語義概念。通常，通過證明類型健全性定理來檢查類型系統(tǒng)的內部一致性。這正是類型系統(tǒng)與語義相結合的地方。對于指稱語義（denotational semantics），我們期望如果 $ \Gamma \vdash M : A $ 成立，那么 $ [ M ] \in [ A ] $ 也成立（即 $ M $ 的值屬于由類型 $ A $ 表示的值的集合）。對于操作語義（operational semantics），我們期望如果 $ \Gamma \vdash M : A $ 且 $ M $ 歸約為 $ M' $，那么 $ \Gamma \vdash M' : A $ 也成立。在這兩種情況下，類型健全性定理都斷言：良類型的程序在計算時不會發(fā)生運行錯誤。

First-order Type Systems

大多數(shù)常見的過程式語言中的類型系統(tǒng)被稱為一階類型系統(tǒng)（first-order type systems）。在類型理論術語中，這意味著它們缺乏類型參數(shù)化（type parameterization）和類型抽象（type abstraction），而這些特性屬于二階特性（second-order features）。令人稍感困惑的是，一階類型系統(tǒng)實際上可以包含高階函數(shù)（higher-order functions）。例如，Pascal 和 Algol68 擁有相對豐富的一階類型系統(tǒng)，而 FORTRAN 和 Algol60 的一階類型系統(tǒng)則非常有限。

一個最小的一階類型系統(tǒng)可以應用于無類型的λ-演算上，其中無類型的 λ-抽象 $ \lambda x.M $ 表示一個以參數(shù) $ x $ 為輸入、以 $ M $ 為結果的函數(shù)。為這個演算提供類型只需要函數(shù)類型和一些基本類型；稍后我們將看到如何添加其他常見的類型結構。

一階類型化的 λ-演算被稱為 \(\text{System F}_1\)。與無類型 λ-演算的主要區(qū)別是為 λ-抽象添加了類型注解，使用的語法是 $ \lambda x:A.M $，其中 $ x $ 是函數(shù)的參數(shù)，$ A $ 是其類型，$ M $ 是函數(shù)的主體。（在一個類型化的編程語言中，我們可能還會包括函數(shù)返回的結果的類型，但在這里并不必要。）從 $ \lambda x.M $ 到 $ \lambda x:A.M $ 的轉變是從無類型語言到類型化語言的典型步驟：綁定變量會獲得類型注解。

由于 \(F_1\) 主要基于函數(shù)值，最有趣的類型是函數(shù)類型：$ A \to B $ 表示具有參數(shù)類型為 $ A $ 且結果類型為 $ B $ 的函數(shù)的類型。不過，為了開始，我們還需要一些基本類型來構建函數(shù)類型。我們用 Basic 表示這樣一組基本類型，并用 $ K \in \text{Basic} $ 表示任意一個這樣的基本類型。目前，基本類型僅僅是技術上的必要性，但很快我們會考慮一些有趣的基本類型，比如 Bool 和 Nat。

\(F_1\) 的語法如表 2 所示。在類型化語言中，討論語法的作用是非常重要的。在無類型 λ-演算中，無上下文語法（context-free syntax）精確地描述了合法的程序。然而在類型化演算中，情況并非如此，因為良好行為通常不是一個無上下文的性質。描述合法程序的任務由類型系統(tǒng)接管。例如，表達式 $ \lambda x:K.x(y) $ 符合表中 \(F_1\) 的語法規(guī)則，但它不是 \(F_1\) 的合法程序，因為它不是類型正確的，因為 $ K $ 不是一個函數(shù)類型。盡管如此，無上下文語法仍然是需要的，但其主要作用是定義自由變量和綁定變量的概念，也就是定義語言的作用域規(guī)則（scoping rules）。基于這些作用域規(guī)則，僅在綁定變量上不同的項，例如 $ \lambda x:K.x $ 和 $ \lambda y:K.y $，在語法上被認為是相同的。這種方便的等同關系在類型規(guī)則中被隱式假定（在應用某些類型規(guī)則時可能需要重命名綁定變量）。

note: 可以通過反證嚴格證明表達式不符合類型規(guī)則

我們只需要為 \(F_1\) 定義三個簡單的判斷規(guī)則，它們如表 3 所示。判斷 $ \Gamma \vdash A $ 在某種意義上是有點多余的，因為所有語法上正確的類型 $ A $ 在任何環(huán)境 $ \Gamma $ 中都自然是良構的。然而，在二階系統(tǒng)中，類型的良構性無法僅通過語法來捕獲，因此判斷 $ \Gamma \vdash A $ 變得至關重要。現(xiàn)在采用這個判斷規(guī)則使得這樣后續(xù)擴展會更加容易。

這些判斷的有效性由表 4 中的規(guī)則定義。其中，規(guī)則 (Env \(\emptyset\)) 是唯一不需要任何前提假設的規(guī)則（即，它是唯一的公理）。它表明空環(huán)境是一個有效的環(huán)境。規(guī)則 (Env x) 用于將環(huán)境 $ \Gamma $ 擴展為更長的環(huán)境 $ \Gamma, x:A $，前提是 $ A $ 是 $ \Gamma $ 中的一個有效類型。需要注意的是，假設 $ \Gamma \vdash A $ 的過程會隱含著 $ \Gamma $ 是有效的環(huán)境，而且這一過程是遞歸的。換句話說，在推導 $ \Gamma \vdash A $ 的過程中，我們必須已經(jīng)推導出 $ \Gamma \vdash \Diamond $。規(guī)則 (Env x) 的另一個要求是變量 $ x $ 不能已經(jīng)在 $ \Gamma $ 中定義。我們特別注意保持環(huán)境中的變量互不相同，因此當 $ \Gamma, x:A \vdash M : B $ 被推導出來時（例如在規(guī)則 (Val Fun) 的假設中），我們可以確定 $ x $ 不會出現(xiàn)在 $ \text{dom}(\Gamma) $ 中（即 $ x $ 不屬于 $ \Gamma $ 的域）。這種約束確保了環(huán)境的變量是唯一的，從而避免了變量沖突的問題。

規(guī)則 (Type Const) 和 (Type Arrow) 用于構造類型。規(guī)則 (Val x) 從環(huán)境中提取假設：我們使用符號 $ \Gamma', x:A, \Gamma'' $（相對非正式地）表示 $ x:A $ 在環(huán)境中的某處出現(xiàn)。規(guī)則 (Val Fun) 為函數(shù)賦予類型 $ A \to B $，前提是函數(shù)體在假設形式參數(shù)具有類型 $ A $ 的情況下被賦予類型 $ B $。請注意，在此規(guī)則中，環(huán)境的大小發(fā)生了變化，因為我們向環(huán)境中添加了新的變量 $ x $ 和它的類型 $ A $。規(guī)則 (Val Appl) 用于將函數(shù)應用于一個參數(shù)：在檢驗前提是否成立時，相同的類型 $ A $ 必須出現(xiàn)兩次。這意味著函數(shù)的參數(shù)類型與實際傳遞給函數(shù)的參數(shù)類型必須一致，從而確保類型安全性。這些規(guī)則共同定義了 \(F_1\) 類型系統(tǒng)中的基本行為，包括如何構造類型、如何從環(huán)境中提取假設，以及如何驗證函數(shù)的類型和應用的類型。

表 5 展示了一個相當長的但是使用了所有規(guī)則的推導：

現(xiàn)在我們已經(jīng)研究了一個簡單一階類型系統(tǒng)的基本結構，可以開始對其進行擴展，使其更接近實際編程語言中的類型結構。我們將為每種新的類型構造添加一組規(guī)則，并遵循一種相當規(guī)律的模式。我們從一些基本數(shù)據(jù)類型開始：類型 \(Unit\)，它只有一個值，即常量 \(unit\)；類型 \(Bool\)，它的值是 \(true\) 和 \(false\)；以及類型 \(Nat\)，它的值是自然數(shù)。

類型 \(Unit\) 通常用于作為無關緊要的參數(shù)和結果的占位符；在某些語言中，它被稱為 \(Void\) 或 \(Null\)。由于 \(Unit\) 類型上沒有任何操作，因此我們只需要一個規(guī)則聲明 \(Unit\) 是一個合法的類型，以及一個規(guī)則聲明 \(unit\) 是 \(Unit\) 類型的合法值（見表 6）。

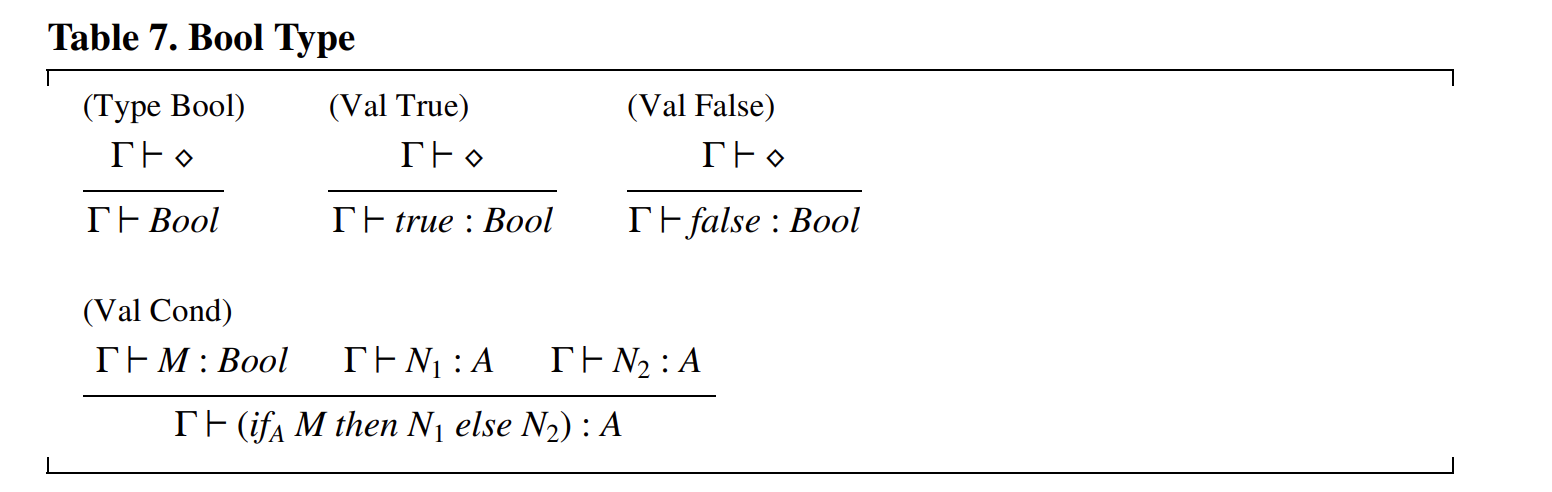
我們對 \(Bool\) 類型的規(guī)則遵循類似的模式，但布爾類型還具有一個有用的操作——條件表達式，它有自己的類型規(guī)則（見表 7）。在規(guī)則 (Val Cond) 中，條件表達式的兩個分支必須具有相同的類型 \(A\)，因為任一分支都可能生成結果。

規(guī)則 (Val Cond) 展示了一個關于類型檢查所需類型信息的微妙問題。當遇到條件表達式時，類型檢查器必須分別推導出 \(N_1\) 和 \(N_2\) 的類型，然后找到一個與兩者兼容的單一類型 \(A\)。在某些類型系統(tǒng)中，從 \(N_1\) 和 \(N_2\) 的類型中確定這個單一類型 \(A\) 可能并不容易，甚至可能無法實現(xiàn)。為了應對這種潛在的類型檢查困難，我們使用“下標類型”來表達額外的類型信息：\(if_A\) 是對類型檢查器的提示，表明結果類型應該是 \(A\)，并且推導出的 \(N_1\) 和 \(N_2\) 的類型應分別與給定的 \(A\) 進行比較。通常，我們使用帶下標的類型來指示在特定類型系統(tǒng)中可能有用或必要的信息。類型檢查器的任務通常是綜合這些額外的信息。當可以綜合這些信息時，下標可以被省略。（大多數(shù)常見的語言不需要這樣的 \(if_A\) 注解。）

自然數(shù)類型 \(Nat\)（見表 8）以 \(0\) 和 \(succ\)（后繼）作為生成器。或者，如我們之前所做的，可以用一條規(guī)則來聲明所有數(shù)值常量都屬于類型 Nat。 對 \(Nat\) 類型的計算由 \(pred\)（前驅）和 \(isZero\)（測試是否為零）這兩個基本操作實現(xiàn)；當然，也可以選擇其他集合的基本操作。

現(xiàn)在我們已經(jīng)有了一些基本類型，可以開始研究結構化類型，從笛卡爾積類型開始（見表 9）。一個笛卡爾積類型 \(A_1 \times A_2\) 表示一對值的類型，其中第一個分量的類型是 \(A_1\)，第二個分量的類型是 \(A_2\)。這些分量可以分別通過投影操作 \(first\) 和 \(second\) 提取出來。除了（或作為補充）使用投影操作，還可以使用 \(with\) 語句來分解一個對 \(M\)，并將其分量分別綁定到兩個獨立的變量 \(x_1\) 和 \(x_2\)，供作用域 \(N\) 使用。\(with\) 這種記法與 ML 語言中的模式匹配有關，同時也與 Pascal 語言中的 \(with\) 語句存在聯(lián)系；當我們進一步討論記錄類型時，與 Pascal 的聯(lián)系會更加清晰。

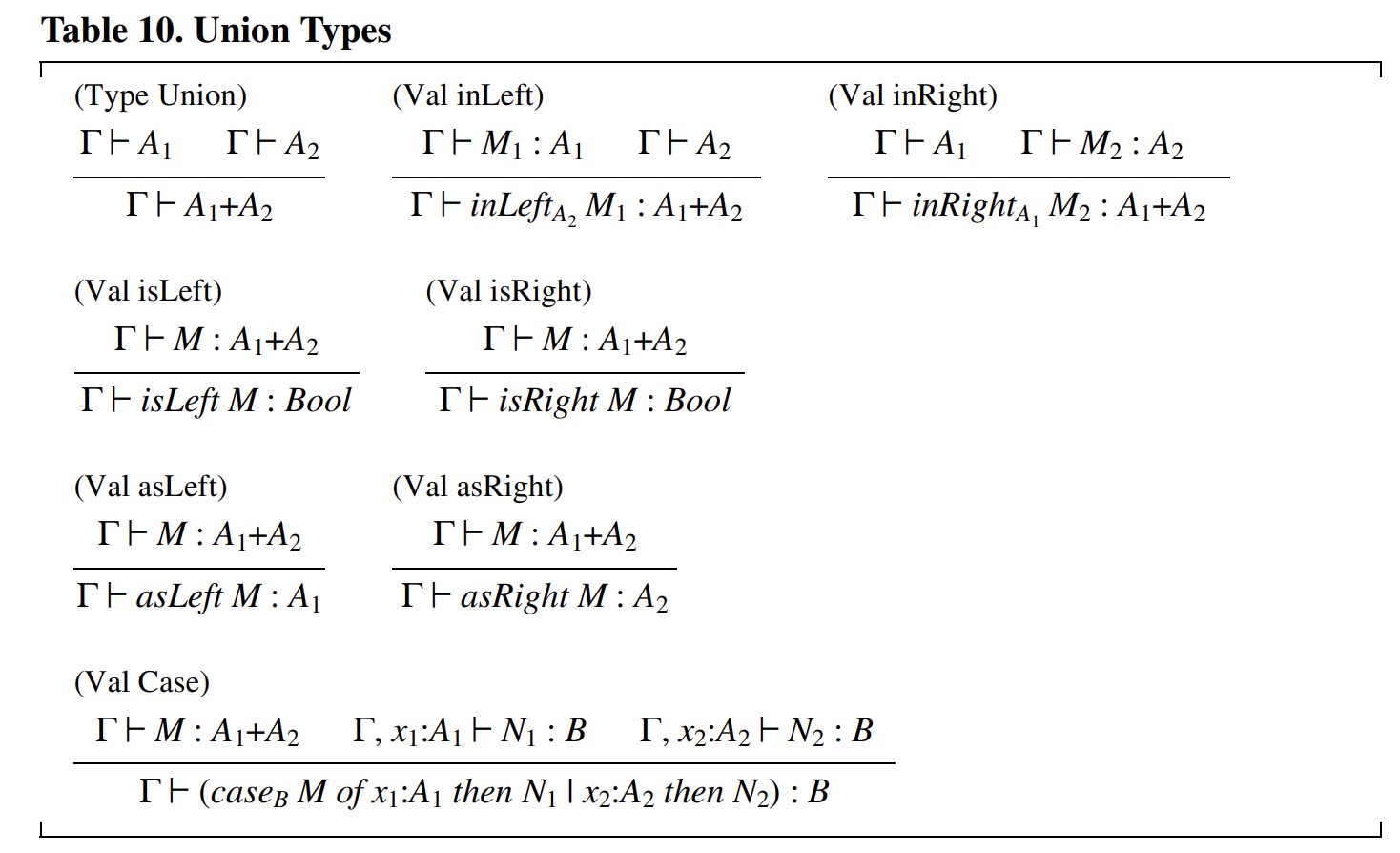
聯(lián)合類型（Union types，見表 10）常常被忽視，但它們在表達能力上與笛卡爾積類型同樣重要。聯(lián)合類型 \(A_1 + A_2\) 的元素可以被看作是一個帶有左標簽（由 \(inLeft\) 創(chuàng)建）的 \(A_1\) 類型的元素，或者是一個帶有右標簽（由 \(inRight\) 創(chuàng)建）的 \(A_2\) 類型的元素。這些標簽可以通過 \(isLeft\) 和 \(isRight\) 進行測試，并且可以通過 \(asLeft\) 和 \(asRight\) 提取對應的值。如果錯誤地將 \(asLeft\) 應用于一個帶右標簽的值，會產生一個捕獲的錯誤或異常；這種捕獲的錯誤不被視為禁止的錯誤。需要注意的是，假設 \(asLeft\) 的任何結果都屬于類型 \(A_1\) 是安全的，因為參數(shù)要么是帶左標簽的，在這種情況下結果確實是 \(A_1\) 類型；要么是帶右標簽的，在這種情況下沒有結果。與條件表達式的情況類似，下標被用來消除某些規(guī)則中的歧義。

規(guī)則 (Val Case) 描述了一種優(yōu)雅的結構，它可以取代 \(isLeft\)、\(isRight\)、\(asLeft\)、\(asRight\) 以及相關的捕獲錯誤。（同時，它也消除了聯(lián)合操作對布爾類型 \(Bool\) 的任何依賴。）這個 \(case\) 結構根據(jù) \(M\) 的標簽執(zhí)行兩個分支之一，并將 \(M\) 的去標簽內容分別綁定到 \(x_1\) 或 \(x_2\)，供 \(N_1\) 或 \(N_2\) 的作用域使用。分支之間用豎線 \(|\) 分隔。這種構造不僅更簡潔，還避免了顯式測試和提取標簽的冗余操作，同時通過綁定去標簽的內容直接進入邏輯分支，從而提高了代碼的可讀性和安全性。

從表達能力的角度來看（盡管不一定是實現(xiàn)的角度），可以注意到類型 \(Bool\) 可以被定義為 \(Unit + Unit\)，在這種情況下，\(case\) 結構可以簡化為條件表達式。類似地，類型 \(Int\) 可以被定義為 \(Nat + Nat\)，其中一個 \(Nat\) 表示非負整數(shù)，另一個 \(Nat\) 表示負整數(shù)。我們還可以定義一個原型的捕獲錯誤，如 $ \text{error}_A = \text{asRight}(\text{inLeft}_A(\text{unit})) : A $。因此，我們可以為每種類型構造一個錯誤表達式。

笛卡爾積類型和聯(lián)合類型可以通過迭代擴展來生成元組類型和多重聯(lián)合類型。然而，這些派生類型相對不夠方便，因此在編程語言中很少見到。相反，通常使用帶標簽的積類型和聯(lián)合類型：它們分別被稱為記錄類型和變體類型。

記錄類型是一種熟悉的類型結構，它是帶有名稱的類型集合，其值級別的操作允許通過名稱提取組件。表 11 中的規(guī)則假設記錄類型和記錄在語法上是等價的，允許對其帶標簽的組件進行重新排序；這種等價性類似于對函數(shù)的語法等價性，即允許對綁定變量進行重命名。

笛卡爾積類型的 \(with\) 語句被推廣至記錄類型，在規(guī)則 \((Val \ Record \ With)\) 中體現(xiàn)。記錄 \(M\) 中帶標簽的組件 \(l_1, \dots, l_n\) 被綁定到變量 \(x_1, \dots, x_n\)，這些綁定變量的作用域為 \(N\)。Pascal 語言中也有類似的結構，也被稱為 \(with\)，但其綁定變量是隱式的。這種設計有一個相當不幸的后果：作用域依賴于類型檢查，從而導致難以追蹤的錯誤，例如隱藏變量沖突。

笛卡爾積類型 \(A_1 \times A_2\) 可以被定義為 \(\text{Record}( \text{first}:A_1, \text{second}:A_2)\)。

變體類型（表 12）是帶名稱的獨立類型的聯(lián)合；它們在語法上可以通過重新排列組成部分來識別。構造 \(is\ l\) 是 \(isLeft\) 和 \(isRight\) 的推廣，而構造 \(as\ l\) 是 \(asLeft\) 和 \(asRight\) 的推廣。與聯(lián)合類型類似，這些構造可以被替換為一個 \(case\) 語句，而該語句現(xiàn)在具有多個分支。

聯(lián)合類型 \(A_1 + A_2\) 可以定義為 \(\text{Variant}(\text{left}:A_1, \text{right}:A_2)\)。枚舉類型，例如 \(\{\text{red}, \text{green}, \text{blue}\}\)，可以定義為 \(\text{Variant}(\text{red}:\text{Unit}, \text{green}:\text{Unit}, \text{blue}:\text{Unit})\)。

引用類型（表 13）可以用作命令式語言中可變存儲位置的基礎類型。類型為 \(\text{Ref}(A)\) 的元素是一個可變單元，包含類型為 \(A\) 的元素。新的單元可以通過規(guī)則 \((\text{Val Ref})\) 分配，通過規(guī)則 \((\text{Val Assign})\) 更新，并通過規(guī)則 \((\text{Val Deref})\) 顯式解引用。由于賦值操作的主要目的是執(zhí)行副作用，其結果值被選擇為 \(\text{Unit}\) 類型。

更有趣的是，數(shù)組及其操作可以如表 14 所示進行建模，其中 (\text{Array}(A)) 是一種數(shù)組類型，表示長度固定且元素類型為 (A) 的數(shù)組。表 14 中的代碼當然是對數(shù)組的一種低效實現(xiàn)，但它說明了一個關鍵點：復雜的類型規(guī)則可以從更簡單的類型規(guī)則中推導出來。表 15 中展示的數(shù)組操作的類型規(guī)則可以根據(jù)表 14 中的實現(xiàn)，結合笛卡爾積、函數(shù)和引用類型的規(guī)則，輕松推導出來。

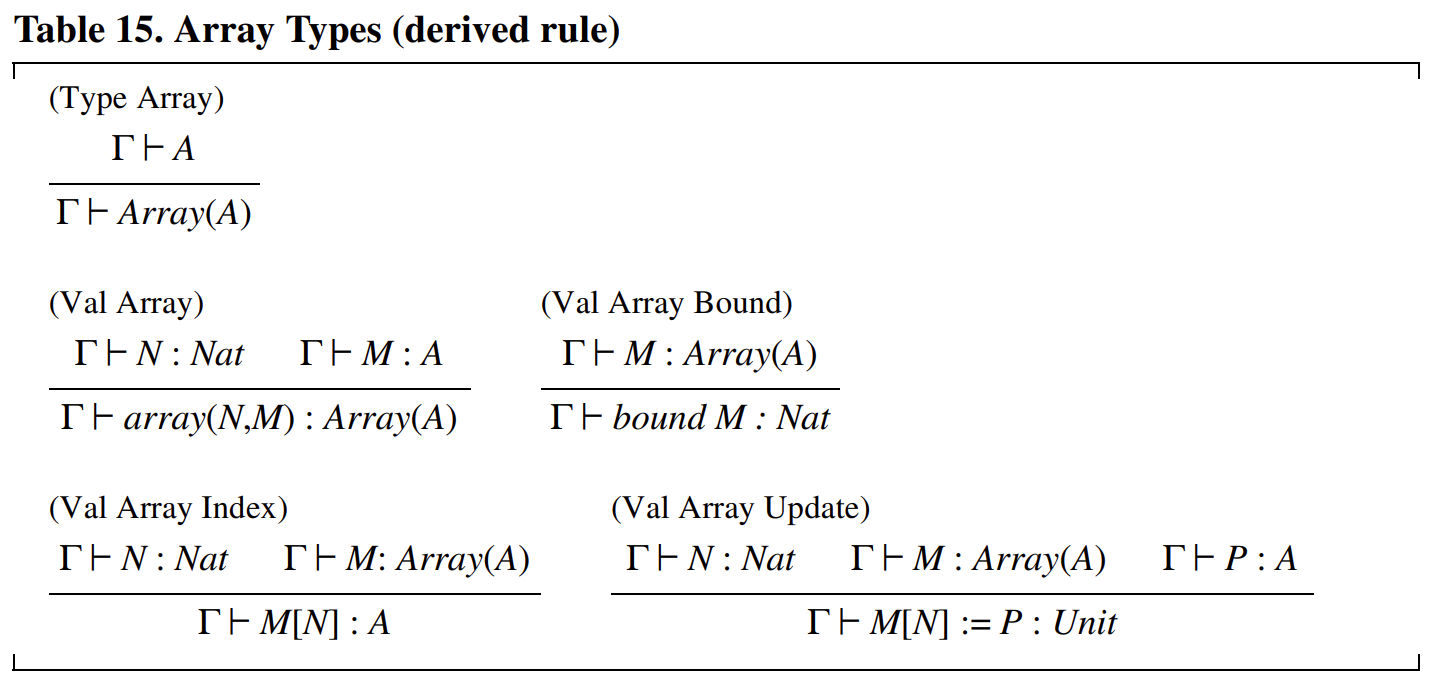
note: 其實還挺好理解的，一個有界數(shù)組是長度和映射組成的一個元組，當然還有別的構造方案

在大多數(shù)編程語言中，類型可以遞歸定義。遞歸類型非常重要，因為它們使其他類型構造更加有用。遞歸類型通常是隱式引入的，或者缺乏精確的解釋，并且它們的特性相當微妙。因此，對遞歸類型進行形式化定義需要特別謹慎。

對遞歸類型的處理需要對 \(F_1\) 進行一個相當基礎的擴展：需要將環(huán)境擴展為包含類型變量 \(X\)。這些類型變量用于形如 \(\mu X.A\) 的遞歸類型（見表 16），其直觀上表示遞歸方程 \(X = A\) 的解，其中 \(X\) 可以出現(xiàn)在 \(A\) 中。操作 \(\text{unfold}\) 和 \(\text{fold}\) 是顯式的類型轉換，它們在遞歸類型 \(\mu X.A\) 和其展開形式 \([\mu X.A / X]A\)（其中 \([B / X]A\) 表示將 \(A\) 中所有自由出現(xiàn)的 \(X\) 替換為 \(B\)）之間進行映射，反之亦然。這些類型轉換在運行時沒有任何實際效果（即滿足 \(\text{unfold}(\text{fold}(M)) = M\) 和 \(\text{fold}(\text{unfold}(M')) = M'\)）。在實際的編程語言語法中，這些操作通常被省略，但它們的存在使得遞歸類型的形式化處理更加容易。

note: 不太記得miu算子是什么了，等會復習下

遞歸類型的一個標準應用是結合乘積類型和并集類型來定義列表和樹的類型。元素類型為 \(A\) 的列表類型 \(\text{List}_A\) 定義如下（見表 17），同時包括列表構造器 \(\text{nil}\) 和 \(\text{cons}\)，以及列表分析器 \(\text{listCase}\)。

遞歸類型可以與記錄類型（record types）和變體類型（variant types）結合使用，用于定義復雜的樹結構，例如抽象語法樹（abstract syntax trees, AST）。通過使用 \(\text{case}\) 和 \(\text{with}\) 語句，可以方便地分析這些樹結構。

當遞歸類型與函數(shù)類型結合使用時，其表達能力令人驚訝。通過巧妙的編碼，可以證明在值層級的遞歸實際上已經(jīng)隱含在遞歸類型中：無需將遞歸作為一個單獨的構造來引入。此外，在遞歸類型的存在下，可以在類型化語言中實現(xiàn)無類型編程。更具體地說，表 18 展示了如何為任意類型 \(A\) 定義一個發(fā)散元素 \(\bot_A\) 以及該類型的一個不動點算子\(\text{fix}_A\)。表 19 展示了如何在類型化計算中對無類型 \(\lambda\)-演算進行編碼。（這些編碼適用于按需調用；在按值調用中，它們的形式略有不同。）

在遞歸類型的背景下，類型等價變得尤為有趣。我們通過以下方式規(guī)避了一些問題：不處理類型定義，要求在遞歸類型與其展開形式之間顯式使用折疊和展開的強制轉換，并且不假設遞歸類型之間的任何等價關系，除了對綁定變量的重命名。在當前的形式化中，我們無需定義一個正式的類型等價判斷：兩個遞歸類型僅在結構上完全相同（允許綁定變量的重命名）時才視為等價。這種簡化的方法可以擴展，以包括類型定義和基于遞歸類型展開的類型等價關系。

First-order Type Systems for Imperative Languages

Second-order Type Systems

Subtyping