KMP 算法
前綴函數
定義
定義字符串 \(s\) 和它的長度 \(n\),字符串 \(s\) 可以寫作 \(s_0s_1s_2s_3...s_n\)
定義真前綴為:從 \(s\) 的首部開始到某個位置 \(i\) 結束的子串,但不包括 \(s\) 本身
定義真后綴為:從 \(s\) 的某個位置 \(i\) 開始到 \(s\) 的尾部結束的子串,但不包括 \(s\) 本身
定義 \(s\) 的前綴函數為:\(\pi(i)\) 為 \(s_0 ... s_i\) 中最長的相同前后綴長度
遞推
遞推基礎:\(\pi(0) = 0\)
證明:因為真前綴/真后綴不包括串本身,長度為\(1\)的子串\(s_0\)不存在真前綴/真后綴,所以長度顯然是 \(0\),前綴函數的值也是 \(0\)
遞推步驟:對于每個 \(i > 0\),比較\(s_{\pi(i-1)}\)和\(s_i\)
-
如果\(s_{\pi(i-1)}=s_i\),那么\(\pi(i) = \pi(i-1) + 1\)
-
如果\(s_{\pi(i-1)}\neq s_i\),那么再次比較\(s_i\)和\(s_{\pi(\pi(i-1)-1)}\),重復這個遞推步驟,直到\(\pi...(\pi(\pi(i-1)-1)) = 0\)仍然不相同,那么\(\pi(i) = 0\)
證明:
-
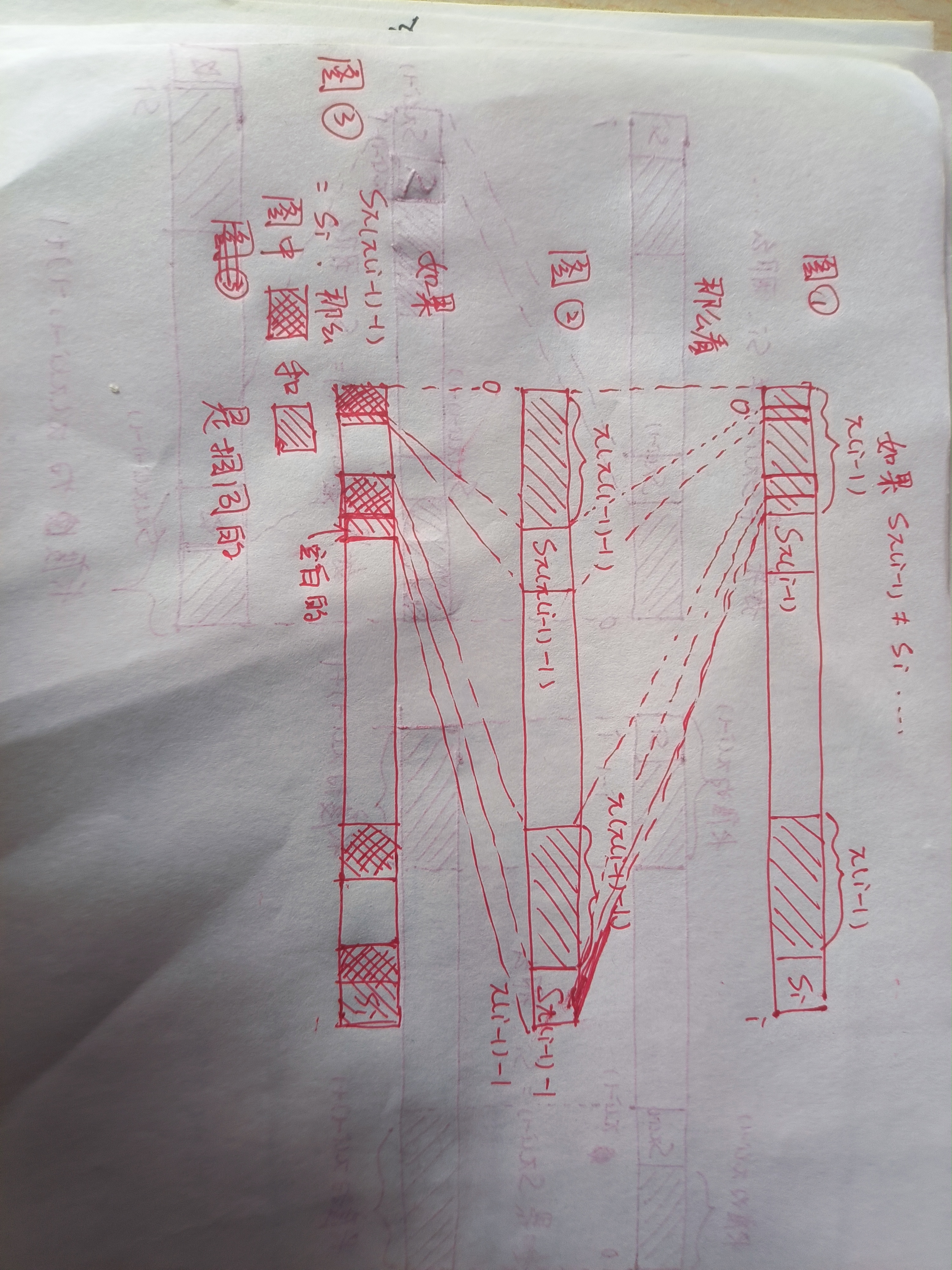
首先考慮求出\(\pi(i-1)\)的時候發生了什么:我們得到 \(s_0...s_{\pi(i-1)-1} = s_{i-\pi(i-1)}...s_{i-1}\),等式左部是真前綴,等式右部是真后綴。那么既然\(s_{\pi(i-1)}=s_i\)的話,我們可以把真前綴和真后綴都往前推進一步,得到:\(s_0...s_{\pi(i-1)-1}s_{\pi(i-1)} = s_{i-\pi(i-1)}...s_{i-1}s_i\),所以\(\pi(i) = \pi(i-1) + 1\)
圖示:

-
\(s_{\pi(i-1)}\neq s_i\) 會稍微麻煩一些,因為這意味著我們已經沒法使用\(s_0...s_{\pi(i-1)-1} = s_{i-\pi(i-1)}...s_{i-1}\)來推進了,我們需要嘗試更短的真前綴/真后綴。容易發現,找更短的真前綴/真后綴的過程和當前問題的結構是一樣的,我們可以利用前綴函數 \(\pi(\pi(i-1)-1)\) 以及其對應的真前綴/真后綴 \(s_0...s_{\pi(\pi(i-1)-1)-1} = s_{\pi(i-1)-\pi(\pi(i-1)-1)}...s_{\pi(i-1)-1}\)。如果我們運氣很好,找到了\(s_i = s_{\pi(\pi(i-1)-1)}\),那么有如下的推理:
因為 \(\pi(\pi(i-1)-1)\) 有:$$s_0...s_{\pi(\pi(i-1)-1)-1} = s_{\pi(i-1)-\pi(\pi(i-1)-1)}...s_{\pi(i-1)-1} ①$$
又因為 \(\pi(i-1)\) 有:$$s_0...s_{\pi(i-1)-1} = s_{i-\pi(i-1)}...s_{i-1}②$$
可以觀察到式子\(①\)等號左部和右部都是式子\(②\)的等號左部的一部分,那么你可以在式子\(②\)的等號右部截取同樣長的一個后綴,使得下面這個等式仍然成立(一種傳遞性):$$s_0...s_{\pi(\pi(i-1)-1)-1} = s_{i-\pi(\pi(i-1)-1)}...s_{i-1}$$
又因為\(s_i = s_{\pi(\pi(i-1)-1)}\),所以$$s_0...s_{\pi(\pi(i-1)-1)-1}s_{\pi(\pi(i-1)-1)} = s_{i-\pi(\pi(i-1)-1)}...s_{i-1}s_i$$
這意味著我們可以推進一步,否則就遞歸的進行這個過程。
圖示:
KMP 算法
KMP 算法被用來高效地解決子串匹配問題:在一個很長的字符串 \(s\)(下面我們簡稱為母串)中查詢是否有子串 \(p\) 出現,比如判定子串hello出現在helloworld中。KMP 算法的核心思想就是用上面定義的前綴函數減少匹配次數。
傳統暴力
傳統暴力的思路非常簡單:枚舉子串在母串中的起始位置,對于一個可能的起始位置,依次檢查字符是否相同,如果不同,那么推進到下一個起始位置。
for (int i = 0; i < s.length(); i++)
for(int j = 0; l < p.length(); j++) {
if (s[i] != p[j]) break;
if (j == p.length() - 1) printf("Find at %d", i);
}
假設母串和子串的長度分別是 \(n\) 和 \(m\),算法復雜度顯然是 \(O(n*m)\) 的
KMP 算法
KMP 算法利用前綴和后綴來避免不必要的比較。假設我們有母串 aaaaaaba 和子串 aaab:
假設我們已經枚舉到母串中 \(i = 2\) 的位置,在檢查中發現母串中 \(i = 5\) 和子串中 \(j = 3\) 的位置符號不相同(簡稱為失配)。那么在下一步,我們有必要從母串中 \(i = 3\) 的位置開始嗎?
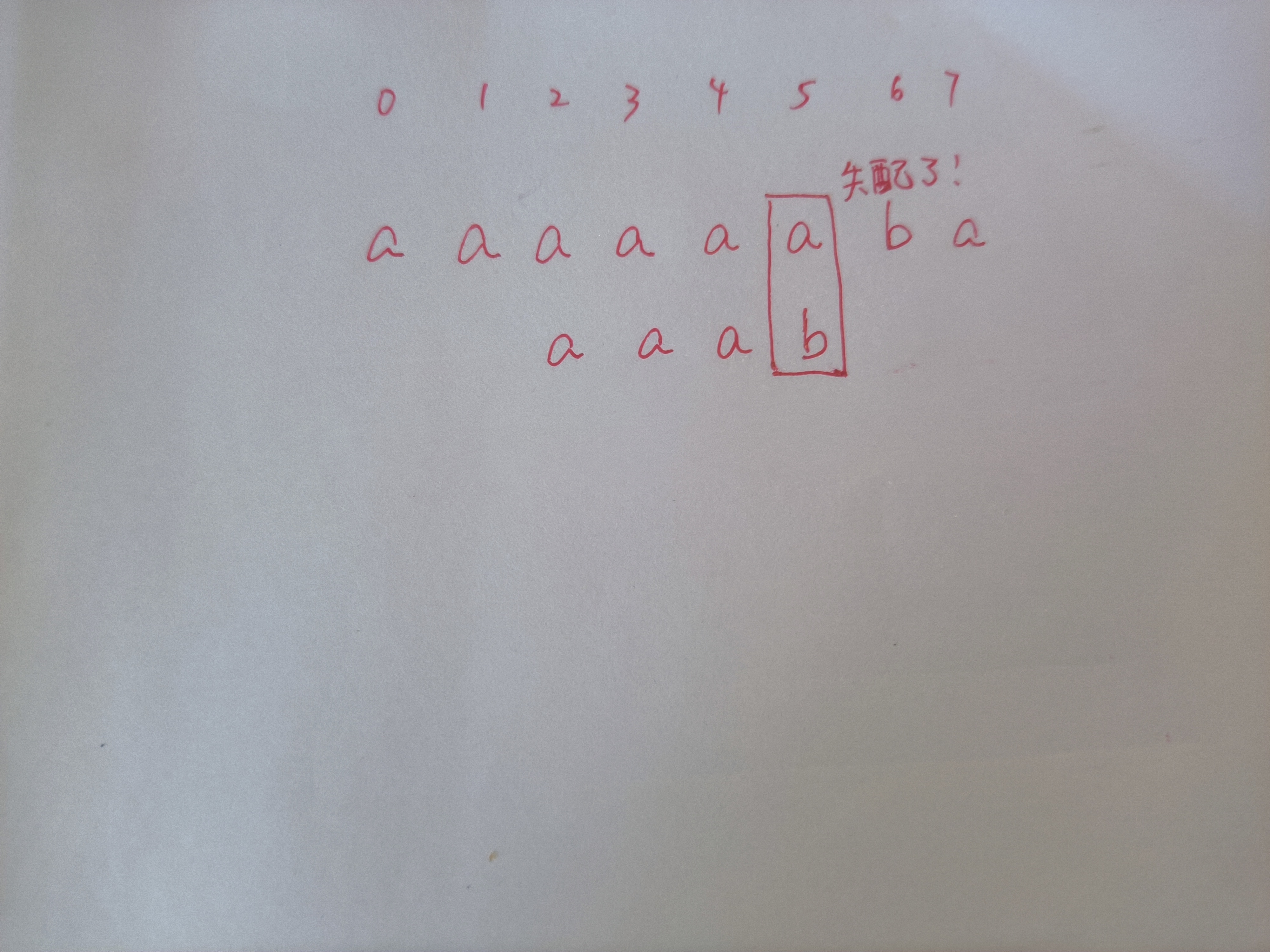
既然都這么問了,肯定不需要。因為母串中的 \(i = 2, 3, 4\) 和子串中的 \(j = 0, 1, 2\) 已經匹配上了,也就是 \(s_2s_3s_4 = p_0p_1p_2\)。經歷過上面前綴函數的磨練,你也能發現對于子串來說 \(\pi(2) = 2\),那么 \(p_0p_1 = p_1p_2\),那么顯然有 \(p_0p_1 = s_3s_4\)(和上面前綴函數相似的“傳遞”)。這意味著在下一個起始位置:母串中的\(i = 3\),我們不再需要檢查\(s_3s_4\)是否等于\(p_0p_1\),直接檢查\(s_5\)和\(p_2\)是否相同。顯然,這么做節省了很多步驟。
讓我們嘗試把情況泛化:
假設在母串的位置 \(i\) 和子串的位置 \(j\) 發生了失配,即\(s_i \neq p_j\):
-
\(j \neq 0\),那么下一個要比較 \(s_i\) 和 \(p_{\pi(j-1)}\)
-
\(j = 0\),應該枚舉母串的下一個位置 \(i\)
如果沒有失配,那么同時推進 \(i\) 和 \(j\)。
證明:TBD
#include<bits/stdc++.h>
using namespace std;
string s1, s2;
#define maxn 2000010
int nxt[maxn];
int main() {
cin >> s1 >> s2;
memset(nxt, 0, sizeof(nxt));
for (int i = 1; i < s2.size(); i++) {
if (s2[i] == s2[nxt[i - 1]]) {
nxt[i] = nxt[i - 1] + 1;
} else {
int j = nxt[i - 1];
while (j > 0 && s2[i] != s2[j]) j = nxt[j - 1];
if (s2[i] == s2[j]) j++;
nxt[i] = j;
}
}
int j = 0;
for (int i = 0; i < s1.size(); i++) {
while (j > 0 && s1[i] != s2[j]) j = nxt[j - 1];
if (s2[j] == s1[i]) j++;
if (j >= s2.size()) {
printf("%d\n", i - s2.size() + 2);
j = nxt[j - 1];
}
}
for (int i = 0; i < s2.size(); i++) {
printf("%d ", nxt[i]);
}
return 0;
}
復雜度分析
KMP 的計算復雜度是 \(O(n + m)\)
證明:
TBD



 浙公網安備 33010602011771號
浙公網安備 33010602011771號