基本概念

1. 散列是一種用于以常數平均時間執行插入、刪除和查找的技術
2. 理想的散列表數據結構是一個包含有關鍵字的具有固定大小的數組，表的大小記作TableSize，習慣上使表從0到TableSize - 1變化，每個關鍵字被映射到0到TableSize - 1范圍中的某個數并被放在合適的單元中，這個映射就叫散列函數
3. 當兩個關鍵字散列到同一個值的時候就會產生沖突，因為單元數目有限而關鍵字無窮多，處理沖突的方法有分離鏈接法和開放定址法等
4. 散列的一般做法是對\(Key\)做一些運算，最后得到一個\(HashVal\)，然后使\(Key\) \(mod\) \(TableSize\)，困難之處在于需要使得\(HashVal\)分布的盡量均勻，一般考慮將\(TableSize\)盡可能為一個素數

• 比如，考慮將字符串的ASCII值相加（一種簡單的散列）

typedef unsigned int Index;

Index Hash(const char *Key, int TableSize)
{
    unsigned int HashVal = 0;
    while (*key != '\0') HashVal += *Key++;
    return HashVal % TableSize;
}

• 比如，取前三個字符，每個給予不同的權重（一種不太好的散列）

Index Hash(const char *Key, int TableSize)
{
    return (Key[0] + 27 * Key[1] + 729 * Key[2]) % TableSize;
}

• 比如，使用一個更復雜的公式\(\sum^{KeySize - 1}_{i = 0}{Key[KeySize - i -1] * 32^i}\)獲得\(HashVal\)

Index Hash(const char *Key, int TableSize)
{
    unsigned int HashVal = 0;
    while (*Key != '\0') HashVal = (HashVal << 5) + *Key++;
    return HashVal % TableSize;
}

解決沖突

分離鏈接法

它的做法就是將散列到同一個值的所有元素保留到一個如圖所示的鏈表數組中

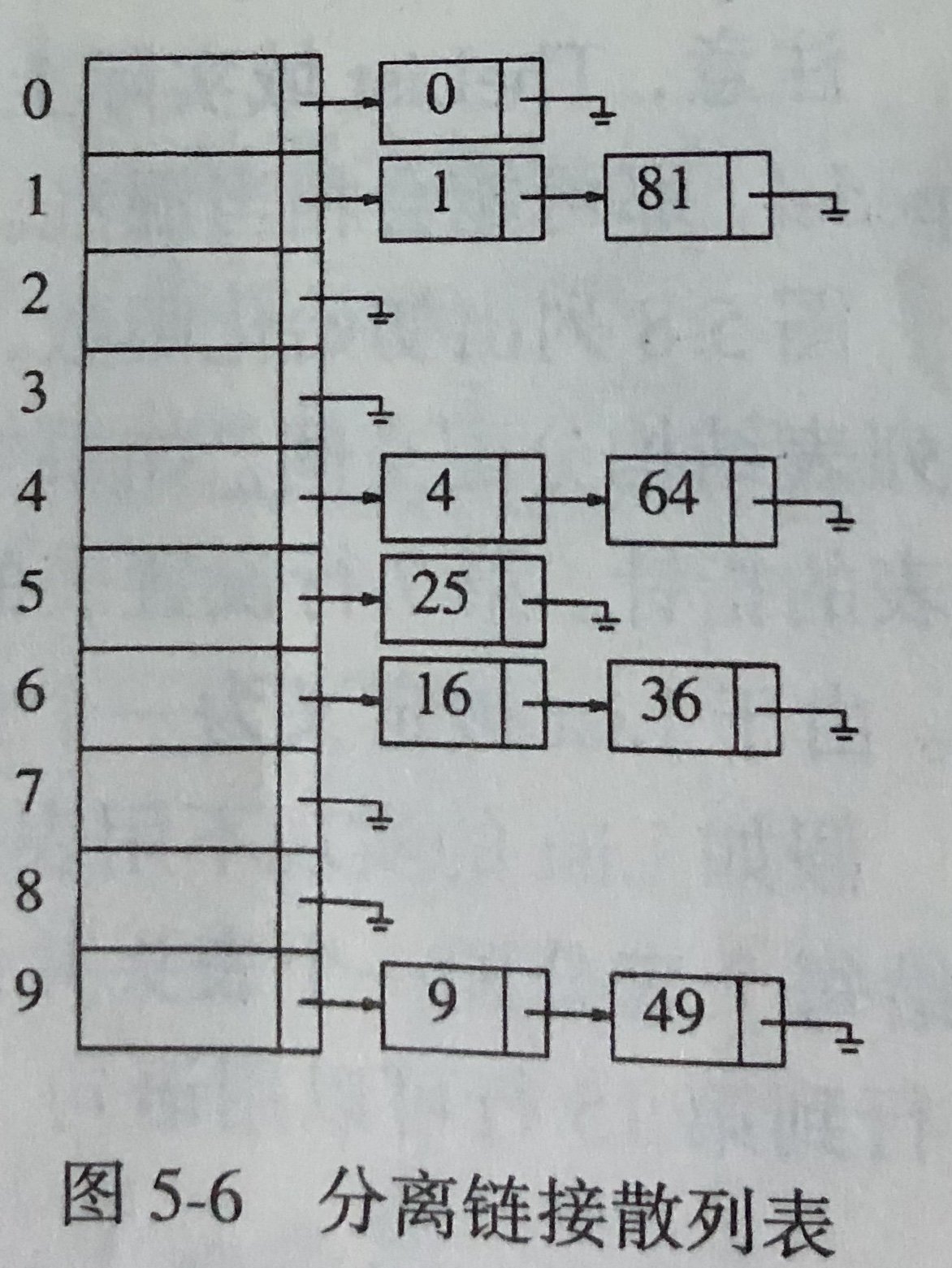
//分離鏈接散列表類型聲明
struct ListNode;
typedef struct ListNode *Position;
struct Hashbl;
typedef struct Hashbl *HashTable;

struct ListNode
{
	ElementType Element;
	Position Next;
};

typedef Position List;
struct Hashbl
{
	int TableSize;
	List* TheLists;
};

//初始化
HashTable InitializeTable(int TableSize)
{
	HashTable H;
	int i;

	if (TableSize < MiniTableSize)
	{
		Error("Table size too small");
		return NULL;
	}

	H = malloc(sizeof(struct HashTbl));
	if (H == NULL) FatalError("out of space");
	H->TableSize = NextPrime(TableSize);
	H->TheLists = malloc(sizeof(List) * H->TableSize);
	if (H->TheLists == NULL) FatalError("out of space");

	for (i = 0; i < H->TableSize; i++)
	{
		H->TheLists[i] = malloc(sizeof(struct ListNode));
		if (H->TheLists[i] == NULL) FatalError("out of space");
		else H->TheLists[i]->Next = NULL;
	}
	return H;
}

//尋找一個值
Position Find(Element Key, HashTable H)
{
	Position P;
	List L;
	L = H->TheLists[Hash(Key, H->TableSize)];
	P = L->Next;
	while (P != NULL && P->Element != Key) P = P->Next;
	return P;
}

//插入一個值
void Insert(ElementType Key, HashTable H)
{
	Position Pos, NewCell;
	List L;
	
	Pos = Find(Key, H);
	if (Pos == NULL)
	{
		NewCell = malloc(sizeof(struct ListNode));
		if (NewCell == NULL) FatalError("out of space");
		else
		{
			L = H->TheLists[Hash(Key, H->TableSize)];
			NewCell->Next = L->Next;
			NewCell->Element = Key;
			L->Next = NewCell;
		}
	}
}

如上面的代碼所示，它將新元素插入到表的最前面，不僅是因為方便，更是因為新插入的元素有可能最先被訪問，這里使用了鏈表，自然還可以想到用二叉查找樹，甚至另一個散列表來實現，這里使用了表頭，在空間不足時可以考慮不使用表頭

定義散列表的裝填因子\(\lambda\)為散列表中的元素個數與散列表大小的比值

開放定址法

簡介

開放定址散列法是另一種不用鏈表解決沖突的辦法，在開放定址法中，如果有沖突發生，就選擇嘗試另外的單元，直到找到空的單元為止，單元\(h_0(X)\)，\(h_1(X)\)，\(h_2(X)\)等相繼被試選，其中\(h_i(X) = (Hash(X) + F(i))\) \(mod\) \(TableSize\)，\(F(0) = 0\)，函數\(F\)為沖突解決方法

線性探測法

即\(F(i) = i\)的情形，就是逐個探測每個單元格以查找出一個空單元，這種方法的一個問題就是即使表格相對較空，占據的單元也會形成一些區塊，其結果稱為一次聚焦

平方探測法

即\(F(i) = i^2\)的情形，它消除了線性探測的一次聚焦問題，關于它有一個定理：如果使用平方探測，且表的發小是素數（兩個條件都要滿足），那么當表至少有一半是空的時候，總能夠插入一個新的值。雖然平方探測消除了一次聚焦，但是散列到同一位置的元素將探測相同的備選單元，稱為二次聚焦，模擬結果指出，它一般要引起另外的少于一半的探測

雙散列

再散列

可擴散列