概念和性質

1. 優先隊列是允許至少下列兩種操作的數據結構：插入（Insert）和刪除最小者（DeleteMin）
2. 實現優先隊列的數據結構叫二叉堆，他有兩個性質，結構性（完全二叉樹）和堆序性（(min)堆或(max)堆），堆的操作必須要到堆的所有性質都被滿足才能終止
3. 堆是一顆被完全填滿的二叉樹，在樹的底層上的元素從左到右填入的，這樣的樹叫完全二叉樹。可以證明一顆高為\(h\)的完全二叉樹有\(2^h\)到\(2^{h + 1} - 1\)個節點，他的高為\(?log N?\)
4. 可以用一個數組來表示一個完全二叉樹，對于數組中任意位置\(i\)上的元素，其左兒子在位置\(2i\)處，右兒子在位置\(2i + 1\)處，它的父親在位置\(?i / 2?\)處，

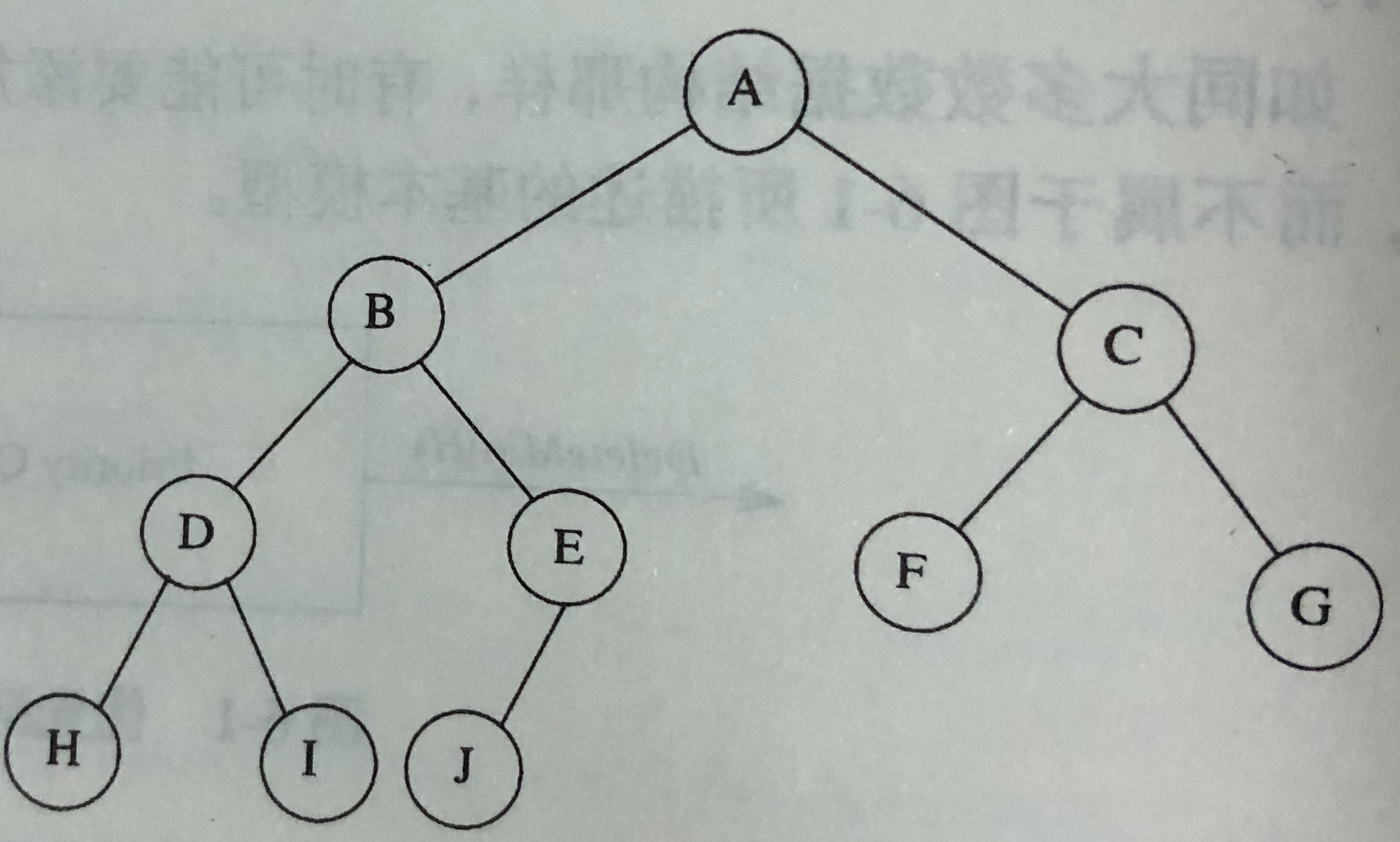
數組中的元素 | | A | B | C | D | E | F | G | H | I | J | |
-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-
數組的下標 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12

• 它的數據結構為

struct HeapStruct;
typedef struct HeapStruct *PriorityQueue;

struct HeapStruct
{
    int Capacity;
    int Size;
    ElementType *Elements;
}

基本操作

插入

void Insert(ElementType X, PriorityQueue H)
{
    int i;
    if (IsFull(H))
    {
        Error("Priority queue is Full");
        return;
    }
    for (i = ++H->Size; H->Element[i / 2] > X; i /= 2) H->Element[i] = H->Element[i / 2];
    H->Element[i] = X;
}

• 它的策略是先在尾部創建一個空穴，然后與它的父節點比較，如果比它的父節點小，則將父節點的值賦給空穴位置，然后與父節點的父節點比較，這種策略叫做上濾，如果插入的元素是新的最小元素，則它將一直上濾到根的位置，所以插入的最壞情形時間復雜度為\(\mathrm{O}(log N)\)

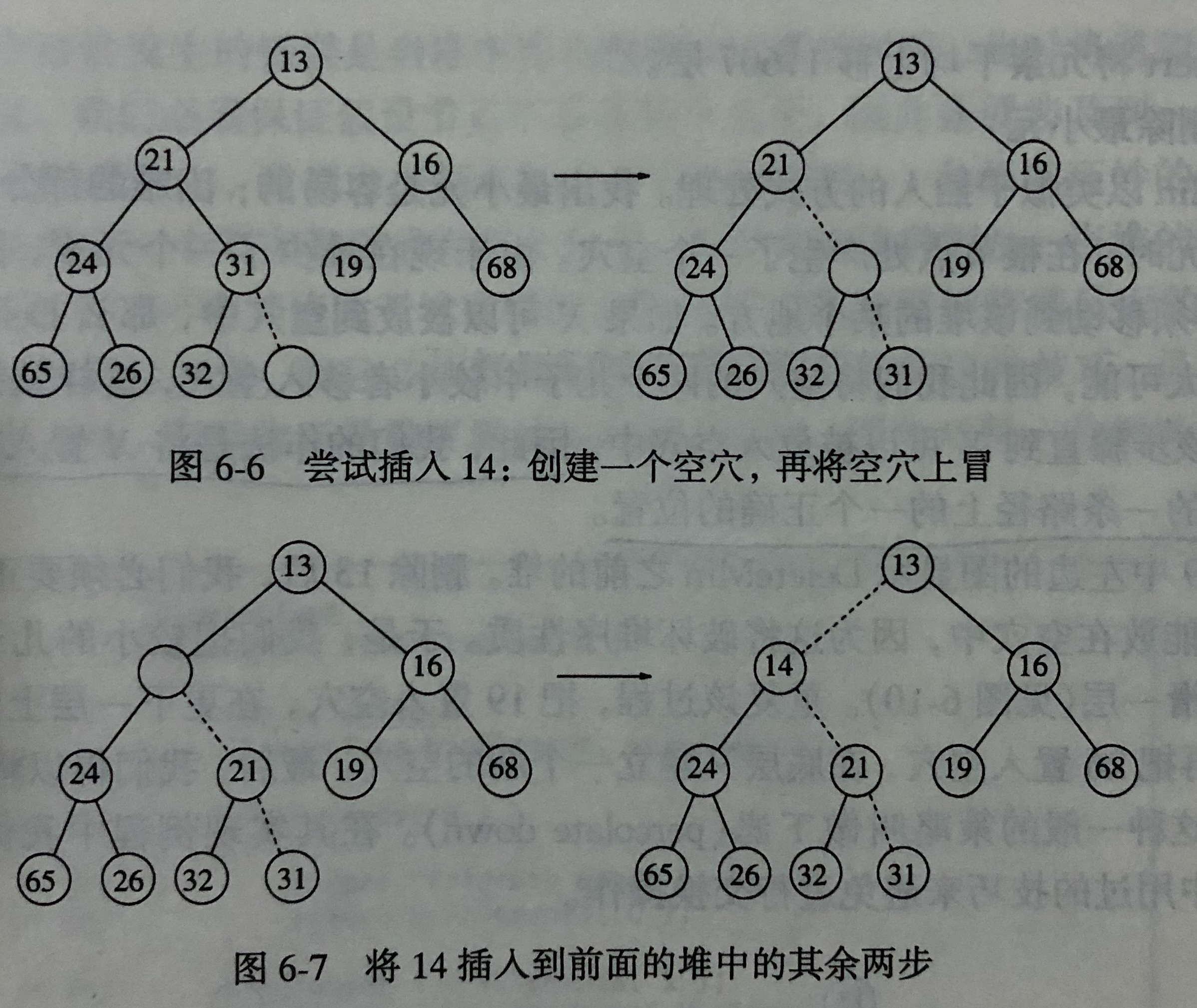
這里還有一個小問題，當\(i = 1\)時程序必須跳出循環，雖然說可以用一個if判斷來跳出，但這里（書上）使用的方法是在位置0處放一個保證小于堆中的任何值的一個值，避免了每次循環都要執行一次測試，個人感覺也是一條思路吧

刪除最小者

ElementType DeleteMin(PriorityQueue H)
{
	int i, Chile;
	ElementType MinElement, LastElement;
	
	if (IsEmpty(H))
	{
		Error("Priority queue is empty")
		return;
	}
	MinElement = H->Elements[1];
	LastElement = H->Elements[H->Size--];

	for (i = 1; i * 2 <= H->Size; i = Child)
	{
		Child = i * 2;
		if (Child != H->Size && H->Elements[Child + 1] < H->Elements[Child]) Child++;
		if (LastElement > H->Elements[Child]) H->Elements[i] = H->Elements[Child];
		else break;
	}
	H->Elements[i] = LastElement;
	return MinElement;
}

• 找到最小元素很簡單，就是根的位置，將其刪除后為了保持堆的堆序性自然要進行一系列的調整，此時在根的位置上就出現了一個空穴，并且位于堆的最后一個元素\(X\)也必須找到一個合適的位置，所以從根開始，對比它的兒子節點與\(X\)的大小，如果是兒子節點中的某一個更小，則將其放入根處的空穴，此時就又出現了一個空穴，按同樣的方法繼續向下推進，直到\(X\)可以正確的放入堆中，這個策略叫下濾,算法的最壞情形時間復雜度為\(\mathrm{O}(log N)\)

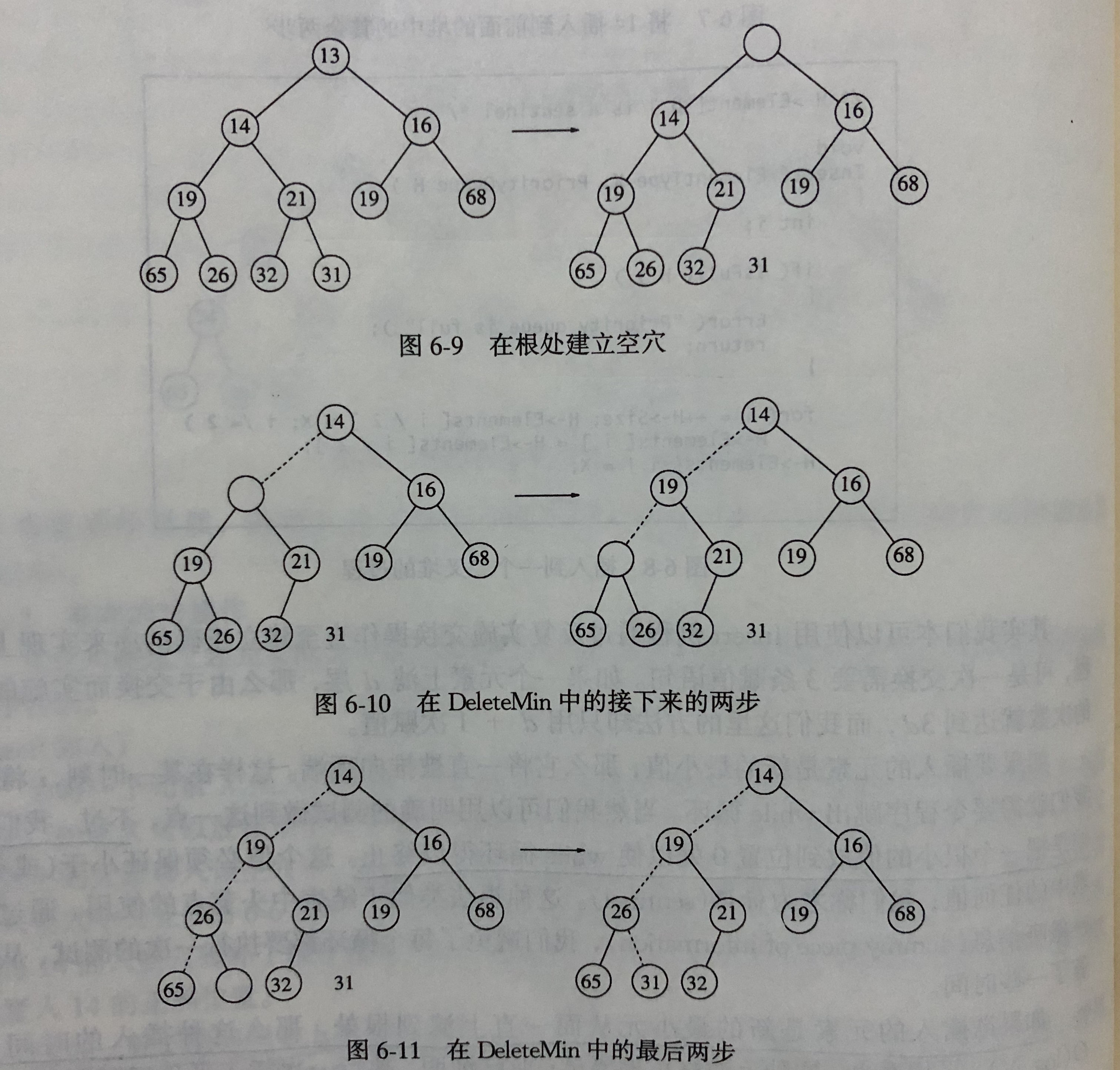
這里需要考慮的一個問題是一個父節點并不總是有兩個兒子節點，所以會有這么一條判斷if (Child != H->Size && H->Elements[Child + 1] < H->Elements[Child]) Child++;，它有效的保證了不會越界訪問元素并且判斷了兩個子節點的大小（如果有的話）