wqs 二分

0.前言

去年 10 月底學(xué)了一遍，當前再次學(xué)習(xí)并記錄。

wqs 二分，也稱帶權(quán)二分，一般用于優(yōu)化決策單調(diào)性優(yōu)化 DP。

1.wqs 二分

對于此類問題：給定 $n$ 個物品，現(xiàn)要求將其分為 $m$ 段，每段存在相應(yīng)的代價 $w$，求代價最值。

如果沒有限制段數(shù)，可以考慮使用決策單調(diào)性優(yōu)化或者斜優(yōu)來做到 $\mathcal{O(n \log n)}$ 或 $\mathcal{O(n)}$，再加上一維段數(shù)的限制，我們可以得到一個 $\mathcal{O(mc)}$（$c = n\log n$ 或 $n$）的算法，即 $f_{i,cnt}$ 表示前 $i$ 個物品，分了 $cnt$ 段的代價最值。那么有如下轉(zhuǎn)移：

\[f_{i,cnt} = f_{j,cnt - 1} + w(j,i) \]

但當 $\mathcal{O(nm)}$ 過大，上述做法會 TLE，此時需要考慮使用 wqs 二分來優(yōu)化 DP。

首先假設(shè)我們討論的情形是，求最小值。將 $(i,g_i = f_{n,i})$ 當作點全部放在平面直角坐標系中，并順次連接，假設(shè)得到的是下凸包。

該函數(shù)圖像就表示了限制分為 $i$ 段時的代價最小值，得到的圖像為下凸包，該條件等價于 $\forall i \in [2,m - 1], g_{i - 1} - g_{i} \ge g_{i} - g_{i + 1} \Leftrightarrow \Delta \downarrow$。

畫出該下凸包。圖中標紅的點 C 即為要求的點 $(m,g_{m})$。

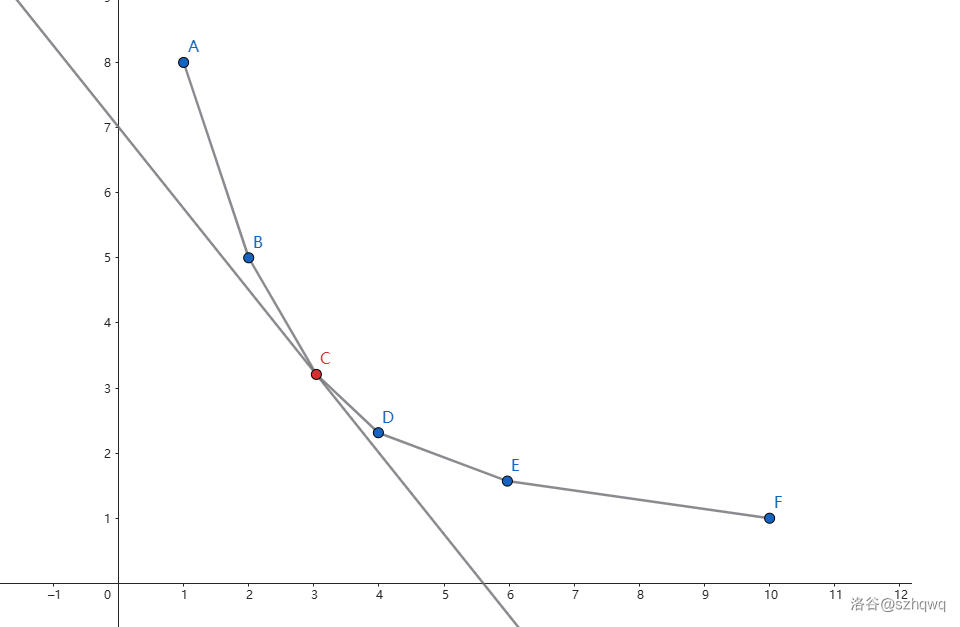
拿一條斜率為 $k$ 直線去截我們需要的答案點，所二分的即為斜率 $k$，如果能夠求出所截到的點 $(p,g_p)$，就能夠通過比較 $p$ 與 $m$，考慮斜率是需要增大還是減小，再調(diào)整二分區(qū)間。

如果我們觀察該斜率的直線與凸包上每個點的相交后的直線，會發(fā)現(xiàn)第一個截到的點的截距最小（上凸包則為截距最大），觀察 $b = y - kx$ 的式子，問題可以等價于求 $\min\limits_{i = 1}^m \{f_i - ki\}$。

相當于每次分段的時候?qū)⒇暙I $- k$，等價于做無段數(shù)限制的 DP。 這就是 wqs 二分的核心。注意并非每次都是將貢獻 $-k$，需要考慮該題求的是最大代價還是最小代價，需要向著與要求最值相反的方向來進行加減，這樣方可起到限制段數(shù)的作用。

在做 DP 的時候可以記錄轉(zhuǎn)移次數(shù)，即得到所截點的橫坐標 $p$。但我們二分完斜率之后，需要將答案斜率再 check 一遍得到答案的 $f_n$，最終答案需要加上 $m \times k$。

2.特別注意

I.多點共線

在題目中，通常會遇到多點共線的情況，如圖，所求點為 D，但是點 C，E 也同樣會被截到。

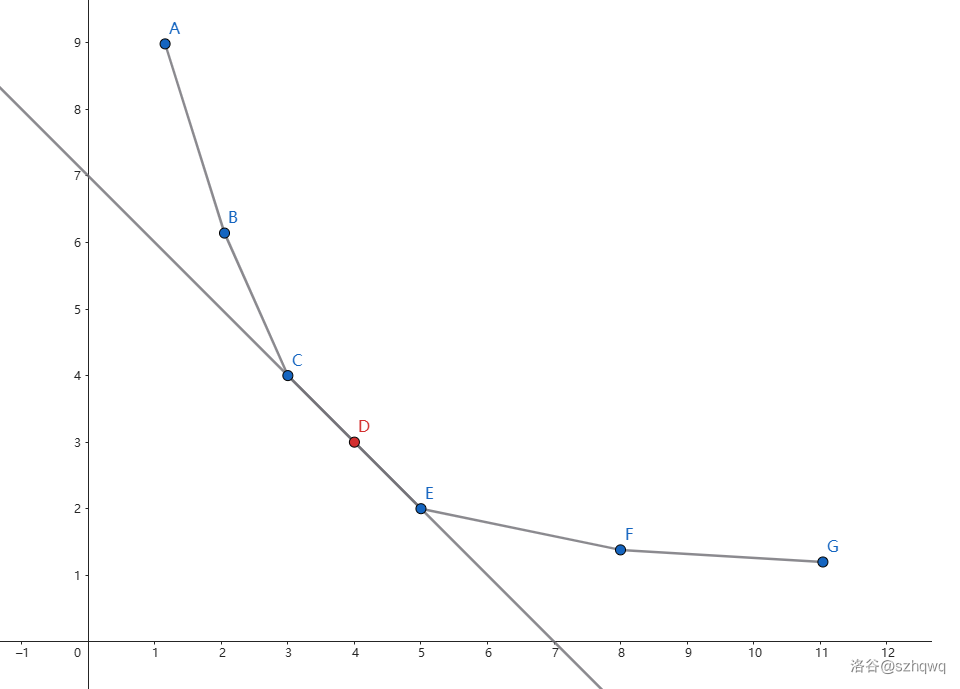
在決策單調(diào)性優(yōu)化 DP一文中我提到過取決策點時，通常需要欽定取最小決策點還是最大決策點，就我個人的寫法而言，取的是最小決策點，此時會取到共線點的左端點，所以此時在 check 的時候我應(yīng)該判斷轉(zhuǎn)移次數(shù) $g_n \le m$（此處的 $g_n$ 指轉(zhuǎn)移次數(shù)，并非上文的 $f_{n,m}$）。如果寫 $g_n \ge m$，那么在共線的時候并不會記錄答案，而是直接改變斜率繼續(xù)二分，此時可能我們就不能再二分到答案斜率了。

關(guān)于該點詳見帖子。

II.斜率

若貢獻均為整數(shù)，則我們二分斜率也為整數(shù)，如果貢獻為小數(shù)，才會采用小數(shù)二分，一般情況下整數(shù)貢獻不會采用小數(shù)二分，時間限制可能不能接受。

III.內(nèi)層 DP 為斜優(yōu)

此時需要極度注意細節(jié)。

思考你在出隊頭隊尾時所取的點是最小決策點還是最大決策點，即取不取等，該點需與 check 的判斷條件相對應(yīng)，與 I. 中所敘述的問題類似。如果取的是最小決策點那么出隊時判斷不應(yīng)該取等。

3.例題

I.P6246 [IOI 2000] 郵局加強版加強版

此題需要嚴格注意細節(jié)才能通過。

做該題前可以先把 $\mathcal{O(pn\log n)}$ 的做法寫出來，即P4767 [IOI 2000] 郵局加強版。

#include <bits/stdc++.h>

// #define int long long
#define ll long long
#define ull unsigned long long
#define db double
#define ld long double
#define rep(i,l,r) for (int i = (int)(l); i <= (int)(r); ++ i )
#define rep1(i,l,r) for (int i = (int)(l); i >= (int)(r); -- i )
#define il inline
#define fst first
#define snd second
#define ptc putchar
#define Yes ptc('Y'),ptc('e'),ptc('s'),puts("")
#define No ptc('N'),ptc('o'),puts("")
#define YES ptc('Y'),ptc('E'),ptc('S'),puts("")
#define NO ptc('N'),ptc('O'),puts("")
#define pb emplace_back
#define sz(x) (int)(x.size())
#define all(x) x.begin(),x.end()
#define get(x) ((x - 1) / len + 1)
#define debug() puts("------------")

using namespace std;
typedef pair<int,int> PII;
typedef pair<int,PII> PIII;
typedef pair<ll,ll> PLL;
namespace szhqwq {
    template<class T> il void read(T &x) {
        x = 0; T f = 1; char ch = getchar();
        while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
        while (ch >= '0' && ch <= '9') { x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar(); }
        x *= f;
    }
    template<class T,class... Args> il void read(T &x,Args &...x_) { read(x); read(x_...); }
    template<class T> il void print(T x) {
        if (x < 0) ptc('-'), x = -x; 
        if (x > 9) print(x / 10); ptc(x % 10 + '0');
    }
    template<class T,class T_> il void write(T x,T_ ch) { print(x); ptc(ch); }
    template<class T,class T_> il void chmax(T &x,T_ y) { x = max(x,y); }
    template<class T,class T_> il void chmin(T &x,T_ y) { x = min(x,y); }
    template<class T,class T_,class T__> il T qmi(T a,T_ b,T__ p) {
        T res = 1; while (b) {
            if (b & 1) res = res * a % p;
            a = a * a % p; b >>= 1;
        } return res;
    }
    template<class T> il T gcd(T a,T b) { if (!b) return a; return gcd(b,a % b); }
    template<class T,class T_> il void exgcd(T a, T b, T_ &x, T_ &y) {
        if (b == 0) { x = 1; y = 0; return; }
        exgcd(b,a % b,y,x); y -= a / b * x; return ;
    }
    template<class T,class T_> il T getinv(T x,T_ p) { T inv,y; exgcd(x,(T)p,inv,y); inv = (inv + p) % p; return inv; }
} using namespace szhqwq;
const int N = 3010,inf = 1e9,mod = 998244353;
const ull base = 131,base_ = 233;
const ll inff = 1e18;
int n,p;
int a[N],f[N][310],s[N];
int q[N],hh = 1,tt;

il int calc(int j,int i) {
    int mid = i + j >> 1;
    int dis = s[i] - s[mid] - (i - mid) * a[mid] + (mid - j + 1) * a[mid] - (s[mid] - s[j - 1]);
    return dis;
}

il int check(int j,int i,int c) {
    if (f[j][c - 1] + calc(j + 1,n) <= f[i][c - 1] + calc(i + 1,n)) return n + 1; // 注意 <=
    int l = i,r = n,ret = -1;
    while (l <= r) {
        int mid = l + r >> 1;
        if (f[j][c - 1] + calc(j + 1,mid) > f[i][c - 1] + calc(i + 1,mid)) r = mid - 1,ret = mid; // 注意 >，兩處地方共同構(gòu)成了取最小決策點的寫法
        else l = mid + 1;
    }
    return ret;
}

il void solve() {
    //------------code------------
    read(n,p);
    rep(i,1,n) read(a[i]),s[i] = s[i - 1] + a[i];
    memset(f,0x3f,sizeof f);
    sort(a + 1,a + n + 1);
    // cerr << calc(1,4) << endl;
    f[0][0] = 0;
    rep(cnt,1,p) {
        hh = 1; tt = 0;
        rep(i,1,n) {
            // cerr << hh << " " << tt << endl;
            while (hh <= tt && check(q[hh - 1],q[hh],cnt) <= i) ++ hh;
            int j = q[hh - 1];
            f[i][cnt] = f[j][cnt - 1] + calc(j + 1,i);
            while (hh <= tt && check(q[tt - 1],q[tt],cnt) >= check(q[tt],i,cnt)) -- tt;
            q[++ tt] = i;
        }
    }
    // rep(i,1,n) {
    //     rep(j,1,p) cerr << f[i][j] << " ";
    //     cerr << '\n';
    // }
    write(f[n][p],'\n');
    return ;
}

il void init() {
    return ;
}

signed main() {
    // init();
    int _ = 1;
    // read(_);
    while (_ -- ) solve();
    return 0;
}

觀察 $(i,f_{n,i})$ 構(gòu)成的函數(shù)圖像，感性猜測該題為斜率為負的下凸包，當然可以嚴謹證明，大多數(shù)情況下我們通常僅進行猜測。所以在取最小決策點的情況下，如果 $g_n \le m$，則增大斜率 $l \gets mid + 1,ret \gets mid$，反之 $r \gets mid - 1$。因為該題要求最小值，所以在 check 里 DP 轉(zhuǎn)移中要限制其的段數(shù)，故我們需要 $ - k$，等價于每次轉(zhuǎn)移會多加上一個正整數(shù)。
最后答案再加上 $p \times k$ 即可。

#include <bits/stdc++.h>

// #define int long long
#define ll long long
#define ull unsigned long long
#define db double
#define ld long double
#define rep(i,l,r) for (int i = (int)(l); i <= (int)(r); ++ i )
#define rep1(i,l,r) for (int i = (int)(l); i >= (int)(r); -- i )
#define il inline
#define fst first
#define snd second
#define ptc putchar
#define Yes ptc('Y'),ptc('e'),ptc('s'),puts("")
#define No ptc('N'),ptc('o'),puts("")
#define YES ptc('Y'),ptc('E'),ptc('S'),puts("")
#define NO ptc('N'),ptc('O'),puts("")
#define pb emplace_back
#define sz(x) (int)(x.size())
#define all(x) x.begin(),x.end()
#define get(x) ((x - 1) / len + 1)
#define debug() puts("------------")

using namespace std;
typedef pair<int,int> PII;
typedef pair<int,PII> PIII;
typedef pair<ll,ll> PLL;
namespace szhqwq {
    template<class T> il void read(T &x) {
        x = 0; T f = 1; char ch = getchar();
        while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
        while (ch >= '0' && ch <= '9') { x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar(); }
        x *= f;
    }
    template<class T,class... Args> il void read(T &x,Args &...x_) { read(x); read(x_...); }
    template<class T> il void print(T x) {
        if (x < 0) ptc('-'), x = -x; 
        if (x > 9) print(x / 10); ptc(x % 10 + '0');
    }
    template<class T,class T_> il void write(T x,T_ ch) { print(x); ptc(ch); }
    template<class T,class T_> il void chmax(T &x,T_ y) { x = max(x,y); }
    template<class T,class T_> il void chmin(T &x,T_ y) { x = min(x,y); }
    template<class T,class T_,class T__> il T qmi(T a,T_ b,T__ p) {
        T res = 1; while (b) {
            if (b & 1) res = res * a % p;
            a = a * a % p; b >>= 1;
        } return res;
    }
    template<class T> il T gcd(T a,T b) { if (!b) return a; return gcd(b,a % b); }
    template<class T,class T_> il void exgcd(T a, T b, T_ &x, T_ &y) {
        if (b == 0) { x = 1; y = 0; return; }
        exgcd(b,a % b,y,x); y -= a / b * x; return ;
    }
    template<class T,class T_> il T getinv(T x,T_ p) { T inv,y; exgcd(x,(T)p,inv,y); inv = (inv + p) % p; return inv; }
} using namespace szhqwq;
const int N = 5e5 + 10,inf = 1e9,mod = 998244353;
const ull base = 131,base_ = 233;
const ll inff = 1e18;
int n,p;
ll a[N],f[N],s[N],g[N];
int q[N],hh = 1,tt;

il ll calc(int j,int i) {
    int mid = i + j >> 1;
    ll dis = s[i] - s[mid] - (i - mid) * a[mid] + (mid - j + 1) * a[mid] - (s[mid] - s[j - 1]);
    return dis;
}

il int check(int j,int i) {
    if (f[j] + calc(j + 1,n) <= f[i] + calc(i + 1,n)) return n + 1;
    int l = i,r = n,ret = -1;
    while (l <= r) {
        int mid = l + r >> 1;
        if (f[j] + calc(j + 1,mid) > f[i] + calc(i + 1,mid)) r = mid - 1,ret = mid;
        else l = mid + 1;
    }
    return ret;
}

il bool check__(int val) {
    hh = 1; tt = 0; f[0] = g[0] = 0;
    rep(i,1,n) {
        // cerr << hh << " " << tt << endl;
        while (hh <= tt && check(q[hh - 1],q[hh]) <= i) ++ hh;
        int j = q[hh - 1];
        f[i] = f[j] + calc(j + 1,i) - val; g[i] = g[j] + 1;
        while (hh <= tt && check(q[tt - 1],q[tt]) >= check(q[tt],i)) -- tt;
        q[++ tt] = i;
    }
    return g[n] <= p;
}

il void solve() {
    //------------code------------
    read(n,p);
    rep(i,1,n) read(a[i]);
    sort(a + 1,a + n + 1);
    rep(i,1,n) s[i] = s[i - 1] + a[i];
    int l = -1e7,r = 0,ret = 0;
    while (l <= r) {
        int mid = l + r >> 1;
        if (check__(mid)) l = mid + 1,ret = mid;
        else r = mid - 1;
    }
    check__(ret);
    write(f[n] + p * ret,'\n');
    return ;
}

il void init() {
    return ;
}

signed main() {
    // init();
    int _ = 1;
    // read(_);
    while (_ -- ) solve();
    return 0;
}

4.練習(xí)題

直接借用他人的題單。Link

5.參考資料

DP 優(yōu)化方法大雜燴 I. - Alex_wei

wqs 二分入門 - MafuyuQWQ

【學(xué)習(xí)筆記】WQS二分詳解及常見理解誤區(qū)解釋 - ikrvxt

作者水平有限，如有錯誤請指出。

posted @ 2025-07-31 19:32 songszh 閱讀(16) 評論(0) 收藏舉報

刷新頁面返回頂部

szhqwq's blogs

aaa

wqs 二分

0.前言

1.wqs 二分

2.特別注意

I.多點共線

II.斜率

III.內(nèi)層 DP 為斜優(yōu)

3.例題

I.P6246 [IOI 2000] 郵局加強版加強版

4.練習(xí)題

5.參考資料

公告

szhqwq's blogs

aaa

wqs 二分

0.前言

1.wqs 二分

2.特別注意

I.多點共線

II.斜率

III.內(nèi)層 DP 為斜優(yōu)

3.例題

I.P6246 [IOI 2000] 郵局 加強版 加強版

4.練習(xí)題

5.參考資料

公告

I.P6246 [IOI 2000] 郵局加強版加強版