結構化概率模型

結構化概率模型(Structured Probabilistic model)，就是利用圖論(graph theory)中的圖來表示概率分布中相互之間作用的隨機變量的關系。深度學習經常面對的問題是如何理解具有豐富結構的高維數據的問題，例如圖片、語音、文本等等。除了經典的分類問題如圖像識別、語音識別等，有的時候我們還要處理比分類更復雜的任務，如分布密度估計，降噪，填補損失數據，取樣等等。我們無法僅僅用一個大型的查找表(look-up table)來處理這些問題，例如假如我們要模擬具有\(n\)個元素每個元素可以取\(k\)個不同值的隨機向量 \(\overrightarrow{x}\) 的分布，我們如果采用查找表就需要 \(k^n\) 個參數，我們需要很大的存儲空間，需要海量的數據才能防止過擬合，而且預測或者取樣的時間也會很長。

使用大型查找表的問題在于我們要模擬所有變量之間的相互關系，但實際問題中常常只有某些變量和其他變量發生直接作用，而圖(graph)就可以很好的表示隨機變量之間的作用關系，其中每個節點(node)代表了一個隨機變量，而每條邊(edge)代表了兩個隨機變量之間有直接作用，而連接不相鄰節點的路徑(path)就代表了簡介相互作用。圖可以分為兩種：有向圖(directed graph)和無向圖(undirected graph)。

有向圖

有向圖又被稱作信念網絡(belief network)或者貝葉斯網絡(bayesian network)，圖中的邊是有方向的，即從一個節點指向另一個節點，其方向代表了條件概率分布，例如從\(a\)指向\(b\)的邊代表了\(b\)的概率分布依賴于\(a\)的值。一個簡單的有向圖如下圖所示：

上圖對應的概率分布可以表示為 \(p\left(t_0, t_1, t_2\right)=p\left(t_0\right) p\left(t_1 \mid t_0\right) p\left(t_2 \mid t_1\right)\) ，一般的圖的概率分布可通過\(p(x)=\prod_i p\left(x_i \mid P a_G\left(x_i\right)\right)\) 來表示，其中 \(P a_G\left(x_i\right)\) 代表了圖G中節點 \(x_i\) 的所有父節點即指向它的節點。和查找表方法相比較，假如條件概率最多出現 \(\mathrm{m}\) 個變量，則有向圖復雜度為 \(O\left(k^m\right)\) ，假如我們設計的模型 \(m \ll n\) ，則其效率遠高于查找表方法。

無向圖

有向圖適用于信息流動方向比較明確的問題，而對于其他因果律不明確的問題，我們需要用無向圖來表示，無向圖也被叫做馬爾科夫隨機場(Markowv random fields)或馬爾科夫網絡(Markov Network)。在無向圖中，邊是沒有方向的，且不代表條件概率，一個簡單的無向圖如下圖所示:

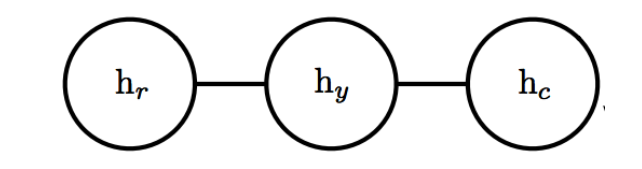
對于無向圖，如果一個子集包含的所有點兩兩之間均相互連接，則這個集合叫做團(clique)，簡記 做 \(C\) ，用 \(\phi(C)\) 來表示團 \(C\) 的所有變量的聯合概率分布，則整個圖的非歸一化的概率分布 (unnormalized probability distribution)可表示為 \(\tilde{p}(x)=\prod_{C \in G} \phi(C)\) ，為了使概率歸一 化，我們需要引入配分函數 (partition function) \(Z=\int \tilde{p}(x) d x\) ，歸一化后的概率即可表示為 \(p(x)=\frac{1}{Z} \tilde{p}(x)\) 。由于\(Z\)的形式是積分形式，這會導致最大似然估計遇到計算難題，這類問題的解決在18章中會介紹用近似方法求配分函數。
處理具體問題時，常常需要假設對于所有的 \(x ， \tilde{p}(x)>0\) ，一個可以保證這一條件的模型是基于能量的模型(energy-based model)，即 \(\tilde{p}(x)=\exp (-E(x))\) ，由于取指數后總是正值，這保證了所有狀態的概率大于零。基于能量的模型也被稱作玻爾茲曼機(Boltzmann machine)。
當我們想從模型中取樣時，對于有向圖，我們可以利用ancestral sampling，即對圖中的變量進行拓撲排序(topological ordering)，使得對于所有 \(i, j\) ，滿足假如 \(x_i\) 是 \(x_j\) 的父節點，則 \(j>i\) 。這樣，我們就可以先取樣 \(x_1 \sim P\left(x_1\right)\), 然后取樣 \(P\left(x_2 \mid P a_G\left(x_2\right)\right)\) ，以此類推，最后取樣 \(P\left(x_n \mid P a_G\left(x_n\right)\right)\)。

Gibbs Sampling

但是對于無向圖，我們無法進行拓撲排序，通常采取的方法是Gibbs sampling。Gibbs Sampling 是一種馬爾科夫鏈蒙特卡洛算法(Markov Chain Monte Carlo，簡稱MCMC)，其基本思想是假設我們有 \(\mathrm{n}\) 個變量，初始的樣本表示為 \(\left(x_1^{(0)}, x_2^{(0)}, \ldots, x_n^{(0)}\right)\) ，之后迭代取樣時每個變量取自依賴于現有其他變量值的條件概率分布，即第 \(i\) 次迭代取樣時，

依此迭代直到取樣趨近于真實分布。

假設我們有許多觀察到的變量 \(\vec{v}\) ，有些有相互作用有些沒有且我們事先不知道這些相互關系，我們該如何訓練出合適的圖來表示它們之間的關系呢? 一種方法被稱作結構學習（structure learning），本質上是一種貪心搜索算法(greedy search)，即先試驗幾種結構的圖，看哪種訓練誤差最小且模型復雜度較低，然后再在這種結構上試驗添加或去除某些邊并選取其中效果最好的結構再如此循環下去。這種算法的缺點是需要不斷的搜索模型結構而且需要多次訓練，另一種更常見的方法是引入一些隱藏變量 \(\vec{h}\) ，則觀察變量 \(v_i\) 與 \(v_j\) 的關系通過 \(v_i\) 與 \(\vec{h}\) 以及 \(\vec{h}\) 與 \(v_j\) 之間的依賴關系而間接的表示出來。我們可以選取固定的圖的結構，令隱藏變量與觀察變量相連接，并且通過梯度下降算法求得代表這些連接強弱的參數。
模型訓練結束后，如何用模型進行對于某些節點的邊緣分布(marginal distribution)或條件概率分布(conditional distribution) 進行推斷也是一大難題，所以常常需要我們進行近似推斷，深度學習中常用到變分推斷(variational inference)，即尋找接近真實分布 \(p(\vec{h} \mid \vec{v})\) 的近似分布 \(q(\vec{h} \mid \vec{v})\) 。

概率圖也可以用深度學習中的計算圖來代表，觀察變量構成輸入層，隱藏變量構成隱藏層，層與層之間的鏈接即代表概率圖中的邊。一個例子是受限玻爾茲曼機(restricted Boltzmann machine，簡稱RBM) ，即網絡中僅有隱藏變量與觀察變量的連接，而觀察變量間沒有連接，隱藏變量間也沒有連接，如下圖所示:

其能量函數可表示為 \(E(\vec{v}, \vec{h})=-\vec{b}^T \vec{v}-\vec{c}^T \vec{h}-\vec{v}^T W \vec{h}\) ，其中 \(\vec{b}, \vec{c}, W\) 為網絡所需要學習的參數。

由于RBM中僅有 \(\vec{v}\) 與 \(\vec{h}\) 間的連接，Gibbs sampling的過程就更簡單了，可以同時sample所有的 \(\vec{h}\) ，然后再同時 sample所有的 \(\vec{v}\) 依次交替進行。另外能量函數的導數為 \(\frac{\partial}{\partial W_{i, j}} E(\vec{v}, \vec{h})=-v_i h_j\) ，方便運算，所以我們可以很高效的進行訓練。

總結

這一章主要講了概率圖模型的基本概念，概率圖模型中很多概念來源于統計物理，如配分函數，能量函數，玻爾茲曼機等，Gibbs sampling名字也是致敬統計物理學家吉布斯。因此，如何在學習過程中發現并促進不同學科的融合也是一個問題。