線性因子模型

線性因子

之前總結(jié)的方法大部分是在 有大量數(shù)據(jù)情況下的監(jiān)督學(xué)習(xí)方法，而假如我們想減小數(shù)據(jù)量的要求，則需要一些無(wú)監(jiān)督學(xué)習(xí)及半監(jiān)督學(xué)習(xí)方法，雖然有很多無(wú)監(jiān)督學(xué)習(xí)方法，但是目前還無(wú)法達(dá)到深度學(xué)習(xí)在監(jiān)督學(xué)習(xí)問(wèn)題中所達(dá)到的精度，這常常是由于我們需要解決的問(wèn)題的維度過(guò)高或計(jì)算量過(guò)大造成的。
無(wú)監(jiān)督學(xué)習(xí)常常需要建立一種依賴(lài)于觀察數(shù)據(jù)的概率模型 \(p_{\text {model }}(x)\) ，但由于實(shí)際觀察的數(shù)據(jù) \(x\) 常常比較雜亂沒(méi)有規(guī)律，通常我們會(huì)用某種代表了更低維基本特征的隱性變量(latent variables) \(h\) 來(lái)更好的表征數(shù)據(jù)，將問(wèn)題轉(zhuǎn)化為 \(p_{\text {model }}(x)=E_h p_{\text {model }}(x \mid h)\) ，這一章主要介紹了最基本的 利用隱性變量的概率模型――線性因子模型(Linear Factor model)，即假定 \(h\) 取自某種先驗(yàn)分布 (prior distribution) \(h \sim p(h)\) ，而我們觀察到的數(shù)據(jù)是 \(h\) 的線性變換與一些隨機(jī)噪聲的疊加， 用式子表示為

之后討論的不同方法會(huì)選擇不同的 \(p(h)\) 和\(noise\)分布。

因子分析(Factor Analysis)模型中，\(h\) 滿足單位高斯分布

而觀察數(shù)據(jù) \(x\) 相對(duì)于 \(h\) 則相互條件獨(dú)立，noise來(lái)自于對(duì)角協(xié)方差高斯分布，其協(xié)方差矩陣 \(\psi=\operatorname{diag}\left(\sigma^2\right)\) ，其中 \(\sigma^2=\left[\sigma_1^2, \sigma_2^2, \ldots, \sigma_n^2\right]^T\) 是每個(gè)變量的協(xié)方差。

常見(jiàn)的因子分析模型

概率主成分分析(Probabilistic PCA)模型與因子分析模型類(lèi)似，但是我們令所有的協(xié)方差 \(\sigma_i^2\) 都相等，即

其中

是單位高斯噪聲。若 \(\sigma \rightarrow 0\) 時(shí)，PPCA收斂至PCA。

獨(dú)立成分分析(Independent Component Analysis)簡(jiǎn)稱(chēng)ICA，希望隱性變量盡量互相獨(dú)立，變成原本每個(gè)人的語(yǔ)音。另外，ICA 并不一定需要生成模型即知道怎樣模擬 \(h\) 的生成概率分布 \(p(h)\) ，許多ICA的變種只是將目標(biāo)定為盡量提高 \(h=W^{-1} x\) 的峰度以盡可能偏離高斯分布，而無(wú)需明確的表示 \(h\) 的生成概率分布 \(p(h)\)。

慢特征分析(Slow Feature Analysis)簡(jiǎn)稱(chēng)SFA，希望學(xué)習(xí)隨時(shí)間變化較為緩慢的特征，其核心思想是認(rèn)為一些重要的特征通常相對(duì)于時(shí)間來(lái)講相對(duì)變化較慢，例如視頻圖像識(shí)別中，假如我們要探 測(cè)圖片中是否包含斑馬，兩幀之間單個(gè)像素可能從黑突變?yōu)榘祝晕覀冃枰恍╇S時(shí)間變化更慢 的特征來(lái)決定我們的預(yù)測(cè)結(jié)果。假設(shè)我們的特征提取函數(shù)為 \(f\) ，則慢特征原則希望減小如下的損失函數(shù)

SFA即假定特征提取函數(shù) \(f(x ; \theta)\) 為線性變換，進(jìn)而解決如下的優(yōu)化問(wèn)題

并要求限制條件 \(E_t\left(f\left(x^{(t)}\right)_i\right)=0\) 及 \(E_t\left[f\left(x^{(t)}\right)_i^2\right]=1\) 以保證解的唯一性。
另外我們還要求各個(gè)不同特征之間是去相關(guān)的 \(\forall i<j, E_t\left[f\left(x^{(t)}\right)_i f\left(x^{(t)}\right)_j\right]=0\) ，否則所有的特征都會(huì)變成最慢的那個(gè)信號(hào)的不同表征。

稀疏編碼(Sparse Coding)希望隱性特征更稀疏，即集中在少數(shù)幾個(gè)特征上，所以它的先驗(yàn)函數(shù)通常選為在零點(diǎn)附近有比較陡峭的峰值的函數(shù)，例如拉普拉斯函數(shù)

由于我們定義了

優(yōu)化問(wèn)題就變成了 \(p(x|h)\) 的最大似然估計(jì)，也就是 \(\operatorname{argmin}_h \lambda\|h\|_1+\beta\|x-W h\|_2^2\) 。這里的稀疏約束是通過(guò)拉普拉斯概率函數(shù)的先驗(yàn)加入的，這在第四章中有介紹。

由于在 \(h\) 上施加 \(L^1\) 范數(shù), 這個(gè)過(guò)程將產(chǎn)生稀疏的 \(h^*\) 。為了訓(xùn)練模型而不僅僅是進(jìn)行推斷, 我們交替迭代關(guān)于 \(h\) 和 \(W\) 的最小化過(guò)程。在本文中, 我們將 \(\beta\) 視為超參數(shù)。我們通常將其設(shè)置為 1 , 因?yàn)樗诖藘?yōu)化問(wèn)題的作用與 \(\lambda\) 類(lèi)似, 沒(méi)有必要使用兩個(gè)超參數(shù)。原則上, 我們還可以將 \(\beta\) 作為模型的參數(shù), 并學(xué)習(xí)它。我們?cè)谶@里已經(jīng)放棄了一些不依賴(lài)于 \(h\) 但依賴(lài)于 \(\beta\) 的項(xiàng)。要學(xué)習(xí) \(\beta\), 必須包含這些項(xiàng)，否則 \(\beta\) 將退化為 0 。

不是所有的稀疏編碼方法都顯式地構(gòu)建了一個(gè) \(p(\boldsymbol{h})\) 和一個(gè) \(p(\boldsymbol{x} \mid \boldsymbol{h})\) 。通常我們只是對(duì)學(xué)習(xí)一個(gè)帶有激活值的特征的字典感興趣, 當(dāng)特征是由這個(gè)推斷過(guò)程提取時(shí), 這個(gè)激活值通常為 0 。

PCA流形解釋

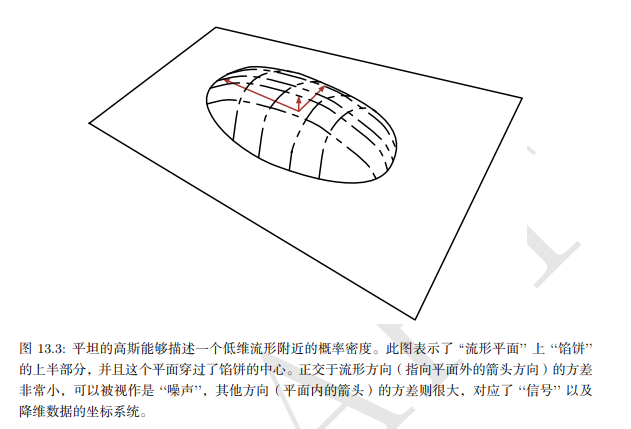
線性因子模型, 包括 PCA 和因子分析, 可以理解為學(xué)習(xí)一個(gè)流形。CA 定義為高概率的薄餅狀區(qū)域, 即一個(gè)高斯分布, 沿著 某些軸非常窄, 就像薄餅沿著其垂直軸非常平坦, 但沿著其他軸是細(xì)長(zhǎng)的, 正如薄餅在其水平軸方向是很寬的一樣。4PCA 可以理解為將該薄餅與更高維空間中的線性流形對(duì)準(zhǔn)。這種解釋不僅適用于傳統(tǒng)PCA, 而且適用于學(xué) 習(xí)矩陣 \(W\) 和 \(V\) 的任何線性自編碼器, 其目的是使重構(gòu)的 \(x\) 盡可能接近于原始的 \(x_0\) 。

編碼器表示為

編碼器計(jì)算 \(h\) 的低維表示。從自編碼器的角度來(lái)看, 解碼器負(fù)責(zé)計(jì)算重構(gòu):

能夠最小化重構(gòu)誤差

的線性編碼器和解碼器的選擇對(duì)應(yīng)著 \(V=W, \mu=b=\mathbb{E}[x], W\) 的列形成一組標(biāo)準(zhǔn)正交基，這組基生成的子空間與協(xié)方差矩陣 \(C\)

的主特征向量所生成的子空間相同。在 PCA 中, \(W\) 的列是按照對(duì)應(yīng)特征值（其全部是實(shí)數(shù)和非負(fù)數(shù)) 幅度大小排序所對(duì)應(yīng)的特征向量。
我們還可以發(fā)現(xiàn) \(C\) 的特征值 \(\lambda_i\) 對(duì)應(yīng)了 \(x\) 在特征向量 \(v^{(i)}\) 方向上的方差。如果 \(\boldsymbol{x} \in \mathbb{R}^D, h \in \mathbb{R}^d\) 并且滿足 \(d<D\), 則 (給定上述的 \(\boldsymbol{\mu}, \boldsymbol{b}, \boldsymbol{V}, \boldsymbol{W}\) 的情況下) 最佳的重 構(gòu)誤差是

因此, 如果協(xié)方差矩陣的秩為 \(d\), 則特征值 \(\lambda_{d+1}\) 到 \(\lambda_D\) 都為 0 , 并且重構(gòu)誤差為 0。 此外, 我們還可以證明上述解可以通過(guò)在給定正交矩陣 \(W\) 的情況下最大化 \(h\) 元素的方差而不是最小化重構(gòu)誤差來(lái)獲得。

小結(jié)

因子分析，概率PCA，ICA，SFA即稀疏編碼等線性因子模型是比較簡(jiǎn)單的學(xué)習(xí)數(shù)據(jù)的高效表征的方法，而且它們也可以擴(kuò)展為之后更復(fù)雜的自編碼網(wǎng)絡(luò)以及深度概率模型，所以有必要對(duì)其有基本的理解。