卷積神經(jīng)網(wǎng)絡(luò)

這一章主要介紹了卷積神經(jīng)網(wǎng)絡(luò)(convolutional neural network，簡(jiǎn)稱(chēng)CNN)，它通常適用于具有網(wǎng)格狀結(jié)構(gòu)的數(shù)據(jù)，例如時(shí)序數(shù)據(jù)可看做是在特定時(shí)間間 隔上的一維網(wǎng)格，圖像可以看做是像素構(gòu)成的二維網(wǎng)格，醫(yī)學(xué)成像如CT等為三維網(wǎng)格數(shù)據(jù)。

基本介紹

卷積神經(jīng)網(wǎng)絡(luò)，顧名思義，利用了數(shù)學(xué)上的卷積操作(convolution)。和前面第六章總結(jié)的基本的 前饋神經(jīng)網(wǎng)絡(luò)相比，CNN只不過(guò)是將某層或某幾層中的矩陣乘法運(yùn)算替換為卷積運(yùn)算，其他的比如說(shuō)最大似然法則，反向傳播算法等等都保持不變。
回顧一下矩陣乘法可以表示為 \(C=A B\) ，矩陣中每個(gè)元素為

而卷積運(yùn)算定義為

其中\(I\)是輸入矩陣(input)， \(K\) 是核矩陣(kernel)，輸出 \(S\) 又稱(chēng)作特征圖(feature map)，而 \(m, n, n\) 則為 \(K\) 的大小。卷積操作即可看做將核矩陣掃過(guò)輸入矩陣并進(jìn)行元素積求和的過(guò)程，如下圖所示:

為什么CNN可以有這么高效的應(yīng)用于具有網(wǎng)格結(jié)構(gòu)的數(shù)據(jù)呢？

主要原因是

1.稀疏連接(sparse connectivity)

2.參數(shù)共享(parameter sharing)

對(duì)于傳統(tǒng)的MLP神經(jīng)網(wǎng)絡(luò)來(lái)說(shuō)，由于其操作是矩陣乘法，每一個(gè)輸入與輸出元之間都需要一個(gè)獨(dú)立的參數(shù)來(lái)表示，這代表每個(gè)輸出元與每個(gè)輸入元之間都有連接，我們就需要很大的空間來(lái)存儲(chǔ)這些參數(shù)，比如說(shuō)圖像有幾擺個(gè)像素點(diǎn)，每個(gè)像素點(diǎn)都代表一個(gè)輸入，而每個(gè)像素點(diǎn)都需要一個(gè)參數(shù)進(jìn)行對(duì)應(yīng)，這很容易造成維度爆炸。而對(duì)于CNN來(lái)說(shuō)，通常其kernel的大小遠(yuǎn)小于其輸入的大小，例如對(duì)于圖像數(shù)據(jù)，輸入常常有成千上萬(wàn)的像素，而對(duì)于檢測(cè)圖像中邊的結(jié)構(gòu)的kernel可能只需要利用十至百個(gè)像素即可，這極大的減小了存儲(chǔ)所需空間，而且減小了計(jì)算輸出時(shí)的計(jì)算量。對(duì)于\(m\)個(gè)輸入和\(n\)個(gè)輸出，矩陣乘法需要\(m*n\)個(gè)參數(shù)，其運(yùn)算時(shí)間為 \(O(m*n)\)，而假如我們限制每個(gè)輸入到輸出的連接為k個(gè)，則我們僅需要 \(k*n\) 個(gè)參數(shù)，且運(yùn)算時(shí)間為 \(O(k*n)\) 。如圖中所示，上圖為卷積操作，下圖為矩陣乘法，可見(jiàn)卷積操作總的連接數(shù)大大減小

另外，對(duì)于傳統(tǒng)神經(jīng)網(wǎng)絡(luò)來(lái)說(shuō)，每一個(gè)輸入至輸出的元素都是獨(dú)立的，只對(duì)于輸入的一個(gè)元素起作用，而對(duì)于CNN來(lái)說(shuō)，kernel的矩陣元素對(duì)于輸入的每一個(gè)元素都起作用，實(shí)現(xiàn)了參數(shù)的共享，如圖中所示，上圖是一個(gè)kernel大小為3的卷積神經(jīng)網(wǎng)絡(luò)，其中深黑色箭頭代表的kernel中間的元素對(duì)于每一個(gè) \(x_i\) 到 \(s_i\) 的運(yùn)算都起作用，而對(duì)于下圖矩陣乘法來(lái)講，黑色箭頭代表的權(quán)重矩陣中的元素僅對(duì) \(x_3\) 到 \(s_3\) 的運(yùn)算起作用。

Pooling

除了卷積層之外，CNN中還有常用的操作是pooling function，其作用是利用附近元素的統(tǒng)計(jì)信息來(lái)代替其原有的值，其目的是可以使結(jié)果在對(duì)于輸入的小量改變的干擾下保持穩(wěn)定。例如，一個(gè)經(jīng)典的pooling function是max pooling，即將周?chē)》礁裰械淖畲笾底鳛檩敵鲋担?dāng)某一輸入值改變時(shí)，對(duì)最大值影響較小，保持了輸出的穩(wěn)定。加入pooling后，卷積的基本單元包括卷積層(convolution layer)，激活函數(shù)的非線性Detector layer，以及pooling layer，如下圖所示

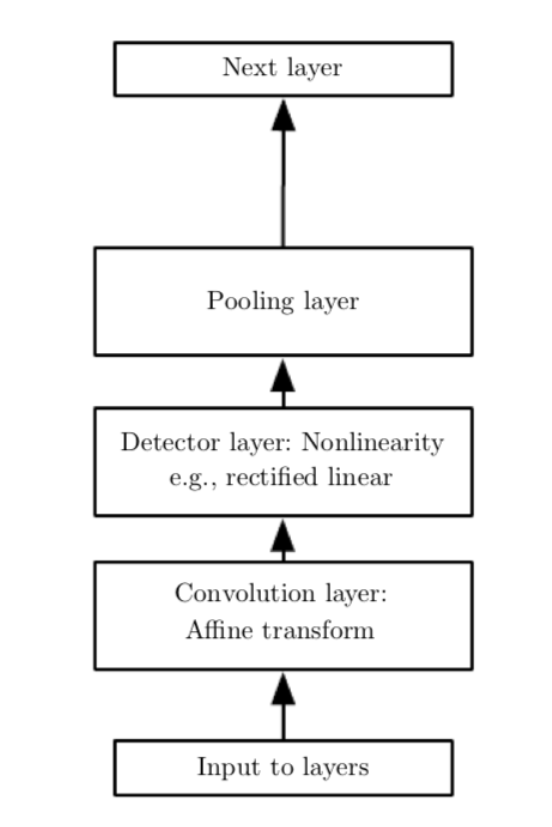
當(dāng)然pooling layer實(shí)際上是假定了數(shù)據(jù)對(duì)于小位移是不變的，比起特定的位置，我們更關(guān)心的是某個(gè)特征是否存在，對(duì)于有些問(wèn)題，假如我們更關(guān)心其特征所在的特定位置，則我們不需用pooling layer。實(shí)際上，對(duì)于卷積操作來(lái)說(shuō)，我們也是假設(shè)了隱藏層中的權(quán)重和其鄰居是相同的只不過(guò)是位移了一下，而且權(quán)重集中在與該單元在空間上連續(xù)的一個(gè)小的空間內(nèi)，而對(duì)于其他元素則權(quán)重為零，即我們的卷積層代表的函數(shù)是局域相互作用且平移不變的，所以我們要注意對(duì)于我們所要研究的數(shù)據(jù)convolution以及pooling是否會(huì)造成欠擬合。

tips：參數(shù)共享的卷積和pooling操作有著非常強(qiáng)的先驗(yàn)，我們假定模型具有平移不變性。若真實(shí)的Task不能由該強(qiáng)假設(shè)模型進(jìn)行你擬合，就會(huì)出現(xiàn)欠擬合?。當(dāng)我們不使用參數(shù)共享的普通卷積，而使用局部連接的卷積，此時(shí)網(wǎng)絡(luò)可以對(duì)于不同的局部進(jìn)行不同的特征探測(cè)，此時(shí)再搭配上max池化，網(wǎng)絡(luò)就可以自己學(xué)習(xí)到新的不變性。

Padding

CNN還有一些其他技巧如strided convolution，即我們每間隔幾個(gè)元素做一次卷積，則輸出相對(duì)于輸入的大小進(jìn)一步減小，如下圖所示，圖中為stride為2的卷積，輸出元素個(gè)數(shù)近似為輸入元素的1/2：

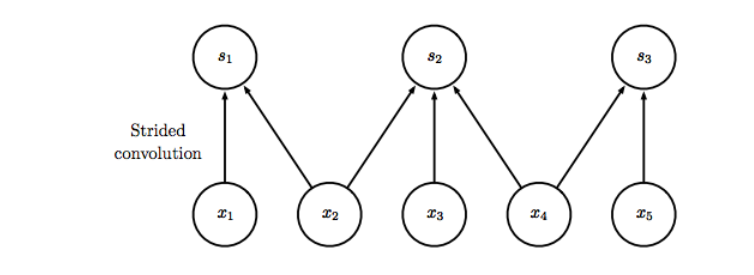
其他的技巧還有zero padding，即如果我們不加任何的padding，假如我們的kernel大小為k，對(duì)于一維網(wǎng)格的CNN，由于邊緣元素的存在，則每層大小會(huì)減小k-1，這導(dǎo)致我們不能建立很深的CNN，所以我們可以采取對(duì)每層邊緣額外補(bǔ)上k-1個(gè)零元素的方式，使每層大小保持一致，從而可以訓(xùn)練更深層的CNN。