正則化

總體來說，一部分正則化方法使給模型施加額外的限制條件，例如限制參數值范圍，有些會在目標函數中添加一些額外懲罰項，本質上也是希望限制參數值。有的時候，這些限制條件或懲罰項代表了特定的先驗經驗，有的時候是希望避免模型過于復雜。正則化常常會增加一些bias但同時會減少variance，好的正則化方法就是在能夠顯著減小variance的情況下又不顯著地增加bias。

解釋一下為什么會增加bias，極大似然估計的漸進估計性質告訴我們，當樣本量趨于無限大時，極大似然估計趨近于無偏估計，這是MLE特有的性質。但是當優化目標不再是似然函數時，此時求出的統計量就不一定是MLE了，通常來說這時的參數是一個有偏估計，但是其在增加了正則化項的批判準則下是最佳估計量。

下面來總結一下常見的幾種正則化方法:

Parameter Norm Penalties

即在目標函數中添加對于參數的懲罰項以減小模型的capacity，即:

其中 \(\alpha \in[0, \infty)\) 是一個標志著懲罰項權重的超參數。當 \(\alpha\) 為零時，正則項為零， \(\alpha\) 越大，則正則化越顯著。由于加入了關于參數大小的懲罰項，模型訓練過程不僅僅是要減小訓練集上的目標函數，而且也要保持懲罰項盡量小，常見的懲罰項有 \(L^2\) regularization和 \(L^1\) regularization。其中 \(L^2\) regularization是減小權重的大小，而 \(L^1\) regularization會使權重更稀硫，具體分析如下:

\(L^2\) regularization也被稱作weight decay(權重衰減)，通過增加 \(\Omega(\theta)=\frac{1}{2}\|w\|_2^2\) 的正則項， 可以使權重大小減小。
為什么 \(L^2\) 可以減小權重w的大小呢? 我們可以先從每次梯度下降更新的大小來理解:

對于 \(\tilde{J}(w ; X, y)=J(w ; X, y)+\frac{\alpha}{2} w^T w\) ，其梯度為 \(\nabla_w \tilde{J}(w ; X, y)=\nabla_w J(w ; X, y)+\alpha w\) ，則每次更新法則為

可以看出， \(L^2\) 的引入使得每次步進時權重有一個常數衰減。對于單次步進如此，那么最終的w結果呢?
我們可以將目標函數在使原目標函數最小的 \(w^*=\operatorname{argmin}_w J(w)\) 附近進行二次展開 \(\tilde{J}(w)=J\left(w^*\right)+\alpha w+\frac{1}{2}\left(w-w^*\right)^T H\left(w-w^*\right)\) ，其中H為Hessian matrix。該函數的極小值應取在滿足 \(\nabla_w \tilde{J}(w)=\alpha w+H\left(w-w^*\right)=0\) 的 \(w\) ，用 \(\tilde{w}\) 代表新的極值點, 則

可以看出當 \(\alpha\) 接近零時， \(\tilde{w}\) 趨近于 \(w^*\) ，而對于 \(\alpha\) 遠離零的情況，我們可對 \(H\) 作特征分解為 \(H=Q \Lambda Q^T\) ，則

可以看出 \(\tilde{w}\) 相對于 \(w^*\) 是沿著 \(H\) 的特征向量的軸線進行了尺度收縮，即沿著 \(i\) 特征向量的方向收縮了 \(\frac{\lambda_i}{\lambda_i+\alpha}\) ，對于特征值較大的 \(\lambda_i \gg \alpha\) 的方向，正則項作用很小，而對于 \(\lambda_i \ll \alpha\) 的方 向，正則項作用顯著， \(\tilde{w}_i\) 趨向于零，如下圖中所示

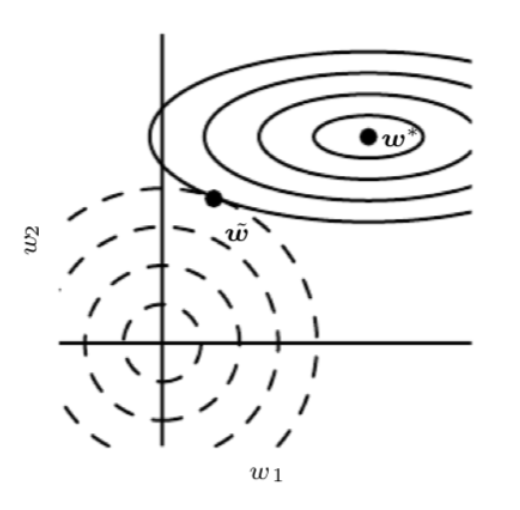
圖中實心線為不含正則項的原目標函數的等高線，虛線為正則項的等高線， \(\tilde{w}\) 為新的目標函數的極值點。對于 \(w_1\) 方向，Hessian matrix的本征值很小，原目標函數對于這一水平方向的移動不敏感，所以正則項可沿 \(w_1\) 方向從原極值點 \(w^*\) 作出較大橫移，使其趨于零，而對于 \(w_2\) 方向，其曲 率較大，本征值較大，目標函數對于這一方向的移動非常敏感，導致正則項不能很大的改變 \(w_2\) 方 向上的值。

\(L^1\) regularization則是加入了對于每一個元素的絕對值的求和懲罰項 \(\Omega(\theta)=\|w\|_1=\sum_i\left|w_i\right|\) ，新的目標函數為 \(\tilde{J}(w ; X, y)=J(w ; X, y)+\alpha\|w\|_1\) ，其梯度為 \(\nabla_w \tilde{J}(w ; X, y)=\nabla_w J(w ; X, y)+\alpha \operatorname{sign}(w)\), 其中sign為正負號函數。
類似于 \(L^2\) regularization的處理過程，我們同樣可以對新的目標函數進行二次展開，為方便討論，假設Hessian matrix是對角矩陣，則新的目標函數可近似為 \(\tilde{J}(w)=J\left(w^*\right)+\sum_i\left[\frac{1}{2} H_{i, i}\left(w_i-w_i^*\right)^2+\alpha\left|w_i\right|\right]\) ，其極值滿足

我們考慮 \(w_i^*>0\) 的情況， \(w_i^*<0\) 可做類似分析，

1. \(w_i^* \leq \frac{\alpha}{H_{i, i}}\) ，則極值點為 \(\tilde{w}_i=0\)

2. \(w_i^*>\frac{\alpha}{H_{i, i}}\) ，則 \(\tilde{w}_i=w_i^*-\frac{\alpha}{H_{i, i}}\) 不為零，而僅僅移動了 \(\frac{\alpha}{H_{i, i}}\) 的距離。

與 \(L^2\) regularization相對比， \(L^1\) regularization使權重更稀疏(sparse)，即使很多項最優值為零，而 對應的 \(L^2\) 僅是使權重更小而不為零。\(L^1\) regularization由于其稀疏化的性質常常被用來做特征選擇(feature selection)，因為它可以使 某些權重為零，說明相對應的特征可以安全地忽略掉，經典的LASSO(least absolute shrinkage and selection operator)就是利用了 \(L^1\) penalty。

Regularization and Underconstrained Problems

在有些情況下我們會遇到欠定的機器學習問題，例如線性回歸中我們需要對 \(X^{T}X\) 求逆以得到閉解，但是在大部分情況下該矩陣是奇異的。此時引入正則化可以讓我們保證該矩陣可逆，例如求解 \(X^TX+\alpha I\) 的逆。這種操作可以理解為將無限的解通過正則化約束將解的數量減小到一個，此時我們就可以獲得閉解。思考Moore-Penrose偽逆 \(X^+\) 的數學定義

偽逆其實就是使用正則化約束來穩定欠定的一種方法。

Dataset Augmentation

使機器學習模型效果更好的很自然的一種辦法就是給它提供更多的訓練數據，當然實際操作中，有時候訓練集是有限的，我們可以制造一些假數據并添加入訓練集中，當然這僅對某些機器學習問題適用，例如對于圖像識別，我們可以平移圖像，添加噪聲，旋轉，色調偏移等等，我們希望模型能夠在這些變換或干擾不受影響保持預則的準確性，從而減小泛化誤差。當然，我們要注意這些變換 不能改變數據的原始標記，如對于識別數字問題，我們就不能對6和9進行180度旋轉。

Multi-task learning

與Dataset augmentation類似，多任務學習也是希望令模型的參數能夠進行很好的泛化，其原理是對多個目標共享模型的一部分 (輸入及某些中間的表示層)，使其對于多個有關聯的目標均有較好的效果，保證模型可以更好的推廣。

tips：參數共享帶有很強的先驗知識(我認定你們學到的東西大差不差！)，只對符合模型的任務有好的效果，且在關聯任務上泛化能力強。

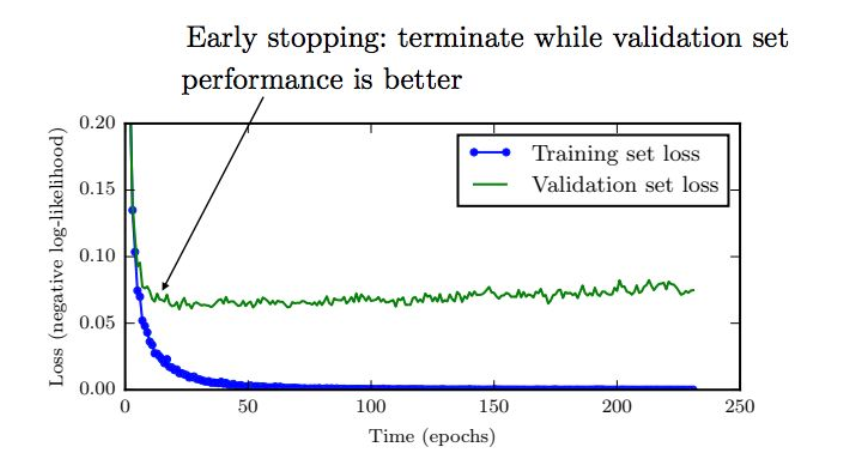
Early stopping

通常對于較大的模型，我們會觀察到訓練集上的誤差不斷減小，但驗證集上的誤差會在某個點之后反而逐漸增大，這意味著為了減小泛化誤差，我們可以在訓伡過程中不斷的記錄驗證集上的誤差及對應的模型參數，最終返回驗證集上誤差最小所對應的模型參數，這個簡單直觀的方法就是early stopping，由于其簡單高效，在深度學習中得到了廣泛應用。其效果和L2正則化類似，由于停止較早，解會靠近原點。

Sparse Representations

\(L^1\) regularization是使參數更稀疏，同樣的我們也可以通過增加對于表征層的norm penalty項使表征 (隱藏層) 更稀疏。即 \(\tilde{J}(\theta ; X, y)=J(\theta ; X, y)+\alpha \Omega(h)\)

Bagging and Ensemble

Bagging(全稱是bootstrap aggregating)通過整合多個模型來減小泛化誤差，其基本思想是多個模型對于訓練集做出同樣錯誤預測的概率較小，Bagging是ensemble methods (集成算法) 的一種方法。
例如假設我們有 \(\mathrm{k}\) 個回歸模型的集合，對于一個數據，每個模型的誤差是 \(\epsilon_i\) ，假設誤差滿足多元正態分布且方差 \(E\left[\epsilon_i^2\right]=v\) ，協方差 \(E\left[\epsilon_i \epsilon_j\right]=c\) ，則ensemble之后的誤差平方的期望為

當誤差間完全相關時，則 \(c=v\) ，均方差仍為 \(v\) ，ensemble并沒有達到更好效果，但如果誤差 間完全不相關，則 \(c=0\) ，則均方差縮小至 \(\frac{1}{k} v\), 說明均方差隨ensemble的集合大小而線性減 小，實際應用中，介于這兩種情況之間，通常ensemble效果會遠好于其中單一模型的效果。
ensemble方法可以是將完全不同的模型結合起來，而Bagging方法則是同一種模型和目標函數， 但是產生k種不同的訓練集，每個訓練集與原訓練集所含數據量相同，但會以某一概率去掉某些樣 本并以其他的重復樣本代替，第i個模型就在第 \(\mathrm{i}\) 個訓?集上進行訓練。例如下圖中所示，我們想鑒 別某個數字是否是 8 ，原數據包含 \(9 ， 6\) 和8，第一個重新取樣的數據集中僅包含 6 和 8 ，9倍替換掉， 則模型1會學習到需要數字有上半圈才能為 8 ，而第二個重新取樣的數據集中去掉 6 ，僅包含 9 和 8 ， 則模型2會學習到數字需有下半圈才能為 8 ，將他們集合起來就可以比較準確的推測需要同時有上下半圈才鑒定數字為 8 。

Dropout

Dropout可以理解做是將ensemble應用到大型神經網絡的一種更為實際有效的方法。由于 ensemble需要訓練多個模型，對于大型神經網絡，其訓練和評估所需時間和存儲資源較大，這種 方法常常不太實際，Dropout就提供了一個更便宜的解決方案：即通過隨機去掉一些節點的方法訓練多個子網絡，并最終將這些子網絡ensemble起來，如下圖所示:

其具體方法是當我們利用minibatch的算法如隨機梯度下降算法來學習時，我們可以隨機的選取一個binary mask(0表示節點輸出為零，1表示正常輸出該節點) 決定哪些輸入和隱藏層節點保留， 每次的mask的選擇是獨立的。而mask為1的概率是我們可以調控的超參數。
和bagging方法相比，bagging中每個模型是完全獨立的，而dropout中，模型間由于繼承了父網絡中的參數的子集會共享一些參數，這使得在有限的存儲空間中我們可以表示多個模型。
以上是訓練過程，而在做inference預測時，我們需要取所有模型的預測的均值，但是這往往計算量過多，Hinton提出inference時我們實際可以只用一個模型但其中每個節點的權重需要乘以包含這個節點的概率，這種方法稱作weight scaling inference rule。實際中，我們常常把weight scaling過程放在訓練過程中，即訓練中每個節點輸出就乘以包含該節點的概率的倒數，則inference時只需要正常的通過一遍前饋過程即可，不需要在進行weight scaling。
Dropout的優勢在于其計算資源占用小，并且對于模型或訓練算法的限制較小，基本上可以適用于各種前饋網絡，循環網絡或概率模型，所以實際工業模型中應用很多。

Adversarial Training

Adversarial Training對抗訓練很有意思，它讓人們深入思考機器學習究竟學到了什么有效信息。 這方面的工作主要是由谷歌的Szegedy和本書作者lan Goodfellow進行的。他們可以制造一些對抗樣本迷惑神經網絡，如下圖中所示，他們對于熊貓圖片加了一些人眼不可見的干擾，形成新樣本，而新的人眼仍可鑒定為熊貓的圖片卻會被機器以較大置信率鑒定為長臂猿。為什么在人類看來類似的樣本機器會得到大相徑庭的結論呢? Ian認為這是由于神經網絡中的大部分組成還是線性的(如ReLU可以看成是分段線性)，而對于不同的輸入，線性函數會受到較大的擾動，產生較大的改變。為了解決這一問題，他們會將這些對抗樣本重新加到訓練集中，使得神經網絡傾向于對于數據集保持局部穩定而不至干擾過大，從而學習到更有效的信息。