區間估計
第九章 區間估計
該筆記基于書本《統計推斷》,筆記省略部分均可在該書上找到對應的詳細解釋。
本章將從第八章的假設檢驗中的LRT入手,再到給出置信區間的自然求解公式。這一個過程符合直覺,且與6,7,8,9章的知識緊密結合。
9.1 前言
? 在第七章中我們學習了如何求解參數 \(\theta\) 的點估計量,這非常有用。但是這具有一些缺點,我們可以想像一下,點估計量 \(T(\boldsymbol{x})\) 是對參數 \(\theta\) 的估計,且估計量本身是一個隨機變量(通常是連續的),所以對于點估計量來說\(P(T(\boldsymbol{x})=\theta)=0\),我們沒法保證其估計的有效性,因此我們需要更精確的估計。但是怎么做呢?既然一個點不行,那就放松這個條件,用區間來包括這一個參數 \(\theta\) 。這也就是為什么這一章的名稱叫做區間估計的原因。我們假設區間為 \(C(\boldsymbol{x})\) , 長度一定不為0,此時我們可以看到 \(P(\theta \in C(\boldsymbol{x}))>0\) 恒成立。我們get了一個不為 0 的概率 !即這個區間 \(C(\boldsymbol{x})\) 包括了這個參數 \(\theta\) 的概率(這里的主語一定是區間 \(C(\boldsymbol{x})\),很重要),這為我們量化這個區間估計的精確性也提供了思路。
? 和前兩章一樣,這章也分為兩個部分,第一部分是如何求一個區間估計,第二部分是區間估計量的評價。
定義 9.1.1: 一個實值參數 \(\theta\) 的區間估計是樣本的任意一對函數 \(L\left(x_1, \cdots\right.\), \(\left.x_n\right)\) 和 \(U\left(x_1, \cdots, x_n\right)\),對于所有的 \(\boldsymbol{x} \in \mathcal{X}\) 滿足 \(L(\boldsymbol{x}) \leqslant U(\boldsymbol{x})\)。如果觀測到樣本 \(\boldsymbol{X}=\boldsymbol{x}\), 就做出推斷 \(L(\boldsymbol{x}) \leqslant \theta \leqslant U(\boldsymbol{x})\)。隨機區間 \([L(\boldsymbol{X}), U(\boldsymbol{X})]\) 叫做區間估計量 (interval estimator)。
定義 9.1.4: 對于一個對參數 \(\theta\) 的區間估計量 \([L(\boldsymbol{X}), U(\boldsymbol{X})],[L(\boldsymbol{X})\), \(U(\boldsymbol{X})]\) 的覆蓋概率 (coverage probability) 是指隨機區間 \([L(\boldsymbol{X}), U(\boldsymbol{X})]\) 覆蓋真實參數 \(\theta\) 的概率。在符號上它記作 \(P_0(\theta \in[L(\boldsymbol{X}), U(\boldsymbol{X})])\) 或 \(P(\theta \in[L(\boldsymbol{X})\), \(U(\boldsymbol{X})] \mid \theta)\)。
定義 9.1.5: 對于一個參數 \(\theta\) 的區間估計量 \([L(\boldsymbol{X}), U(\boldsymbol{X})],[L(\boldsymbol{X}), U(\boldsymbol{X})]\) 的置信系數 (confidence coefficient) 是指覆蓋概率的下確界 \(\inf _\theta P_\theta(\theta \in[L(\boldsymbol{X})\), \(U(\boldsymbol{X})]\)。
從這些定義里我們認識到很多事情. 首先, 一定牢記這個區間是隨機的量, 而 參數不是, 因此, 當我們書寫像 \(P_\theta(\theta \in[L(\boldsymbol{X}), U(\boldsymbol{X})])\) 這樣的概率陳述時, 是針對 \(\boldsymbol{X}\) 而非針對 \(\theta\) 的。 也就是說 \(P_\theta(\theta \in[L(\boldsymbol{X}), U(\boldsymbol{X})])\) 等同于 \(P_\theta(L(\boldsymbol{X}) \leqslant\) \(\theta, U(\boldsymbol{X}) \geqslant \theta)\),隨機變量為 \(\boldsymbol{X}\) 。
區間估計量, 加之信心的一個量度 (通常為置信系數), 有時被稱為一個置信區間。這個術語一般和區間估計量交替使用。一個置信系數為 \(1-a\) 的置信區間被稱為 \(1-a\) 置信區間。
9.2 區間估計量的求解
以下將從反轉一個LRT開始,介紹幾種求解區間估計量的方法。
9.2.1 反轉一個LRT統計量
舉個例子,設\(X_1, \cdots, X_n\) 是 iid \(\mathrm{n}\left(\mu, \sigma^2\right)\) 的并考 慮檢驗 \(H_0: \mu=\mu_0\) 對 \(H_1: \mu \neq \mu_0\). 對于固定的水平 \(\alpha\), 一個合理的檢驗(事實上是 最大功效無偏檢驗) 具有拒絕區域 \(\left\{x:\left|\bar{x}-\mu_0\right|>z_{\alpha / 2} \sigma / \sqrt{n}\right\}\). 注意到對于符合 \(\left|\bar{x}-\mu_0\right| \leqslant z_{\alpha / 2} \sigma / \sqrt{n}\) 或者等價地滿足
的樣本點, \(H_0\) 則被接受。
因為這個檢驗具有真實水平 \(\alpha\), 這意味著 \(P\left(H_0\right.\) 被拒絕 \(\left.\mid \mu=\mu_0\right)=\alpha\), 或者換 言之, \(P\left(H_0\right.\) 被接受 \(\left.\mid \mu=\mu_0\right)=1-\alpha\). 把它和上面接受區域描述結合起來,得到
但是這里對概率的陳述對于每一個 \(\mu\) 都真. 因此陳述
為真. 通過反轉這個水平為 \(\alpha\) 的檢驗的接受區域而獲得的區間 \(\left[\bar{x}-z_{\alpha / 2} \sigma / \sqrt{n}, \bar{x}+\right.\) \(\left.z_{\alpha / 2} \sigma / \sqrt{n}\right]\) 就是一個 \(1-\alpha\) 置信區間。
可以看到樣本空間中使得 \(H_0: \mu=\mu_0\) 被接受的集合由下式給出
而置信區間是由參數空間中似乎可信的參數值構成的集合, 由下式給出
這兩個集合通過等價關系
建立起聯系,下面的圖9.2.1很好的給出了兩者的對應關系。
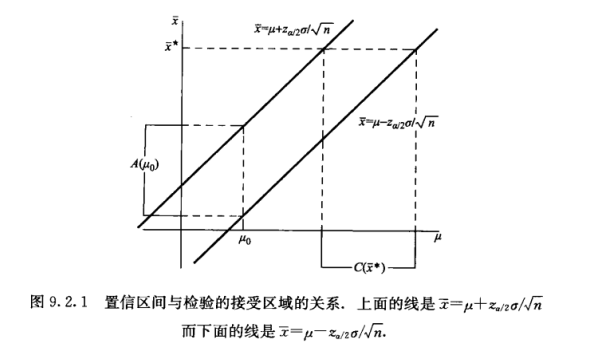
直到此為止,置信區間和假設檢驗在原理和本質上依舊是相同的,兩者都是從 \(\boldsymbol{x}\) 角度,給出了區間范圍,但是置信區間是在接收區域上進行了不等式的形式調整,使得變量看起來變成了 \(\theta\) ,但是參數 \(\theta\) 在這是固定的值,這一定一定要切記。那么對于一族參數為 \(\theta\) 的函數族來說,就會形成一個參數與隨機變量的空間區域。此時 \(\theta\) 在參數族的背景下,才搖身一變成為了一個變量(但是還不是一個隨機變量,因為它沒有概率分布,在之后的bayes法中我們可以看到在將參數 \(\theta\) 考慮為一個隨機變量的時候,如何構造一個信任區間)。
上述的例子為特例,接下來將其推廣到通解方法。
定理 9.2.2: 對每一個 \(\theta_0 \in \Theta\), 設 \(A\left(\theta_0\right)\) 是 \(H_0: \theta=\theta_0\) 的一個水平為 \(\alpha\) 的檢驗的接受區域。對每一個 \(x \in \mathcal{X}\), 在參數空間里定義一個集合 \(C(x)\)
則隨機集合 \(C(\boldsymbol{x})\) 是一個 \(1-\alpha\) 置信集合. 反之, 設 \(C(\boldsymbol{x})\) 是一個 \(1-\alpha\) 置信集合。對任意的 \(\theta_0 \in \Theta\), 定義
則 \(A\left(\theta_0\right)\) 是 \(H_0: \theta=\theta_0\) 的一個水平為 \(\alpha\) 的檢驗的接受區域。
證明:第一部分, 因為 \(A\left(\theta_0\right)\) 是一個水平為 \(\alpha\) 的檢驗的接受區域, 所以 \(P_{\theta 0}\left(\boldsymbol{X} \notin A\left(\theta_0\right)\right) \leqslant \alpha\) 并且因此 \(P_{\theta 0}\left(\boldsymbol{X} \in A\left(\theta_0\right)\right) \geqslant 1-\alpha\)
由于 \(\theta_0\) 是任意的, 可以把 \(\theta_0\) 改寫成 \(\theta\)。把上面的不等式與 (9.2.1) 合在一起, 就 證明了集合 \(C(\boldsymbol{X})\) 的覆蓋概率是
證明了 \(C(\boldsymbol{X})\) 是一個 \(1-\alpha\) 置信集合。
第二部分, 對 \(H_0: \theta=\theta_0\) 的以 \(A\left(\theta_0\right)\) 作接受區域的檢驗, 犯第一類錯誤的概率是
所以是一個水平為 \(\alpha\) 的檢驗。
9.2.2 樞軸量
有的時候,置信區間的概率是依賴于 \(\theta\) 的,而有些則與 \(\theta\) 無關。如果一個置信區間可以由一個概率分布與 \(\theta\) 無關的統計量的范圍來表示,這個統計量就被稱為樞軸量 (pivotal quantity) 或樞軸 (pivot)。
定義 9.2.6: 一個隨機變量 \(Q(\boldsymbol{X}, \theta)=Q\left(X, \cdots, X_n, \theta\right)\) 是一個樞軸量或樞軸,如果 \(Q(\boldsymbol{X}, \theta)\) 的分布獨立于所有的參數. 就是說, 如果 \(X \sim F(\boldsymbol{x} \mid \theta)\), 則 \(Q(\boldsymbol{X}, \theta)\) 對于所有的 \(\theta\) 值具有同樣的分布。
函數 \(Q(x, \theta)\) 通常會明顯地同時包含參數與統計量, 但是對任何集合 \(A\), \(P_\theta(Q(\boldsymbol{X}, \theta) \in A)\) 不能依賴于 \(\theta\)。從樞軸構造置信集合的技術靠的是能求出一個樞軸與一個集合 \(A\) 使得集合 \(\{\theta: Q(\boldsymbol{X}, \theta) \in A\}\) 是 \(\theta\) 的一個集估計。
(位置-尺度樞軸) 在位置和尺度情況里有很多樞軸量。設 \(X, \cdots, X_n\) 是來自一個指定的概率密度 函數的隨機樣本, 并設 \(\bar{X}\) 和 \(S\) 是樣本均值和樣本標準差。為了證明中的量是樞軸, 只需證明它們的概率密度函數與參數是無關的。特別地, 注意到當 \(X, \cdots, X_n\) 是來自正態總體 \(\mathrm{n}\left(\mu, \sigma^2\right)\) 的隨機樣本時, \(t\) 統計量 \((\bar{X}-\mu) /(S / \sqrt{n})\) 是一個樞軸, 因為 \(t\) 分布不依賴于參數 \(\mu\) 和 \(\sigma^2\)。
位置-尺度樞軸
| pdf 的形式 | pdf 的類型 | 樞軸量 |
|---|---|---|
| \(f(x-\mu)\) | 位置 | \(\bar{X}-\mu\) |
| \(\frac{1}{\sigma} f\left(\frac{x}{\sigma}\right)\) | 尺度 | \(\frac{\bar{X}}{\sigma}\) |
| \(\frac{1}{\sigma} f\left(\frac{x-\mu}{\sigma}\right)\) | 位置-尺度 | \(\frac{\bar{x}-\mu}{S}\) |
使用檢驗反轉法構造的那些區間當中, 有些實際上是基于樞軸的,有些則不是。沒有通用的求樞軸的策略, 但是 可以略微聰明一些而不是完全依靠猜測。例如, 求出位置或尺度參數的樞軸就 是相對容易的事情。一般講, 差是位置問題的樞軸而比(或乘積)是尺度問題的樞軸。那么在得到樞紐量后如何構造一個置信區間呢,接下來用伽瑪分布舉一個例子。
例: 設 \(X, \cdots, X_n\) 是指數分布 \(\operatorname{EXPO}(\lambda)\) 的 iid 樣本, 則 \(T=\sum X_i\) 是關于 \(\lambda\) 的充分統計量并且 \(T \sim\) gamma \((n, \lambda)\)。在伽瑪分布的概 率密度函數中 \(t\) 和 \(\lambda\) 以 \(t / \lambda\) 的形式一起出現,并且事實上 gamma \((n, \lambda)\) 的概率密度函數 \(\left(\Gamma(n) \lambda^n\right)^{-1} t^{n-1} \mathrm{e}^{-t / \lambda}\) 是一個尺度族。這樣, 如果 \(Q(T, \lambda)=2 T / \lambda\), 則
它不依賴于 \(\lambda\). 所以, 量 \(Q(T, \lambda)=2 T / \lambda\) 是一個樞軸, 服從 gamma \((n, 2)\) 分布, 或者說 \(\chi_{2 n}^2\) 分布。
有時我們能夠通過觀察概率密度函數的形式看出是否存在樞軸. 在上例中, 量 \(t / \lambda\) 出現在概率密度函數里并且它實際上就是一個樞軸。在正態概率密度函數中, 有\((\bar{x}-\mu) / \sigma\) 出現并且這個量也是一個樞軸。一般, 設一個統計量 \(T\) 的概率密度函數 \(f(t \mid \theta)\) 能夠表示成如下形式
其中 g 是某個函數而 \(Q\) 是某個單調(對于每個 \(t\), 關于 \(\theta\) 單調)函數。由于 \(Q(\boldsymbol{X}, \theta)\) 是一個樞軸, 則對于一個指定的 \(\alpha\) 值, 我們能夠求出數 \(a\) 和 \(b\), 它們不依賴于 \(\theta\), 滿足
則對于每個 \(\theta_0 \in \Theta\)
就是關于 \(H_0: \theta=\theta_0\) 的一個水平為 \(\alpha\) 的檢驗的接受區域. 我們將用檢驗反轉法構造 置信集合, 但現在用樞軸指出了接受區域的具體形式。利用定理 \(9.2 .2\), 反轉檢驗而得到
并且 \(C(\boldsymbol{X})\) 是關于 \(\theta\) 的一個 \(1-\alpha\) 置信集合. 如果 \(\theta\) 是一個實值參數并且對于每個 \(x\) \(\in X, Q(\boldsymbol{x}, \theta)\) 是 \(\theta\) 的一個單調函數, 則 \(C(\boldsymbol{x})\) 將是一個區間. 事實上, 如果 \(Q(\boldsymbol{x}\), \(\theta)\) 是 \(\theta\) 的一個增函數, 則 \(C(\boldsymbol{x})\) 具有 \(L(\boldsymbol{x}, a) \leqslant \theta \leqslant U(x, b)\) 的形式. 如果 \(Q(\boldsymbol{x}\), \(\theta\) ) 是 \(\theta\) 的一個減函數 (這是典型的), 則 \(C(\boldsymbol{x})\) 具有 \(L(\boldsymbol{x}, b) \leqslant \theta \leqslant U(\boldsymbol{x}, a)\) 的 形式。
9.2.3 樞軸化累積分布函數
前面我們看到樞軸量對于求解置信區間的幫助非常大,它可以極大程度上簡化求解的過程。但是這些樞軸量都有著比較嚴格的前提條件,都是在位置-尺度中才成立。接下來,我們將從積分變換入手,對樞軸量進行前提更少的推廣。
首先回想一下,在第三章中我們得到過一個結論,即概率積分變換,隨機變量的累計分布量是服從均勻分布的,這是一個概率分布與參數 \(\theta\) 無關的量,也是一個樞軸量,因此我們可以通過這個樞軸來求解置信區間。而這需要分為連續隨機變量和離散隨即變量兩種情況。
定理 9.2.12: (連續型累積分布函數) 設 \(\mathcal{T}\) 是一個以 \(F_T(t \mid \theta)\) 為 其累積分布函數的連續型統計量。設 \(\alpha_1+\alpha_2=\alpha\) 其中 \(0<\alpha<1\) 是固定值。假定對于 每個 \(t \in T\), 函數 \(\theta_L(t)\) 和 \(\theta_U(t)\) 可以被如下定義。
i. 如果對于每個 \(t, F_T(t \mid \theta)\) 都是 \(\theta\) 的一個減函數, 則由
定義 \(\theta_L(t)\) 和 \(\theta_U(t)\)。
ii. 如果對于每個 \(t, F_T(t \mid \theta)\) 都是 \(\theta\) 的一個增函數, 則由
定義 \(\theta_L(t)\) 和 \(\theta_U(t)\)。
那么隨機區間 \(\left[\theta_L(T), \theta_U(T)\right]\) 是 \(\theta\) 的一個 \(1-\alpha\) 置信區間。
定理 9.2.14: (離散型累積分布函數) 設 \(T\) 是一個以 \(F_T(t \mid \theta)=\) \(P(T \leqslant t \mid \theta)\) 為其累積分布函數的離散型統計量。設 \(\alpha_1+\alpha_2=\alpha\) 其中 \(0<\alpha<1\) 是固定值。假定對于每個 \(t \in \mathcal{T}\), 函數 \(\theta_L(t)\) 和 \(\theta_U(t)\) 可以被如下定義。
i. 如果對于每個 \(t, F_T(t \mid \theta)\) 都是 \(\theta\) 的一個減函數, 則由
定義 \(\theta_L(t)\) 和 \(\theta_U(t)\)。
ii. 如果對于每個 \(t, F_T(t \mid \theta)\) 都是 \(\theta\) 的一個增函數, 則由
定義 \(\theta_L(t)\) 和 \(\theta_U(t)\)。
那么隨機區間 \(\left[\theta_L(T), \theta_U(T)\right]\) 是關于 \(\theta\) 的一個 \(1-\alpha\) 置信區間。
9.2.4 Bayes區間
與之前的置信區間不同,bayes學派認為參數是由先驗分布的,此時的參數 \(\theta\) 是一個真正的隨機變量,所以我們可以考慮 \(\theta\) 的后驗分布,從參數的角度來計算置信系數。
Bayes 集合和經典的集合有相當不同的概率解釋。為了把它們區別開來, 稱 Bayes 估計集合為可信集合 (credible sets) 而不是置信集合。
這樣, 若 \(\pi(\theta \mid \boldsymbol{x})\) 是給定 \(\boldsymbol{X}=\boldsymbol{x}\) 條件下 \(\theta\) 的后驗分布, 則對任意的集合 \(A \subset \Theta\), \(A\) 的可信概率就是
而 \(A\) 是關于 \(\theta\) 的一個可信集合。如果 \(\pi(\theta \mid x)\) 是一個概率質量函數, 則把以上表達式中的積分換成求和。
通常,可信區間的長度要小于置信區間,且更靠近0點,從直覺上來看這是一個比較好的結果。但是請記住這是需要代價的,對于可信區間來說,求解需要概率分布和先驗分布。需要的信息比置信區間要多。Bayes方法和經典方法這兩者沒有誰優誰劣,因為兩者的評判標準并不相同,所以對于不同的問題,要選擇性地用更適合的方法。
9.3 區間估計量的評價方法
? 集合估計量有兩個互相對立競爭的量, 就是尺寸和覆蓋概率。自然, 人們希望集合具有小的尺寸和大的覆蓋概率, 但是這樣的集合通常難以構造。(顯然可以通過增加集合的尺寸獲取大的覆蓋概率。區間 \((-\infty, \infty)\) 的覆蓋概率是 1)在尺寸和覆蓋概率來最優化一個集合之前, 必須決定怎樣度量這些量。
? 一個置信集合的覆蓋概率除特殊情況之外是參數的一個函數, 所以要考慮的不是一個而是無窮個值。然而大多數情況將通過置信系數, 即覆蓋概率的下確界, 去度量覆蓋概率性能。這是一種方式, 但不是唯一的總括覆蓋概率信息的可用方式。
9.3.1 尺寸和覆蓋概率
? 等分概率 \(\alpha\) 的策略在一些例子中比如正態分布中是最優的, 但不總是最優的。現在證明一個定理, 從而論證這個事實。該定理可以在較一般的情況下使用, 它只需要假定概率密度函數是單峰的 (unimodal)。單峰的定義: 一個概率密度函數 \(f(x)\) 是單峰的, 如果存在 \(x^*\) 使得 \(f(x)\) 在 \(x \leqslant x^*\) 非淢而 \(f(x)\) 在 \(x \geqslant x^*\) 非增。
定理 9.3.2: 設 \(f(x)\) 是一個單峰的概率密度函數。如果區間 \([a, b]\) 滿足 i. \(\int_a^b f(x) \mathrmw0obha2h00 x=1-\alpha\),
ii. \(f(a)=f(b)>0\),
iii. \(a \leqslant x^* \leqslant b\), 其中 \(x^*\) 是 \(f(x)\) 的一個眾數 (mode),
則 \([a, b]\) 是所有滿足 (i) 的區間中最短的.
9.3.2 與檢驗相關的最優性
覆蓋假值的概率, 或假值覆蓋概率 (probability of false coverage)間接地度量一個置信集合的尺寸. 直觀地看, 較小的集合覆蓋較少的值, 因此較少可能覆蓋假值.
首先考慮一般情況, 這里 \(\boldsymbol{X} \sim f(\boldsymbol{x} \mid \theta)\), 并且通過反轉接受區域 \(A(\theta)\) 來構造一個對于 \(\theta\) 的置信集合 \(C(\boldsymbol{x}) . C(\boldsymbol{x})\) 的覆蓋概率, 即真值覆蓋概率是由 \(P_\theta(\theta \in\) \(C(\boldsymbol{X})\) ) 給出的 \(\theta\) 的函數. 假值覆蓋概率是 \(\theta\) 和 \(\theta^{\prime}\) 的函數, 它定義為當 \(\theta\) 為真值時, 覆蓋 \(\theta^{\prime}\) 的概率
分別地對于單側和雙側區間定義假值覆蓋概率是有意義的. 例如, 若有一個置信下界, 就是說肯定 \(\theta\) 比一個值大, 于是覆蓋假值只有在我們的區間覆蓋了過小的 \(\theta\) 值的情況下才發生. 類似的論證引導我們給出用于置信上界與雙側置信界的假值覆蓋概率定義.
一個在一類 \(1-\alpha\) 置信集合上最小化假值覆蓋概率的 \(1-\alpha\) 置信集合叫做一致最精確 (uniformly most accurate, UMA) 置信集合. 例如, 我們可以考慮在形如 \([L(\boldsymbol{x}), \infty)\) 的集合中尋找一個 UMA 置信集合. 下面我們將要證明, UMA 置信 集合是通過反轉 UMP 檢驗的接受區域來構造的. 遺憾的是, 雖然 UMA 置信集合 是一個理想的集合, 但是它僅在 (就像做 UMP 檢驗) 相當稀少的情況下才存在. 特別地, 因為 UMP 檢驗一般是單側的, 所以 UMA 區間也是這樣. 然而它們在理 論上是優美的, 從下面的定理我們就會看到 \(H_0: \theta=\theta_0\) 對 \(H_1: \theta>\theta_0\) 的一個 UMP 檢驗產生一個 UMA 置信下界。
定理 9.3.5: 設 \(\boldsymbol{X} \sim f(\boldsymbol{x} \mid \theta)\), 其中 \(\theta\) 是一個實值參數. 對于每個 \(\theta_0 \in \Theta\), 設 \(A^*\left(\theta_0\right)\) 是關于 \(H_0: \theta=\theta_0\) 對 \(H_1: \theta>\theta_0\) 的一個 UMP 水平 \(\alpha\) 檢驗的接受區域. 設 \(C^*(\boldsymbol{x})\) 是通過反轉上述 UMP 接受區域所建立的 \(1-\alpha\) 置信集合. 則對于任何其他的 \(1-\alpha\) 置信集合 \(C\), 有
\(P_\theta\left(\theta^{\prime} \in C^{\cdot}(\boldsymbol{X})\right) \leqslant P_\theta\left(\theta^{\prime} \in C(\boldsymbol{X})\right)\) 對于所有的 \(\theta^{\prime}<\theta\) 成立
定義 9.3.7: 一個 \(1-\alpha\) 置信集合 \(C(\boldsymbol{x})\) 是無偏的 (unbiased), 如果 \(P_\theta\left(\theta^{\prime} \in\right.\) \(C(\boldsymbol{X})) \leqslant 1-\alpha\) 對于所有的 \(\theta \neq \theta^{\prime}\) 成立。
這樣, 對于一個無偏的置信集合, 假值覆蓋概率決不會大于最小的真值覆蓋概率. 可以通過反轉無偏檢驗得到無偏置信集合。 就是說, 如果設 \(A\left(\theta_0\right)\) 是關于 \(H_0\) : \(\theta=\theta_0\) 對 \(H_1: \theta \neq \theta_0\) 的一個無偏的水平 \(\alpha\) 檢驗的接受區域, 而 \(C(\boldsymbol{x})\) 是由反轉該接受 區域得到的 \(1-\alpha\) 置信集合, 則 \(C(\boldsymbol{x})\) 就是一個無偏的 \(1-\alpha\) 置信集合。
定理 9.3.9 (Pratt): 設 \(X\) 是一個實值隨機變量, \(X \sim f(x \mid \theta)\), 其中 \(\theta\) 是一個 實值參數。設 \(C(x)=[L(x), U(x)]\) 是一個關于 \(\theta\) 的置信區間. 如果 \(L(x)\) 和 \(U(x)\) 都是 \(x\) 的增函數, 則對于任意的值 \(\theta^*\), 有
\(C(X)\) 的期望長度等于假值覆蓋概率的和, 積分域取遍參數的所有假值。
9.3.3 Bayes最優
獲得具有指定覆蓋概率的最小置信集合的目標也能利用 Bayes 準則達到。如果有一個后驗分布 \(\pi(\theta \mid x)\), 即給定 \(\boldsymbol{X}=x\) 時 \(\theta\) 的后驗分布, 而欲求集合 \(C\) \((\mathrm{x})\), 滿足
(i) \(\int_{C(x)} \pi(\theta \mid \boldsymbol{x}) \mathrmw0obha2h00 \theta=1-\alpha\) (原文中積分變元為 \(\boldsymbol{x}\))
(ii) 尺寸 \((C(x)) \leqslant\) 尺寸 \(\left(C^{\prime}(x)\right)\)
對于任何滿足 \(\int_{C^{\prime}(x)} \pi(\theta \mid x) \mathrmw0obha2h00 \theta \geqslant 1-\alpha\) 的集合 \(C^{\prime}(\boldsymbol{x})\) 成立。
如果用長度當作尺寸大小的測度, 則我們可以應用定理 \(9.3 .2\) 得到以下的 結果。
推論 9.3.10: 如果后驗密度 \(\pi(\theta \mid x)\) 是單峰的, 則對于一個給定的 \(\alpha\) 值, 關于 \(\theta\) 的最短可信區間由
給出。
上式中給出的可信集合叫做最高后驗密度 (highest posterior density, HPD)區域, 因為它由那些后驗密度最高的參數的值所組成. 注意 HPD 區域在形式上與似然區域是類似的。


 浙公網安備 33010602011771號
浙公網安備 33010602011771號