W

e

l

c

o

m

e

: )

[字符串] 基本子串結(jié)構(gòu)

沒事就學(xué)點(diǎn)新東西

Update in 2025.08.09 回坑了x，打算有時間翻新一下這篇糞文，順便加點(diǎn)可做的題。

提示

~~這個博客是差不多就是學(xué)習(xí)筆記，因此有些重要的但是比較顯然的定義/定理被省略掉了，并且有些符號用得很奇怪，建議看看參考資料。~~

原論文的定義/定理/推論的標(biāo)記號我看不懂關(guān)聯(lián)，于是按照自己的方式編了個號（引理/推論的第一個數(shù)字表示與哪個定義相關(guān)，推論第二個數(shù)字表示與哪個引理相關(guān)）。

符號約定

兩個串 $A, B$，若 $A\subseteq B$，則表示 $A$ 是 $B$ 的子串。

注意區(qū)分本文中等價類，行等價類（endpos 等價類），列等價類（startpos 等價類）的區(qū)別。以及 SAM（SAM 的 DAWG）和 SAM 的 parent 樹的區(qū)別。

拓展串

定義 0（出現(xiàn)次數(shù)）

定義 $s$ 的一個子串 $t$ 在 $s$ 的出現(xiàn)次數(shù)為 $\operatorname{occ}(t)$。

定理 0

若 $t\subseteq T$，那么 $\operatorname{occ}(T)\le\operatorname{occ}(t)$

證明：若 $T$ 出現(xiàn)一次則 $t$ 必然會出現(xiàn)一次。

定義 1（拓展串）

定義 $t$ 的拓展串 $\operatorname{ext}(t)=T \to (\max_{t\subseteq T, \operatorname{occ}(T)=\operatorname{occ}(t)} |T|)$。

定理 1.1

$\operatorname{ext}(t)$ 存在且唯一。

證明：$t$ 自身即為 $\operatorname{ext}(t)$ 一個合法的選項(xiàng)，這是存在性；若兩個不同串 $T1, T2$ 均為為 $\operatorname{ext}(t)$，那么 $T1\cup T2$ 是一個更大且合法的串，矛盾，唯一性得證。

不難進(jìn)一步得出：

推論 1.1.1

若 $t\subseteq p \subseteq T$，且 $\operatorname{ext}(t)=T$，那么 $\operatorname{ext}(q)=T$。

等價類

定義 2（等價類）

對于兩個子串 $x, y$，若 $\operatorname{ext}(x)=\operatorname{ext}(y)$，則我們說 $x, y$ 是一個等價類。

對比 SAM，我們發(fā)現(xiàn)這里的“等價類”其實(shí)是一些等效位置的子串，而 SAM 的 endpos 等價類是一些等效結(jié)束位置的子串，相當(dāng)于 $\operatorname{ext}(t)$ 只向左拓展。

定義 3（代表元）

若 $\operatorname{ext}(t)=t$，則稱 $t$ 是其所在的等價類 $a$ 的代表元 $\operatorname{rep}(a)$。

不難發(fā)現(xiàn) $\operatorname{rep}(a)$ 存在且唯一。

定理 0/2.1

若 $t_{1}\subseteq t_{2}$，且 $\operatorname{occ}(t_{1})=\operatorname{occ}(t_{2})$，那么 $t_{1},t_{2}$ 屬于同一個等價類。

定理 2.2

如果 $s[l, r_1]$ 與 $s[l, r_2]$ 在同一個等價類中，那么對 $\forall 1 \le i < l$，$s[i, r_1]$ 與 $s[i, r_2]$ 在同一個等價類中。
如果 $s[l_1, r]$ 與 $s[l_2, r]$ 在同一個等價類中，那么對 $\forall r< i\le |s|$，$s[l_1, i]$ 與 $s[l_2, i]$ 在同一個等價類中。

證明：不妨設(shè) $r_1<r_2$，因?yàn)?$s_{[l, r_{1}]}\subseteq s_{[i, r_1]}$，$s_{[i, r_1]}$ 的一次出現(xiàn)意味著 $s_{[l, r_{1}]}$ 作為其后綴出現(xiàn)，同時因?yàn)?$s_{[l, r_{1}]}, s_{[l, r_{2}]}$ 屬于同一等價類，所以 $s_{[i, r_1]}$ 后還跟著 $s_{(r_{1}, s_{r_{2}}]}$，即 $s_{[i, r_2]}$ 也出現(xiàn)了。即 $s_{[i, r_1]}，s_{[i, r_2]}$ 一一對應(yīng)，在一個等價類中。第二條同理

階梯狀圖形

定義 4（首次出現(xiàn)位置 first occurence）

對于子串 $t$，定義 $\operatorname{posl}(t), \operatorname{posr}(t)$ 為最小的一對數(shù)使得 $s_{[\operatorname{posl}(t), \operatorname{posr}(t)]}=t$。

以 $s=\texttt{aababcd}$ 為例，我們建立如下一個格點(diǎn)圖：橫軸為 $l$，豎軸為 $r$，一個點(diǎn) $[l, r]$ 為 $s_{[l, r]}$（$y=x$ 下面為空）。

我們先將等價類列出來：

\[\begin{aligned} {\color{red}{g_1}}=&\{\texttt{aa},\texttt{aab},\texttt{aaba},\texttt{aabab},\texttt{aababc},\texttt{aababcd}\}\cup\\ &\{\texttt{aba},\texttt{abab},\texttt{ababc},\texttt{ababcd}\}\cup\\ &\{\texttt{ba},\texttt{bab},\texttt{babc},\texttt{babcd}\}\cup\\ &\{\texttt{abc},\texttt{abcd}\}\cup\\ &\{\texttt{bc},\texttt{bcd}\}\cup\\ &\{\texttt{c},\texttt{cd}\}\cup\{\textttw0obha2h00\}\\ {\color{blue}{g_2}}=&\{\texttt{b},\texttt{ab}\}\\ {\color{green}{g_3}}=&\{\texttt{a}\} \end{aligned} \]

在格點(diǎn)圖上標(biāo)記。

定義 4.1（格點(diǎn)圖）

~~名字是瞎起的哦~~ 平面直角坐標(biāo)系上一點(diǎn) $(l, r)$ 表示子串 $s_{[l, r]}$。$\frac{n(n+1)}{2}$ 個子串形成格點(diǎn)圖。

crashed 大神的圖，侵刪

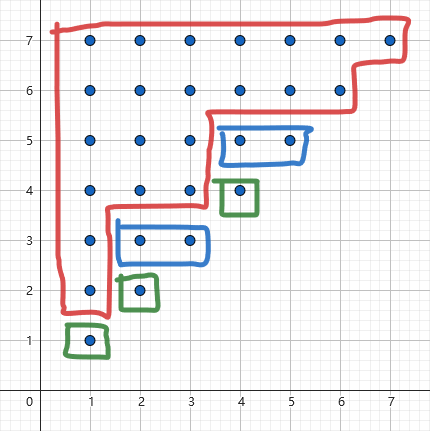
定理 2/5.1

等價類形成了若干個上側(cè)與左側(cè)對齊，右側(cè)與下側(cè)呈階梯狀上升的點(diǎn)陣。

證明：取一等價類 $a$，不妨設(shè) $[\operatorname{posl}(\operatorname{rep}(a)), \operatorname{posr}(\operatorname{rep}(a))]=[l_{0}, r_{0}]$，對于等價類的另一個非代表元的子串 $s_{[x, y]}$，由 定理 2.2 得 $\forall l_{0}\le a\le x \le y \le b\le r_{0}$，$s_{[a, b]}$ 仍在這個等價類中，即 $[a, b]$ 在這個等價類點(diǎn)陣中，那么一個等價類其實(shí)就是若干個左上角為 $[l_{0}, r_{0}]$ 的矩形的并，即階梯狀點(diǎn)陣。

定義 5（點(diǎn)陣）

設(shè) $\operatorname{G}(a)$ 為 $a$ 代表的一個階梯點(diǎn)陣，記 $\operatorname{rowsize}(a), \operatorname{colsize}(a)$ 分別為 $G(a)$ 的行數(shù)和列數(shù)。

~~論文中沒有明確一個符號來表示它，但是用符號確實(shí)能少打幾個字。~~

推論 5.1

某個 $\operatorname{G}(a)$ 會出現(xiàn) $\operatorname{occ}(\operatorname{rep}(a))$ 次。

定義 6（周長）

定義等價類 $a$ 的周長 $\operatorname{per}(a)=\operatorname{rowsize}(a)+\operatorname{colsize}(a)$，即 $\operatorname{G}(a)$ 的行數(shù)和列數(shù)和。

定理 2/5.2（重要）

對于一個等價類 $a$，$\operatorname{G}(a)$ 的每一行對應(yīng)了一個 endpos 等價類，每一列對應(yīng)了一個 startpos 等價類。換言之，每一行對應(yīng)了正串 SAM parent 樹上的一個結(jié)點(diǎn)，每一列對應(yīng)了反串 SAM parent 樹上的一個結(jié)點(diǎn)。

證明：以行為例，設(shè)這一行縱坐標(biāo)為 $r$，由于該行表示的字符串互為后綴，且 $\operatorname{occ}$ 相等，所以它們必然在一個 endpos 等價類 $U$ 里，假設(shè) $U$ 內(nèi)若干個串不在 $a$ 中，由 endpos 等價類的連續(xù)性得出必然有個某個不合法串為 $t=s_{[\operatorname{posl}(\operatorname{rep}(a))-1, r]}$，又 $\operatorname{occ}(t)=\operatorname{occ}(\operatorname{rep}(a))=\operatorname{occ}(\text{行內(nèi)某個串} q)$，由 $\operatorname{ext}(q)$ 的唯一性（引理 1.1）得知其矛盾。因此得到對應(yīng)關(guān)系。

由次不難導(dǎo)出：

定理 5/6.1

$\sum\operatorname{per}(a)=O(n)$，即正反串 SAM 的結(jié)點(diǎn)個數(shù)和。

構(gòu)建

定義 7（基本子串結(jié)構(gòu)）

基本子串的定義十分籠統(tǒng)，不過你可以看成它是正反串 SAM 的結(jié)合體，即對于所有本質(zhì)不同子串狀態(tài)之間的自動機(jī)。

對于一個子串 $s_{[l, r]}$ 在前/后面接一個字符 $c$ 進(jìn)行匹配，這對應(yīng)在格點(diǎn)圖上其實(shí)就是“向左走”（$l-1$）和“向上走”（$r+1$），因此，基本子串結(jié)構(gòu)中的字符邊可以看為某個點(diǎn)對四聯(lián)通結(jié)點(diǎn)的連邊。但邊的數(shù)量實(shí)在太大，于是就有了等價類，等價類中的某行和相鄰行的連邊，此時邊上的字符變成了一個可長可短的字符串（視改行某個點(diǎn)而定）。

考慮先找出一個等價類的標(biāo)識——代表元，由定理 2/5.2可得 $\operatorname{rep}(a)$ 在所在的行 endpos 等價類的最左側(cè)、列 startpos 等價類最上側(cè)，都是它們中的最長串，而對于 $a$ 中的非代表元串，其總是不能同時滿足這兩個條件。換言之，所有滿足 $r-l+1=len_{\text{正} \operatorname{SAM}}=len_{\text{反} \operatorname{SAM}}$ 的子串 $s_{[l, r]}$ 與等價類的代表元一一對應(yīng)。這些代表元可以通過枚舉正串 SAM 的結(jié)點(diǎn)，在反串 SAM 上倍增查詢，做到 $O(n\log n)$ 復(fù)雜度。

接下來考慮不包含代表元的 endpos 等價類和 startpos 等價類，一個非常笨比的做法是按 $\operatorname{occ}$ 掃描線后找最小包含區(qū)間，但是這樣碼量過于抽象，所以想想一個稍微要點(diǎn)腦子的做法，這里給出一個引理。

定理 2/5.3

對于一個 endpos 等價類 $X$，若它不是所屬等價類 $\operatorname{G}(a)$ 中的上邊界，那么其在正 SAM 上有且只有一條出邊，且該出邊指向其在 $\operatorname{G}(a)$ 的上一行。startpos 等價類同理。

~~其實(shí)這個定理還有另外一部分，但是我看不懂，看懂的老哥給我講講。~~

證明：我們之前說過，“向上走”意味著向后接一個字符，這在 SAM 上就是一條轉(zhuǎn)移邊，而如果一個 endpos 等價類 $p$ 向后只有一條轉(zhuǎn)移邊 $(p, q, ch)$。則說明 $\operatorname{occ}(p)=\operatorname{occ}(q)$，由推論 1.1.1可得 $p,q$ 屬于同一個等價類。而這個關(guān)系是雙向的（一一對應(yīng)）。

于是可以按 DAG 的拓?fù)湫騺砗喜ⅲ鋵?shí)也就是按 $len$ 從大到小來合并。

而論文指出，按 SAM 結(jié)點(diǎn)順序倒序合并也是可以的：

將兩個 SAM 的等價類對應(yīng)起來只需分別找到代表元的 posl, posr 即可。每塊中網(wǎng)格圖
的構(gòu)建只需將所有 SAM 節(jié)點(diǎn)按照 r 或 l 進(jìn)行排序，但其天然與 SAM 構(gòu)建時加入的順序相
同。至此所有信息都已構(gòu)建完畢，總時間復(fù)雜度為 O(n)。

我們考慮在同一個等價類 $a$ 中的所有 endpos 等價類，根據(jù) 定理 2/5.3，這些 endpos 等價類在 SAM 中成一條除首尾外沒有其它出邊的鏈，它們各自的最長串其實(shí)就是 $G(a)$ 中最左側(cè)的一列點(diǎn)，在這一列 $l$ 不變 $r$ 遞增，聯(lián)系的 SAM 的構(gòu)建過程，我們發(fā)現(xiàn)越靠上的 endpos 等價類越晚形成（因?yàn)?$r$ 更大），也就是說編號也更大，所以我們直接倒序遍歷所有點(diǎn)進(jìn)行合并即可，

于是合并時間就~~莫名奇妙地~~變成 $O(n)$ 的了。

參考代碼

#define vi vector
const int N=1e5+5;
const int M=N<<1;
int n, Ec;char s[N];
struct SAM{
	int ndc, lst, pos[N], mnpos[M], siz[M], id[M];
	struct node{int fa, len, son[26];}sam[M];
	int clr(int x){sam[x]=sam[0];return x;}
	void init(){clr(ndc=lst=1);}
	int insert(char cr){
		int c=cr-'a';int cur=clr(++ndc), p=lst;
		sam[cur].len=sam[lst].len+1;
		for(; p&&!sam[p].son[c]; p=sam[p].fa) sam[p].son[c]=cur;
		int q=sam[p].son[c];
		if(!q) sam[cur].fa=1;
		else if(sam[q].len==sam[p].len+1) sam[cur].fa=q;
		else{
			int nxt=clr(++ndc);sam[nxt]=sam[q], sam[nxt].len=sam[p].len+1;
			for(; p&&sam[p].son[c]==q; p=sam[p].fa) sam[p].son[c]=nxt;
			sam[cur].fa=sam[q].fa=nxt;
		}
		return lst=cur;
	}
	vi G[M];int fa[M][20];
	void chk(int &x, int v){if(!x) x=v;else if(v) x=min(x, v);}
	void dfs(int x){
		for(int i=1; i<20; ++i) fa[x][i]=fa[fa[x][i-1]][i-1];
		for(auto v:G[x]) fa[v][0]=x, dfs(v), chk(mnpos[x], mnpos[v]);
	}
	int FindR(int l, int r){
		int x=pos[r];
		for(int i=19; i>=0; --i) if(sam[fa[x][i]].len>=r-l+1) x=fa[x][i];
		return x;
	}
	void ins(char *t, int m){
		init();
		for(int i=1; i<=m; ++i) mnpos[pos[i]=insert(t[i])]=i;
		for(int i=2; i<=ndc; ++i) 
			G[sam[i].fa].pb(i), siz[i]=sam[i].len-sam[sam[i].fa].len;
		dfs(1);
	}
	void merge(){
		for(int i=ndc; i>1; --i) if(!id[i]) 
			for(int c=0; c<26; ++c) if(sam[i].son[c])
				{id[i]=id[sam[i].son[c]];break;}
	}
}S, T;
vi row[M], col[M];
void build(){
	S.ins(s, n);reverse(s+1, s+n+1);T.ins(s, n);
	for(int i=2; i<=S.ndc; ++i){
		int r=S.mnpos[i], l=r-S.sam[i].len+1, u=T.FindR(n-r+1, n-l+1);
		if(r-l+1==T.sam[u].len) S.id[i]=T.id[u]=++Ec;
	}
	S.merge();T.merge();
	for(int i=S.ndc; i>=2; --i) row[S.id[i]].pb(i);
	for(int i=T.ndc; i>=2; --i) col[T.id[i]].pb(i);
}

其中 $\operatorname{row}, \operatorname{col}$ 分別存儲了第 $i$ 個等價類包含的 endpos/startpos 等價類在正/反串 SAM 的編號。

為什么要這里也要從末尾開始？因?yàn)檫@樣加入使得 $\operatorname{row},\operatorname{col}$ 中的 endpos/startpos 等價類都按照了自身集合大小加入（從大到小），也就是說 $\operatorname{row}_{a}[0]=\operatorname{col}_{a}[0]=\operatorname{rep}(a)$。

SAM 之死

這里先給出另一個引理：

定理 2/5.4

對于一個等價類 $a$，其包含的某個行等價類（endpos 等價類），經(jīng)過上移若干單位后，仍被某一等價類 $b$ 完全包含。
而對于某個列等價類（startpos 等價類），經(jīng)過左移若干單位后，仍被某一等價類 $b$ 完全包含。

其實(shí)本質(zhì)上就是 定理 2.2

這個定理說明了在等價類階梯點(diǎn)圖中，等價類向上/左只會碰到一個等價類。

考慮串 $s=\operatorname{ababababba}$：

劃分等價類后的點(diǎn)圖

正串 SAM

反串 SAM

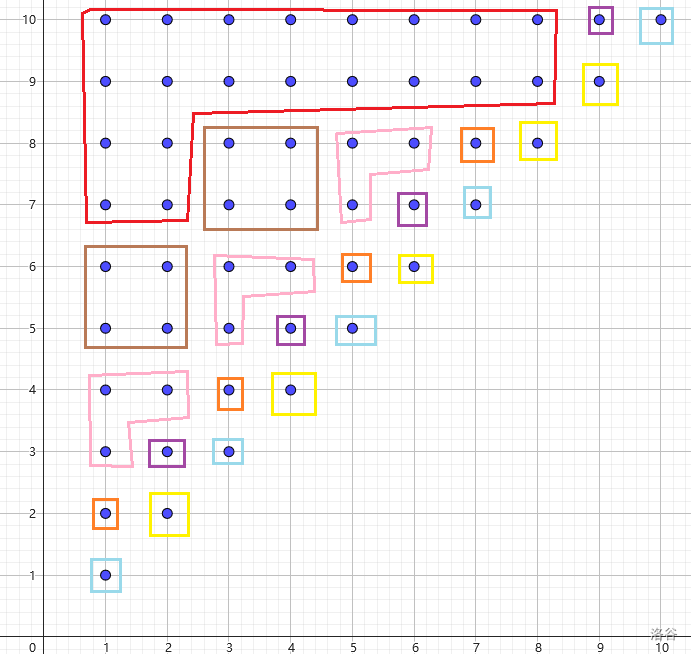
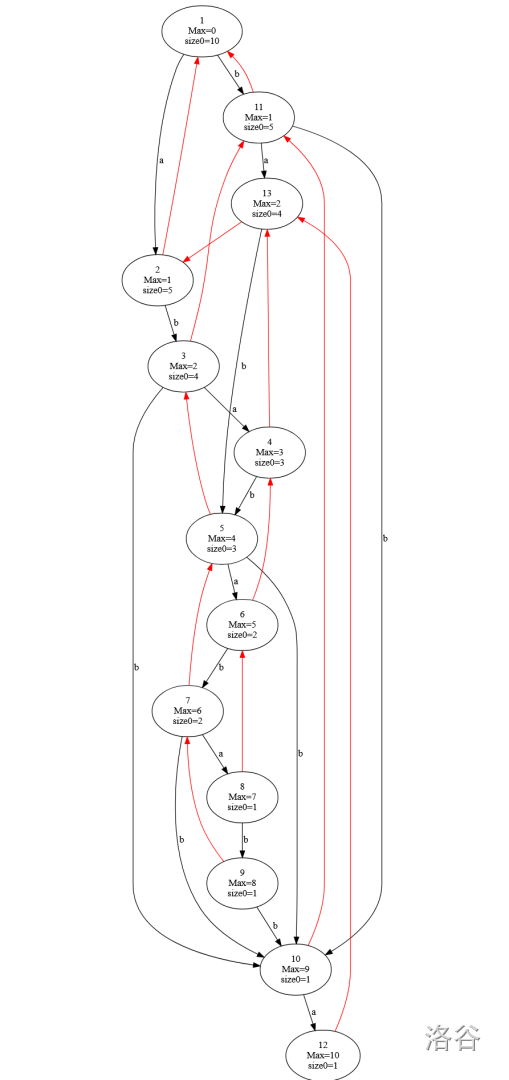
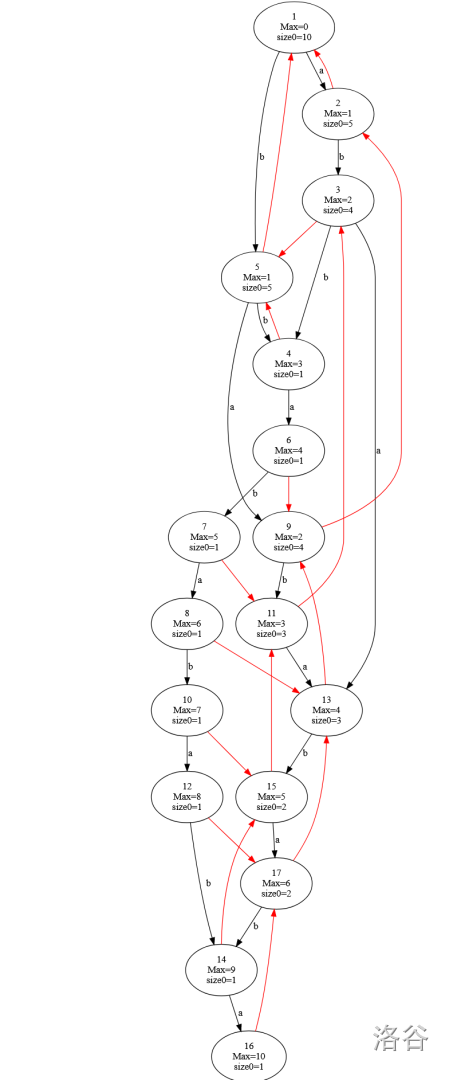
考慮等價類 $a=\{\texttt{aba}, \texttt{bab}, \texttt{abab}\}$（粉色的階梯狀點(diǎn)陣），讓它在 $r=4$ 的位置 “向上走”，走完了另一等價類，$\{\texttt{aba},\texttt{abab}\}_{13}\to \{\texttt{ababa}, \texttt{ababab}\}_{17}+\{\texttt{ababb}, \texttt{ababba}\}_{8}$，$\texttt{bab}_{11}\to\{\texttt{baba}, \texttt{babab}\}_{15}+\{\texttt{babb}, \texttt{babba}\}_{7}$（右下角的數(shù)字表示它們在反串 SAM 上對應(yīng)的結(jié)點(diǎn)），注意到它們向上走分別對應(yīng)了一個完整的 startpos 等價類，我們考慮將 $a$ 也劃分為 startpos 等價類，不難發(fā)現(xiàn)這種“向上走”的轉(zhuǎn)移恰好就是反 SAM parent 樹上的邊。

從這里，我們可以導(dǎo)出定理 2/5.3的下半部分。~~沒錯我最后看懂了~~

定理 2/5.3（完整）

對于一個 endpos 等價類 $X$，若它不是所屬等價類 $\operatorname{G}(a)$ 中的上邊界，那么其在正 SAM 上有且只有一條出邊，且該出邊指向其在 $\operatorname{G}(a)$ 的上一行。如果其對應(yīng)的是上邊界，則它的所有出邊即連向（（從該上邊界用另一棵 SAM 的 parent 樹邊連出能到的所有下邊界）表示的 SAM 節(jié)點(diǎn)）。startpos 等價類同理。

而在定義 7，我們說明了“向上走”同時也相當(dāng)于在后面接上一個字符，一個在等價類 $a$ 最上面部分的 endpos 等價類 $q$，它在正 SAM DAWG 上的轉(zhuǎn)移邊等效于某條反 SAM parent 樹上的邊，而這些邊又相當(dāng)于不同等價類之間列 startpos 等價類的轉(zhuǎn)移！于是，我們用階梯狀點(diǎn)圖和等價類劃分完美描述了兩個 SAM 的結(jié)構(gòu)！

定理 2/5.5（重要）

正 SAM parent 樹上的邊與列等價類之間的轉(zhuǎn)移有對應(yīng)關(guān)系，正 SAM DAWG 的轉(zhuǎn)移邊與行等價類的轉(zhuǎn)移有對應(yīng)關(guān)系；
反 SAM parent 樹上的邊與行等價類之間的轉(zhuǎn)移有對應(yīng)關(guān)系，反 SAM DAWG 的轉(zhuǎn)移邊與列等價類的轉(zhuǎn)移有對應(yīng)關(guān)系。

~~這個定理是我瞎捏的，跟論文無關(guān)，其實(shí)本質(zhì)上就是 定理 2/5.3 的籠統(tǒng)描述~~。

SAM 已死，基本子串當(dāng)立！

線性構(gòu)造

回頭看看我們 $O(n\log n)$ 建立基本子串的過程，發(fā)現(xiàn)瓶頸在于如何快速地處理代表元。

首先根據(jù)定理 2/5.5，不難發(fā)現(xiàn)代表元所在的等價類的最上面/左邊的行/列等價類在 SAM 的 DAWG 上，要么沒有出邊，要么出邊連向的 endpos/startpos 等價類與自己的 $\operatorname{occ}$ 不同（這種關(guān)系是一一對應(yīng)的，即不存在一個滿足條件的 endpos/startpos 等價類，它的最長串不是代表元），于是可以很簡單的找到代表元的個數(shù)。

參考代碼

int repcnt=0;
for(int i=ndc; i>1; --i){
    bool flg=0;int p=0;
	for(int c=0; c<26; ++c) 
        if(sam[i].son[c]){
	        ++p;
			if(cnt[sam[i].son[c]]!=cnt[i]){flg=1;break;}
		}	
	if(flg||p==0) ++repcnt;
}

但是這樣是遠(yuǎn)遠(yuǎn)不行的，我們真正要做的事是將正反串的代表元對應(yīng)起來。

將 $O(n\log n)$ 找代表元做法還原，我們枚舉每一個 endpos 等價類中的最長串，直接在反串 SAM 的 DAWG 上去匹配到對應(yīng)節(jié)點(diǎn)。

這樣做顯然是 $O(n^2)$ 級別的復(fù)雜度，能不能做到類似于雙指針一樣的操作呢？

這里給出一個性質(zhì)：在 SAM 的 DAWG 上，如果我們只走 $len_{x}+1=len_{sam_{x, c}}$ 的點(diǎn)，是能夠走完全部節(jié)點(diǎn)的。（證明很簡單，除根節(jié)點(diǎn)外每個點(diǎn)都必然找得到這么一條連向自己的邊，于是形成了一棵樹）。

為什么要這么走呢？

若 $x$ 與 $son_{x, c}$ 屬于同一個等價類，那么根據(jù) 定理 2/5.3，$x$ 只有一條出邊 $(x, son_{x, c}, c)$，且 $x$ 代表的 endpos 等價類與 $son_{x, c}$ 代表的 endpos 等價類在階梯狀點(diǎn)圖中是相鄰兩行的關(guān)系，由于 $len$ 是 endpos 等價類中最長的串，即只跟行等價類的左端點(diǎn)有關(guān)，而我們知道等價類的點(diǎn)圖左側(cè)對齊，因此兩個 endpos 等價類最長串 $l$ 相同，$r$ 相差 1，因此就有 $len_{x}+1=len_{sam_{x, c}}$。
若 $x$ 與 $son_{x, c}$ 屬于不同等價類，根據(jù) 定理 2.2 這時候我們所有的出邊都指向了同一個等價類，只能走最短的行等價類，于是就走 $len_{x}+1=len_{sam_{x, c}}$ 的邊即可。

接下來我們考慮如何在反串 SAM 上執(zhí)行這個“向前面加字符”的匹配過程。

向前加單個字符，滿足原串是新串的一個后綴，因此它們在 parent 樹上必然是父子，我們考慮預(yù)處理時用兒子去更新父親的匹配邊：設(shè)某個出現(xiàn)的位置末是 $pos$（實(shí)際上應(yīng)該是開始的位置，但是由于是反串的 SAM，于是變成了末位置），父親最大串長為 $len$，那么父親到兒子的匹配邊字符即為 $s_{pos-len}$。

參考代碼

for(int i=2; i<=ndc; ++i)
  son[sam[i].fa][s[pos[i]-sam[sam[i].fa].len]-'a']=i;

但是，注意我們實(shí)際上維護(hù)的是最長串的位置，在同等價類中行等價類的鏈上轉(zhuǎn)移中，我們維護(hù)的最長串一直在最左邊的列等價類（一直在左邊界向上走），因此，只有在 DAWG 的轉(zhuǎn)移邊中，兩端不屬于同一等價類時才要用 son 轉(zhuǎn)移，此時必然滿足起點(diǎn)是代表元之一，可以參考代碼理解。

參考代碼

const int M=N<<1;
int n, Ec;char s[N];
struct SAM{
	int ndc, lst, pos[N], mnpos[M], siz[M], id[M], cnt[M], fail[M][26];
	struct node{int fa, len, son[26];}sam[M];
	int clr(int x){sam[x]=sam[0];return x;}
	void init(){clr(ndc=lst=1);}
	int insert(char cr){
		int c=cr-'a';int cur=clr(++ndc), p=lst;
		sam[cur].len=sam[lst].len+1;
		for(; p&&!sam[p].son[c]; p=sam[p].fa) sam[p].son[c]=cur;
		int q=sam[p].son[c];
		if(!q) sam[cur].fa=1;
		else if(sam[q].len==sam[p].len+1) sam[cur].fa=q;
		else{
			int nxt=clr(++ndc);sam[nxt]=sam[q], sam[nxt].len=sam[p].len+1;
			for(; p&&sam[p].son[c]==q; p=sam[p].fa) sam[p].son[c]=nxt;
			sam[cur].fa=sam[q].fa=nxt;
		}
		return lst=cur;
	}
	vi G[M];
	void chk(int &x, int v){if(!x) x=v;else if(v) x=min(x, v);}
	void dfs(int x){for(auto v:G[x]) dfs(v), chk(mnpos[x], mnpos[v]), cnt[x]+=cnt[v];}
	void ins(char *t, int m){
		init();
		for(int i=1; i<=m; ++i) mnpos[pos[i]=insert(t[i])]=i, ++cnt[pos[i]];
		for(int i=2; i<=ndc; ++i) 
			G[sam[i].fa].pb(i), siz[i]=sam[i].len-sam[sam[i].fa].len;
		dfs(1);
		for(int i=2; i<=ndc; ++i)
  			fail[sam[i].fa][s[mnpos[i]-sam[sam[i].fa].len]-'a']=i;
	}
	void merge(){
		for(int i=ndc; i>1; --i) if(!id[i]) 
			for(int c=0; c<26; ++c) if(sam[i].son[c])
				{id[i]=id[sam[i].son[c]];break;}
	}
}S, T;
vi row[M], col[M];
void DFS(int u, int v){
	int lenu=S.sam[u].len, lenv=T.sam[v].len;
	if(lenu==lenv&&u!=1&&v!=1) S.id[u]=T.id[v]=++Ec;//兩邊的代表元對應(yīng)
	for(int c=0, x, y; c<26; ++c)
		if((x=S.sam[u].son[c])&&(S.sam[x].len==lenu+1)&&(y=(lenu==lenv)?T.fail[v][c]:v))
			DFS(x, y);
}
void build(){
	S.ins(s, n);reverse(s+1, s+n+1);T.ins(s, n);
	DFS(1, 1);//識別代表元
    S.merge();T.merge();//合并
	for(int i=S.ndc; i>=2; --i) row[S.id[i]].pb(i);
	for(int i=T.ndc; i>=2; --i) col[T.id[i]].pb(i);
}

應(yīng)用

字符串匹配

給定一個串 $s$ 和另一個空串 $w$，每次向前/后添加/刪除一個字符，若加入字符后 $w$ 不是 $s$ 的子串則撤銷操作，每次操作后輸出是否成功操作，以及當(dāng)前的 $\operatorname{occ}(w)$。

對 $s$ 建立基本子串結(jié)構(gòu)，這樣我們能顯式地觀察 $w$ 在階梯狀點(diǎn)陣圖的位置，維護(hù) $w$ 在正反 SAM 上對應(yīng)的結(jié)點(diǎn)，那么每次添加字符無外乎兩種可能：在同等價類中走，走出邊界。對于第一種情況，我們顯然珂以通過簡單計(jì)算判斷應(yīng)該接上的字符，對于第二種情況，這相當(dāng)于直接走正/反 SAM 上的字符轉(zhuǎn)移邊，同樣很容易做到。

CF1817F Entangled Substrings

$acb$ 打包出現(xiàn)，因此有 $\operatorname{occ}(a)=\operatorname{occ}(b)$，即 $a, b$ 屬于同一個等價類，因此我們對等價類內(nèi)部計(jì)數(shù)。

考慮枚舉 $acb$ 計(jì)算合法的 $(a, b)$ 對數(shù)，設(shè) $c$ 在階梯狀點(diǎn)圖的坐標(biāo)為 $(l_{c}, r_{c})$，其向右拓展到 $(l_{p}, r_{c})$，向下拓展到 $(l_{c}, r_{p})$，其中 $l_{c}\le l_{p},r_{p}\le r_{c}$，又因?yàn)辄c(diǎn)陣的點(diǎn)全在 $y=x$ 上方，所以右 $l_{p}\le r_{c}, l_{c}\le r_{p}$。

可選的 $a$ 為 $s_{[l_{c}, [r_{p}, r_{c}]]}$，可選的 $b$ 為 $s_{[[l_{c}, l_{p}], r_{c}]}$，并且要滿足 $a$ 的右端點(diǎn)小于 $b$ 的左端點(diǎn)，即 $r_{p}\le r_{a}\le r_{c}, l_{c}\le l_{b}\le l_{p}, r_{a}<l_{b}$。

綜合幾個不等關(guān)系，我們發(fā)現(xiàn) $r_{p}\le l_{p}$ 才會出現(xiàn)合法的 $(a, b)$，此時 $a$ 的右端點(diǎn)和 $b$ 的左端點(diǎn)都落在 $[r_{p}, l_{p}]$ 中，貢獻(xiàn)即為 $C_{l_{p}-r_{p}+1}^{2}$。

因此我們枚舉 $r_{p}$，雙指針維護(hù) $l_{p}$，統(tǒng)計(jì) $\sum 1, \sum l, \sum l^2$ 即可。

注意我們在構(gòu)建基本子串結(jié)構(gòu)時，加入行/列時都是按等價類大小從大到小加入，對應(yīng)到 $l_{p}$ 遞減，$r_{p}$ 遞增。

$O(n\log n)$ 實(shí)現(xiàn) $O(n)$ 實(shí)現(xiàn)

注意到我們實(shí)際上只需要用到行列等價類的長度，可以通過行的長度來推出列的長度，只建一個 SAM。實(shí)現(xiàn) 2

UOJ 577 打擊復(fù)讀

注意到只需要計(jì)算 $wl_{i}$ 的系數(shù)就能支持 $O(1)$ 修改。

注意到 $vl(s[l, r])$ 和 $vr(s[l, r])$ 其實(shí)就是 $[l, r]$ 在反串/正串 SAM parent 樹上對應(yīng)結(jié)點(diǎn)內(nèi)的所有后綴/前綴的 $wl_{i}/wr_{i}$ 的和，并且在基本子串結(jié)構(gòu)中，同一列的 $vl$ 相等，同一行的 $vr$ 相等。

考慮一個點(diǎn) $(l, r)$ 的貢獻(xiàn)是 $vl(s[l, r])\times vr(s[l, r])$，于是我們可以通過基本子串結(jié)構(gòu)得到一列 $vl(s[l, [r1, r2]])$ 的總貢獻(xiàn)系數(shù)為 $\sum_{i=r1}^{r2} vr(s[l, i])\times \operatorname{occ}(s[l, r])$，前面的和式本質(zhì)上是行等價類的一個 $vr$ 前綴和，再由 $vl$ 的定義就可以在反串 SAM 的 parent 樹上反推 $wl$ 的系數(shù)了，復(fù)雜度 $O(n)$。代碼。

UOJ 697 廣為人知題

考慮在格點(diǎn)圖上將所有模式串出現(xiàn)的位置的點(diǎn) +1，于是詢問就是求以 $[ql, qr]$ 為左上角的矩形和，直接做是 $O(n^{2})$ 的。

這樣的做法太過冗余了，我們發(fā)現(xiàn)答案本質(zhì)上只跟 $s_{[ql, qr]}$ 有關(guān)，而與 $[ql, qr]$ 無關(guān)（即兩個詢問的答案與位置無關(guān)，只跟是否為本質(zhì)不同子串有關(guān)），也由此可以推導(dǎo)出一個結(jié)論：

定理 2/5.6

在格點(diǎn)圖中，以 $\operatorname{rep}(a)$ 出現(xiàn)的所有位置開始，向右、向下完拓展出來的 $\operatorname{occ}(\operatorname{rep}(a))$ 個大階梯完全相等。

“相等”指對應(yīng)位置的每個點(diǎn)屬于同一個等價類 $b$，且在 $\operatorname{G}(b)$ 的同一個位置。

仍以 $s=\operatorname{ababababba}$ 為例，其劃分等價類后的格點(diǎn)圖為：

考慮一個詢問 $[1, 5]=[3, 7]$，將其答案統(tǒng)計(jì)劃為兩個部分：$[[1, 2], 5]$ 這條線段以下的部分，以及 $[3, 5]$ 這個子問題詢問。

對于前半部分，我們繼續(xù)將所求劃為兩個部分：與 $[1, 5]$ 在同一等價類中的點(diǎn)/與 $[1, 5]$ 不在同一等價類中的點(diǎn)。對于同等價類中的點(diǎn)，我們可以直接做一個二維數(shù)點(diǎn)，對于非等價類中的點(diǎn)，由于這部分是若干條緊貼著等價類的下邊界的豎線段，每條豎線段相當(dāng)于每個列等價類在反串 SAM 上到根的鏈的和，所有的和是一個后綴。

對于后半部分，發(fā)現(xiàn)我們詢問的點(diǎn)在另一個等價類 $b$ 中最靠左的一個列等價類，考慮先計(jì)算出并加上 $\operatorname{rep}(b)$ 的答案，那么需要減掉的部分的答案是一列的前綴的后綴后的和，這部分是可以簡單預(yù)處理的。

于是總復(fù)雜度 $O((n+q)\log n)$，代碼。

[SDOI/SXOI2022] 子串統(tǒng)計(jì)

SDOI 緊跟論文步伐！

列出 $O(n^{2})$ DP 式子后，在基本子串結(jié)構(gòu)的階梯點(diǎn)圖上優(yōu)化。詳細(xì)題解

parent 樹的樹鏈剖分

通過前面的理論，我們知道，SAM 的 parent 樹上的邊本質(zhì)上是同行不同等價類的行（列）等價類的之間的轉(zhuǎn)移，我們現(xiàn)在通過基本子串結(jié)構(gòu)來反推一些 parent 樹的性質(zhì)。

推論 2.2.1

對于屬于同一等價類 $a$ 兩個行（列）等價類 $u, v$，其所代表的正（反） SAM endpos （startpos）等價類結(jié)點(diǎn)在 parent 樹上的子樹除根節(jié)點(diǎn)外同構(gòu)。

這里同構(gòu)指可將兩棵子樹中的點(diǎn)重編號，使得對應(yīng)結(jié)點(diǎn)的出邊一致，endpos 等價類的大小一致，且對應(yīng)節(jié)點(diǎn)所在同一個等價類，亦即 $\operatorname{occ}$ 一致。

證明：我們同時讓 $u, v$ 從最左邊同時向左邊走（即沿著 parent 樹邊走），由于定理 2.2，每次走到的兩個點(diǎn) $p_{u'}, p_{v'}$ 屬于同一等價類的兩個不同行等價類 $u', v'$，向左走的時候同時從 $u', v'$ 的最右側(cè)走到了最左側(cè)，也就是說 $u', v'$ 的長度（endpos 等價類的大小）相等，考慮每次跨行等價類的時候都是走 parent 樹的出邊從葉子結(jié)點(diǎn)可以歸納證明從 $u, v$ 的任意的鏈?zhǔn)峭耆葍r的，再次對 $u, v$ 的每次出現(xiàn)位置進(jìn)行合并即可得到子樹同構(gòu)結(jié)論。順帶一提，根節(jié)點(diǎn)只有 endpos 大小不同。

我們嘗試對 SAM 每個結(jié)點(diǎn)在階梯狀點(diǎn)圖上確定一個位置，使得 SAM 能更好地刻畫等價類。

定義 8（結(jié)點(diǎn)位置）

令 $occ=1$ 的行/列等價類的位置就是它唯一出現(xiàn)的位置，接著對于每個重兒子，將其父親放在其右/下側(cè)，依次類推。

理論上選哪個點(diǎn)進(jìn)行標(biāo)記都沒有關(guān)系，但是考慮到復(fù)雜度，優(yōu)先選擇重剖。

仍以 $s=\operatorname{ababababba}$ 為例：

行等價類被分到的坐標(biāo)以及傳遞關(guān)系

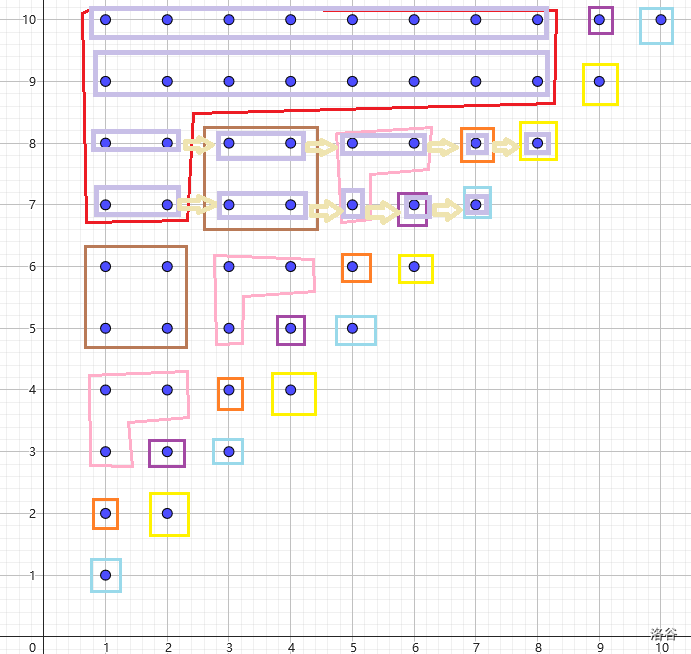
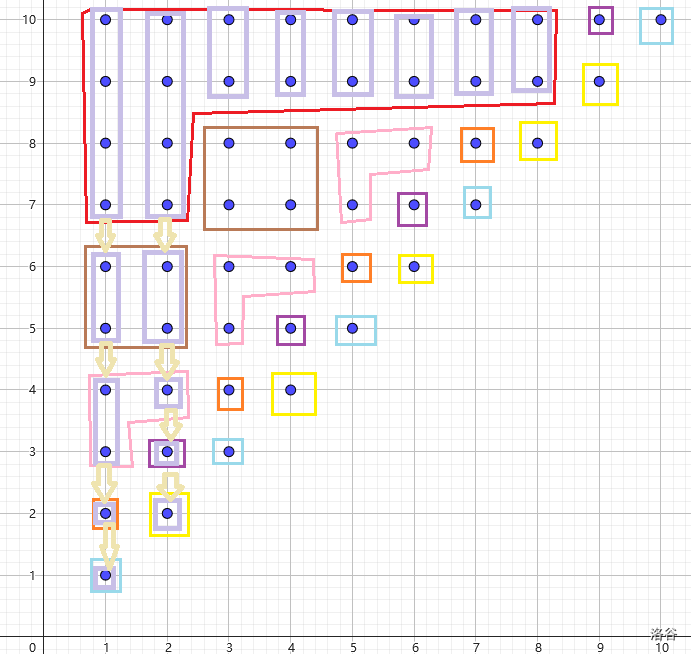
回到 推論 2.2.1，不難得到同等價類中的行等價類在 SAM 上的子樹的每個點(diǎn)的重兒子也一一對應(yīng)。

繼續(xù)考察。

首先，無論我們鏈剖以怎樣的方式（長剖、短剖、輕剖等），為一條鏈上的所有點(diǎn)安排的位置的縱坐標(biāo) $r$ 一定相同（或者橫坐標(biāo) $l$ 一定相同）。

我們考慮每一個等價類 $a$ 中的所有行等價類結(jié)點(diǎn)，考慮它們所在鏈的鏈底，parent 樹邊只會在 $l$ 產(chǎn)生改變（換句話說就是一條鏈的縱坐標(biāo)不變，因?yàn)榭傆泻缶Y關(guān)系），因此這 $\operatorname{rowsize}(a)$ 條重鏈的鏈底的縱坐標(biāo)連續(xù)。

定理 5/8.1

以重鏈鏈底所在位置 $[l, r]$ 的 $r$ 為整條重鏈標(biāo)號，則對于任意一個等價類，其行等價類的重鏈標(biāo)號為一個連續(xù)區(qū)間。

同時注意到一條鏈上的所有本質(zhì)不同子串（注意這里是子串而并非等價類）的長度互不相同，因此我們可以用 $(\text{反串重鏈標(biāo)號},\text{串長})$ 來表示所有的本質(zhì)不同子串，而根據(jù)定理 5/8.1，對于一個行等價類，其包含的所有串的反串重鏈標(biāo)號隨著串長變大依次 +1 ，即其為一條斜率為 $1$ 的線段。我們用 $O(n)$ 的信息量刻畫出了所有本質(zhì)不同子串！

事實(shí)上普通的 SAM 也能刻畫本質(zhì)不同子串，在反串 SAM 上，對于一個列等價類，其代表的所有子串是一條豎線段（第一維相同，第二維的區(qū)間為 $(fa.len, len]$）。

[BJWC2018] Border 的四種求法

區(qū)間最長 border，同時也可以做到數(shù)區(qū)間 border 個數(shù)。

先在正反 SAM 上定位 $s[l, r]$ 得到兩個節(jié)點(diǎn) $u, $，$u, v$ 到各自 parent 樹根的鏈分別為 $s[l, r]$ 后綴和前綴的信息，同時注意 $u, v$ 所在的等價類會包含一個更大的串，需要加長度 $\le r-l+1$ 的限制。詢問則等價于查詢鏈交。

一個很暴力的做法是，從 $u$ 開始向上跳，將每個正串 SAM 結(jié)點(diǎn)加入到集合中，然后從 $v$ 開始跳，每次跳到一個點(diǎn)，相當(dāng)于詢問一條橫線段與集合中的線段交點(diǎn)信息。

考慮優(yōu)化：我們發(fā)現(xiàn)在 $v$ 跳的過程中，對于某條重鏈，其詢問的橫線段的第一維都是相同的，而第二維都是連續(xù)的，這里的連續(xù)的意思是，這重鏈長度個點(diǎn)的橫線段可以接在一起，變成一條長線段。右側(cè)的詢問個數(shù)變?yōu)?$O(\log n)$。

考慮繼續(xù)對正 SAM 重剖，這時也出現(xiàn)了 $O(\log n)$ 條鏈，然而由于交集的長度限制，正反 SAM 的交叉詢問并不是 $O(\log^2 n)$ 級別，而是 $O(\log n)$ 條重鏈對的交。

將這些重鏈對離線下來，枚舉正 SAM 處的重鏈對處理詢問，那么就變成了 $O(n)$ 次加斜線段，$O(q\log n)$ 次查詢豎線段與斜線段交集信息的問題。總復(fù)雜度 $(n+q\log n)\log n$

更詳細(xì)的題解和代碼見此。

【UNR #6】Border 的第五種求法

~~你到底有幾種求法~~

同樣類似于區(qū)間 border，交點(diǎn)的代價變?yōu)?$f_{occ}$，對于正串的一個結(jié)點(diǎn)所代表的斜線段上的點(diǎn)，其代價是相同的，同樣做二維數(shù)點(diǎn)，掃到詢問的時候變?yōu)榍髤^(qū)間和，復(fù)雜度不變。代碼

Border 的第六種求法

xtq 鴿鴿的論文的最后一題，同第五種求法，Border $t$ 的貢獻(xiàn)變?yōu)?$f_{\operatorname{occ}}\times g_{|t|}$。

我們發(fā)現(xiàn)做法并不能直接套上去了，這是因?yàn)橐粋€ SAM 結(jié)點(diǎn)的 $len$ 并不相同（貢獻(xiàn)并不呈線性），我們需要考慮一個更好的做法來統(tǒng)一 $\operatorname{occ}, len$。

繼續(xù)從一個等價類 $a$ 入手，注意到 $G(a)$ 中一條斜率為 $1$ 的線段，它們的 $len$ 相同，我們考慮對這些斜線計(jì)數(shù)。

對于這些斜線，它們的 $(\text{正串重鏈標(biāo)號}, \text{反串重鏈標(biāo)號})$ 跟原下標(biāo)是一樣的一條斜率為 $1$ 的線段。對于詢問，我們發(fā)現(xiàn)這兩個重鏈標(biāo)號已經(jīng)被定死了，只剩長度的限制。

具體的，考慮三維坐標(biāo) $(\text{正串重鏈標(biāo)號}, \text{反串重鏈標(biāo)號}, \text{串長})=(x, y, len)$，$O(n)$ 條 $len$ 一定，$y=x+k$ 代價為 $f_{\operatorname{occ}}g_{len}$ 的線段，$O(q\log n)$ 次詢問給出一條 $(x, y)$ 一定的線段，查詢與 $O(n)$ 條線段的交集信息。直接對 $(x-y, len)$ 二維數(shù)點(diǎn)即可。

mod 1e9+7 下的實(shí)現(xiàn)

#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <cctype>
#include <vector>
#include <queue>
#include <bitset>
#include <set>
#include <assert.h>
#define mcy(arra, arrb) memcpy(arra, arrb, sizeof(arra))
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define st first
#define nd second
using namespace std;
typedef long long ll;
typedef pair <int, int> Pii;
const int INF=0x3f3f3f3f;
const int cp=1e9+7;
inline int mod(int x){return x+(x<0?cp:0)-(x>=cp?cp:0);}
inline void plust(int &x, int y){x=mod(x+y);return ;}
inline void minut(int &x, int y){x=mod(x-y);return ;}
inline int read(){
	char ch=getchar();int x=0, f=1;
	while(!isdigit(ch)){if(ch=='-') f=-1; ch=getchar();}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*f;
}
inline void write(int x){
    if(x<0) putchar('-'), x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline int ksm(int a, int b=cp-2){
	int ret=1;
	for(; b; b>>=1, a=1ll*a*a%cp)
		if(b&1) ret=1ll*ret*a%cp;
	return ret;
}
const int N=5e5+5;
const int M=N<<1;
struct SAM{
	int tr[M][26], len[M], fa[M][21], ndc, lst;
	inline int clr(int x){len[x]=fa[x][0]=0;mcy(tr[x], tr[0]);return x;}
	inline int rmk(){return lst=clr(ndc=1);}
	inline int insert(char cc){
		int p=lst, cur=clr(++ndc), c=cc-'a';len[cur]=len[p]+1;
		for(; p&&!tr[p][c]; p=fa[p][0]) tr[p][c]=cur;int q=tr[p][c];
		if(!q) fa[cur][0]=1;else if(len[p]+1==len[q]) fa[cur][0]=q;
		else{
			int nex=clr(++ndc);len[nex]=len[p]+1, fa[nex][0]=fa[q][0], mcy(tr[nex], tr[q]);
			for(; p&&tr[p][c]==q; p=fa[p][0]) tr[p][c]=nex;fa[q][0]=fa[cur][0]=nex;
		}
		return lst=cur;
	}
	vi G[M];int mxp[M], pos[N], siz[M], son[M], top[M], edr[M], occ[M];;
	void dfs(int x){
		for(int i=1; i<=20; ++i) fa[x][i]=fa[fa[x][i-1]][i-1];int y;siz[x]=1;
		for(auto v:G[x]) dfs(v), occ[x]+=occ[v], siz[x]+=siz[v], mxp[x]=max(mxp[x], mxp[v]),
		y=son[x], son[x]=(siz[y]==siz[v])?(mxp[y]<mxp[v]?v:y):(siz[y]<siz[v]?v:y);
	}
	void dfs(int x, int rt){
		top[x]=rt;if(son[x]) dfs(son[x], rt);edr[x]=son[x]?edr[son[x]]:mxp[x];
		for(auto v:G[x]) if(!top[v]) dfs(v, v);
	}
	void build(char *str, int len, bool rev){
		rmk();for(int i=1; i<=len; ++i) mxp[pos[i]=insert(str[i])]=(rev)?(len-i+1):i, occ[pos[i]]=1;
		for(int i=2; i<=ndc; ++i) G[fa[i][0]].pb(i);dfs(1), son[1]=0;dfs(1, 1);
	}
	inline int mnl(int x){return len[fa[x][0]]+1;}
	inline int find(int x, int y){
		int u=pos[y], k=y-x+1;for(int i=20; i>=0; --i) 
		if(len[fa[u][i]]>=k) u=fa[u][i];return u;
	}
	int id[M];
	void merge(){
		for(int i=ndc; i>1; --i) if(!id[i]) 
			for(int c=0; c<26; ++c) if(tr[i][c])
				{id[i]=id[tr[i][c]];break;}
	}
}A, B;
char s[N];int n, m, occ[M], len[M], ans[N], f[N], g[N];
vi row[M], col[M];int Ec;vector <Pii> cm[M];
set <Pii> S;inline void add(int x){
	int l=x, r=x;
	set <Pii> :: iterator it1=S.lower_bound({x, x});--it1;
	if((*it1).nd==x-1) l=(*it1).st, S.erase(*it1);
	set <Pii> :: iterator it2=S.lower_bound({x, x});
	if((*it2).st==x+1) r=(*it2).nd, S.erase(*it2);
	S.insert({l, r});
}
inline void del(int x){
	set <Pii> :: iterator it=S.lower_bound({x+1, x});--it;Pii me=(*it);S.erase(*it);
	if(me.st<x) S.insert({me.st, x-1});if(x<me.nd) S.insert({x+1, me.nd});
}
struct seg{int val, x, len, tp;}; 
vector <seg> W[M];
void build(){
	A.build(s, n, 0);reverse(s+1, s+n+1);B.build(s, n, 1);
	for(int i=2; i<=A.ndc; ++i){
		int r=A.mxp[i], l=r-A.len[i]+1, u=B.find(n-r+1, n-l+1);
		if(r-l+1==B.len[u]) A.id[i]=B.id[u]=++Ec, occ[Ec]=(A.occ[i]+B.occ[u])>>1, len[Ec]=r-l+1;
	}
	A.merge();B.merge();
	for(int i=A.ndc; i>=2; --i) row[A.id[i]].pb(i);
	for(int i=B.ndc; i>=2; --i) col[B.id[i]].pb(i);
	auto K=[&](int u, int v){return A.edr[u]-B.edr[v];};
	for(int i=1; i<=Ec; ++i){
		int R=row[i].size(), C=col[i].size(), u=row[i][R-1], v=col[i][C-1], maxl=K(row[i][0], col[i][0]), minl=n;
		for(auto x:row[i]) minl=min(minl, K(x, B.find(n-A.mxp[x]+1, n-(A.mxp[x]-A.mnl(x)+1)+1)));
		vector <Pii> clp;for(auto y:col[i]) clp.pb({K(A.find(B.mxp[y], B.mxp[y]+B.mnl(y)-1), y), 
		K(A.find(B.mxp[y], B.mxp[y]+B.len[y]-1), y)}), minl=min(minl, clp.back().st);
		S.clear();S.insert({-2, -2}), S.insert({n+5, n+5});
		for(int c=0; c<C; ++c) cm[clp[c].st-minl].pb({c, 1}), cm[clp[c].nd+1-minl].pb({c, 0});
		for(int k=minl, lenk, v; k<=maxl; ++k){//k=x-y
			lenk=len[i]-(maxl-k), v=1ll*f[occ[i]]*g[lenk]%cp;
			for(auto [u, op]:cm[k-minl]) if(op) add(u);else del(u);
			for(auto [l, r]:S) if(l<0||l>n) continue;else 
			W[k+n].pb((seg){v, B.edr[col[i][l]]+k, lenk, 0}),
			W[k+n].pb((seg){mod(-v), B.edr[col[i][r]]+k+1, lenk, 0});
		}
		for(int i=0; i<=maxl-minl+1; ++i) vector <Pii> ().swap(cm[i]);
	}
}
inline void wrk(int id, int l, int r){
	int u=A.find(l, r), v=B.find(n-r+1, n-l+1);plust(ans[id], 1ll*f[A.occ[u]]*g[r-l+1]%cp);
	for(u=A.fa[u][0], v=B.fa[v][0]; u!=1&&v!=1; ){
		int fu=A.top[u], a=A.mnl(fu), b=A.len[u], fv=B.top[v], c=B.mnl(fv), d=B.len[v];
		int x=A.edr[fu], y=B.edr[fv];W[x-y+n].pb((seg){id, x, min(r-l, min(A.len[u], B.len[v])), 1});
		if(a<c) v=B.fa[fv][0];else u=A.fa[fu][0];
	}
}
namespace BIT{
	#define lowbit(x) (x&(-x))
	int bit[N];void modify(int k, int v){for(; k<=n; k+=lowbit(k)) plust(bit[k], v);}
	int query(int k, int res=0){for(; k; k-=lowbit(k)) plust(res, bit[k]);return res;}
	#undef lowbit(x)
}
using namespace BIT;
inline void slv(int k){
	sort(W[k+n].begin(), W[k+n].end(), [&](seg a, seg b){return (a.x==b.x)?(a.tp<b.tp):(a.x<b.x);});
	for(auto sg:W[k+n]) if(sg.tp) plust(ans[sg.val], query(sg.len));else modify(sg.len, sg.val);
}
signed main(){
	freopen("border.in", "r", stdin);
	freopen("border.out", "w", stdout);
	n=read(), m=read();scanf("%s", s+1);
	for(int i=1; i<=n; ++i) f[i]=read();for(int i=1; i<=n; ++i) g[i]=read();
	build();for(int i=1, l, r; i<=m; ++i) l=read(), r=read(), wrk(i, l, r);
	for(int i=-n; i<=n; ++i) slv(i);for(int i=1; i<=m; ++i) printf("%d\n", ans[i]);
	return 0;
}

參考資料

一類基礎(chǔ)子串?dāng)?shù)據(jù)結(jié)構(gòu) - rdfz xtq

字符串技術(shù)巡禮-ix35_的博客

《一類基礎(chǔ)子串?dāng)?shù)據(jù)結(jié)構(gòu)》摘抄及注解 crashed

~~仍然是復(fù)讀參考資料~~

posted @ 2023-07-25 09:59 127_127_127 閱讀(828) 評論(4) 收藏舉報

刷新頁面返回頂部

提示

符號約定

拓展串

定義 0（出現(xiàn)次數(shù)）

定理 0

定義 1（拓展串）

定理 1.1

推論 1.1.1

等價類

定義 2（等價類）

定義 3（代表元）

定理 0/2.1

定理 2.2

階梯狀圖形

定義 4（首次出現(xiàn)位置 first occurence）

定義 4.1（格點(diǎn)圖）

定理 2/5.1

定義 5（點(diǎn)陣）

推論 5.1

定義 6（周長）

定理 2/5.2（重要）

定理 5/6.1

構(gòu)建

定義 7（基本子串結(jié)構(gòu)）

定理 2/5.3

SAM 之死

定理 2/5.4

定理 2/5.3（完整）

定理 2/5.5（重要）

線性構(gòu)造

應(yīng)用

字符串匹配

定理 2/5.6

parent 樹的樹鏈剖分

推論 2.2.1

定義 8（結(jié)點(diǎn)位置）

定理 5/8.1

Border 的第六種求法

參考資料

公告