深度學習神經網絡訓練過程主要涉及到兩個過程，一個是數據前向傳播(data forward-propagation)，輸入數據經過網絡正向計算，輸出最終結果；另一個是誤差反向傳播(error backward-propagation)，網絡輸出結果的誤差和梯度反向傳播，并更新權重。反向傳播過程又可以細分為兩部分：1）求梯度；2）梯度下降法更新權重。現在大家所說的backward-propagation，一般只是指第一步：求梯度，采用的策略就是鏈式法則。

最早在1974年，有個Harvard博士生Paul Werbos首次提出了backprop，不過沒人理他，到了1986年，Rumelhart和Hinton一起重新發現了backprop，并且有效訓練了一些淺層網絡，一下子開始有了名氣。

1. backward-propagation的重要性

前面已經說了，BP(Backward Propagation)的作用主要是將網絡輸出結果的誤差和梯度反向傳遞，從而采用梯度下降法進行權重更新。所以其實我們需要的只是每個權重的梯度，完全可以不采用BP，直接對每個權重計算下梯度就可以了，但是這樣會有很多冗余的計算過程，而采用BP，一層一層的反向傳播梯度，就能避免這些冗余的計算，加速網絡訓練，這應該就是BP最重要的地方了。

如下面的計算圖，若要分別計算a，b的梯度。

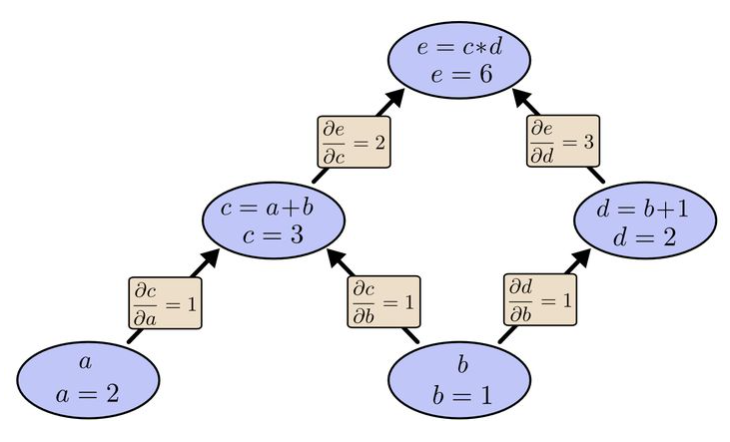
直接計算梯度

先計算a的梯度， 根據鏈式法則：

再計算b的梯度，根據鏈式法則：

很明顯，\(\frac{\partial e}{\partial c}\)計算了兩遍，是一個冗余的計算過程。

采用BP逐層計算梯度

BP是一層一層的反向計算，先計算e對c，d的梯度\(\frac{\partial e}{\partial c}，\frac{\partial e}{\partial d}\)，并將梯度信息\(\frac{\partial e}{\partial c}，\frac{\partial e}{\partial d}\)存儲在c，d兩個節點, 即：

再計算c，d對a，b的梯度，同時將梯度存儲在a，b節點，即：

對比上述兩個過程，很明顯BP能節省計算量。經常刷算法題的同學，應該能感受到BP就是一個動態規劃的過程，中間存儲梯度就類似于dp數組值。

2.pytorch中反向傳播

pytorch中的autograd模塊實現了自動的反向傳播，示例代碼如下：

import torch
from torch import nn

def show_param(net):
    # print(list(net.parameters()))
    for index, param in enumerate(net.parameters()):
        print("第{}層結點權重參數".format(index+1), param.data)  # 打印權重參數
        print("第{}層結點梯度".format(index+1), param.grad)  # 打印梯度值

# 搭建網絡
net = nn.Sequential(
    nn.Linear(4, 3, bias=False),  # 不采用bias
    nn.ReLU(),
    nn.Linear(3, 3, bias=False),
    nn.ReLU(),
    nn.Linear(3, 2, bias=False),
)
# 初始化網絡
for m in net.modules():
    if isinstance(m, nn.Linear):
        nn.init.normal_(m.weight, mean=0, std=1e-3)
        # nn.init.constant_(m.bias, 0)

criterion = nn.CrossEntropyLoss()  # 交叉熵損失函數
lr = 0.01    # 學習速率

input = torch.randn((2, 4), requires_grad=True)  # 輸入數據， shape為(2, 4)
label = torch.empty(2, dtype=torch.long).random_(2)  # 輸入數據標簽（隨機賦值為0， 1, 必須是torch.long類型）
# print(net[0](input))

# 訓練過程
for i in range(1):
    output = net(input)
    loss = criterion(output, label)
    print("********反向傳播前參數*********")
    show_param(net)
    loss.backward()  # 反向傳播，計算梯度值
    
    print("********反向傳播后參數*********")
    show_param(net)

    for param in net.parameters():  # 更新參數
        param.data.sub_(param.grad.data*lr)  # w = w-grad*lr

    print("********梯度下降后參數*********")
    show_param(net)

上面代碼中搭建了一個三層的網絡，其結構畫出來如下：

在上圖中，可以自己手動計算下權重參數的梯度，如w7，w4的梯度如下：

那么可以將下圖中圈出來的部分存儲在節點處，方便bp傳遞過程中使用：

參考： https://www.zhihu.com/question/27239198?rf=24827633

? https://zhuanlan.zhihu.com/p/25081671

? https://zhuanlan.zhihu.com/p/25416673

3. 采用Numpy實現backward

在看完pytorch中的backward的步驟后，應該能明白backward的作用了，但還是想看下backward過程中的細節問題，可以嘗試自己用numpy實現下簡單的神經網絡和backward。

下面代碼中采用numpy實現了一個簡單的神經網絡訓練和推理過程，可以看到在Network類中我們維持了三個字典， 如下：

• self.params = {} : 儲存網絡中的權重參數
• self.grads = {}: 儲存網絡中權重參數的梯度值
• self.cache = {}：緩存中間數據值，方便backward中使用

上面的self.cache = {}，就是我們一直在強調的，在bp過程中儲存的數據，方便bp過程中使用

# coding:utf-8
import numpy as np


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def sigmoid_backward(dz, x):
    z = sigmoid(x)
    return dz * z * (1 - z)


def relu(x):
    x = np.copy(x)
    x[x <= 0] = 0  # relu: max(0, x)
    return x


def relu_backward(dz, x):
    dx = np.copy(dz)
    dx[x <= 0] = 0
    return dx


def cross_entropy_loss(pred, target):
    # target: (batch_size,), pred: (batch_size, nClass)
    label = np.zeros((target.shape[0], pred.shape[1])) # one-hot encoding，編碼

    for i in range(target.shape[0]):
        label[i, target[i]] = 1

    pred_sft = np.exp(pred)/(np.sum(np.exp(pred), axis=1)[:, None])  # softmax求概率
    loss = -np.sum(np.log(pred_sft)*label)           # crossEntropy 求交叉熵損失
    grad = cross_entropy_loss_backward(pred_sft, label)     # 求交叉熵梯度，反向傳播使用
    return loss/pred.shape[0], grad                     #loss/pred.shape[0]:是為了將整個batch的loss平均后返回，方便外層調用使用，

    # 注意：求導只是求-np.sum(np.log(pred_sft)*label)這一項的梯度, 這里不需要考慮batch_zie,后面backward過程中考慮了


def cross_entropy_loss_backward(pred_softmax, one_hot_label):
    return pred_softmax - one_hot_label
    # 詳細推導過程：https://zhuanlan.zhihu.com/p/131647655


class Network(object):

    def __init__(self, net_architecture, learning_rate):
        assert len(net_architecture) > 0 and isinstance(net_architecture[0], dict), \
            print("wrong format of net_architecture:{}".format(net_architecture))
        self.params = {}  # 權值參數
        self.grads = {}  # 梯度
        self.cache = {}  # 緩存，方便backward propagation
        self.net_arch = net_architecture
        self.lr = learning_rate
        for idx, layer in enumerate(net_architecture):
            self.params["w{}".format(idx + 1)] = np.random.normal(0, pow(layer["output_dim"], -0.5),
                                                                  (
                                                                  layer["output_dim"], layer["input_dim"]))  # 初始化weight
            self.params["b{}".format(idx + 1)] = np.random.randn(layer["output_dim"], 1) * 0.1  # 初始化bias

    def train(self, data, target, batch_size, loss_func="cross_entropy_loss"):
        epoch_loss = 0
        for j in range(0, data.shape[0], batch_size):
            batch_data = data[j:j + batch_size]
            batch_target = target[j:j + batch_size]
            pred = self.forward(batch_data)         # pred: shape(batch_size, nClass)
            if loss_func == "cross_entropy_loss":
                loss, loss_grad = cross_entropy_loss(pred, batch_target)   # loss為一個batch的平均loss
                self.backward(loss_grad)
            else:
                raise Exception("Unimplemented loss func")
            self.update()
            epoch_loss += loss
        return epoch_loss*batch_size/data.shape[0]   # 一個epoch的平均loss

    def query(self, data):
        pred = self.forward(data)
        return np.argmax(pred, axis=1)   # shape(batch_size, )

    def forward_once(self, input_prev, w_cur, b_cur, activation="relu"):
        output_cur = np.dot(w_cur, input_prev) + b_cur
        if activation == "relu":
            activation_func = relu
        elif activation == "sigmoid":
            activation_func = sigmoid
        else:
            raise Exception("Unimplemented activation func")
        return activation_func(output_cur), output_cur

    def forward(self, x):
        input = x.T    # x shape : from (batch_size, input_dim) to (input_dim, batch_size)
        for idx, layer in enumerate(self.net_arch):
            w = self.params["w{}".format(idx+1)]
            b = self.params["b{}".format(idx+1)]
            output, output_cur = self.forward_once(input, w, b, activation=layer["activation_func"])

            self.cache["input{}".format(idx+1)] = input
            self.cache["output{}".format(idx+1)] = output_cur   # 儲存wx+b，未經過激活函數的值
            input = output
        return output.T   # output shape : from (output_dim, batch_size) to (batch_size, output_dim)

    def backward_once(self, dx, w_cur, b_cur, input_cur, output_cur, activation="relu"):
        n = input_cur.shape[1]  # batch_size
        if activation == "relu":
            activation_backward = relu_backward
        elif activation == "sigmoid":
            activation_backward = sigmoid_backward
        else:
            raise Exception("Unimplemented activation func")
        activation_grad = activation_backward(dx, output_cur)
        bp_grad = np.dot(w_cur.T, activation_grad)

        # 注意！！！： weight_grad: shape(5 10), 和w_cur的shape相同，但這個梯度是4組數據(batch_size=4)的梯度之和，除4表示求整個batch的平均梯度
        weight_grad = np.dot(activation_grad, input_cur.T)/n

        # 注意！！！： b_cur:shape(5, 1); activation_grad:shape(5, 4); 這里的4表示batch_size, 求和除4，相當于求整個batch的平均梯度
        bias_grad = np.sum(activation_grad, axis=1, keepdims=True)/n

        return bp_grad, weight_grad, bias_grad

    def backward(self, dy):
        bp_grad_input = dy.T  # dy shape: from (batch_size, output_dim) to (output_dim, batch_size)
        for idx, layer in reversed(list(enumerate(self.net_arch))):
            w = self.params["w{}".format(idx + 1)]
            b = self.params["b{}".format(idx + 1)]
            input = self.cache["input{}".format(idx+1)]
            output = self.cache["output{}".format(idx+1)]
            bp_grad_output, weight_grad, bias_grad = self.backward_once(bp_grad_input, w, b, input, output, activation=layer["activation_func"])
            self.grads["weight_grad{}".format(idx + 1)] = weight_grad
            self.grads["bias_grad{}".format(idx + 1)] = bias_grad
            bp_grad_input = bp_grad_output

    def update(self):  # 梯度下降，更新權重參數
        for idx, layer in enumerate(self.net_arch):
            self.params["w{}".format(idx + 1)] -= self.lr*self.grads["weight_grad{}".format(idx + 1)]
            self.params["b{}".format(idx + 1)] -= self.lr*self.grads["bias_grad{}".format(idx + 1)]


if __name__ == "__main__":
    net_architecture = [
        {"input_dim": 10, "output_dim": 20, "activation_func": "relu"},
        {"input_dim": 20, "output_dim": 10, "activation_func": "relu"},
        {"input_dim": 10, "output_dim": 5, "activation_func": "sigmoid"},
    ]

    learning_rate = 0.01
    net = Network(net_architecture, learning_rate)

    # 隨機訓練數據
    train_data = np.random.randn(100, 10)
    train_target = np.random.randint(0, 5, 100)

    # 模擬訓練train()
    epoch = 1000
    batch_size = 4
    loss_list = []
    for i in range(epoch):
        epoch_loss = net.train(train_data, train_target, batch_size, loss_func="cross_entropy_loss")
        loss_list.append(epoch_loss)
        print("[Epoch {}/{}] training loss: {:.4f}".format(i+1, epoch, epoch_loss))

    # 采用隨機測試數據，模擬evaluate
    test_data = np.random.randn(100, 10)
    test_target = np.random.randint(0, 5, 100)
    test_pred = net.query(test_data)
    print(test_target, test_pred)
    precision = np.sum(test_pred == test_target)/test_target.shape[0]
    print("Test precision: {:.4f}%".format(precision*100))

參考：https://zhuanlan.zhihu.com/p/47051157

? https://github.com/SkalskiP/ILearnDeepLearning.py

? https://zhuanlan.zhihu.com/p/131647655