一、分治法的設計思想
分治法將一個難以直接解決的大問題劃分為一些規模較小的子問題,分別求解各個子問題,再合并子問題的解得到原問題的解。
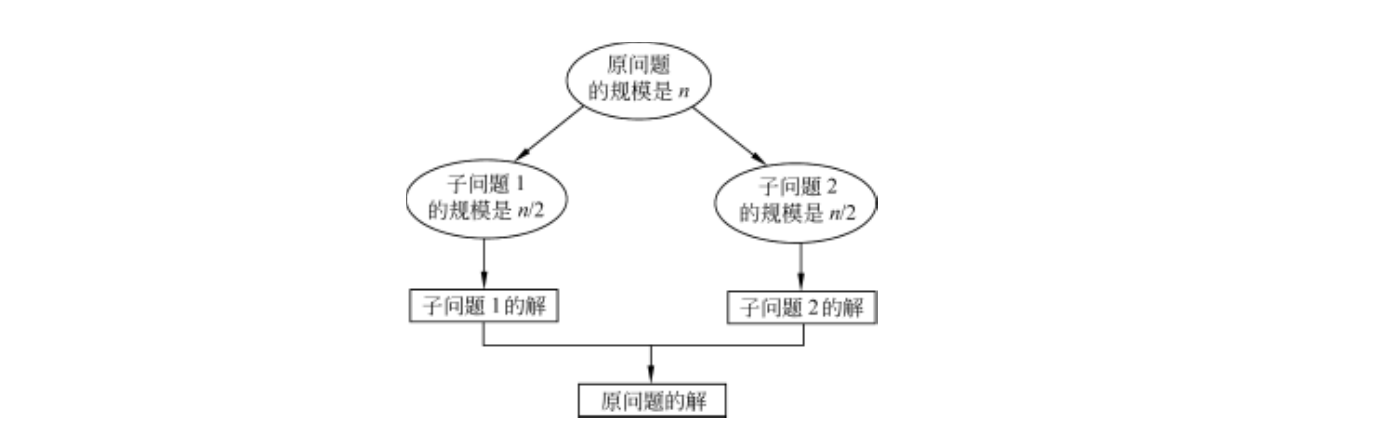
分治法的典型情況
二、分治法的求解過程
一般來說,分治法的求解過程主要由以下三個階段組成:
- 劃分:吧規模為n的原問題劃分為k個規模較小的子問題。
- 求解子問題:各子問題的解法與原問題的解法通常是相同的,可以用遞歸或者迭代的方法求解各個子問題,有時遞歸處理也可以用循環來實現。
- 合并:把各個子問題的解合并起來,合并的代價因情況不同有很大差異。分治算法的效率很大程度上依賴于合并的實現。
三、幾種典型的分治策略算法
- 歸并排序
歸并排序首先執行劃分過程,將序列劃分成2個子序列,如果子序列的長度為1,則劃分結束,否則,繼續執行劃分,直到將n個待排序的序列劃分為n個長度為1的有序子序列,然后再兩兩合并,得到?n/2?個長度為2的有序子序列,再進行兩兩合并,得到?n/4?個長度為4的有序子序列,直到得到一個長度為n的有序序列。
代碼實現
點擊查看代碼
void Merge(int r[],int r1[],int s,int m,int t)
{
int i = s,j = m + 1,k = s;
while(i <= m && j <= t)
{
if(r[i] <= r[j])
r1[k++] = r[k++];//取r[i]和r[j]中較小的放入r1[k]中
else
r1[k++] = r[j++];
}
while(i <= m)//若第一個子序列未處理完,則進行收尾處理
r1[k++] = r[i++];
while(j <= t)//若第二個子序列未處理完,則進行收尾處理
r1[k++] = r[j++];
}
void MergeSort(int r[],int s,int t)//對數組r[s]~r[t]進行歸并排序
{
int m,r1[1000];//數組r1為臨時數組,假設最多能存1000個元素
if(s==t) return;
else
{
m = (s+t)/2;//對記錄進行劃分
MergeSort(r,s,m);//求解子問題1,歸并排序前半個子序列
MergeSort(r,m+1,t);//求解子問題2,歸并排序后半個子序列
Merge(r,r1,s,m,t);//合并兩個有序子序列,將結果存到數組r1中
for(int i = s;i <= t;i++)//將有序序列傳回數組r中
r[i] = r1[i];
}
}該算法的時間復雜度為:O(nlog2n)
- 快速排序
再待排序表L[1...n]中任取一個元素pivot作為樞軸(通常取首元素),通過一趟排序將待排序表劃分成獨立的兩部分L[1...k-1]和L[k+1...n],使得L[1...k-1]中的所有元素小于pivot,L[k+1...n]中的所有元素大于等于pivot,,則pivot放在了其最終位置L[k]上,這個過程稱為一趟快速排序(一次劃分)。對兩個子表重復上述過程,直至每部分內只有一個元素或空為止。
代碼實現
點擊查看代碼
int Partition(int r[], int first,int end)//對待排序表進行劃分
{
while(first < end)
{
int i = first,j = end;
while(i < j && r[i] <= r[j]//掃描右側
j--;
if(i < j)
{
int temp = r[i];
r[i] = r[j];
r[j] = temp;
i++;
}
while(i < j && r[i] <= r[j])//掃描左側
i++;
if(j < j)
{
int temp = r[i];
r[i] = r[j];
r[j] = temp;
j--;
}
}
return i;//返回軸值記錄的位置
}
void QuickSort(int r[],int firsr,int end)
{
int pivot;
if(first < end)
{
pivot = Partition(r,first,end);//劃分,pivot是軸值再序列中的位置
QuickSort(r,first,pivot - 1);//求解子問題1,對左側子序列進行快速排序
QuickSort(r,pivot + 1,end);//求解子問題2,對右側子序列進行快速排序
}
}
該算法的時間復雜度為:O(nlog2n)



 浙公網安備 33010602011771號
浙公網安備 33010602011771號