

直接用二進(jìn)制處理,不斷對2取余,除2,如果奇數(shù),那肯定就是不行的
#include<bits/stdc++.h>
using namespace std;
const int maxn=10100;
const int INF=0x3fffffff;
typedef long long LL;
int n;
int a[maxn];
int main(){
//二進(jìn)制??
cin>>n;
int i=0;
if(n==0) {
printf("-1");
return 0;
}
while(n!=0){
a[++i]=n%2;
n/=2;
}
if(a[1]==1) printf("-1");
else {
for(int j=i;j>=1;j--){
if(a[j]) {
LL ans=pow(2,j-1);
printf("%lld ",ans);
}
}
}
return 0;
}

每個(gè)人的成績都不大于600----->桶排序,直接倒著累加,看人數(shù)有沒有達(dá)到當(dāng)前人數(shù)的w
注意細(xì)節(jié)喲,應(yīng)該是判斷有沒有大于max(1,i*w/100)這個(gè)數(shù),因?yàn)殚_始的肯定是人數(shù)很少的
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3fffffff;
typedef long long LL;
int n,w;
int t[606];
//每個(gè)選手的成績均為不超過 600600 的非負(fù)整數(shù)!!!桶排序
int main(){
scanf("%d %d",&n,&w);
int x;
for(int i=1;i<=n;i++){
cin>>x;
int summ=0;
t[x]++;
for(int j=600;j>=0;j--){
summ+=t[j];
if(summ>=max(1,i*w/100)){
printf("%d ",j);
break;
}
}
}
return 0;
}
這道題好難。。。。又是后綴表達(dá)式,看到題目肯定要反應(yīng)過來,有的值改變了對結(jié)果也沒有影響
題目里有個(gè)信息是“每個(gè)變量在表達(dá)式中出現(xiàn)恰好一次”,而每個(gè)詢問只改變一個(gè)變量的值,這對原答案來說就產(chǎn)生兩個(gè)可能:變或不變。這聽起來是一句廢話,其實(shí)蘊(yùn)含的意思是:
有些變量對整個(gè)表達(dá)式其決定作用,其改變則原答案也改變;有些變量對整個(gè)表達(dá)式根本沒用,其變不變原答案都不變。
1 & x = x ,0 | x= x ,這兩個(gè)公式里的 x 就起了決定性作用,而 0 & x = 0 ,1 | x= 1 的 x 就是一個(gè)廢物。
那我們就給樹上每個(gè)結(jié)點(diǎn)建一個(gè)廢物標(biāo)記,對& 來說,如果一棵子樹是 0,那另外一棵子樹內(nèi)所有葉結(jié)點(diǎn)都應(yīng)該打上廢物標(biāo)記,對|同理。
先計(jì)算出原表示答案ans,這樣我們在查詢的時(shí)候,沒被標(biāo)記的就說明它往上到根節(jié)點(diǎn)都不存在一種讓它變成廢物的運(yùn)算,所以答案是!ans,如果有標(biāo)記則答案依舊為ans。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<cstdlib>
#include<stack>
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7;
const int N = 1000005;
//好難啊。。。建立表達(dá)式樹,然后標(biāo)記(逆轉(zhuǎn)、無用標(biāo)記)
/*
題目里有個(gè)信息是“每個(gè)變量在表達(dá)式中出現(xiàn)恰好一次”,而每個(gè)詢問只改變一個(gè)變量的值,這對原答案來說就產(chǎn)生兩個(gè)可能:變或不變。這聽起來是一句廢話,其實(shí)蘊(yùn)含的意思是:
有些變量對整個(gè)表達(dá)式其決定作用,其改變則原答案也改變;有些變量對整個(gè)表達(dá)式根本沒用,其變不變原答案都不變。
1 & x = x ,0 | x= x ,這兩個(gè)公式里的 x 就起了決定性作用,而 0 & x = 0 ,1 | x= 1 的 x 就是一個(gè)廢物。
那我們就給樹上每個(gè)結(jié)點(diǎn)建一個(gè)廢物標(biāo)記,對& 來說,如果一棵子樹是 0,那另外一棵子樹內(nèi)所有葉結(jié)點(diǎn)都應(yīng)該打上廢物標(biāo)記,對|同理。
先計(jì)算出原表示答案ans,這樣我們在查詢的時(shí)候,沒被標(biāo)記的就說明它往上到根節(jié)點(diǎn)都不存在一種讓它變成廢物的運(yùn)算,所以答案是!ans,如果有標(biāo)記則答案依舊為ans。
*/
string s; //字符串
int a[N]; //每個(gè)值0/1
int son[N][2], ck;
int flag[N], c[N];//兩個(gè)標(biāo)記
int n, q;
int dfs(int u, int g) {
a[u] ^= g;
if (u <= n) {
return a[u];
}
int x = dfs(son[u][0], g ^ flag[son[u][0]]);
int y = dfs(son[u][1], g ^ flag[son[u][1]]);
if (a[u] == 2) {
if (x == 0) c[son[u][1]] = 1; //廢物標(biāo)記
if (y == 0) c[son[u][0]] = 1;
return x & y;
} else {
if (x == 1) c[son[u][1]] = 1;
if (y == 1) c[son[u][0]] = 1;
return x | y;
}
}
void dfs2(int u) {
if (u <= n) return;
c[son[u][0]] |= c[u];
c[son[u][1]] |= c[u];//合并廢物標(biāo)記
dfs2(son[u][0]);
dfs2(son[u][1]); //因?yàn)槿绻项^有廢物標(biāo)記,那就往下傳,下面的都是改變了對結(jié)
}
int main() {
getline(cin,s);
scanf("%d", &n);
ck = n;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
stack<int> b; //這個(gè)存放的是編號
for (int i = 0; s[i]; i += 2) { //注意是+=2
if (s[i] == 'x') {
int x = 0;
i++;
while (s[i] != ' ') {
x = x * 10 + s[i] - '0';
i++;
}
i--;//因?yàn)槭莍+=2
b.push(x);
} else if (s[i] == '&') {
int x = b.top();
b.pop();
int y = b.top();
b.pop();
b.push(++ck);
a[ck] = 2;
son[ck][0] = x;
son[ck][1] = y;
} else if (s[i] == '|') {
int x = b.top();
b.pop();
int y = b.top();
b.pop();
b.push(++ck);
a[ck] = 3;
son[ck][0] = x;
son[ck][1] = y;
} else if(s[i] == '!'){
flag[b.top()] ^= 1;
}
}
int ans = dfs(ck, flag[ck]);
dfs2(ck);
scanf("%d", &q);
while (q--) {
int x;
scanf("%d", &x);
printf("%d\n", c[x] ? ans : !ans);
}
return 0;
}
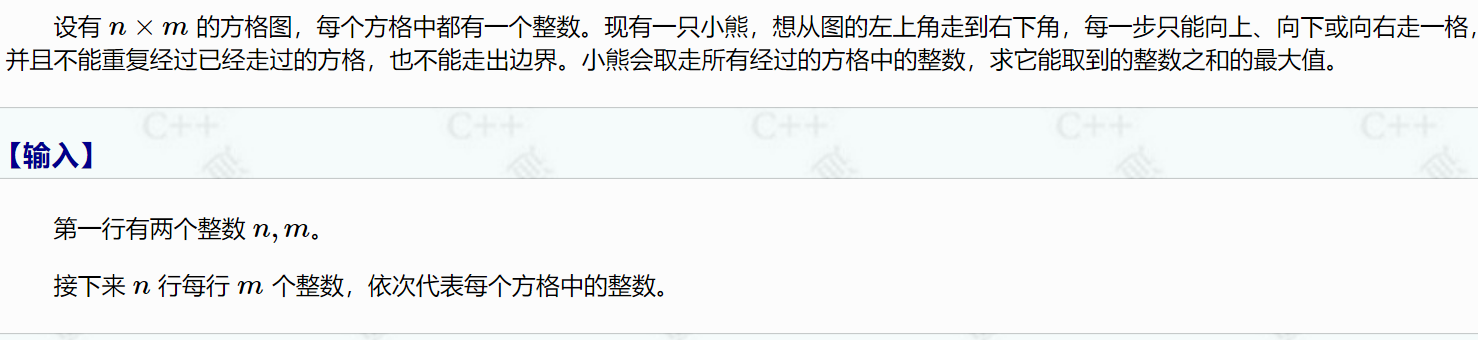
注意這里的方向有三種,而且不能走經(jīng)過的地方,所以上下下上這樣走是不行的,用dfs+記憶化搜索,從終點(diǎn)搜索到起點(diǎn)
記憶化搜索:記錄每個(gè)點(diǎn)從上來,從下來的值,如果上一步是向上,那么只能走到再上一格,或者是左邊(上下都可以
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
typedef long long LL;
const int maxn=1e3+10;
const LL INF=1e18;
typedef unsigned long long ull;
//記憶化搜索的方法,要判斷上一步是向上還是向右走的
//從終點(diǎn)搜到起點(diǎn)(注意)
//如果上一步是向上,那么只能走到再上一格,或者是左邊(上下都可以
int n,m;
int w[maxn][maxn];
LL mp[maxn][maxn][2]; //0表示從一個(gè)格子上方走到該格子的路徑最大和 1表表示從一個(gè)格子下方走到該格子的路徑最大和
LL mx(LL p,LL q,LL r){
return p > q ? (p > r ? p : r) : (q > r ? q : r);
}
LL dfs(int x,int y,int from){
if(x<1||x>n||y<1||y>m) return -INF;
if(mp[x][y][from]!=-INF) return mp[x][y][from];
if(from==0) mp[x][y][from]=mx(dfs(x+1,y,0),dfs(x,y-1,0),dfs(x,y-1,1))+w[x][y];
else mp[x][y][from]=mx(dfs(x-1,y,1),dfs(x,y-1,0),dfs(x,y-1,1))+w[x][y];
return mp[x][y][from];
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&w[i][j]);
mp[i][j][0]=mp[i][j][1]=-INF;
}
}
mp[1][1][0]=mp[1][1][1]=w[1][1];
LL ans=dfs(n,m,1);
printf("%lld",ans);
return 0;
}
另一種做法:dp,記錄從哪里來的(思路是差不多的)
#include <bits/stdc++.h>
typedef long long LL;
using namespace std;
const int maxn=1e3+10;
//dp好理解一點(diǎn)
int n,m;
int a[maxn][maxn];
LL up[maxn],down[maxn],f[maxn];
//分別表示從下面走上來到j(luò)列時(shí)的最大值和從上面走下來到j(luò)列時(shí)的最大值。
//f代表i行j列最終可取到的最大值
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) cin>>a[i][j];
f[1]=a[1][1];
//減了一維
for(int i=2;i<=n;i++) f[i]=f[i-1]+a[i][1];
for(int j=2;j<m;j++){
memset(down,0,sizeof(down));memset(up,0,sizeof(up));
down[1]=f[1]+a[1][j]; //從上面來的
up[n]=f[n]+a[n][j]; //從下面來的
for(int i=2;i<=n;i++) down[i]=max(down[i-1],f[i])+a[i][j];
for(int i=n-1;i>=1;i--) up[i]=max(up[i+1],f[i])+a[i][j];
for(int i=1;i<=n;i++) f[i]=max(down[i],up[i]);
}
f[1]+=a[1][m];
//最后一列
for(int i=2;i<=n;i++) f[i]=max(f[i],f[i-1])+a[i][m];
cout<<f[n]<<endl;
return 0;
}


 posted on
posted on

 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號