這篇文檔非常長所以我們會分成5篇來連載，因為機器學習并不是純軟件開發，簡單地調用庫函數 API，需要有一定的理論支撐，如果完全不介紹理論部分，可能就不知道為什么模型要這樣設計，模型出了問題應該怎樣改善。不過文檔如果寫太長大家可能很難有耐心看完，特別是理論部分會有很多公式，但是機器學習確實又對 理論基礎 和 編程能力 都有一些要求，相信堅持看下去還是會有很多收獲的，我也盡可能把理論和應用都介紹清楚。

前兩篇的連載會以機器學習理論為主，之后的文檔就基本是純實際應用了，不會有太多理論內容了：[ Darknet 訓練目標檢測模型 ]、[ RT-Thread 連接 ROS 小車控制 ]。

操作系統相關內容請由此入>>>>

這篇文章假定大家都已經會用 RT-Thread 的 env 工具下載軟件包，并且生成項目上傳固件到 stm32 上，因為這幾天的兩篇連載文章重點在于加載 onnx 通用機器學習模型，關于 RT-Thread 的教程大家可以在官網文檔中心：https://www.rt-thread.org/document/site/上找一找。

如果對機器學習理論比較清楚，可以直接看第二部分 Keras 訓練模型
如果對 Keras 機器學習框架也比較熟悉了，可以直接跳轉到第三部分 RT-Thread 加載 onnx 模型
如果對 RT-Thread 和 onnx 模型都很熟悉了，那我們可以一起交流下如何在嵌入式設備上高效實現機器學習算法

這篇文章假定大家都已經會用 RT-Thread 的 env 工具下載軟件包，并且生成項目上傳固件到 stm32 上，畢竟這篇文章重點在于加載 onnx 通用機器學習模型，關于 RT-Thread 的教程大家可以在官網上找一找。

首先，簡單介紹一下上面提到的各個話題的范圍 (Domain)，人工智能 (Artifitial Intelligence) 是最大的話題，如果用一張圖來說明的話：

然后機器學習 (Machine Learning) 就是這篇文檔的主題了，但是 機器學習 依舊是一個非常大的話題：

這里簡單介紹一下上面提到的三種類型：

監督學習 (Supervised Learning): 這應當是應用最多的領域了，例如人臉識別，我提前先給你大量的圖片，然后告訴你當中哪些包含了人臉，哪些不包含，你從我給的照片中總結出人臉的特征，這就是訓練過程。最后我再提供一些從來沒有見過的圖片，如果算法訓練得好的話，就能很好的區分一張圖片中是否包含人臉。所以監督學習最大的特點就是有訓練集，告訴模型什么是對的，什么是錯的。

非監督學習 (Unsupervised Learning): 例如網上購物的推薦系統，模型會對我的瀏覽記錄進行分類，然后自動向我推薦相關的商品。非監督學習最大的特點就是沒有一個標準答案，比如水杯既可以分類為日用品，也可以分類為禮品，都沒有問題。

強化學習 (Reinforcement Learnong): 強化學習應當是機器學習當中最吸引人的一個部分了，例如 Gym 上就有很多訓練電腦自己玩游戲最后拿高分的例子。強化學習主要就是通過試錯 (Action)，找到能讓自己收益最大的方法，這也是為什么很多都例子都是電腦玩游戲。

所以文檔后面介紹的都是關于 監督學習，因為手寫體識別需要有一些訓練集告訴我這些圖像實際上應該是什么數字，不過監督學習的方法也有很多，主要有分類和回歸兩大類：

分類 (Classification): 例如手寫體識別，這類問題的特點在于最后的結果是離散的，最后分類的數字只能是 0, 1, 2, 3 而不會是 1.414, 1.732 這樣的小數。

回歸 (Regression): 例如經典的房價預測，這類問題得到的結果是連續的，例如房價是會連續變化的，有無限多種可能，不像手寫體識別那樣只有 0-9 這 10 種類別。

這樣看來，接下來介紹的手寫體識別是一個 分類問題。但是做分類算法也非常多，這篇文章要介紹的是應用非常多也相對成熟的 神經網絡 (Neural Network)。

人工神經網絡 (Artifitial Neural Network):這是個比較通用的方法，可以應用在各個領域做數據擬合，但是像圖像和語音也有各自更適合的算法。

卷積神經網絡 (Convolutional Neural Network):主要應用在圖像領域，后面也會詳細介紹。

循環神經網絡 (Recurrent Neural Network):比較適用于像聲音這樣的序列輸入，因此在語言識別領域應用比較多。

最后總結一下，這篇文檔介紹的是人工智能下面發展比較快的機器學習分支，然后解決的是機器學習監督學習下面的分類問題，用的是神經網絡里的卷積神經網絡 (CNN) 方法。

1 神經網絡相關理論

這一部分主要介紹神經網絡的整個運行流程，怎么準備訓練集，什么是訓練，為什么要訓練，怎么進行訓練，以及訓練之后得到了什么。

1.1 線性回歸 (Linear Regression)

1.1.1 回歸模型

要做機器學習訓練預測，我們首先得知道自己訓練的模型是什么樣的，還是以最經典的線性回歸模型為例，后面的人工神經網絡 (ANN) 其實可以看做多個線性回歸組合。那么什么是線性回歸模型呢？

比如下面圖上這些散點，希望能找到一條直線進行擬合，線性回歸擬合的模型就是

$y = k x + b$

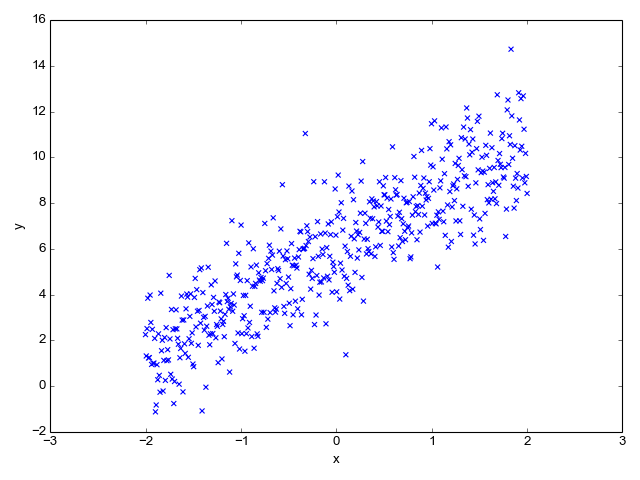
這樣如果以后有一個點 x = 3，不在圖上這些點覆蓋的區域，我們也可以通過訓練好的線性回歸模型預測出對應的 y。

不過上面的公式通常使用另外一種表示方法，最終的預測值也就是 y 通常用 $h_{θ}$

h θ = θ 0 + θ 1 x 1

所以 $θ_{0}$

h θ = θ 0 x 0 + θ 1 x 1 = [θ 0 θ 1] [x 0 x 1] =

這就是線性回歸的模型了，只要會向量乘法，上面的公式計算起來還是挺輕松的。

順便一提， $θ$

h θ = θ T x

1.1.2 評價指標

為了讓上面的模型能夠很好的擬合這些散點，我們的目標就是改變模型參數 $θ_{0}$

可以看到，一開始是一條幾乎水平的直線，但是慢慢地它的斜率和截距就移動到一個比較好的位置，那么問題來了，我們要怎么評價這條直線當前的位置滿不滿足我們的需求呢？

一個很直接的想法就是求出所有散點實際值 y 和我們模型的測試值 $h_{θ}$

J (θ) = 1 2 m \sum i = 1 m ( h θ ( x i ) ? y i ) 2

函數右邊之所以除以了2是為了求倒數的時候更加方便，因為如果右邊的公式求導，上面的平方就會得到一個2，剛好和分母里的2抵消了。

這樣我們就有了評價指標了，損失函數計算出來的值越小越好，這樣就知道當前的模型是不時能很好地滿足需求，下一步就是告訴模型該如何往更好的方向優化了，這就是訓練 (Training) 過程。

1.1.3 模型訓練

為了讓模型的參數 $θ$

那么什么是"下坡"的方向呢？其實就是導數的方向，從上面的動畫也可以看出來，黑點一直是沿著切線方向逐漸走到最低點的，如果我們對損失函數求導，也就是對 $J (θ)$

J (θ)' = 1 m x θ ( h ? y )

我們現在知道 $θ$

θ = θ ? α 1 m ( x T ( h ? y ) )

這種訓練方法就是很有名的 梯度下降法(Gradient Descent)，當然現在也有很多改進的訓練方法例如 Adam，其實原理都差不多，這里就不做過多的介紹了。

1.1.4 總結

機器學習的流程總結出來就是，我們先要設計一個模型，然后定義一個評價指標稱之為損失函數，這樣我們就知道怎么去判斷模型的好壞，接下來就是用一種訓練方法，讓模型參數能朝著能讓損失函數減少的方向運動，當損失函數幾乎不再減少的時候，我們就可以認為訓練結束了。最終訓練得到的就是模型的參數，使用訓練好的模型我們就可以對其他的數據進行預測了。

順便一提，上面的線性回歸其實是有標準理論解的，也就是說不需要通過訓練過程，一步得到最優權值，我們稱之為 Normal Equation：

θ = (X T X) ? 1 X T y

那么，明明有一步到位的理論解，我們為什么還需要一步一步的訓練呢？因為上面的公式里有矩陣的逆運算，當矩陣規模比較小時，對矩陣求逆運算量并不大，但是一旦矩陣的規模提升上去，用現有的計算能力求逆是幾乎不可能了，所以這個時候就需要用梯度下降這樣的訓練方法一步一步的逼近最優解。

1.2 非線性回歸 (Logistic Regression)

我們回到手寫體識別的例子，上面介紹的線性回歸最后得到的是一個連續的數值，但是手寫體識別最后的目標是得到一個離散的數值，也就是 0-9，那么這要怎么做到呢？

h θ = θ T x

這個就是上一部分的模型，其實很簡單，只需要在最后的結果再加一個 sigmoid 函數，把最終得到的結果限制在 0-1 就可以了。

就像上面圖中的公式那樣，sigmoid 函數就是：

g (t) = 1 1 + e ? t

如果把它應用到線性回歸的模型，我們就得到了一個非線性回歸模型，也就是 Logistic Regression：

h θ = g (θ T x)

這樣就可以確保我們最后得到的結果肯定是在 0-1 之間了，然后我們可以定義如果最后的結果大于 0.5 就是 1，小于 0.5 就是 0，這樣一個連續的輸出就被離散了。

1.3 人工神經網絡 (ANN)

現在我們介紹了連續的線性回歸模型 Linear Regression，和離散的非線性回歸模型 Logistic Regression，模型都非常簡單，寫在紙上也就不過幾厘米的長度。那么這么簡單的模型到底是怎么組合成非常好用的神經網絡的呢？

其實上面的模型可以看做是只有一層的神經網絡，我們輸入 $x$

h θ = g (θ T x)

如果我們不那么快得到計算結果，而是在中間再插入一層呢？就得到了有一層隱藏層的神經網絡了。

上面這張圖里，我們用 $a$

另外，我們用帶括號的上標代表神經網絡的層數。例如 $a^{(1)}$

于是，我們可以總結一下上面的神經網絡結構：

輸入層： $a^{(1)} = x$
隱藏層： $a^{(2)} = g (θ^{(1)} a^{(1)})$
輸出層： $h (θ) = g (θ^{(2)} a^{(2)})$

如果我們設置最后的輸出層節點是 10 個，那就剛好可以用來表示 0-9 這 10 個數字了。

如果我們再多增加幾個隱藏層，是不是看起來就有點像是互相連接的神經元了？

如果我們再深入一點 Go Deeper (論文里作者提到，他做深度學習的靈感其實源自于盜夢空間)

這樣我們就得到一個深度神經網絡了：

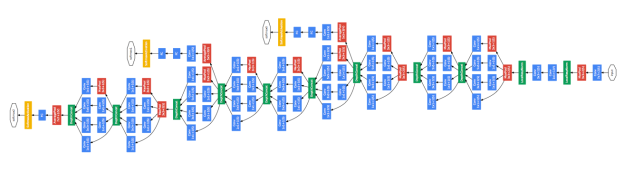
如果你想知道，具體應當選多少層隱藏層，每個隱藏層應該選幾個節點，這就跟你從哪里來，要到哪里去一樣，是神經網絡的終極問題了 ??

最后，神經網絡的訓練方法是用的 反向傳播 (Back Propagation)，如果感興趣可以在這里找到更加詳細的介紹。

1.4 卷積神經網絡 (CNN)

終于到了后面會用到的卷積神經網絡了，從前面的介紹可以看到，其實神經網絡的模型非常簡單，用到的數學知識也不多，只需要知道矩陣乘法，函數求導就可以了，而深度神經網絡只不過是反復地進行矩陣乘法和激活函數的運算：

h θ = g (θ T x)

這樣重復相同的運算顯得有些單調了，下面要介紹的卷積神經網絡就引入了更多更有意思的操作，主要有：

Cov2D
Maxpooling
Relu
Dropout
Flatten
Dense
Softmax

接下來就對這些算子逐一介紹。

1.4.1 Conv2D

首先圖像領域的神經網絡最大的特點就是引入了卷積操作，雖然這個名字看起來有點神秘，其實卷積運算非常簡單。

這里說明一下為什么要引入卷積運算，盡管前面的矩陣乘法其實已經可以解決很多問題了，但是一旦到了圖像領域，對一個 1920*1080 的圖像做乘法，就是一個 [1, 2,073,600] 的矩陣了，這個運算量已經不算小了，而用卷積操作，計算量就會大大縮減；另一方面，如果把一個二維的圖像壓縮成一個一維的向量，其實就丟失了像素點在上下左右方向相互關聯的信息，例如一個像素點和周圍的顏色通常比較相近，這些信息很多時候是很重要的圖像信息。

介紹完了卷積操作的優勢，那么到底什么是卷積運算呢？其實卷積就是簡單的加減乘除，我們需要一幅圖像，然后是一個卷積核 (Kernel)：

上面這張圖像經過一個 3x3 的卷積核操作，就很好地把圖像的邊緣提取出來了，下面這個動畫就很清晰地介紹了矩陣運算：

上面動畫用到的卷積核是一個 3x3 的矩陣：

??? 1 0 1 0 1 0 1 0 1 ???

如果我們把動畫暫停一下：

可以看到卷積操作實際上就是把卷積核在圖像上按照行列掃描一遍，把對應位置的數字相乘，然后求和，例如上面的左上角的卷積結果 4 是這么計算得到的 (這里用 $*$

??? 1 0 0 1 1 0 1 1 1 ??? (圖 像) ? (卷 積

= ??? 1 \times 1 0 \times 0 0 \times 1 1 \times 0 1 \times 1 0 \times 0 1 \times 1 1 \times 01

= ??? 1 0 0 0 1 0 1 0 1 ??? = 1 + 1 + 1 + 1 = 4

當然上面的計算過程用等號連接是不嚴謹的，不過可以方便地說明卷積的計算過程。可以看到，卷積的計算量相比全連接的神經網絡是非常小的，而且保留了圖像在二維空間的關聯性，所以在圖像領域應用地非常多。

卷積操作非常好用，但是卷積后圖像大小變小了，例如上面的 5x5 矩陣經過一個 3x3 的卷積核運算最后得到的是一個 3x3 的矩陣，所以有的時候為了保持圖像大小不變，會在圖像周圍一圈用 0 填充，這個操作稱之為 padding。

但是 padding 也沒有辦法完全保證圖像大小不變，因為上面動畫的卷積核每次都只向一個方向運動一格，如果每次運動 2 格，那么 5x5 的圖像經過 3x3 的卷積就成了 2x2 的矩陣了，卷積核每次移動的步數我們稱之為 stride。

下面是一幅圖像經過卷積運算后得到的圖像大小計算公式：

o u t p u t = W ? F + 2 P S + 1

比如上面圖像寬度 W = 5，卷積核大小 F = 3，沒有使用 padding 所以 P = 0，每次移動步數 S = 1：

o u t p u t = 5 ? 3 + 2 \times 0 1 + 1 = 3

這里說明一下，上面的計算都是針對一個卷積核而言的，實際上一層卷積層可能有多個卷積核，而且實際上很多 CNN 模型也是卷積核隨著層數往后，越來越多的。

1.4.2 Maxpooling

上面提到卷積可以通過 padding 保持圖像大小不變，但是很多時候我們希望能隨著模型的推進，逐漸減小圖像大小，因為最后的輸出例如手寫體識別，實際上只有 0-9 這 10 個數字，但是圖像的輸入卻是 1920x1080，所以 maxpooling 就是為了減少圖像尺寸的。

其實這個計算比卷積要簡單多了：

比如左邊 4x4 的輸入，經過 2x2 的 maxpooling，其實就是把左上角 2x2 的方塊取最大值：

max ([1 5 1 6]) = max (1, 1, 5, 6) = 6

所以這樣一個 4x4 的矩陣經過 2x2 的 maxpooling 一下尺寸就縮小了一半，這也就是 maxpooling 的目的了

1.4.3 Relu

之前介紹 sigmoid 函數的時候，提到過它是激活函數的一種，而 Relu 就是另一種在圖像領域更為常用的激活函數， Relu 相比 sigmoid 就非常簡單了：

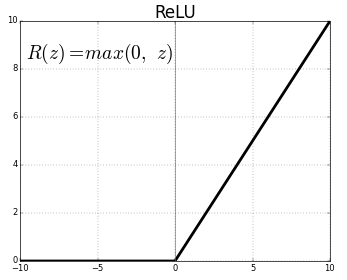
其實就是當數字小于0的時候取0，大于0的時候保持不變。

就這么簡單。

1.4.4 Dropout

到這里一共介紹了3個算子，conv2d， maxpooling，relu，每一個的運算都非常簡單，但是 Dropout 甚至更簡單，連計算都沒有，于是在這個部分一個公式都沒有。

之前沒有提到模型過擬合的問題，因為神經網絡模型在訓練過程中，很有可能出現模型對自己提供的訓練集擬合非常好，但是一旦碰到沒有見過的數據，就完全預測不出正確的結果了，這種時候就是出現了過擬合。

那么，怎么解決過擬合問題呢？Dropout 就是一種非常簡單粗暴的方法，從已經訓練好的參數當中，隨機挑一些出來丟棄掉重置為 0，這也是為什么它的名字叫 Dropout，就是隨機丟掉一些參數。

這是個簡單到不可思議的方法，但是卻意外地好用，例如僅僅是在 maxpooling 后隨機丟棄掉 60% 訓練好的參數，就可以很好地解決過擬合問題。

1.4.5 Flatten

依舊是卷積神經網絡的簡單風格，這里也不會有公式。

Flatten 就是像字面意思那樣，把一個2維的矩陣壓平，比如這樣一個矩陣：

[1 5 1 6] \to [1 1 5 6]

就是這么簡單。。。

1.4.6 Dense

Dense 其實前面已經介紹過了，就是矩陣的乘法，然后加法：

Y = W T X

所以卷積部分其實確實不需要知道太多的數學運算。

1.4.7 Softmax

這一個就是最后一個算子了，比如我們要做手寫體識別，那么最后的輸出就會是 0-9，這將是一個 1x10 的矩陣，例如下面的預測結果 (實際上是一行，為了方便顯示寫成兩行了)：

[0.001 0.002 0.000 0.000 0.017 0.753 0.028 0.027 0.001 0.172]

上面的 1x10 的矩陣可以看到第 7 個數 0.753 遠遠大于其他幾個數 (下標我們從 0 開始)，所以我們可以知道當前預測結果是 7。 所以 softmax 會作為模型的輸出層輸出 10 個數字，每個數字分別代表圖片是 0-9 的概率，我們取最大的一個概率就是預測結果了。

另一方面，上面 10 個數相加剛好是 1，所以其實每個數就代表一個概率，模型認為這個數是1個概率是 0.000498，是 2 的概率是 0.000027，以此類推，這么直觀方便的結果就是用 softmax 計算得到的。

s o f t m a x = e i \sum j e j

比如有兩個數 [1, 2] 經過 softmax 運算：

s (1) = e 1 e 1 + e 2 = 2.72 2.72 + 7.39 = 0.27

s (2) = e 2 e 1 + e 2 = 7.39 2.72 + 7.39 = 0.73

最后得到的兩個數字就是 [0.269, 0.731]。

到這里第一部分卷積神經網絡相關的算子就終于介紹完了，第二部分部分就會介紹實際如何用 Keras (Tensorflow) 機器學框架訓練一個手寫體識別模型，最后第三部分就是介紹如何利用把生成的模型導入到 stm32 上面運行。

2 訓練卷積神經網絡模型

這里會介紹如何訓練圖像領域應用非常廣的卷積神經網絡 (Convolutional Neural Network)

這一部分應當不會涉及到很多理論了，其實用 Keras 訓練模型寫起代碼來非常簡單，如果發現不太清楚代碼為什么要這么寫，可以看看上一部分對應的算子。

2.1 MNIST 手寫體訓練集

首先我們需要介紹一下訓練集，畢竟在訓練之前我們得先看看訓練集長什么樣子。

這就是手寫體識別數據庫的官網了，風格比較跨世紀：

這個圖上就是全球各地大家用不同方法做手寫體識別得到的準確率匯總，可以看到我用紅圈畫出來的部分，用前面介紹的 Logistic Regression (Linear Classifier) 做手寫體識別效果是最差的，所以我們之后要使用的是卷積神經網絡 CNN (之后我就都用 CNN 簡寫了)。

在網站的下面給出了訓練集的二進制格式定義：

當然，這是指自己從網站下載原始訓練集，從當中提取圖片才需要了解的，我們使用 tensorflow 不需要自己解析數據集。

2.2 開發環境搭建

首先介紹一下機器學習的開發環境，現在主流開發環境都是 Python，但是我們也不是一個裸 Python 打開記事本就直接開始寫代碼了，實際上數據科學家用的最多的開發環境是 Anaconda，里面集成了 Python 和 R 開發環境。

我們從官網下載 Anaconda 安裝包 https://www.anaconda.com/distribution/ 根據自己的操作系統選擇就可以了，因為安裝過程基本就是單純地下一步、下一步，所以這里就不介紹了。

安裝好之后，我們打開 Anaconda Prompt：

Anaconda 其實是有圖形界面的，叫 Anaconda Navigator，但是這里以控制臺為主，因為圖形界面其實用起來反而比較麻煩，因為控制臺一行命令就解決了更加快速方便。

然后我們輸入：

# 如果你是用的 CPU
conda create -n tensorflow-cpu tensorflow

# 如果你是用的 GPU (NVIDIA 顯卡會自動安裝顯卡驅動，CUDA，cudnn，簡直方便)
conda create -n tensorflow-gpu tensorflow-gpu

這樣開發環境就搭好了，我們激活一下當前的開發環境：

# 如果你是用的 CPU
conda activate tensorflow-cpu

# 如果你是用的 GPU 
conda activate tensorflow-gpu

這里激活開發環境是指，在 Anaconda 下我們可以有多個開發環境，比如如果你想對比一下 CPU 和 GPU 計算速度的差距，可以同時安裝 2 個開發環境，然后根據需要切換到 CPU 開發環境，或者 GPU 開發環境，非常方便。如果不用 Anaconda 而是一個 Python 裸奔的話，要么使用 VirtualEnv，要么就只能反復安裝卸載不同的開發環境了。

接下來就可以啟動我們寫代碼的位置了：

# 這里的軟件包 anaconda 可能已經都裝好了，以防萬一再確認一遍
pip install numpy scipy sklearn pandas pillow matplotlib keras onnx jupyter -i https://pypi.tuna.tsinghua.edu.cn/simple

# 啟動編輯器
jupyter notebook

這樣就會自動打開瀏覽器，看到我們的開發環境了，在這里新建一個 notebook：

可以把它重命名為 mnist-keras：

接下來就可以開始訓練模型了。

2.3 Keras 訓練模型

2.3.1 導入庫函數

我們首先導入需要的庫函數，在 In[1] 后面的方框內寫入代碼：

#coding:utf-8
from tensorflow.examples.tutorials.mnist import input_data

import numpy as np
np.set_printoptions(suppress=True)

import matplotlib.pyplot as plt
%matplotlib inline

這些代碼寫進去之后就是這個樣子，后面我就不一一截圖了。

如果你對上面 導入庫 這一個注釋比較感興趣，可以在一個把光標移到到一個輸入框，按下 Esc 再按下 m，這個輸入框就從 代碼段 變成 注釋段 了，Anaconda 也是代碼、注釋、輸出可以同時保存所以用起來體驗非常好。更多的快捷鍵可以在菜單欄的 Help --> Keyboard Shortcuts 找到。

把光標移動到剛剛輸入的代碼塊，按下鍵盤的 Shift + Enter 就自動執行了，并且會自動在下面增加一行代碼輸入框，導入庫根據電腦的配置可能需要一些時間，耐心等待一下。

2.3.2 下載 MNIST 訓練集

在代碼塊輸入一行代碼：

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) #MNIST數據輸入

這樣就會自動下載數據集了，國內可能下載速度比較慢，可以從這個地址下載 MNIST數據集然后解壓到 Anaconda Prompt 啟動 Jupyter Notebook 的位置就不用等它慢慢下載了，默認是 C:/Users/你的用戶名/

2.3.3 看一看 MNIST 數據

我們把下載下來的數據集分成訓練集和測試集，訓練集用來訓練模型，測試集用來檢測最后模型預測的正確率：

X_train = mnist.train.images
y_train = mnist.train.labels
X_test = mnist.test.images
y_test = mnist.test.labels

# 輸入圖像大小是 28x28 大小
X_train = X_train.reshape([-1, 28, 28, 1])
X_test = X_test.reshape([-1, 28, 28, 1])

如果比較好奇這是一個怎樣的圖片，可以看看它長什么樣子，比如我們看看訓練集的第一張圖片

plt.imshow(X_train[0].reshape((28, 28)), cmap='gray')

也可以看看第二張圖片：

plt.imshow(X_train[1].reshape((28, 28)), cmap='gray')

下面就正式開始建立訓練模型了。

2.3.4 構建模型

同樣先導入一下 Keras 庫：

# Importing the Keras libraries and packages
# Importing the Keras libraries and packages
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Dropout
from keras.layers import Flatten

接下來就可以建模了，可以看到這里的模型和上一部分介紹的 CNN 算子是一模一樣的，熟悉的 conv2d, maxpooling, dropout, flatten, dense, softmax, adam, 如果忘了它們是什么意思，隨時可以切換到上一個部分回憶一下。

def build_classifier():

    classifier = Sequential()

    # 第一層 Conv2D，激活函數 Relu
    classifier.add(Conv2D(filters = 2, kernel_size = 3, strides = 1, padding = "SAME", activation = "relu", input_shape = (28, 28, 1)))
 
    # 第二層 Maxpooling, 使用保持圖像大小的 padding
    classifier.add(MaxPooling2D(pool_size=(2, 2),  padding='SAME'))

    # 第三層 Dropout
    classifier.add(Dropout(0.5))

    # 第四層 Conv2D，激活函數 Relu
    classifier.add(Conv2D(filters = 2, kernel_size = 3, strides = 1, padding = "SAME", activation = "relu"))

    # 第五層 Maxpoling，使用保持圖像大小的 padding
    classifier.add(MaxPooling2D(pool_size=(2, 2),  padding='SAME'))

    # 第六層 Dropout
    classifier.add(Dropout(0.5))

    # 第七層 Flatten
    classifier.add(Flatten())

    # 第八層 Dense
    classifier.add(Dense(kernel_initializer="uniform", units = 4))

    # 第九層 softmax 輸出
    classifier.add(Dense(kernel_initializer="uniform", units = 10, activation="softmax"))
    
    #  使用 adam 訓練
    classifier.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics=['accuracy'])

    return classifier

這樣模型就建完了。

代碼真的就是一層只要一行，但是一定要知道自己的模型為什么要這么建，比如為什么 maxpooling 要放在 con2d 之后，為什么要加 dropout，最后的 softmax 到底是在干什么，可不可以不要？

我們可以看看自己建立的模型長什么樣：

classifier = build_classifier()
classifier.summary()

可以看到確實是和上一部分的理論是一一對應的。

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 28, 28, 2)         20        
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 2)         0         
_________________________________________________________________
dropout_1 (Dropout)          (None, 14, 14, 2)         0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 14, 14, 2)         38        
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 7, 7, 2)           0         
_________________________________________________________________
dropout_2 (Dropout)          (None, 7, 7, 2)           0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 98)                0         
_________________________________________________________________
dense_1 (Dense)              (None, 4)                 396       
_________________________________________________________________
dense_2 (Dense)              (None, 10)                50        
=================================================================
Total params: 504
Trainable params: 504
Non-trainable params: 0
_________________________________________________________________

2.3.5 訓練模型

接下來我們就可以開始訓練模型了：

from keras.callbacks import ModelCheckpoint
checkpointer = ModelCheckpoint(filepath='minions.hdf5', verbose=1, save_best_only=True, monitor='val_loss',mode='min')

history = classifier.fit(X_train, y_train, epochs = 50, batch_size = 50, validation_data=(X_test, y_test), callbacks=[checkpointer])

這個模型非常小，不過我用 CPU 訓練才迭代 50 步，也差不多花了 10 分鐘，所以 能用 GPU 我們是堅決不用 CPU 的。

我們可以看看剛剛的訓練過程：

def plot_history(history) :
    SMALL_SIZE = 20
    MEDIUM_SIZE = 22
    BIGGER_SIZE = 24

    plt.rc('font', size=SMALL_SIZE)          # controls default text sizes
    plt.rc('axes', titlesize=SMALL_SIZE)     # fontsize of the axes title
    plt.rc('axes', labelsize=MEDIUM_SIZE)    # fontsize of the x and y labels
    plt.rc('xtick', labelsize=SMALL_SIZE)    # fontsize of the tick labels
    plt.rc('ytick', labelsize=SMALL_SIZE)    # fontsize of the tick labels
    plt.rc('legend', fontsize=SMALL_SIZE)    # legend fontsize
    plt.rc('figure', titlesize=BIGGER_SIZE)  # fontsize of the figure title

    fig = plt.figure()
    fig.set_size_inches(15,10)
    plt.plot(history['loss'])
    plt.plot(history['val_loss'])
    plt.title('Model Loss')
    plt.xlabel('epoch')
    plt.ylabel('loss')
    plt.legend(['train', 'test'],loc='upper left')
    plt.show()

用圖片顯示一下訓練過程：

plot_history(history.history)

可以看到，模型在訓練集和測試集的 cost function 計算出來的 loss 都在減小，很神奇的是模型在測試集上的表現竟然比訓練集還要好，不過模型精度不算太高才 60% 多一點的準確率，大家可以試著優化一下，在嘗試改進模型的過程中，就會加深對模型的理解，如果我在這里直接就給出一個表現非常好的模型，可能對大家幫助反而不是那么大。

2.4 保存模型為 onnx

我們可以把模型保存為原生的 Keras 模型：

classifier.save("mnist.h5")

當然，為了在 stm32 上面加載，我們更想保存為通用機器學習模型 onnx 的格式：

import onnx
import keras2onnx

onnx_model = keras2onnx.convert_keras(classifier, 'mnist')
onnx.save_model(onnx_model, 'mnist.onnx')

這樣在 Anaconda Prompt 默認目錄下 C:/Users/你的用戶名 可以看到 mnist.h5 和 mnist.onnx 兩個文件，這就是訓練好的模型。

這樣我們模型也訓練好了，也保存好了，下一步就是怎么使用訓練好的模型了。

(大家可以試試把 Dropout 的概率從 0.5 改為 0.3，訓練集準確度就會從 60% 提升到 80%，測試集則有 90% 以上，為什么呢？??)

2.5 參考文獻

MNIST 訓練集
Anaconda GPU 環境

3 運行卷積神經網絡模型

這一部分會介紹模型訓練好之后要如何使用，也就是模型的推斷過程 (Inference)

3.1 python 導入模型并運行

我們先用 python 加載模型，看看用剛剛訓練好的模型能不能進行很好的預測，下面的代碼就是導入了剛剛訓練完保存的 mnist.onnx 模型。

import onnxruntime as rt
sess = rt.InferenceSession("mnist.onnx")

為了運行模型，我們需要先得到模型的輸出和輸入層，輸出層上一部分提到了，應當是 softmax：

input_name = sess.get_inputs()[0].name
output_name = sess.get_outputs()[0].name

接下來就是用測試集對模型進行預測了：

res = np.array(sess.run([output_name], {input_name: X_test}))

我們可以看看模型的測試集是個什么數字，然后看看模型計算得到了什么結果：

plt.imshow(X_test[0].reshape((28, 28)), cmap='gray')
print(res[0][0])

可以看到模型最后一層 softmax 輸出了 10 個數字，其中第 7 個數字 0.99688894 (下標從 0 開始) 明顯遠大于其他的數，這說明這張圖片里的數字是 7 的概率是 99% 以上，這張圖片也確實就是 7。

這樣看來，剛剛訓練得到的模型還是可以正常預測的，當然，并不能保證有 100% 的正確率，如果大家感興趣也可以改變一下上面代碼里 X_test[0] 的序號，看看其他的測試集預測效果怎么樣

到這里為止，我們就不需要在 Anaconda 的 Jupyter Notebook 里寫任何 Python 代碼了，完整的代碼可以在這里看到。

https://github.com/wuhanstudio/onnx-backend/blob/master/examples/model/mnist-keras.ipynb

3.2 Google Protobuf

3.2.1 Protobuf 簡介

從這里開始，我們的目的就是在 stm32 上面加載訓練好的 onnx 模型了，那么為什么這里突然提到 Google Protobuf 呢？因為 onnx 的模型結構是用 Google Protobuf 的格式保存的。

之前我們提到，模型訓練的目的就是為了得到變量的權值，只不過是純數字罷了，但是我們也不能就這樣把這些數字一個一個地寫入文件，因為在要保存的模型文件里，不光要保存權值，也要告訴之后用這個模型的人，模型結構是怎么樣的，所以需要合理地設計保存文件的格式。不同的機器學習框架都有自己的模型保存格式，例如 Keras 的模型格式是 h5，而 Tensorflow 和 onnx 的保存格式就是 protobuf。

那么到底什么是 protobuf? 為什么 protobuf 這么受歡迎？

其實 protobuf 使用起來非常簡單方便，就是自己先定義一個數據保存格式，然后用 protoc 自動生成各個語言的解析代碼，現在支持 C, C++, C#, Java, Javascript, Objective-C, PHP, Python, Ruby。

舉個例子，我們創建這么個文件 amessage.proto

syntax = "proto3";

message AMessage {
  int32 a=1; 
  int32 b=2;
}

那么我們就定義了一種二進制的數據存儲格式，里面包含 2 個數字，其中 a = 1，代表 id 為 1 的數據是個 int32 類型，它的名字是 a，并不是代表 a 這個變量數值是 1，同樣的道理，id 為 2 的數據是個 int32 類型，它的名字是 b。這里 id 是不能重復的。

所以使用 protobuf 需要先定義一個數據格式，然后自動生成編碼和解碼的代碼，供不同語言使用，因為能自動生成代碼，所以 protobuf 簡單好用，非常受歡迎，建議大家使用 protov3。

3.2.2 RT-Thread 使用 Protobuf

在 RT-Thread 也是有 protobuf 的庫的，可以幫助我們用 C 語言解析和保存 protobuf 文件，畢竟我們之后要解析的 onnx 模型就是 protobuf 協議保存的。

protobuf 軟件包地址： http://packages.rt-thread.org/itemDetail.html?package=protobuf-c

雖然在文章的開頭已經假定大家熟練使用 RT-Thread 軟件包了，還是提醒一下 menuconfig 之前記得 pkgs --upgrade 一下才能看到最新的軟件包。

可以看到這個軟件包下有 2 個例程，一個直接創建一個 protobuf 格式的數據，然后直接解碼；另一個例程則是先把數據編碼保存到文件，再從二進制文件讀取數據并解碼。

關于 protobuf 這里就不做更多的介紹了，因為 onnx 的模型格式已經定義好了，我們只需要直接拿來用就可以了。

3.3 onnx 模型解析

現在我們已經有了 RT-Thread 支持的 protobuf 軟件包，下一步就是弄清楚 onnx 模型的格式到底是怎么定義的了，關于 onnx 數據格式的完整定義可以在這里看到。

onnx 數據格式定義： https://github.com/onnx/onnx/blob/master/onnx/onnx.proto3

為了幫助我們更加直觀的看到模型結構，這里推薦一個工具 protobuf editor，可以很方便地解析 protobuf 文件。

軟件下載下來后，按照下面的流程就可以解析之前我們生產的 mnist.onnx 文件了，圖上面提到的 onnx.proto3 文件之前提到過可以在這里下載。

然后我們就可以在彈出來的界面看到之前訓練生成的模型里到底有哪些數據了。

可以看到里面有模型的版本信息、模型結構、模型權值、模型輸入和模型輸出，這也就是我們需要的信息了。

這里大家看到的權值不一定和我完全一樣，因為每個人訓練得到的模型都是略有差異的。

3.4 RT-Thread 導入模型并運行

在介紹了神經網絡的基本理論，如何用 Python 訓練 MNIST 手寫體識別模型，以及 onnx 模型的 protobuf 文件格式后，終于到了最后一步，從 stm32 上加載這個模型并運行了。

到這里你應該準備好了：

訓練好的模型 mnist.onnx
一個帶 SD 卡的 stm32 開發板，畢竟我們要把模型保存進去才能加載

項目源碼：

RT-Thread 加載模型: https://github.com/wuhanstudio/onnx-backend
直接在上電腦上體驗: https://github.com/wuhanstudio/onnx-parser

首先，我們需要在 env 里通過 menuconfig 選中軟件包：

RT-Thread online packages → IoT - internet of things → onnx-backend

這里忍不住再提醒大家一下，記得先在 env 里：

pkgs --upgrade

可以看到這里一共有三個例程，下面就對這三個例程分別介紹，在看下面的源碼解析之前也可以直接下載代碼到板子上體驗一下，不過記得打開文件系統，并且復制模型到 SD 卡里面，如果希望得到相同的輸出，請使用 examples/mnist-sm.onnx 這個模型。

3.4.1 純手動構建模型和參數

第一個例程是純手動構建模型和參數，這樣可以幫助我們理解模型結構和參數的位置，后面自動加載權值和模型結構就顯得很自然簡單了。

既然是純手動構建模型，我們肯定得先知道模型長什么樣子，這里再推薦另外一個 onnx 模型可視化根據 netron，下面的圖就是 netron 根據我們之前訓練生成的 mnist.onnx 模型生成的，非常漂亮：

可以看到我們的模型大致是這么個流程，中間重復的層我就沒有寫 2 次了，但是我們手動建模的時候自然是要加進去的。

Conv2D -> Relu -> Maxpool -> Dense ->Softmax

這里解釋一下為什么訓練時候用到的 Dropout 這里看不到，因為 Dropout 只是為了防止過擬合，在訓練的時候隨機將訓練好的參數丟棄置 0，所以一旦模型訓練好，我們就不再需要 Dropout 操作了。

那么，接下來就要手動構建上面這個模型了。

模型的權值可以在 mnist.h 這個頭文件里看到，其實這里面的權值就是我從 Protocol Buffer Editor 里面復制過來的，大家訓練好的模型權值不一定和我完全一樣。

static const float W3[] = {-0.3233681, -0.4261553, -0.6519891, 0.79061985, -0.2210753, 0.037107922, 0.3984157, 0.22128074, 0.7975414, 0.2549885, 0.3076058, 0.62500215, -0.58958095, 0.20375429, -0.06477713, -1.566038, -0.37670124, -0.6443057};
static const float B3[] = {-0.829373, -0.14096421};

static const float W2[] = {0.0070440695, 0.23192555, 0.036849476, -0.14687373, -0.15593372, 0.0044246824, 0.27322513, -0.027562773, 0.23404223, -0.6354651, -0.55645454, -0.77057034, 0.15603222, 0.71015775, 0.23954256, 1.8201442, -0.018377468, 1.5745461, 1.7230825, -0.59662616, 1.3997843, 0.33511618, 0.56846994, 0.3797911, 0.035079807, -0.18287429, -0.032232445, 0.006910181, -0.0026898328, -0.0057844054, 0.29354542, 0.13796881, 0.3558416, 0.0022847173, 0.0025906325, -0.022641085};
static const float B2[] = {-0.11655525, -0.0036503011};

static const float W1[] = {0.15791991, -0.22649878, 0.021204736, 0.025593571, 0.008755621, -0.775102, -0.41594088, -0.12580238, -0.3963741, 0.33545518, -0.631953, -0.028754484, -0.50668705, -0.3574023, -3.7807872, -0.8261617, 0.102246165, 0.571127, -0.6256297, 0.06698781, 0.55969477, 0.25374785, -3.075965, -0.6959133, 0.2531965, 0.31739804, -0.8664238, 0.12750633, 0.83136076, 0.2666574, -2.5865922, -0.572031, 0.29743987, 0.16238026, -0.99154145, 0.077973805, 0.8913329, 0.16854058, -2.5247803, -0.5639109, 0.41671264, -0.10801031, -1.0229865, 0.2062031, 0.39889312, -0.16026731, -1.9185526, -0.48375717, 0.057339806, -1.2573057, -0.23117211, 1.051854, -0.7981992, -1.6263007, -0.26003376, -0.07649365, -0.4646075, 0.755821, 0.13187818, 0.24743222, -1.5276812, 0.1636555, -0.075465426, -0.058517877, -0.33852127, 1.3052516, 0.14443535, 0.44080895, -0.31031442, 0.15416017, 0.0053661224, -0.03175326, -0.15991405, 0.66121936, 0.0832211, 0.2651985, -0.038445678, 0.18054117, -0.0073251156, 0.054193687, -0.014296916, 0.30657783, 0.006181963, 0.22319937, 0.030315898, 0.12695274, -0.028179673, 0.11189027, 0.035358384, 0.046855893, -0.026528472, 0.26450494, 0.069981076, 0.107152134, -0.030371506, 0.09524366, 0.24802336, -0.36496836, -0.102762334, 0.49609017, 0.04002767, 0.020934932, -0.054773595, 0.05412083, -0.071876526, -1.5381132, -0.2356421, 1.5890793, -0.023087852, -0.24933836, 0.018771818, 0.08040064, 0.051946845, 0.6141782, 0.15780787, 0.12887044, -0.8691056, 1.3761537, 0.43058, 0.13476849, -0.14973496, 0.4542634, 0.13077497, 0.23117822, 0.003657386, 0.42742714, 0.23396699, 0.09209521, -0.060258932, 0.4642852, 0.10395402, 0.25047097, -0.05326261, 0.21466804, 0.11694269, 0.22402634, 0.12639907, 0.23495848, 0.12770525, 0.3324459, 0.0140223345, 0.106348366, 0.10877733, 0.30522102, 0.31412345, -0.07164018, 0.13483422, 0.45414954, 0.054698735, 0.07451815, 0.097312905, 0.27480683, 0.4866108, -0.43636885, -0.13586079, 0.5724732, 0.13595985, -0.0074526076, 0.11859829, 0.24481037, -0.37537888, -0.46877658, -0.5648533, 0.86578417, 0.3407381, -0.17214134, 0.040683553, 0.3630519, 0.089548275, -0.4989473, 0.47688767, 0.021731026, 0.2856471, 0.6174715, 0.7059148, -0.30635756, -0.5705427, -0.20692639, 0.041900065, 0.23040071, -0.1790487, -0.023751246, 0.14114629, 0.02345284, -0.64177734, -0.069909826, -0.08587972, 0.16460821, -0.53466517, -0.10163383, -0.13119817, 0.14908728, -0.63503706, -0.098961875, -0.23248474, 0.15406314, -0.48586813, -0.1904713, -0.20466608, 0.10629631, -0.5291871, -0.17358926, -0.36273107, 0.12225631, -0.38659447, -0.24787207, -0.25225234, 0.102635615, -0.14507034, -0.10110793, 0.043757595, -0.17158166, -0.031343404, -0.30139172, -0.09401665, 0.06986169, -0.54915506, 0.66843456, 0.14574362, -0.737502, 0.7700305, -0.4125441, 0.10115133, 0.05281194, 0.25467375, 0.22757779, -0.030224197, -0.0832025, -0.66385627, 0.51225215, -0.121023245, -0.3340579, -0.07505331, -0.09820366, -0.016041134, -0.03187605, -0.43589246, 0.094394326, -0.04983066, -0.0777906, -0.12822862, -0.089667186, -0.07014707, -0.010794195, -0.29095307, -0.01319235, -0.039757702, -0.023403417, -0.15530063, -0.052093383, -0.1477549, -0.07557954, -0.2686017, -0.035220042, -0.095615104, -0.015471024, -0.03906604, 0.024237331, -0.19604297, -0.19998372, -0.20302829, -0.04267139, -0.18774728, -0.045169186, -0.010131819, 0.14829905, -0.117015064, -0.4180649, -0.20680964, -0.024034742, -0.15787442, -0.055698488, -0.09037726, 0.40253848, -0.35745984, -0.786149, -0.0799551, 0.16205557, -0.14461482, -0.2749642, 0.2683253, 0.6881363, -0.064145364, 0.11361358, 0.59981894, 1.2947721, -1.2500908, 0.6082035, 0.12344158, 0.15808935, -0.17505693, 0.03425684, 0.39107767, 0.23190938, -0.7568858, 0.20042256, 0.079169095, 0.014275463, -0.12135842, 0.008516737, 0.26897284, 0.05706199, -0.52615446, 0.12489152, 0.08065737, -0.038548164, -0.08894516, 7.250979E-4, 0.28635752, -0.010820533, -0.39301336, 0.11144395, 0.06563818, -0.033744805, -0.07450528, -0.027328406, 0.3002447, 0.0029921278, -0.47954947, -0.04527057, -0.010289918, 0.039380465, -0.09236952, -0.1924659, 0.15401903, 0.21237805, -0.38984418, -0.37384143, -0.20648403, 0.29201767, -0.1299253, -0.36048025, -0.5544466, 0.45723814, -0.35266167, -0.94797707, -1.2481197, 0.88701195, 0.33620682, 0.0035414647, -0.22769359, 1.4563162, 0.54950374, 0.38396382, -0.41196275, 0.3758704, 0.17687413, 0.038129736, 0.16358295, 0.70515764, 0.055063568, 0.6445265, -0.2072113, 0.14618243, 0.10311305, 0.1971523, 0.174206, 0.36578146, -0.09782787, 0.5229244, -0.18459272, -0.0013945608, 0.08863555, 0.24184574, 0.15541393, 0.1722381, -0.10531331, 0.38215113, -0.30659106, -0.16298945, 0.11549875, 0.30750987, 0.1586183, -0.017728966, -0.050216004, 0.26232007, -1.2994286, -0.22700997, 0.108534105, 0.7447398, -0.39803517, 0.016863048, 0.10067235, -0.16355589, -0.64953077, -0.5674107, 0.017935256, 0.98968256, -1.395801, 0.44127485, 0.16644385, -0.19195901};
static const float B1[] = {1.2019119, -1.1770505, 2.1698284, -1.9615222};

static const float W[] = {0.55808353, 0.78707385, -0.040990848, -0.122510895, -0.41261443, -0.036044, 0.1691557, -0.14711425, -0.016407091, -0.28058195, 0.018765535, 0.062936015, 0.49562064, 0.33931744, -0.47547337, -0.1405672, -0.88271654, 0.18359914, 0.020887045, -0.13782434, -0.052250575, 0.67922074, -0.28022966, -0.31278887, 0.44416663, -0.26106882, -0.32219923, 1.0321393, -0.1444394, 0.5221766, 0.057590708, -0.96547794, -0.3051688, 0.16859075, -0.5320585, 0.42684716, -0.5434046, 0.014693736, 0.26795483, 0.15921915};
static const float B[] = {0.041442648, 1.461427, 0.07154641, -1.2774754, 0.80927604, -1.6933714, -0.29740578, -0.11774022, 0.3292682, 0.6596958};

接下來就是利用這些權值進行計算了，也就是把這些權值帶入到理論部分介紹的各個運算里面，其中各個算子都可以在源代碼的目錄下看到，一個算子對應一個 c 文件：

conv2d.c     maxpool.c    softmax.c    transpose.c    
matmul.c     add.c        dense.c      relu.c

這些算子的代碼如果對應理論部分的公式，就很好理解了，這里就不再重復介紹每個算子對應的含義了，在 mnist.c 里也可以看到，其實就只是輸入圖像，經過各個算子的運算，加上一些內存的釋放操作，最后就得到了 softmax 的輸出，如果我把內存部分的操作隱藏掉：

    // 1. Conv2D
    float* W3_t = transpose(W3, shapeW3, dimW3, permW3_t);
    conv2D(img[img_index], 28, 28, 1, W3, 2, 3, 3, 1, 1, 1, 1, B3, conv1, 28, 28);

    // 2. Relu
    relu(conv1, 28*28*2, relu1);

    // 3. Maxpool
    maxpool(relu1, 28, 28, 2, 2, 2, 0, 0, 2, 2, 14, 14, maxpool1);

    // 4. Conv2D
    float* W2_t = transpose(W2, shapeW2, dimW2, perm_t);
    conv2D(maxpool1, 14, 14, 2, W2_t, 2, 3, 3, 1, 1, 1, 1, B2, conv2, 14, 14);

    // 5. Relu
    relu(conv2, 14*14*2, relu2);

    // 6. Maxpool
    maxpool(relu2, 14, 14, 2, 2, 2, 0, 0, 2, 2, 7, 7, maxpool2);

    // Flatten NOT REQUIRED

    // 7. Dense
    float* W1_t = transpose(W1, shapeW1, dimW1, permW1_t);
    dense(maxpool2, W1_t, 98, 4, B1, dense1);

    // 8. Dense
    float* W_t = transpose(W, shapeW, dimW, permW_t);
    dense(dense1, W_t, 4, 10, B, dense2);

    // 9. Softmax
    softmax(dense2, 10, output);

可以看到，這些操作和前面圖片里的模型是一一對應的，所以理解了理論部分模型為什么這么建立之后，再看代碼就有一種恍然大悟的感覺，只不過相比 Python 而言, C 需要手動把權值和輸入保存的數組里，并合理地管理內存的分配和釋放。

如果我們把 mnist.c 編譯上傳到板子里，就可以看到成功地輸出了預測結果：

msh />onnx_mnist 1
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@        @@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@              @@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@                    @@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@          @@@@@@@@    @@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@        @@@@@@@@@@    @@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@  @@@@@@    @@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@  @@@@      @@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@          @@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@              @@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@            @@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@          @@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@      @@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@    @@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@    @@@@@@@@@@@@@@@@@@  @@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@    @@@@@@@@@@@@@@@@@@    @@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@  @@@@@@@@@@@@@@@@@@      @@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@    @@@@@@@@@@@@        @@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@                      @@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@                  @@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@    @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

Predictions:
0.007383 0.000000 0.057510 0.570970 0.000000 0.105505 0.000000 0.000039 0.257576 0.001016

The number is 3

由于這個模型是完全手動構建的，所以內存消耗非常少，大約在 16KB 左右，下面的例子由于需要從文件系統加載模型，所以內存消耗會增大許多。

這里需要說明的是，大家可能聽說過機器學習的模型在 MCU 上運行需要做量化 (Quantization)，而這里為了說明方便是沒有做量化的，所以當前是以浮點數進行計算，速度會比做了量化之后要慢，不過因為這個模型比較小，幾乎還是瞬間就能看到結果的。

這里可以看到跟多關于 模型量化 的介紹。

3.4.2 手動構建模型自動加載參數

之前我們是手動構建模型，并且從 Protocol Buffer Editor 里手動復制權值到 mnist.h 里面，這樣非常辛苦，所以這個例子就是會根據當前計算的模型的名稱，自動加載權值。

比如我們在 Protocol Buffer Editor 軟件里可以看到：

如果我們想計算 “dense_5” 這一層模型，那么我們需要權值 W1，接下來就會根據 “W1” 這個名字取尋找對應的權值：

所以這個例程只是多了自動尋找權值這個功能，因此我們傳入的參數只需要是模型各層的名字就可以了，如果去掉內存釋放相關的代碼，每一層的計算還是非常清晰的。

    // 2. Conv2D
    float* conv1 = conv2D_layer(model->graph, img[MNIST_TEST_IMAGE], shapeInput, shapeOutput, "conv2d_5");

    // 3. Relu
    float* relu1 = relu_layer(model->graph, conv1, shapeInput, shapeOutput, "Relu1");

    // 4. Maxpool
    float* maxpool1 = maxpool_layer(model->graph, relu1, shapeInput, shapeOutput, "max_pooling2d_5");

    // 5. Conv2D
    float* conv2 = conv2D_layer(model->graph, maxpool1, shapeInput, shapeOutput, "conv2d_6");

    // 6. Relu
    float* relu2 = relu_layer(model->graph, conv2, shapeInput, shapeOutput, "Relu");

    // 7. Maxpool
    float* maxpool2 = maxpool_layer(model->graph, relu2, shapeInput, shapeOutput, "max_pooling2d_6");

    // 8. Transpose

    // 9. Flatten

    // 10. Dense
    float* matmul1 = matmul_layer(model->graph, maxpool2, shapeInput, shapeOutput, "dense_5");

    // 11. Add
    float* dense1 = add_layer(model->graph, matmul1, shapeInput, shapeOutput, "Add1");

    // 12. Dense
    float* matmul2 = matmul_layer(model->graph, dense1, shapeInput, shapeOutput, "dense_6");

    // 13. Add
    float* dense2 = add_layer(model->graph, matmul2, shapeInput, shapeOutput, "Add");

    // 14. Softmax
    float* output = softmax_layer(model->graph, dense2, shapeInput, shapeOutput, "Softmax");

如果大家對上面這些算子的名字有些陌生了，可以再回憶一下第一部分理論介紹。

3.4.3 自動構建模型并加載參數

這三個例程越往下是越簡單的，可以看到最后一個例程幾乎就這兩行代碼了，加載模型，然后運行模型 ??

只需要指定模型的輸入就可以了，畢竟后面模型各層的輸入輸出是完全可以自動計算出來的。

// 加載模型
Onnx__ModelProto* model = onnx_load_model(ONNX_MODEL_NAME);

// 計算模型
float* output = onnx_model_run(model, input, shapeInput);

這個例子使用 valgrind 測試發現大約需要 64KB 內存，所以大家記得檢查一下自己的開發板內存夠不夠。

這里還有最后一點前面沒有提到，對于圖像而言數據順序是非常重要的，比如 NWHC 和 NCWH 這兩就略有不同，其中 N 代表輸入圖像數量, W 代表圖像寬度, H 代表圖像高度，C 代表圖像的通道數，比如彩色圖像就有 RGB 三個通道。所以 NWHC 和 NCWH 的區別就在于到底應該把通道 C 放在前面還是放在后面呢？

關于這個問題，有一篇論文做了一些研究，在 CPU 和 GPU 上通常選擇 NCWH 效率更高，這也是為什么大部分機器學習框架都是默認 NCWH 的格式，但是在 MCU 上例如 Cortex-M 系列使用 NWHC 計算效率就更高了。

論文地址：

https://arxiv.org/abs/1801.06601

3.5 參考文獻

完整 Jupyter Notebook 源碼
protobuf editor 解析工具
onnx 數據格式定義
onnx 模型可視化
模型量化
NWHC 還是 NCWH
RT-Thread Protobuf 軟件包
RT-Thread Protobuf 軟件包
RT-Thread Protobuf 軟件包

4 總結

不知不覺這個文檔已經寫得這么長了，不知道大家有沒有耐心看到最后，相信靜下心來看得話還是有很多收獲的，這里最后總結一下這篇文檔介紹了哪些內容。

機器學習算法分類
Linear Regression (損失函數，梯度下降)
Logistic Regression (sigmoid 函數)
ANN (反向傳播)
CNN (conv2d, maxpooling, relu, dropout, flatten, dense, softmax)
Protobuf (RT-Thread 軟件包 protobuf-c)
onnx 模型結構 (RT-Thread 軟件包 onnx-parser)
RTT 加載 onnx 模型并運行 (RT-Thread 軟件包 onnx-backend)

下一篇文檔 Draknet 訓練目標檢測模型 就會比較短了，因為理論部分這里基本介紹完了，主要就是 darknet 框架的使用，甚至都不怎么需要寫代碼。

最后，如果大家對在 MCU 上運行機器學習模型感興趣，希望這篇文檔還是能有所幫助。

posted @ 2019-12-17 11:02 RT-Thread小師妹閱讀(3450) 評論(0) 收藏舉報

刷新頁面返回頂部

RT-Thread小師妹

入門機器學習（1）——手寫體識別模型