你是否曾仰望星空，驚嘆于宇宙那宏大而精準的秩序？行星億萬年如一日地圍繞恒星旋轉，仿佛背后有一只無形的手在精確地指揮。然而，在這看似和諧的宇宙樂章之下，其實涌動著混沌的暗流。今天，我想通過我最新的一個開源項目，帶大家一窺這美麗而又脆弱的天體之舞。

這個項目就是 n-body，一個我用 C# 結合 ode45 高精度常微分方程求解器和 Direct2D 圖形渲染，專門用來模擬二維天體運動的“宇宙沙盤”。

從我們熟悉的家園開始

讓我們先從最經典的場景開始：太陽-地球-月球系統。這是一個我們從小就熟知的穩定模型。

下面是它的初始參數定義：

public static SystemDef CreateSolarEarthMoon1() => new([
    new(0.3534,  0, 0, -0.2658, BodyType.Solar, 1.0),
    new(-1.1466, 0, 0, 0.8183 , BodyType.Planet, 0.3),
    new(-0.9466, 0, 0, 2.0430 , BodyType.Moon, 0.01)
]);

運行起來的效果，正如你我所預料的那樣和諧而穩定：

可以清楚地看到，地球圍繞著太陽公轉，月球則圍繞著地球旋轉。但如果你再仔細觀察，會發現一個有趣的細節：地球的軌道并非一個完美的橢圓，它在月球引力的作用下，會產生輕微的、周期性的擺動。這正是萬有引力定律在微小尺度上展現的魅力。

蝴蝶效應：失之毫厘，謬以千里

天體運動的迷人之處在于其對初始條件的極端敏感性。如果我們將初始參數做一些看似微不足道的調整，宇宙的劇本可能就會完全不同。

比如，我們微調參數，將太陽的質量和位置稍作改變：

public static SystemDef CreateSolarEarthMoon2() => new([
    new(-0.2013, 0, 0, 0.16041, BodyType.Solar, 2.0),
    new(1.2987, 0, 0, -1.0744, BodyType.Planet, 0.3),
    new(1.4987, 0, 0, 0.1503, BodyType.Moon, 0.01)
]);

再來看模擬結果，整個系統的動態就變得狂野起來：

月球被地球和太陽的引力反復拉扯，上演了一出驚險的“太空芭蕾”，最終才勉強穩定下來。這正是混沌理論中“蝴蝶效應”的直觀體現：初始狀態的微小差異，足以導致最終結果的天壤之別。

完美環狀三星：脆弱的平衡藝術

除了我們熟悉的這種主星-行星-衛星模型，宇宙中還存在著更令人著迷的結構，比如劉慈欣《三體》中提到的，也是困擾了無數物理學家和數學家的“三體問題”。

我的模擬器提供了一個可以生成任意數量星體、并讓它們進行穩定環狀運動的函數：

public static SystemDef CreateStableRing(int N, double scale = 1.0, double G = 1.0, double M = 1.0, double R = 1.0)
{
    if (N < 2)
    {
        throw new ArgumentException("星體數量 N 必須大于等于 2", nameof(N));
    }

    double forceSumFactor = 0;
    for (int k = 1; k < N; ++k)
    {
        forceSumFactor += 1.0 / Math.Sin(Math.PI * k / N);
    }

    double v_squared = (G * M / (4.0 * R)) * forceSumFactor;
    double v = Math.Sqrt(v_squared) * scale;

    BodyDef[] stars = new BodyDef[N];
    for (int i = 0; i < N; ++i)
    {
        double angle = 2.0 * Math.PI * i / N;

        double px = R * Math.Sin(angle);
        double py = R * -Math.Cos(angle);

        double vx = v * Math.Cos(angle);
        double vy = v * Math.Sin(angle);

        stars[i] = new BodyDef(new BodyState(px, py, vx, vy), BodyType.Solar, M);
    }

    return new SystemDef(stars, G);
}

利用這個函數，我們可以創造一個理論上完美而穩定的環狀三體系統。它們的軌跡如同精密的時鐘，優雅而迷人：

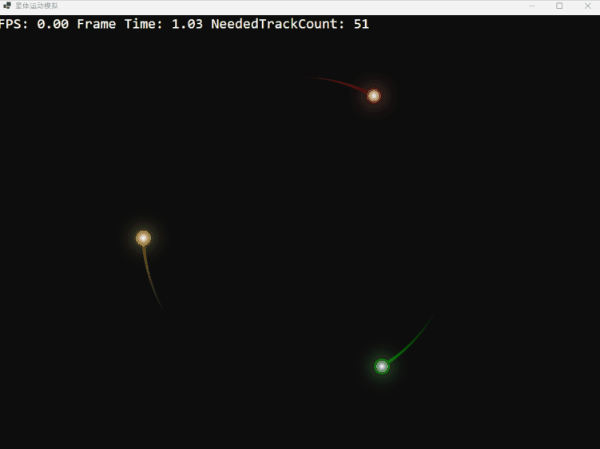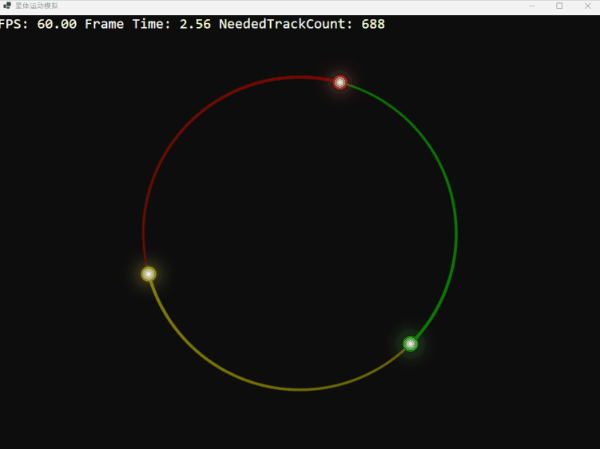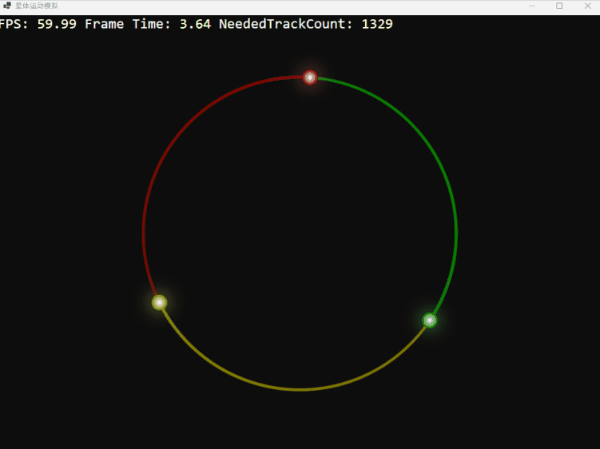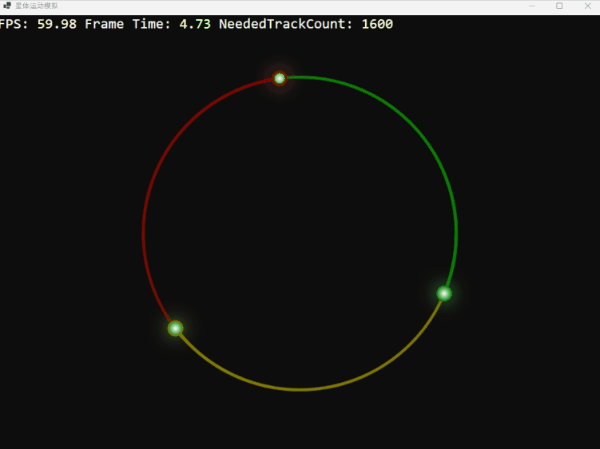
三顆星體在引力的束縛下，跳著一曲永不終結的華爾茲。這畫面充滿了數學和物理上的和諧之美，不是嗎？

然而，這種美麗，是建立在一種極其脆弱的平衡之上的。

秩序的瞬間崩潰

在真實的宇宙中，絕對的“完美”是不存在的。任何一絲微小的擾動，都可能成為壓垮這個精密系統的最后一根稻草。在我的模擬中，盡管已經使用了 ode45 這樣高精度的求解器，但計算過程中累積的微小誤差，足以打破這種脆弱的平衡。

于是，在一段時間的完美運行后，末日來臨了：

曾經優雅的舞蹈瞬間化為混亂的掙扎，星體被無情地拋向遠方。秩序在剎那間崩潰，混沌取而代之。這就是三體問題最本質的恐怖與魅力——穩定是偶然，混亂是必然。

為了更清晰地展示這種不穩定性，我們可以人為地給這個系統施加一點點“擾動”。

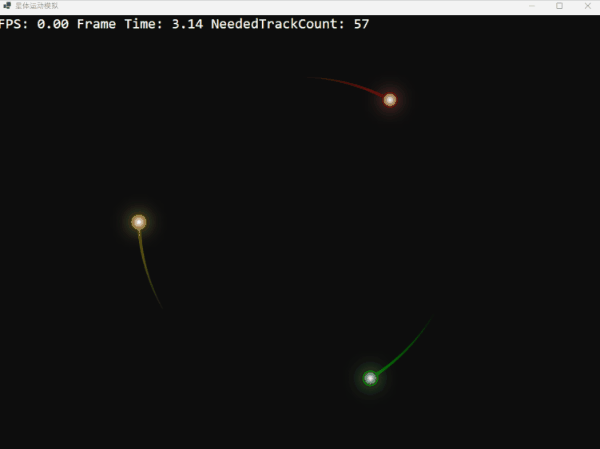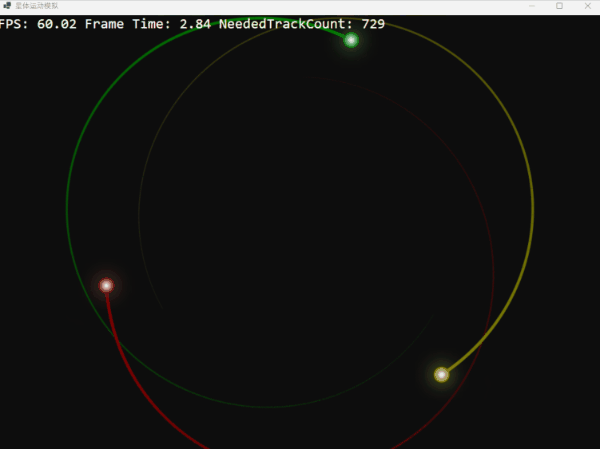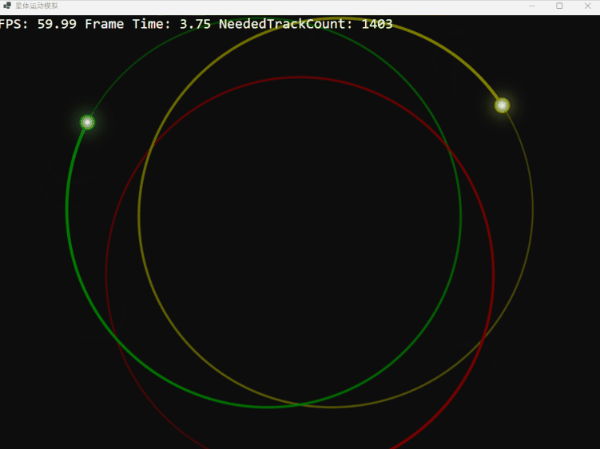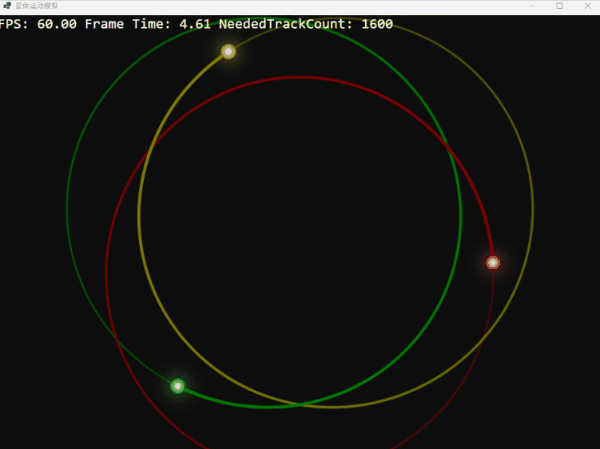
如果我們將三體的初始速度降低 10%，它們將無法維持圓形軌道，最終螺旋式地坍然后重生：

反之，如果我們將初始速度提高 10%，它們則會掙脫引力的束縛，漸行漸遠，但由于失去速度最終又回歸：

更多奇異的宇宙之舞

當然，三體運動的可能性遠不止于此。宇宙的想象力遠超人類。比如下面這個被稱為 "Henon5" 的初始配置：

public static SystemDef CreateHenon5() => new([
    new(-0.9353825545, 0, 0, 3.3166932522),
    new(1.9545571553, 0, 0, 0.1654488998),
    new(-1.0191746008, 0, 0, -3.4821421520)
]);

它會產生一種更加復雜、更加奇特的運行軌跡，宛如一幅不斷變換的抽象畫：

總結

從和諧的日地月系統，到美麗而脆弱的三體環舞，再到最終不可避免的混沌結局，我們通過代碼管中窺豹，領略了宇宙法則的兩個側面：它可以創造出令人贊嘆的秩序，也可以在瞬間將一切歸于混亂。

這種從有序到無序的張力，正是天體運動乃至整個物理世界最迷人的地方。

感謝你閱讀到這里！如果感覺本文對您有幫助，請不吝 評論 和 點贊，這也是我持續創作的最大動力！

如果你覺得我的 N 體運行模擬項目很有趣，歡迎來 GitHub 給一個 Star ?：
https://github.com/sdcb/n-body

也歡迎加入我的 .NET騷操作 QQ群：495782587，在這里我們可以一起交流 .NET 和 AI 領域各種最新、最酷、最“騷”的玩法！