原題鏈接：link。

自然想到建立坐標系，以速度為縱軸，初始點為橫軸。

以樣例二為例來分析：

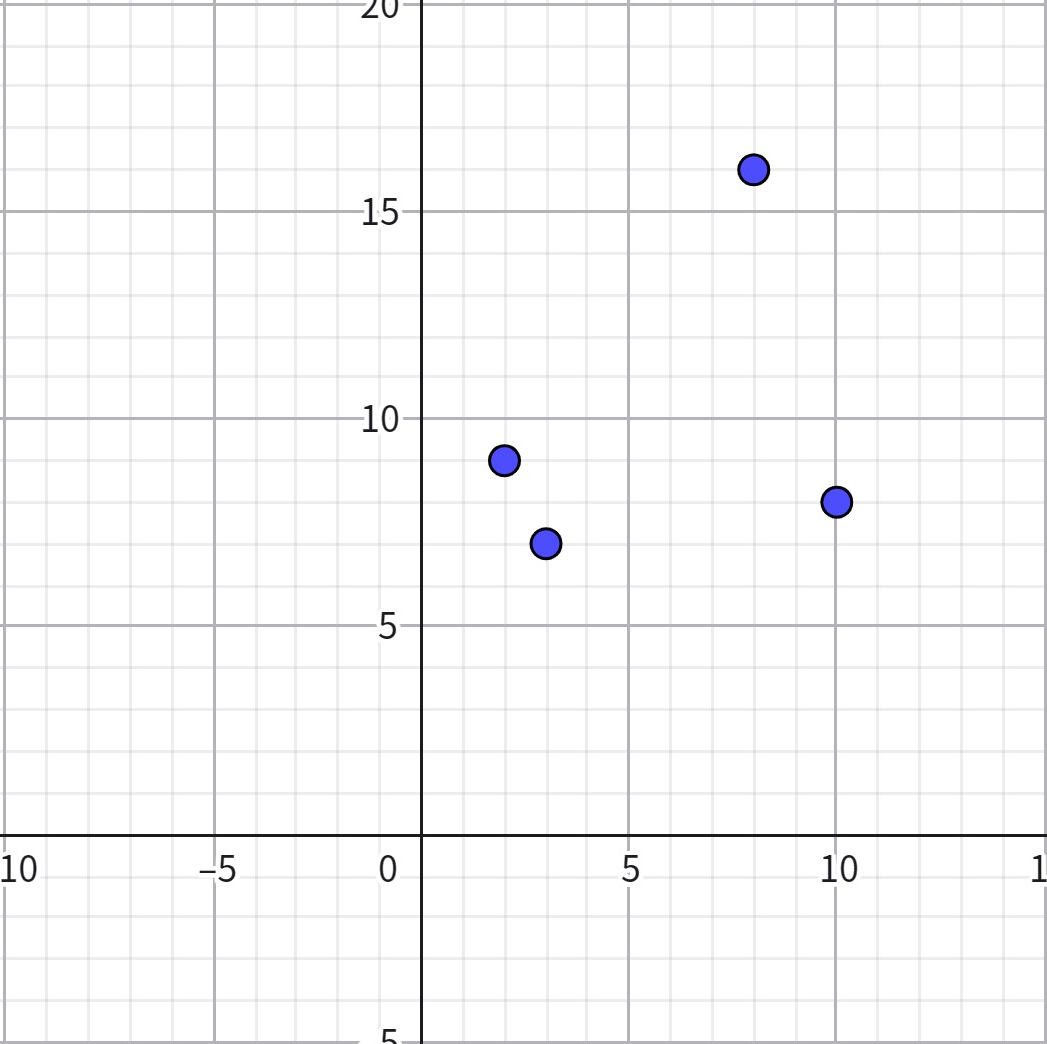
考慮將點兩兩連線：

`

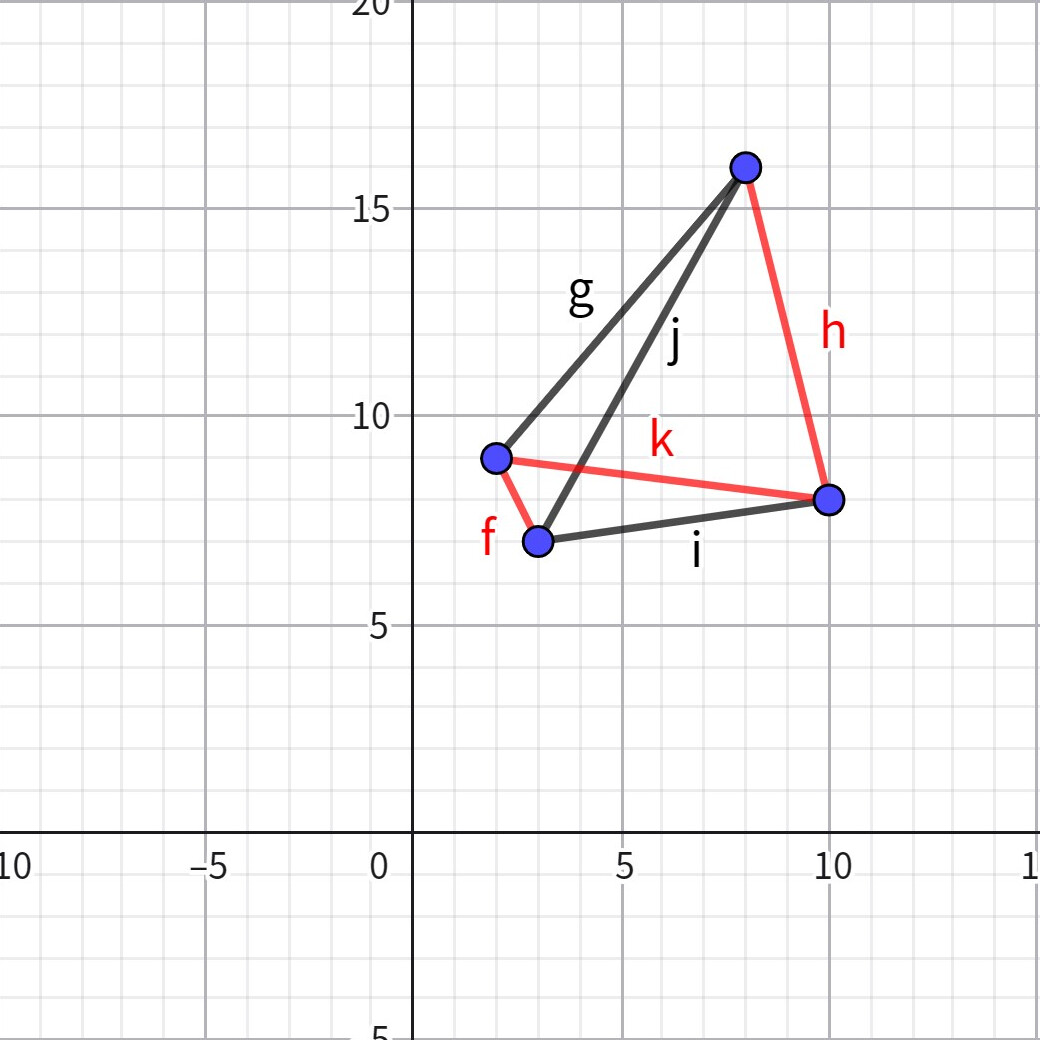其中紅線為斜率為負數的線，容易知道點 \((x_i,v_i)\) 與點 \((x_j,v_j)\) 所連成的線的斜率為 \(\frac{x_j-x_i}{v_j-v_i}\)，注意到他們相遇的時間與斜率互為相反數，即若斜率為負數，則相遇的時間為正數，也就是兩人會相遇。

接下來，我們將點編號：

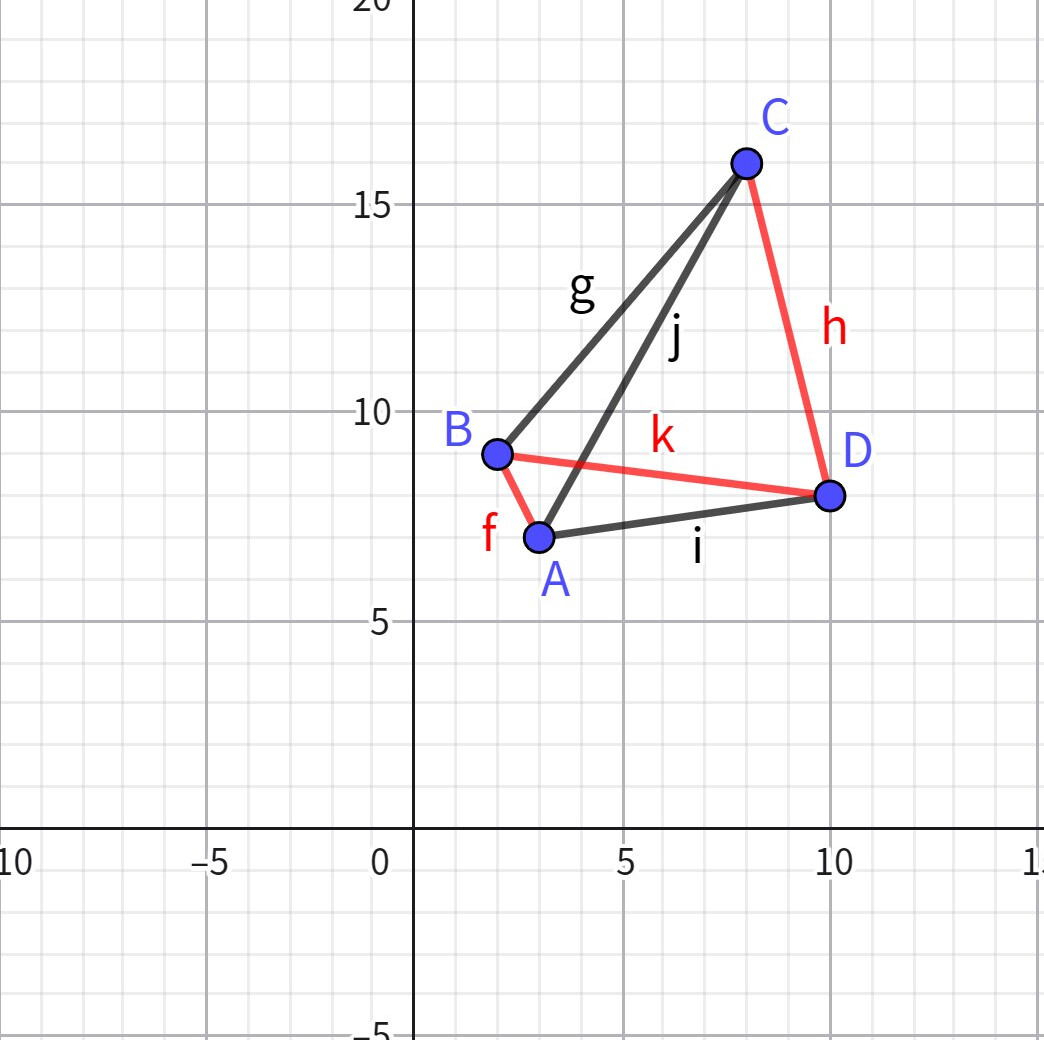
這里我們先考慮 \(B,C,D\) 三個點，注意到 \(CD\) 的斜率比 \(BD\) 的斜率小，即 \(D\) 先于 \(C\) 相遇，后與 \(B\) 相遇。

翻譯一下就是如果一開始 \(C\) 就被感染，那么 \(C\) 先與 \(D\) 相遇，那么 \(D\) 也被感染，接著 \(D\) 與 \(B\) 相遇，三人都被感染。

那么問題就出現了，我們如何處理這種間接感染的問題。

首先總結出規律，如果一個點 \(n\) 想要感染點 \(m\) 那么，點 \(n\) 與點 \(m\) 之間需要有一條斜率都是負的且單調上升的路徑。

考慮關注一個點 \(k\) 的影響范圍，容易想到點 \(k\) 的影響范圍為 \(\left\{(x,y)\mid y\ge l,y\le r\right\}\) 其中 \(l\) 為最小的使與 \(k\) 連線的斜率小于 \(0\) 的點的縱坐標，類似的，\(r\) 為最大的使與 \(k\) 連線的斜率小于 \(0\) 的點的縱坐標，我們拿上圖中的 \(D\) 點舉例：

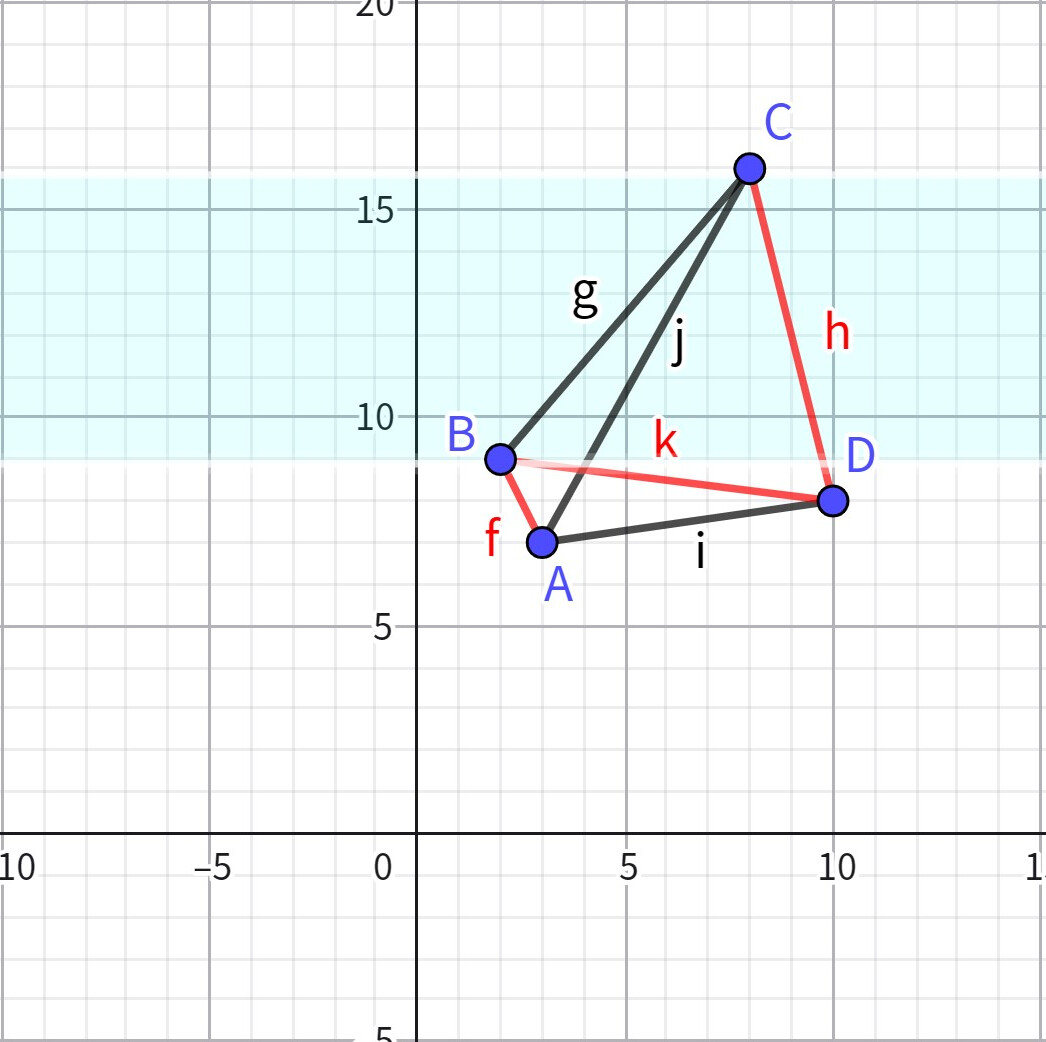
如圖，藍色區域就是點 \(D\) 的影響范圍。

然后我們不考慮單個的點，我們考慮這個點的影響范圍 \([l_i,r_i]\) 現在，問題轉換為求線段覆蓋區間的方案數，使用 dp。

設 \(dp_i\) 為覆蓋前 \(i\) 個點的方案數，有狀態轉移方程：

自然想到使用前綴和優化，使用樹狀數組，復雜度 \(\mathcal{O}(n\log n)\)。