MPK（Mirage Persistent Kernel）源碼筆記（2）--- 多層結構化圖模型

0x00 概要

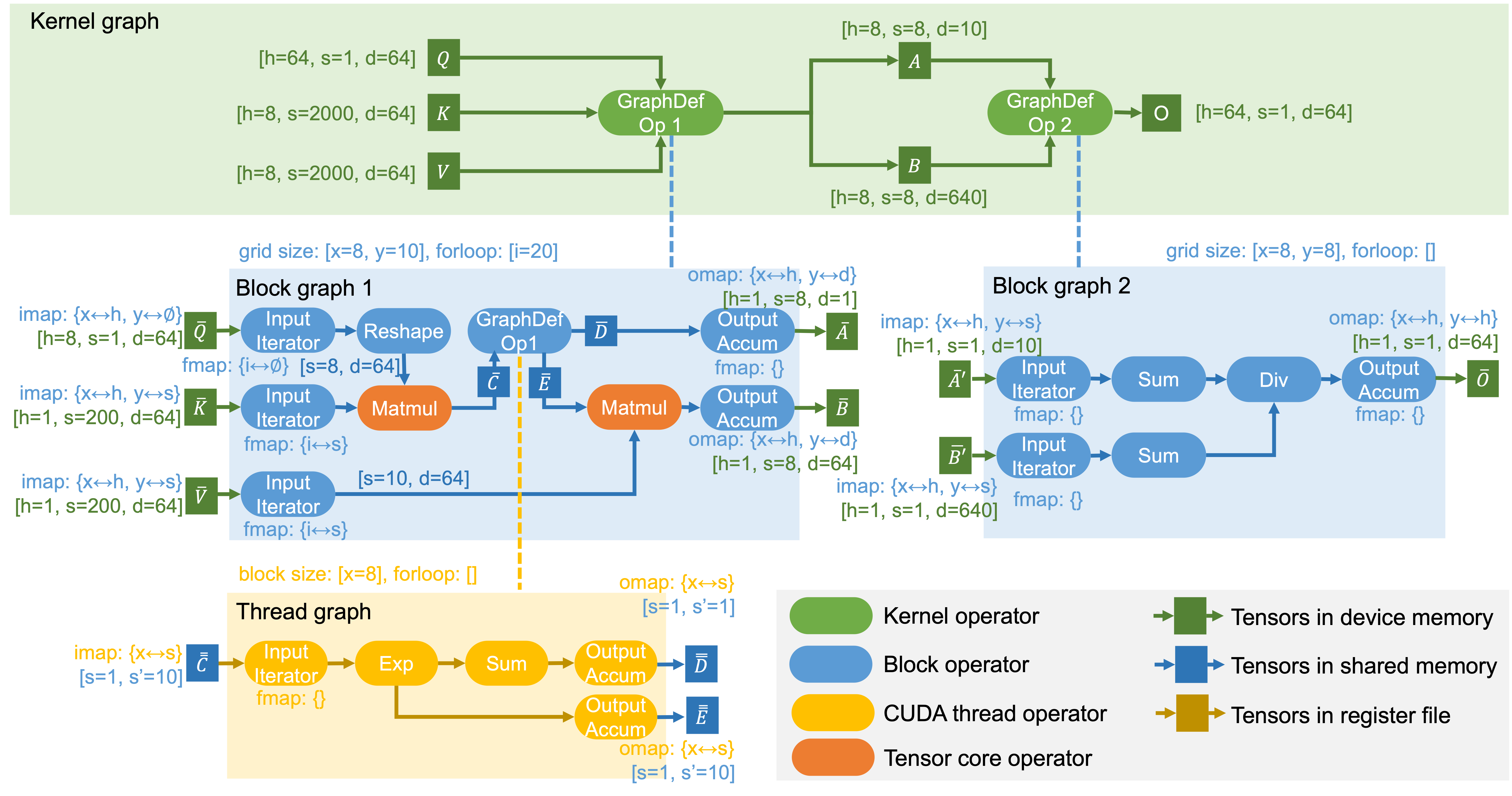
Mirage 使用 uGraph 來指定在 GPU 上執行張量程序。uGraph 包含多個級別的層次化圖，以表示在內核、塊和線程級別的計算。下圖是GQA對應的μGraphs，顯示了一個用于計算GQA的 uGraph。我們用它作為運行示例來解釋 uGraph 的關鍵組成部分。

0x01 機制

1.1 當前問題

LLM 的計算過程通常以計算圖的形式表示，其中每個節點對應一個計算算子（如矩陣乘法、注意力機制）或集合通信原語（如 all-reduce），邊表示算子間的數據依賴關系。現有系統通常為每個算子啟動獨立的 GPU 內核。然而，這種“單算子單內核”的執行模型難以實現 pipeline 優化，因為依賴關系是在整個內核的粗粒度層面強制執行的，而非實際數據單元層面。

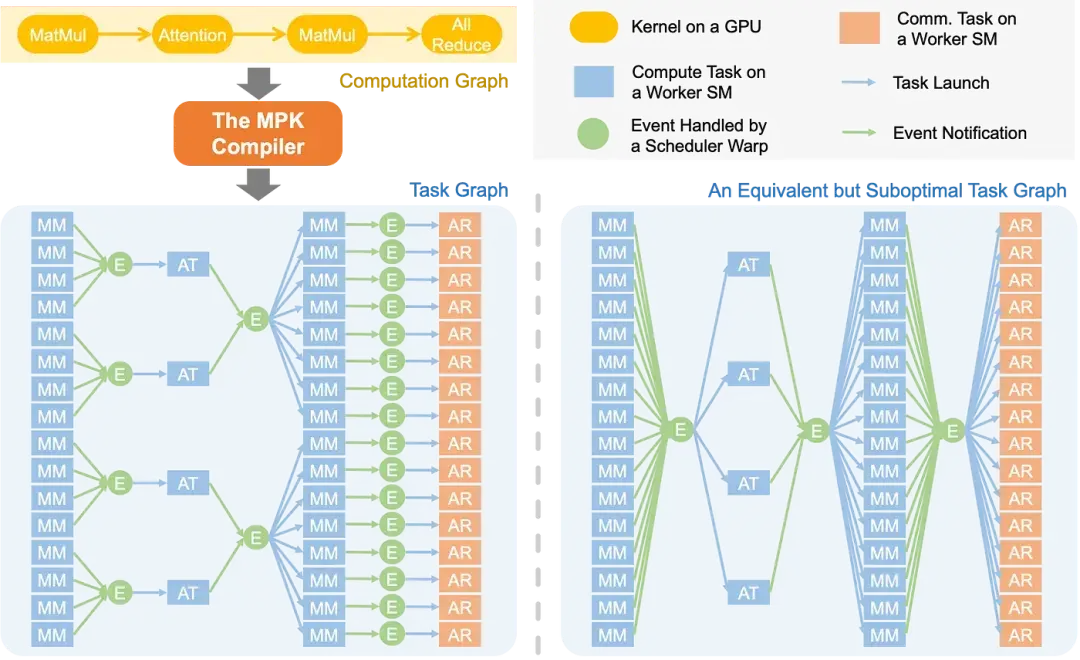
例如，矩陣乘法（matmul）后接 all-reduce 操作：現有系統中，all-reduce 內核必須等待整個 matmul 內核完成。而實際上，all-reduce 的每個數據分塊僅依賴 matmul 輸出的局部結果。這種邏輯依賴與實際依賴的錯配，嚴重限制了計算與通信的重疊潛力。下圖的右側展示次優方案 —— 其引入不必要的數據依賴與全局屏障，導致跨層流水線優化機會受限。

1.2 解決方案

為了解決這一問題，Mirage實現了多層次計算圖表示（μGraphs）與歸納式程序合成（Inductive Program Synthesis）。這兩大機制協同作用，實現了從宏觀調度到微觀計算的全鏈路優化，高效生成GPU程序，顯著提升了張量計算的性能。

Mirage 的編譯流程清晰且目標明確：

• 輸入：來自預定義算子集合的計算圖子圖（如 GQA 注意力計算子圖），確保輸入邏輯的規范性與可優化性；
• 核心優化步驟：包含圖重寫（Graph Rewrite，調整圖結構以適配 GPU 架構）、算子融合（Operator Fusion，減少內存訪問次數）等，所有優化均基于 μGraphs 的跨層級表示展開；
• 輸出：優化后的 CUDA 程序，直接適配 GPU 硬件執行，可直接JIT嵌入pytorch。

1.2.1 μGraphs：多層次計算圖表示

MPK 編譯器將 LLM 計算圖自動轉化為細粒度任務圖，最大化暴露并行性。該任務圖在子內核級別顯式捕獲依賴關系，實現更激進的跨層流水線優化。具體而言，在 MPK 任務圖中（參見上圖）：

• 任務（矩形表示）：代表分配給單個 GPU 流式多處理器（SM）的計算或通信單元。
• 事件（圓形表示）：表示任務間的同步點。
• 觸發機制：每個任務發出指向觸發事件的邊，該事件在關聯任務全部完成后激活。
• 依賴機制：每個任務接收來自依賴事件的邊，表明事件激活后任務立即啟動。

任務圖使 MPK 能夠發掘計算圖中無法實現的 pipeline 優化機會。例如，MPK 可以構建優化任務圖 —— 其中每個 all-reduce 任務僅依賴于生成其輸入的對應 matmul 任務，從而實現分塊執行與計算通信重疊。

除生成優化任務圖外，MPK 還通過 Mirage 內核超優化器自動為每個任務生成高性能 CUDA 實現，確保任務在 GPU 流式多處理器（SM）上高效執行。

1.2.2 歸納式程序合成：優化范式

歸納式程序合成是Mirage的另一大核心機制。與傳統的演繹式程序合成（如基于規則的重寫系統）不同，歸納式程序合成直接從語法出發構造程序，并借助SMT求解器驗證構造程序與原程序的等價性。這種方法能夠突破傳統優化方法的局限，發現將代數變換、調度變換和新自定義內核生成相結合的創新優化路徑。

通過歸納式程序合成，Mirage能夠自動生成高性能的GPU內核代碼，不僅簡化了開發流程，還提升了程序的運行效率，使得開發者能夠更專注于高層邏輯的設計，而無需深入底層硬件細節。

傳統機器學習編譯器（如 TVM、TensorRT）采用演繹式程序合成（Deductive Program Synthesis，又稱 Term Rewrite） ：從原始程序出發，通過等價重寫規則（如圖模式匹配、循環調度原語）逐步變換，始終在 “程序等價類” 內搜索更優實現 —— 這種方式依賴手工設計規則，難以突破現有等價類的性能上限。

Mirage 則采用歸納式程序合成：不依賴原始程序的逐步變換，而是直接基于算子語法構造全新候選程序，再通過 “μGraphs 語義校驗 + 概率等價驗證”（如有限域隨機測試）確認候選程序與原始程序的功能一致性。這種范式無需受限于等價重寫規則，可探索更靈活的跨層級優化方案（如 Kernel-Graph 合成算子與 Block-Graph 共享內存復用的協同），同時通過概率驗證保障正確性。

下圖是Mirage找出的最佳μGraphs。

0x02 多層次計算圖表示

Mirage 實現了多層次計算圖表示（μGraphs），通過 kernel-graph（內核圖）、block-graph（塊圖）和 thread-graph（線程圖）這三層結構化圖模型，精確映射 GPU 程序從內核到線程的執行邏輯與存儲層級。這種三層結構與 CUDA 程序的執行層級及 GPU 的存儲體系緊密對應，每層均清晰定義了 “算子類型 — 張量存儲 — 核心功能” 的關聯關系。

2.1 概念

三層的概念如下：

1. kernel-graph（內核圖）：屬于高層次抽象，用于表示整個計算圖（即完整的計算任務），包含粗粒度的高層操作（如完整的矩陣乘法、規約運算等）與對應數據。該層負責全局調度，重點關注數據流與任務間的依賴關系，對應 GPU 的全局內存，主要處理宏觀層面的任務分配與協同。其包含的算子（舉例）類型有：
   1. 高層操作：KN_INPUT_OP（輸入算子）、KN_OUTPUT_OP（輸出算子）、KN_MATMUL_OP（矩陣乘法算子）；
   2. 數學操作：KN_EXP_OP（指數運算算子）、KN_ADD_OP（加法算子）、KN_MUL_OP（乘法算子）；
   3. 規約操作：KN_REDUCTION_0_OP（零階規約算子）等；
   4. 自定義操作：KN_CUSTOMIZED_OP（自定義算子）等。
2. block-graph（塊圖）：屬于中等層次抽象，嵌套在 KN_CUSTOMIZED_OP（自定義內核算子）中，定義 threadblock（線程塊）級別的計算邏輯。該層包含細粒度操作，負責管理線程塊級別的并行計算，重點關注內存訪問模式、循環結構等中觀細節，對應 GPU 的共享內存，核心目標是優化中觀層面的資源利用與數據共享效率。其包含的算子類型（舉例）有：
   1. 輸入操作：TB_INPUT_OP（線程塊輸入算子）；
   2. 內存操作：TB_MATMUL_OP（線程塊矩陣乘法算子）、TB_EXP_OP（線程塊指數運算算子）；
   3. 特殊操作：TB_FORLOOP_ACCUM_NO_RED_OP（線程塊循環累加無規約算子）、TB_RMS_NORM_OP（線程塊 RMS 歸一化算子）。
3. thread-graph（線程圖）：在 block-graph 的具體操作中體現，定義線程級別的執行細節。該層專注于線程級別的微觀計算邏輯，對應 GPU 的寄存器，核心作用是確保每個線程的高效執行，最大化單線程的計算吞吐量。

這種三層結構支持系統在不同抽象層級開展針對性優化：

• 在 kernel-graph 層，主要進行全局任務調度與數據流優化，明確整體計算流程與資源分配方向；
• 在 block-graph 層，側重線程塊級別的并行策略優化，提升中觀層面的并行效率與數據共享能力；
• 在 thread-graph 層，聚焦具體的內存訪問模式優化與計算指令調度，確保微觀執行的高效性。

若用通俗語言概括三層結構的分工：kernel-graph 決定 “要做什么”（明確整體計算任務與目標），block-graph 決定 “該怎么做”（規劃線程塊級的執行方案），thread-graph 負責 “具體執行”（完成線程級的微觀計算）。

這種從宏觀到微觀的層次化設計，使 μGraphs 能夠實現從全局調度到局部執行的全鏈路優化，有效減少計算冗余與資源浪費，確保 GPU 計算資源的高效利用。

2.2 層級關系

三級圖結構的關系如下圖所示。

  muGraph(Kernel Graph)                                    
  │                                                        
  ├────? KNOperator(各種標準操作)                                       
  │                                   
  │                                                        
  └────? KNCustomizeOp(自定義操作)                                   
            │                                              
            └───? block-graph(Threadblock Graph)           
                   │                                       
                   ├────? TBOperator(各種線程塊操作)                     
                   │                                       
                   └────? TBInputOp(連接到muGraph的張量)                      
                             │                             
                             └───? thread-level execution(線程級執行)

2.3 對比

三層的對比如下。

計算圖層級	對應 CUDA 執行層級	張量存儲位置	算子類型與功能	核心屬性 / 邏輯
Kernel-Graph	整個 GPU 內核（多流處理器 SM 協同）	設備全局內存（Device DRAM）	1. 預定義算子：直接調用廠商庫內核（如 cuBLAS 的 GEMM 矩陣乘、cuDNN 的卷積）； 2. 合成算子：需通過更低層級的 Block-Graph 描述，承載算子融合、自定義算法等復雜邏輯	無額外屬性，核心是 “調度多 SM 協同”，通過預定義算子復用成熟庫性能，合成算子支持靈活優化
Block-Graph	單個流處理器 SM（線程塊協作）	共享內存（Shared Memory）	1. 預定義算子：調用 CUTLASS、ThunderKittens 等庫的共享內存操作（如塊內矩陣乘、累加）； 2. 合成算子：由 Thread-Graph 描述，實現線程塊內細粒度計算	1. 并行切分屬性：imap（輸入分塊，映射 Grid 維度到輸入張量維度）、omap（輸出拼接，映射 Grid 維度到輸出張量維度）、fmap（循環迭代，映射 For-Loop 維度到數據迭代器 / 累加器維度）； 2. 執行邏輯：支持線程塊循環迭代，通過共享內存復用與 “計算 - 訪存重疊”，將全局內存讀寫延遲隱藏在計算過程中
Thread-Graph	單個線程（寄存器操作）	線程私有寄存器（Register File）	僅含預定義算子，描述單個線程內的寄存器級流水操作（如 load 數據→元素級計算→store 結果），支持循環迭代與寄存器累加；默認通過 “規則化融合” 快速生成，避免細粒度層級的冗余搜索	核心是 “單線程高效流水”，通過寄存器操作最小化內存訪問，提升計算密度

2.4 執行關系

persistent_kernel.py是 Persistent Kernel的Python接口，本質是Python到CUDA持久化內核系統的橋梁，允許用戶用python定義復雜的計算圖，然后在GPU上高效執行。

persistent_kernel.py與三層計算圖的關系如下：

1. Persistent Kernel 創建并管理 Kernel Graph
2. Kernel Graph 通過 KN_CUSTOMIZED_OP 包含多個 Block Graph
3. 每個 Block Graph 定義線程塊內的操作序列
4. Kernel Graph 轉換為 Task Graph 用于執行
5. Task Execution Engine 在 Persistent Kernel 中執行任務
6. Event System 管理任務間的依賴和同步
7. Thread Graph 在實際GPU線程中執行具體操作

0x03 內核圖

每個張量程序對應一個內核圖，其中每個節點代表在整個 GPU 上運行的內核，每條邊是內核之間共享的張量。內核圖中的所有張量都存儲在 GPU 設備內存中，因為不同的內核不能在寄存器文件或共享內存中共享數據。內核圖中的每個節點都可以是現有內核庫（如 cuDNN 的卷積和 cuBLAS 的矩陣乘法）支持的預定義內核操作符。此外，為了啟用細粒度的內核間優化（如內核融合），內核圖中的節點也可以是圖定義的內核操作符，其語義和行為由較低級別的（即塊）圖定義。下圖中的兩個內核操作符都是圖定義的操作符，每個都由塊圖指定。

3.1 PersistentKernel調用

在PersistentKernel內部，kn_graph負責實際的計算圖構建。

self.kn_graph = KNGraph(CyKNGraph(disable_fingerprint=True))

每個attach_input和new_tensor調用都會在kn_graph中創建張量節點。每個layer調用也會在kn_graph中添加相應的計算節點。最后compile()調用self.kn_graph.generate_task_graph生成任務圖。

3.2 Python 代碼

內核圖在Python中的類是KNGraph。KNGraph用于構建和管理內核計算圖。比如，new_input會創建新的輸入變量。attach_torch_tensor管理PyTorch變量。attach_cuda_tensor關聯CUDA變量。compile會生成最終的執行代碼。

KNGraph的特點如下：

• Kernel graph的節點是：

  • 預定義算子（pre-defined operator），比如cuBLAS GEMM、cuDNN Conv
  • 合成算子（graph-defined operator），用更低一層的block graph描述，可承載fusion/新算法。

• Kernel graph的邊是：位于全局內存（Device DRAM）的Tensor。

KNGraph 代碼舉例如下：

class KNGraph:
    def __init__(self, graph):
        self.cygraph = graph
        self._is_compiled = False
        self.run = None
        self._valid_cuda_kernels = False
        self._cached_results = None
        self.visualizer = None

        self.backend = "cuda"
        
    def new_input(
        self, dims: tuple, strides: tuple = None, dtype: dtype = float16
    ) -> DTensor:
        # use the default strided layout if strides = None
        if strides is None:
            total_elements = 1
            strides = []
            for d in reversed(dims):
                strides.append(total_elements)
                total_elements *= d
            strides = reversed(strides)
        return self.cygraph.new_input(dims, tuple(strides), dtype)      
    

    def compile(self, async_=False, **kwargs):
        if self._is_compiled:
            return self._cached_results
        input_tensors = kwargs.get("inputs", [])
        input_strides = []

        for i in range(len(dtensors)):
            dims, strides = self.cygraph.get_input_dtensor_shape_and_stride(dtensors[i])
            input_strides.append(strides)
        target_cc = kwargs.get(
            "target_cc",
            torch.cuda.get_device_properties(0).major * 10
            + torch.cuda.get_device_properties(0).minor,
        )
        num_warp_groups = kwargs.get("num_warp_groups", 2)
        pipeline_stages = kwargs.get("pipeline_stages", 2)
        enable_online_softmax = kwargs.get("enable_online_softmax", False)

        result = generate_cuda_program(
            self.cygraph,
            target_cc=target_cc,
            input_strides=input_strides,
            num_warp_groups=num_warp_groups,
            pipeline_stages=pipeline_stages,
            profiling=profiling,
            enable_online_softmax=enable_online_softmax,
        )
        if result["max_smem_size"] > get_shared_memory_capacity(target_cc):
            self._is_compiled = True
            self._valid_cuda_kernels = False
            self._error_message = "shared memory usage exceed limit"

            if async_:
                return Handle([], None)
            else:
                return None

        MIRAGE_ROOT, INCLUDE_PATH, DEPS_PATH = get_key_paths()
        tempdir_obj = tempfile.TemporaryDirectory()
        tempdir = tempdir_obj.name
        saved_addr = ""
        file_id = kwargs.get("file_id", -1)
        if file_id != -1:
            print(f"file_id: {file_id}")
            saved_addr = f"./generated_codes/{file_id}/"
        FILE_NAME = os.path.join(tempdir, "test.cu")
        so_path = os.path.join(tempdir, "test.cpython-38-x86_64-linux-gnu.so")

        with open(FILE_NAME, "w") as f:
            f.write(result["code"] + HARD_CODE)
            if saved_addr != "":
                print(f"saved_addr: {saved_addr}")
                os.makedirs(saved_addr, exist_ok=True)
                with open(saved_addr + "test" + str(file_id) + ".cu", "w") as f:
                    f.write(result["code"] + HARD_CODE)

        cc = shutil.which("nvcc")
        # This function was renamed and made public in Python 3.10
        if hasattr(sysconfig, "get_default_scheme"):
            scheme = sysconfig.get_default_scheme()
        else:
            scheme = sysconfig._get_default_scheme()
        if scheme == "posix_local":
            scheme = "posix_prefix"
        py_include_dir = sysconfig.get_paths(scheme=scheme)["include"]
        cc_cmd = get_cc_cmd(
            target_cc,
            cc,
            FILE_NAME,
            py_include_dir,
            INCLUDE_PATH,
            DEPS_PATH,
            so_path,
            profiling,
        )

        def remain_op():
            import importlib.util

            try:
                spec = importlib.util.spec_from_file_location(
                    "__mirage_launcher", so_path
                )
                mod = importlib.util.module_from_spec(spec)
                spec.loader.exec_module(mod)
                self.run = getattr(mod, "launch")
                self._is_compiled = True
                self._valid_cuda_kernels = True
                self._cached_results = result
                self._error_message = "No error"
                tempdir_obj.cleanup()
                return self._cached_results
            except ImportError:
                self._is_compiled = True
                self._valid_cuda_kernels = False
                self._cached_results = None
                self._error_message = "CUDA compilation error"
                return None

        if async_:
            if global_config.bypass_compile_errors:
                ret = subprocess.Popen(
                    cc_cmd, stdout=subprocess.DEVNULL, stderr=subprocess.STDOUT
                )
            else:
                ret = subprocess.Popen(cc_cmd)
            return Handle([ret], remain_op)
        else:
            ret = subprocess.check_call(cc_cmd)
            return remain_op()

3.3 橋梁

PersistentKernel 中，通過如下方式進行設置 Kernel Graph。

self.kn_graph = KNGraph(CyKNGraph(disable_fingerprint=True))

在python\mirage_cython\core.pyx 文件中，CyKNGraph 中有定義 CppKNGraph。

cdef class CyKNGraph:
    cdef CppKNGraph *p_kgraph #Hold a CppKNGraph instance

    def __cinit__(self, graph = None, bool disable_fingerprint = False):
        cdef unsigned long long ptr
        cdef dim3 c_gpu_dim
        if graph is None:
            c_gpu_dim.x = 1
            c_gpu_dim.y = 1
            c_gpu_dim.z = 1
            self.p_kgraph = new CppKNGraph(c_gpu_dim, disable_fingerprint)
        else:
            ptr = ctypes.cast(graph, ctypes.c_void_p).value
            self.p_kgraph = <CppKNGraph*>(ptr)

在 python\mirage_cython\CCore.pxd 文件中，指明 CppKNGraph 對應了 "mirage::kernel::Graph"，這便是C++代碼中，Kernel Graph 的實現。

    cdef cppclass CppKNGraph "mirage::kernel::Graph":
        CppKNGraph(dim3 gpu_dim, bool disable_fingerprint)
        CppDTensor* new_input_ptr(vector[int] dims,
                                  vector[size_t] strides,
                                  DataType data_type,
                                  DmemLayout layout)
        void mark_output(const CppDTensor* A, vector[size_t] strides)
        CppDTensor* matmul(const CppDTensor* A, const CppDTensor* B)
        CppDTensor* reduction(const CppDTensor* input, int dim, int size)
        CppDTensor* rms_norm(const CppDTensor* input, vector[int])
        CppDTensor* exp(const CppDTensor* input)
        CppDTensor* silu(const CppDTensor* input)
        CppDTensor* gelu(const CppDTensor* input)
        CppDTensor* relu(const CppDTensor* input)
        CppDTensor* clamp(const CppDTensor* input, float min_val, float max_val)
        CppDTensor* sqrt(const CppDTensor* input)
        CppDTensor* square(const CppDTensor* input)
        CppDTensor* add(const CppDTensor* op1, const CppDTensor* op2)
        CppDTensor* mul(const CppDTensor* op1, const CppDTensor* op2)
        CppDTensor* div(const CppDTensor* op1, const CppDTensor* op2)
        CppDTensor* pow(const CppDTensor* op1, const CppDTensor* op2)
        int customized(vector[const CppDTensor*] inputs,
                       CppDTensor** outputs,
                       CppTBGraph* bgraph)
        int get_num_input_dtensors()
        int get_num_output_dtensors()
        int get_input_dtensors(CppDTensor** cinputs)
        int get_input_dtensor_shape_and_stride(const CppDTensor *input, int *strides, int *dims)
        void generate_triton_program(const char *filepath)
        void generate_cuda_program(const char *filepath)
        size_t get_owner_independent_hash() const
        # Persistent kernel functions
        void attach_torch_tensor(const CppDTensor *input,
                                 void *torch_data_ptr,
                                 const char *name)
        void attach_cuda_tensor(const CppDTensor *input,
                                const char *name)
        void attach_nvshmem_tensor(const CppDTensor *input,
                                   const char *name)
        CppDTensor* fuse_tensors(vector[const CppDTensor*] inputs,
                                 int fused_dim,
                                 int num_groups,
                                 const char *name)
        void register_task(const char *task_type,
                           vector[int] params)
        TaskGraphResult generate_task_graph(int num_gpus, int my_gpu_id)

        vector[CppKNOperator*] operators

3.4 C++ 代碼

muGraph在c++代碼中體現為mirage::kernel::Graph類，這是最高層次的計算圖。

namespace mirage {
namespace kernel {

class Graph {
private:
  struct pair_hash {
    size_t operator()(std::pair<int, int> const &p) const;
  };

public:
  Graph(dim3 gpu_dim = {1, 1, 1}, bool disable_fingerprint = false);
  ~Graph();
  Graph(Graph const &) = delete;
  Graph &operator=(Graph const &) = delete;
  // input operator
  DTensor new_input(std::vector<int> const &dims,
                    std::vector<size_t> const &strides,
                    mirage::type::DataType data_type,
                    mirage::layout::DmemLayout layout);
  DTensor elementunary(DTensor const &input,
                       mirage::type::KNOperatorType _type);
  // 忽略其它函數  

public:
  std::vector<mirage::kernel::KNOperator *> operators; // 操作符列表
  dim3 gpu_dim;
  off_t dmem_data_offset, dmem_fp_offset;
  std::vector<std::pair<off_t, size_t>> allocated_data_tensors,
      allocated_fp_tensors;
  // Fields for persistent kernels
  std::map<mirage::type::GuidType, mirage::runtime::IODesc> io_config;
  std::unordered_map<mirage::kernel::KNOperator const *,
                     std::tuple<int, int, runtime::TaskType, int>>
      task_config;

  using OpType = KNOperator;
  using TensorType = DTensor;
};  

mirage::kernel::Graph的主要特征是：

• 操作符類型：使用KNOperatorType 枚舉定義操作類型。
• 張量表示：使用DTensor（Device Tensor）表示數據。
• 操作節點：包括輸入（KN_INPUT_OP），輸出（KN_OUTPUT_OP），矩陣乘法（KN_MATMUL_OP）等。

mirage::kernel::Graph的成員函數以 elementunar 為例，代碼如下：

DTensor Graph::elementunary(DTensor const &input,
                            mirage::type::KNOperatorType type) {
  KNOperator *op = create_elementunary_op(input, type);
  assert(op != nullptr);
  operators.push_back(op);
  assert(op->output_tensors.size() == 1);
  DTensor output = op->output_tensors[0];
  return output;
}

3.5 KNOperator

Graph包含多個KNOperator對象。

KNOperator是內核級別的操作符基類，用于表示計算圖中的節點。作為計算圖中每個操作的基本單元，可以維護輸入和輸出張量的信息，提供操作類型表示。而且，通過輸入輸出張量的連接關系，可以建立操作間的依賴關系，為后續的任務調度和事件管理提供基礎。

在runtime.cc中，系統通過遍歷Graph中的operators來生成任務圖。

class KNOperator {
public:
  KNOperator(Graph *graph, mirage::type::KNOperatorType _type);
  KNOperator(Graph *graph,
             mirage::type::KNOperatorType _type,
             DTensor const &input1);
  KNOperator(Graph *graph,
             mirage::type::KNOperatorType _type,
             DTensor const &input1,
             DTensor const &input2);
  KNOperator(Graph *graph,
             mirage::type::KNOperatorType _type,
             std::vector<DTensor> const &inputs);
  int get_input_dtensors(DTensor **inputs);
  int get_output_dtensors(DTensor **inputs);

  virtual ~KNOperator();
  virtual bool fingerprint(void) = 0;
  virtual operator json() const = 0; // 將操作序列轉換為JSON格式

  // hash related functions
  virtual size_t get_owner_independent_hash() const;

public:
  Graph *kgraph; // 通過該指針維護與所屬計算圖的關聯
  mirage::type::KNOperatorType op_type; // 標識操作類型
  std::vector<DTensor> input_tensors; // 存儲操作的輸入張量
  std::vector<DTensor> output_tensors; // 存儲操作的輸出張量
};

KNCustomizedOp，KNInputOp，KNOutputOp是KNOperator的派生類。KNOperator的派生類舉例。

class KNInputOp : public KNOperator {
public:
  KNInputOp(Graph *_graph,
            std::vector<int> const &dims,
            std::vector<size_t> const &strides,
            mirage::type::DataType data_type,
            mirage::layout::DmemLayout layout,
            int3 input_map = {-1, -1, -1});
  ~KNInputOp();
  bool fingerprint(void);

  operator json() const override;

public:
  std::vector<size_t> input_strides;
  int3 input_map;
};

class KNOutputOp : public KNOperator {
public:
  KNOutputOp(Graph *_graph,
             DTensor const &A,
             std::vector<size_t> const &strides,
             int3 output_map = {-1, -1, -1});
  ~KNOutputOp();
  bool fingerprint(void);

  operator json() const override;

public:
  std::vector<size_t> output_strides;
  int3 output_map;
};

class KNCustomizedOp : public mirage::kernel::KNOperator {
public:
  KNCustomizedOp(Graph *_kgraph,
                 std::vector<DTensor> const &inputs,
                 mirage::threadblock::Graph const &_graph);
  virtual ~KNCustomizedOp();
  bool fingerprint(void);
  size_t get_owner_independent_hash() const override;

  operator json() const override;

public:
  mirage::threadblock::Graph bgraph;
  void get_bgraph(mirage::threadblock::Graph **bgraph);
};

KNOperatorType 的全量為：

enum KNOperatorType {
  KN_UNKOWN = 1000,
  KN_INPUT_OP = 1001,
  KN_OUTPUT_OP = 1002,
  KN_MATMUL_OP = 1003,
  // ElementUnary
  KN_EXP_OP = 1100,
  KN_SQUARE_OP = 1101,
  KN_SQRT_OP = 1102,
  KN_MUL_SCALAR_OP = 1103,
  KN_SILU_OP = 1104,
  KN_SIGMOID_OP = 1105,
  KN_GELU_OP = 1106,
  // non-lax elementunary ops
  KN_RELU_OP = 1150,
  KN_CLAMP_OP = 1151,
  KN_LOG_OP = 1160,
  // ElementBinary
  KN_ADD_OP = 1200,
  KN_MUL_OP = 1201,
  KN_DIV_OP = 1202,
  KN_POW_OP = 1203,
  // Reduction & Normalization
  KN_REDUCTION_0_OP = 1300,
  KN_REDUCTION_1_OP = 1301,
  KN_REDUCTION_2_OP = 1302,
  KN_RMS_NORM_OP = 1350,
  // Concat & Split
  KN_CONCAT_FIRST_OP_ID = 1400,
  KN_CONCAT_0_OP = 1400,
  KN_CONCAT_1_OP = 1401,
  KN_CONCAT_2_OP = 1402,
  KN_CONCAT_LAST_OP_ID = 1409,
  KN_SPLIT_FIRST_OP_ID = 1420,
  KN_SPLIT_0_OP = 1420,
  KN_SPLIT_1_OP = 1421,
  KN_SPLIT_2_OP = 1422,
  KN_CHUNK_0_OP = 1423,
  KN_CHUNK_1_OP = 1424,
  KN_CHUNK_2_OP = 1425,
  KN_SPLIT_LAST_OP_ID = 1429,
  // Communication
  KN_ALLREDUCE_OP = 1900,
  KN_CUSTOMIZED_OP = 1999,
};

3.6 生成樣例

Kernel & block圖的生成邏輯如下：

• 從輸入節點出發，以x，y，z輸入張量為起點，初始化一個空前綴。
• 迭代增長，枚舉算子來構造新節點，每次枚舉一個算子加入（枚舉matmul、add、exp...，合成算子），當枚舉到合成算子，馬上進入block graph的synthesis，每次擴張會檢查合法性：形狀、顯存/SMEM容量、路徑約束。
• 抽象剪枝，計算當前前綴的抽象表達式E，當和canonical form E0不一致時剪枝，生成結束后會得到沒有thread graph的kernel/block圖候選集合。

下面代碼中給出了kernel graph和block graph的生成樣例。

import mirage as mi

def new_kernel_graph():
    kgraph = core.CyKNGraph()
    return KNGraph(kgraph)

def get_rms_linear():
    graph = mi.new_kernel_graph() # kernel graph
    X = graph.new_input(dims=(num_tokens, 4096), dtype=mi.float16)
    W = graph.new_input(dims=(4096, n_local_heads * head_dim + 2 * n_local_kv_heads * head_dim), dtype=mi.float16)
    # block graph
    tb_graph = mi.new_threadblock_graph(grid_dim=(384,1,1), block_dim=(128,1,1), forloop_range=32, reduction_dimx=64)
    tX = tb_graph.new_input(dtensor=X, input_map=(-1, -1, -1), forloop_dim=1)
    tW = tb_graph.new_input(dtensor=W, input_map=(1, -1, -1), forloop_dim=0)
    tM = tb_graph.matmul(tX, tW)
    tAccX = tb_graph.forloop_accum(tX, "rms")
    tAccM = tb_graph.forloop_accum(tM)
    tO = tb_graph.div(tAccM, tAccX)
    tb_graph.new_output(stensor=tO, output_map=(1, -1, -1))
    O = graph.customized([X, W], tb_graph)
    return graph, O
    
def mirage_llama(X, Wqkv, Wo, W13, W2, Kcache, Vcache, kernels):
    func = kernels[0]
    outputs = func(inputs=[X, Wqkv])
    Xqkv = outputs[0]
    Xq = Xqkv[:, : (n_local_heads * head_dim)]
    output_shape = Xq.shape
    Xkv = Xqkv[:, (n_local_heads * head_dim) :]
    Xk, Xv = Xkv.chunk(2, 1)
    Xq = Xq.view(Xq.shape[0], n_local_heads, head_dim)
    Xk = Xk.view(Xk.shape[0], n_local_kv_heads, head_dim)
    Xv = Xv.view(Xv.shape[0], n_local_kv_heads, head_dim)
    output = flashinfer.single_prefill_with_kv_cache(Xq, Kcache, Vcache, causal=True)
    output = torch.matmul(output.reshape(output_shape), Wo)
    X = output
    func = kernels[1]
    outputs = func(inputs=[X, W13])
    X13 = outputs[0]
    X1, X3 = X13.chunk(2, -1)
    output = torch.matmul(X1, W2)
    return output    
 
if __name__ == "__main__":
    X = torch.randn(num_tokens, 4096, dtype=torch.float16, device='cuda:0')
    Wqkv = torch.randn(4096, n_local_heads * head_dim + 2 * n_local_kv_heads * head_dim, dtype=torch.float16, device='cuda:0')
    Wo = torch.randn(n_local_heads * head_dim, 4096, dtype=torch.float16, device='cuda:0')
    W13 = torch.randn(4096, intermediate_size * 2, dtype=torch.float16, device='cuda:0')
    W2 = torch.rand(14336, 4096, dtype=torch.float16, device='cuda:0')
    Kcache = torch.rand(num_kv_tokens, n_local_kv_heads, head_dim, dtype=torch.float16, device='cuda:0')
    Vcache = torch.rand(num_kv_tokens, n_local_kv_heads, head_dim, dtype=torch.float16, device='cuda:0')

    k1 = get_rms_linear() # 此處生成計算圖
    k2 = get_rms_linear2() # 此處生成計算圖
    kernels = [k1, k2]

    for _ in range(16):
        mirage_llama(X, Wqkv, Wo, W13, W2, Kcache, Vcache, kernels)
    torch.cuda.synchronize()

from_json()函數也會生成。以下是創建操作。g是內核圖。

void from_json(json const &j, Graph &g) {
    switch (op_type) {
      case type::KNOperatorType::KN_INPUT_OP: {
        int num_dim, dim[mirage::config::MAX_TENSOR_DIMS];
        type::DataType data_type;
        layout::DmemLayout layout;
        std::vector<size_t> input_strides;
        size_t guidO;
        jop.at("output_tensors")[0].at("num_dims").get_to(num_dim);
        jop.at("output_tensors")[0].at("dim").get_to(dim);
        jop.at("input_strides").get_to(input_strides);
        jop.at("output_tensors")[0].at("data_type").get_to(data_type);
        jop.at("output_tensors")[0].at("layout").get_to(layout);
        jop.at("output_tensors")[0].at("guid").get_to(guidO);
        std::vector<int> dims = to_vector(num_dim, dim);
        // 調用KNGraph的函數
        DTensor const &output =
            g.new_input(dims, input_strides, data_type, layout);
        guid_mapping[output.guid] = guidO;
        break;
      }

new_input是KNGraph的函數。

class KNGraph:
    def new_input(
        self, dims: tuple, strides: tuple = None, dtype: dtype = float16
    ) -> DTensor:
        # use the default strided layout if strides = None
        if strides is None:
            total_elements = 1
            strides = []
            for d in reversed(dims):
                strides.append(total_elements)
                total_elements *= d
            strides = reversed(strides)
        return self.cygraph.new_input(dims, tuple(strides), dtype)

最終到CyTBGraph

cdef class CyTBGraph:
    cdef CppTBGraph *p_bgraph #Hold a CppTBGraph instance

    def __cinit__(self, tuple grid_dim = (), tuple block_dim = (), int forloop_range = -1, int dimx = -1, bgraph = None):
        cdef unsigned long long ptr
        cdef dim3 c_grid_dim
        cdef dim3 c_block_dim
        if bgraph is None:
            c_grid_dim.x = grid_dim[0]
            c_grid_dim.y = grid_dim[1]
            c_grid_dim.z = grid_dim[2]
            c_block_dim.x = block_dim[0]
            c_block_dim.y = block_dim[1]
            c_block_dim.z = block_dim[2]
            self.p_bgraph = new CppTBGraph(c_grid_dim, c_block_dim, forloop_range, dimx)
        else:
            ptr = ctypes.cast(bgraph, ctypes.c_void_p).value
            if isinstance(bgraph, int):
                self.p_bgraph = <CppTBGraph*>(ptr)
            elif isinstance(bgraph, ctypes.c_void_p):
                self.p_bgraph = <CppTBGraph*>(ptr)
    
    def new_input(self, DTensor dtensor, tuple input_map, int forloop_dim, bool store_in_dmem = False):

        cdef int3 c_input_map
        c_input_map.x = input_map[0]
        c_input_map.y = input_map[1]
        c_input_map.z = input_map[2]
        cdef CppDTensor* dtensor_cptr = NULL
        if dtensor is not None:
            dtensor_cptr = dtensor.c_ptr
        cdef CppSTensor* ptr = self.p_bgraph.new_input(dtensor_cptr, c_input_map, forloop_dim, SmemRowMajor, store_in_dmem)
        t = ctypes.cast(<unsigned long long>ptr, ctypes.c_void_p)
        return STensor(t)

    def new_output(self, STensor stensor, tuple output_map, int forloop_dim, str epilogue = None):
        cdef int3 c_output_map
        c_output_map.x = output_map[0]
        c_output_map.y = output_map[1]
        c_output_map.z = output_map[2]
        epilogue_type = string_to_tbepilogue(epilogue)
        self.p_bgraph.new_output(stensor.c_ptr, c_output_map, forloop_dim, epilogue_type)  

    def matmul(self, STensor A, STensor B):
        cdef CppSTensor* ptr = self.p_bgraph.matmul(A.c_ptr, B.c_ptr)
        t = ctypes.cast(<unsigned long long>ptr, ctypes.c_void_p)
        return STensor(t)

    def exp(self, STensor A):
        cdef CppSTensor* ptr = self.p_bgraph.exp(A.c_ptr)
        t = ctypes.cast(<unsigned long long>ptr, ctypes.c_void_p)
        return STensor(t)

    def silu(self, STensor A):
        cdef CppSTensor* ptr = self.p_bgraph.silu(A.c_ptr)
        t = ctypes.cast(<unsigned long long>ptr, ctypes.c_void_p)
        return STensor(t)

0x04 線程塊圖

kernel graph 管理整體計算流，block_graph 管理線程塊級別的并行計算，從而實現高效的 GPU 執行。

塊圖指定與線程塊相關的計算，其中每個節點表示一個塊操作符，指定線程塊內的計算，每條邊是線程塊操作符之間共享的張量。Mirage 將塊圖中的所有中間張量保存在 GPU 共享內存中，有兩個考慮。首先，GPU 共享內存提供的帶寬遠高于設備內存，這種設計允許 Mirage 通過最大限度地將中間結果保存在共享內存中來減少設備內存訪問。其次，對于大小超過共享內存容量且必須存儲在設備內存中的張量，Mirage 使用這些張量將計算分割成多個塊圖，每個塊圖僅包含共享內存中的張量。這種分離不會引入對設備內存的額外訪問。

4.1 屬性

每個塊圖還與一些屬性相關聯，以指定其執行。

4.1.1 網格尺寸

內核中的所有線程塊都由最多 3 維的網格組織，標識為 x、y 和 z。相應地，塊圖與最多三個網格尺寸相關聯，指定沿 x、y 和 z 尺寸的塊數。上圖中的兩個塊圖啟動了 80（即 8 × 10）和 64（即 8 × 8）個塊。

首先，對于圖定義的內核操作符（例如內核圖中的 Q、K 和 V）的每個輸入張量，相關的塊圖包含一個 imap，它指定如何將輸入張量劃分為各個塊的子張量。對于每個網格尺寸（即 x、y 或 z），imap 將其映射到（1）輸入張量的數據維度或（2）特殊的副本維度 ??。對于（1），映射的數據維度在網格尺寸上的塊之間均勻劃分。對于（2），輸入張量在這些線程塊之間復制。

其次，對于塊圖的每個輸出張量，塊圖包括一個 omap，它指定所有塊的輸出如何連接以構建內核操作符的最終輸出。在 omap 中，每個網格尺寸必須映射到輸出張量的數據維度，因為不同的塊必須保存到設備內存中的不相交張量。對于上圖中形狀為 [h=1, s=8, d=64] 的 B，其 omap={x<->h, y<->d} 表示具有相同 x 索引的塊沿 h 維度連接，具有相同 y 索引的塊沿 d 維度連接，從而得到形狀為 [h=8, s=8, d=640] 的張量 B。

4.1.2 For-loop 尺寸

為了適應大輸入張量在共享內存中并允許緩存重用，與每個塊圖相關的第二個屬性是 for-loop 尺寸，它們共同指定塊圖執行多少次以完成內核。相應地，每個輸入張量首先被發送到輸入迭代器，該迭代器從設備內存加載張量的一部分到共享內存。每個輸入迭代器都與 fmap 關聯，以指定每次迭代加載輸入張量的哪一部分。形式上，fmap 將每個 for-loop 維度映射到（1）輸入張量的數據維度或（2）副本維度 ??。與 imap 的語義類似，輸入張量沿該維度均勻劃分為（1）并在（2）中復制。

此外，塊圖包含輸出累加器，以在共享內存中跨迭代累積其輸出，并將最終結果保存回設備內存。與輸入迭代器類似，輸出累加器也與 fmap 關聯，以指定不同迭代的輸出張量如何組合以產生最終結果。具體來說，fmap 將每個 for-loop 維度映射到數據維度，這導致輸出沿該維度連接，或副本維度 ??，這導致輸出在共享內存中累積。

4.2 Python 代碼

TBGraph 是塊圖的實現。每個自定義操作（embedding，attention，MLP）都會創建對應的thread block，用于定義該級別的具體執行方式，這些thread block 被編譯為CUDA 內核，在GPU上以warp和線程方式并行執行。

TBGraph的特點如下：

• 節點分類如下：

  • 預定義算子，對應CUTLASS或者ThunderKittens等CUDA組件庫中封裝好的共享內存上的一些操作（例如MatMul、Mul、Accum等block ops）
  • 合成算子，包含一個thread graph

• 邊的特點是：

  • Tensor，SEME tensor，所有暫存tensor默認放在共享內存，減少DRAM訪問

class TBGraph:
    def __init__(self, graph):
        self.cygraph = graph

    def new_input(
        self,
        dtensor: DTensor,
        input_map: tuple,
        forloop_dim: int,
        store_in_dmem: bool = False,
    ):
        return self.cygraph.new_input(dtensor, input_map, forloop_dim, store_in_dmem)

    def new_output(self, stensor: STensor, output_map: tuple, forloop_dim: int = -1):
        return self.cygraph.new_output(stensor, output_map, forloop_dim)

    def matmul(self, A: STensor, B: STensor):
        return self.cygraph.matmul(A, B)

    def exp(self, A: STensor):
        return self.cygraph.exp(A)

    def silu(self, A: STensor):
        return self.cygraph.silu(A)

    def gelu(self, A: STensor):
        return self.cygraph.gelu(A)

    def relu(self, A: STensor):
        return self.cygraph.relu(A)

    def clamp(self, A: STensor, min_val: float, max_val: float):
        return self.cygraph.clamp(A, min_val, max_val)

    def square(self, A: STensor):
        return self.cygraph.square(A)

    def sqrt(self, A: STensor):
        return self.cygraph.sqrt(A)

    def mul_scalar(self, A: STensor, scalar: float):
        return self.cygraph.mul_scalar(A, scalar)

    def add(self, A: STensor, B: STensor):
        return self.cygraph.add(A, B)

    def mul(self, A: STensor, B: STensor):
        return self.cygraph.mul(A, B)

    def div(self, A: STensor, B: STensor):
        return self.cygraph.div(A, B)

    def sub(self, A: STensor, B: STensor):
        return self.cygraph.sub(A, B)

    def reduction(self, A: STensor, dim: int):
        return self.cygraph.reduction(A, dim)

    def reduction_max(self, A: STensor, dim: int):
        return self.cygraph.reduction_max(A, dim)

    def rms_norm(self, A: STensor):
        return self.cygraph.rms_norm(A)

    def concat(self, A: STensor, B: STensor, dim: int):
        return self.cygraph.concat(A, B, dim)

    def forloop_accum(self, A: STensor, acc: str = None):
        return self.cygraph.forloop_accum(A, acc)

    def forloop_accum_rescale(self, A: STensor, B: STensor, acc: str = None):
        return self.cygraph.forloop_accum_rescale(A, B, acc)

    def forloop_accum_max(self, A: STensor):
        return self.cygraph.forloop_accum_max(A)

TBGraph 構造函數傳參 graph 是 CyTBGraph 類型。因此，TBGraph 的所有操作都轉交給 CyTBGraph 進行處理。

TBGraph(CyTBGraph(grid_dim, block_dim, 1, 64))

生成時候TBGraph，傳入

grid_dim=(X,Y,Z) // 線程塊網格維度

block_dim=(128,1,1) // 線程塊內線程維度

這表明每個thread block包含128個線程，按一維方式組織。

grid_dim和block_dim這兩個參數被CyTBGraph使用。

4.3 橋梁

new_threadblock_graph函數中，會看到CyTBGraph。

def new_threadblock_graph(
    grid_dim: tuple, block_dim: tuple, forloop_range: int, reduction_dimx: int
):
    bgraph = core.CyTBGraph(grid_dim, block_dim, forloop_range, reduction_dimx)
    return TBGraph(bgraph)

CyTBGraph會調用到CppTBGraph。

cdef class CyTBGraph:
    cdef CppTBGraph *p_bgraph #Hold a CppTBGraph instance

    def __cinit__(self, tuple grid_dim = (), tuple block_dim = (), int forloop_range = -1, int dimx = -1, bgraph = None):
        cdef unsigned long long ptr
        cdef dim3 c_grid_dim
        cdef dim3 c_block_dim
        if bgraph is None:
            c_grid_dim.x = grid_dim[0]
            c_grid_dim.y = grid_dim[1]
            c_grid_dim.z = grid_dim[2]
            c_block_dim.x = block_dim[0]
            c_block_dim.y = block_dim[1]
            c_block_dim.z = block_dim[2]
            self.p_bgraph = new CppTBGraph(c_grid_dim, c_block_dim, forloop_range, dimx)
        else:
            ptr = ctypes.cast(bgraph, ctypes.c_void_p).value
            if isinstance(bgraph, int):
                self.p_bgraph = <CppTBGraph*>(ptr)
            elif isinstance(bgraph, ctypes.c_void_p):
                self.p_bgraph = <CppTBGraph*>(ptr)
            else:
                assert False, "bgraph must be an integer or ctypes.c_void_p, but got " + str(type(bgraph))

CppTBGraph 對應 "mirage::threadblock::Graph"，這就是 C++的實現。

cdef cppclass CppTBGraph "mirage::threadblock::Graph"

4.4 C++代碼

塊圖在代碼中是mirage::threadblock::Graph類，這是中間層次的計算圖。下面是精簡版代碼。

Block graph主要包含以下屬性來表示程序并行切分的信息

• Grid Dims(x, y, z)：kernel啟動多少block
• imap：作用是輸入分塊，grid-dims到input tensor dims的映射
• omap：作用是輸出拼接，grid-dims到output tensor dims的映射
• For-loop body：允許block多次迭代來復用SMEM，流水線形式來充分計算和訪存重疊，把DRAM讀寫完全隱藏到計算時間里，同時也充分服用SMEM，形如InputIterator->...->Accum->...->OutputSaver
• fmap：決定每次迭代取哪一塊數據，比如 fmap={i?h} 沿 h 維滑窗。

namespace mirage {
namespace threadblock {

class Graph {
private:
  struct pair_hash {
    size_t operator()(std::pair<int, int> const &p) const;
  };

public:
  Graph();
  Graph(dim3 grid_dim, dim3 block_dim, int forloop_range, int reduction_dimx);
  ~Graph();
  Graph(Graph const &) = delete;
  Graph &operator=(Graph const &) = delete;
  // input operator

  STensor new_input(mirage::kernel::DTensor const &dtensor,
                    int3 input_map,
                    int forloop_dim,
                    mirage::layout::SmemLayout layout,
                    bool store_in_dmem = false);
  STensor *new_input(mirage::kernel::DTensor const *dtensor,
                     int3 input_map,
                     int forloop_dim,
                     mirage::layout::SmemLayout layout,
                     bool store_in_dmem = false);
  TBOperator *create_input_op(mirage::kernel::DTensor const &dtensor,
                              int3 input_map,
                              int forloop_dim,
                              mirage::layout::SmemLayout layout,
                              bool store_in_dmem = false);
  // matmul operator
  STensor matmul(STensor const &A, STensor const &B);
  STensor *matmul(STensor const *A, STensor const *B);
  TBOperator *create_matmul_op(STensor const &A, STensor const &B);
  // element unary operator
  STensor exp(STensor const &A);
  STensor *exp(STensor const *A);
  STensor square(STensor const &A);
  STensor *square(STensor const *A);
  STensor sqrt(STensor const &A);
  STensor *sqrt(STensor const *A);
  STensor silu(STensor const &A);
  STensor *silu(STensor const *A);
  STensor gelu(STensor const &A);
  STensor *gelu(STensor const *A);
  STensor relu(STensor const &A);
  STensor *relu(STensor const *A);

  // element binary operators
  STensor add(STensor const &A, STensor const &B);
  STensor *add(STensor const *A, STensor const *B);
  STensor mul(STensor const &A, STensor const &B);
  STensor *mul(STensor const *A, STensor const *B);
  STensor div(STensor const &A, STensor const &B);
  STensor *div(STensor const *A, STensor const *B);
  STensor sub(STensor const &A, STensor const &B);
  STensor *sub(STensor const *A, STensor const *B);
  STensor pow(STensor const &A, STensor const &B);
  STensor *pow(STensor const *A, STensor const *B);

  // reduction operator
  STensor reduction(STensor const &A, int dim);
  STensor *reduction(STensor const *A, int dim);
  TBOperator *create_reduction_op(STensor const &A, int dim);

  // reduction_to_dimx operator
  STensor reduction_to_dimx(STensor const &A, int dim);
  TBOperator *create_reduction_to_dimx_op(STensor const &A, int dim);

  // reduction_max operator
  std::vector<STensor> reduction_max(STensor const &A, int dim);
  std::vector<STensor *> reduction_max(STensor const *A, int dim);
  TBOperator *create_reduction_max_op(STensor const &A, int dim);

  // rms_norm operator
  STensor rms_norm(STensor const &A);
  STensor *rms_norm(STensor const *A);
  TBOperator *create_rms_norm_op(STensor const &A);

public:
  dim3 grid_dim, block_dim, cluster_dim{4, 4, 1};
  int forloop_range;
  int reduction_dimx;
  std::vector<mirage::threadblock::TBOperator *> operators;
  // memory allocator
  off_t smem_offset;
  std::vector<std::pair<off_t, size_t>> allocated_tensors;

  using OpType = TBOperator;
  using TensorType = STensor;
};

void from_json(json const &j, Graph &g);

} // namespace threadblock
} // namespace mirage

以 reduction_max 為例，代碼如下：

std::vector<STensor *> Graph::reduction_max(STensor const *input, int dim) {
  TBOperator *op = create_reduction_max_op(*input, dim);
  assert(op != nullptr);
  operators.push_back(op);
  return std::vector<STensor *>{&op->output_tensors[0], &op->output_tensors[1]};
}

TBOperator *Graph::create_reduction_max_op(STensor const &input, int dim) {
  TBOperator *op =
      new TBReductionOp(this, input, dim, -1 /*size = -1 for max*/);
  // Check shmem usage
  size_t smem_usage = calculate_shared_memory_usage(op);
  if (smem_usage > mirage::config::MAX_SMEM_SIZE) {
    delete op;
    return nullptr;
  } else {
    return op;
  }
}

4.5 TBOperator

塊圖在CUDA thread block級別執行，使用TBOperator來表示所包含的操作。也使用TBInputOp連接到上層的mu'Graph的張量。

以 Attention 層為例，其 thread block 可能包含如下結構：

Thread Block for Attention:
TB_INPUT_OP（輸入QKV張量）
    ↓
TB_MATMUL_OP（計算QK^T）
    ↓
TB_REDUCTION_OP（Softmax歸一化）
    ↓
TB_MATMUL_OP（計算Attention輸出）
    ↓
TB_FORLOOP_ACCUM_NO_RED_OP（累積計算）

TBOperator的定義如下：

namespace mirage {
namespace threadblock {

class Graph;

class TBOperator {
public:
  TBOperator(Graph *graph, mirage::type::TBOperatorType);
  TBOperator(Graph *graph, mirage::type::TBOperatorType, STensor const &input1);
  TBOperator(Graph *graph,
             mirage::type::TBOperatorType,
             STensor const &input1,
             STensor const &input2);
  TBOperator(Graph *graph,
             mirage::type::TBOperatorType,
             std::vector<STensor> const &inputs);
  int get_input_stensors(STensor **inputs);
  int get_output_stensors(STensor **inputs);

  virtual ~TBOperator();

  virtual operator json() const = 0;

public:
  Graph *bgraph;
  mirage::type::TBOperatorType op_type;
  std::vector<STensor> input_tensors;
  std::vector<STensor> output_tensors;
};

TBOperator 的派生類舉例。

class TBInputOp : public TBOperator {
public:
  TBInputOp(Graph *_graph,
            mirage::kernel::DTensor const &dtensor,
            int3 input_map,
            int forloop_dim,
            mirage::layout::SmemLayout layout,
            bool store_in_dmem);
  ~TBInputOp();

  operator json() const override;
  size_t get_dtensor_guid();

public:
  mirage::kernel::DTensor dtensor;
  int3 input_map;
  int forloop_dim;
};

class TBOutputOp : public TBOperator {
public:
  TBOutputOp(Graph *_graph,
             STensor const &stensor,
             int3 output_map,
             int forloop_dim,
             mirage::type::TBEpilogueType allreduce);
  ~TBOutputOp();

  operator json() const override;
  size_t get_dtensor_guid();

public:
  mirage::kernel::DTensor dtensor;
  int3 output_map;
  int forloop_dim;
  mirage::type::TBEpilogueType epilogue;
};

TBOperatorType的類型為：

enum TBOperatorType {
  TB_UNKOWN = 2000,
  TB_INPUT_OP = 2001,
  TB_OUTPUT_OP = 2002,
  TB_MATMUL_OP = 2003,
  // ElementUnary
  TB_EXP_OP = 2100,
  TB_SQUARE_OP = 2101,
  TB_SQRT_OP = 2102,
  TB_MUL_SCALAR_OP = 2103,
  TB_SILU_OP = 2104,
  TB_SIGMOID_OP = 2105,
  TB_GELU_OP = 2106,
  // non-lax elementunary ops
  TB_RELU_OP = 2150,
  TB_CLAMP_OP = 2151,
  TB_LOG_OP = 2160,
  // ElementBinary
  TB_ADD_OP = 2200,
  TB_MUL_OP = 2201,
  TB_DIV_OP = 2202,
  TB_SUB_OP = 2203,
  TB_POW_OP = 2204,
  // Reduction and Normalization
  TB_REDUCTION_FIRST_OP_ID = 2300,
  TB_REDUCTION_0_OP = 2301,
  TB_REDUCTION_1_OP = 2302,
  TB_REDUCTION_2_OP = 2303,
  TB_REDUCTION_0_TO_DIMX_OP = 2304,
  TB_REDUCTION_1_TO_DIMX_OP = 2305,
  TB_REDUCTION_2_TO_DIMX_OP = 2306,
  TB_REDUCTION_0_MAX_OP = 2307,
  TB_REDUCTION_1_MAX_OP = 2308,
  TB_REDUCTION_2_MAX_OP = 2309,
  TB_REDUCTION_LAST_OP_ID = 2349,
  TB_RMS_NORM_OP = 2350,
  // Concat & Split
  TB_CONCAT_FIRST_OP_ID = 2400,
  TB_CONCAT_0_OP = 2400,
  TB_CONCAT_1_OP = 2401,
  TB_CONCAT_2_OP = 2402,
  TB_CONCAT_LAST_OP_ID = 2409,
  TB_CONCAT_THEN_MATMUL_OP = 2411,
  TB_SPLIT_FIRST_OP_ID = 2420,
  TB_SPLIT_0_OP = 2420,
  TB_SPLIT_1_OP = 2421,
  TB_SPLIT_2_OP = 2422,
  TB_SPLIT_LAST_OP_ID = 2429,
  // Forloop Accum
  // LD indicates last dimension
  TB_FORLOOP_ACCUM_FIRST_OP = 2500,
  TB_FORLOOP_ACCUM_NO_RED_OP = 2500,
  TB_FORLOOP_ACCUM_RED_LD_SUM_OP = 2501,
  TB_FORLOOP_ACCUM_RED_LD_MEAN_OP = 2502,
  TB_FORLOOP_ACCUM_RED_LD_RMS_OP = 2503,
  TB_FORLOOP_ACCUM_REDTOX_LD_SUM_OP = 2504,
  TB_FORLOOP_ACCUM_NO_RED_RESCALE_OP = 2505,
  TB_FORLOOP_ACCUM_RED_LD_SUM_RESCALE_OP = 2506,
  TB_FORLOOP_ACCUM_MAX_OP = 2507,
  TB_FORLOOP_ACCUM_LAST_OP = 2599,
  TB_CUSTOMIZED_OP = 2999
};

我們用 TBReductionOp 來看看具體實現。

class TBReductionOp : public TBOperator {
public:
  TBReductionOp(Graph *graph,
                STensor const &_input,
                int reduce_dim,
                int reduce_size);
  ~TBReductionOp();

  operator json() const override;

public:
  int reduce_dim, reduce_size;
};

TBReductionOp::TBReductionOp(Graph *bgraph,
                             STensor const &input,
                             int dim,
                             int size)
    : TBOperator(bgraph,
                 size == 1 ? (mirage::type::TBOperatorType)(
                                 mirage::type::TB_REDUCTION_0_OP + dim)
                 : size == -1
                     ? (mirage::type::TBOperatorType)(
                           mirage::type::TB_REDUCTION_0_MAX_OP + dim)
                     : (mirage::type::TBOperatorType)(
                           mirage::type::TB_REDUCTION_0_TO_DIMX_OP + dim),
                 input),
      reduce_dim(dim), reduce_size(size) {
  STensor output = input;
  assert(output.num_dims > reduce_dim);
  assert(output.layout == mirage::layout::SmemRowMajor);
  output.dim[reduce_dim] = reduce_size == -1 ? 1 : reduce_size;
  output.owner_op = this;
  output.owner_ts_idx = 0;
  output.guid = STensor::next_guid++;
  output.after_accum = input.after_accum;
  output.smem_offset = bgraph->allocate_fingerprint(output);
  output_tensors.push_back(output);
  if (reduce_size == -1) {
    // For max reduction, we need to allocate another tensor for difference
    STensor diff = output;
    diff.owner_ts_idx = 1;
    diff.guid = STensor::next_guid++;
    diff.smem_offset = bgraph->allocate_fingerprint(diff);
    output_tensors.push_back(diff);
  }
}

4.6 生成樣例

在Mirage項目中，block_graph是在創建自定義操作時插入得。

• 可以在Python代碼直接通過mi.new_threadblock_graph()直接構建。
• 在 demo.py 中逐層構建模型時，每一層都會插入相應的 block_graph 來定義該層在線程塊級別的具體執行方式。即，每個自定義操作的創建過程中：每當調用 PersistentKernel 的 layer 方法時，都會在內部創建一個包含具體線程塊級計算的 block_graph。比如，attention_layer()，rmsnorm_linear_layer()， def embed_layer()內部都會構建block_graph。
• 也可以在C++代碼直接構建。

4.6.1 Python代碼直接構建

原始的rms_linear公式為：

邏輯如下：

針對rms_linear，MPK的轉換代碼如下：

def get_rms_linear():
    graph = mi.new_kernel_graph() # kernel graph
    X = graph.new_input(dims=(num_tokens, 4096), dtype=mi.float16)
    W = graph.new_input(dims=(4096, n_local_heads * head_dim + 2 * n_local_kv_heads * head_dim), dtype=mi.float16)
    # block graph
    tb_graph = mi.new_threadblock_graph(grid_dim=(384,1,1), block_dim=(128,1,1), forloop_range=32, reduction_dimx=64)
    tX = tb_graph.new_input(dtensor=X, input_map=(-1, -1, -1), forloop_dim=1)
    tW = tb_graph.new_input(dtensor=W, input_map=(1, -1, -1), forloop_dim=0)
    tM = tb_graph.matmul(tX, tW)
    tAccX = tb_graph.forloop_accum(tX, "rms")
    tAccM = tb_graph.forloop_accum(tM)
    tO = tb_graph.div(tAccM, tAccX)
    tb_graph.new_output(stensor=tO, output_map=(1, -1, -1))
    O = graph.customized([X, W], tb_graph)
    return graph, O

其中，new_threadblock_graph()內部會直接構建TBGraph(bgraph)。

def new_threadblock_graph(
    grid_dim: tuple, block_dim: tuple, forloop_range: int, reduction_dimx: int
):
    bgraph = core.CyTBGraph(grid_dim, block_dim, forloop_range, reduction_dimx)
    return TBGraph(bgraph)

調整之后，其對應的邏輯如下：

4.6.2 PersistentKernel 的 layer 方法間接構建

比如：rmsnorm_linear_layer()，attention_layer()等函數中，都構建了TBGrapattach_inputh(CyTBGraph(grid_dim, block_dim, 1, 64))。

mpk.embed_layer(input=x, weight=w_embed, output=embed_out, grid_dim=(1, 1, 1), block_dim=(128, 1, 1))
mpk.rmsnorm_linear_layer(input=x, weight_norm=w_norm_attn, weight_linear=w_qkv, output=attn_in, grid_dim=(96, 1, 1), block_dim=(128, 1, 1))

在embed_layer函數內部，會構建 TBGraph(bgraph)。

    def embed_layer(
        self,
        input: DTensor, # [batch_size, num_spec_tokens]
        weight: DTensor, # [vocab_size, hidden_size]
        output: DTensor, # [batch_size, hidden_size]
        grid_dim: tuple,
        block_dim: tuple,
        input_source: int = 0, # 0: all_tokens, 1: input_token
    ):
        tb_graph = TBGraph(CyTBGraph(grid_dim, block_dim, 1, 64))
        tb_graph.new_input(input, (-1, 1, -1), -1, True)
        tb_graph.new_input(weight, (1, -1, -1), -1, True)
        tb_graph.new_input(output, (1, 0, -1), -1, True)
        self.kn_graph.customized([input, weight, output], tb_graph)
        self.kn_graph.register_task(tb_graph, "embedding", [input_source])

4.6.3 C++代碼直接構建

在graph.cc，自定義操作也會構建block graph。這個是把python定義的圖進行轉換到c++。

void from_json(json const &j, Graph &g) {
      case type::KNOperatorType::KN_CUSTOMIZED_OP: {
        std::vector<DTensor> inputs;
        for (auto const &jinput : jop.at("input_tensors")) {
          size_t guid;
          jinput.at("guid").get_to(guid);
          inputs.push_back(get_tensor_from_guid(guid));
        }
        threadblock::Graph bgraph;
        from_json(jop.at("bgraph"), bgraph);
        // 將muGraph的張量連接到block-graph的輸入
        for (size_t i = 0; i < bgraph.operators.size(); ++i) {
          if (bgraph.operators[i]->op_type == type::TB_INPUT_OP) {
            static_cast<threadblock::TBInputOp *>(bgraph.operators[i])
                ->dtensor = inputs[i];
          }
        }
        std::vector<DTensor> outputs = g.customized(inputs, bgraph);
        for (size_t i = 0; i < outputs.size(); ++i) {
          size_t guidO;
          jop.at("output_tensors")[i].at("guid").get_to(guidO);
          guid_mapping[outputs[i].guid] = guidO;
        }

        break;
      }

0x05 線程圖

線程圖進一步將計算范圍從塊縮小到單個線程。與塊圖類似，每個線程圖也與塊尺寸相關聯，指定塊內線程的組織，以及 for-loop 尺寸，定義完成定義計算的總迭代次數。每個線程圖包括輸入迭代器，每個迭代器從 GPU 共享內存加載輸入張量到寄存器文件，以及輸出累加器，每個累加器從寄存器文件保存輸出張量回到共享內存。線程圖是 uGraph 中的最低級別圖，僅包含預定義的線程操作符。

線程圖是最底層的計算圖，在代碼中沒有顯式定義為獨立的圖結構，而是在block-graph的操作中體現。

主要特征：

• 執行單位：在CUDA thread warp或者單個thread級別執行
• 操作細節：包含具體的線程級別計算和內存訪問模式

• Thread graph

• • 邊：Tensor，thread graph的張量位于寄存器

  • 節點：描述單個thread內寄存器上的流水，load->emelent-wise->store。只包含預定義算子，對應封裝好的寄存器上的一些操作，也支持for loop維+寄存器累加，不過mirage默認用規則化融合快速合成，避免在最細層再做大搜索

• 對每個候選內的block圖，找出符合form的子圖（通常是一串element-wise+reduce），把它們融成thread graph節點，表示這段計算可以放在寄存器里完成

• 規則化、無需大搜索。thread只做局部融合和固定模式的for-loop，避免搜索指數爆炸，這樣仍能讓大多數逐元素算子留在寄存器中，減少shared-memory訪問

0xFF 參考

如何評價CMU將LLM轉化為巨型內核的Mirage Persistent Kernel(MPK)工作？

Mirage: A Multi-Level Superoptimizer for Tensor Programs 簡記 塵伊光

OSDI2025論文筆記：Mirage: A Multi-Level Superoptimizer for Tensor Programs 畫餅充饑

Mirage: A Compiler for High-Performance Tensor Programs on GPUs

https://mirage-project.readthedocs.io/en/latest/mugraph.html

https://mirage-project.readthedocs.io/en/latest/transpiler.html

https://zhihaojia.medium.com/compiling-llms-into-a-megakernel-a-path-to-low-latency-inference-cf7840913c17

舍棄CUDA編程！CMU等用代碼將LLM編譯成巨型內核，推理延遲降6.7倍 機器之心Pro