從零開始解析Transformer，目標(biāo)是：(1) 解析Transformer如何運(yùn)作，以及為何如此運(yùn)作，讓新同學(xué)可以入門；(2) 力爭融入一些比較新的或者有特色的論文或者理念，讓老鳥也可以有所收獲。

探秘Transformer系列之（36）--- 大模型量化方案

0x00 概述

繼前一篇介紹了大模型量化基礎(chǔ)之后，本篇我們來看看一些量化方案。

因?yàn)榇蠹夷壳岸加脡嚎s到某個(gè)bit來衡量量化方案，因此我們接下來就按照量化比特來進(jìn)行分類學(xué)習(xí)。

0x01 8位量化

因?yàn)槟壳坝布?(例如 NVIDIA GPU、Intel CPU、高通 DSP 等) 普通都支持INT8 GEMM，因此為了加快推理速度，研究人員提出了將 weight 和 activation 量化為 INT8 (即 W8A8)的方案。

下圖給出了幾種8bit量化方案的對(duì)比。

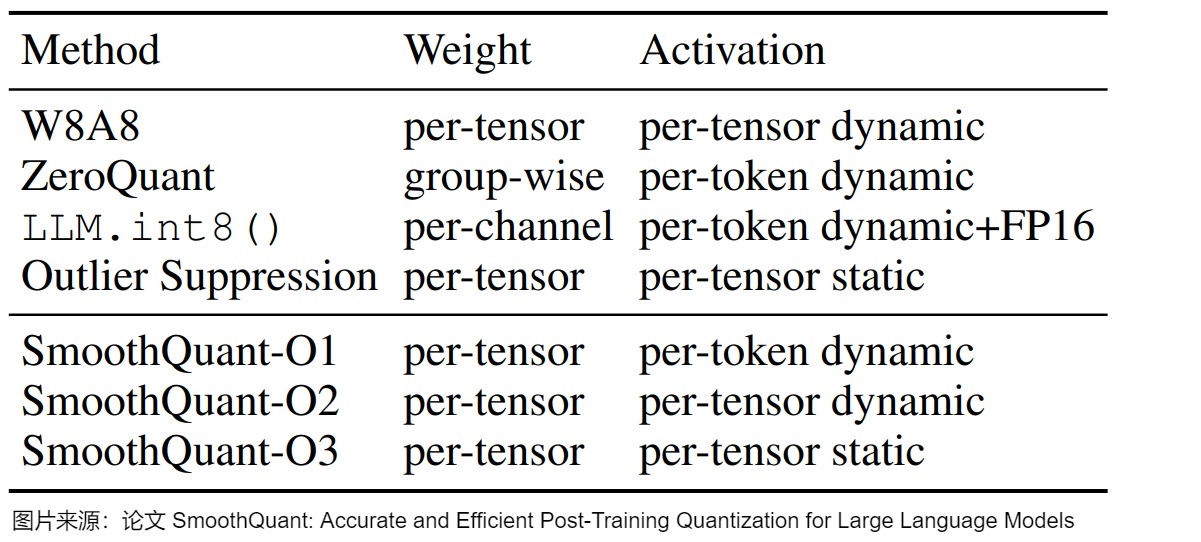
本節(jié)介紹的三種方案特點(diǎn)摘要如下。

方法	量化權(quán)重與激活	特點(diǎn)
LLM.int8()	W8A8	混合精度量化，離群點(diǎn)保持FP16，其它值量化為INT8
ZeroQuant	W8A8	應(yīng)用Dynamic per-token activation 量化和分組 weight 量化。
SmoothQuant	W8A8	提出了一種按通道縮放的方法，將高精度量化的復(fù)雜性從激活轉(zhuǎn)移到權(quán)重，借此平滑激活異常值。

1.1 LLM.int8()

LLM.int8()出自論文“ LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale”，是 LLM 量化早期工作之一。論文的核心思想是分而治之。對(duì)絕大部分權(quán)重（Per-channel）和激活（Per-token）用8bit量化（vector-wise）。對(duì)離群特征的幾個(gè)維度保留16bit，不進(jìn)行量化。

1.1.1 動(dòng)機(jī)

作者首先提出了activation outlier概念，這是后續(xù)大模型量化一直都在注重的點(diǎn)，這兩年大模型的優(yōu)化主要集中在保持activation outlier對(duì)應(yīng)的權(quán)重的基礎(chǔ)上如何做量化。

LLMs的激活非常難以量化，是因?yàn)榧せ钪袝?huì)出現(xiàn)具有大幅度的activation outlier，導(dǎo)致較大的量化誤差和準(zhǔn)確性下降。這些離群值與正常值相比會(huì)有數(shù)百倍的數(shù)值差距。activation outlier影響巨大，容易導(dǎo)致量化失敗。因?yàn)槿绻凑諒埩苛炕姆桨福瑫?huì)一個(gè)tensor共享一個(gè)縮放值，這樣，只要有一個(gè)異常值就能破壞量化的精度。試想一下，張量的大部分值都在0到1之間，假設(shè)有一個(gè)異常值等于一萬，量化之后，這一個(gè)異常值就把其它的值拉到0了，會(huì)產(chǎn)生很大的精度損失。但同時(shí)又有研究表明，這部分離群值會(huì)對(duì)模型的性能產(chǎn)生顯著影響，因此必須想辦法保留離群值而不是直接清零，這就產(chǎn)生了一個(gè)難以調(diào)和的矛盾。

作者發(fā)現(xiàn)激活中的異常值集中在一小部分通道中，且outliers占據(jù)的維度很少(不到1%)。于是作者思考，是否可以把異常值單獨(dú)分出來處理。剩下的部分只使用一個(gè)縮放值就可以得到很好的結(jié)果了。另外，作者認(rèn)為，其實(shí)換個(gè)角度來看，矩陣乘法可以看成是左邊矩陣的行和右邊矩陣的列在做點(diǎn)乘。如果我們把左邊矩陣按行做量化，右邊矩陣按列做量化，那么就可以得到更加精確的量化值，可以進(jìn)一步得到更高的精度。

1.1.2 方案

基于以上思考，論文提出了一個(gè)兩步量化方法 LLM.int8()。

• 逐向量量化 。具體是：
  • 從輸入的隱含狀態(tài)中，按列提取異常值 (離群特征，即大于某個(gè)閾值的值)。
  • 根據(jù)輸入通道內(nèi)的離群值分布將激活和權(quán)重分成離群值和普通值兩個(gè)不同的部分。包含激活值和權(quán)重的異常數(shù)據(jù)的通道以FP16格式存儲(chǔ)，其他通道則以INT8格式存儲(chǔ)。后續(xù)會(huì)對(duì)每個(gè)向量內(nèi)積使用不同的歸一化常數(shù)。
• 混合精度矩陣分解。具體是：
  • 對(duì)絕大部分權(quán)重和激活的正常特征仍然用8bit量化（vector-wise）后計(jì)算（W8A8），計(jì)算完成后再量化為FP16。對(duì)離群特征的幾個(gè)維度保留FP16，對(duì)其做高精度的矩陣乘法（W16A16）。
  • 把反量化非離群值的矩陣乘結(jié)果與離群值矩陣乘結(jié)果相加，獲得最終的 FP16 結(jié)果。

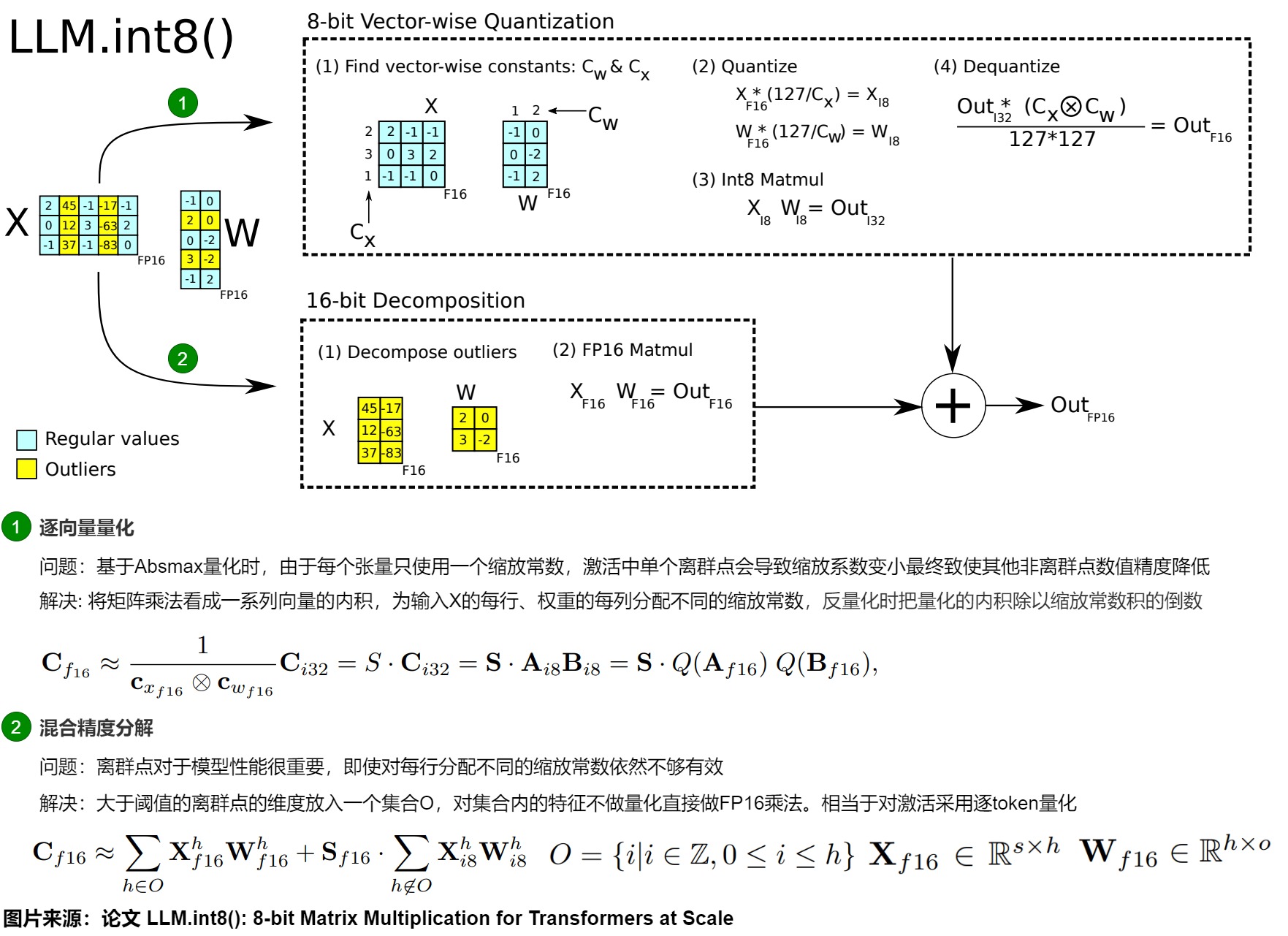
具體如下圖所示，通過離群(Outlier)檢測，把輸入X和權(quán)重W中包含異常值的行、列挑選出來直接做fp16的浮點(diǎn)矩陣乘法，然后剩下的正常點(diǎn)（X每一行用absmax進(jìn)行量化、W每一列用absmax進(jìn)行量化）量化后進(jìn)行int8乘法再反量化回fp16，最后把它們累加起來作為最終結(jié)果輸出。

8位數(shù)據(jù)類型和量化

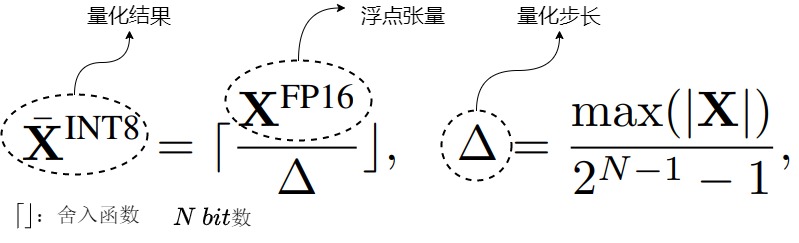
我們首先看看8位數(shù)據(jù)類型和量化的特點(diǎn)。這里介紹的是高精度非對(duì)稱量化 (Zeropoint quantization) 和對(duì)稱量化 (Absmax quantization)。雖然 Zeropoint 量化通過使用數(shù)據(jù)類型的全位范圍來提供高精度，但由于實(shí)際的限制，它很少使用。Absmax 量化是最常用的技術(shù)。

下圖(a)表示Absmax量化，b)表示Zeropoint量化。[β，α]分別表示區(qū)間最小和最大值。

• Absmax量化：除以絕對(duì)值的最大值乘127從而把輸入縮放到8位寬 [?127,127] ， ?? 表示取最近鄰整數(shù)，記\(s_{xfl16}\)為縮放系數(shù)。該方法即為縮放量化。
• Zeropoint量化：上述量化方案對(duì)于ReLU的輸出只有正區(qū)間被使用，而Zeropoint提出使用動(dòng)態(tài)區(qū)間 ndx 縮放，使用零點(diǎn) zpx 平移，從而可使用全區(qū)間數(shù)值。該方法即為仿射量化，更準(zhǔn)確但由于實(shí)際限制該方法較少使用。

逐向量量化（vector-wise quantization）

當(dāng)進(jìn)行Absmax量化時(shí)，會(huì)為每個(gè) tensor 使用一個(gè) scaling 常數(shù)。由于每個(gè)tensor只使用一個(gè)縮放常數(shù)，激活中存在單個(gè)離群點(diǎn)會(huì)導(dǎo)致縮放系數(shù)變小，最終致使其他非離群點(diǎn)數(shù)值精度降低。如果每個(gè)張量有多個(gè) scaling 常數(shù)就可以緩解此問題。因此，作者使用了 Vector-wise Quantization。

Vector-wise Quantization具體為：將矩陣乘法看成一系列向量（獨(dú)立的行與列）的內(nèi)積，可對(duì)每個(gè)內(nèi)積使用不同的歸一化常數(shù)。對(duì)于給定輸入 \(X_{f16}\)和權(quán)重 \(W_{f16}\)，輸入為FP16的int8矩陣乘法，我們?yōu)檩斎?\(X_{f16} \in R^{s×?}\) 的每行、權(quán)重 \(W_{f16} \in R^{?×o}\) 的每列分配不同的縮放常數(shù) \(c_{xf16}\) 和 \(c_{wf16}\) ，反量化時(shí)把量化的內(nèi)積除以縮放常數(shù)積的倒數(shù)。對(duì)于整個(gè)矩陣乘法，這相當(dāng)于外積\(c_{xf16}?c_{wf16}\)的反規(guī)范化（denormalization）。并且，可以在下一個(gè)操作前，通過反歸一化恢復(fù)矩陣乘法的輸出。

混合精度分解（mixed precision decomposition）

參數(shù)規(guī)模達(dá)到十億級(jí)的 8-bit Transformer 的一個(gè)重要問題是，它們具有異常值特征，需要高精度的量化。然而， Vector-wise Quantization（量化隱藏狀態(tài)的每一行）對(duì)異常值特征依然不夠有效。作者觀察到，這些異常值特征在實(shí)踐中既非常稀疏又有規(guī)律，僅占所有特征維度的 0.1%。因此，作者開發(fā)了一種新的矩陣乘法的混合精度分解技術(shù)：將大于閾值 \(\alpha\) 的離群點(diǎn)的維度放入一個(gè)集合O，對(duì)集合內(nèi)的特征不做量化、直接做FP16乘法，而其他維度進(jìn)行8位乘法。實(shí)驗(yàn)發(fā)現(xiàn)，當(dāng)\(\alpha\)=6.0，就足以抵消量化帶來的降級(jí)影響（performance degradation） 。因?yàn)楫惓Ｖ堤卣骶S度通常小于7即 |O|≤7 ，因此分解操作基本只消耗很少內(nèi)存。

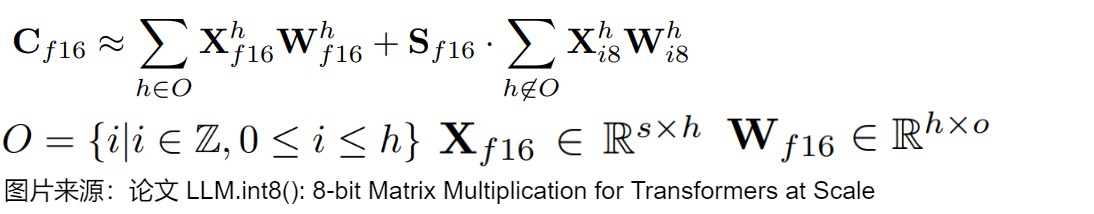
1.1.3 缺點(diǎn)

論文不足點(diǎn)如下：

• 很難在硬件加速器上高效實(shí)現(xiàn)outlier的分解，而且運(yùn)行時(shí)進(jìn)行異常值檢測，這導(dǎo)致推理速度比fp16還慢
• 模型量化僅到8bit，仍是4bit的2倍大。

1.2 ZeroQuant

1.2.1 主要貢獻(xiàn)

ZeroQuant的主要貢獻(xiàn)如下：

• 對(duì)激活按 per-token 的動(dòng)態(tài)量化，每個(gè)token都有獨(dú)立的量化參數(shù)。對(duì)權(quán)重矩陣進(jìn)行分組量化，每組都有獨(dú)立的量化參數(shù)。這樣兼顧了性能和精度。
• 提出一種無需訪問原始訓(xùn)練數(shù)據(jù)的逐層知識(shí)蒸餾算法（LKD）來提取量化網(wǎng)絡(luò)，降低了顯存開銷。

1.2.2 方案

用于激活的按token量化

現(xiàn)有 PTQ 中對(duì)激活進(jìn)行量化常見做法是靜態(tài)量化，其中最小/最大范圍是在離線校準(zhǔn)階段計(jì)算的。

對(duì)于激活范圍方差較小的小模型來說，這種方法可能就足夠了。然而，LLM的激活范圍存在巨大差異。因此，靜態(tài)量化方案（通常應(yīng)用于所有tokens/樣本）將導(dǎo)致準(zhǔn)確度顯著下降。克服這個(gè)問題的一個(gè)辦法就是采用更細(xì)粒度的token-wise量化并動(dòng)態(tài)計(jì)算每個(gè)token的最小/最大范圍，以減少激活引起的量化誤差。然而，使用現(xiàn)有的深度學(xué)習(xí)框架直接應(yīng)用 token-wise 量化會(huì)導(dǎo)致顯著的量化和反量化成本，因?yàn)?token-wise 量化引入了額外的操作，導(dǎo)致 GPU 計(jì)算單元和主存之間產(chǎn)生昂貴的數(shù)據(jù)移動(dòng)開銷。

為了解決這個(gè)問題，ZeroQuant 構(gòu)建了一個(gè)高度優(yōu)化的推理后端，用于Transformer模型 token-wise 量化。例如，ZeroQuant 的推理后端采用算子融合技術(shù)將量化算子與其先前的算子（如Layer Norm）融合，以減輕 token-wise 量化的數(shù)據(jù)移動(dòng)成本。類似地，在將最終 FP16 結(jié)果寫回到下一個(gè) FP16 算子（如：GeLU）的主存之前，使用權(quán)重和激活量化 scales 縮放 INT32 accumulation，可以減輕不同 GeMM 輸出的反量化成本。

Token-wise 量化可以顯著減少量化激活的表示誤差，它不需要校準(zhǔn)激活范圍，對(duì)于ZeroQuant 的量化方案（INT8 權(quán)重和 INT8 激活）不存在與量化相關(guān)的成本（例如，激活范圍校準(zhǔn)）。

用于權(quán)重矩陣的分組量化

將 INT8 PTQ 應(yīng)用于 BERT/GPT-3 模型會(huì)導(dǎo)致準(zhǔn)確性顯著下降。關(guān)鍵的挑戰(zhàn)是 INT8 的表示無法完全捕獲權(quán)重矩陣中不同行和不同激活Token的不同數(shù)值范圍。解決這個(gè)問題的一種方法是對(duì)權(quán)重矩陣（激活）使用group-wise（token-wise）量化。

分組量化最先在Q-BERT中提出，其中權(quán)重矩陣被劃分為 g 個(gè)組，每個(gè)組單獨(dú)量化。然而，在Q-BERT中，作者僅將其應(yīng)用于量化感知訓(xùn)練。更重要的是，他們沒有考慮硬件效率約束，也沒有系統(tǒng)后端支持，因此沒有降低時(shí)延。

ZeroQuant 的設(shè)計(jì)中考慮了 GPU Ampere 架構(gòu)（例如: A100）的硬件約束，其中計(jì)算單元基于 Warp Matrix Multiply and Accumulate (WMMA) 的分片（Tiling）大小，以實(shí)現(xiàn)最佳加速。與單矩陣量化相比，ZeroQuant 的分組量化由于其更細(xì)粒度的量化而具有更好的精度，同時(shí)極大的降低了延遲。

逐層知識(shí)蒸餾

知識(shí)蒸餾（KD）是緩解模型壓縮后精度下降的最有力方法之一。然而，當(dāng)應(yīng)用到LLM上時(shí)，KD 存在一些局限性：

• KD 需要在訓(xùn)練過程中將教師和學(xué)生模型放在一起，這大大增加了內(nèi)存和計(jì)算成本；
• KD 通常需要對(duì)學(xué)生模型進(jìn)行充分訓(xùn)練。因此，需要在內(nèi)存中存儲(chǔ)權(quán)重參數(shù)的多個(gè)副本來更新模型；
• KD 通常需要原始訓(xùn)練數(shù)據(jù)，有時(shí)由于隱私/機(jī)密問題而無法訪問。

為了解決這些限制，ZeroQuant 提出了逐層蒸餾（LKD）算法緩解精度損失。該算法將原始模型作為教師模型，量化后的模型作為學(xué)生模型，通過逐層傳遞知識(shí)的方式，引導(dǎo)學(xué)生模型模仿教師模型的輸出。這種方法不需要原始訓(xùn)練數(shù)據(jù)，且能夠在不增加額外計(jì)算成本的情況下，有效提升量化模型的精度。

第二版ZeroQuant-V2分析了權(quán)重量化和激活值量化對(duì)精度的敏感性，比較了常用PTQ算法的模型效果，最后引入了一種稱為低秩補(bǔ)償（LoRC）的優(yōu)化技術(shù)，它可以與 PTQ 的協(xié)同工作，以最小的模型參數(shù)大小的增加來改善整個(gè)模型質(zhì)量的恢復(fù)，但這種方法的擴(kuò)展性似乎不是很好。

第三版ZeroQuant-FP主要探索了浮點(diǎn)（FP）量化的可行性，特別關(guān)注FP8和FP4格式。對(duì)于LLM，F(xiàn)P8激活在性能上優(yōu)于INT8，而在權(quán)重量化方面，F(xiàn)P4在性能上與INT4相比具有可比性，甚至更優(yōu)越；LoRC有助于提升W4A8的整體表現(xiàn)。同時(shí)為了解決由權(quán)重和激活之間的差異(從FP4到FP8)引起的挑戰(zhàn)，ZeroQuant-FP要求所有縮放因子為2的冪，并將縮放因子限制在單個(gè)計(jì)算組內(nèi)。

第四版ZeroQuant-HERO是一種新的硬件增強(qiáng)型訓(xùn)練后 W8A8 量化框架，它考慮了內(nèi)存帶寬限制和計(jì)算密集型運(yùn)算，總體偏工程方向，將transformer中更多子模塊進(jìn)行了量化改造，分別是：Embedding層量化、Attention模塊量化、MLP 模塊量化，同時(shí)采用不同量化精度對(duì)各個(gè)模塊進(jìn)行量化組合，按需選取量化等級(jí)。

1.3 SmoothQuant

SmoothQuant由論文“SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models”給出，其量化位寬為 W8A8，即權(quán)重和激活都是用 8bit 量化。

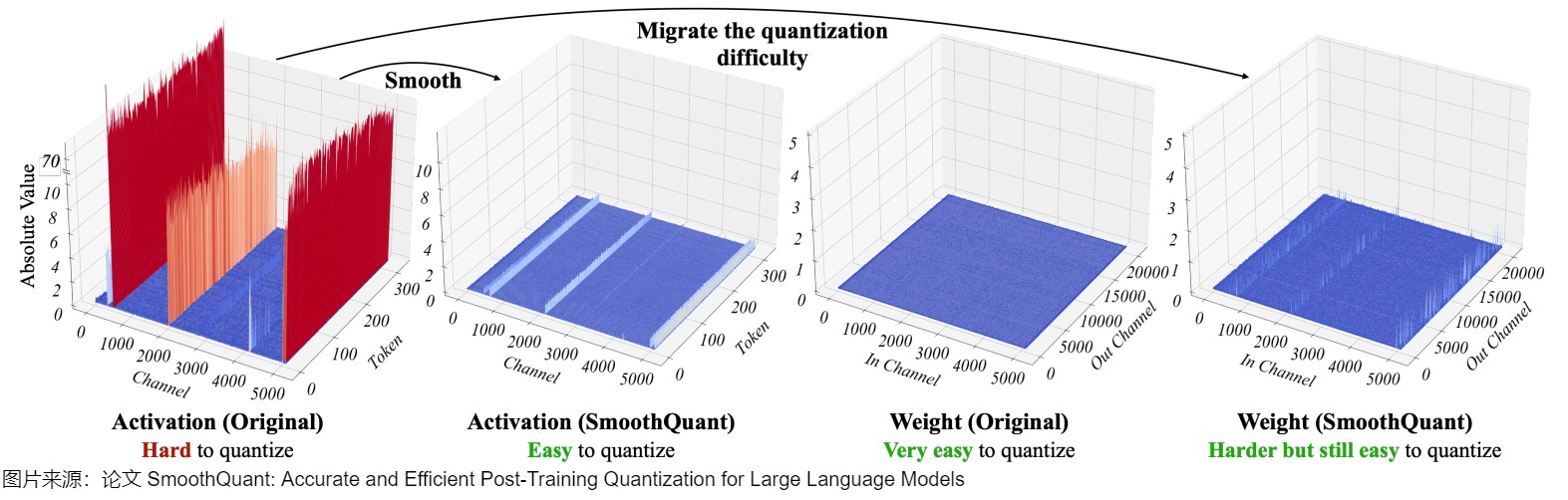
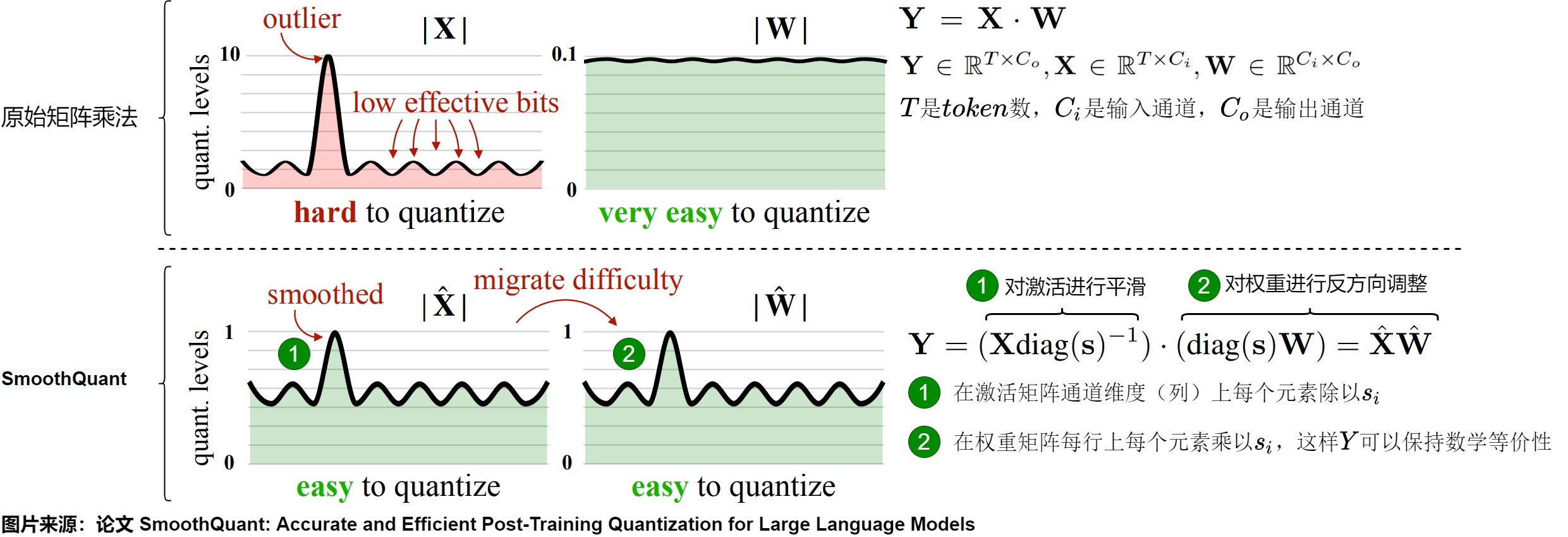
SmoothQuant 的核心思路是，激活 X 之所以難以量化，是因?yàn)榇嬖陔x群值拉伸了量化的線性映射范圍，導(dǎo)致大部分?jǐn)?shù)值的有效位數(shù)減少。而且，不同token在激活通道之間具有相似變化。因此，論文提出了一種按通道縮放的方法，在離線階段引入平滑因子 s 來平滑激活中的異常值，并通過數(shù)學(xué)上的等效轉(zhuǎn)換將量化的難度從激活遷移至權(quán)重 W 上（逐通道對(duì)權(quán)重乘上縮放因子，在激活上乘上縮放因子矩陣的逆，從而保持整體的輸出不變，激活值整體變小，權(quán)重整體變大，激活值更好量化了），從而降低激活的量化難度。經(jīng)過平滑處理的激活 X 和調(diào)整后的權(quán)重 W 均易于量化。

1.3.1 動(dòng)機(jī)

現(xiàn)狀

針對(duì)異常值，ZeroQuant 和 LLM.int8() 提出了各自的解決辦法：

1. ZeroQuant 應(yīng)用了動(dòng)態(tài)逐 token 激活量化和分組權(quán)重量化來解決激活離群值問題。雖然該方法實(shí)現(xiàn)效率較高，但對(duì)于 175B 參數(shù)的 OPT 模型的準(zhǔn)確性較差。
2. LLM.int8() 通過引入混合精度分解（即對(duì)異常值保持 FP16，其他激活使用 INT8）解決了該準(zhǔn)確性問題，但是這種方法在工程上很難在 AI 加速器上高效實(shí)現(xiàn)，是一種硬件不友好的量化方案。

因此，需要尋找到一種高效、對(duì)硬件友好且無需訓(xùn)練的量化方案，使得 LLMs 中所有計(jì)算密集型操作均采用 INT8。

量化方案的問題

根據(jù)量化參數(shù) s（數(shù)據(jù)量化的間隔）和 z（數(shù)據(jù)偏移的偏置）的共享范圍，即量化粒度的不同，量化方法也可以分為逐層量化（per-tensor）、逐通道（per-channel）量化，逐token（per-token）量化和逐組量化（per-group，Group-wise）。SmoothQuant 作者對(duì)比了這幾種量化方案，得出結(jié)論如下：

• per-tensor量化是在硬件上最高效的實(shí)現(xiàn)方式。
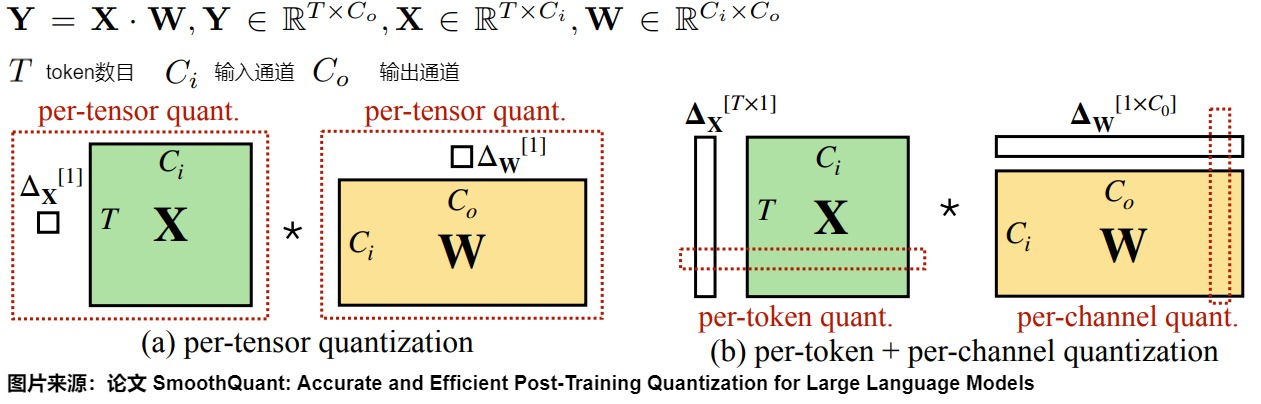
• per-channel量化保留了精度，但是它與 INT8 GEMM 內(nèi)核不兼容（要求權(quán)重和激活都是INT8）。即per-channel量化不能很好地映射到硬件加速的GEMM內(nèi)核（硬件不能高效執(zhí)行，從而增加了計(jì)算時(shí)間）。在這些內(nèi)核中，縮放只能沿著矩陣乘法的外部維度執(zhí)行 (即激活的 token 維度、權(quán)重 \(??_??\) 的輸出通道維度)，不能在內(nèi)部維度\(C_i\)進(jìn)行。具體參見下圖。
• 因此，盡管 per-token 量化精度較低，為了不降低GEMM 內(nèi)核本身的吞吐量，過往的研究依然還是在線性層中采用了它。但是它們無法解決 activation 量化的問題。

因?yàn)榫碗x群值來說，不同 tokens 在其通道上表現(xiàn)出類似的變化，于是 SmoothQuant 提出了一種數(shù)學(xué)上等價(jià)的逐通道縮放變換（per-channel scaling transformation）方案，可顯著平滑通道間的幅度，從而使模型易于量化，保持精度的同時(shí)，還能夠保證推理提升推理速度。

我們再來梳理下為何per-channel量化不能很好地映射到硬件加速的GEMM內(nèi)核。其根本原因是：如果不考慮加速的話，只是為了壓縮參數(shù)，那么怎么量化都行。如果想加速矩陣乘法，就要考慮整個(gè)矩陣乘法的反量化。只能在矩陣乘法的外側(cè)維度進(jìn)行量化，否則無法反量化。

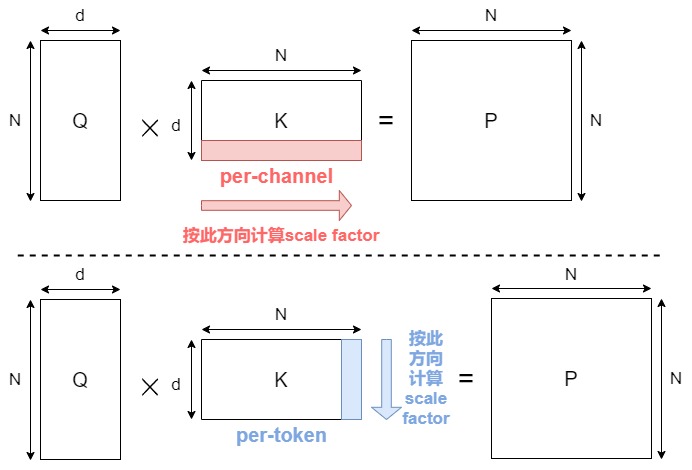
我們以注意力機(jī)制量化為例來繼續(xù)分析。假如對(duì)K 做 channel-wise 量化，是可以避免不同 channel 之間的值共享scale factor。然而這在注意力機(jī)制計(jì)算中會(huì)有問題。這是因?yàn)樵谶M(jìn)行矩陣乘法 \(QK^T\) 后，得到的結(jié)果矩陣的維度是 N × N。如果我們對(duì) K 進(jìn)行了per-channel 量化（上圖上方，總共 d 個(gè)channel，每個(gè) channel 包含 N 個(gè)元素），每個(gè)通道都有一個(gè)獨(dú)立的scale factor，總共是 d 個(gè) scale factor。在反量化（dequantization）時(shí)，我們需要將量化后的結(jié)果乘以對(duì)應(yīng)的scale factor，而\(QK^T\) 的結(jié)果矩陣的維度是 NxN，沒有 d 的通道維度直接對(duì)應(yīng)，無法使用 K 的通道維度的縮放因子進(jìn)行正確的反量化。因此，注意力乘法中，對(duì)于每個(gè)矩陣，我們只能沿著公共維度進(jìn)行量化（如上圖下方）。根據(jù)這個(gè)簡單的原則，Attention 中四個(gè)矩陣可以量化的組合如下。

	Q	K	P	V
per-channel	N	N	N	Y
per-token	Y	Y	Y	N
per-block	Y	Y	Y	N

1.3.2 方案

SmoothQuant提出了8bit weight，8bit activation(W8A8)的量化方法，此方案其實(shí)可以看做數(shù)據(jù)的預(yù)處理，處理完之后的數(shù)據(jù)可以適配int8量化方法。主要思路就是，由于權(quán)重很容易量化，而激活則較難量化，因此將量化難度從激活遷移到下一層的權(quán)重內(nèi)，利用weight的細(xì)粒度量化來承擔(dān)該量化困難。方案特點(diǎn)如下：

• 引入平滑因子s來平滑激活異常值，將量化難度從激活等價(jià)轉(zhuǎn)移到權(quán)重上；
• 平滑因子的作用是建立一個(gè)數(shù)學(xué)上等效的變換，即將input的動(dòng)態(tài)范圍除上scale（該scale > 1）即可以實(shí)現(xiàn)動(dòng)態(tài)范圍減小，從而改善量化結(jié)果，然后將該scale吸到下一層的weight內(nèi)；
• 利用weight的細(xì)粒度量化來承擔(dān)該權(quán)重的量化困難（因?yàn)閕nput往往使用token-wise quantization，而weight通常使用channel-wise quantization或group-wise quantization）；

SmoothQuant 算法有兩個(gè)難點(diǎn)：如何通過數(shù)學(xué)上的等效轉(zhuǎn)換將量化的難度從激活遷移至權(quán)重上，以及如何實(shí)現(xiàn)逐通道的等效縮放轉(zhuǎn)換。這具體是通過矩陣乘法升級(jí)和合理計(jì)算平滑因子來達(dá)到目的。

計(jì)算平滑因子

SmoothQuant 的目標(biāo)是為每個(gè) channel 選擇一個(gè)平滑因子 ?? ，使得 \(\hat X=??diag(??)^{?1}\) 易于量化。為了減少量化誤差，應(yīng)該增加所有通道的有效量化位。當(dāng)所有 channel 都具有相同的最大幅值時(shí)，總有效量化位將是最大的。

• 一種做法是讓 \(s_j = max(|X_j|),j=1,2,...,C_j\)， \(C_j\)代表第 j 個(gè) input channel。各 channel 通過除以 \(s_j\)后，激活 channels 都將有相同的最大值，這時(shí)激活比較容易量化。但是這會(huì)使得激活值的離群值全部轉(zhuǎn)移到權(quán)重上面，激活值變得很好量化，權(quán)重反而難以量化。

• 另一種做法是讓\(s_j=1/max(|W_j|)\)，這樣權(quán)重 channels 都將有相同的最大值，權(quán)重易量化。即將所有量化難度從權(quán)重遷移到激活，這會(huì)使得原本方差較小的權(quán)重方差更小，激活值方差更大，更難以量化激活。

因此，我們需要在 weight 和 activation 中平衡量化難度，讓彼此均容易被量化。論文作者通過加入一個(gè)超參 \(\alpha\) （遷移強(qiáng)度），來控制從激活值遷移多少難度到權(quán)重值。一個(gè)合適的遷移強(qiáng)度值能夠讓權(quán)重和激活都易于量化。\(\alpha\) 太大，權(quán)重難以量化，\(\alpha\) 太小，則激活難以量化。下圖中。

• \(\alpha\) 表示遷移強(qiáng)度，為一個(gè)超參數(shù)，控制將多少激活值的量化難度遷移到權(quán)重量化。
• C 表示激活的輸入通道數(shù)。

對(duì)于縮放系數(shù)，其實(shí)可以離線使用一個(gè)小的標(biāo)定數(shù)據(jù)集進(jìn)行計(jì)算，考慮到 X一般都是從前一個(gè)線性操作得到的，我們事實(shí)上可以把對(duì)X的scale融合到前一個(gè)線性層。而對(duì)于weight的量化，也可以在計(jì)算好當(dāng)前層的縮放系數(shù)(以及下一層X的縮放系數(shù))后乘起來再做量化。這樣就可以避免在推理的時(shí)間計(jì)算縮放矩陣的乘法。

矩陣乘法升級(jí)

有了平滑因子，就可以實(shí)現(xiàn)離群值平滑了，其本質(zhì)上是通過將激活難度轉(zhuǎn)移至權(quán)重來實(shí)現(xiàn)的。

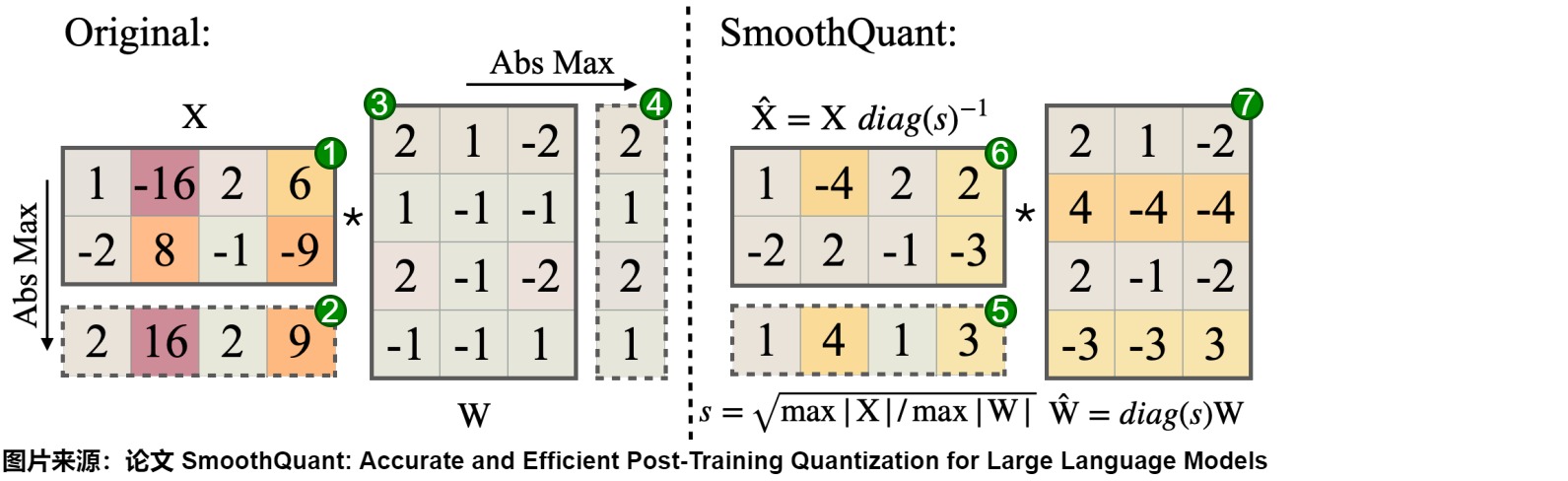
常規(guī)的矩陣乘為\(Y=XW\)。SmoothQuant 通過按通道除以 smoothing factor 來對(duì)激活進(jìn)行平滑。即為了保持線矩陣乘法在數(shù)學(xué)上的等價(jià)性，以相反的方式對(duì)權(quán)重進(jìn)行對(duì)應(yīng)調(diào)整。X 在 channel 維度（列）上每個(gè)元素除以 \(s_i\) ，W則在每行上每個(gè)元素乘以 \(s_i\) 。這樣 Y 在數(shù)學(xué)上是完全相等的。

具體轉(zhuǎn)換過程如下圖。

考慮到輸入 X 通常由前面的線性操作（如線性層、層歸一化等）產(chǎn)生，我們可以輕松地將平滑因子離線地融合到前一層的參數(shù)中\(diag(s) \times W_{pre}\)，不會(huì)因額外的縮放操作而導(dǎo)致增加內(nèi)核調(diào)用開銷。在一些其他情況下，例如當(dāng)輸入來自殘差相加時(shí)，我們可以在殘差分支中添加額外的縮放。

示例

下圖給出了計(jì)算流程。其中，平滑因子 s 是離線在校準(zhǔn)樣本上獲得的。

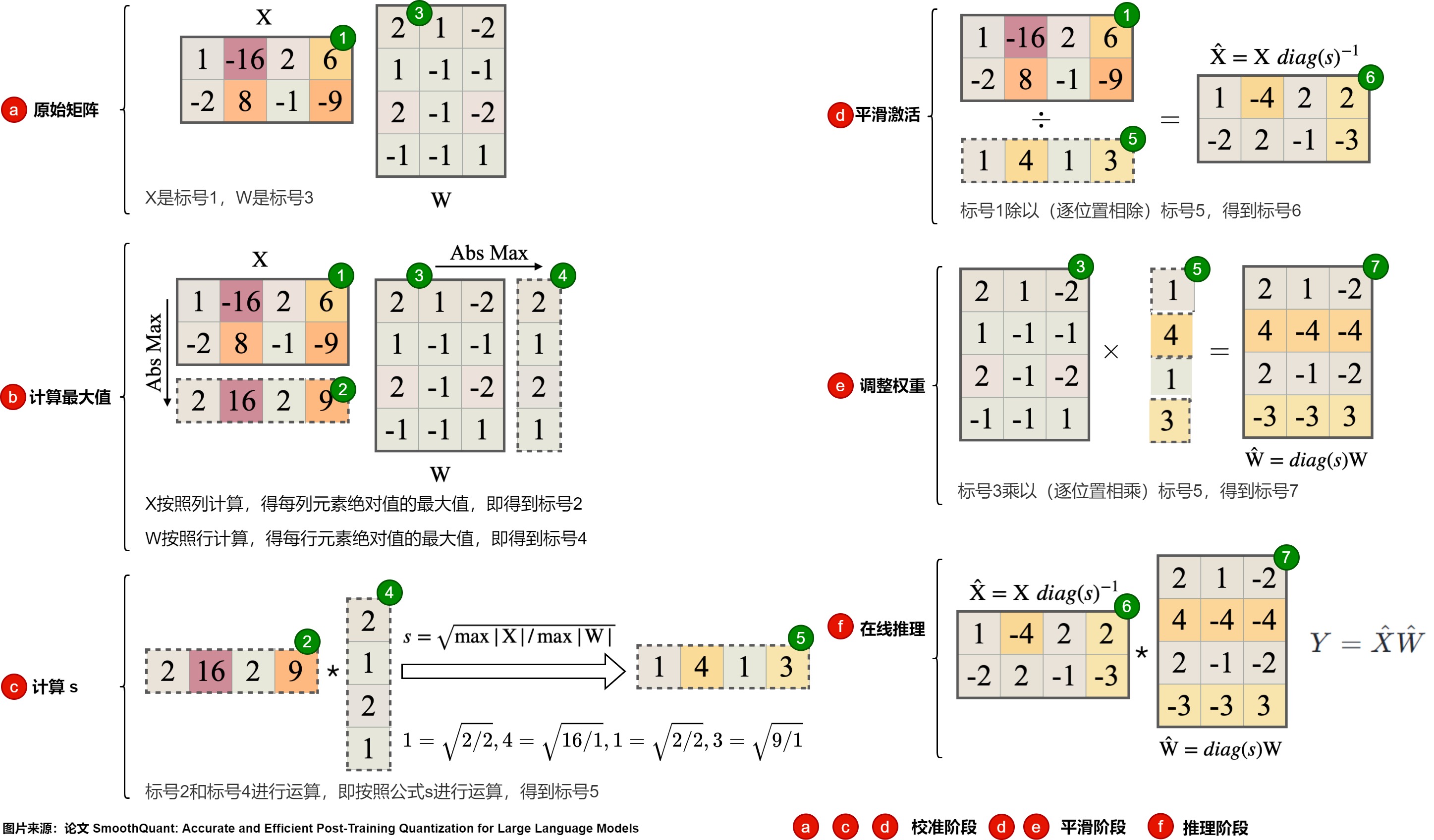
具體步驟如下圖，其中，圖上的紅色標(biāo)號(hào)b，d，d是離線校準(zhǔn)階段。e和f是平滑階段，e是推理階段。

• 準(zhǔn)備階段

  • X是標(biāo)號(hào)1，W是標(biāo)號(hào)3。

• 校準(zhǔn)階段（離線）

  • X按照列計(jì)算，得每列元素絕對(duì)值的最大值，即標(biāo)號(hào)2。
  • W按照行計(jì)算，得每行元素絕對(duì)值的最大值，即4號(hào)。
  • 標(biāo)號(hào)2和標(biāo)號(hào)4進(jìn)行運(yùn)算，即按照公式s進(jìn)行運(yùn)算，得到標(biāo)號(hào)5。

• 平滑階段（離線）

  • 1號(hào)除以5號(hào)，得到6號(hào)。$ \hat{W}$ 的計(jì)算公式如下：\(\hat{W}=diag(s)\)

  • 3號(hào)乘以以5號(hào)，得到7號(hào)。\(\hat{X}\)的計(jì)算公式如下：\(\hat{X}=X diag(s)^{-1}\)

• 推理階段（在線，部署模型）

  • 6號(hào)乘以以7號(hào)，得到Y(jié)。平滑之后的激活的計(jì)算公式如下：\(Y = \hat{X} \hat{W}\)

應(yīng)用

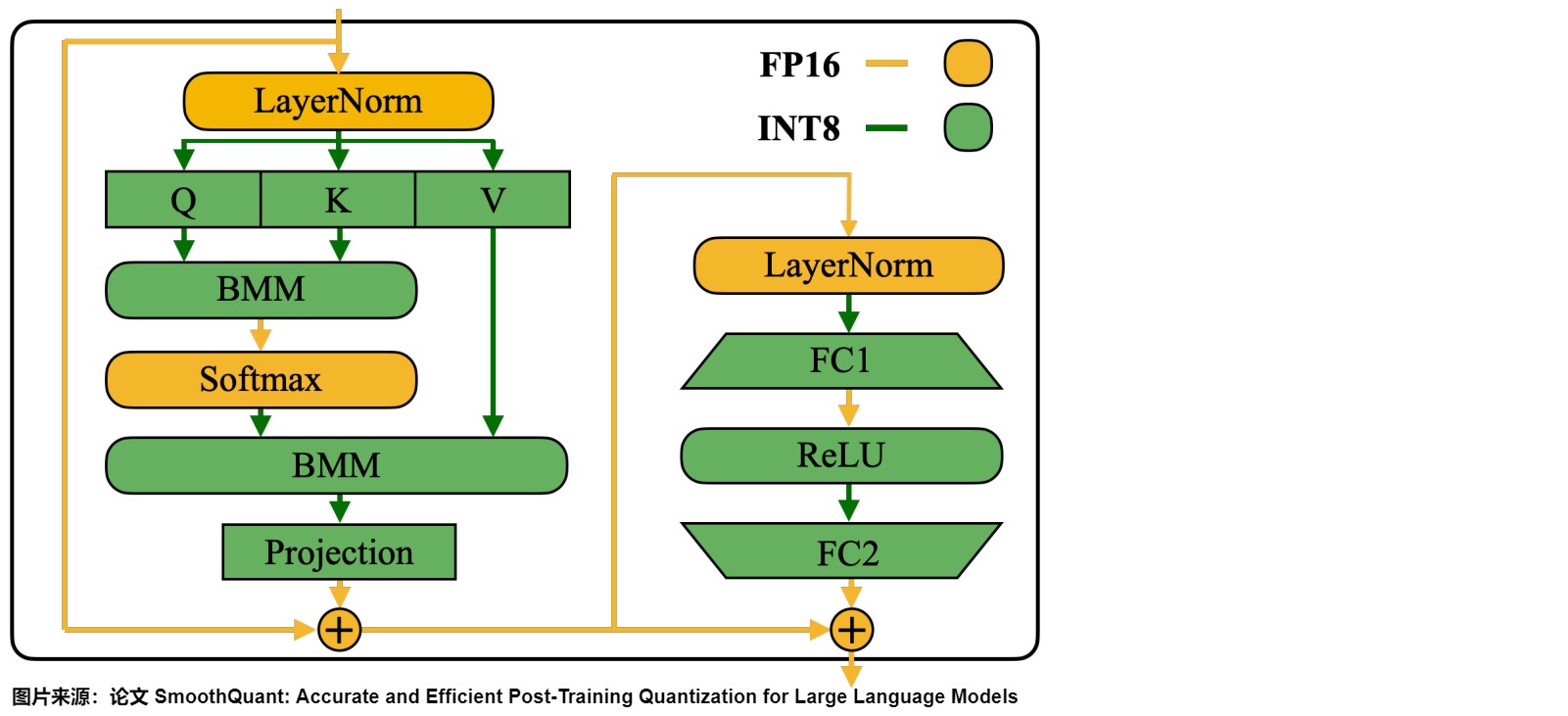
因?yàn)榫€性層占據(jù)了大型語言模型中大部分的參數(shù)量和計(jì)算開銷。默認(rèn)情況下，作者對(duì)自注意力和前饋層的輸入激活進(jìn)行平滑處理，并將所有線性層量化為 W8A8。同時(shí)，作者也對(duì)注意力機(jī)制中的 BMM 操作進(jìn)行量化。下圖展示了作者針對(duì) Transformer 模塊設(shè)計(jì)的量化流程：

• 對(duì)線性層和注意層的 BMM（批量矩陣乘法） 等計(jì)算量大的算子的輸入和權(quán)重進(jìn)行INT8量化（W8A8）。

• 對(duì)于 Softmax 和 LayerNorm 等其他輕量級(jí)逐元素（element-wise）操作模塊，則保持激活為 FP16。

這樣設(shè)計(jì)有助于平衡準(zhǔn)確性和推理效率。不量化 Token Embedding 層的原因，可能是因?yàn)槠鋮?shù)冗余性較小且不存在權(quán)重稀疏現(xiàn)象。

1.3.3 不足

SmoothQuant 不足點(diǎn)如下：

• 適用于LLM，在stable diffusion上表現(xiàn)欠佳；

• 使用小批量數(shù)據(jù)離線進(jìn)行標(biāo)定，有過擬合標(biāo)定數(shù)據(jù)的風(fēng)險(xiǎn)。
• 精度沒有LLM.int8()有保證, 且容易受到calibration-set的影響), 同時(shí)一旦weight精度調(diào)至4bit, 則模型精度下滑嚴(yán)重)

0x02 4位量化

當(dāng)LLM參數(shù)變大時(shí)，上述提到的INT8量化方案在低比特位精度下會(huì)存在顯著的性能劣化。例如，SmoothQuant在 W4A4、W3A4、W2A16 和 W2A8 等低比特位設(shè)置下表現(xiàn)出較大的精度下降，從而影響了量化模型的實(shí)際使用體驗(yàn)。因此，需要更低比特位的方案，比如GPTQ和AWQ提出的4比特方案。

GPTQ和AWQ成功地將LLMs的權(quán)重矩陣壓縮到4bit，同時(shí)保持了LLMs的主要能力。這代表了LLM優(yōu)化的重大進(jìn)展，通過在時(shí)間和空間效率以及模型性能之間實(shí)現(xiàn)平衡。論文“The case for 4-bit precision: k-bit inference scaling laws”深入探討了LLM中模型大小和比特精度之間在零樣本性能方面的權(quán)衡。他們在各種LLM家族之間進(jìn)行了廣泛的實(shí)驗(yàn)，在全部的模型比特?cái)?shù)和零樣本準(zhǔn)確性之間，發(fā)現(xiàn)4比特精度幾乎普遍是實(shí)現(xiàn)平衡的最佳選擇。

本節(jié)介紹的幾種方案特點(diǎn)如下。

方法	量化權(quán)重與激活	特點(diǎn)
GPTQ	W3A16, W4A16	根據(jù)海森矩陣順序量化一列權(quán)重并調(diào)整未量化的權(quán)重補(bǔ)償損失，提出順序并行量化、延遲更新和Cholesky分解加速。
AWQ	W4A16	Weight：Per-group，Activation：FP16。根據(jù)激活幅值選擇重要權(quán)重并單獨(dú)縮放這些權(quán)重和激活，通過網(wǎng)格搜索最優(yōu)縮放因子。
LLM-QAT	W4A16	大模型量化感知訓(xùn)練的開山之作。除了量化權(quán)重和激活之外，還量化了 KV 緩存，這對(duì)于提高吞吐量和支持當(dāng)前模型規(guī)模的長序列依賴至關(guān)重要。
QLoRA	W4A16	將低秩自適應(yīng)與量化相結(jié)合，以實(shí)現(xiàn)大型模型的有效微調(diào)，同時(shí)最大限度地降低計(jì)算成本和內(nèi)存使用。
FlatQuant	W4A4	探索平坦分布與量化損失的優(yōu)化路徑

2.1 GPTQ

GPTQ出自論文“GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers”，其思路是通過二 階Hessian信息對(duì)剩余權(quán)重進(jìn)行矯正，補(bǔ)償量化引入的誤差，從而最小化量化前后模型的輸出差異。即，GPTQ 對(duì)當(dāng)前權(quán)重進(jìn)行量化，然后更新剩余權(quán)重以最小化量化前后，層輸出的損失。

GPTQ建立在傳統(tǒng)算法OBQ的基礎(chǔ)上。OBQ通過相對(duì)于未量化權(quán)重的Hessian矩陣的重建誤差的方法，來實(shí)現(xiàn)每行權(quán)重矩陣的最優(yōu)量化順序。在每個(gè)量化步驟之后，OBQ迭代調(diào)整未量化的權(quán)重以減輕重建誤差。然而，量化過程中頻繁更新Hessian矩陣增加了計(jì)算復(fù)雜度。

GPTQ作者認(rèn)為當(dāng)今模型過于復(fù)雜，導(dǎo)致求解整個(gè)模型的海森矩陣太復(fù)雜。如果假設(shè)參數(shù)矩陣的同一行參數(shù)互相之間是相關(guān)的，而不同行之間的參數(shù)互不相關(guān)，則只需計(jì)算行內(nèi)海森矩陣即可。GPTQ作者認(rèn)為剪枝是一種特殊的量化，同時(shí)提出OBQ：逐層求海森矩陣并按影響從小到大給層內(nèi)權(quán)重排個(gè)序，然后依次量化。

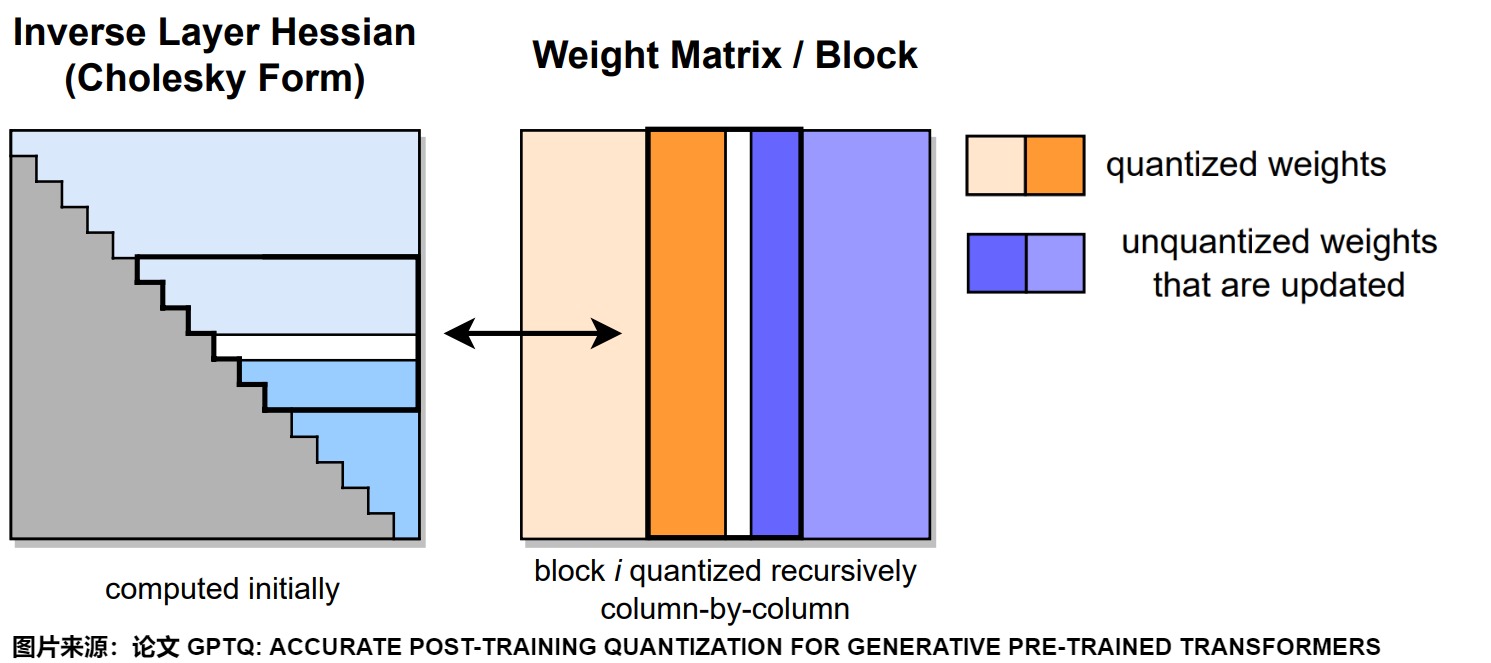
下圖給出了GPTQ量化過程。在給定的步驟中，GPTQ 使用Cholesky分解中存儲(chǔ)的逆Hessian信息對(duì)連續(xù)列的塊（粗體）進(jìn)行量化，并在步驟結(jié)束時(shí)更新剩余的權(quán)重（藍(lán)色）。量化過程在每個(gè)塊內(nèi)遞歸應(yīng)用。白色中間列代表當(dāng)前正在被量化的部分。右圖黑色方框就是一個(gè)block，表示當(dāng)前正在進(jìn)行量化的組。

2.1.1 背景

在GPTQ之前，主要PTQ方案最高只能實(shí)現(xiàn)8位量化，GPTQ進(jìn)一步探索更低比特的量化。GPTQ 并不是憑空出現(xiàn)的，它的基礎(chǔ)有兩個(gè)：

• 逐層量化。
• Optimal Brain Quantization (OBQ)。

逐層量化

GPTQ使用非對(duì)稱量化，并且逐層進(jìn)行，每層獨(dú)立處理完畢后再繼續(xù)到下一層。采樣逐層量化相當(dāng)于對(duì)每層求解一個(gè)重建問題。給定線性層 ? 的權(quán)重 W? 和輸入 X? ，優(yōu)化目標(biāo)為找到一個(gè)量化的權(quán)重矩陣 \(\widehat W\) ，使得其相對(duì)于全精度層的輸出的平方差最小。下面公式中，W和\(\widehat W\)分別表示原始權(quán)重和剪枝后的權(quán)重矩陣，X 表示矩陣形式的輸入。

若將權(quán)重矩陣按行分解，則剪枝損失又可以表示為按行求和的形式。由于每次迭代我們都只對(duì)某一行中的一個(gè)權(quán)重進(jìn)行剪枝，也就是說只影響一行的剪枝損失。進(jìn)而，每一次迭代只影響當(dāng)前行的 Hessian 矩陣，不同行之間的 Hessian 矩陣計(jì)算是相互獨(dú)立的，所以不同行之間的迭代是可以并行的。

OBQ

GPTQ的原理來自于另一個(gè)量化方法OBQ(Optimal Brain Quantization)，OBQ 實(shí)際上是對(duì) OBS(Optimal Brain Surgeon，一種比較經(jīng)典的剪枝方法）的魔改， 而OBS則來自于OBD（Optimal Brain Damage，由 Yann LeCun 在1990年提出的剪枝方法）。

• OBD的作用是：引入二階導(dǎo)數(shù)信息對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行最小損失剪枝。

• OBS的作用是：引入刪除權(quán)重補(bǔ)償概念，使得剪枝損失降到最小。

因此，我們要梳理一下脈絡(luò)。我們的核心問題是：如何選擇性的刪除一些權(quán)重來減少網(wǎng)絡(luò)大小的同時(shí)，不要引入太多的誤差？由此而來的是，如何定義刪除權(quán)重帶來的誤差是什么？或者說如何衡量？

OBD

OBD是剪枝方案，模型剪枝實(shí)際上就是將 W 的某個(gè)值調(diào)整為 0。因此，我們可以通過刪除某權(quán)重參數(shù)所帶來的損失函數(shù)的變化來衡量該權(quán)重參數(shù)的重要性。即，如果要在模型中去除一些參數(shù)（即剪枝），我們希望去除對(duì)目標(biāo)函數(shù)E影響小的參數(shù)。但是，刪除一個(gè)參數(shù)再重新評(píng)估目標(biāo)函數(shù)的方法是在是太繁雜了。因此OBD建立了一個(gè)誤差函數(shù)的局部模型來預(yù)測擾動(dòng)參數(shù)向量（刪除部分權(quán)重參數(shù)）對(duì)優(yōu)化目標(biāo)造成的影響。

假設(shè)模型的權(quán)重為 W，損失函數(shù)為 f，則在當(dāng)前權(quán)重下，模型的訓(xùn)練損失為 L=L(W)。OBD 的基本思想是以模型訓(xùn)練損失為目標(biāo)函數(shù)，迭代地選擇剪枝參數(shù)使目標(biāo)函數(shù)最小化。OBD 作者對(duì)目標(biāo)函數(shù) E 做泰勒展開來估計(jì)權(quán)重調(diào)整造成的影響。同時(shí)，作者做了一些假設(shè)（如：假設(shè)刪除任意一個(gè)參數(shù)后，其他參數(shù)對(duì)目標(biāo)函數(shù)的影響不變。也就是說，每個(gè)參數(shù)對(duì)目標(biāo)函數(shù)的影響是獨(dú)立的），然后進(jìn)行簡化。最終得到一個(gè)方案：對(duì)目標(biāo)函數(shù)的變化量被簡化為\(\frac{1}{2}h_{ii}w_i^2\)，只要計(jì)算海森矩陣 \(h_{ii}\) ，就可以知道每個(gè)參數(shù)對(duì)目標(biāo)的影響。然后就可以按照影響從小到大給參數(shù)排個(gè)序，這樣就確定了參數(shù)剪枝的次序。具體參加下圖。

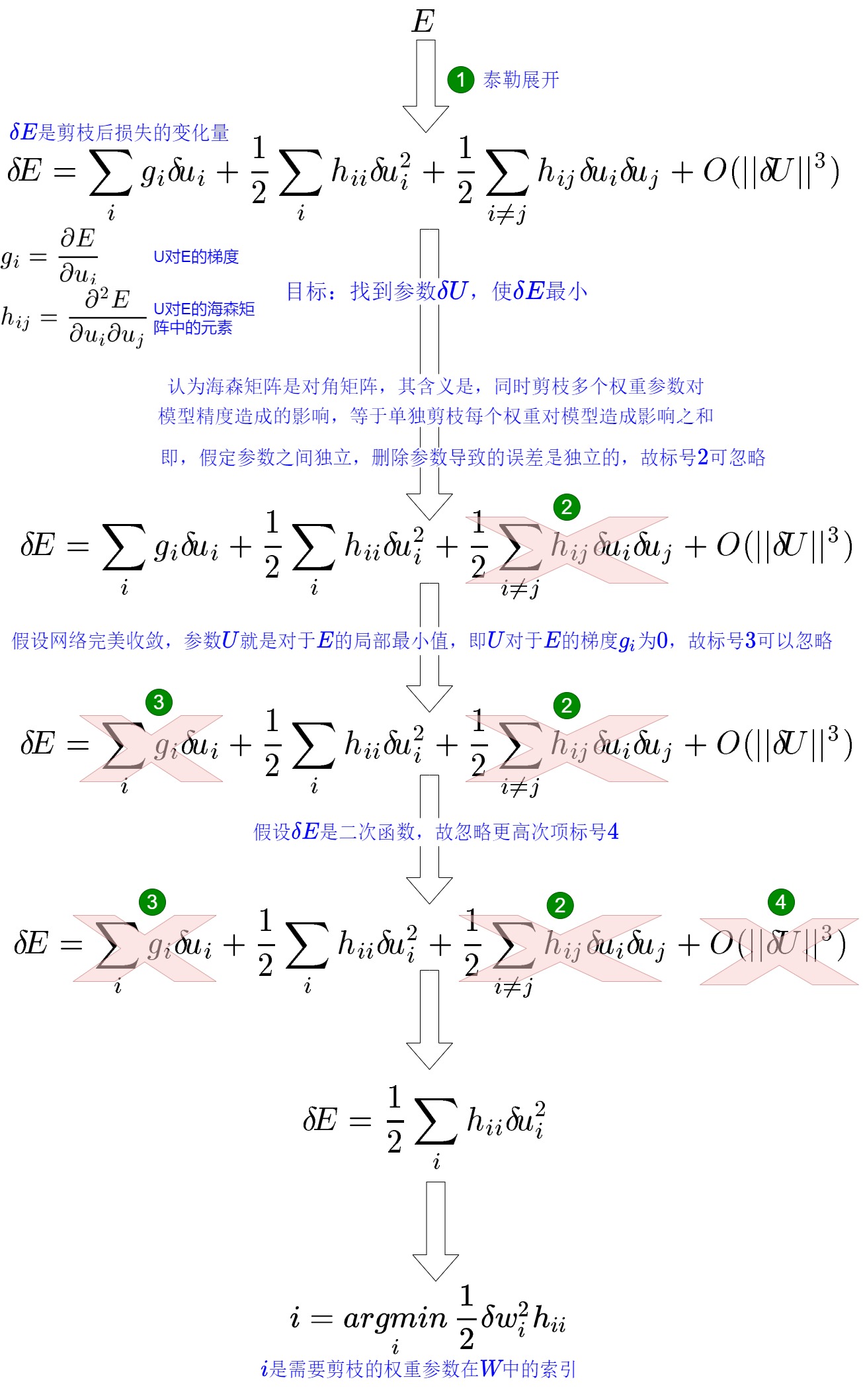
OBD剪枝算法如下：

1. 構(gòu)建神經(jīng)網(wǎng)絡(luò)；
2. 訓(xùn)練神經(jīng)網(wǎng)絡(luò)直到收斂；
3. 計(jì)算每個(gè)參數(shù)的二階導(dǎo)數(shù)\(?_{????}\)；
4. 按照Δ??計(jì)算每個(gè)參數(shù)會(huì)帶來的損失函數(shù)增加值；
5. 刪除一些Δ??小的系數(shù)；
6. 重復(fù)2-5直到刪除的數(shù)量達(dá)到預(yù)設(shè)要求。

OBS

OBS 肯定了 OBD 關(guān)于減小模型剪枝對(duì)損失函數(shù)影響的思路，但是OBS認(rèn)為OBD中提出的參數(shù)之間的獨(dú)立性假設(shè)不成立，OBS 認(rèn)為權(quán)重剪枝之間是有關(guān)聯(lián)的，我們還是要考慮交叉項(xiàng)，所以不能簡單地將 Hessian 矩陣假設(shè)為對(duì)角矩陣。

具體而言，OBS 認(rèn)為，參數(shù)之間的獨(dú)立性不成立，因此，還是要考慮交叉項(xiàng)。假設(shè)我們要抹去一個(gè)權(quán)重記為 \(w_q\)，使得其對(duì)整體的誤差增加最少，但是，同時(shí)應(yīng)該再計(jì)算出一個(gè)補(bǔ)償\(\delta_q\)應(yīng)用于剩余的權(quán)重上，使得抹去的這個(gè)權(quán)重所帶來的誤差被抵消。

OBS作者找到了一個(gè)方法：通過求解海森矩陣的逆，就可以計(jì)算每個(gè)參數(shù)權(quán)重\(w_q\)對(duì)目標(biāo)的影響\(\frac{1}{2}\frac{w_q^2}{[\mathbf{H^{-1}]_{qq}}}\)，然后就可以按照影響從小到大給參數(shù)排個(gè)序，這樣就確定了參數(shù)剪枝的次序。同時(shí)，每次剪枝一個(gè)參數(shù)，其他的參數(shù)也更新一次從而減少誤差。

OBS 最終算法如下圖所示：把權(quán)重直接展開，計(jì)算對(duì)應(yīng)的海森矩陣，然后按照順序進(jìn)行量化。

其實(shí)，OBS研究的是量化視角下的參數(shù)敏感度。并非神經(jīng)網(wǎng)絡(luò)中的所有參數(shù)都同等重要。直觀地說，如果某個(gè)權(quán)重的舍入誤差（rounding error）較大，則可以將其視為具有較大的量化參數(shù)敏感度，即這個(gè)權(quán)重和量化點(diǎn)不接近。直接統(tǒng)計(jì)權(quán)重的舍入誤差忽略了 LLM 向量相關(guān)性非常大的事實(shí)，需要進(jìn)行合理補(bǔ)償：權(quán)重 \(w_a\) 可能有較大的舍入誤差，但 \(w_a\) 與另一個(gè)權(quán)重 \(w_b\) 密切相關(guān)，這意味著可以通過向下舍入 \(w_b\) 很好地補(bǔ)償對(duì)\(w_a\)進(jìn)行舍入的誤差。

OBS 在每次迭代中，都涉及到計(jì)算 Hessian 矩陣的逆矩陣。設(shè)權(quán)重參數(shù)總量為 d，則計(jì)算 Hessian 矩陣的逆矩陣的時(shí)間復(fù)雜度為 \(O(d^3)\)，且每次迭代都需要計(jì)算一次，因此 OBS 的時(shí)間復(fù)雜度為 \(O(d^4)\)。顯然對(duì)于動(dòng)則上百萬甚至上億參數(shù)的模型來說，這種方式的計(jì)算量是非常巨大的。

OBQ

OBQ 把OBS 推廣到模型量化中，同時(shí)加上分行運(yùn)算的方式。模型剪枝是把某些權(quán)重變成 0，而模型量化則是把權(quán)重近似到一個(gè)值。因此，可以把剪枝理解成為一種特殊的量化。OBQ 使用貪心算法對(duì)權(quán)重W矩陣分行獨(dú)立計(jì)算，每一行內(nèi)部量化的時(shí)候按照Δ??最小的原則來選擇量化的順序。具體而言，OBQ 逐層量化的公式可寫成 W 每一行的平方差的和，從而以貪婪的方式進(jìn)行量化：

• 利用海森矩陣信息作為準(zhǔn)則判定每個(gè)權(quán)重量化后對(duì)輸出loss造成的影響。選擇讓當(dāng)前權(quán)重 W 量化誤差（通過Δ??找到在本行內(nèi)量化導(dǎo)致?lián)p失函數(shù)增加的最小的系數(shù)）最小的一行權(quán)重 w 進(jìn)行量化；
• 對(duì)其它未量化的權(quán)重進(jìn)行更新以彌補(bǔ)量化損失。

具體推導(dǎo)如下圖所示，其中 quant(w) 是把 w 近似到最近的quant grid的點(diǎn)上，簡單說就是四舍五入到指定位數(shù)上。可以看到假如quant(q)永遠(yuǎn)返回零，其實(shí)就是原版的OBS。

這個(gè)方法之所以行之有效，是因?yàn)闄?quán)重通常是相互關(guān)聯(lián)的。所以當(dāng)一個(gè)權(quán)重發(fā)生量化誤差時(shí)，相關(guān)的權(quán)重會(huì)相應(yīng)地更新（通過逆海森矩陣）。具體過程如下圖所示：

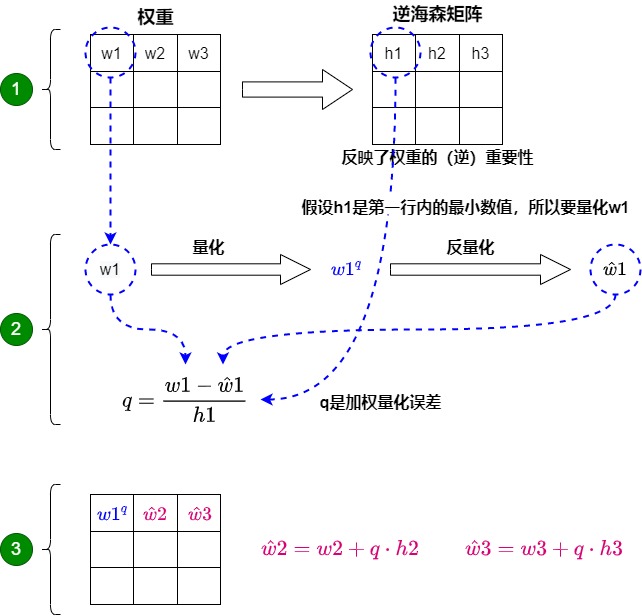
• 首先將層的權(quán)重轉(zhuǎn)換為逆海森矩陣（Hessian）。海森矩陣是模型損失函數(shù)的二階導(dǎo)數(shù)，它告訴我們模型輸出對(duì)每個(gè)權(quán)重變化的敏感度，本質(zhì)上展示了每個(gè)權(quán)重在層中的（逆）重要性。在逆-海森矩陣中，較低的值表示更“重要”的權(quán)重。因?yàn)檫@些權(quán)重的小變化可能會(huì)導(dǎo)致模型性能的顯著變化。即，調(diào)整過程會(huì)優(yōu)先考慮對(duì)精度至關(guān)重要的權(quán)重，有效地生成加權(quán)量化誤差，從而保留更重要的細(xì)節(jié)。
• 對(duì)權(quán)重矩陣中的第一行的第一個(gè)權(quán)重進(jìn)行量化，然后反量化。這個(gè)過程允許我們計(jì)算量化誤差（q），我們可以使用之前計(jì)算的逆海森（h_1）來加權(quán)這個(gè)量化誤差。本質(zhì)上是根據(jù)權(quán)重的重要性創(chuàng)建了一個(gè)加權(quán)量化誤差。
• OBQ不會(huì)讓量化誤差孤立地存在于單個(gè)權(quán)重上，而是將這個(gè)加權(quán)量化誤差重新分配到行中的其他權(quán)重上。這有助于維持網(wǎng)絡(luò)的整體功能和輸出。例如，如果我們對(duì)第一行的第一個(gè)權(quán)重（w1）進(jìn)行量化，我們會(huì)將量化誤差（q）乘以第一行的另外兩個(gè)權(quán)重來進(jìn)行彌補(bǔ)誤差損失。即，對(duì)其他權(quán)重進(jìn)行更新來調(diào)整權(quán)重，補(bǔ)償權(quán)重w1量化導(dǎo)致的影響。我們重復(fù)這個(gè)過程，將加權(quán)量化誤差重新分配，直到所有值都被量化。

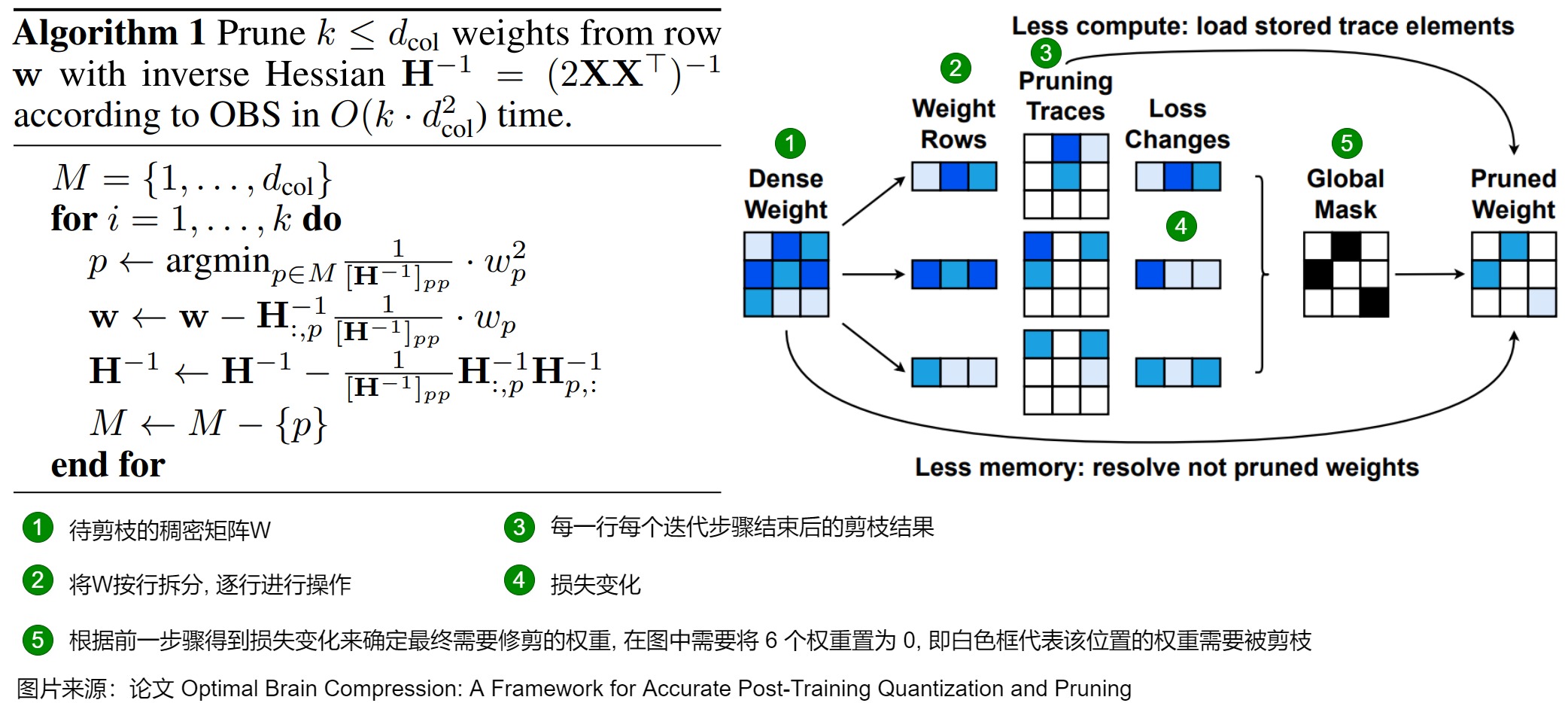
論文給出的算法如下。

• 左數(shù)第一列是待剪枝的稠密矩陣 W。
• 左數(shù)第二列表示將 W 按行拆分, 準(zhǔn)備逐行進(jìn)行操作。
• 左數(shù)第三和第四列表示逐行按照算法進(jìn)行剪枝。
  • Pruning Traces 表示每一行每個(gè)迭代步驟結(jié)束后的剪枝結(jié)果。
  • Loss Changes 表示每個(gè)迭代步驟后損失的變化量，顏色越深表示損失越大。
• 左數(shù)第五列表示根據(jù)前一步驟得到 Loss Changes 確定最終需要修剪的權(quán)重, 在圖中需要將 6 個(gè)權(quán)重置為 0, 即白色框代表該位置的權(quán)重需要被剪枝。
• Less compute: load stored trace elements, 表示如果存儲(chǔ)了 Pruning Traces 時(shí)，可以不用重新跑剪枝過程.
• Less memory: resolve not pruned weights, 表示如果沒有足夠空間可以存儲(chǔ) Pruning Traces 時(shí)，再逐行重跑一遍剪枝過程或者直接進(jìn)行一次參數(shù)更新就能得到這一行的剪枝結(jié)果。

總的來說，OBQ方法通過迭代和更新權(quán)重的方式，以貪心策略找到最佳的量化參數(shù)，以最小化量化引入的誤差，同時(shí)控制模型的大小。這種方法允許在后訓(xùn)練階段將神經(jīng)網(wǎng)絡(luò)的權(quán)重量化為所需的精度，而無需重新訓(xùn)練整個(gè)模型。這種策略對(duì)于大型語言模型如GPT非常有用，因?yàn)樗鼈兺ǔＰ枰诒３指邷?zhǔn)確性的同時(shí)減小模型尺寸。

雖然 OBQ 不錯(cuò)，但是太慢，因?yàn)閷?duì)于包含\(d_{row} \times d_{col}\)的權(quán)重矩陣 W，OBQ的計(jì)算復(fù)雜度是O \((d_{row}?d_{col}^3)\)。OBQ 使用一小時(shí)左右量化一個(gè) ResNet50，在大模型（如：GPT3）上可能要數(shù)天。

2.1.2 GPTQ 方案

特色

GPTQ 的特點(diǎn)或者說主要改進(jìn)如下：

• 逐層量化。GPTQ進(jìn)行逐層進(jìn)行非對(duì)稱量化，每層獨(dú)立處理完畢后再繼續(xù)到下一層。

• 按固定順序量化。GPTQ作者覺得對(duì)于LLMs來說，每次都要挑選需要量化的參數(shù)是不必要的。因?yàn)椋诹炕倪^程中，雖然以貪心算法來每次以最小的誤差來量化權(quán)重的方法表現(xiàn)良好，但相比固定順序并沒有明顯提升，尤其是在大模型上可能固定順序更好。因此，GPTQ將每一行的量化權(quán)重選擇方式從OBQ的貪心策略改成固定地按索引順序選擇。這種方法使得在大型模型上的計(jì)算效率更高，因?yàn)樗鼫p少了計(jì)算復(fù)雜性。

• Lazy Batch-Updates。如果我們每次量化一個(gè)參數(shù)就進(jìn)行一次權(quán)重更新的話，更多的時(shí)間都被花到訪存，不能充分利用GPU的算力，所以 GPTQ 選擇分批進(jìn)行更新，批內(nèi)完成后再更新全局的矩陣。這樣可以延遲一部分參數(shù)的更新，緩解 I/O 壓力。

• Cholesky(喬萊斯基) 分解。GPTQ發(fā)現(xiàn)逐權(quán)重量化需要頻繁更新整個(gè)海森矩陣的逆，這會(huì)引入數(shù)值誤差。因此用 Cholesky 分解求海森矩陣的逆，在增強(qiáng)數(shù)值穩(wěn)定性的同時(shí)，不再需要對(duì)海森矩陣做更新計(jì)算，進(jìn)一步減少了計(jì)算量。結(jié)合 Lazy Batch-Updates, 可以將權(quán)重更新式限制在 block 內(nèi), 然后再通過一次更新將此 block 之后的全部列進(jìn)行更新. 這樣就起到了節(jié)省內(nèi)存帶寬的作用, 從而顯著提升算法效率。

• GPTQ首次將4bit/3bit權(quán)重量化應(yīng)用在176B的模型上，同時(shí)也提供了對(duì)應(yīng)的kernel。

取消貪心算法

OBQ采用貪心策略，獨(dú)立量化權(quán)重矩陣W的每一行，每一行內(nèi)部量化的順序不同，都在維護(hù)自己的最優(yōu)量化順序：按照ΔE最小的原則來選擇量化的順序。即，每個(gè)權(quán)重是按“貪心順序”選擇的，總是優(yōu)先量化當(dāng)前對(duì)整體誤差影響最小的那個(gè)權(quán)重。這個(gè)策略雖然理論上更優(yōu)，但在大模型中效率極低。原因是：每次量化一個(gè)權(quán)重都需要更新 Hessian 的逆矩陣，且每行都需要獨(dú)立執(zhí)行，導(dǎo)致總時(shí)間復(fù)雜度極高。

GPTQ發(fā)現(xiàn)對(duì)于參數(shù)量很大的層，這樣嚴(yán)格選擇順序的量化結(jié)果和任意順序的量化結(jié)果差別并不大，即使不使用貪心策略，只要采用任意固定順序來量化每一行中的權(quán)重，最終的誤差幾乎和貪心順序一致。GPTQ 作者分析：少數(shù)權(quán)重帶來較大的量化損失，這些損失可以被剩余未量化的權(quán)重平衡掉，因此量化順序可能不重要。因此，GPTQ提出所以決定對(duì)所有的行都使用同樣的順序進(jìn)行量化，雖然理論上不是局部最優(yōu)，但整體誤差變化非常小，尤其在參數(shù)數(shù)量大的時(shí)候幾乎無影響。

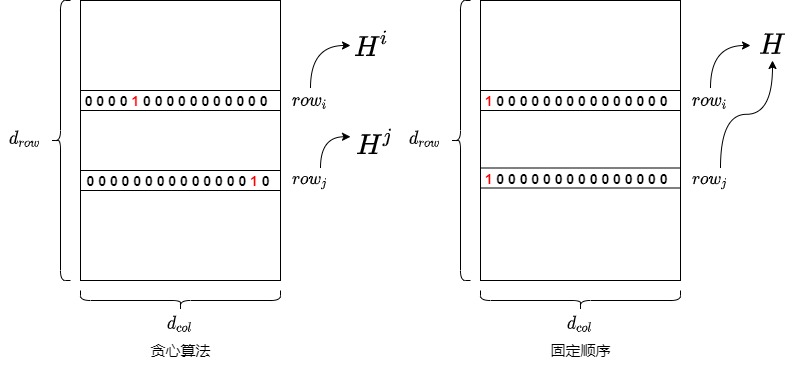
這樣做的好處如下：

• 對(duì)于權(quán)重矩陣的每一行來說，其初始 Hessian 矩陣\(H=2XX^T\)只與輸入矩陣 X相關(guān)，因此初始 Hessian 矩陣都是相同的。
• 在 OBQ 中，隨著剪枝過程的進(jìn)行，每一行權(quán)重的優(yōu)化順序都可能不一樣，因此每一行相關(guān)的 Hessian 矩陣都會(huì)發(fā)生不同的變化。具體而言，每量化一個(gè)參數(shù)，都需要更新\(H^{?1}\)。如果每一行的量化順序不一致，那么每一步中，各行的\(H^{?1}\)是不一樣的，需要各自單獨(dú)計(jì)算。
• 而如果每一行的量化順序一致，那么每一步各行的\(H^{?1}\)是一樣的，所有行共享一個(gè)逆 Hessian 矩陣只，且需要計(jì)算一次即可，這種方式也節(jié)省了每次構(gòu)造 H(i) 的時(shí)間。再考慮到所有行都是按照一樣的順序來量化權(quán)重，那么一次迭代就可以量化同一列的所有行。這項(xiàng)改進(jìn)使得數(shù)矩陣每一行的量化可以做并行的矩陣計(jì)算。
• 由于大模型極度冗余，單個(gè)權(quán)重引入的誤差影響微小，統(tǒng)一順序?qū)е碌淖幼顑?yōu)選擇不會(huì)積累為顯著性能損失。GPTQ 中使用的 Hessian-based 誤差補(bǔ)償機(jī)制會(huì)在每一步自動(dòng)對(duì)未量化權(quán)重進(jìn)行調(diào)整，進(jìn)一步抑制誤差傳播。

這項(xiàng)改進(jìn)使得參數(shù)矩陣每一行的量化可以做并行的矩陣計(jì)算（即 per-channel quantization）。對(duì)于大模型場景，使得量化速度快了一個(gè)數(shù)量級(jí)。

Lazy Batch-Updates

因?yàn)榇竽Ｐ蜋?quán)重的海森矩陣很大，OBQ 每次迭代都需要更新整個(gè)海塞矩陣的逆以及對(duì)整個(gè)權(quán)重進(jìn)行更新，這一過程涉及大量的內(nèi)存訪問，但實(shí)際的計(jì)算量卻較少。所以算法的計(jì)算訪存比相對(duì)較低，性能瓶頸實(shí)際在于GPU的內(nèi)存帶寬。具體而言，因?yàn)槊苛炕?列參數(shù)，就需要更新1次海森矩陣的逆，假設(shè)逆矩陣的大小為 \(d_{row} \times d_{col}\) ，共需更新 \(d_{col}\)次，帶來的訪存總量為 \(d_{row} \times d_{col}^2\) 。當(dāng)維度較大時(shí)，則會(huì)導(dǎo)致運(yùn)行時(shí)間都被訪存占用。例如，在量化某個(gè)參數(shù)矩陣的情況下，每次量化一個(gè)參數(shù)，其他所有未量化的參數(shù)都要按公式全都要更新一遍。

作者發(fā)現(xiàn)：同一個(gè)特征矩陣W不同列間的權(quán)重更新是不會(huì)互相影響的，具體如下：

• 當(dāng)前列 i 的量化只受到前序列量化的影響（前序列量化后會(huì)更新后續(xù)列參數(shù)）。
• 當(dāng)前列 i 的量化不會(huì)影響前序已經(jīng)量化的列（前序列量化完成后其參數(shù)固定）。
• 當(dāng)前列 i 的量化會(huì)更新后續(xù)列的參數(shù)，但后續(xù)列的更新不會(huì)影響當(dāng)前列 i 的量化。換句話說，當(dāng)前列的量化不會(huì)受到尚未更新的列的影響。

具體如下圖所示，由于參數(shù)量化是一列一列按次序進(jìn)行的，第 i 列的參數(shù)的量化結(jié)果受到前 i-1 列量化的影響，但第 i 列的量化結(jié)果不影響前面列的量化。因此我們不需要每次量化前面的列，就更新一遍第 i 列的參數(shù)，而是可以先逐步記錄量化前面列給第 i 列帶來的更新量，在量化到第 i 列時(shí)，再一次性更新參數(shù)，這樣就可以減少 IO 的次數(shù)。

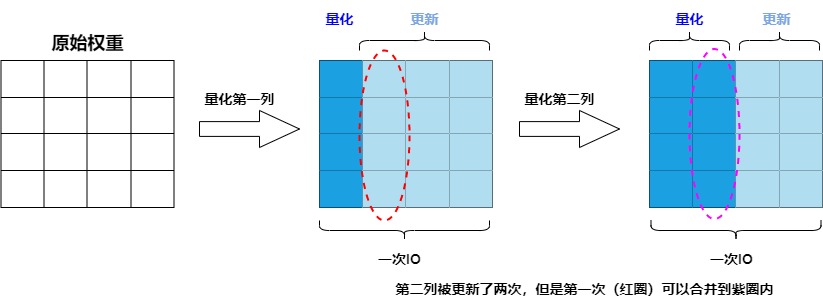
因此作者提出了延遲批處理的方法：先延遲一部分參數(shù)的更新，再后續(xù)一次處理多個(gè)列，以此來緩解帶寬的壓力，大幅提升了計(jì)算速度。具體如下：

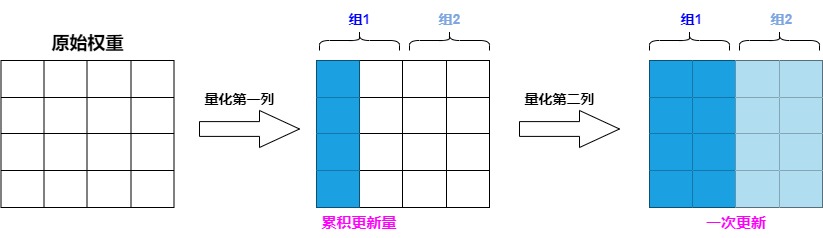
• 對(duì)權(quán)重矩陣按每 B= 128 列進(jìn)行分組（分成group/block），量化當(dāng)前列后，調(diào)整該組剩余的權(quán)重，以補(bǔ)償量化引入的誤差，這樣可以將更新限制在這些列和的對(duì)應(yīng)BxB塊中。

• 當(dāng)一個(gè) group 的參數(shù)全部量化完成，我們才使用下面這個(gè)多權(quán)重版本的公式統(tǒng)一對(duì) \(H^{?1}\) 和 W 進(jìn)行一次全局更新，即處理完當(dāng)前組的所有列后，再更新整個(gè)矩陣的其他列組（其他128列組），以進(jìn)一步修正誤差。這一完整過程就是"惰性批量更新”（Lazy Batch Update）。

這種方法沒有減少理論的計(jì)算總量，但避免了大量更新Hessian矩陣的需要，有效緩解了訪存的瓶頸，從而加快了整個(gè)量化過程。

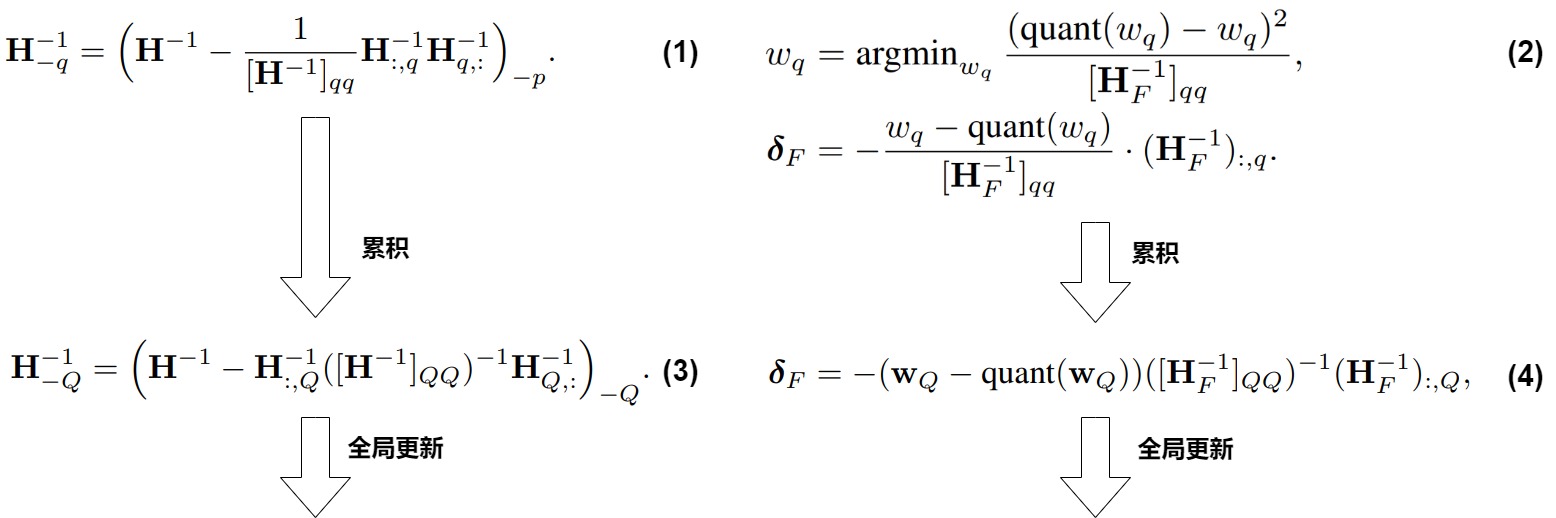
Cholesky(喬萊斯基) 分解

GPTQ 還應(yīng)用 Cholesky 分解來解決 H?? 逆矩陣計(jì)算的數(shù)值穩(wěn)定性問題。 GPTQ 作者在實(shí)驗(yàn)過程中注意到在大規(guī)模參數(shù)矩陣上重復(fù)的應(yīng)用如下公式會(huì)累積誤差，進(jìn)而使得數(shù)值計(jì)算不準(zhǔn)確。確切的說，矩陣\(H^{-1}_F\)會(huì)出現(xiàn)無窮的情況，這回導(dǎo)致算法更新剩余權(quán)重錯(cuò)誤，導(dǎo)致量化效果變差。

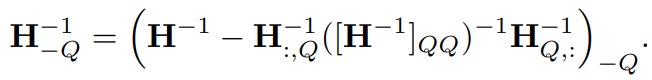
想解決此問題，對(duì)于小模型，在 H 的對(duì)角線元素添加小的常數(shù)項(xiàng) \(\lambda\) 即可，對(duì)于大模型需要更穩(wěn)定和通用的辦法。為了解決這個(gè)問題，作者用Cholesky 分解（一種分解矩陣的方法）來求海森矩陣的逆，提前計(jì)算好所有需要的信息，并使用優(yōu)化的Cholesky核進(jìn)行加速。

總體算法

GPTQ根據(jù)輸入的Hessian逆矩陣\(??^{?1}\) 和其他參數(shù)來量化權(quán)重W，并且核心思想是通過迭代逐步量化權(quán)重以減小誤差。GPTQ算法的主要步驟如下。

• 初始化量化結(jié)果Q為一個(gè)零矩陣，初始化誤差矩陣E為一個(gè)零矩陣。
• 對(duì)\(??^{?1}\) 進(jìn)行Cholesky分解，得到H?1的逆矩陣信息。
• 迭代處理權(quán)重列的量化（逐列量化權(quán)重矩陣，并在每一步調(diào)整尚未量化的部分以補(bǔ)償上述量化誤差）：
  • 對(duì)每個(gè)列進(jìn)行量化，更新Q矩陣中的對(duì)應(yīng)列。
  • 計(jì)算量化誤差，更新誤差矩陣E。
  • 更新權(quán)重矩陣W中的權(quán)重，以減小誤差。
  • 重復(fù)上述步驟，直到所有的權(quán)重列都被量化。
• 最終，返回量化后的權(quán)重矩陣Q。

為了降低計(jì)算復(fù)雜度，GPTQ 采用了逐列優(yōu)化的方法。將權(quán)重矩陣 W 的列表示為 wi，對(duì)每一列進(jìn)行量化，同時(shí)考慮之前列量化引入的誤差累積。逐列優(yōu)化的主要優(yōu)勢在于：

• 降低計(jì)算復(fù)雜度：將高維的矩陣優(yōu)化問題分解為多個(gè)低維的向量優(yōu)化問題。
• 考慮誤差累積：在每一步更新中，考慮了之前量化引入的誤差，保證了整體誤差的最小化。

這里做幾點(diǎn)簡要說明:

• 這里的算法流程對(duì)權(quán)重的每一行是并行處理的
• 算法第 3 行左側(cè)的 \(??^{?1}\) 實(shí)際上是 \(??^{?1}=????^??\) 中的 \(??^??\)
• 算法的倒數(shù)第 5 行的分子進(jìn)行平方后除以 2 才代表了本次迭代造成的損失增量
• 算法的倒數(shù)第 4 行實(shí)際上還更新了被量化的權(quán)重項(xiàng)本身, 更新后其權(quán)重為 0, 而被量化的權(quán)重所在列靠前的權(quán)重的更新項(xiàng)實(shí)際上是 0, 因此可以統(tǒng)一這么寫
• 算法倒數(shù)第 2 行表示對(duì) block 之后的全部權(quán)重進(jìn)行一次性更新, 實(shí)際上也就是倒數(shù)第 4 行將列的范圍 ??:(??+??) 擴(kuò)展到 ??+??。

雖然前面的 GPTQ 通過校準(zhǔn)數(shù)據(jù)最小化量化誤差，提升量化效果。但是可能過擬合校準(zhǔn)集，導(dǎo)致模型在分布外域上的性能下降。

2.2 AWQ

論文“AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration”是SmoothQuant的續(xù)作。論文作者發(fā)現(xiàn)：對(duì)模型的性能來說，權(quán)重并不是同等重要的。極少量（0.1%~1%）的參數(shù)可能主導(dǎo)的量化過程中損失的性能。保留這些顯著權(quán)重（Salient weight）不做量化，就可以顯著減少量化誤差。什么樣的權(quán)重值得保護(hù)呢，作者指出，應(yīng)該參考 activation 分布而不是 weight 分布。在推理時(shí)被顯著激活的權(quán)重肯定更重要，因?yàn)檫@些權(quán)重處理更重要的特征。即用激活值來發(fā)現(xiàn)重要的weight，較大激活值對(duì)應(yīng)的權(quán)重比較重要。在此觀察的基礎(chǔ)上，AWQ采用了激活感知方法。該方法是一種數(shù)據(jù)驅(qū)動(dòng)的方法，采用逐通道縮放技術(shù)來自動(dòng)搜索最佳縮放因子，通過保護(hù)更多的 "重要" 權(quán)重來提高準(zhǔn)確性，從而在量化所有權(quán)重的同時(shí)最小化量化誤差。

2.2.1 動(dòng)機(jī)

AWQ作者有以下發(fā)現(xiàn)：

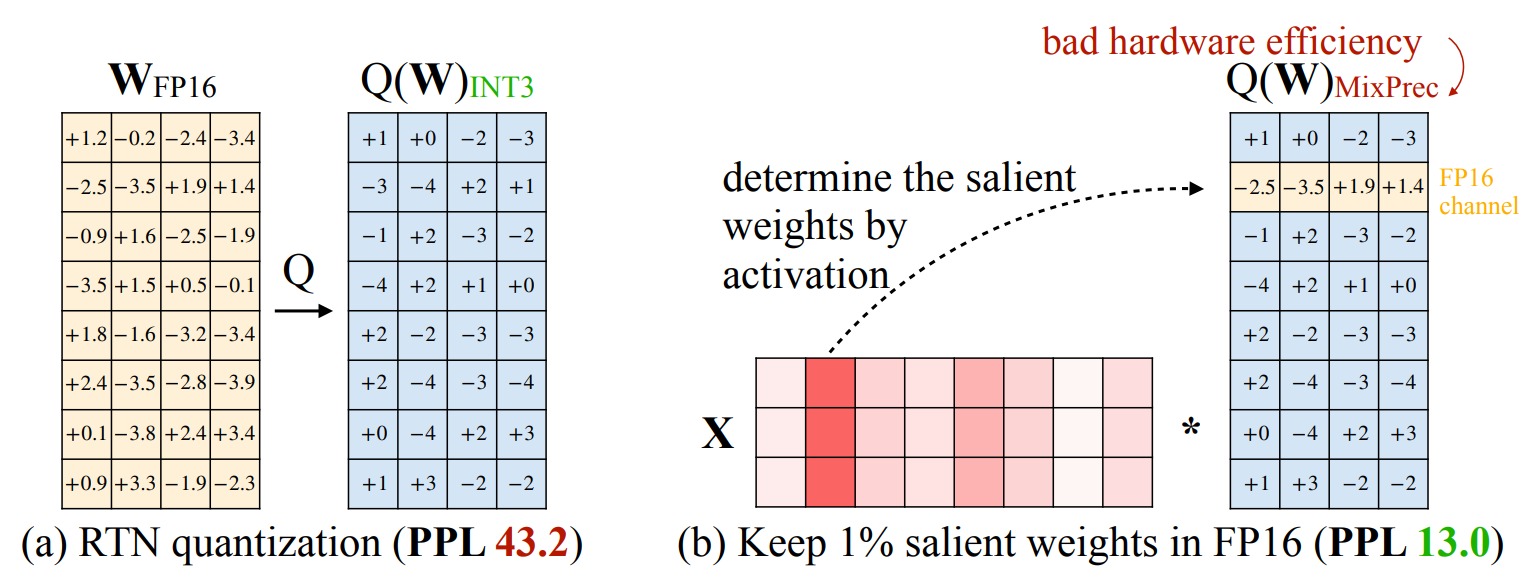
• LLM 的權(quán)重并非同等重要。與其他權(quán)重相比，有一小部分顯著權(quán)重對(duì) LLM 的性能更為重要。作者認(rèn)為，保留這些顯著權(quán)重不進(jìn)行量化（維持這些權(quán)重的精度為FP16），其他權(quán)重使用低比特量化推理，就可以在不進(jìn)行任何訓(xùn)練的情況下，彌補(bǔ)量化損失造成的性能下降。
• 激活大的值所對(duì)應(yīng)的權(quán)重為重要權(quán)重。可以根據(jù)激活幅度（magnitude）選擇權(quán)重，通過只保留 0.1%-1% 的較大激活對(duì)應(yīng)權(quán)重通道，對(duì)顯著權(quán)重進(jìn)行放大，就可以防止高影響力權(quán)重的退化，保留了大型語言模型中的關(guān)鍵知識(shí)，顯著提高量化性能。

2.2.2 方案

選擇權(quán)重

通常評(píng)估權(quán)重重要性的方法是查看其大小（magnitude）或 L2-norm（L2-范數(shù)）。

但是AWQ作者發(fā)現(xiàn)，保留那些具有較大 Norm的權(quán)重通道對(duì)量化性能的提升有限。與隨機(jī)選擇效果相比，僅僅有少量改進(jìn)。而根據(jù)激活幅度（magnitude）選擇權(quán)重可以顯著提高模型量化效果。作者推測是，幅度較大的輸入特征通常更重要，保留相應(yīng)的權(quán)重為 FP16 可以更好地保護(hù)這些特征，從而提升模型性能。具體實(shí)現(xiàn)上，作者是對(duì)激活值的每一列求絕對(duì)值的平均值，然后把平均值較大的一列對(duì)應(yīng)的通道視作顯著通道，保留 FP16 精度。

然而在實(shí)現(xiàn)中遇到一個(gè)問題：盡管將 0.1% 的權(quán)重保留為 FP16 可以在不明顯增加模型大小的情況下提高量化性能，但這種混合精度數(shù)據(jù)類型會(huì)給系統(tǒng)實(shí)現(xiàn)帶來困難（硬件效率低下）。因此，我們需要想出一種方法，即保護(hù)重要的權(quán)重，同時(shí)又不用實(shí)際保留它們?yōu)?FP16。具體如下圖所示，RTN代表vanilla round-to-nearest baseline。

激活感知縮放

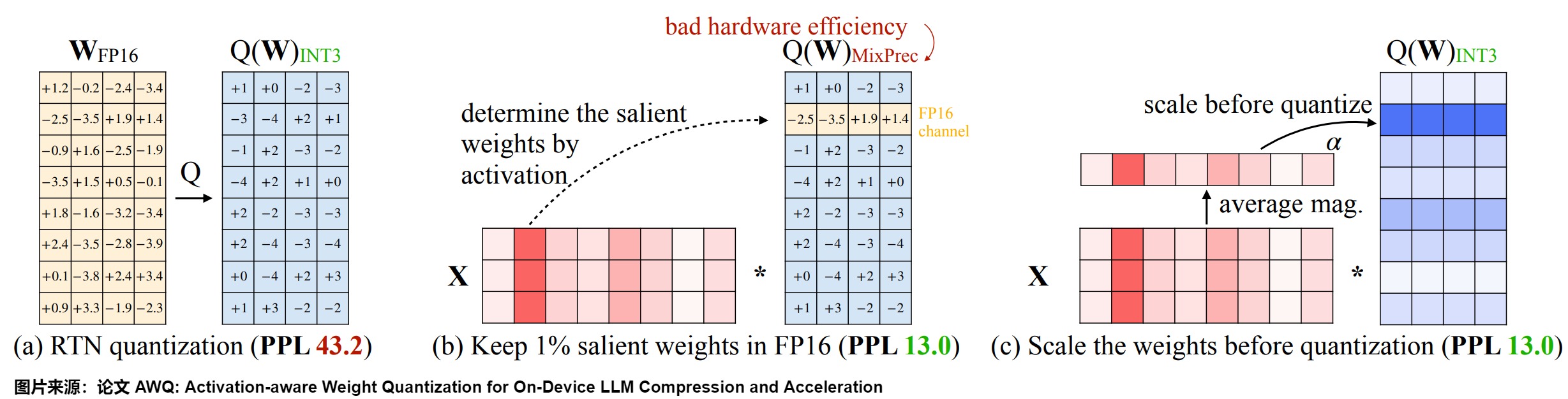
AWQ的思路是：通過激活感知縮放（Activation-aware Scaling）保護(hù)顯著權(quán)重。即，識(shí)別每一層中最重要的權(quán)重，通過按逐通道（per-channel）縮放 (Scaling) 來減少重要權(quán)重（Salinet Weight ）的量化誤差。這些權(quán)重對(duì)于維持模型性能至關(guān)重要。通過關(guān)注與高激活特征對(duì)應(yīng)的權(quán)重，AWQ最小化了可能導(dǎo)致顯著精度下降的量化誤差。具體如下圖所示。

推導(dǎo)

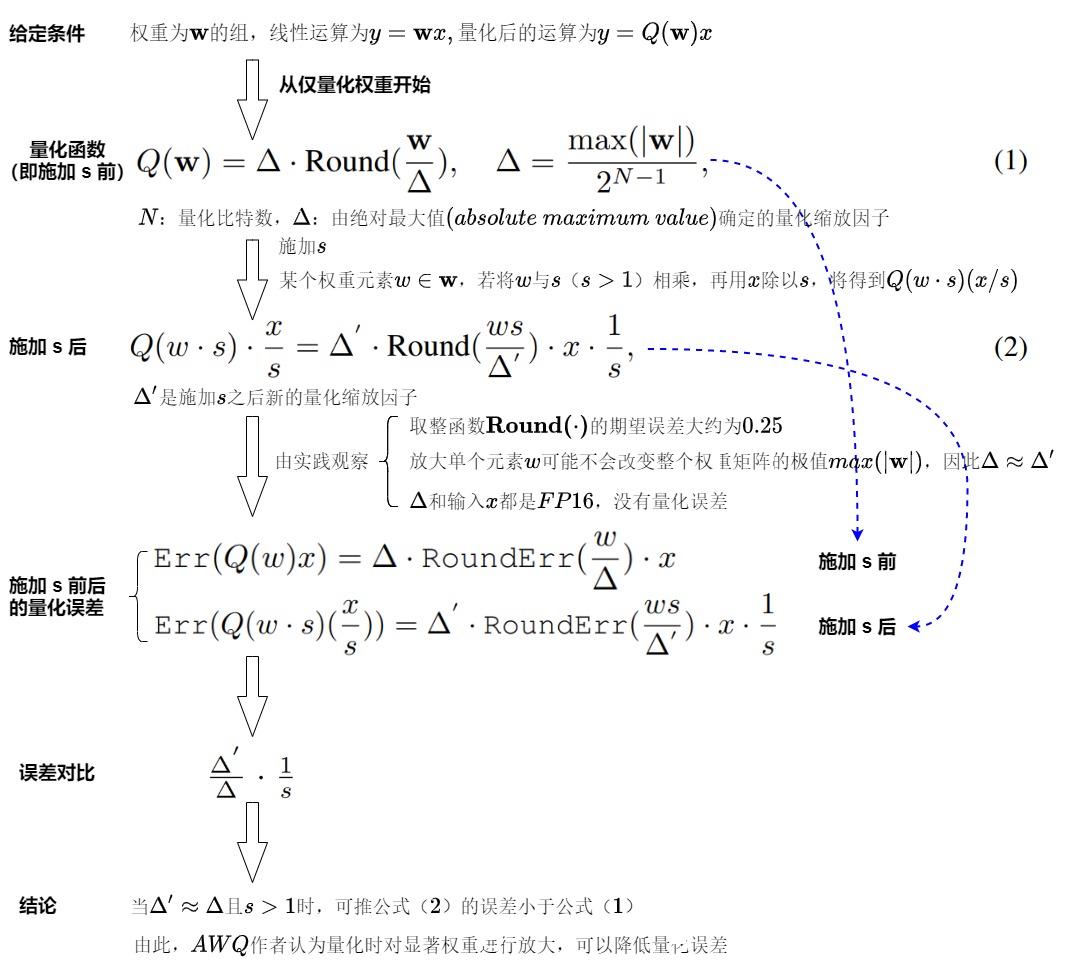
保護(hù)異常值權(quán)重通道的一種直接方法是將通道乘以一定的縮放比(scaling ratio >1)，這樣它們就可以精確量化。我們接下來分析采用縮放比前后，Weight-only的量化誤差。由下圖可知，方案基本可行。

問題

如果希望重要的權(quán)重被更好地表示出來，就需要設(shè)置更大的縮放比，這樣量化效果更好。但如果我們使用非常大的縮放比，非顯著權(quán)重的channel（(Non-salient channels）會(huì)被迫使用更小的動(dòng)態(tài)范圍，這可能會(huì)損害模型的整體精度。即，s進(jìn)一步增大時(shí)，\(\Delta' \approx \Delta\)不再成立，當(dāng) Δ 增加時(shí)，非顯著通道的相對(duì)誤差將會(huì)增加（非顯著通道的誤差將被放大），從而使得量化精度下降，沒有保留 1%權(quán)重方法效果好。因此，在保護(hù) Salient Channels 時(shí)，還需要考慮如何減少 Non-salient channels 的錯(cuò)誤。

最優(yōu)縮放因子搜索

為了同時(shí)考慮 Salient Weight 和 Non-salient Weight，AWQ 提出了自動(dòng)搜索 (每個(gè)輸入通道) 最優(yōu)縮放比的方法（找到一個(gè)合適的縮放因子s），使得減少顯著權(quán)重量化損失的同時(shí)也不能增加其它權(quán)重的量化損失，讓某一層量化后的輸出差最小。

下圖給出了思路。形式上，希望優(yōu)化下圖中標(biāo)號(hào)1的目標(biāo)函數(shù)。但是因量化函數(shù)是不可微的，故無法用反向傳播直接優(yōu)化問題。有些優(yōu)化技術(shù)因?yàn)橐蕾囉诮铺荻龋匀匀淮嬖谑諗坎环€(wěn)定的問題。為了使整個(gè)過程更加穩(wěn)定，AWQ 作者通過分析影響比例因子選擇的因素，來定義最優(yōu) Scaling 的搜索空間。

如前文所述，權(quán)重通道的顯著性實(shí)際上是由 activation 的尺度（scale）決定的（故此稱之為 activation-awareness）。因此，作者簡單地使用非常簡單的搜索空間（如下圖標(biāo)號(hào)2）。此方法會(huì)自動(dòng)搜索一個(gè)最優(yōu)（每個(gè)輸入通道）比例因子，并進(jìn)一步應(yīng)用權(quán)重裁剪來最小化量化的 MSE 誤差，即，讓某一層量化后的輸出差異最小化。

如何確定超參數(shù) \(\alpha\)？作者認(rèn)為可以通過在區(qū)間 [0,1] 上進(jìn)行快速網(wǎng)格搜索來找到最佳的 \(\alpha\)（0 表示不進(jìn)行縮放；1 表示在搜索空間中最激進(jìn)的縮放）。通過閱讀源碼發(fā)現(xiàn)該方法實(shí)際上就是在 [0,1] 區(qū)間平均取 20 個(gè)數(shù)，0, 0.05, 0.10, 0.15 …… 然后逐個(gè)計(jì)算不同 \(\alpha\)下的 MSE 損失，損失最小的就是最佳的 \(\alpha\)。

應(yīng)用

awq 中需要根據(jù)模塊類型，分別處理不同的線性層組，分開計(jì)算不同模塊的權(quán)重縮放因子，比如可以將llm 模型分成以下幾個(gè)模塊分別計(jì)算 scales。

• self-attention 的查詢、鍵、值投影層
• self-attention 的輸出投影層
• mlp 的 第一個(gè)全連接層
• mlp 的 第二個(gè)全連接層
• mlp 的 gate_proj 和 up_proj 線性層
• mlp 的 down_proj 線性層

與 SmoothQuant 的關(guān)系

因?yàn)閮善撐淖髡叨紒碜灾?MIT HAN LAB 團(tuán)隊(duì)，所以我們進(jìn)行分析。

相同點(diǎn)

• 都是后訓(xùn)練量化 (Post-Training Quantization PTQ)。
• 都有對(duì)一些 weight (及其對(duì)應(yīng)的 input activation) 做 scaling，即 weight 乘以一個(gè) scaling factor，對(duì)應(yīng)的 input activation 除以這個(gè) scaling factor。
• 都需要校準(zhǔn)集確定 scaling factor 的值 (無需額外的訓(xùn)練)。

區(qū)別

• 量化精度不同：SmoothQuant 量化精度為 W8A8；AWQ 量化精度為 W4A16。
• Scaling factor 的確定方法不同：SmoothQuant 的 scaling factor 是算出來的： \(??_??=max(|??_??|)^??/max(|??_??|)^{1???}\) ；AWQ 的 scaling factor 是搜出來的 $??=??_{??^??},???=arg?\ min_?????(??_{??^??}) $，其中 ???? 是 activation 的平均幅值。
• Scaling factor 施加的 weight 不同：SmoothQuant 平等地對(duì)每個(gè) weight (及其對(duì)應(yīng)的 input activation) 做 scaling；AWQ 只對(duì)少量 (約 0.1%) 的 salient weight (及其對(duì)應(yīng)的 input activation) 做 scaling。
• AWQ 作者還開發(fā)了 TinyChat，一個(gè)高效靈活的 4 位設(shè)備端 LLM/VLM 推理框架。

2.3 LLM-QAT

論文“LLM-QAT: Data-Free Quantization Aware Training for Large Language Models”是大模型量化感知訓(xùn)練的開山之作。目前一些針對(duì)大模型的PTQ方法已被證明在低至 8 bit 的情況下也能表現(xiàn)良好。但是論文作者發(fā)現(xiàn)這些方法在較低比特精度下會(huì)出現(xiàn)問題。因此，論文研究了 LLM 的QAT，以進(jìn)一步提高量化水平。作者還提出了一種 data-free 蒸餾方法，該方法利用預(yù)訓(xùn)練模型產(chǎn)生的生成，可以更好地保留原始輸出分布，并允許獨(dú)立于其訓(xùn)練數(shù)據(jù)來量化任何生成模型，類似于訓(xùn)練后量化方法。文中除了量化權(quán)重和激活之外，還量化了 KV 緩存，這對(duì)于提高吞吐量和支持當(dāng)前模型規(guī)模的長序列依賴至關(guān)重要。

2.3.1 動(dòng)機(jī)

與后訓(xùn)練相比，QAT通常會(huì)帶來更好的準(zhǔn)確性，因?yàn)槟Ｐ蛷囊婚_始就被訓(xùn)練來考慮精度降低的問題。此外，它允許模型繼續(xù)訓(xùn)練或進(jìn)行fine tune，這對(duì)大型語言模型至關(guān)重要。但是，使用QAT量化LLM在幾個(gè)主要方面面臨挑戰(zhàn)：

• 大模型的訓(xùn)練從技術(shù)上來說很困難，對(duì)于算力資源要求比較集中。而且，QAT需要引入模擬量化的操作, 會(huì)引起顯存&計(jì)算量進(jìn)一步上漲，以及梯度mismatch的問題，從而增加訓(xùn)練成本以及影響Scaling Laws。
• QAT需要訓(xùn)練數(shù)據(jù)，但是對(duì)于大模型來說，很難獲取到這些訓(xùn)練數(shù)據(jù)。而預(yù)訓(xùn)練數(shù)據(jù)的龐大規(guī)模和多樣性本身就是一個(gè)障礙，數(shù)據(jù)的預(yù)處理也很困難。
• LLM 在 zero-shot 生成方面表現(xiàn)出色，并在量化后保持這種能力至關(guān)重要。因此，選擇合適的微調(diào)數(shù)據(jù)集很重要。 如果 QAT 數(shù)據(jù)域太窄或者與原始預(yù)訓(xùn)練數(shù)據(jù)分布存在顯著不同，則可能會(huì)損害模型的性能。
• 由于 LLM 表現(xiàn)出獨(dú)特的權(quán)重和激活分布，其特點(diǎn)是存在大量的異常值。 因此，針對(duì)小型模型的最好的量化裁剪（clipping）方法，但該方法對(duì)于LLM來說并不是開箱即用的。
• 此外，尚不清楚量化感知訓(xùn)練是否遵循模型的縮放規(guī)律。

2.3.2 方案

Data-free 蒸餾

為了應(yīng)對(duì)訓(xùn)練數(shù)據(jù)方面的挑戰(zhàn)，需要將預(yù)訓(xùn)練數(shù)據(jù)的分布與有限數(shù)量的微調(diào)數(shù)據(jù)緊密的結(jié)合，論文提出了從原始預(yù)訓(xùn)練模型生成下一個(gè) Token 數(shù)據(jù)的方法，并結(jié)合知識(shí)蒸餾來規(guī)避這個(gè)問題，該方法被稱為 data-free 知識(shí)蒸餾，適用于任何生成模型，無論原始訓(xùn)練數(shù)據(jù)是否可用。

如下圖(a)所示，我們從詞匯表中隨機(jī)化第一個(gè)Token：<start>，并讓預(yù)訓(xùn)練模型生成下一個(gè)Token：<out1>，然后將生成的Token附加到起始Token以生成新的輸出：<out2>。 重復(fù)這個(gè)迭代過程，直到達(dá)到句子Token的結(jié)尾或最大生成長度。在數(shù)據(jù)生成過程中，從分布中采樣下一個(gè)Token是非常重要的，作者在下一個(gè)Token生成時(shí)測試三種不同的采樣策略。

• 最直接的方法是選擇第 1 個(gè)候選者作為下一個(gè)Token。 但是，下一個(gè)Token不一定代表訓(xùn)練學(xué)生模型的最佳標(biāo)簽，因?yàn)椴蓸訒?huì)引入固有的噪聲。 所以，該策略生成的句子缺乏多樣性，并且會(huì)循環(huán)重復(fù)幾個(gè)Token。
• 為了解決這個(gè)問題，論文使用預(yù)訓(xùn)練模型的 SoftMax 輸出作為概率，從分布中隨機(jī)采樣下一個(gè)Token。 這種采樣策略會(huì)產(chǎn)生更加多樣化的句子，并大大提高了微調(diào)學(xué)生模型的準(zhǔn)確性。
• 此外，論文還發(fā)現(xiàn)最初的幾個(gè)Token在確定預(yù)測趨勢方面起著至關(guān)重要的作用。 因此，對(duì)他們來說擁有更高的置信度很重要。 在生成過程中，論文采用了混合采樣策略，針對(duì)前 3~5 個(gè)Token確定性地選擇 top-1 預(yù)測，然后剩余的Token進(jìn)行隨機(jī)采樣。

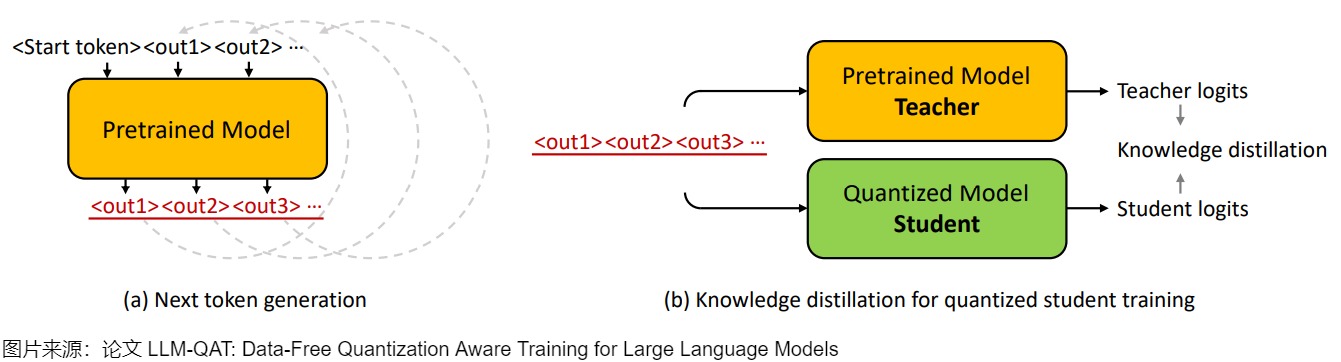
實(shí)驗(yàn)表明，即使與使用原始訓(xùn)練集的大型子集進(jìn)行訓(xùn)練相比，該方法也能夠更好地保留原始模型的輸出分布。 此外，我們可以僅使用一小部分（100k）采樣數(shù)據(jù)成功地提取量化模型，從而保證一個(gè)合適的計(jì)算成本。

知識(shí)蒸餾

論文作者使用基于交叉熵的 logits 蒸餾從全精度預(yù)訓(xùn)練教師網(wǎng)絡(luò)來訓(xùn)練量化的學(xué)生網(wǎng)絡(luò)，公式如下所示：

其中， i 表示當(dāng)前批次中的第 i 個(gè)樣本，總共有 n 個(gè)句子。 c 表示類的數(shù)量，在論文的例子中，它等于詞匯量的大小。 T和S分別是教師網(wǎng)絡(luò)和學(xué)生網(wǎng)絡(luò)。

量化函數(shù)

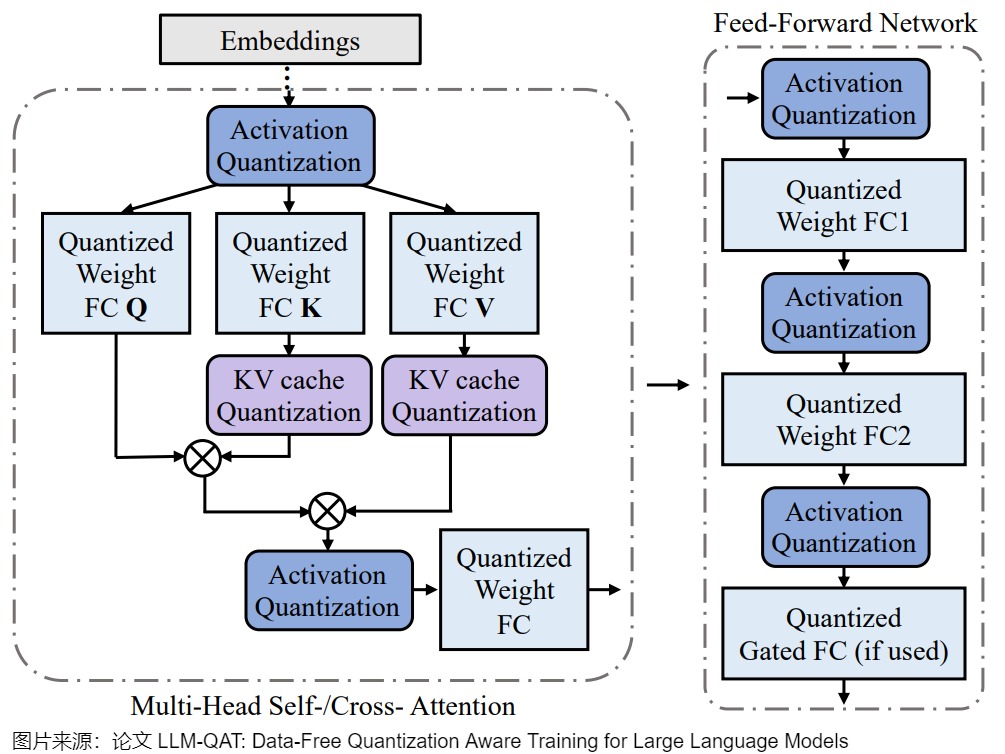
上圖為量化 Transformer 模型的示例圖。根據(jù) Llm.int8 () 和 Smoothquant 中的發(fā)現(xiàn)，在LLM中，權(quán)重和激活都存在顯著的異常值 。 這些異常值對(duì)量化過程有顯著影響，因?yàn)樗鼈儠?huì)增加量化步長，同時(shí)降低中間值的精度。

但事實(shí)證明，在量化過程中裁剪這些異常值不利于 LLM 的性能。 在訓(xùn)練的初始階段，任何基于裁剪的方法都會(huì)導(dǎo)致異常高的困惑度（perplexity）分?jǐn)?shù)（即> 10000），從而導(dǎo)致大量信息丟失，并且事實(shí)證明很難通過微調(diào)來恢復(fù)。 因此，論文選擇保留這些異常值。 此外，論文還發(fā)現(xiàn)在具有門控線性單元（GLU）的模型中，激活權(quán)重大多是對(duì)稱分布的。 根據(jù)論文的分析和經(jīng)驗(yàn)觀察，論文為權(quán)重和激活選擇對(duì)稱 MinMax 量化，公式如下所示：

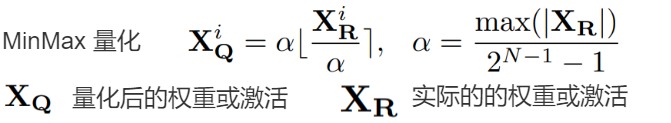
其中， XQ 表示量化后的權(quán)重或激活，XR 表示實(shí)際的權(quán)重或激活。 為了確保有效的量化，論文采用 per-token 激活量化和 per-channel 權(quán)重量化，如下圖所示。

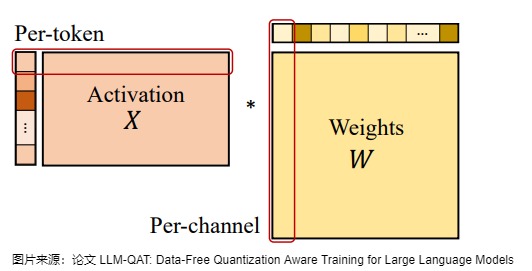
KV Cache的量化感知訓(xùn)練

除了權(quán)重和激活之外，大語言模型（LLM）中的鍵值緩存（KV 緩存）也會(huì)消耗不少的內(nèi)存。 然而，之前只有少數(shù)工作解決了 LLM 中的 KV 緩存的量化問題，且方法主要局限于訓(xùn)練后量化（論文“FlexGen: High-Throughput Generative Inference of Large Language Models with a Single GPU”）。 而本論文證明了可以采用用于激活量化的類似量化感知訓(xùn)練方法來量化 KV 緩存。

在訓(xùn)練過程中，LLM-QAT對(duì) key 和 value 的整個(gè)激活張量進(jìn)行量化，如下圖所示。通過將量化函數(shù)集成到梯度計(jì)算中，確保使用量化的鍵值對(duì)進(jìn)行有效的訓(xùn)練。

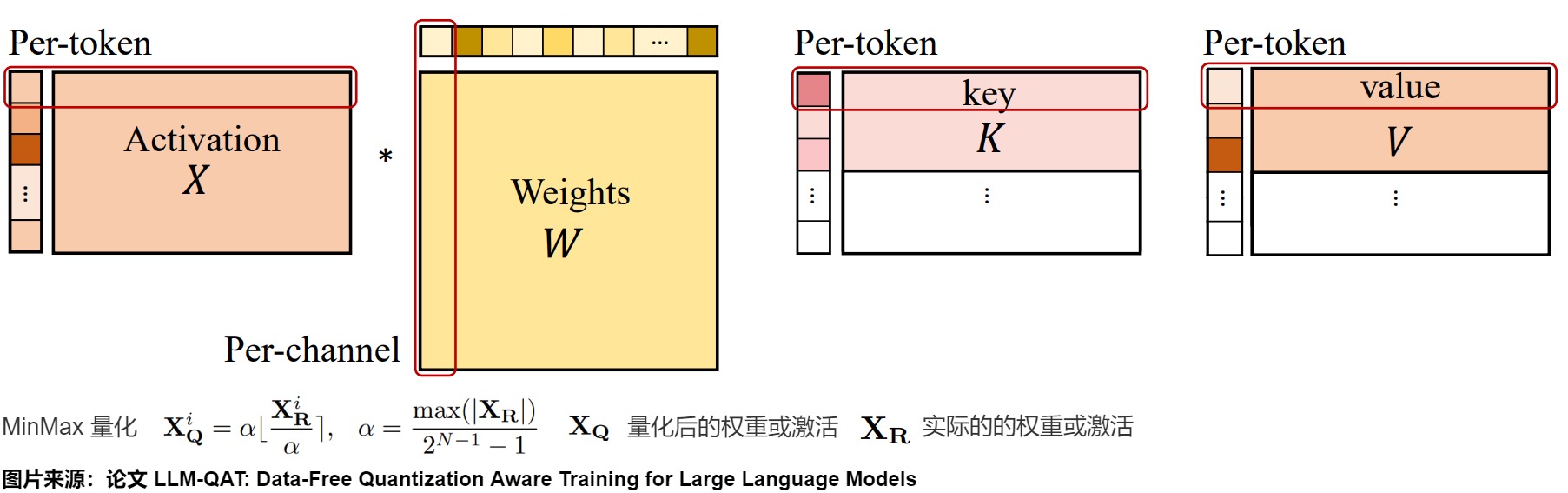
結(jié)論

論文采用了三種訓(xùn)練后量化方法 round-to-nearest(RTN)、 GPT-Q 和 SmoothQuant 作為基線，在BoolQ、PIQA、SIQA、HellaSwag、WinoGrande、ARC和 OBQA 數(shù)據(jù)集上針對(duì)不同的量化方法對(duì)比了常識(shí)推理任務(wù)的零樣本性能，還在 TriviaQA 和 MMLU數(shù)據(jù)集上評(píng)估了不同的量化方法的小樣本性能，同時(shí)，也在 WikiText2和 C4 數(shù)據(jù)集上對(duì)比了不同的量化方法的困惑度分?jǐn)?shù)。其中，困惑度評(píng)估用于驗(yàn)證量化模型是否能夠在其訓(xùn)練域的不同樣本上保留模型的輸出分布。 零樣本和少樣本評(píng)估則衡量模型在下游任務(wù)上的能力是否得到保留。

對(duì)于從業(yè)者來說，一個(gè)重要的問題是是選擇使用全精度的小模型，還是選擇具有類似推理成本的較大的量化模型？雖然確切的權(quán)衡可能會(huì)因多種因素而異，但作者根據(jù)本文的結(jié)果提出了一些建議。

• 使用8比特量化的大模型應(yīng)該優(yōu)于較小的全精度模型，PTQ 方法足以滿足這種情況。

• 使用 LLM-QAT 量化的 4 比特的模型應(yīng)該優(yōu)于類似大小的 8 比特模型。

因此，作者建議使用 4 比特的 LLM-QAT 模型，以實(shí)現(xiàn)最佳效率與精度的權(quán)衡。

2.4 QLoRA

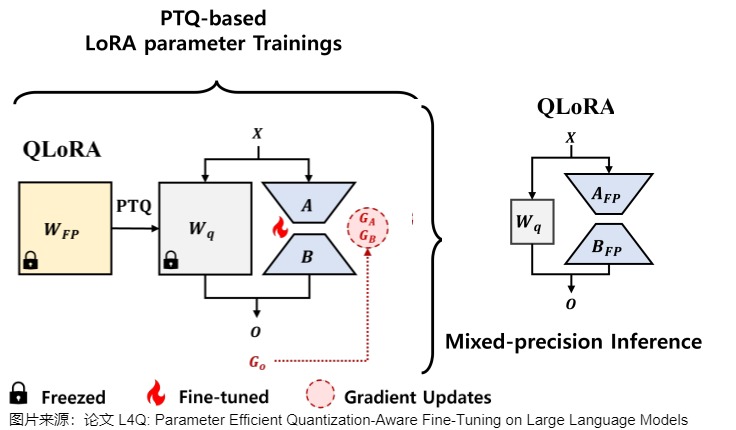
QLoRA（Quantized Low-Rank Adapter）出自論文“QLORA: Efficient Finetuning of Quantized LLMs”，是首個(gè)基于LoRA（Low-rank Adapter）的PTQ方法，其中適配器位于每個(gè)網(wǎng)絡(luò)層。通過一系列創(chuàng)新工作，如引入4位NormalFloat、雙量化和Paged Optimizers（分頁優(yōu)化器）等方法，QLoRA對(duì)LoRA方法進(jìn)行了更好的調(diào)優(yōu)，在降低內(nèi)存使用的同時(shí)，也可以保持性能。

在微調(diào)階段，QLoRA首先將LLM量化為4位，然后，鎖定原模型參數(shù)不參與訓(xùn)練，在更高的精度（如BFloat16或Float16）下，對(duì)量化模型的每個(gè)4位權(quán)重矩陣使用LoRA來進(jìn)行微調(diào)。在推理階段，QLoRA將LLM反量化到與LoRA相同的精度，然后將LoRA的更新添加到LLM中。

2.4.1 動(dòng)機(jī)

由于模型量化前后存在量化誤差，一個(gè)自然的想法就是用LoRA去學(xué)習(xí)這個(gè)量化誤差。QLoRA就是在PTQ的過程中用一個(gè)全精度的LoRA矩陣去學(xué)這個(gè)量化誤差。量化時(shí)權(quán)重采用NF4格式編碼。

然而，由于LoRA參數(shù)上的額外前向路徑，QLoRA在推理過程中還是需要和一個(gè)全精度的LoRA一起推理，計(jì)算全精度模型的加和，沒法將LoRA融入到量化的模型里。這引入了計(jì)算效率低下的問題。這種低效是因?yàn)楦呔萀oRA參數(shù)和低精度量化權(quán)重不能合并為低精度值。本來想用量化的方式加速推理，現(xiàn)在只降低了顯存開銷。

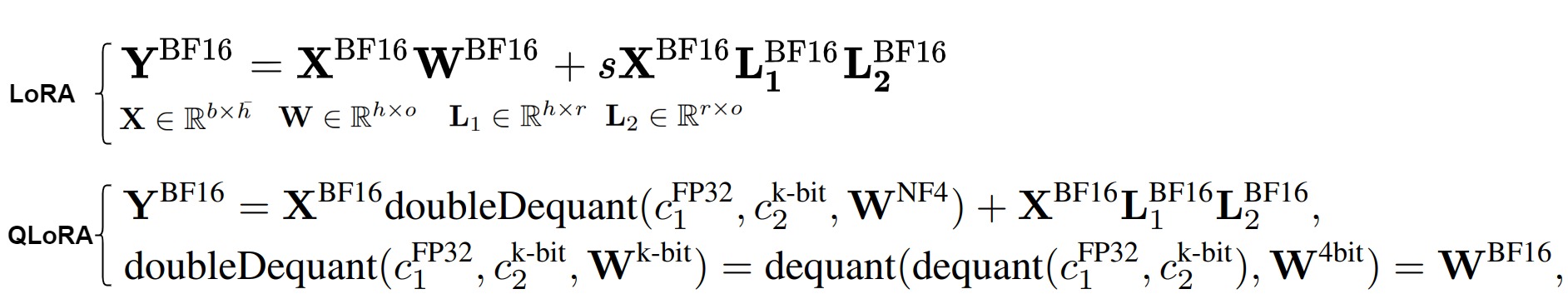
2.4.2 方案

QLoRA的主要?jiǎng)?chuàng)新如下：

• 4-bit NormalFloat (NF4) Quantization：QLoRA引入了一種新的4位量化數(shù)據(jù)類型，稱為NormalFloat（NF4），它在信息理論上對(duì)于正態(tài)分布的權(quán)重是最優(yōu)的，因此可以將權(quán)重量化為4位來減少內(nèi)存占用的同時(shí)，也保持模型性能。
• Double Quantization：QLoRA采用雙重量化技術(shù)，即對(duì)普通參數(shù)進(jìn)行一次量化，對(duì)量化常數(shù)再進(jìn)行一次量化，這樣可以進(jìn)一步減少平均內(nèi)存占用。
• Paged Optimizers：為了管理內(nèi)存峰值，QLoRA引入了分頁優(yōu)化器，它們使用NVIDIA統(tǒng)一內(nèi)存來處理長序列長度的小批量數(shù)據(jù)時(shí)出現(xiàn)的內(nèi)存需求。
• Forward and Backward Propagation：在前向計(jì)算時(shí)，QLoRA首先通過反量化函數(shù)將原始模型的參數(shù)反量化成fp16，然后加上LoRA適配層。LoRA的參數(shù)不量化，因?yàn)樗鼈冃枰聪騻鞑?yōu)化。而原始模型的參數(shù)是凍結(jié)的，因此可以量化。在參數(shù)更新時(shí)，只需要計(jì)算LoRA適配器權(quán)重對(duì)誤差的梯度，而不需要4位權(quán)重的梯度。

4位正態(tài)浮點(diǎn)量化

\(\text{4-bit NormalFloat}\)（正態(tài)浮點(diǎn)）是一種數(shù)據(jù)類型，它在量化過程中保留了零點(diǎn)，并使用所有\(2^k\)位來表示k位數(shù)據(jù)類型。這種數(shù)據(jù)類型通過估計(jì)兩個(gè)范圍的分位數(shù)\(q^i\)來創(chuàng)建一個(gè)非對(duì)稱的數(shù)據(jù)類型，這兩個(gè)范圍分別是負(fù)數(shù)部分\([-1,0]\)的 \(2^{k-1}\)和正數(shù)部分\([0,1]\)的\(2^{k-1}+1\)。然后，它統(tǒng)一了這兩組分位數(shù)\(q^i\)，并從兩組中都出現(xiàn)的兩個(gè)零中移除一個(gè)。這種結(jié)果數(shù)據(jù)類型在每個(gè)量化bin中都有相等的期望值數(shù)量，因此被稱為\(\text{k-bit NormalFloat}\space (\text{NF}_k)\)，這種數(shù)據(jù)類型對(duì)于以零為中心的正態(tài)分布數(shù)據(jù)在信息論上是最優(yōu)的。

NormalFloat 數(shù)據(jù)類型是建立在Block-wise k-bit Quantization和分位數(shù)量化（Quantile Quantization）基礎(chǔ)之上的。

分塊k位量化（Block-wise k-bit Quantization）

量化是將數(shù)據(jù)從一個(gè)表示更多信息的形式轉(zhuǎn)換為一個(gè)表示較少信息的形式的過程。通常情況下，這涉及將數(shù)據(jù)類型從一個(gè)占用更多比特的形式轉(zhuǎn)換為一個(gè)占用較少比特的形式，例如從32位浮點(diǎn)數(shù)轉(zhuǎn)換為8位整數(shù)。為了確保較少比特的數(shù)據(jù)類型能夠充分利用其范圍，通常會(huì)對(duì)輸入數(shù)據(jù)進(jìn)行歸一化處理，使其適應(yīng)目標(biāo)數(shù)據(jù)類型的范圍。 例如，將FP32張量量化為范圍為[-127, 127]的Int8張量。

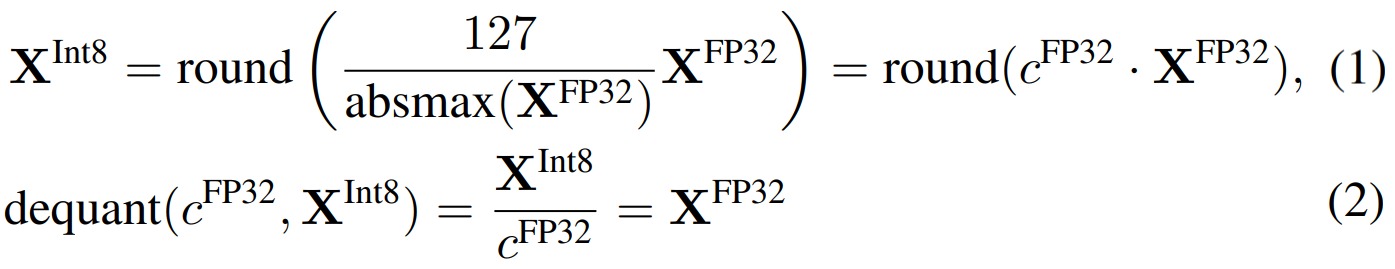
上圖是int8量化和反量化。在式(1)中，\(\frac{127}{absmax(X^{FP32})}\) 的作用是依據(jù)參數(shù)中的最大值來確定縮放尺度。這種方法的問題是，如果輸入張量中出現(xiàn)較大的幅度值（即異常值），那么使用它計(jì)算縮放尺度就不合適了，因?yàn)樗鼤?huì)造成整個(gè)張量的絕大多數(shù)值在量化后都在0附近，從而破壞了量化后特征分布的均勻性。分塊k位量化（block-wise k-bit quantization）的策略是一批一批的量化：通過將張量分成若干個(gè)塊，讓每個(gè)塊都有獨(dú)立的量化常數(shù)c，從而解決模型參數(shù)的極大極小的異常值的問題。分塊量化的另外一個(gè)好處是減少了核之間的通信，可以實(shí)現(xiàn)更好的并行性，并充分利用硬件的多核的能力。

分位數(shù)量化（Quantile Quantization）

QLoRA 是把參數(shù)量化到4bit，我們可以使用的數(shù)字就是\(2^4\) ，即16個(gè)。如果采用四舍五入到最近值（RTN, round-to-nearest）方法，則在某些分布下，可能大部分原始數(shù)值都被量化到同一個(gè)4bit數(shù)上，本有的差異或者說信息在這個(gè)量化過程中就丟掉了，沒有充分利用現(xiàn)有的數(shù)位。比如，原始的float32浮點(diǎn)數(shù)都在0上下波動(dòng)，用 RTN 方法，這些數(shù)字可能量化完全變成零了。

為了更有效利用現(xiàn)有的16個(gè)數(shù)字，我們可以采用分位數(shù)（Quantile）量化。分位數(shù)在數(shù)學(xué)上的定義指的是把順序排列的一組數(shù)據(jù)分割為若干個(gè)相等塊的分割點(diǎn)的數(shù)值。分位數(shù)量化是一種信息論上的最優(yōu)數(shù)據(jù)類型，其主要思想便是將數(shù)值盡量落到均值為0，標(biāo)準(zhǔn)差為[-1,1]的正態(tài)分布的固定期望值上。

由于預(yù)訓(xùn)練的神經(jīng)網(wǎng)絡(luò)權(quán)值通常具有標(biāo)準(zhǔn)差為0的正態(tài)分布性質(zhì)，因此我們可以通過縮放系數(shù)將所有的神經(jīng)網(wǎng)絡(luò)權(quán)重轉(zhuǎn)換為固定期望值，從而使該分布完全適合我們的數(shù)據(jù)類型范圍。一旦權(quán)重范圍和數(shù)據(jù)類型范圍匹配，我們就可以像往常一樣進(jìn)行量化。比如把所有數(shù)字由小到大排列，再分成十六等分，最小的一塊映射到量化后的第一個(gè)數(shù)，第二塊映射到量化后的第二個(gè)數(shù)，以此類推。這樣做原始數(shù)據(jù)在量化后的數(shù)字上分布就是均勻的。通過使用分位數(shù)將張量分成了大小相同的若干個(gè)塊，我們得到更加均勻的量化特征，這也就是分位數(shù)量化。分位數(shù)量化技術(shù)使得每個(gè)量化分區(qū)中具有相等的期望值，相等的期望值可以避免昂貴的分位數(shù)估計(jì)和近似誤差，使得精確的分位數(shù)估計(jì)在計(jì)算上可行。

4位正態(tài)浮點(diǎn)量化

分位數(shù)量化有一個(gè)問題：過于繁瑣。每一批數(shù)字都要計(jì)算對(duì)應(yīng)的分位，開銷較大。因此，QLoRA 給出了正態(tài)浮點(diǎn)量化的加速方法。

預(yù)訓(xùn)練的參數(shù)基本上是符合均值為0的正態(tài)分布的，因此可以直接縮放到指定的范圍內(nèi)，比如 [?1,1] 。對(duì)于范圍在 [?1,1] 內(nèi)的零均值正態(tài)分布，其標(biāo)準(zhǔn)差為任意 \(\delta\) 的信息論上最優(yōu)數(shù)據(jù)類型的計(jì)算方式如下：

• 估算理論上的 N(0,1) 分布的 \(2^k+1\) 個(gè)分位數(shù)，以獲得 k 位的正態(tài)分布量化數(shù)據(jù)類型；
• 通過絕對(duì)最大值重縮放將輸入權(quán)重張量規(guī)范化到 [?1,1] 范圍內(nèi)來進(jìn)行量化。此步驟相當(dāng)于重新縮放權(quán)重張量的標(biāo)準(zhǔn)差，以匹配 k 位數(shù)據(jù)類型的標(biāo)準(zhǔn)差。更具體地，數(shù)據(jù)類型的 \(2^k\) 個(gè)值 \(q_i\) 的估算方式為：\(\begin{equation} q_i=\frac{1}{2}\left(Q_X\left(\frac{i}{2^k+1}\right)+Q_X\left(\frac{i+1}{2^k+1}\right)\right) \end{equation}\) ，其中 $Q_X(\cdot) $是標(biāo)準(zhǔn)正態(tài)分布 N(0,1) 的分位數(shù)函數(shù)。
• 這樣的做法存在一個(gè)缺點(diǎn)，0可能會(huì)被映射到一個(gè)不為零的數(shù)值上，損失了0的特殊性質(zhì)。為了解決這點(diǎn)，QLoRA用兩個(gè)\(2^{k-1}\)的[0, 1]范圍分別代表正負(fù)0~1， 再去掉重疊的一個(gè)0值。

如下圖所示，對(duì)于4比特量化，我們希望需要找到15個(gè)分位數(shù)來將這個(gè)曲線下面的面積（積分）等分成16份。兩個(gè)分位數(shù)的中點(diǎn)便是模型量化到這個(gè)區(qū)間映射的值\(q_i\)。

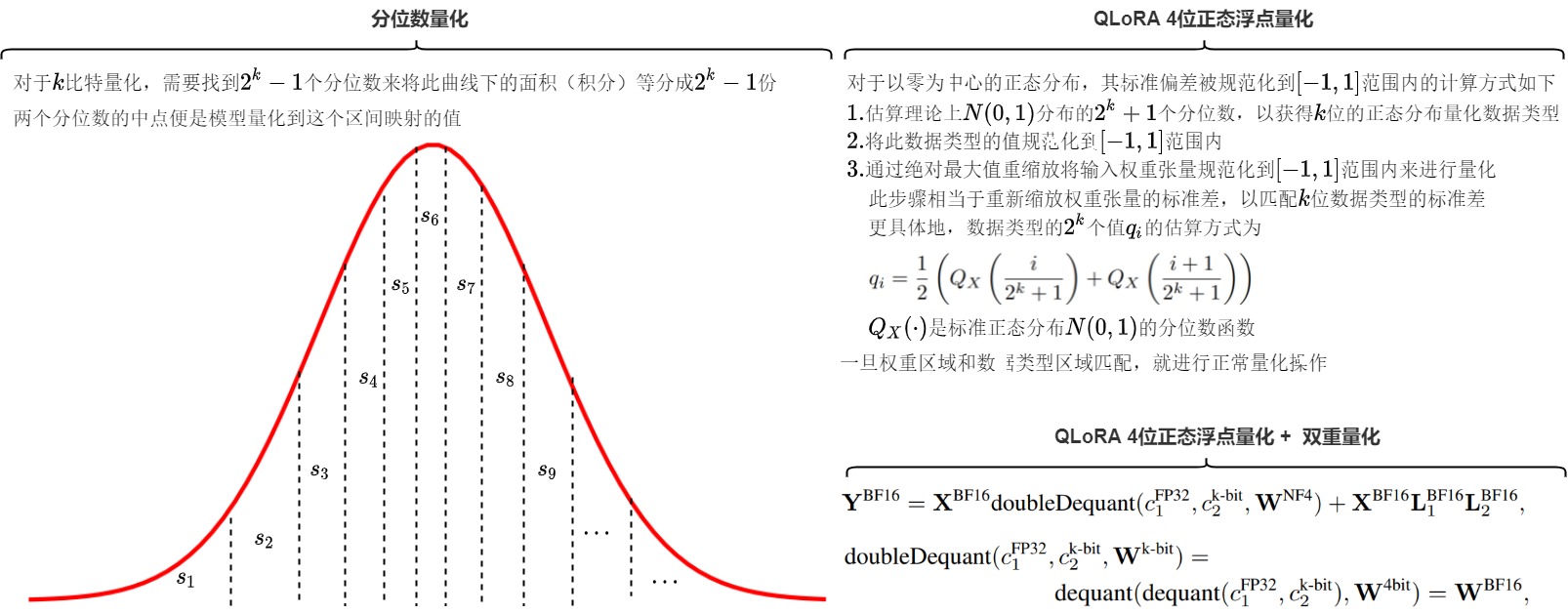
雙重量化

在量化的過程中，為了降低Outlier的影響，QLoRA采用分塊的方式進(jìn)行進(jìn)行量化。具體來說就是每64個(gè)參數(shù)共享一個(gè)量化常數(shù)(Absmax, 32bit)， 相當(dāng)于每一個(gè)參數(shù)的量化額外開銷為$$32/64 = 0.5 \text{bit}$$。對(duì)于4bit量化來說額外的0.5bit相當(dāng)于多12.5%的顯存耗用，總體來說也是比較大的一個(gè)開銷。

為了進(jìn)一步優(yōu)化這個(gè)量化開銷，QLoRA對(duì)其進(jìn)行二次量化($$\text{Double Quantization}$$)，對(duì)量化常數(shù)進(jìn)行進(jìn)一步的量化。即把第一次32bit量化的輸出作為第二次量化的輸入。考慮到c一般出現(xiàn)outliner的概率較小，LoRA采用256的塊大小對(duì)量化常數(shù)進(jìn)行$$\text{FP8}$$量化，平均來說，對(duì)于64的塊大小，這種量化方法將每個(gè)參數(shù)的內(nèi)存占用從 32/64=0.5 位降低到 \(\begin{equation} 8/64 + 32/(64 * 256) = 0.127 bit \end{equation}\)，每個(gè)參數(shù)減少了0.373位的內(nèi)存占用。因?yàn)槭褂昧穗p重量化，在進(jìn)行反量化時(shí)，我們也需要進(jìn)行兩次反量化才能把量化后的值還原。

優(yōu)化器狀態(tài)分配分頁內(nèi)存

梯度檢查點(diǎn)（Gradient Checkpointing）是用于解決模型訓(xùn)練時(shí)顯存占用過高的問題的一個(gè)技術(shù)方案。在模型訓(xùn)練時(shí)，我們通常需要將所有前向傳播的激活值保存下來以在模型進(jìn)行反向傳播的時(shí)候使用，但是這樣就會(huì)非常占用模型顯存。當(dāng)然我們也可以不保存激活值，而是在計(jì)算梯度時(shí)重新計(jì)算，但是這樣雖然減少了緩存占用，但是卻增大了計(jì)算量，減慢了訓(xùn)練速度。

梯度檢查點(diǎn)就是一個(gè)介于全不丟和全丟棄的一個(gè)這種的技術(shù)方案，即只在前向傳播過程中保存部分激活值。當(dāng)運(yùn)行反向過程時(shí)，如果有保存的梯度，我們就直接使用這個(gè)保存的值， 沒有保存的梯度時(shí)，我們再根據(jù)它損失函數(shù)重新計(jì)算這個(gè)梯度。

分頁優(yōu)化是針對(duì)梯度檢查點(diǎn)做的進(jìn)一步優(yōu)化，以防止在顯存使用峰值時(shí)發(fā)生顯存OOM的問題。QLoRA分頁優(yōu)化其實(shí)就是當(dāng)顯存不足時(shí)，這些梯度檢查點(diǎn)狀態(tài)會(huì)自動(dòng)被逐出到CPU RAM，然后在優(yōu)化器更新步驟中需要內(nèi)存時(shí)，再分頁回GPU內(nèi)存，和計(jì)算機(jī)的內(nèi)存數(shù)據(jù)轉(zhuǎn)移到硬盤上的常規(guī)內(nèi)存分頁一個(gè)道理。

2.5 FlatQuant

目前的 W4A4 （權(quán)重4位，激活值4位）量化模型相比全精度模型還存在著較大的量化損失，難以在實(shí)際應(yīng)用中使用，也就難以利用峰值算力最高的 INT4 Tensor Core 加速 LLM 的實(shí)際推理部署。FlatQuant作者發(fā)現(xiàn)，量化前權(quán)重和激活值分布的平坦度 (flatness) 是影響 LLM 量化誤差的關(guān)鍵因素。

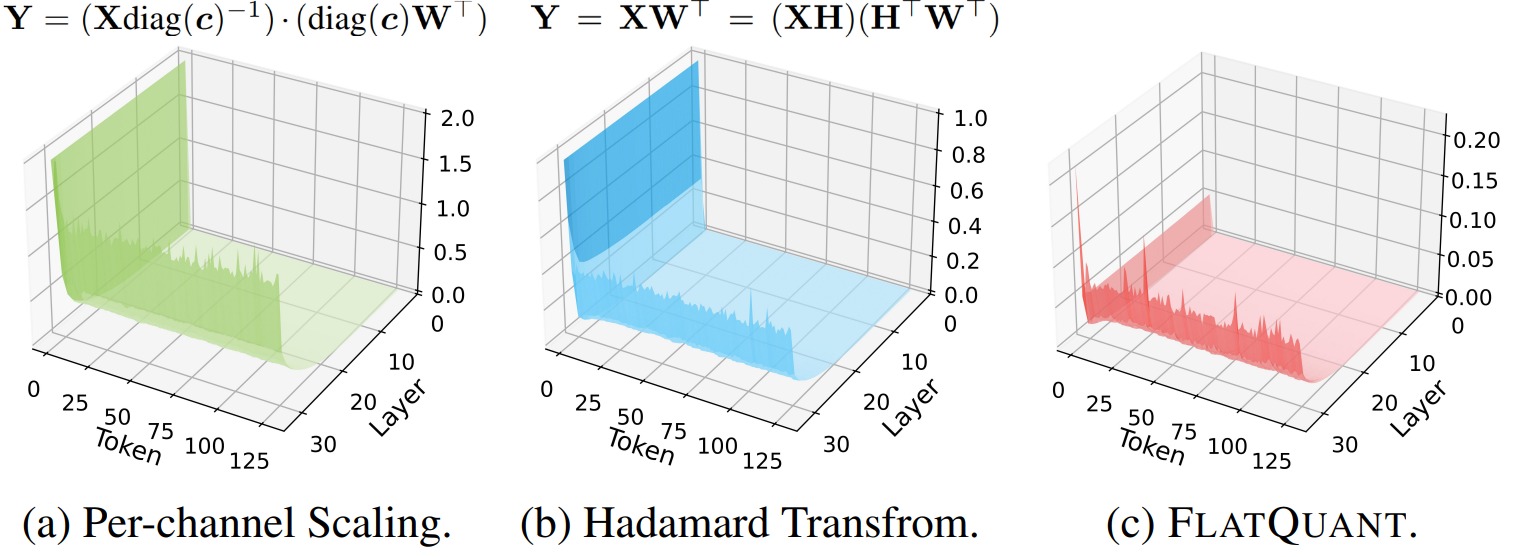
直觀來看，分布越平坦，離群值就越少，量化時(shí)的精度也就越高。已有方法大多使用 pre-quantization transformations，通過在量化前對(duì)權(quán)重和激活值做等價(jià)變換得到更平坦的分布來降低量化誤差，常用的變換主要有 Per-channel Scaling 和 Hadamard 變換。

然而，F(xiàn)latQuant作者發(fā)現(xiàn)這些變換并不是最優(yōu)的，這些變換后的權(quán)重和激活值仍然可能保持陡峭和分散。為此FlatQuant作者提出 FlatQuant (Fast and Learnable Affine Transformation)，其目標(biāo)是通過一些等價(jià)變換使得權(quán)重和激活值的分布盡量的平坦。具體而言，就是為每個(gè)線性層學(xué)習(xí)一個(gè)最優(yōu)的仿射變換來有效緩解權(quán)重和激活值上的離群值，，這組仿射變換矩陣的值是通過校準(zhǔn)數(shù)據(jù)調(diào)校訓(xùn)練而來的。 從而得到平坦的權(quán)重和激活值分布，有效提升了量化精度。此外，針對(duì)推理中的在線變換，F(xiàn)latQuant作者進(jìn)行了算子融合進(jìn)一步降低訪存開銷，使得在線變換僅帶來極小的推理開銷。

2.5.1 動(dòng)機(jī)

LLM 的權(quán)重和激活值上存在較多的離群值，特別是激活值上常常存在離群值通道 (outlier channels)，導(dǎo)致 LLM 難以量化。目前針對(duì) LLM WA 量化的方法大多在量化前對(duì)權(quán)重和激活值做等價(jià)變換來用其他通道吸收離群值，從而得到更加平坦的分布以降低量化損失。例如：

• Per-channel Scaling 對(duì)應(yīng)的等價(jià)變換為 \(\mathbf{Y}= (\mathbf{X}diag(\mathbf{c})^{-1}) \cdot (diag(\mathbf{c}) \mathbf{W}^{\top})\)，通過 scaling 將激活值上的離群值轉(zhuǎn)移到權(quán)重的相同通道上，使得激活值分布更加平坦；
• Hadamard 變換 \(\mathbf{Y} = \mathbf{X}\mathbf{W}^{\top} = (\mathbf{XH})(\mathbf{H}^{\top}\mathbf{W}^{\top} , \mathbf{H}^{\top}\mathbf{H} = \mathbf{I}\)則是通過給權(quán)重和激活值同時(shí)做 Hadamard 變換來將離群值重新分配到權(quán)重/激活值的其他通道上。

然而，已有的等價(jià)變換得到的分布仍然可能是不平坦的。權(quán)重和激活值分布可以看作兩個(gè)斜坡，變換就類似于用鏟子搬土，土不會(huì)憑空增加或者減少，所以目標(biāo)是通過把兩個(gè)坡中高處（離群值）的土填到低處（非離群值通道），從而把這兩個(gè)坡填平。

• Per-channel Scaling 就相當(dāng)于只能把一個(gè)坡上的土填到另一個(gè)坡的相同位置上，比較局限。離群值仍然被限制在了權(quán)重和激活值的相同通道上，非離群值通道得不到有效利用。因此不管是權(quán)重還是激活值，變換后的分布都非常陡峭，呈現(xiàn)出非常明顯的離群值通道。
• Hadamard 變換 相當(dāng)于在每個(gè)坡的內(nèi)部把高處的土填到自身的低處，但不能在兩個(gè)坡之間轉(zhuǎn)移土。并且由于不同坡的形狀不同，相同的 Hadamard 變換（坡內(nèi)搬土方式）不一定適用于所有土坡。Hadamard 變換對(duì)所有權(quán)重和激活值都施加相同的變換，而不同層的權(quán)重和激活值分布是不同的，這意味著 Hadamard 變換并不是對(duì)于每個(gè)層的最優(yōu)解，例如下圖 (b) 中，LLaMA-3-8B 的權(quán)重和激活值經(jīng)過 Hadamard 變換后仍然比較陡峭，特別是激活值上的離群值無法得到有效平滑。此外，Hadamard 變換作為一種正交變換不會(huì)改變向量的模長，而 LLM 激活值上大量的離群值會(huì)導(dǎo)致激活值模長顯著大于權(quán)重，這導(dǎo)致正交變換后的激活值量化難度也會(huì)顯著高于權(quán)重，無法像 Per-channel Scaling 一樣靈活地平衡權(quán)重和激活值上的量化難度。

具有 massive outlier 的關(guān)鍵詞元 (pivot token)對(duì)于模型性能十分重要，關(guān)鍵詞元上的量化誤差會(huì)比較嚴(yán)重地影響模型的量化精度。下圖展示了在LLaMA-3-8B施加不同變換后，Transformer層和輸入序列的量化均方誤差（MSE）。可以發(fā)現(xiàn)，per-channel scaling 和 Hadamard 變換都無法很好處理具有 massive outlier 的關(guān)鍵詞元 (pivot token)，導(dǎo)致在首詞元上具有非常大的量化誤差。而 FlatQuant 方法的 MSE 更小，因此可以顯著降低關(guān)鍵詞元上的量化損失，并有效抑制量化誤差的逐層傳播，帶來更加平坦的量化損失平面。

2.5.2 方案

FlatQuant方案關(guān)鍵步驟如下：

1. 輕量仿射變換：通過學(xué)習(xí)每個(gè)線性層的最優(yōu)仿射變換來平滑離群值。
2. Kronecker 分解：將大的變換矩陣分解為小矩陣，減少存儲(chǔ)和計(jì)算開銷。
3. Per-channel Scaling：為每個(gè)通道提供獨(dú)立的縮放因子，增加變換的靈活性。
4. Learnable Clipping Thresholds：通過可學(xué)習(xí)的裁剪閾值進(jìn)一步減少離群值的影響。

相比于Per-channel Scaling和Hadamard 變換，F(xiàn)latQuant 方法可以被看作是一種更加精細(xì)和智能的“搬土”策略。在這個(gè)方法中，我們不再局限于只在單個(gè)斜坡內(nèi)部移動(dòng)土，也不只是在兩個(gè)斜坡的相同位置上進(jìn)行土的轉(zhuǎn)移。FlatQuant 允許我們對(duì)每個(gè)斜坡進(jìn)行定制化的調(diào)整，這意味著我們可以針對(duì)每個(gè)斜坡的獨(dú)特形狀和需求，設(shè)計(jì)出最佳的“搬土”方案。這就相當(dāng)于為模型的每一層學(xué)習(xí)一個(gè)特定的仿射變換，不僅可以得到平坦的分布，還可以自適應(yīng)地平衡權(quán)重和激活值的量化難度。

輕量的仿射變換

FlatQuant 通過輕量的仿射變換來平滑權(quán)重和激活值上的離群值，需要為每個(gè)線性層學(xué)習(xí)最優(yōu)的仿射變換。學(xué)到可逆矩陣P后，變換\(P^{-1}W^T\)可以融到權(quán)重中不會(huì)帶來額外推理開銷，但XP必須作為在線變換，這會(huì)使得線性層的存儲(chǔ)和計(jì)算開銷翻倍，這顯然是不現(xiàn)實(shí)的。因此，為了解決上述問題，F(xiàn)latQuant 對(duì)P使用 Kronecker 分解。具體推導(dǎo)如下。

Per-channel Scaling

Kronecker 分解本質(zhì)上還是對(duì)P的 rank-1 近似，我們進(jìn)一步使用 learnable Per-channel Scaling 提升 Kronecker 分解的表征能力。Per-channel Scaling 可以融到前序的 LN/線性層中不會(huì)帶來額外推理開銷。

Learnable Clipping Thresholds

我們對(duì)變換后的權(quán)重和激活值進(jìn)一步采用了 learnable clipping 來更好地消除離群值。

模型架構(gòu)

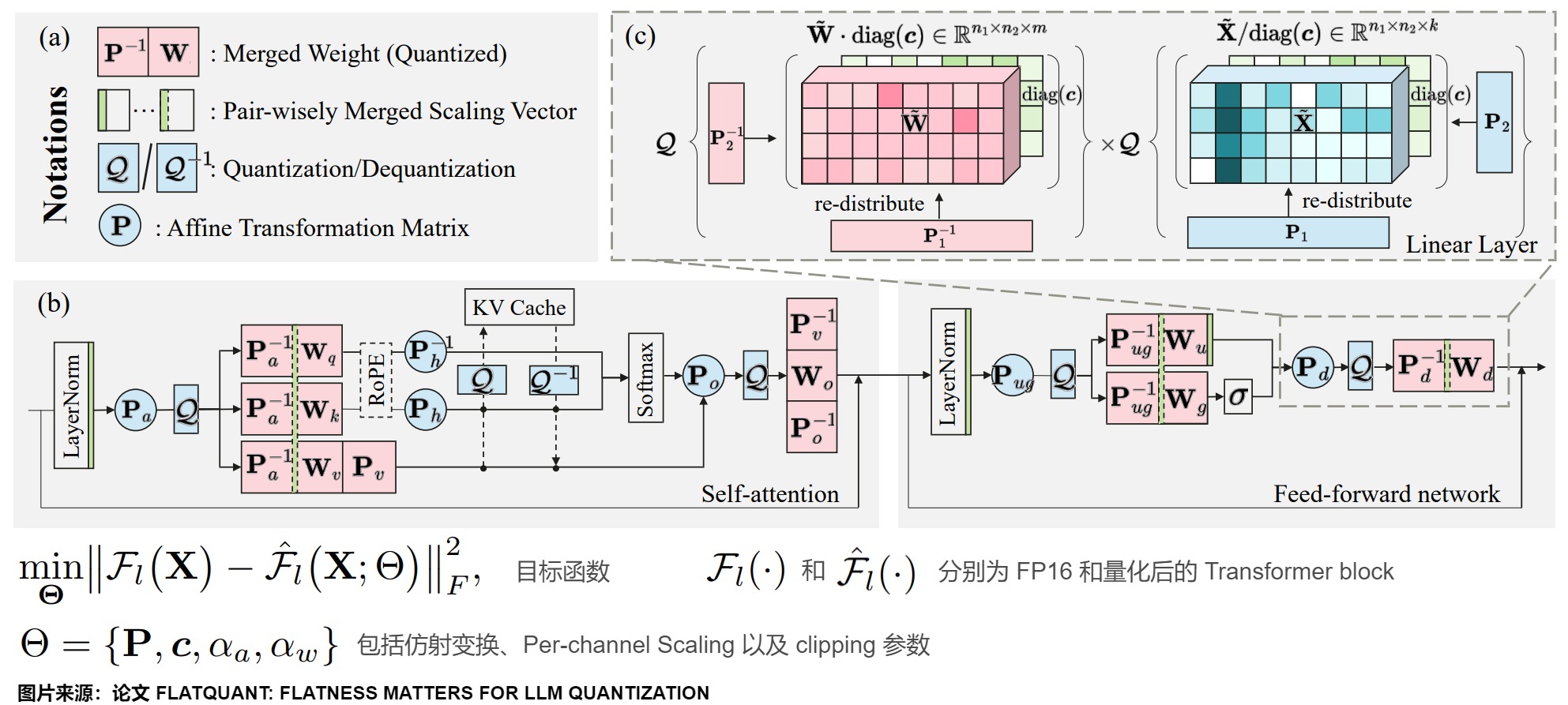
下圖展示了模型架構(gòu)，F(xiàn)latQuant 在單個(gè) Transformer 內(nèi)會(huì)引入 5 種不同的在線變換。損失函數(shù)采用 Layer-wise MSE loss。

0x03 低位量化

將量化位數(shù)降低到低于8位已被證明是一項(xiàng)艱巨的任務(wù)，因?yàn)槊繙p少一位，量化誤差都會(huì)增加。但是內(nèi)存和運(yùn)算速度的壓力迫使研究人員絞盡腦汁繼續(xù)探究。于是就有了低位量化方案。

本節(jié)介紹的幾種方案特點(diǎn)如下。

方法	量化權(quán)重與激活	特點(diǎn)
SqueezeLLM	W3~W4/A16	先把極端值分離出來，對(duì)剩余的權(quán)重用加權(quán)的k-means聚類的非均勻量化方法
SpQR	W3~W4/A16	用分治方法分離出敏感權(quán)重，然后對(duì)非敏感權(quán)重采用二級(jí)壓縮方法，轉(zhuǎn)化為3bit存儲(chǔ)
BitNet	W1	BitNet使用-1或1來表示模型權(quán)重的單一位，并且將activation量化成8-bit來執(zhí)行矩陣乘法。模型其余部分則會(huì)維持一個(gè)高精度，比如FP16
BitNet b1.58	W1.58	主要將weights的取值從{-1, 1}變?yōu)閧-1, 0, 1}，這賦予了模型忽略（ignore）特定feature的能力，提升了模型性能
OneBit	W1	提出一種新穎的1bit參數(shù)表示方法，和一種基于矩陣分解的有效參數(shù)初始化方法，以提高QAT框架的收斂速度

3.1 SqueezeLLM

SqueezeLLM是一個(gè)訓(xùn)練后量化框架，它不僅使 lossless 壓縮到 ultra-low 精度到 3 位，同時(shí)也在相同的內(nèi)存限制下實(shí)現(xiàn)了更高的量化性能。SqueezeLLM提出將離群值存儲(chǔ)在全精度稀疏矩陣中，并對(duì)剩余權(quán)重應(yīng)用非均勻量化。根據(jù)量化靈敏度確定非均勻量化的值，能夠提高量化模型的性能。

3.1.1 動(dòng)機(jī)

SqueezeLLM 發(fā)現(xiàn)，生成式推理的主要瓶頸在于內(nèi)存帶寬即內(nèi)存墻，而非算術(shù)計(jì)算，特別是針對(duì)單個(gè)批次推理時(shí)。既然把權(quán)重加載到內(nèi)存是主要瓶頸，因此最小化內(nèi)存即可。比如僅僅把權(quán)重位寬降低而不對(duì)激活量化，即可實(shí)現(xiàn)運(yùn)行加速（相當(dāng)于把權(quán)重加載到內(nèi)存后，再反量化回FP16，這種方式雖然增加了計(jì)算開銷但降低了訪存開銷）。另外，權(quán)重存在不同敏感度，少量權(quán)重非常敏感，需要針對(duì)性進(jìn)行量化。

3.1.2 方案

SqueezeLLM 主要貢獻(xiàn)有如下兩點(diǎn)：

• 基于敏感性的非均勻量化。權(quán)重分布是不均勻的，使用非均勻量化可以實(shí)現(xiàn)3比特量化。
  • 它采用近似的Fisher information來度量敏感度，這是一種新的度量方式。然后基于敏感度進(jìn)行低比特非均勻量化，使用kmeans聚類來生成靠近敏感值的量化定點(diǎn)，其它點(diǎn)以MSE最小來安置，從而最小化量化誤差。
• 稠密和稀疏分解，針對(duì)離群點(diǎn)的稠密和稀疏量化：把權(quán)重分為稠密和稀疏，稀疏權(quán)重不量化，只量化稠密權(quán)重。高效的稀疏格式來存儲(chǔ)outlier和敏感權(quán)重(FP16)，稠密格式來存儲(chǔ)大量的低比特常規(guī)權(quán)重值。分別開發(fā)了kernel來處理稠密和稀疏的矩陣向量乘kernel。

基于敏感度的非均勻量化

均勻量化的主要優(yōu)勢是計(jì)算高效，但在LLM推理中，計(jì)算不是主要瓶頸，并且權(quán)重本身是非均勻分布的。因此，作者提出非均勻量化的方式縮小這些敏感權(quán)重的量化誤差。即通過loss的二階hessian信息來確定量化敏感的權(quán)重, 將量化點(diǎn)安置在這些敏感權(quán)重附近。具體推導(dǎo)如下圖所示。其中核心點(diǎn)是：

• 在3bit的時(shí)候，只有8個(gè)量化slot，因此需要謹(jǐn)慎選擇量化值。一種常見的思路就是用k-mean聚類，這里的關(guān)鍵是損失函數(shù)的定義。作者嘗試用task loss，而不是簡化版的單層重建誤差。

• 這里的H求解還是太貴了，作者使用了費(fèi)舍爾信息矩陣(FIM, fisher information matrix)矩陣來替換，具體來說就是計(jì)算一階梯度的協(xié)方差。

• 因此對(duì)于每個(gè)\(Q(w_i)\)，可以使用k-means算法（3比特的時(shí)候k=8）來最小化上面的\(L(W_Q)\)損失誤差，最終得到k個(gè)離散的一維浮點(diǎn)值。

針對(duì)離群點(diǎn)的稠密稀疏量化

作者分析了一下MHA的輸出proj矩陣和FFN的contraction矩陣的權(quán)重分布，如下所示，發(fā)現(xiàn)

• 99.9%的權(quán)重?cái)D在最大區(qū)間的10%以內(nèi)的地方。
• 剩下0.1%的權(quán)重在最大區(qū)間的10%-90%的地方，屬于outlier。

這表明去除離群點(diǎn)可以將量化閾值縮小10倍。

因此，作者采用了簡單而有效的分解思路，如下圖所示，把權(quán)重W分解成容納異常值權(quán)重的稀疏矩陣(S)和包含剩余的大多數(shù)權(quán)重的稠密矩陣(D)。前者保持FP16后者量化。SqueezeLLM 通過迭代過程將權(quán)重矩陣分解為一個(gè)稀疏矩陣和一個(gè)密集矩陣，分解成稀疏矩陣的過程中實(shí)現(xiàn)了壓縮和量化。另外，除了把離群點(diǎn)放入稀疏矩陣，還可以根據(jù)Fisher信息度量把小部分敏感權(quán)重也放入稀疏矩陣。

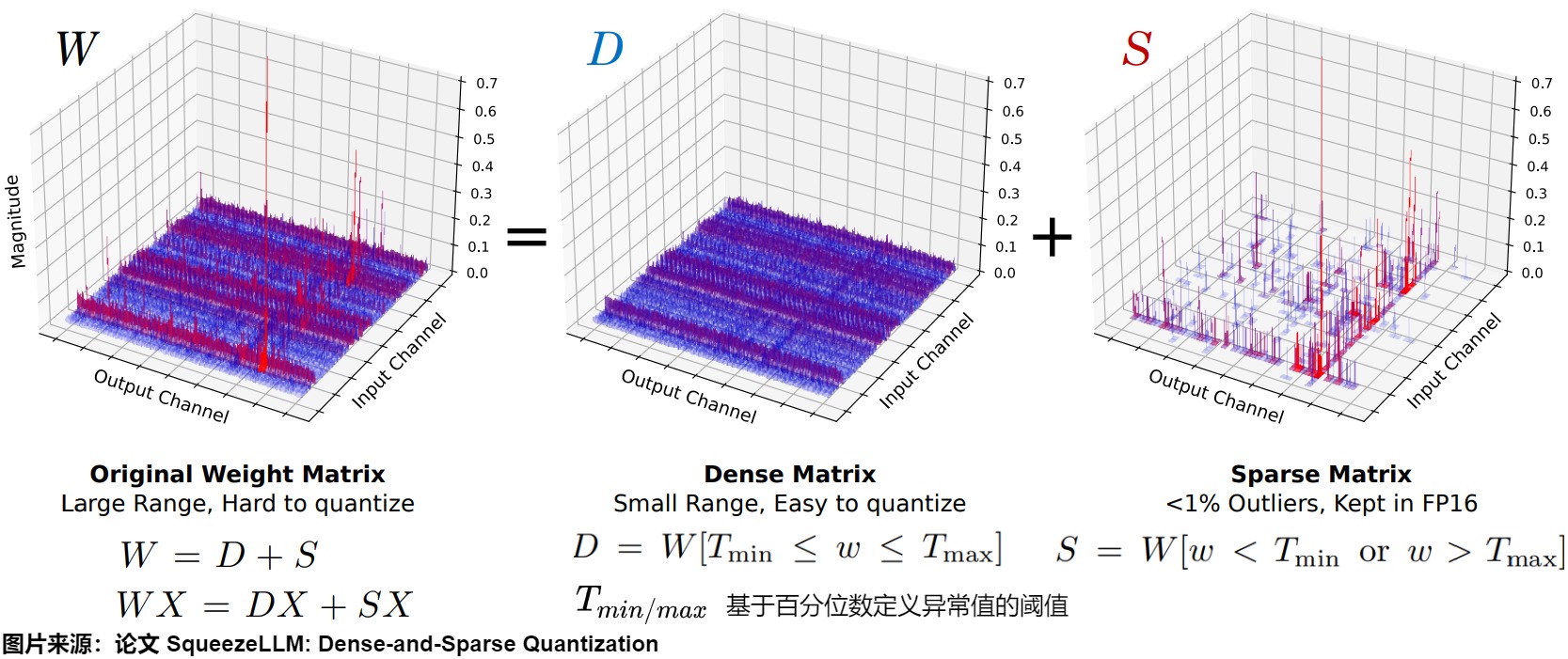
這里，\(T_{min/max}\)是基于百分位數(shù)定義異常值的閾值。

重要的是，因?yàn)楫惓Ｖ档臄?shù)量很小。因此，可以使用高效的稀疏格式來存儲(chǔ)outlier和敏感權(quán)重(FP16)，使用稠密格式來存儲(chǔ)大量的低比特常規(guī)權(quán)重值。

3.2 SpQR

論文“SpQR: A Sparse-Quantized Representation for Near-Lossless LLM Weight Compression”提出了SpQR。SpQR也像AWQ一樣發(fā)現(xiàn)了weight對(duì)模型的重要程度存在極強(qiáng)的不均衡性，1%的參數(shù)可能主導(dǎo)的量化過程中損失的性能這一事實(shí)。但是它對(duì)識(shí)別敏感weight和保護(hù)敏感weight的做法和AWQ不一樣，其工作原理是識(shí)別和單獨(dú)處理會(huì)導(dǎo)致大量化誤差的異常值權(quán)重，并以更高的精度存儲(chǔ)它們，同時(shí)將所有其他權(quán)重壓縮到 3-4 比特。

3.2.1 動(dòng)機(jī)

隨著大模型的參數(shù)越來越大，通常需要通過量化將此類LLMs壓縮為每個(gè)參數(shù)3-4比特，以適合筆記本電腦和移動(dòng)電話等內(nèi)存有限的設(shè)備，從而實(shí)現(xiàn)個(gè)性化使用。但現(xiàn)有的技術(shù)方案（如：GPTQ）將參數(shù)量化至 3-4 比特通常會(huì)導(dǎo)致顯著的精度損失，特別是對(duì)于 1-10B 參數(shù)范圍內(nèi)的較小模型，而這些模型卻非常適合邊緣部署。為了解決這個(gè)精度的問題，作者引入了稀疏量化表示（SpQR），這是一種新的壓縮格式和量化技術(shù)，首次實(shí)現(xiàn)了跨模型參數(shù)規(guī)模的近乎無損的（near-lossless） LLM 壓縮，同時(shí)達(dá)到與以前的方法類似的壓縮水平。

離群值

早期的工作[LLM.int8()、Smoothquant]觀察到在大語言模型的輸入/輸出中存在顯著較高值的“離群特征”，這會(huì)導(dǎo)致更高的量化誤差，并提出不同的緩解策略。而本文的作者從權(quán)重量化的角度來分析這個(gè)現(xiàn)象。特別是，作者研究了除權(quán)重矩陣中的輸入特征離群值之外的離群值結(jié)構(gòu)。結(jié)果發(fā)現(xiàn)，雖然當(dāng)前層的輸入特征異常值與前一層的隱藏單元異常值權(quán)重相關(guān)，但并不存在嚴(yán)格的對(duì)應(yīng)關(guān)系。論文首次證明，與輸入特征異常值不同，輸出隱藏維度異常值（output hidden dimension outliers）僅出現(xiàn)在特定輸出隱藏維度的小片段中（small segments for a particular output hidden dimension）。這種部分結(jié)構(gòu)化的異常值模式需要一種細(xì)粒度的混合壓縮格式。

針對(duì)離群值特點(diǎn)，SpQR 作者提出的量化算法隔離此類異常值，并以 SpQR 格式有效地對(duì)給定模型進(jìn)行編碼。

參數(shù)靈敏度分析

首先它用類似OBC(Optimal Brain Compression)的方式來計(jì)算參數(shù)的敏感度，求解結(jié)果如下所示。

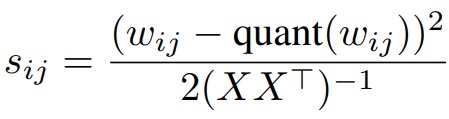
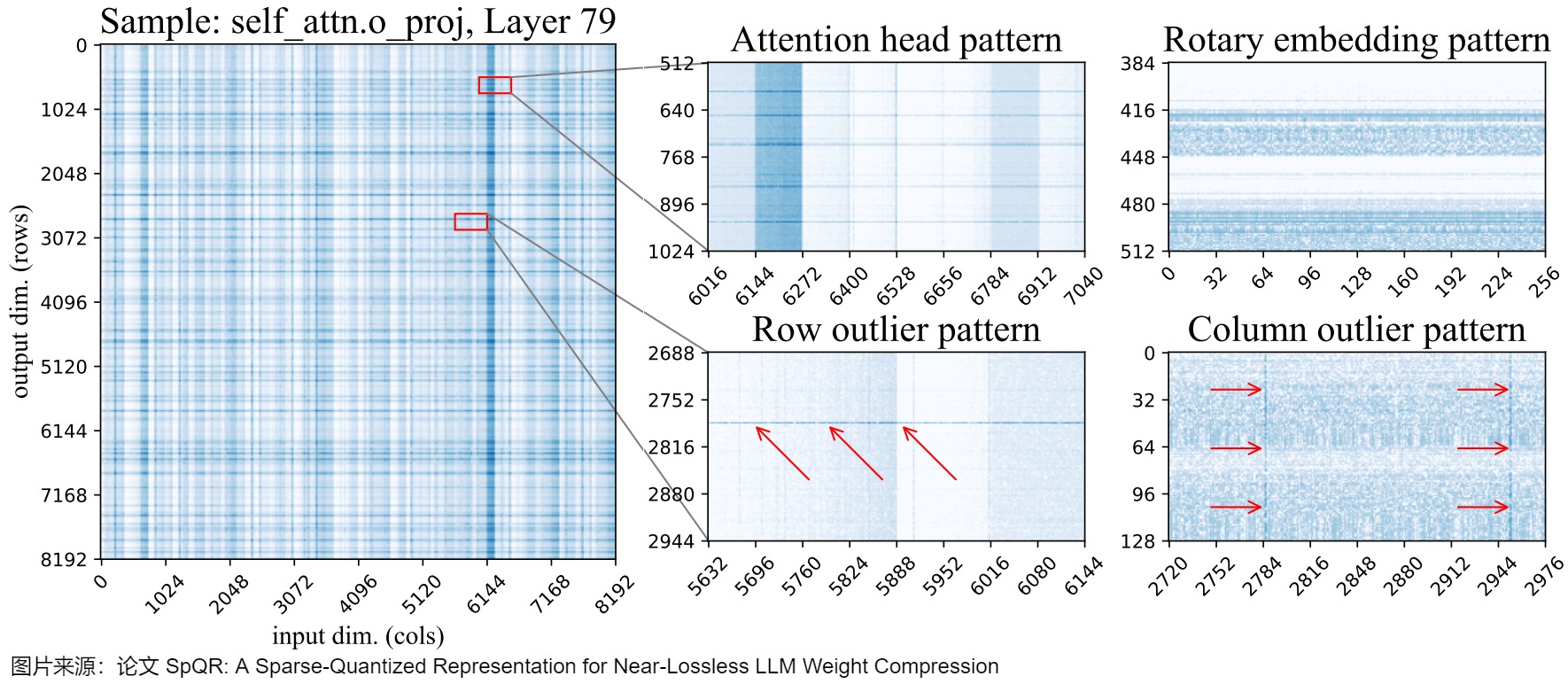
其次，論文對(duì)權(quán)重的參數(shù)敏感度進(jìn)行了分析，結(jié)果發(fā)現(xiàn)，敏感權(quán)重在權(quán)重矩陣中的位置不是隨機(jī)的，而是具有特定結(jié)構(gòu)（行、列、注意力頭、非結(jié)構(gòu)化等）。下圖展示了LLaMA-65B最后一個(gè)自注意力層的權(quán)重對(duì)數(shù)敏感度（log-sensitivities）。深藍(lán)色陰影表示敏感度較高。通過敏感度分析，作者觀察到在權(quán)重矩陣中存在的幾種模式：

• 行異常值：圖底部中心對(duì)應(yīng)于輸出特征的高敏感度區(qū)域。其中一些模式橫跨整行，而另一些模式則占據(jù)了行的部分。在注意力層中，一些部分行異常值對(duì)應(yīng)于注意力頭的某個(gè)子集。
• 列異常值：圖右下角底部顯示了跨越所有行（across all rows）的選擇輸入維度（列）的高靈敏度。
• 敏感注意力頭：圖頂部中心區(qū)域出現(xiàn)了寬度為 128 的規(guī)則條紋，這對(duì)應(yīng)了一個(gè)注意力頭的所有權(quán)重。這些的“條紋”在 Q & K 投影矩陣中是水平形狀，在輸出投影矩陣中是垂直形狀，但是在 V 投影矩陣和任何 MLP 權(quán)重中都沒有出現(xiàn)。值得注意的是，即使在敏感的頭（sensitive heads）內(nèi)，單獨(dú)的權(quán)重敏感性也存在顯著差異。
• 旋轉(zhuǎn)嵌入模式：圖右上角所展示了 64 個(gè)單位周期的重復(fù)垂直敏感度模式，這是旋轉(zhuǎn)嵌入位置編碼的特有模式。任何不使用旋轉(zhuǎn)嵌入的層都沒有這種模式。
• 非結(jié)構(gòu)化異常值：除此之外，每一層都有許多單獨(dú)的敏感度權(quán)重，這些權(quán)重不適合任何上述模式。這些非結(jié)構(gòu)化異常值更頻繁地出現(xiàn)在具有最大輸入索引的列中（即在圖像的右側(cè)）。但在熱力圖上很難看到這種效果。

因此，作者希望使用一個(gè)壓縮方案來維持所有這些不同的離群值類型。

3.2.2 方案

針對(duì)離群值，作者提出用量化算法隔離此類異常值（敏感值group和單個(gè)異常值），然后將它們存儲(chǔ)在更高的精度中；將所有其他權(quán)重壓縮為3-4比特。并以 SpQR 格式有效地對(duì)給定模型進(jìn)行編碼。

量化算法

之前的 LLM 量化算法同等對(duì)待低敏感度權(quán)重和高敏感度權(quán)重，這可能會(huì)導(dǎo)致次優(yōu)量化。理想情況下，我們應(yīng)該為更高敏感度的權(quán)重分配更多的存儲(chǔ)資源（size budge）。然而，這些權(quán)重多為非結(jié)構(gòu)化異常（單獨(dú)權(quán)重)或形成小組分散在權(quán)重矩陣中，例如：部分行或注意力頭。為了捕捉這種結(jié)構(gòu)，本文將量化過程分為兩部分：捕捉小的異常組；捕獲單個(gè)異常值。

通過雙層（bilevel）量化捕獲小組（small groups ）權(quán)重

在上圖中，我們觀察到了在幾種模式中，權(quán)重在連續(xù)的小組中表現(xiàn)相似，但組之間發(fā)生突然變化。例如：某些注意力頭和部分行異常值。當(dāng)應(yīng)用標(biāo)準(zhǔn)方法時(shí)，在很多情況下，這些權(quán)重將被分組在一起，共享相同的量化統(tǒng)計(jì)數(shù)據(jù)。為了減少此類情況，我們使用極小的組進(jìn)行分組量化，通常為 β1=8~32 個(gè)權(quán)重。也就是說，對(duì)于每 β 個(gè)連續(xù)權(quán)重，都有一個(gè)單獨(dú)的量化 scale 和 zero-point。

為了避免"存儲(chǔ)量化統(tǒng)計(jì)數(shù)據(jù)的開銷抵消精度優(yōu)勢"，我們使用與權(quán)重相同的量化算法——非對(duì)稱（最小-最大）量化來量化分組統(tǒng)計(jì)數(shù)據(jù)本身。換句話說，我們對(duì)來自 β2=16 個(gè)連續(xù)值的分組統(tǒng)計(jì)數(shù)據(jù)進(jìn)行分組，并以相同的位數(shù)將它們一起量化，這樣具有非典型量化參數(shù)的組最終會(huì)使用更多的“量化預(yù)算”。

高靈敏度異常值

事實(shí)上，存在一小部分敏感權(quán)重以小組形式（在 Self Attention 層）或單獨(dú)“異常值”形式（在 MLP 中）出現(xiàn)的情況。這些異常權(quán)重往往只占全部權(quán)重的 1%，但卻會(huì)導(dǎo)致占據(jù)總體 75% 以上的量化誤差。由于這些離群值通常是非結(jié)構(gòu)化的，因此本文選擇將這些異常值保持在高精度（16 位），并以類似于壓縮稀疏行（CSR）表示 [5]的行排列對(duì)它們進(jìn)行單獨(dú)編碼。

檢測高靈敏度異常值的算法如下圖所示：左側(cè)片段描述了完整的過程，右側(cè)包含用于bilevel量化和查找異常值的子例程。左側(cè)片段具體如下：

• 第一步是“異常值檢測”步驟：查找異常值，并將其保持為 16 位權(quán)重。我們發(fā)現(xiàn)量化異常值會(huì)導(dǎo)致不成比例的高誤差。因此，將這些權(quán)重保持高精度。敏感權(quán)重的計(jì)算參照了OBS里面的結(jié)論。這里使用了逐層的重建誤差。在全局范圍內(nèi)，對(duì)于每個(gè)矩陣，該算法的目標(biāo)是選擇一個(gè)敏感度閾值 τ 以獲得整個(gè)模型中所需的異常值數(shù)量，通常約為權(quán)重的 1%。
• 第二步是“實(shí)際壓縮步驟”：將大多數(shù)（≥99%）的非異常值權(quán)重近似量化為 3~4 比特，并將剩余的量化轉(zhuǎn)移到 16 比特異常值權(quán)重中。

在第一個(gè)異常值檢測步驟之后，SpQR 會(huì)忽略同一量化組中的所有異常值，只量化非異常權(quán)重。同時(shí)，在最小-最大量化后，該算法還會(huì)繼續(xù)應(yīng)用 GPTQ 來量化剩余權(quán)重。最后，該算法通過分級(jí)量化對(duì)稀疏異常值矩陣以及最終的量化統(tǒng)計(jì)量進(jìn)行收集和壓縮，并返回壓縮后的權(quán)重及其元數(shù)據(jù)。

稀疏量化表示的實(shí)現(xiàn)和利用

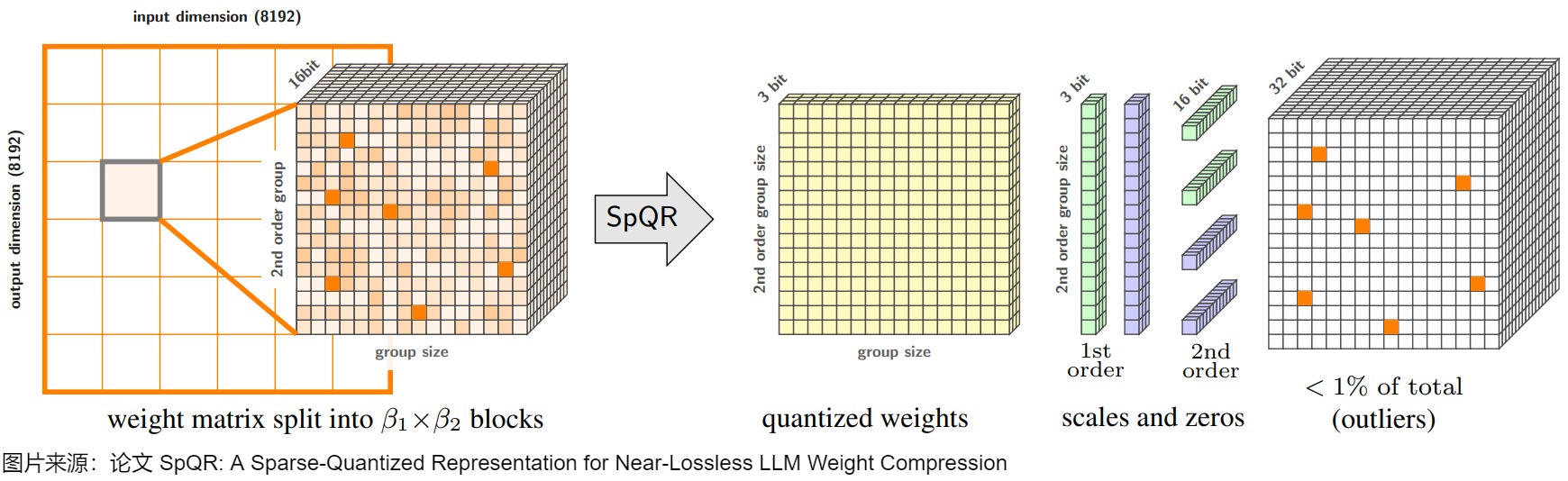
SpQR將均勻權(quán)重轉(zhuǎn)換為不同大小和精度的多種數(shù)據(jù)結(jié)構(gòu)。總體而言，該表示由(1)量化權(quán)重、(2)一級(jí)量化統(tǒng)計(jì)數(shù)據(jù)、二級(jí)量化統(tǒng)計(jì)和 (3) CSR 異常值索引和值組成。下圖總結(jié)了 SpQR 的總體結(jié)構(gòu)。 左側(cè)是單個(gè)權(quán)重張量的 SpQR 表示方法的概述，右側(cè)描繪了所有存儲(chǔ)的數(shù)據(jù)類型及其維度。

下面是每個(gè)組件的描述。

存儲(chǔ)量化組（Storing quantized groups）。所有非異常值權(quán)重都被編碼為一個(gè)結(jié)構(gòu)，該結(jié)構(gòu)包含：

• 一個(gè)\(b_w\)-bit的獨(dú)立權(quán)重
• 每組（組的大小是B）對(duì)應(yīng)的\(b_q\)-bit的scale 和 zero point（一級(jí)量化）
• 用于量化 \(B_q\)個(gè)量化組（scale 和 zero point）的 16 比特統(tǒng)計(jì)數(shù)據(jù)（二級(jí)量化）

存儲(chǔ)異常值（Storing outliers）。由于異常值是非結(jié)構(gòu)化的，SpQR 按照它們的行和列對(duì)它們進(jìn)行排序，這樣同一行中的異常值在內(nèi)存中是連續(xù)的。對(duì)于每個(gè)異常值，本文存儲(chǔ)兩個(gè)標(biāo)量：16 位權(quán)重值和 16 位列索引。對(duì)于每一行，還存儲(chǔ)一個(gè) 32 位的數(shù)字，用于表示行中異常值的總數(shù)。每個(gè)異常權(quán)重的平均存儲(chǔ)成本為 32.03 至 32.1 比特。

3.3 BitNet

BitNet使用-1或1來表示模型權(quán)重的單一位，即將weight matrix量化成1-bit（即取值1或-1），并且將activation量化成8-bit來執(zhí)行矩陣乘法。然后使用1-bit矩陣乘上8-bit activation的矩陣運(yùn)算，代替一般神經(jīng)網(wǎng)絡(luò)中的矩陣乘法nn.Linear。模型其余部分則會(huì)維持一個(gè)高精度，比如FP16，包括梯度、優(yōu)化器狀態(tài)、以及Attention里的運(yùn)算。

3.3.1 方案

架構(gòu)

BitNet將量化過程直接注入到Transformer 架構(gòu)中。Transformer 架構(gòu)是大多數(shù)LLM的基礎(chǔ)，該架構(gòu)在計(jì)算中嚴(yán)重依賴線性層。這些線性層通常以更高的精度（例如FP16）表示，模型的大部分權(quán)重都存在于此。因此，BitNet對(duì)此進(jìn)行了修改，引入了BitLinear層來替換這些線性層。

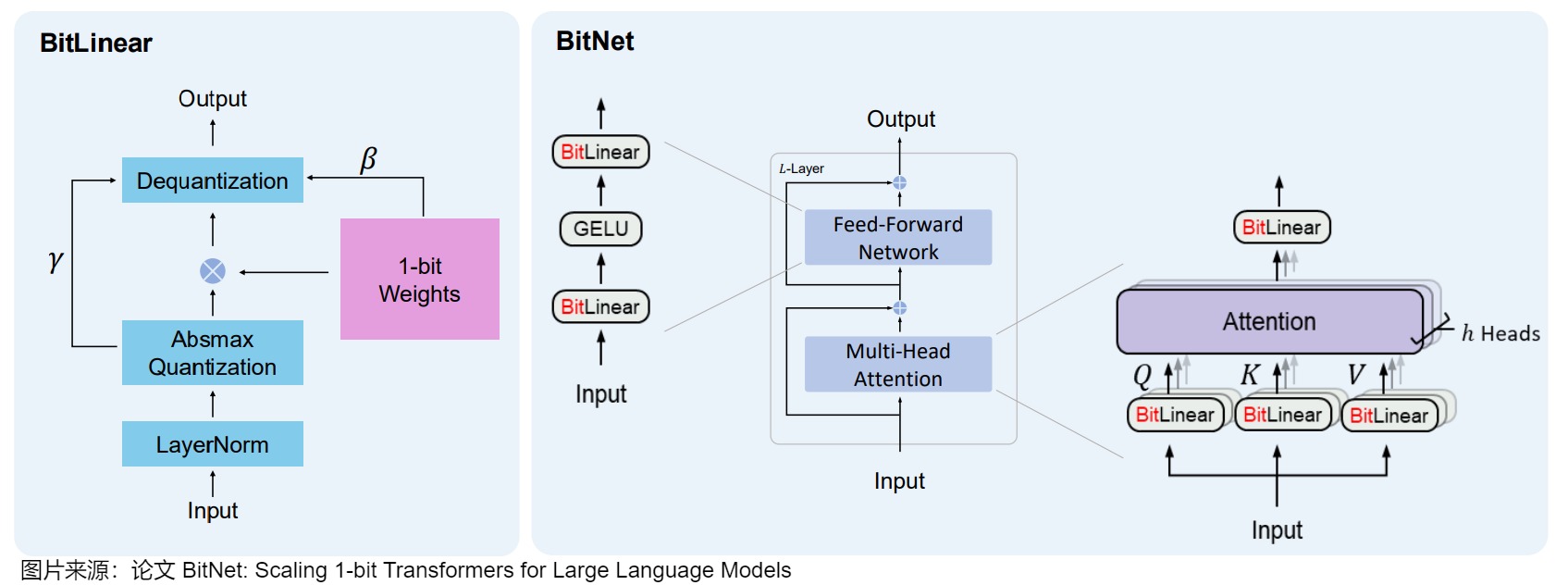
BitLinear層的工作方式與普通線性層相同，根據(jù)權(quán)重乘以激活來計(jì)算輸出。但是BitLinear層使用1位來表示模型的權(quán)重，并使用INT8來表示激活。這種方法顯著減少了模型的存儲(chǔ)和計(jì)算需求，使得在資源受限的環(huán)境中部署大型語言模型變得可行。同時(shí)，通過這種極端的量化方法，BitNet在維持性能的同時(shí)大幅降低了能耗和運(yùn)行成本。

另一方面，作者希望維持梯度更新操作的高精度，因此還會(huì)在訓(xùn)練過程中維持一個(gè)高精度的隱含的權(quán)重矩陣（當(dāng)然在計(jì)算的時(shí)候會(huì)進(jìn)行1-bit量化，只是在更新參數(shù)的時(shí)候是高精度的），另一方面作者認(rèn)為Transformer計(jì)算的主要workload在于矩陣乘法，因此優(yōu)化nn.Linear操作最為重要。

流程

BitLinear在訓(xùn)練時(shí)的流程如下。

• 一開始有一個(gè)高精度的input activation，一個(gè)高精度的weight matrix。
• 用零初始化weight，然后用一個(gè)sign函數(shù)將它轉(zhuǎn)變成1-bit（1或-1）。
• 用LayerNorm歸一化input，然后做8-bit quantization。
• 用1-bit weight乘上這個(gè)8-bit input，得到8-bit的output。
• 用之前量化的參數(shù)做dequantization，得到高精度的output。

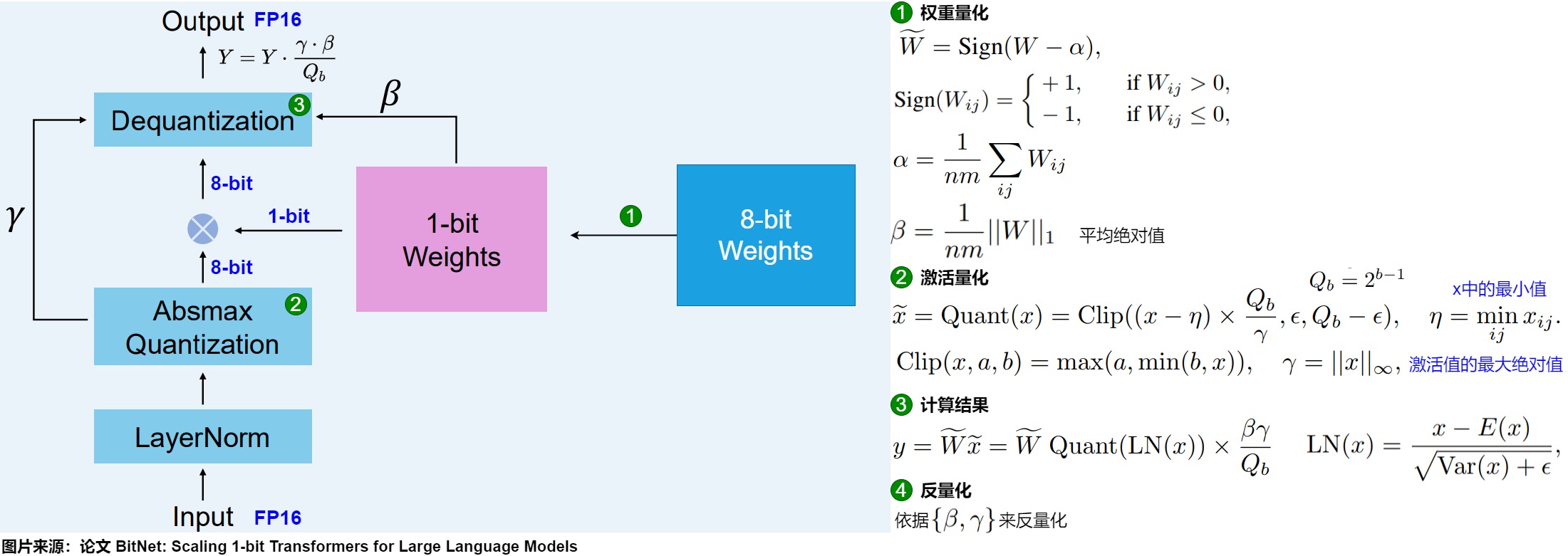
權(quán)重量化

在訓(xùn)練過程中，權(quán)重存儲(chǔ)在INT8中，然后使用一種稱為符號(hào)函數(shù)的基本策略，將其量化為1位。具體而言，它將權(quán)重的分布移動(dòng)到以0為中心，然后將0左邊的所有值賦值為-1，右邊的所有值賦值為1。

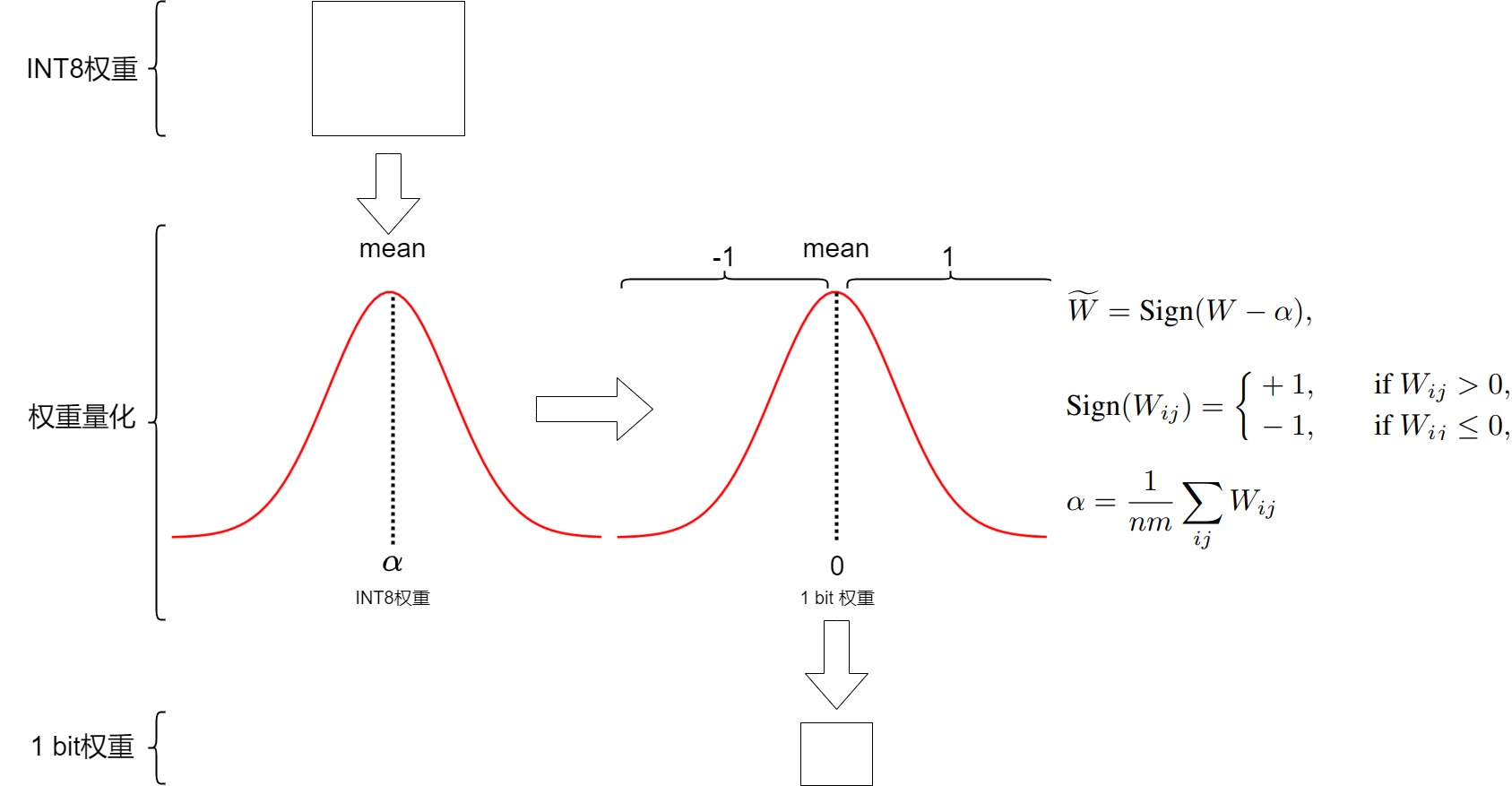
此外，它還跟蹤一個(gè)值 β（平均絕對(duì)值），因?yàn)樯院髮⒂盟M(jìn)行去量化。

激活量化

為了量化激活值，BitLinear使用absmax（絕對(duì)最大）量化將激活值從FP16轉(zhuǎn)換為INT8，因?yàn)樵诰仃嚦朔ㄖ兴鼈冃枰叩木取４送猓€記錄了激活值的最高絕對(duì)值α，因?yàn)樯院髮⒂盟M(jìn)行去量化。

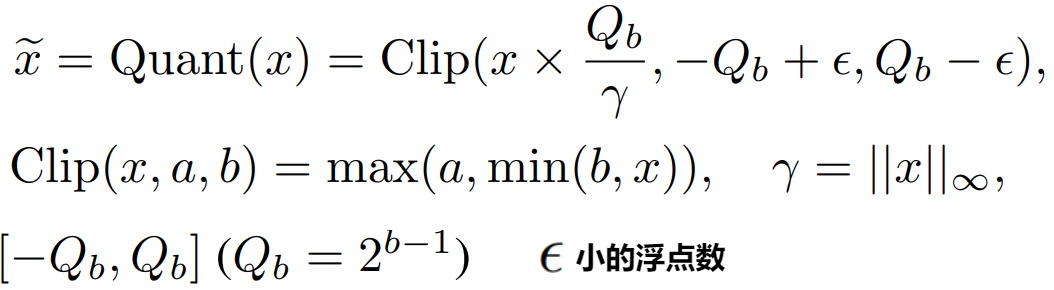
反量化

上面跟蹤了 α（激活值的最大絕對(duì)值） 和 β（權(quán)重的平均絕對(duì)值），這些值將幫助我們將激活值反量化回FP16。輸出激活值使用 {α, γ} 重新縮放，以將其反量化到原始精度：

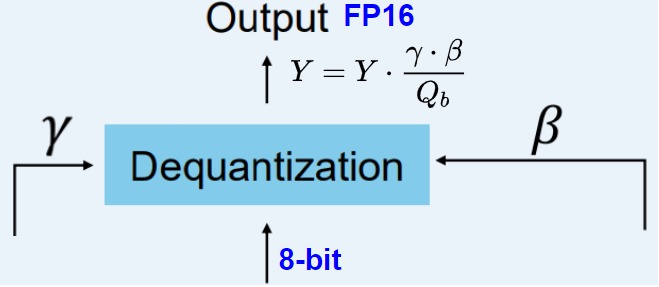
QAT

BitLinear層像QAT那樣，在訓(xùn)練期間執(zhí)行一種“假”量化形式，以分析權(quán)重和激活量化的效果。

反向傳播的時(shí)候會(huì)遇到quantization和sign操作無法傳遞梯度的問題，論文用STE (straight-through estimator) 將梯度直接傳遞回去。在Inference的時(shí)候是不需要維持一個(gè)高精度的weights的，直接用1-bit量化版本即可。同時(shí)論文發(fā)現(xiàn)1-bit模型在訓(xùn)練時(shí)比高精度模型更穩(wěn)定，而且由于weight不是1就是-1，如果gradient太小，一步更新后模型可能沒有什么變化，因此論文推薦使用更大的學(xué)習(xí)率。

3.3.2 結(jié)果

BitNet體現(xiàn)出了良好的scaling law，即通過小參數(shù)模型的訓(xùn)練loss和參數(shù)量，可以準(zhǔn)確地預(yù)測更大參數(shù)量模型的訓(xùn)練結(jié)果，而且與FP16精度模型的差距隨著參數(shù)量增大而減少。同時(shí)由于使用1-bit weights，原先nn.Linear中的矩陣乘法如今只要做加法就可以了，乘法主要是在scaling的時(shí)候用一下，使得計(jì)算量大減。

BitNet和Post-training quantization主要區(qū)別在于BitNet需要從頭訓(xùn)練模型，這確實(shí)是一些劣勢，但在推理階段的優(yōu)勢非常明顯，擁有極低的顯存占用和計(jì)算量。

3.4 BitNet b1.58

BitNet b1.58 是 BitNet 的一個(gè)改良版本，主要將weights的取值從{-1, 1}變?yōu)閧-1, 0, 1}，這也是為什么說這個(gè)模型是1.58-bit的原因，這賦予了模型忽略（ignore）特定feature的能力，提升了模型性能，并且增加一個(gè)0的選擇，進(jìn)行矩陣乘法時(shí)也還是只需要進(jìn)行加法即可。

3.4.1 方案

1.58位量化主要需要兩個(gè)技巧：

• 添加 0 創(chuàng)建三元表示 [-1, 0, 1]。
• absmean 量化用于權(quán)重。

這樣就得到了輕量級(jí)模型，因?yàn)樗鼈冎恍枰?.58位的計(jì)算效率。

0的力量

添加 0 的作用是可以消除一次乘法操作。所以如果權(quán)重量化到1.58位，只需要進(jìn)行加法操作。

矩陣乘法在計(jì)算輸出時(shí)，將一個(gè)權(quán)重矩陣乘以一個(gè)輸入向量。這種乘法涉及兩個(gè)動(dòng)作，即乘輸入和單個(gè)權(quán)重，然后將它們加在一起。

BitNet 1.58b 通過使用三元權(quán)重基本上可以避免乘法操作，因?yàn)槿獧?quán)重本質(zhì)上告訴你以下信息：

• 1 — 我想添加這個(gè)值
• 0 — 我不需要這個(gè)值
• -1 — 我想減去這個(gè)值

通過將給定的權(quán)重設(shè)置為0，就可以忽略它，而不是像1位表示那樣要么添加要么減去權(quán)重。這不僅可以顯著加速計(jì)算，還允許進(jìn)行特征過濾。

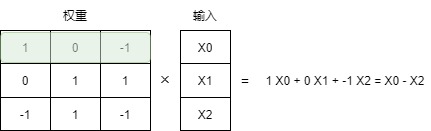
量化

為了進(jìn)行權(quán)重量化，BitNet 1.58b 使用了 absmean 量化（絕對(duì)均值量化）。它簡單地壓縮權(quán)重的分布，并使用絕對(duì)平均值（α）來量化值，即將權(quán)重分布?jí)嚎s在絕對(duì)均值（α）附近。然后這些值被四舍五入為 -1、0 或 1。與BitNet相比，激活量化基本相同，但是激活不再縮放到范圍 [0, 2??1]，而是使用 absmax 量化 縮放到 [-2??1, 2??1]。

3.5 OneBit

論文“Onebit: Towards extremely low-bit large language models”引入了一個(gè)名為OneBit的1bit量化感知訓(xùn)練（QAT，quantization-aware training）框架，包括一種新穎的1bit參數(shù)表示方法，和一種基于矩陣分解的有效參數(shù)初始化方法，以提高QAT框架的收斂速度。

3.5.1 主要貢獻(xiàn)

Onebit的貢獻(xiàn)是如下：

• 提出了一種新穎高效的1-bit模型架構(gòu)，用于LLMs，它可以在模型推理過程中提高時(shí)間和空間效率，架構(gòu)在量化LLMs時(shí)更穩(wěn)定。
• 提出了SVID（符號(hào)-值獨(dú)立分解）來將高比特矩陣分解為低比特矩陣，這對(duì)于1-bit架構(gòu)的初始化至關(guān)重要。實(shí)驗(yàn)表明，基于SVID的初始化可以提高模型性能和收斂速度。

3.5.2 挑戰(zhàn)

模型量化的主要思想是將模型中的每個(gè)權(quán)重矩陣W從FP32或FP16格式壓縮成低比特的對(duì)應(yīng)物。具體來說，我們通常將Transformer中線性層的權(quán)重矩陣量化為8比特、4比特，甚至2比特。大多數(shù)量化研究主要采用四舍五入到最近值（RTN, round-to-nearest）方法，即將權(quán)重w四舍五入到量化網(wǎng)格中最接近的值。這可以表示為：

其中s表示量化比例參數(shù)，z表示零點(diǎn)參數(shù)，N是量化比特寬度。Clip(·)將結(jié)果截?cái)嘣?到 2^N?1 的范圍內(nèi)。

隨著比特寬度越來越低，量化網(wǎng)格也變得更加稀疏。當(dāng)我們將LLM量化為1bit時(shí)，量化模型中只有2個(gè)可用數(shù)字可供選擇。此外，當(dāng)N等于1時(shí)，基于RTN方法的量化本質(zhì)上等同于設(shè)置一個(gè)閾值，權(quán)重w在它的兩側(cè)被轉(zhuǎn)換為相應(yīng)的整數(shù)值 \(\hat w\)。這種情況下，方程中的參數(shù)s和z實(shí)際上失去了實(shí)際意義。因此，當(dāng)將權(quán)重量化為1比特時(shí)，基于元素的RTN操作嚴(yán)重破壞了權(quán)重矩陣W的精度，造成了權(quán)重矩陣 W 中極低比特寬度下的巨大精度損失，顯著增加了LLMs核心操作符線性投影WX 的損失。導(dǎo)致量化模型性能下降。

3.5.3 方案

Onebit在BitNet上改進(jìn)。

1-bit線性層架構(gòu)

由于1-bit權(quán)重量化的嚴(yán)重精度損失，直接按照RTN將線性層中的權(quán)重矩陣從FP32/16格式轉(zhuǎn)換為1-bit格式是難度非常大的。BitNet通過研究純粹1-bit權(quán)重矩陣的能力，從頭開始訓(xùn)練1-bit模型，探索了這種可能性。在W1A16設(shè)置下，BitNet的線性層被設(shè)計(jì)如上圖左側(cè)。其中 W 表示形狀為m×n的量化權(quán)重矩陣， W±1 表示1-bit量化矩陣。X是線性層的輸入，Y是輸出。Sign(·)、Mean(·)和Abs(·)函數(shù)分別返回符號(hào)矩陣、平均值和絕對(duì)值矩陣。不幸的是，這種方法雖然減少了計(jì)算需求，但也導(dǎo)致了顯著的性能下降。

受到 BitNet 的啟發(fā)，OneBit 也使用Sign(·)函數(shù)量化權(quán)重矩陣，并將量化矩陣的元素設(shè)置為+1或-1。此外，我們還注意到，盡管 W±1 保持了 W 的高秩，但缺失的浮點(diǎn)精度仍然破壞了模型性能。與以前的工作不同，OneBit 引入了兩個(gè)FP16格式的值向量來彌補(bǔ)量化過程中的精度損失。OneBit 提出的線性層被設(shè)計(jì)為：

其中 g 和 h 是兩個(gè)FP16值向量。注意在上述公式中使用括號(hào)指定了計(jì)算順序，這樣可以最小化時(shí)間和空間成本。BitNet 和OneBit之間的主要區(qū)別在于額外的參數(shù) g 和 h。即使引入了額外的參數(shù)，其帶來的好處也遠(yuǎn)遠(yuǎn)超過了其小成本。例如，當(dāng)我們量化一個(gè)形狀為4096×4096的權(quán)重矩陣時(shí)，量化結(jié)果的平均比特寬度為1.0073。

下圖給出了OneBit 方法的主要思想。左側(cè)是原始的 FP16 線性層，其中激活值 X 和權(quán)重矩陣 W 都采用 FP16 格式。右側(cè)是 OneBit 提出的架構(gòu)，只有值向量 g 和 h 保持 FP16 格式，而權(quán)重矩陣由 ±1 組成。?：哈達(dá)瑪積（Hadamard product）。

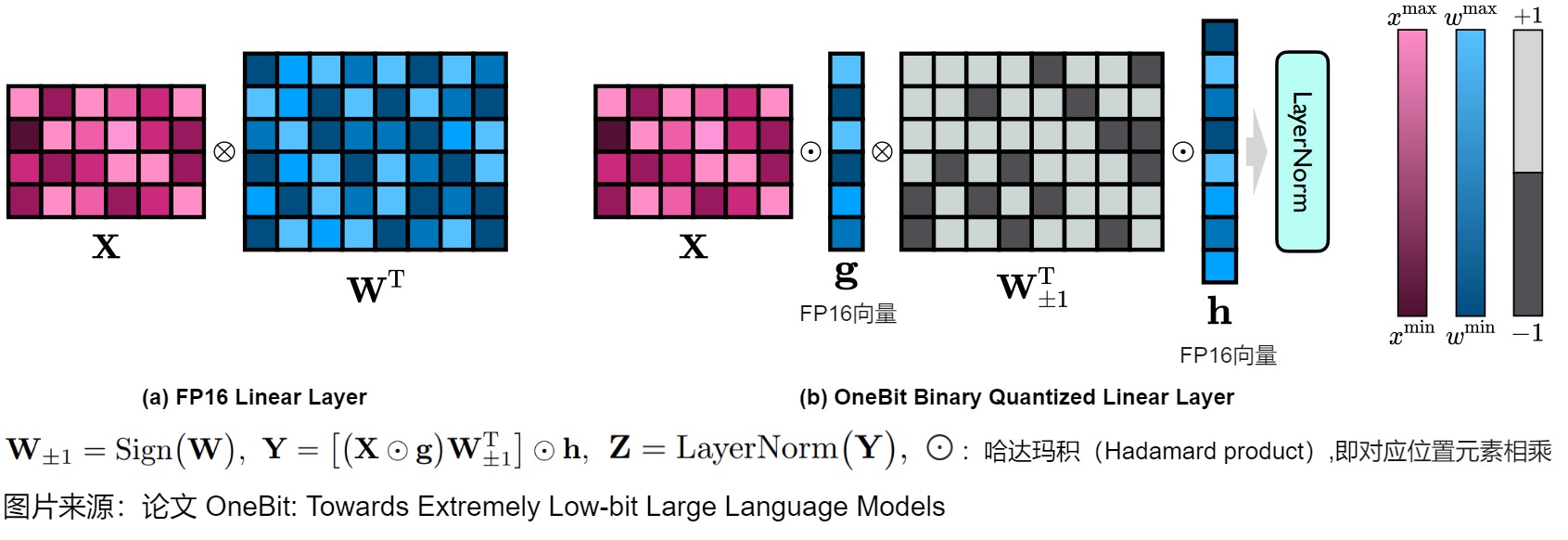
符號(hào)-值獨(dú)立分解（SVID）

在SVID（Sign-Value-Independent Decomposition）中，每個(gè)原始的高比特權(quán)重矩陣被分解成一個(gè)INT1格式的符號(hào)矩陣（W±1）和兩個(gè)FP16值向量g和h。值向量在很小的代價(jià)下為線性投影提供了必要的浮點(diǎn)精度，并幫助模型輕松訓(xùn)練。符號(hào)矩陣以很小的空間成本保持了原始權(quán)重矩陣的高秩，從而保留了高信息容量。

具體推導(dǎo)如下：

知識(shí)轉(zhuǎn)移

SVID為1bit模型提供了更好的參數(shù)初始化，OneBit采用量化感知的知識(shí)蒸餾將原始模型的能力轉(zhuǎn)移到提出的1比特對(duì)應(yīng)物。具體而言，OneBit采用量化感知知識(shí)蒸餾，將知識(shí)從原始模型（即教師模型）轉(zhuǎn)移到量化模型（即學(xué)生模型）。在學(xué)生模型中訓(xùn)練矩陣W和向量g/h的元素。使用基于交叉熵的logits和基于均方誤差的全精度教師模型隱藏狀態(tài)來指導(dǎo)量化的學(xué)生模型。

0xFF 參考

Onebit: Towards extremely low-bit large language models

https://arxiv.org/pdf/2402.17764

H. Wang, S. Ma, L. Dong, S. Huang, H. Wang, L. Ma, F. Yang, R. Wang, Y. Wu, and F. Wei. BitNet: Scaling 1-bit transformers for large language models. arXiv preprint arXiv:2310.11453, 2023.

Yuzhuang Xu, Xu Han, Zonghan Yang, Shuo Wang, Qingfu Zhu, Zhiyuan Liu, Weidong Liu, and Wanxiang Che. 2024. Onebit: Towards extremely low-bit large language models. CoRR, abs/2402.11295.

Fast and Efficient 2-bit LLM Inference on GPU: 2/4/16-bit in a Weight Matrix with Asynchronous Dequantization

大模型量化技術(shù)原理-SpQR 吃果凍不吐果凍皮

SqueezeLLM

LLM 量化新篇章，4-bit 權(quán)重激活量化幾乎無損！FlatQuant 的平坦之道 NeuralTalk

LLM-QAT: Data-Free Quantization Aware Training for Large Language Models

https://www.armcvai.cn/2024-11-01/llm-quant-awq.html

LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

https://www.armcvai.cn/2024-10-30/llm-smoothquant.html

https://www.armcvai.cn/2024-10-31/smoothquant-inplement.html

https://www.armcvai.cn/2024-11-03/awq-code.html

[源碼] [萬字] SmoothQuant量化深入探究

https://github.com/mit-han-lab/smoothquant/

https://github.com/Guangxuan-Xiao/torch-int/

[LLM量化系列] PTQ量化經(jīng)典研究解析 進(jìn)擊的Killua

LLM-QAT: Data-Free Quantization Aware Training for Large Language Models

大模型輕量化 (二)：AWQ：適合端側(cè)的 4-bit 大語言模型權(quán)重量化 科技猛獸

GPTQ&OBQ：量化你的GPT 楊新宇

QLoRA: 訓(xùn)練更大的GPT 楊新宇

LLM 推理加速技術(shù)原理 —— GPTQ 量化技術(shù)演進(jìn) Fenrier Lab

(Alpha) GPTQ 詳解 buxianchen

LeCun, Yann, John Denker, and Sara Solla. “Optimal brain damage.” Advances in neural information processing systems 2 (1989).

Hassibi, Babak, David G. Stork, and Gregory J. Wolff. “Optimal brain surgeon and general network pruning.” IEEE international conference on neural networks. IEEE, 1993.

Frantar, Elias, and Dan Alistarh. “Optimal brain compression: A framework for accurate post-training quantization and pruning.” Advances in Neural Information Processing Systems 35 (2022): 4475-4488.

Frantar, Elias, et al. “Gptq: Accurate post-training quantization for generative pre-trained transformers.” arXiv preprint arXiv:2210.17323 (2022).

GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers https://arxiv.org/abs/2210.17323

Optimal Brain Compression: A Framework for Accurate Post-Training Quantization and Pruning https://arxiv.org/abs/2208.11580v2

Optimal Brain Surgeon and general network pruning https://www.babak.caltech.edu/pubs/conferences/00298572.pdf

Optimal Brain Damage https://proceedings.neurips.cc/paper/1989/file/6c9882bbac1c7093bd25041881277658-Paper.pdf

GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers （https://arxiv.org/abs/2210.17323）

Wu H, Judd P, Zhang X, et al. Integer quantization for valuation[J]. arXiv preprint arXiv:2004.09602, 2020.

Zhewei Yao, Reza Yazdani Aminabadi, Minjia Zhang, Xiaoxia nt and affordable post-training quantization for .01861, 2022.

Tim Dettmers, Mike Lewis, Younes Belkada, and Luke n for transformers at scale. arXiv preprint

Elias Frantar, Sidak Pal Singh, and Dan r accurate post-training quantization and pruning. arXiv S 2022, to appear.

Bondarenko, Y., Nagel, M., and Blankevoort, T. Understanding and overcoming the challenges of efficient transformer quantization. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, pp. 7947–7969, Online and Punta Cana, Dominican Republic, November 2021. Association for Computational Linguistics. URL https://aclanthology.org/2021. emnlp-main.627.

模型量化技術(shù)綜述：揭示大型語言模型壓縮的前沿技術(shù) [DeepHub IMBA](javascript:void(0)??

大模型性能優(yōu)化（一）：量化從半精度開始講，弄懂fp32、fp16、bf16

便捷的post training quantization方案: GPTQ

【AI不惑境】模型量化技術(shù)原理及其發(fā)展現(xiàn)狀和展望 龍鵬-筆名言有三

AWQ, Activation-aware Weight Quantization

LLM.int8()

SqueezeLLM

SmoothQuant

ZeroQuant系列(v1, v2)

GPTQ

大模型量化感知訓(xùn)練開山之作：LLM-QAT 吃果凍不吐果凍皮

LLM-QAT: Data-Free Quantization Aware Training for Large Language Models

https://link.zhihu.com/?target=https%3A//github.com/facebookresearch/LLM-QAT)

關(guān)于大模型推理的量化算法總結(jié) 孫培欽

、王文廣萬字長文揭秘大模型量化的GPTQ方法：從OBS經(jīng)OBQ到GPTQ，海森矩陣的魔力

王文廣萬字長文揭秘大模型量化技術(shù)：探究原理，理解大模型高效推理最重要的技術(shù)

akaihaoshuai：從0開始實(shí)現(xiàn)LLM：6、模型量化理論+代碼實(shí)戰(zhàn)（LLM-QAT/GPTQ/BitNet 1.58Bits/OneBit）
akaihaoshuai：從0開始實(shí)現(xiàn)LLM：6.1、模型量化（AWQ/SqueezeLLM/Marlin）

https://zhuanlan.zhihu.com/p/703513611

AI大模型高效推理的技術(shù)綜述！ 花哥 [AI大模型前沿](javascript:void(0)??

[LLM量化系列] DuQuant、AffineQuant和FlatQuant 進(jìn)擊的Killua

Rishabh Agarwal, Nino Vieillard, Piotr Stanczyk, Sabela Ramos, Matthieu Geist, and Olivier Bachem. 2023. GKD: Generalized knowledge distillation for auto-regressive sequence models. arXiv preprint arXiv:2306.13649.

E Beltrami. 1990. Sulle funzioni bilineari, giomale di mathematiche ad uso studenti delle uniersita. 11, 98–106. (an English translation by d boley is available as University of Minnesota, Department of Computer Science). Technical report, Technical Report 90–37.

Stella Biderman, Hailey Schoelkopf, Quentin Gregory Anthony, Herbie Bradley, Kyle O’Brien, Eric Hallahan, Mohammad Aflah Khan, Shivanshu Purohit, USVSN Sai Prashanth, Edward Raff, et al. 2023. Pythia: A suite for analyzing large language models across training and scaling. In ICML, pages 2397– 2430.

Yonatan Bisk, Rowan Zellers, Jianfeng Gao, Yejin Choi, et al. 2020. PIQA: Reasoning about physical commonsense in natural language. In Proceedings of the AAAI, volume 34, pages 7432–7439.

Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. 2020. Language models are few-shot learners. Advances in NeurIPS, 33:1877–1901.

Sébastien Bubeck, Varun Chandrasekaran, Ronen Eldan, Johannes Gehrke, Eric Horvitz, Ece Kamar, Peter Lee, Yin Tat Lee, Yuanzhi Li, Scott Lundberg, et al. 2023. Sparks of artificial general intelligence: Early experiments with gpt-4. arXiv preprint arXiv:2303.12712.

Christopher Clark, Kenton Lee, Ming-Wei Chang, Tom Kwiatkowski, Michael Collins, and Kristina Toutanova. 2019. BoolQ: Exploring the surprising difficulty of natural yes/no questions. arXiv preprint arXiv:1905.10044.

Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. 2018. Think you have solved question answering? try arc, the ai2 reasoning challenge. arXiv preprint arXiv:1803.05457.

Tim Dettmers, Mike Lewis, Younes Belkada, and Luke Zettlemoyer. 2022. LLM.int8(): 8-bit matrix multiplication for transformers at scale. arXiv preprint arXiv:2208.07339.

Tim Dettmers, Artidoro Pagnoni, Ari Holtzman, and Luke Zettlemoyer. 2023a. QLoRA: Efficient finetuning of quantized LLMs. In Advances in NeurIPS.

Tim Dettmers, Ruslan Svirschevski, Vage Egiazarian, Denis Kuznedelev, Elias Frantar, Saleh Ashkboos, Alexander Borzunov, Torsten Hoefler, and Dan Alistarh. 2023b. SpQR: A sparse-quantized representation for near-lossless llm weight compression. arXiv preprint arXiv:2306.03078.

Tim Dettmers and Luke Zettlemoyer. 2023. The case for 4-bit precision: k-bit inference scaling laws. In ICML, pages 7750–7774.

Elias Frantar and Dan Alistarh. 2023. SparseGPT: Massive language models can be accurately pruned in one-shot. In ICML, pages 10323–10337.

Elias Frantar, Saleh Ashkboos, Torsten Hoefler, and Dan Alistarh. 2022. GPTQ: Accurate post-training quantization for generative pre-trained transformers. arXiv preprint arXiv:2210.17323.

Dan Hendrycks, Collin Burns, Steven Basart, Andy Zou, Mantas Mazeika, Dawn Song, and Jacob Steinhardt. 2021. Measuring massive multitask language understanding. In ICLR.

Cheng-Yu Hsieh, Chun-Liang Li, Chih-kuan Yeh, Hootan Nakhost, Yasuhisa Fujii, Alex Ratner, Ranjay Krishna, Chen-Yu Lee, and Tomas Pfister. 2023. Distilling step-by-step! outperforming larger language models with less training data and smaller model sizes. In Findings of the ACL, pages 8003–8017.

Jeonghoon Kim, Jung Hyun Lee, Sungdong Kim, Joonsuk Park, Kang Min Yoo, Se Jung Kwon, and Dongsoo Lee. 2023a. Memory-efficient fine-tuning of compressed large language models via sub-4-bit integer quantization. arXiv preprint arXiv:2305.14152.

Sehoon Kim, Coleman Hooper, Amir Gholami, Zhen Dong, Xiuyu Li, Sheng Shen, Michael W Mahoney, and Kurt Keutzer. 2023b. SqueezeLLM: Dense-and-sparse quantization. arXiv preprint arXiv:2306.07629.

Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.

Ji Lin, Jiaming Tang, Haotian Tang, Shang Yang, Xingyu Dang, and Song Han. 2023. AWQ: Activation-aware weight quantization for llm compression and acceleration. arXiv preprint arXiv:2306.00978.

Zechun Liu, Barlas Oguz, Changsheng Zhao, Ernie Chang, Pierre Stock, Yashar Mehdad, Yangyang Shi, Raghuraman Krishnamoorthi, and Vikas Chandra. 2023. LLM-QAT: Data-free quantization aware training for large language models. arXiv preprint arXiv:2305.17888.

Xinyin Ma, Gongfan Fang, and Xinchao Wang. 2023. LLM-Pruner: On the structural pruning of large language models. In Advances in NeurIPS.

Stephen Merity, Caiming Xiong, James Bradbury, and Richard Socher. 2016. Pointer sentinel mixture models. arXiv preprint arXiv:1609.07843.

Matan Ben Noach and Yoav Goldberg. 2020. Compressing pre-trained language models by matrix decomposition. In Proceedings of the AACL-IJCNLP, pages 884–889.

Pentti Paatero and Unto Tapper. 1994. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics, 5(2):111–126.

Baolin Peng, Chunyuan Li, Pengcheng He, Michel Galley, and Jianfeng Gao. 2023. Instruction tuning with gpt-4. arXiv preprint arXiv:2304.03277.

Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, Ilya Sutskever, et al. 2019. Language models are unsupervised multitask learners. OpenAI blog, 1(8):9.

Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J Liu. 2020. Exploring the limits of transfer learning with a unified text-to-text transformer. The Journal of Machine Learning Research, 21(1):5485–5551.

Keisuke Sakaguchi, Ronan Le Bras, Chandra Bhagavatula, and Yejin Choi. 2021. Winogrande: An adversarial winograd schema challenge at scale. Communications of the ACM, 64(9):99–106.

Wenqi Shao, Mengzhao Chen, Zhaoyang Zhang, Peng Xu, Lirui Zhao, Zhiqian Li, Kaipeng Zhang, Peng Gao, Yu Qiao, and Ping Luo. 2023. OmniQuant: Omnidirectionally calibrated quantization for large language models. arXiv preprint arXiv:2308.13137.

Mingjie Sun, Zhuang Liu, Anna Bair, and J. Zico Kolter. 2023. A simple and effective pruning approach for large language models. arXiv preprint arXiv:2306.11695.

Siqi Sun, Yu Cheng, Zhe Gan, and Jingjing Liu. 2019. Patient knowledge distillation for BERT model compression. In Proceedings of the EMNLP-IJCNLP, pages 4323–4332.

Rohan Taori, Ishaan Gulrajani, Tianyi Zhang, Yann Dubois, Xuechen Li, Carlos Guestrin, Percy Liang, and Tatsunori B. Hashimoto. 2023. Stanford alpaca: An instruction-following llama model. https://github.com/tatsu-lab/stanford_alpaca.

Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, et al. 2023. LLaMA: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971.

Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, ?ukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. Advances in NeurIPS, 30.

Zhongwei Wan, Xin Wang, Che Liu, Samiul Alam, Yu Zheng, Zhongnan Qu, Shen Yan, Yi Zhu, Quanlu Zhang, Mosharaf Chowdhury, et al. 2023. Efficient large language models: A survey. arXiv preprint arXiv:2312.03863.

Hongyu Wang, Shuming Ma, Li Dong, Shaohan Huang, Huaijie Wang, Lingxiao Ma, Fan Yang, Ruiping Wang, Yi Wu, and Furu Wei. 2023. BitNet: Scaling 1-bit transformers for large language models. arXiv preprint arXiv:2310.11453.

Guangxuan Xiao, Ji Lin, Mickael Seznec, Hao Wu, Julien Demouth, and Song Han. 2023. SmoothQuant: Accurate and efficient post-training quantization for large language models. In ICML, pages 38087– 38099.

Mingxue Xu, Yao Lei Xu, and Danilo P Mandic. 2023. TensorGPT: Efficient compression of the embedding layer in llms based on the tensor-train decomposition. arXiv preprint arXiv:2307.00526.

Rowan Zellers, Ari Holtzman, Yonatan Bisk, Ali Farhadi, and Yejin Choi. 2019. Hellaswag: Can a machine really finish your sentence? arXiv preprint arXiv:1905.07830.

Peiyuan Zhang, Guangtao Zeng, Tianduo Wang, and Wei Lu. 2024. TinyLlama: An open-source small language model. arXiv preprint arXiv:2401.02385.

Xunyu Zhu, Jian Li, Yong Liu, Can Ma, and Weiping Wang. 2023. A survey on model compression for large language models. arXiv preprint arXiv:2308.07633.

The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits：https://arxiv.org/abs/2402.17764

BitNet: Scaling 1-bit Transformers for Large Language Models：https://arxiv.org/abs/2310.11453

The Era of 1-bit LLMs: Training Tips, Code and FAQ：https://github.com/microsoft/unilm/blob/master/bitnet/The-Era-of-1-bit-LLMs__Training_Tips_Code_FAQ.pdf

OLMo-Bitnet-1B：NousResearch/OLMo-Bitnet-1B · Hugging Face

1bitLLM/bitnet_b1_58-3B · Hugging Face

Touvron, Hugo, et al. "Llama: Open and efficient foundation language models." arXiv preprint arXiv:2302.13971 (2023).

[2] Taori, Rohan, et al. "Stanford alpaca: An instruction-following llama model." (2023).

Dettmers, Tim, et al. "Llm. int8 : 8-bit matrix multiplication for transformers at scale." arXiv preprint arXiv:2208.07339 (2022).

[4] Frantar, Elias, et al. "Gptq: Accurate post-training quantization for generative pre-trained transformers." arXiv preprint arXiv:2210.17323 (2022).

Hoefler, Torsten, et al. "Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks." The Journal of Machine Learning Research 22.1 (2021): 10882-11005.

QLORA: Efficient Finetuning of Quantized LLMs

2w字解析量化技術(shù)，全網(wǎng)最全的大模型量化技術(shù)解析 柏企閱文

SageAttention：即插即用的8-bit Attention 最佳實(shí)踐 方佳瑞

decoupleQ 2bit 量化技術(shù)介紹 行云流水

[LLM量化系列] PTQ量化經(jīng)典研究解析 進(jìn)擊的Killua

Outlier Suppression: Pushing the Limit of Low-bit Transformer Language Models

Outlier Suppression+: Accurate quantization of large language models by equivalent and optimal shifting and scaling

大模型量化技術(shù)祛魅 不歸牛頓管的熊貓

[ICML2023] [W8A8] SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models

[Frantar et al., NIPS2022] Optimal Brain Compression: A Framework for Accurate Post-Training Quantization and Pruning

[ICLR2023][W3A16] GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers
QLoRA、GPTQ：模型量化概述

[MLSys2024] [W3A16] AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration

NF4 Isn't Information Theoretically Optimal (and that's Good)

SpQR: A Sparse-Quantized Representation for Near-Lossless LLM Weight Compression

目前針對(duì)大模型進(jìn)行量化的方法有哪些？ 絕密伏擊

QLoRA: Efficient Finetuning of Quantized LLMs https://arxiv.org/abs/2305.14314

QLoRA: 4bit量化+LoRA訓(xùn)練=瞬間起飛 LokLok