探秘Transformer系列之(22)--- LoRA
探秘Transformer系列之(22)--- LoRA
0x00 概述
大語言模型(LLMs)在各種自然語言處理任務中取得了顯著的成功,推動了語言理解、生成和推理能力的突破。類似其他領域中的自監督學習方法,LLMs通常在大量未標注文本數據上進行預訓練,然后針對特定下游任務進行微調,以使其知識適應目標領域。然而,LLMs的巨大規模,往往達到數十億參數量,在微調過程中帶來了計算復雜度和資源需求上的重大挑戰。
為應對這些挑戰,一種名為參數高效微調(PEFT)的有前途的方法有望在不增加大量可訓練參數的前提下將大語言模型適應于下游任務,從而減少計算和內存開銷。在這類方法中,由于其有效性和簡潔性,低秩適應(LoRA)受到了廣泛關注。
LoRA 的核心思想是利用低秩矩陣來近似模型參數的變化,從而以極小的參數量來實現大模型的間接訓練。LoRA 凍結預訓練模型的權重,引入低秩矩陣和來近似模型參數的變化量。通過僅在微調過程中更新這些低秩矩陣,LoRA在保持預訓練模型大部分參數不變的情況下,實現對特定任務的適應。LoRA的目標就是以小博大,以極小的參數量來實現大模型的間接訓練,逼近全量微調的效果。這種方法在減少存儲和計算需求的同時,也保持了模型的性能。
本文主要基于兩篇論文進行學習:
- A Survey on LoRA of Large Language Models
- Low-Rank Adaptation for Foundation Models: A Comprehensive Review
注:全部文章列表在這里,估計最終在35篇左右,后續每發一篇文章,會修改文章列表。
cnblogs 探秘Transformer系列之文章列表
0x01 背景知識
1.1 微調
隨著開源預訓練大型語言模型變得更加強大和開放,越來越多的開發者將大語言模型納入到他們的項目中。預訓練的 LLMs 通常被稱為基礎模型(在多樣、大規模數據集上訓練的大規模神經網絡),因為它們在各種任務中具有多功能性。然而,由于LLMs的知識邊界,基礎模型在某些下游任務上的能力仍然有限。為了擴展知識邊界,仍然需要在下游任務上對LLMs進行微調,即針對特定數據集或任來調整預訓練的 LLM。而且,訓練大型語言模型需要消耗大量的計算資源和時間。這為人工智能的發展帶來了瓶頸并引發了環境問題。為了緩解這一問題,人也通常也會選擇微調預訓練模型。
微調允許模型適應特定領域,而無需進行昂貴的預訓練。但是傳統上,適應預訓練模型到特定下游任務需要全面微調所有參數。而對于較大的模型來說,更新所有層的計算成本仍然很高,而且大模型全量微調時的顯存占用也容易過大。隨著這些模型的復雜性和規模增加,這種傳統的微調方法在計算和資源方面變得不再可行。
1.2 PEFT
為了應對上述挑戰,出現了更多參數高效微調技術,統稱為PEFT(Parameter-Efficient Tuning/參數高效微調)。PEFT方法已經成為了資源有限的機構和研究者微調大模型的標配,其總體思路是凍結住大模型的主干參數,引入一小部分可訓練的參數作為適配模塊進行訓練,這樣通過微調少量(額外)模型參數或者減少迭代次數,可以使LLM適應下游任務,在不影響任務性能的情況下大幅降低計算需求,節省模型微調時的顯存和參數存儲開銷,降低微調成本。雖然這些PEFT方法有著很大的潛力,但往往在效率、性能和適應性之間需要做出權衡,因此仍然有巨大優化空間。
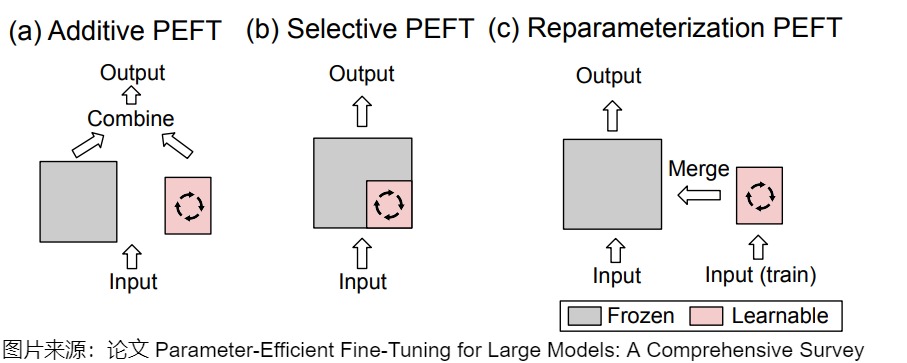
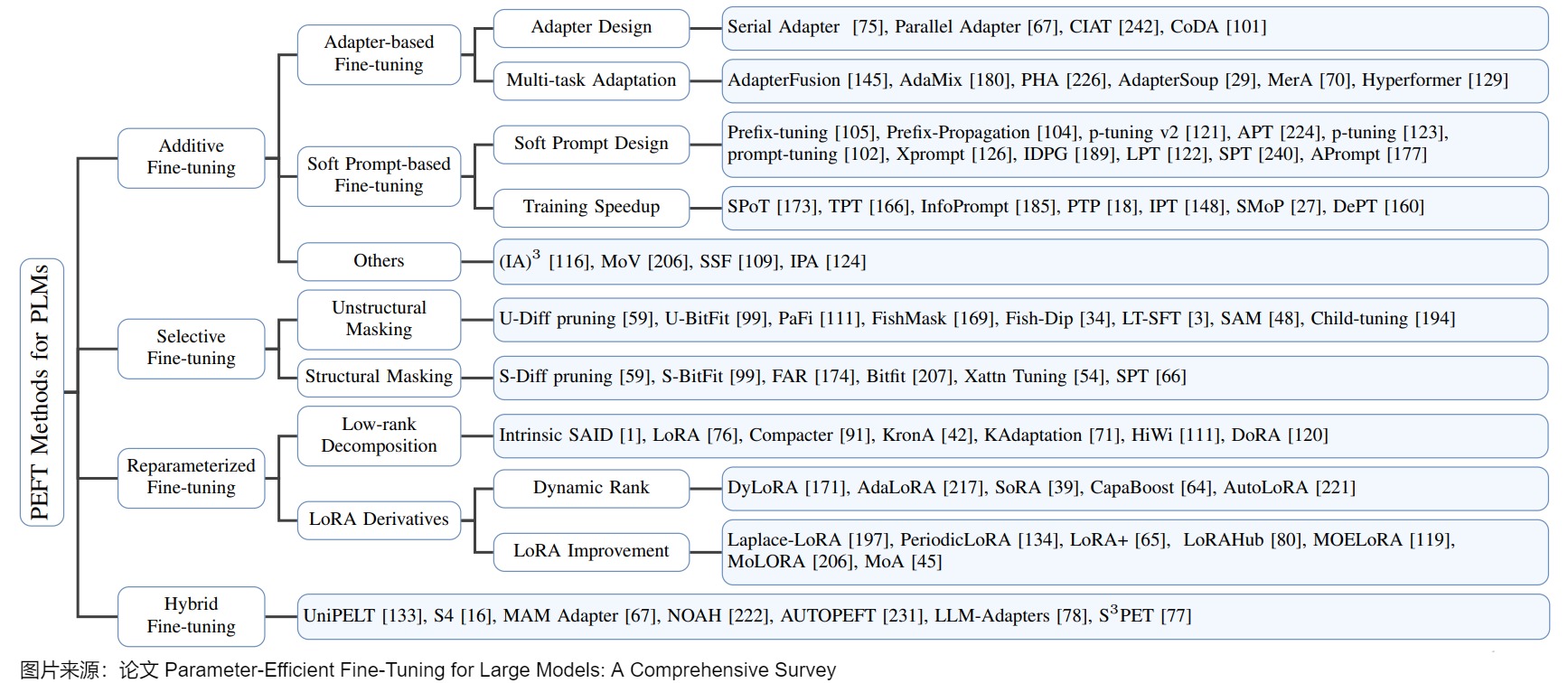
PEFT的分類方法沒有統一的規范,這里采用論文"Parameter-Efficient Fine-Tuning for Large Models: A Comprehensive Survey"的說法,將PEFT策略可大致分為四類:
- 可加性PEFT,通過注入新的可訓練模塊或參數來修改模型架構;
- 選擇性PEFT,使參數子集在微調過程中可訓練;
- 重參數化PEFT,它構建了原始模型參數的(低維)重參數化訓練,然后等效地將其轉換回來進行推理;
- 混合PEFT,它結合了不同PEFT方法的優點,構建了一個統一的PEFT模型。
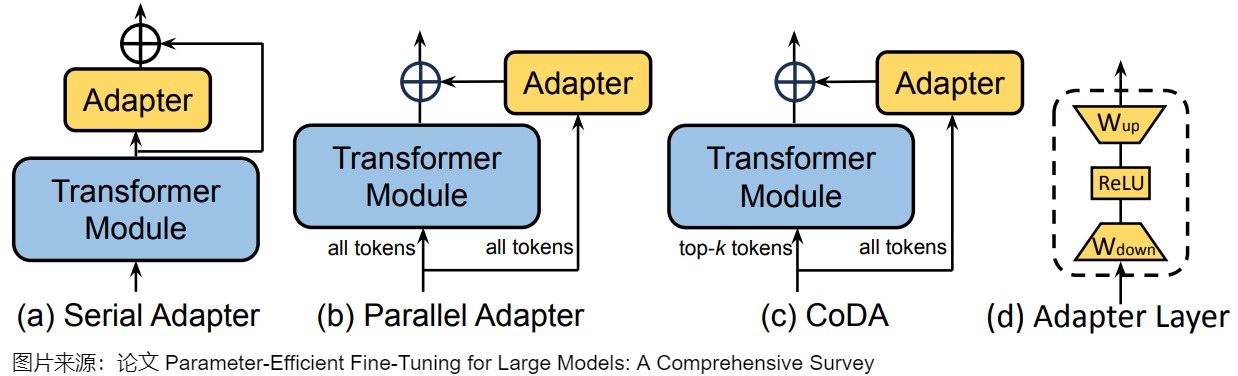
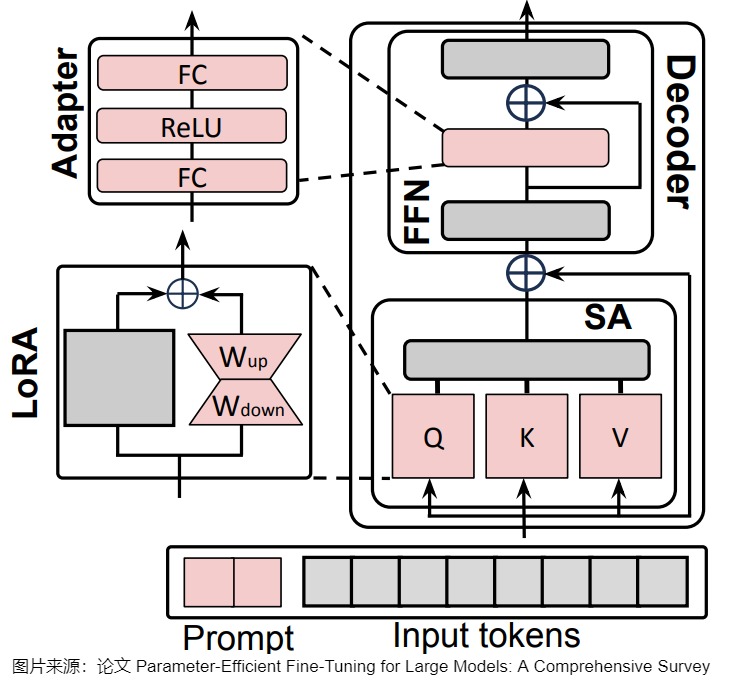
不同類型的PEFT算法的概述如下圖所示。
下圖則給出了詳細分類。
另外,上述的PEFT方法中,有些是可以混用的。比如下圖中,所有可學習的組件是紅色的,凍結的組件是灰色的。LoRA被應用到Q,K和V上,adapter 被用用到FFN上。Soft-Prompt則對每個解碼器的輸入激活進行調節。
1.3 秩
秩(Rank)是指矩陣的秩,也就是在一個矩陣中,有多少行(或列)是“唯一的”,即這些行(或列)無法由其他行(或列)線性組合而得到。例如:
第二行是第一行的三倍,所以上述矩陣的秩是1。對于列來說,第二列是第一列的2倍,第三列是第一列的3倍,所以,秩還是1。
而如下矩陣:
第二行不能由第一行組成,所以秩至少為2。乍一看第三行跟第一行和第二行無關,但仔細一算,第三行可以由第一行減去第二行的兩倍得到,所以這個矩陣的秩是2。對于列來說,也是類似的,第二列可以由第一列和第三列相加而得到。
事實上,不管根據行還是根據列來計算秩,對于同一個矩陣來說總是相同的。這也說明了,矩陣的秩一定小于等于行數或列數中小的那個。
1.4 SVD分解
由于網絡總是可以用矩陣和張量的語言來描述,線性代數為研究網絡屬性提供了重要的工具。SVD分解(Singular Value Decomposition / 奇異值分解)是線性代數的一個矩陣分解技術。SVD 的作用在于將矩陣分解為若干個不同重要性的分量之和。奇異值分解常用于降維和壓縮,通過保留較大的奇異值,可以近似表示原始矩陣。
在SVD分解中,給定大小為 ??×?? 的實數矩陣 A,對 A 進行 SVD 后得到的輸出為 \(A=UΣV^T\) 。即,原始權重矩陣被分解為三個主要組件,它們共同涵蓋了原始矩陣空間的全部。
- \(\mathbf{U}\):左奇異向量,形成列空間的正交基,其大小為??×??;
- \(\mathbf{\Sigma}\):對角矩陣,對角線上的元素稱為奇異值。奇異值用來測量每個主軸的強度或重要性,并在子空間內調整維度和縮放,其大小為??×??;
- \(\mathbf{V}\):右奇異向量,構成行空間的正交基,其大小為??×??。
我們把三個矩陣展開,得到:
由于正交矩陣的逆就是其轉置矩陣,因此 \(UU^T=I_m\) 和\(VV^T=I_n\),其中兩個單位矩陣的下標表示它們的大小分別為 ??×?? 和 ??×??。
進一步, 矩陣 A 可以寫成各個奇異值及其對應向量的求和形式,這樣的分解能分解出重要性。如果矩陣中某幾個奇異值已經占據了所有奇異值的90%,我們就只要保存對應的奇異向量和奇異值,就可以恢復這個矩陣的 90%。
SVD幾何意義本質是變基(變到 V 表示的正交基,對應向量乘以 \(V^T\),再拉伸壓縮(對應向量乘以 Σ ),再旋轉(對應向量乘以 ??)。即,空間中的一個向量到另一個向量的運動,就是一個向量分解到V上,然后分別做\(\sum\)描述的拉伸,再分解到U上,變成另一個向量。
0x02 LoRA
2.1 定義
LoRA 是低秩適配(Low-Rank Adaptation)的縮寫,是一種用于減少內存需求的微調方法。
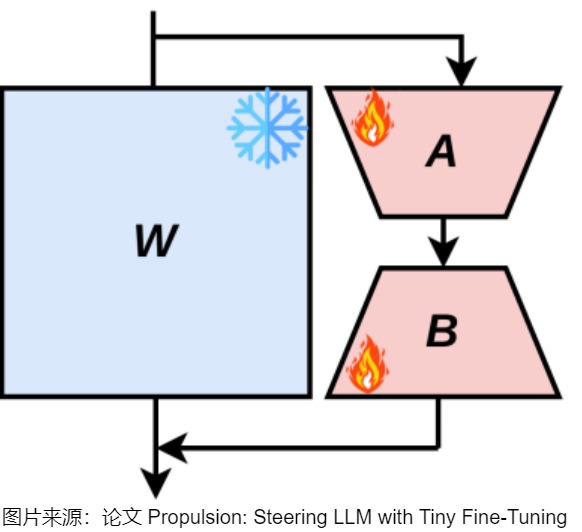
在抽象的層面上,基礎大模型可以抽象為一個函數:\(y=f(x, W)\)。函數f()對輸入x進行處理,并輸出y。W是模型的權重,也可以認為是大模型本身。對于現在的大語言模型來說,W是數以百億(或者千億、萬億)計的浮點數組成的權重集合,是大模型發揮其“魔法”之所在。通常來說,訓練一個大模型就是通過大規模語料學習出模型的權重W。形式化來說就是通過利用數據集的不斷迭代來實現權重的調整,即:\(W = W + \Delta W\),直到訓練出一個好的W。其中,\(\Delta W\)就是每次訓練數據中通過損失函數計算出來的權重的變化值。
LoRA 凍結基礎大模型的模型權重參數,引入低秩矩陣和來近似模型參數的變化量。LoRA方法背后的邏輯是:可以使用低秩矩陣有效捕獲對特定任務的適應。與原始權重相比,新增加的知識 ΔW只占一小部分。因此LoRA會凍結一個預訓練模型的原始矩陣權重參數,以低秩分解格式來模擬訓練期間層的權重變化 ΔW。從而以極小的參數量來實現大模型的間接訓練。即,通過將更新矩陣約束為低秩,利用矩陣分解減少參數學習量。通過針對每個任務優化這些低秩矩陣并凍結原始模型參數,LoRA 實現了高效適應,并能夠組合多個特定任務的適應,且不會增加推理延遲。
LoRA的這種設計不僅減少了參數量,還保持了模型的原有結構和性能。由于原始模型參數保持不變,只是通過添加少量的可訓練參數來適應新的任務,因此LoRA可以在不同的任務上進行靈活應用,而不會對模型的原有能力造成影響。
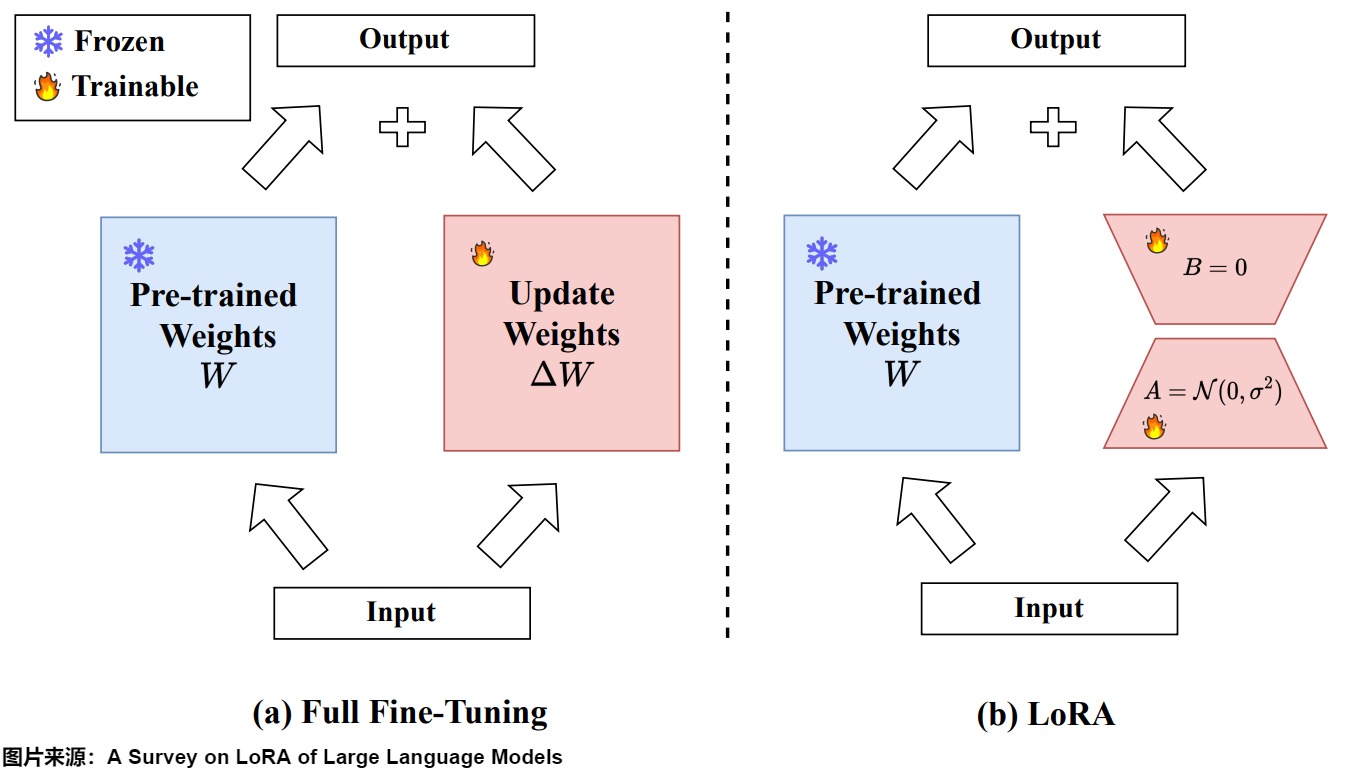
下圖展示了全量微調和LoRA的區別。B和A的維度分別為d×r和r×d,其中r遠小于d,d是原始權重矩陣的維度。因此,微調的參數量從原來的d×d減少到了2×r×d,顯著降低了參數量和計算成本。
2.1.1 訓練
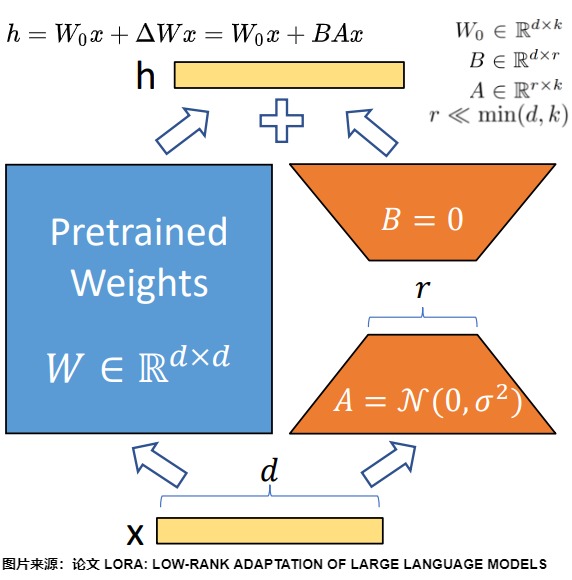
假設要針對某下游任務來微調一個預訓練語言模型。LoRA在原始矩陣的基礎上增加一個旁路矩陣,在此旁路上做降維再升維的操作(通過在已經預訓練的模型權重基礎上添加兩個低秩矩陣的乘積來進行微調)。當針對下游任務時,只更新旁路矩陣的參數。即,LoRA的數學公式核心是:在微調期間將更新矩\(\Delta W\)約束為低秩矩陣。通過將\(\Delta W\)限制為低秩,LoRA最大限度地減少了微調過程中需要學習的參數量,從而提高了計算和存儲效率。具體操作如下:
- 假設模型矩陣為\(W\),由\(W_0 ∈ R^{d \times k}\)參數來初始化。訓練時,原始的預訓練權重保持凍結,在訓練期間不接收梯度更新(即 \(W_0\) 是固定不變的),只計算需要更新的參數權重的變化\(\Delta W\)。
- 把增量矩陣\(\Delta W\)分解為兩個低秩矩陣A和B。用A和B這兩個矩陣的乘法來低秩近似\(\Delta W\)。即\(\Delta W = B \times A\)。
- LoRA采用特定的初始化策略來確保穩定和有效的訓練。通常用隨機高斯分布初始化 A ,用 0 矩陣初始化 B。這意味著訓練開始時\(\Delta W = B \times A = 0\),這樣可以保證初始狀態模型和預訓練一致。
- 只有 A 和 B 是需要更新的訓練參數,會針對特定任務進行調整。訓練時的更新可表示為:\(W_0+ΔW=W_0+BA,W_0∈R^{d×r},B∈R^{d×r},A∈R^{r×k}\)。其中秩$ r?min(d,k)$。
- 在訓練中,每次迭代都會計算\(\Delta W\)。如果每一次迭代中,我們并不直接更新模型的權重\(W\),而是將這些權重的變化累積到一個矩陣\(\Delta W\)中,等待訓練的所有迭代都完成后一次性更新\(W\),我們也可以得到相同的模型。
2.1.2 推理
在推理時,可以原始LLM輸出和可學習的矩陣的輸出相加,得到最終的輸出。即,給定形狀為[H1, H2]的預訓練參數矩陣W,針對某下游任務微調訓練一個形狀為[H1, r]的小矩陣A和形狀為[r, H2]的B。當訓練好 LoRA 模型之后,我們使用\((W_0+BA)\)作為微調模型的權重。
從矩陣角度看,W0 與 ΔW 都會乘以相同的輸入x,相加得到最終結果,模型的輸入輸出維度不變。即,\(y = f(x,W_0 + W_A \times W_B) = f(x, W_0) + f(x,W_A \times W_B)\),對應上圖的\(h=W_0+ΔWx=W_0x+BAx\)。
合并權重
上述推理還是有一定的延遲,如果希望消除推理延遲,則可以把將訓練好的低秩矩陣(B*A)和凍結的原模型權重合并(相加),計算出新的權重,然后使用新的權重進行推理。這么做的原因是LoRA本身可以合并回原模型,推理時可以做到兼容原模型結構。
另外,如何在已有LoRA模型上繼續訓練?其實也是同理。可以把之前的LoRA跟原始模型合并,然后繼續訓練就可以,這樣可以保留之前LoRA帶來的知識和能力。
可插拔性
LoRA還具有可插拔性,即訓練后的LoRA參數可與模型分離。
在面對大量下游任務和微型定制化需求時,因為不同任務之間的干擾可能對訓練過程產生負面影響。所以在參數數量相同的情況下,與其對整個域數據集使用單個 LoRA,不如部署多個較小的 LoRA 模塊,每個模塊專注于特定的下游任務。LoRA的可插拔性讓我們可以凍結分享的模型,通過替換矩陣A與B實現不同下游任務之間的切換。
比如,我們并不使用來\(\Delta W\)更新W,而是將其保存為單獨的模型\(\Delta W\),并在推理階段再進行更新,這樣我們就可以針對不同的任務,來微調模型,形成針對任務的\(\Delta W\)。也就是:
- 針對任務1,有\(\Delta W_1\)
- 針對任務2,有\(\Delta W_2\)
- 針對任務3,有\(\Delta W_3\)
當我們面對預期的某個新任務k 時,假如當前任務是W0+B1A1,我們將LoRA部分B1A1減掉,再加上BkAk,即可實現任務切換,用\(\Delta W_k\)來做任務k的推理。這樣,我們就可以自如地在不同的任務之間快速切換模型。
由于LoRA適配器可以與基礎LLM分開存儲,因此在添加新功能的同時,保留原始能力非常簡單。因此人們會結合兩種方法,通過全微調進行知識更新,隨后使用LoRA進行專業化。
組合性
多個LoRA也可以堆疊一起組合使用,實現組合任務的增強和跨任務泛化,即不同任務可以訓練不同的lora,通過混合它們來實現在不同任務間的知識和技能遷移。當然,堆疊不同的\(\Delta W_k\)需要精心選擇和訓練,隨便堆疊不一定能夠達到預期的效果。比如在文生圖任務中把人物LoRA、風景LoRA和服飾LoRA組合起來一起生成一個照片。
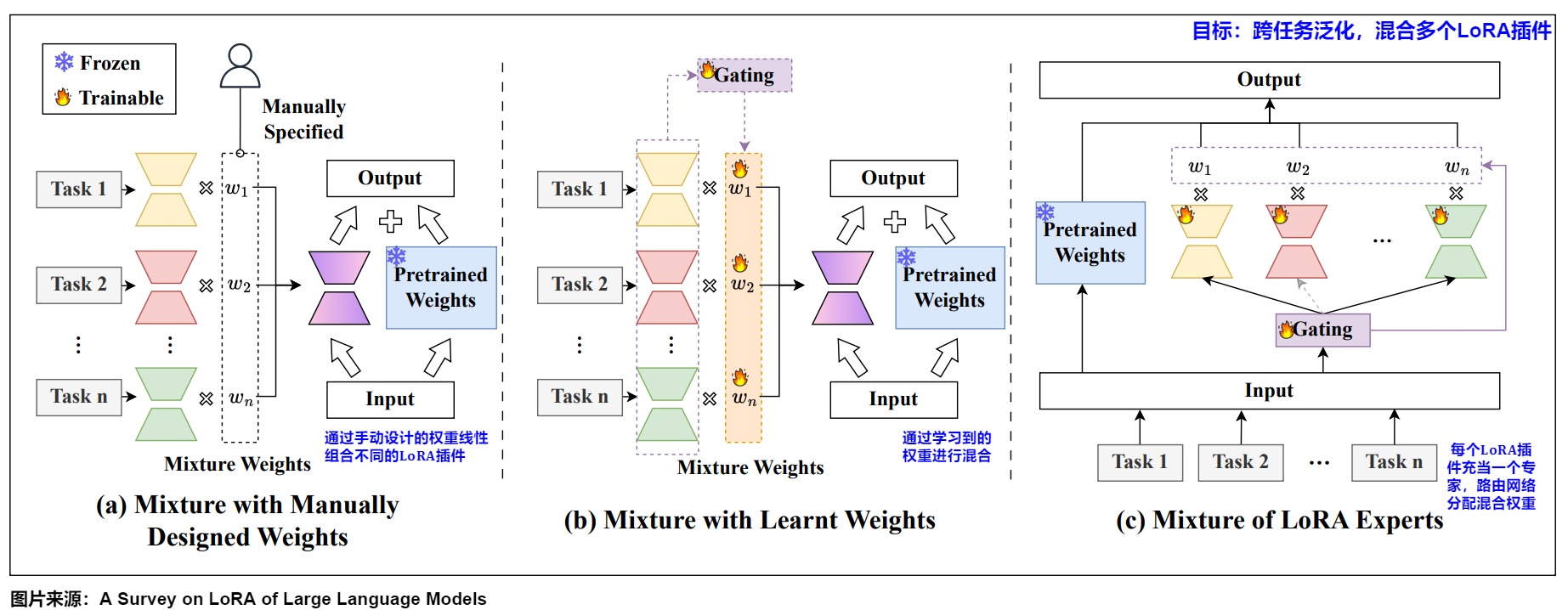
這種將多個LoRA插件混合在一起,叫做LoRA混合,其有多種方案。現有的LoRA混合方法可分為(1)手動設計權重的混合;(2)學習權重的混合;(3)LoRA專家混合。
-
手動設計權重的混合。早期的LoRA混合方法嘗試通過手動設計的權重線性組合不同的LoRA插件。一些研究表明,通過簡單地平均插件或其相關輸出,可以實現適當的跨任務泛化能力。此外,研究人員還提出了幾種方法,通過采用手動設計的權重來進一步提高LoRA混合的性能。比如:
- 線性組合:一些研究嘗試通過簡單的平均或者加權平均的方式來混合不同任務的LoRA插件,其中權重是手動設計的。
- 超參數調整:ControlPE等方法將權重作為超參數,并通過超參數搜索來確定最佳的LoRA插件組合。
- 特征相似度權重:Token-level Adaptation等方法使用輸入特征與適配器數據集中心之間的余弦相似度作為權重。
- 模型融合方法:BYOM等方法應用基本的模型融合技術,如任務算術、Fisher合并和RegMean等。
手動設計權重的混合可以快速混合多個LoRA,無需額外訓練,體現了簡單性和計算效率。然而,它往往無法找到最優權重,導致性能不穩定和泛化能力有限。隨后,研究人員探索使用基于學習的方法來實現更精確和自適應的混合。
-
學習權重的混合。為了學習最優混合權重,研究人員提出了幾種方法,分別在任務級、實例級和token級來滿足不同需求。
- 任務級方法側重于增強任務可遷移性,可以是基于梯度的,或無梯度的。LoRAHub采用了一種名為CMA-ES的黑盒算法來優化LoRA插件的權重因子,簡化了訓練過程。ComPEFT和L-LoRA使用LoRAHub混合量化LoRA插件,進一步提高了計算效率。
- 與任務級方法相比,實例級和token級方法能夠為復雜輸入提供靈活性和精確性。在多模態指令調優方面,MixLoRA根據輸入實例動態選擇適當的低秩分解向量,這些向量隨后被集成到LoRA矩陣中進行訓練。為了進行蛋白質力學分析和設計任務,X-LoRA開發了一種動態門控機制,以在token級別和層粒度上為LoRA插件分配權重。這些方法在特定任務或應用場景中展現出更好的性能。
-
LoRA專家混合體。為了聯合學習混合權重和LoRA插件,LoRA專家混合體(LoRA MoE)是一個自然的選擇,其中每個LoRA插件充當一個專家,而路由網絡通常分配混合權重。
2.2 AB矩陣的作用
研究人員也對A 和 B 矩陣之間的區別做了深入研究,這為提升參數效率和有效性提供了重要見解。
人們觀察到,當多個 LoRA 模塊在不同數據上獨立訓練時,不同頭的矩陣 A 參數趨于一致,而矩陣 B 的參數則明顯可區分。針對這種線性,人們分析如下:
- A矩陣:主要用來降維,從輸入中提取特征,傾向于捕捉跨領域的共性。因此, A 矩陣的參數可以在多個頭部之間共享,從而減少冗余。
- B矩陣:主要用來升維,利用這些特征生成期望的輸出(進行預測),因此更加適應領域特定的差異。不同頭的 B 矩陣參數分散,說明使用單一頭部來適應多個領域的效果可能不如為每個領域使用獨立頭部更為有效,因為這能最大程度地減少領域之間的干擾。
我們要針對矩陣B做進一步說明。研究人員發現,B的重要性遠遠大于A,比如。
- 凍結B會投影掉大部分輸出,而凍結A只會投影掉部分輸入特征空間,這通常影響較小。
- 僅更新B矩陣的性能始終好于僅更新A矩陣。不更新A的參數,只更新B的參數的效果和LoRA差別不大,可以在參數減少一半的情況下提高表現力。
- 隨機初始化并凍結A矩陣,僅更新B矩陣通常能獲得更好的域外(out-of-domain)測試準確率。
這種不對稱性表明,單獨微調B可能比微調A更有效。
論文"Asymmetry in Low-Rank Adapters of Foundation Models"給出了不同LoRA變體的泛化界限( generalization bound)。下圖中分別是更新BA,只更新A,只更新B的泛化界限。其中 r 是秩,q 是量化位,\(\sigma\) 與損失的次高斯性( sub-Gaussianity)相關,n 是樣本大小,\(d^{(i)}_{in},d^{(i)}_{out}\)分別是第 i 層的輸入、輸出維度。可以看到,只更新B與更新A和B兩者相比,該界限更緊,這表明將A凍結為隨機正交矩陣并且僅更新B,可能會潛在地增強對未見過數據的泛化能力。

FLoRA論文則對LoRA中的B矩陣主導了權重的更新提供了證明,具體如下圖。

2.3 部署位置
2.3.1 原始論文
在原始研究中,LoRA被應用于注意力層的權重矩陣。HuggingFace PEFT庫就僅將 LoRA 加到q_proj和v_proj。
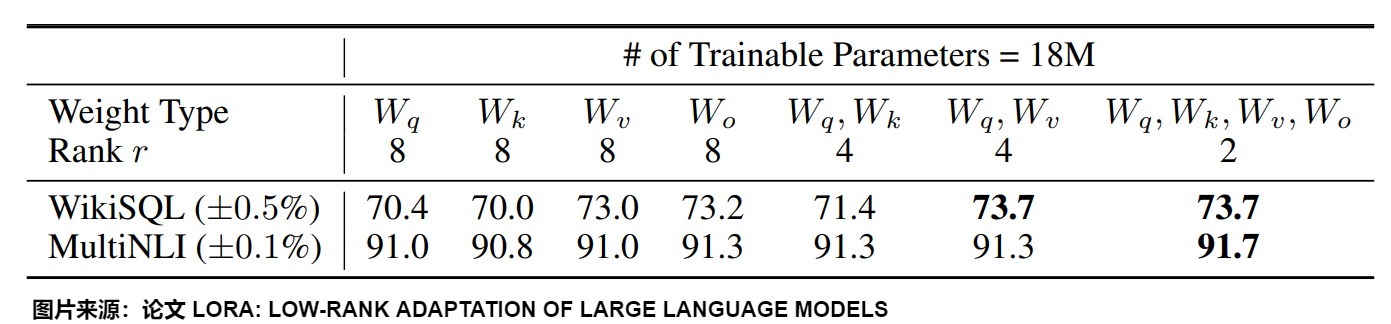
然而,從上圖我們可以看到:
- 將所有參數微調放在\(\Delta W^Q\) 或 \(\Delta W^K\) (或者說,放在注意力機制中的某個矩陣)中會導致性能顯著降低,但同時對 \(\Delta W^Q\) 和 \(\Delta W^V\) 進行調整會得到最佳結果。
- 即使是 r=4 ,也能在\(\Delta W\)訓練中得到足夠的信息。
綜上可知,最好應當將可微調參數分配到多種類型權重矩陣中,而不應該用更大的秩單獨微調某種類型的權重矩陣。
2.3.2 拓展
從原理上說,LoRA 可以集成到 Transformer 層中的任何位置。一些研究,如QLoRA就主張將其包含在所有的密集投影中。

對于基于Transformer的大型語言模型(LLM),密集層通常包含兩種類型的權重矩陣:注意力模塊中的投影矩陣和前饋神經網絡(FFN)模塊中的矩陣。下圖中的藍色就是密集層。在Transformer架構中,Self-Attention中有四個權重矩陣( \(W^Q\) , \(W^K\) , \(W^V\) , \(W^O\) ),而MLP模塊中有兩個權重矩陣。下圖藍色就是這些密集層。因此,可以把LoRA應用到這些密集層上。
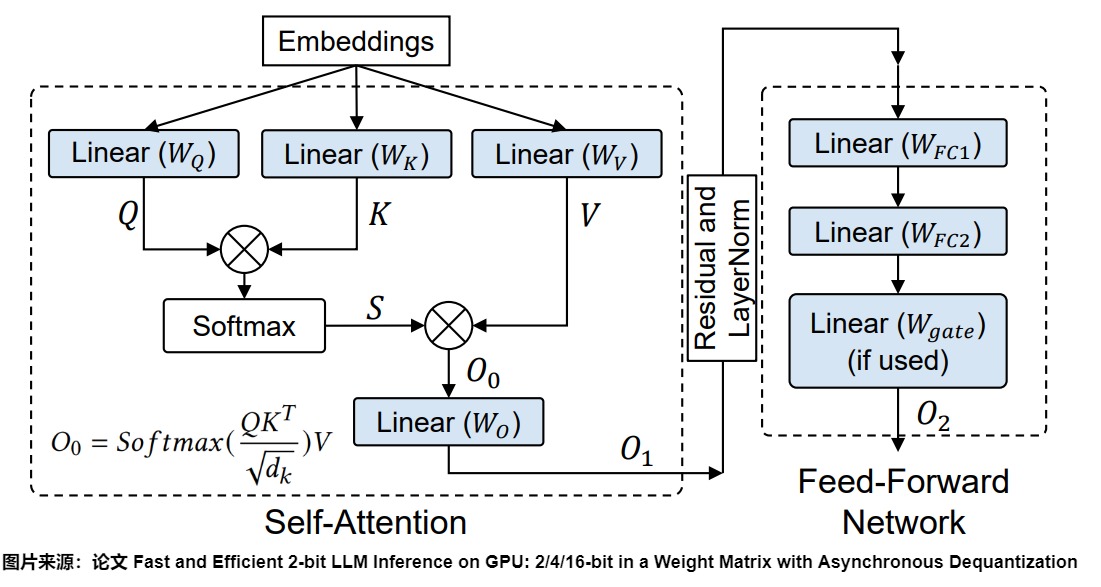
另外,為了解決長上下文導致的計算量和資源占用過大的問題、以及LoRA和全參數微調之間的gap,LongLoRA 在LoRA訓練時,把嵌入層、歸一化層也都打開,參與權重更新。
2.3.3 動態選擇
理論上,LoRA矩陣可以添加到神經網絡的任何一層,但是因為在實際性能與理論最優值之間仍存在差距,所以也有工作在研究是否可以跳過某些層進行訓練。
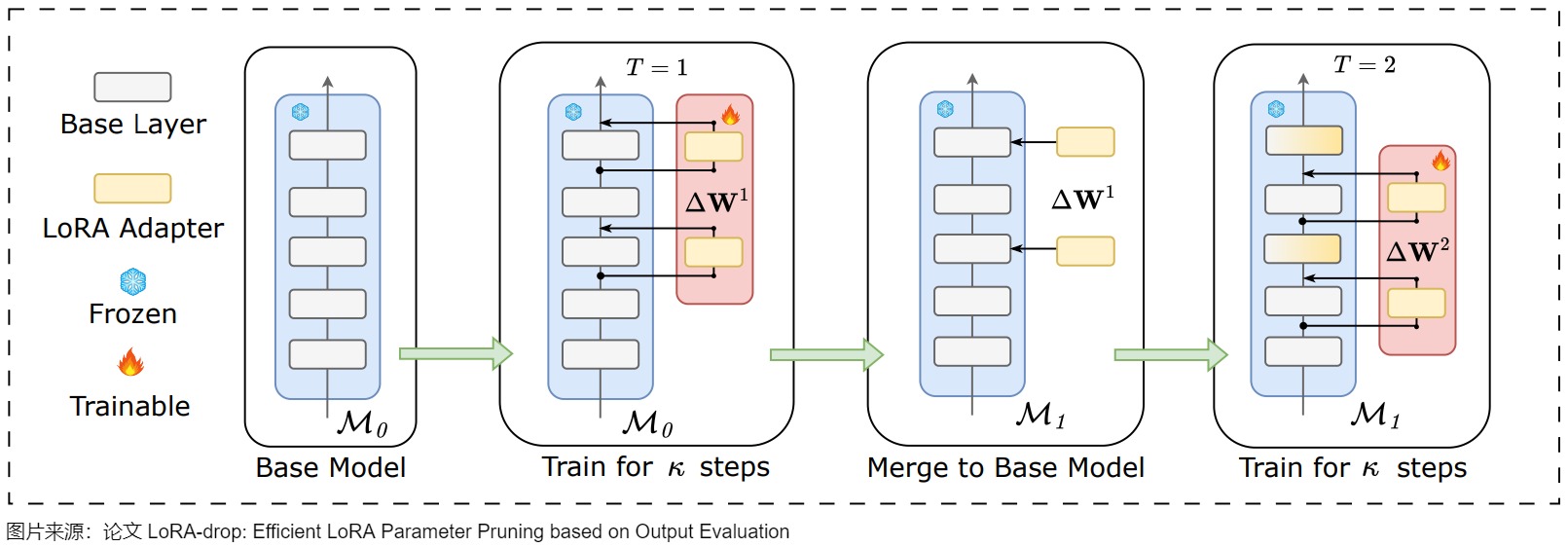
LoRA-drop引入了一種算法來決定哪些層由LoRA微調,哪些層不需要。LoRA-drop算法允許只使用LoRA層的一個子集來訓練模型。根據作者提出的證據表明,與訓練所有的LoRA層相比,準確度只有微小的變化,但由于必須訓練的參數數量較少,因此減少了計算時間。
LoRA-drop的步驟如下:
- 用數據集的一個子集進行采樣訓練,然后計算出每個LoRA適配器的重要性分數。如果分數很大,說明該適配器對模型的影響很大,如果很小,則說明該適配器對模型的影響很小,可以忽略。
- 然后,LoRA-drop會匯總重要性分數,直到達到一個閾值,從中只取最重要的n個固定n的LoRA層。
- 最后,LoRA-drop會在整個數據集上進行完整的訓練,其他層固定為一組共享參數,在訓練期間不會再更改。
XGBLoRA也可以進行隨機層選擇。作者不是對語言模型(LM)的所有層進行修改,而是隨機選擇\(L_s\)層添加LoRA以構建增強器。通過在每次迭代中僅適應一部分層,增強器改變模型的能力受到限制。這種有意的約束讓每個增強器在其預測能力上仍然相對“弱”。但是,這種策略向最終集成模型中注入了隨機性,從而在增強器之間創造了多樣性。每個增強器專注于模型的不同部分,捕獲數據的不同方面。這種多樣性對于集成方法的成功至關重要。
2.4 初始化
在初始化時,通常用隨機高斯分布初始化 A ,用 0 矩陣初始化 B。這意味著訓練開始時\(\Delta W = B \times A = 0\),這樣可以保證初始狀態模型和預訓練一致。
如果B,A全都初始化為0,那么很容易導致梯度消失。 如果B,A全部高斯初始化,那么在網絡訓練剛開始就會有概率為得到一個過大的偏移值Δ W 從而引入太多噪聲,導致難以收斂。 因此,一部分初始為0,一部分正常初始化是為了在訓練開始時維持網絡的原有輸出,但同時也保證在開始學習后能夠更好的收斂。
當然,也有研究人員認為A或B之一使用全零初始化會帶來不對稱問題(一個全零,一個非全零)。因此可以將A和B都使用非全零初始化,只要事先將預訓練權重減去\(A_0B_0\)即可,或者等價地說,將W參數化為\(W = W_0 - A_0B_0 + AB\),這樣即保證了初始狀態一致,也增強了對稱性。
2.5 超參數
2.5.1 秩
LoRA微調中的秩 R 對于理解適應的表現力和保持計算效率至關重要。
- R 越小,則對應的低秩矩陣簡單,LoRA 模型越小,在適應過程中需要學習的參數更少,這可以帶來更快的訓練并可能減少計算要求。然而,隨著 r 的減小,但所能存儲的信息也越少,低秩矩陣捕獲特定任務信息的能力會降低,難以捕捉復雜模式。通常適用于特別狹小領域的任務;
- R 越大,LoRA 模型則更大,能夠存儲的信息越多,更具備表現力,通常適合于更寬泛領域的任務。但會增加計算和內存需求。
通常認為LoRA等微調技術不如正常微調(Finetune)的原因是,LoRA被認為是對Finetune微調的一種低秩近似,通過增加Rank,LoRA可以達到類似Finetune的微調效果。在實踐中,嘗試不同的 r 值以找到適當的平衡以在新任務中實現所需的性能非常重要。通常是根據下游任務和訓練語料的數量來選擇秩 R。
intrinsic rank
如果LoRA 能夠以非常小的 r 得到較好的效果,這表明更新矩陣 \(\Delta W\) 具有非常小的本征秩(intrinsic rank)。或者說,第一個矩陣A負責降維,第二個矩陣B負責升維,中間層維度為r,從而來模擬所謂的本征秩(intrinsic rank)。
下圖給出了在WikiSQL和MultiNLI上,不同不同秩r的驗證準確性。可以發現,在非常小的r下,LoRA已經表現出競爭力(把\(W_q,W_v\)一起調整比僅僅調整\(W_q\)效果更好)。這表明更新矩陣?W可能具有非常小的“內在秩”。LoRA作者認為,增加r并不能覆蓋更有意義的子空間,進而表明低秩自適應矩陣對于微調就已經足夠了。
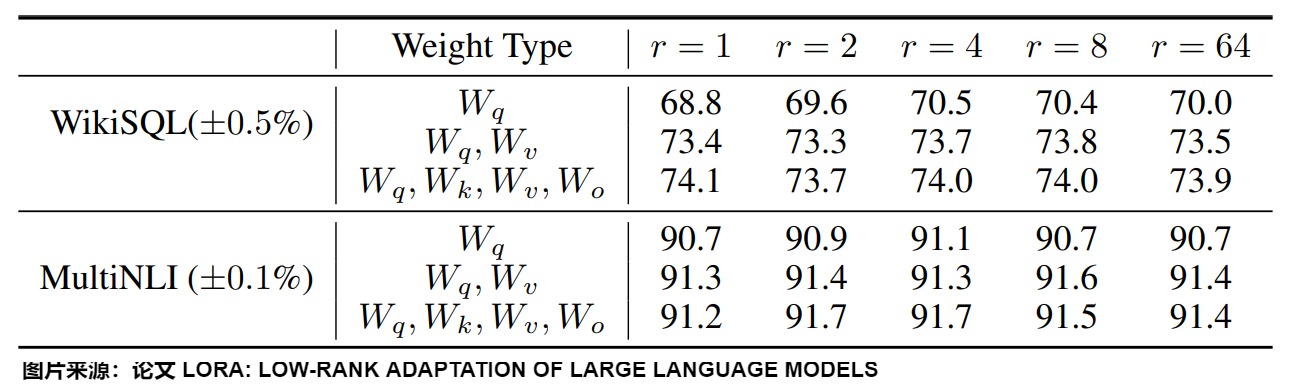
然而,按理來說,任務與預訓練之間的差異越大,所需的 rank 應該越高,因為這意味著可調節的參數也應該越多。
最佳性能
需要多少個秩才能獲得最佳LoRA性能?有些論文對此做了深入的研究。
論文"THE EXPRESSIVE POWER OF LOW-RANK ADAPTATION"指出:
- 對于全連接的神經網絡,如果LoRA秩r滿足以下條件(見下圖藍色),則LoRA可以調整任何預訓練模型 f 以準確地匹配較小的目標模型\(\tilde f\)的功能。
- 對于Transformer網絡,他們證明了只要適應的秩滿足 \(r \ge {embedding\_size} / 2\),則任何模型都可以用LoRA來適配到一個目標模型。

但是,在實踐中,通常使用較小的秩(例如,\(r\in [8,16]\))來權衡性能與效率之間的關系。理論上的最優值與實際使用之間的差異導致了性能差距。為了滿足上述理論要求而增加秩會增加內存使用和計算復雜度,從而抵消了 LoRA 的優勢,使其成本與完全微調策略相當。
論文“LoRA Training in the NTK Regime has No Spurious Local Minima”在神經切線核(NTK)框架內分析了LoRA的微調過程,表明:
-
全量微調(無LoRA)允許秩為 \(r ? \sqrt N\)的低秩解,N是訓練數據點的數目。
-
采用秩 ( \(r ? \sqrt N\) ) 的LoRA有助于避免虛假的局部最小值,并可以促進發現具有良好泛化能力的低秩解。
R的分布
在原始LoRA中,所有矩陣的秩都是相同的。而AdaLoRA則根據重要程度(比如,根據LoRA矩陣的奇異值作為重要程度指標的)來選擇不同矩陣秩的大小。重要的矩陣的秩高一些,次要的矩陣的秩低一些,所以最終的參數總數是相同的。
我們會在后文進行詳解。
2.5.2 學習率
原始 LoRA 方法的適配器矩陣A和B都是以相同的學習率更新。而LoRA+的作者可以證明,因為對于A和B使用相同的學習率并不能有效學習特征,所以,單一學習率會帶來的效果不一定合適。比如在對層數非常多的神經網絡或寬度較大的神經網絡進行微調時,會導致次優結果。原因在于,對A和B的更新對學習動態的貢獻不同。
因此,LoRA+為兩個矩陣A和B引入不同的學習率,即將矩陣B的學習率設置為遠高于矩陣A的學習率,可以使得訓練更加高效。為了有效學習,來自A和B的特征更新的幅度應該是Θ(1)。這就需要對學習率進行縮放,使得\(η_B = Θ(1)\) 和\(η_A =Θ(n^{-1})\),其中n表示模型寬度。在實踐中,LoRA+引入了一個固定的比率\(λ = η_B/η_A > 1\),允許使用者在調整一個學習率的同時自動調整另外一個學習率。

縮放因子 \(\gamma\)
LoRA的輸出會按比例因子\(\gamma_r = \alpha / r\)進行縮放。當使用Adam進行優化時,調整比例因子α大致類似于調整學習速率。實際上,α的值可以根據秩r來設置,這種縮放機制的引入有助于在調整超參數時減少過多的重新調節需求。
然而,當增加適配器秩時,該比例因子會導致梯度崩潰,從而導致學習速度減慢,以及秩較高的適配器性能下降。為了克服這一限制,rsLoRA將比例因子重新定義為$\gamma_r = \alpha /\sqrt r $。這種調整確保了適配器的秩穩定,這意味著即使秩變大,前向和后向通道也能保持穩定的幅度,防止梯度崩潰。
2.5.3 Dropout
盡管基于 LoRA 的模型可訓練參數數量減少,但過擬合仍然是一個問題,特別是在微調小型或專用數據集時。在這種情況下,傳統的dropout技術可能不足以減輕過擬合。
HiddenKey的作者強調了這個問題,并提出了一個全面的框架,通過三個維度來解決此問題:Dropout位置、結構模式和補償措施。Dropout位置指定了引入噪聲的位置,例如在注意力 logits、權重或隱藏表示中。結構模式定義了單元Dropout的粒度,包括元素級、列級或跨度級模式。補償措施旨在通過諸如歸一化重縮放或 Kullback-Leibler 散度損失等技術來最小化訓練和推理階段之間的差異。BiLoRA則采用了一種雙層優化策略。它交替在訓練數據的不同子集上訓練低秩增量矩陣的奇異向量和奇異值。這種方法避免了在單一數據集上同時優化不同層次的參數,從而減輕了過擬合問題。
2.6 優勢
與全量微調相比,LoRA 具有以下關鍵優勢:
- 參數效率(Parameter Efficiency):LoRA 通過低秩分解引入了極少的可訓練參數,通常將特定任務的參數數量減少幾個數量級,在資源受限的環境和需要對基礎模型進行多次適應的多任務場景中,這種方法特別有利。 減少了微調時所需的內存和計算需求,同時沒有增加推理延遲。
- 內存使用減少(Reduced Memory Usage):LoRA顯著降低了微調大型語言模型(LLMs)時的內存使用量。LoRA減少了優化內存和梯度內存的顯著用量,雖然引入了一些額外的“增量參數”,導致激活內存和權重內存略有增加,但考慮到整體內存的減少,這種增加是可以忽略不計的。
- 增強的訓練效率:傳統的全量微調更新所有模型參數,LoRA 僅優化低秩適應矩陣。這種方法大大降低了計算成本和內存需求,尤其是對于具有數十億參數的模型。減少的參數空間通常會導致訓練期間更快的收斂。
- 無延遲推理:LoRA 不會引入額外的推理延遲,因為更新矩陣可以明確地合并到原始凍結權重中。這種集成確保了適應后的模型在部署和推理期間保持高效。 另外,減少內存使用也會帶來前向傳播的加速。
- 靈活的模塊化適應:LoRA 能夠創建輕量級的、特定任務的適配器,這些適配器可以在不修改基礎模型架構的情況下進行互換。與為每個任務維護單獨的模型實例相比,這種模塊化有助于高效的多任務學習和任務切換,同時最小化存儲需求。
- 穩健的知識保留:通過保留預訓練權重,LoRA 有效地減輕了災難性遺忘,這是傳統微調中的一個常見挑戰。這種方法在獲取特定任務能力的同時保持了模型的基礎知識。
- 擴展上下文窗口(Extended Context Window):LoRA也被用于擴展大型語言模型的上下文窗口大小,例如LongLoRA通過結合LoRA和移位稀疏注意力,有效地將LLaMA2-7B的上下文窗口從4k擴展到100k個token。
- 其他應用案例(Beyond Fine-tuning):除了微調之外,LoRA還可以應用于其他學習范式,例如預訓練和持續訓練。在預訓練中,LoRA可以用于訓練高秩網絡;在持續訓練中,LoRA可以解決災難性遺忘問題。
通過這些優勢,LoRA 能夠在保持模型性能的同時有效地適應基礎模型,并顯著降低計算需求。另外,論文“LoRA Learns Less and Forgets Less”比較了低秩適應(LoRA)和全微調在大型語言模型(LLMs)上的表現,重點關注兩個領域(編程和數學)和兩個任務(指令微調和持續預訓練)。該論文發現:
- LoRA學習更少。新任務與模型的預訓練數據的距離越遠,全微調在學習能力方面的優勢越明顯。
- LoRA遺忘更少。在考察喪失之前獲得的知識時,LoRA的遺忘始終較少。這在適應跟源領域數據差異較大時尤為明顯。
總體而言,存在一種權衡:全微調更適合從更遠領域吸收新知識,但會導致對先前學習任務的更多遺忘。LoRA通過改變較少的參數,學習較少的新信息,但保留了更多的原始能力。
0x03 復雜度&資源占用
LoRA因其僅更新模型參數的一小部分子集,在微調過程中減少了內存和計算需求,且不增加推理延遲而具有極高的參數效率。
3.1 計算量分析
理論上計算量分析:LoRA的計算量和全參數微調相當。
| 計算項 | 全參數微調 | LoRA |
|---|---|---|
| 主干模型(前向計算) | √ | √ |
| 主干模型(梯度) | √ | √ |
| LoRA部分(前向+梯度) | × | √ |
3.1.1 訓練
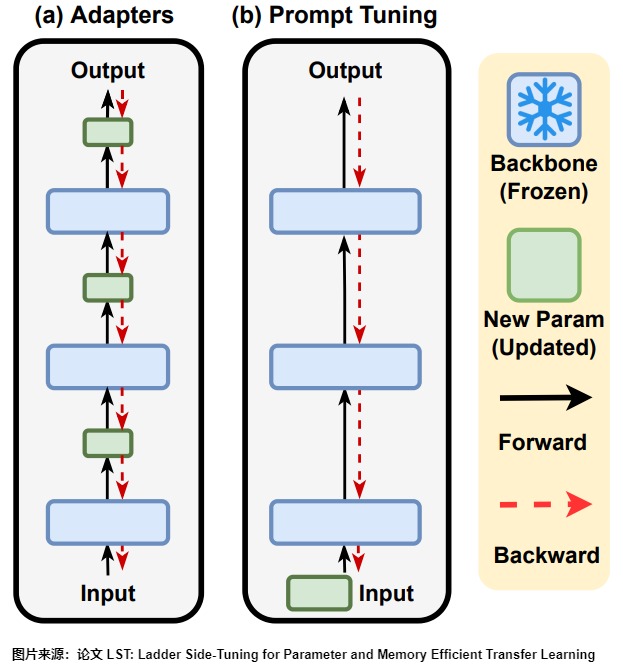
很多參數高效的微調實際上只是降低了顯存需求,并沒有降低計算量。比如 Adapter、P-Tuning等很多參數高效的微調技巧,它們能夠通過只微調很少的參數來達到接近全量參數微調的效果。然而,這些技巧通常只是“參數高效”而并非“訓練高效”,因為它們依舊需要在整個模型中反向傳播來獲得少部分可訓練參數的梯度,說白了,就是可訓練的參數確實是少了很多,但是訓練速度并沒有明顯提升。問題的原因在于反向傳播的特點。反向傳播,也就是求模型梯度,是從輸出層向輸入層逐步計算的,因此反向傳播的深度/計算量,主要取決于最靠近輸入層的可訓練參數的深度,跟可訓練的參數量沒有太必然的聯系。
以下圖為例,對于Adapter來說,它在每一層后面都插入了一個小規模的層,雖然其余參數都固定了,只有新插入的層可訓練,但每一層都存在新模塊,所以反向傳播還是要從輸出層傳到輸入層;對于P-tuning來說,本質上,它是只有在Embedding層中有少量可訓練參數,但Embedding層是輸入層,因此它的反向傳播也要貫穿整個模型。因此,所以,這兩種方案并不能顯著降低計算量。
LoRA 其實也不例外。在 LoRA 的訓練過程中, \({W}_0\) 是固定不變的,只有 A和B是訓練參數。假設模型的損失函數是 \(\mathcal{L}\),那么訓練過程中參數A和B的梯度計算如下所示: \(\frac{\partial \mathcal{L}}{\partial{B}}=\frac{\partial \mathcal{L}}{\partial{W}}{A}^{T},\frac{\partial \mathcal{L}}{\partial{A}}={B}^{T}\frac{\partial \mathcal{L}}{\partial{W}}\)。在訓練過程中,求模型梯度是主要的計算量,如果全參數微調,那么所用的梯度是\(\frac{\partial \mathcal{L}}{\partial {W}}\),而LoRA所用的梯度則是\(\frac{\partial \mathcal{L}}{\partial {B}}\)和\(\frac{\partial \mathcal{L}}{\partial {A}}\),它們是建立在全量更新的梯度\(\frac{\partial \mathcal{L}}{\partial {W}}\)基礎上的,所以理論上LoRA的計算量比全參數微調還大。
但是從實際角度來看,LoRA訓練速度更快。為什么使用LoRA時,實際訓練的速度會變快呢?這主要有以下幾個原因:
- 低精度加速:使用LoRA時,我們可以對主干模型采用各種低精度加速技術,如FP16、FP8或者INT8量化等。這樣可以減少主干模型的前向傳播和反向傳播的耗時。
- 只更新部分參數。在訓練時,原始參數W0被凍結,即雖然W0會參與前向傳播和反向傳播,但不會計算其對應的梯度,更不會更新其參數。這樣,模型在微調過程中主要學習的是低秩矩陣B和A,而不是直接更新原始的權重矩陣W0。比如LoRA原論文就選擇只更新Self Attention的參數,實際使用時我們還可以選擇只更新部分層的參數;
- 使用多卡訓練(數據并行)時,我們只需要同步LoRA模型部分的梯度,這樣可以大大減少卡間通信的壓力,也可以提高總訓練速度。 減少了通信時間:由于更新的參數量變少了,所以(尤其是多卡訓練時)要傳輸的數據量也變少了,從而減少了傳輸時間;
- 此外,減少內存還帶來了前向傳播的加速。
3.1.2 推理
在推理過程中,LoRA 的低秩調整矩陣可以直接與原始模型的權重合并,因此不會帶來額外的推理延遲(No Additional Inference Latency)。這意味著,在推理階段,計算效率與原始模型基本相同。
3.2 內存占用
理論上,LoRA顯存占用比全參數微調更低。其省顯存的本質是,在使用 Adam 優化器時可以避免計算全量權重的一階動量和二階動量(這兩個都必須用 fp32 表示,非常占顯存)。具體參見下圖。
| 顯存占用 | 全參數微調 | LoRA |
|---|---|---|
| 主干模型(模型參數) | √ | √ |
| 主干模型(梯度) | √ | √ |
| 主干模型(中間激活) | √ | √ |
| 主干模型(優化器) | √ | × |
| LoRA部分 | × | √ |
3.2.1 全參數微調
全參數微調是一種需要大量資源的微調方法,它會對模型的所有參數進行優化。這樣做的缺點是,優化器狀態和梯度的內存開銷比模型本身還要大。因此,即使對于參數較少的模型,全參數微調也需要消耗很多計算資源。大型語言模型(LLM)的內存使用,這可以分為四個部分:
- 模型內存(權重內存):存儲模型權重所需的內存;
- 激活內存:前向傳播過程中中間激活所占用的內存,主要取決于批次大小和序列長度等因素;
- 梯度內存:反向傳播過程中存儲梯度所需的內存,梯度僅針對可訓練參數計算;
- 優化器內存:存儲優化器狀態所用的內存。例如,Adam優化器存儲可訓練參數的“第一矩”和“第二矩”。
3.2.2 LoRA
主干模型
- 首先,主干模型的權重都要存儲到顯存中,這部分顯存無法省掉。
- 其次,由于LoRA模型的梯度依賴于主干模型的梯度,所以我們必須計算主干模型的梯度,即使我們不需要優化主干模型。
- 第三,激活也無法省略。
- 最后,由于不需要優化主干模型,所以主干模型對應的優化器不需要存儲,這部分顯存可以節省(像Adam優化器需要維護每個參數的一階動量和二階動量,分別是梯度的指數移動平均值和梯度平方的指數移動平均值)。
分支模型
LoRA 模型的權重、梯度、優化器狀態都需要存儲。
結論
LoRA不需要保存主干模型的優化器狀態,而是引入了額外的增量參數。雖然增量參數會導致激活內存和權重內存略有增加,但是遠小于主干模型的優化器狀態所占據的內存,因此考慮到整體內存的減少,這種增加可以忽略不計。另外,實際使用中,我們可以利用主干模型不需要優化的特點,使用fp16,甚至int8,int4等低精度的數據類型,進一步減少顯存消耗。
0x04 支撐機理 & 分析
LoRA是建立在以下的假設上的。在預訓練階段,模型需要處理多種復雜的任務和數據,因此其權重矩陣通常是高秩的,具有較大的表達能力,以適應各種不同的任務。然而,當模型被微調到某個具體的下游任務時,發現其權重矩陣在這個特定任務上的表現實際上是低秩的。也就是說,盡管模型在預訓練階段是高維的,但在特定任務上,只需要較少的自由度(低秩)就可以很好地完成任務,即微調期間的權重更新通常位于低維子空間。基于這一觀察,LoRA提出在保持預訓練模型的高秩結構不變的情況下,通過添加一個低秩的調整矩陣來適應特定的下游任務。
本節要分析一些內容:比如本征維度和子空間微調,以此來探究LoRA為何有效以及如何使其更有效。
- 本征維度是LoRA的思路來源,也是理解和優化大型模型復雜行為的一個有用工具。
- 子空間微調將所有已知的PEFT方法統一在一個理論下。并從分解理論的角度闡明了每種方法的數學原理。
- 復雜系統的低秩表示理論:創新性地驗證了低秩結構在復雜系統中的普遍存在,為構建大規模復雜網絡的統一降維理論方法,提供了一種可行的思路。
4.1 本征維度
在LoRA論文中提到,其思路是來自兩篇論文提到的本征維度(Intrinsic dimension)。即,常見的預訓練模型表現出異常低的內在維度。換句話說,可以找到一種低維的重新參數化,它對整個參數空間的微調是有效的。

因此我們要研究下本征維度。
4.1.1 定義
本征維度(Intrinsic dimension)是指一個數據集的實際有效維度的數量,即可以用最少的維度(Intrinsic dimension)來表達數據集的大部分信息。這個概念通常用于處理高維數據的降維問題。
在實際應用中,許多數據集看似是高維的,但實際上存在一個低維子空間,其包含了數據的絕大部分信息。一個目標函數的本征維度描述了解決其定義的優化問題所需的最小維度。在本征維度代表的子空間中,人們可以將原始目標函數優化到一定程度的近似誤差內。
通過確定數據集的本征維度,可以有效地降低數據的維度,從而更好地理解和分析數據。確定數據集的本征維度是一個復雜的問題,通常需要使用各種數學方法和算法,如主成分分析(PCA)、獨立成分分析(ICA)、多維縮放(MDS)等。這些方法可以幫助我們找到一個最優的低維表示,以最小化信息丟失,并盡可能保留數據的特征。
4.1.2 模型的本征維度
本征維度是理解和優化大型模型復雜行為的一個有用工具。
在深度學習領域,過參數化(over parameterization)現象指的是模型參數的數量超過了插值訓練數據所需的數量。然而,過參數化的優勢也伴隨著計算成本的顯著增加。即,神經網絡實際上對于它們所做的大多數預測來說都太大了。盡管每次預測都要運行整個網絡,但實際上只有很小一部分模型能夠發揮作用。因此,在處理一個細分的小任務時,是不需要那么復雜的大模型的,可能只需要在模型參數的某個子空間范圍內就可以解決,那么也就不需要對全量參數進行優化了。
而在深度過參數化分解中,每個權重矩陣的學習動態(梯度下降過程GD)只在一個大約不變的低維子空間內發生。因此,需要通過在更少的參數上運行梯度下降來實現與原始全參數分解幾乎相同的端到端軌跡。這一分解允許我們只優化低秩核心 ,而忽略不隨梯度更新變化的正交部分。
現實中我們難以精確找到某個問題所對應的子空間,但是我們可以進行粗略逼近,當對某個子空間參數進行優化時,能夠達到全量參數優化的性能的一定水平(如90%精度)時,那么這個子空間所對應的維度就可以稱為對應當前待解決問題的本征維度。即,本征維度代表了最低維度的子空間,在這個子空間中,人們可以將模型的原始目標函數優化到一定程度的近似誤差內。
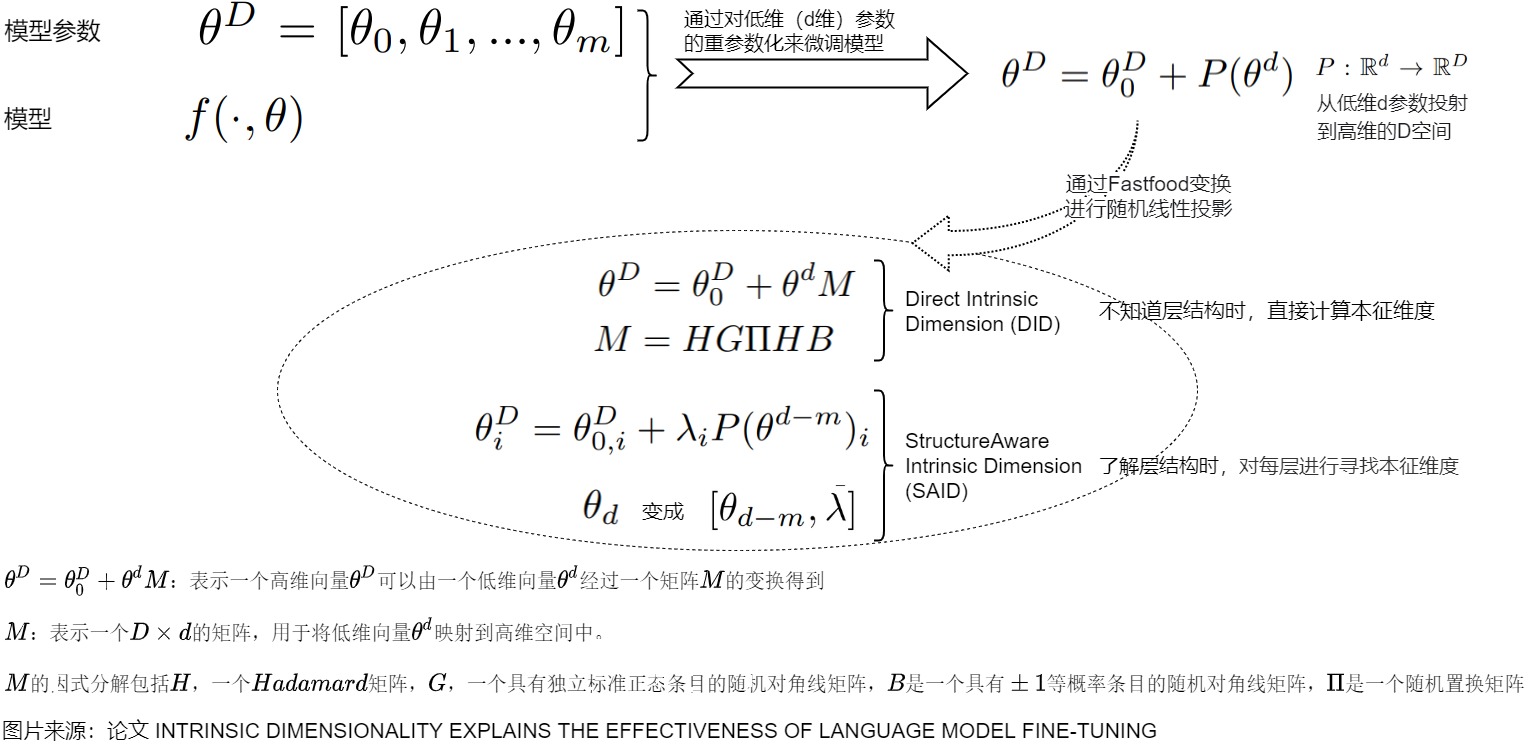
比如,那么對于一個參數量為D的模型 \(\theta^{(D)} \in R^{(D)}\) ,我們訓練該模型,也就意味著在D維空間上尋找有效的解。因為D可能是冗余的,可能實際上只需要優化其中的d個參數就可以找到一個有效的解。即對某個模型\(f(\cdot ,\theta)\)進行參數化,而不是對原始參數\(\theta^{(D)}\)的經驗損失進行優化。用公式表示如下:\(\theta^{(D)} = \theta_0^{(D)} + P\theta^{(d)}\) ,其中
- $\theta_0^{(D)} $是隨機初始化的一個參數并且在訓練時是不進行更新的。
- P是一個隨機初始化的D×d大小的矩陣且訓練時也不進行更新。
- \(\theta^{(d)}\)表示待優化的d維參數。
也就是說,如果在訓練網絡時只更新d維參數,就可以達到該網絡應有的效果。那么這個d就是所謂的該模型的本征維度。計算目標函數的確切本征維度是難以計算的;因此,我們采用啟發式方法來計算一個上界,具體如下:
對于大模型而言,進行本征維度的測試就可以知道在解決某一類下游問題時,需要調整多少參數就能近似的解決當前的問題。從某種角度來看,訓練過程就是在objective landscape中遍歷某個路徑。只要訓練數據集和網絡的架構是確定的,那么該andscape就是完全確定的。landscape被實例化并固定之后,后續的參數初始化、前向、反向、梯度優化都是在該空間中進行探索。
4.1.3 預訓練和本征維度
有研究人員對現有的預訓練方法及其各自的本征維度進行了實證研究,其洞見如下:
- 可以通過本征維數來解釋預訓練模型有效性。可以將預訓練解釋為一個壓縮框架,該壓縮框架會隱含地優化了自然語言任務的平均描述長度(降低了本征維度)。即存在一個低維度的重新參數化(reparameterization),其在低維子空間內的優化效果和對預訓練模型的全參數微調一樣有效。
- 較大的模型往往具有較小的本征維度。從本征維度的角度來說,大模型具有更強的信息壓縮能力,經過一段時間訓練,可以得到更低的本征維度——當模型參數越多的時候,我們需要用來表示一個任務的信息量 越少(因為可以在一個更低維的子空間中進行對應任務的學習)。隨著預訓練的表示參數的增加,本征維度也在減少。而越簡單的下游任務,有著越低的本征維度。在預訓練表征的背景下,常見的NLP任務的本征維度比完整的參數化要小幾個數量級。
- 越低的本征維度,有著越好的泛化性能。泛化不一定必須由預訓練模型的參數數或復雜度來衡量的,也可以被用預訓練模型壓縮下游任務的效果來衡量。在某種意義上,如果我們想更好地壓縮下游任務,我們必須期望預訓練的表征有相當大的復雜度。
4.1.4 LoRA和本征維度
為什么LoRA思路能有效?我們可以從本征維度角度來看。
- 一個目標函數的本征維度衡量的是達到目標的滿意解所需的最小參數的數目。對于大模型來說,就是在降維或者壓縮過程中,為了最大程度的保持數據特征,你最低限度需要保留哪些特征。測量本征維度將告訴我們需要調整多少個自由參數來近似解決優化問題。
- 過度參數化的模型存在一個較低的內在維度。這表明僅通過更新與內在秩相關的參數即可實現適當的學習性能,就能在下游任務上得到很好的效果。
基于上述推導,LoRA才提出使用低秩矩陣更新模型中的密集層,從而實現參數和計算效率的雙重提升。
4.2 子空間微調
論文“See Further for Parameter Efficient Fine-tuning by Standing on the Shoulders of Decomposition”則讓我們可以從子空間角度來分析LoRA。該論文利用分解理論--包括矩陣(分解)和子空間(分解)理論--提出了一種新的框架,稱為子空間微調。該框架將所有已知的PEFT方法統一在一個理論下。并從分解理論的角度闡明了每種方法的數學原理,提供了理解不同PEFT策略內在動態的全面理論基礎。此外,論文也分析了為什么這些方法會導致性能差異。
4.2.1 子空間微調
考慮\(\mathbf{W} \in R^{n \times m}\)作為任何給定主干網絡層的凍結權重矩陣,且\(n \leq m\),在不失一般性的情況下。我們用權重矩陣\(\mathbf{W}\)的性能來量化模型的性能\(P(\mathbf{W})\),其中值越高表示性能越好。對于特定任務,假設存在最優權重矩陣\(\mathbf{W}^*\),我們斷言$P(\mathbf{W}^*) \geq P(\mathbf{\overline W}) \(對于所有\)\forall \mathbf{\overline W} \in R^{n \times m}$。PEFT的目標因此被公式化為
其中\(l\)衡量兩個矩陣之間的差異。在以前的工作中,\(\phi\)函數被概念化為增量調優,表示對矩陣\(\mathbf{W}\)的每個元素的修改。雖然這種表征是準確的,但它過于籠統,無法充分捕捉每種方法的內在邏輯。
從分解理論的角度來看,調整矩陣本質上涉及修改其對應的子空間。子空間微調方法主要集中于調整原始參數的子空間,涉及子空間的重構和擴展。因此,所有PEFT方法都可以視為子空間微調。
4.2.2 分類
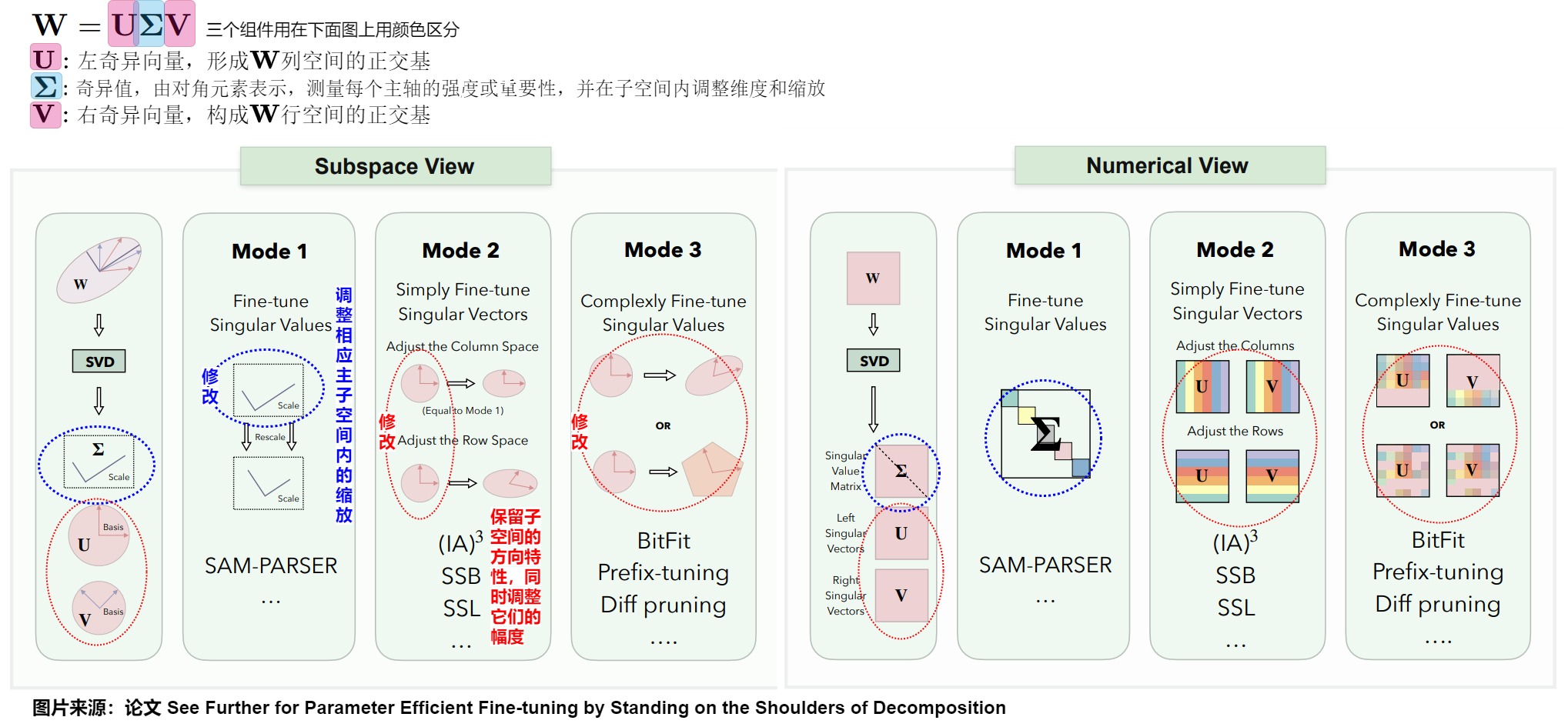
論文建議將\(\phi(\cdot)\)視為一種轉換函數,用于修改與權重矩陣\(\mathbf{W}\)相關的子空間。轉換函數的目標是找到\(\mathbf{W}^*\)在基\(\phi(\mathbf{W})\)所生成的子空間內的最大投影,然后將\(\mathbf{W}\)與其對齊。顯然有兩種方法可以實現這一目標:
- Subspace Reconstruction:直接修改對應\(\mathbf{W}\)的子空間,以更好地對齊\(\mathbf{W}^*\),即通過調整\(\mathbf{W}\)來逼近\(\mathbf{W}^*\)的投影。函數是\(\phi(\mathbf{W}) = f(\mathbf{W})。\)
- Subspace Extension:引入一個新子空間并與原始子空間結合,以此操作\(\phi(\mathbf{W})\)的子空間以接近或包含\(\mathbf{W}^*\)。函數是\(\phi(\mathbf{W}) = g(\mathbf{W})\)。
這些過程可以通過以下公式數學表示:
在這里,\(f(\mathbf{W})\)概括了的子空間重構過程,而\(g(f(\mathbf{W}))\)描述了子空間的聯合。我們將這些操作分別稱為“子空間重構”和“子空間擴展”。因此,我們將現有方法分為以下三類:基于子空間重構、基于子空間擴展和基于子空間組合的方法。
- 子空間重構:將與原始權重矩陣\(\mathbf{W}\)相關的復雜空間分解為更直觀和易于理解的子空間,并調整這些派生子空間的基;
- 子空間擴展:引入一個新的子空間。它們尋求在由新子空間和原始權重矩陣\(\mathbf{W}\)對應的子空間基所生成的空間內找到最優權重\(\mathbf{W}^*\)的最大投影;
- 子空間組合:同時采用子空間的重建和擴展對子空間進行調整。
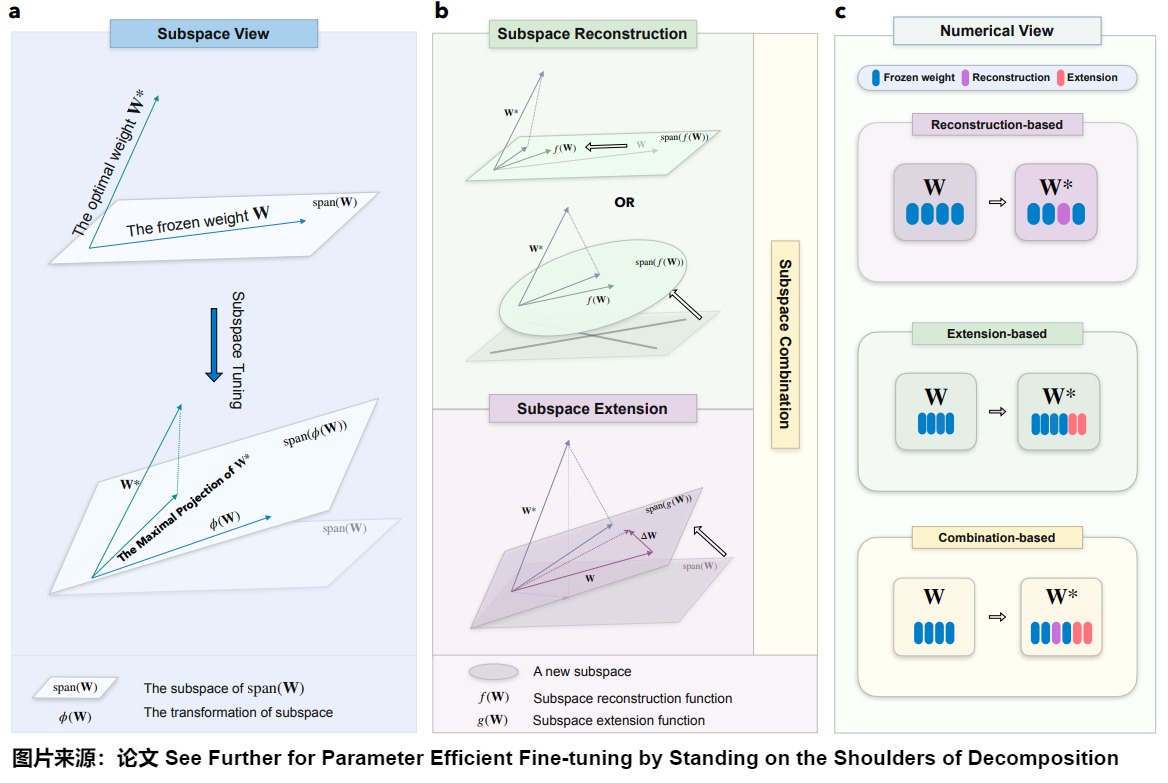
下圖展示了子空間調優的框架。
- a:子空間調優(tuning)致力于識別最優權重W在由?(W)基組成的子空間上的最大投影。這里,?(W)表示原始凍結權重W。
- b:子空間重構。子空間重構涉及將原始權重W的子空間重新縮放來逼近\(\mathbf{W}^*\),或通過構造一個從原始權重導出的新子空間W來逼近\(\mathbf{W}^*\)。子空間擴展涉及調整原始權重W的子空間來逼近或者包括(encompasses)\(\mathbf{W}^*\)。
- c:子空間調優的數值視角。重建涉及修改原始的凍結參數,而擴展則需要添加新的可調參數。
4.2.3 子空間重構
基于先前概述的框架,利用子空間重構的方法首先將的空間分割為可解釋的子空間。這些子空間然后被細化以提高模型效率。即先分解,再優化某些子空間。許多PEFT策略集中于直接重構與原始權重矩陣相關的子空間。著名例子包括SAM-PARSER、Diff Pruning、(IA)3、BitFit、Prefix-tuning和Prompt-tuning等。
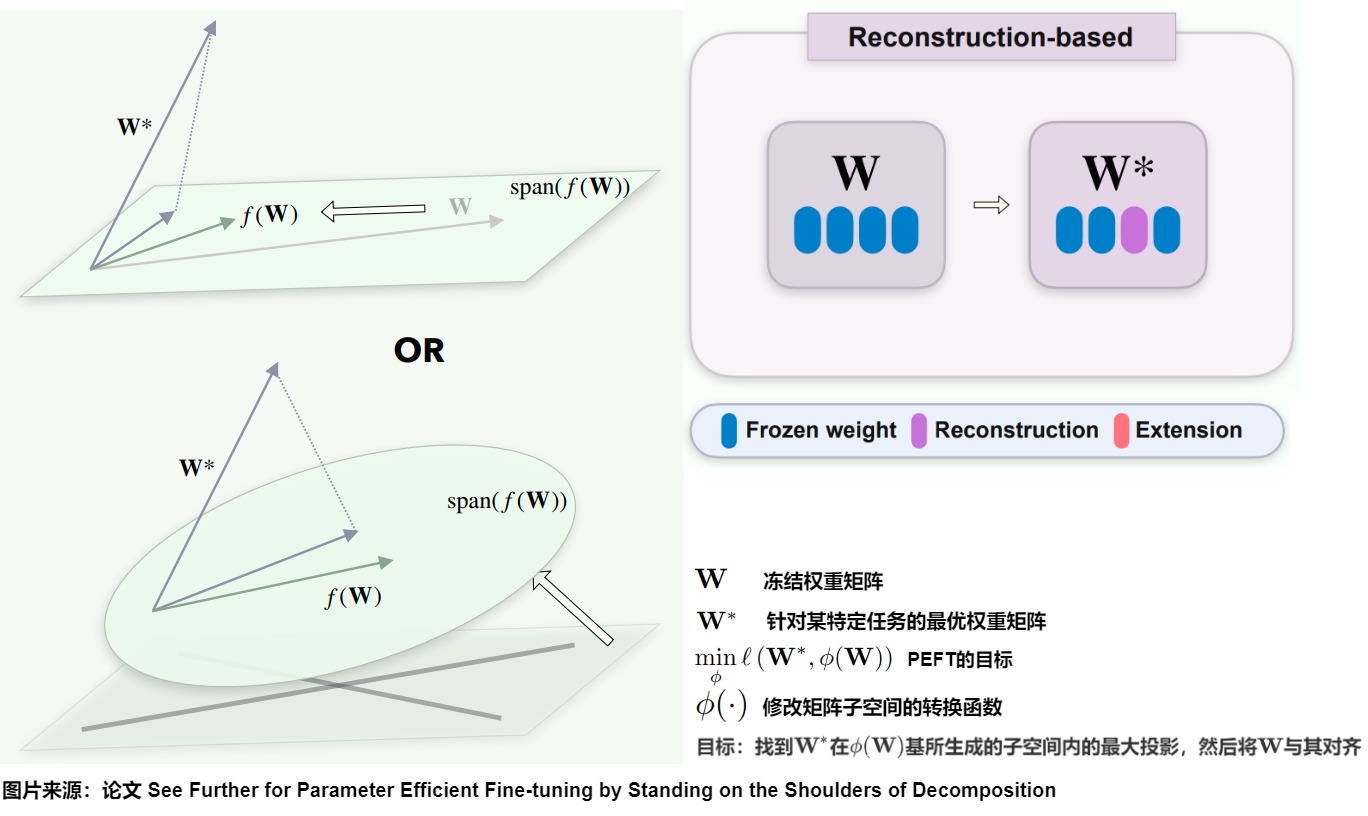
我們從奇異值分解(SVD)開始探索,這種分解系統地將W分成三個主要組件:
- \(\mathbf{U}\):左奇異向量,形成列空間的正交基;
- \(\mathbf{\Sigma}\):奇異值,由對角元素表示,測量每個主軸的強度或重要性,并在子空間內調整維度和縮放;
- \(\mathbf{V}\):右奇異向量,構成行空間的正交基。
SVD闡明了結構所依據的基本子空間,通過巧妙地調整通過分解過程獲得的子空間,可以重構原始空間。這些子空間的細化分為三種不同的模式:
- 模式1,奇異值調整:此模式涉及對中的奇異值進行調整,從而調整相應主子空間內的縮放。改變這些值可以在不影響和定義的子空間方向特性的情況下,修改每個主成分的權重;
- 模式2,簡單奇異向量調整:此模式涉及通過縮放它們生成的子空間來對和中的奇異向量進行簡單調整。它保留了子空間的方向特性,同時調整它們的幅度以提高性能;
- 模式3,復雜奇異向量調整:此模式包含對奇異向量的更復雜的變換,涉及子空間的重新定向或重塑。它同時影響子空間的方向和尺度,促進對矩陣結構的全面調整。
4.2.4 子空間擴展
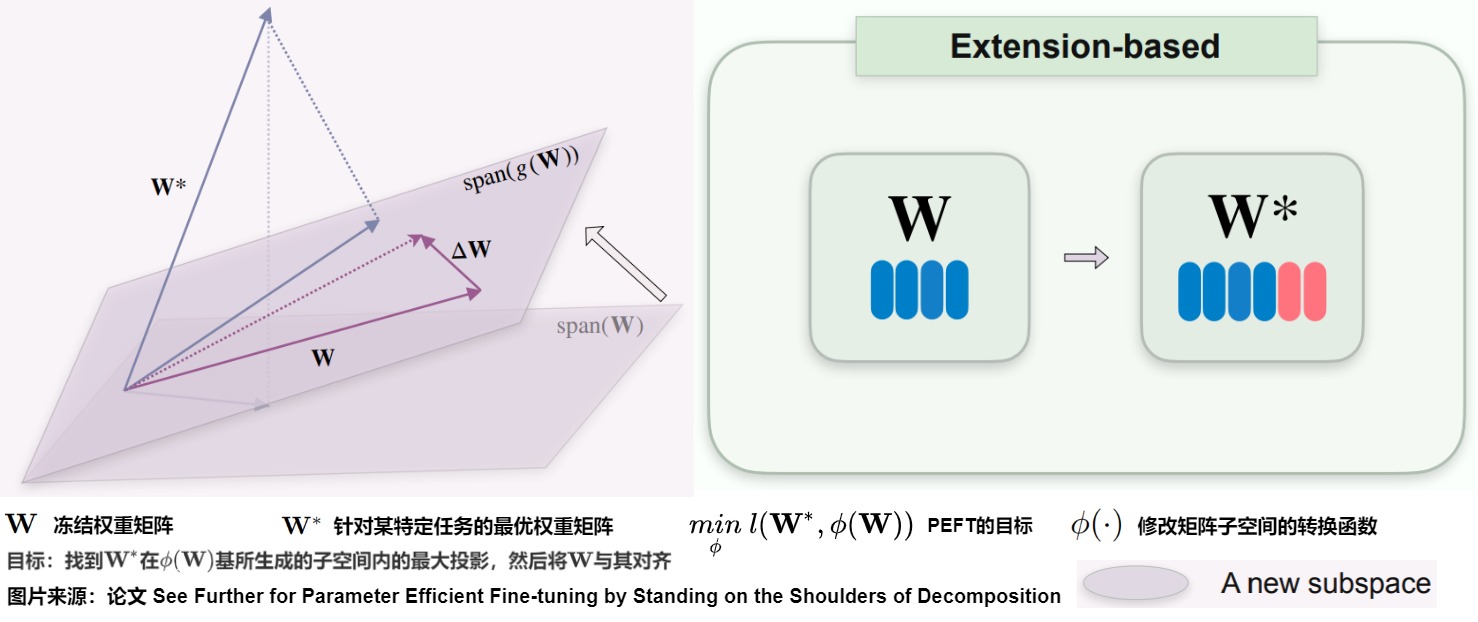
基于擴展的方法引入一個新子空間,結合該新子空間和原始權重矩陣\(\mathbf{W}\)的基來生成一個擴展空間。這些方法旨在找到最優權重\(\mathbf{W}^*\)在此新空間內的最接近投影,實質上是通過引入額外的權重矩陣來擴大原始子空間的基以覆蓋更大的維度區域(如下圖)。通常,這些方法的轉換函數定義為\(\phi(\mathbf{W}) = g(\mathbf{W}) = \mathbf{W} + s \Delta \mathbf{W}\),其中 s 代表縮放因子。這里\(\Delta \mathbf{W}\) 對應于引入的新子空間,也稱為附加項。
考慮權重矩陣\(\mathbf{W} \in R^{n \times m}\) ,在不失一般性的情況下假設\(n \leq m\)。理想情況下,我們有\(\phi(\mathbf{W}) = \mathbf{W}^*\)。這種設置意味著\(\mathbf{W} + s \Delta \mathbf{W}\)和\(\mathbf{W}^*\)占據相同的行和列空間,將它們定位在同一超平面內。如果\(\mathbf{W}\)秩為n,其列空間的維度也等于n,使其能夠生成子空間\(R^n\)。由于我們不知道\(\mathbf{W}^*\)列空間的基,一個保守的假設是\(\Delta \mathbf{W}\)和\(\mathbf{W}\)的列空間基可以生成整個空間。在最優情況下,\(\Delta \mathbf{W}\)的列基向量應理想地補充\(\mathbf{W}\)的列基。因為\(\mathbf{W}^*\)可能與\(\mathbf{W}\)的子空間共享大量共同基。因此,\(\Delta \mathbf{W}\)可能只需要考慮\(\mathbf{W}\)中缺少的,但\(\mathbf{W}^*\)中存在的一小部分基,從而使\(\Delta \mathbf{W}\)成為一個低秩矩陣。
對于基于擴展的方法,我們的目標是確定\(\mathbf{W}^*\)在由\(\mathbf{W}\)和\(\Delta \mathbf{W}\)形成的超平面內的最大投影,確保\(\mathbf{W} + s \Delta \mathbf{W}\)盡可能與\(\mathbf{W}^*\)對齊。給定固定的\(\mathbf{W}\)和\(\Delta \mathbf{W}\),只有一個縮放因子s值會使的\(\mathbf{W} + s \Delta \mathbf{W}\)方向與\(\mathbf{W}^*\)的方向對齊。因此,值對性能的影響可能非常顯著或甚至關鍵。
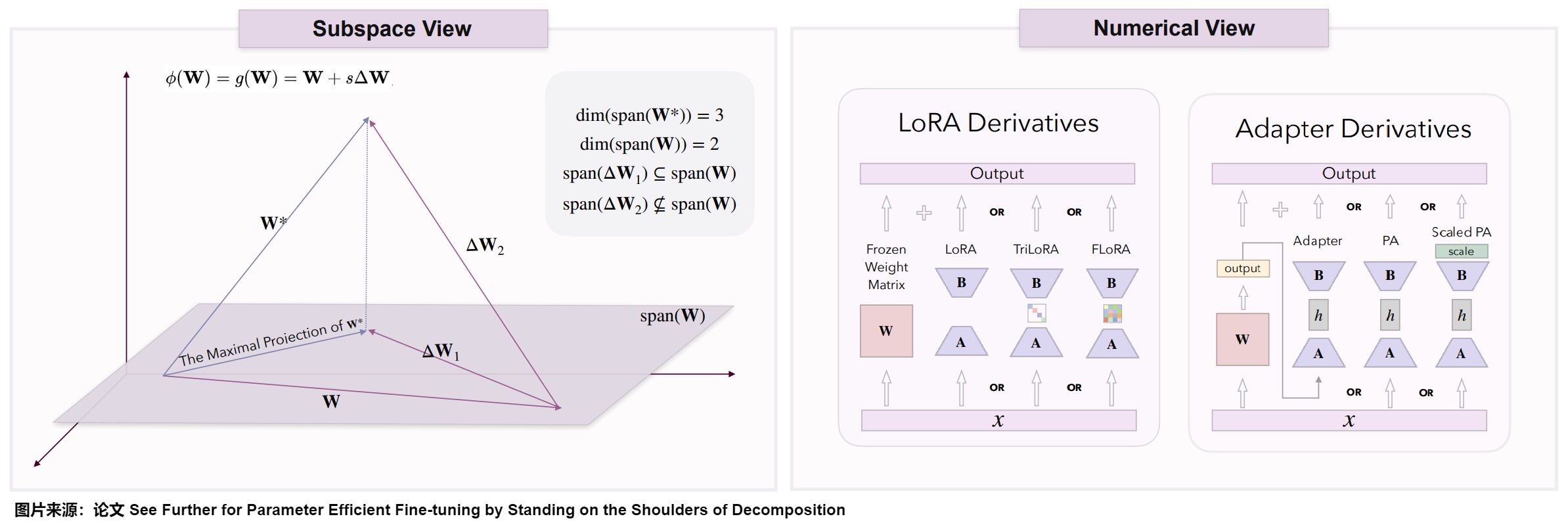
在參數高效微調中,有兩大系列基于擴展的方法。第一個系列是LoRA及其衍生方案,包括LoRA、AdaLoRA、TriLoRA、FLoRA、VeRA和LoTR。這些方法主要依賴于低秩矩陣分解技術。第二個系列是適配器衍生,這些方法在現有架構中引入了小規模神經模塊或適配器。具體參見下圖。
下圖是基于擴展方法的子空間和數值視圖。基于擴展的方法引入了一個額外的權重矩陣,然后試圖在這個額外的權重和原始權重所跨越的子空間內找到最優的權重投影。為了實現這一點,由附加矩陣構建的子空間的基應盡可能地補充原始權重的基。圖右側列出了一些常見的基于擴展的方法及其對矩陣的操作。
4.2.5 子空間組合
子空間組合同時執行子空間重構和擴展,結合了這兩種方法的原理。此外,對于某些方法,它們既可以分類為基于重構的方法,也可以分類為基于擴展的方法,我們也將它們分類為基于組合的方法。幾種代表性的基于組合的方法為:DoRA,Spectral Adapter和SVDiff。
4.3 復雜系統的低秩表示理論
復雜系統是高維非線性的動力系統,其組成成分之間存在異質相互作用。為了對復雜系統的大規模行為做出可解釋的預測,復雜系統通常被假設可以簡化為涉及低秩矩陣的少量方程。
論文"The low-rank hypothesis of complex systems"探討了低秩假設(low-rank hypothesis)的有效性,證實許多復雜系統可以被簡化,并且仍然保留初始高維網絡的基本特征。從這個角度來看,降維技術基于一個隱含的假設,即高維復雜系統的動力學取決于低秩矩陣的行為。
下圖中:
- 黑腹果蠅的半腦是復雜系統的一個例子。
- b 表示黑腹果蠅連接體的復雜網絡圖,其中為了可視化,從21733個頂點中隨機擇了5%進行展示。
- c 表示秩為r的實數矩陣的奇異值分解。截斷的(truncated )SVD是矩陣的最佳低秩近似。

4.4 Neural Tangent Kernel (NTK)
論文“A kernelbased view of language model fine-tuning”從NTK角度對LoRA作用進行了研究。論文發現,LoRA在微調過程中近似保留了原始模型的內核。具體參見下圖。

雖然LoRA將更新限制在低秩子空間中,但是它有效地關注到了對網絡行為變化影響最大的梯度。通過關注這些臨界梯度,LoRA保留了模型的泛化能力,確保網絡對基本輸入變化保持敏感,同時具有高度的參數效率。具體如下圖所示。
4.5 對模型的改變
論文“The impact of lora on the emergence of clusters in transformers”分析了注意力矩陣的動態特性,證明LoRA引入的低秩修改在token聚類中保持了短期穩定性,同時促進了學習到的表征的顯著長期差異。
引入LoRA之后,對注意力動態行為改變如下。

通過讓在加入擾動的token和未加入擾動的token之間的Wasserstein distance(Wasserstein距離)保持有界,LoRA可以維持token聚類的短期穩定性。
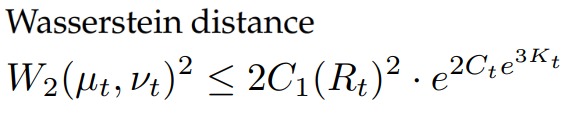
一個關鍵的結果是識別相變,在相變中,tokn在臨界時間\(T^*(δ)\)之后分叉成新的聚類,該臨界時間由value矩陣的特征值間隙(eigenvalue gap)λ1-|λ2|所控制。這顯示了LoRA如何在沒有災難性遺忘的情況下微調模型,在訓練早期保留token結構,同時允許受控發散。
0x05 實現
我們使用HuggingFace PEFT 代碼來進行學習。
5.1 使用
通過指定配置,我們可以使用LoRA。
model = prepare_model_for_kbit_training(model)
config = LoraConfig(
r=16,
lora_alpha=32,
target_modules=["q_proj", "v_proj"],
lora_dropout=0.05,
bias="none",
task_type="CAUSAL_LM",
)
model = get_peft_model(model, config)
5.2 創建
5.2.1 LoraModel
LoRA微調方法對應LoraModel類,我們跳過一些代碼,直接通過PEFT_TYPE_TO_MODEL_MAPPING找到LoraModel。
PEFT_TYPE_TO_MODEL_MAPPING = {
PeftType.LORA: LoraModel,
PeftType.LOHA: LoHaModel,
PeftType.LOKR: LoKrModel,
PeftType.PROMPT_TUNING: PromptEmbedding,
PeftType.P_TUNING: PromptEncoder,
PeftType.PREFIX_TUNING: PrefixEncoder,
PeftType.ADALORA: AdaLoraModel,
PeftType.BOFT: BOFTModel,
PeftType.ADAPTION_PROMPT: AdaptionPromptModel,
PeftType.IA3: IA3Model,
PeftType.OFT: OFTModel,
PeftType.POLY: PolyModel,
PeftType.LN_TUNING: LNTuningModel,
PeftType.VERA: VeraModel,
PeftType.FOURIERFT: FourierFTModel,
PeftType.XLORA: XLoraModel,
PeftType.HRA: HRAModel,
PeftType.VBLORA: VBLoRAModel,
PeftType.CPT: CPTEmbedding,
PeftType.BONE: BoneModel,
}
因為LoraModel的基類是BaseTuner,所以我們要看看BaseTuner。
class LoraModel(BaseTuner):
"""
Creates Low Rank Adapter (LoRA) model from a pretrained transformers model.
The method is described in detail in https://arxiv.org/abs/2106.09685.
"""
5.2.2 BaseTuner
基類BaseTuner,里面最主要的是兩個函數:
- inject_adapter()函數。
inject_adapter()函數首先把模型每一層的名字存儲在key_list中,然后通過遍歷key_list獲取當前層的父模塊類,層名,層名對應的模塊類。 _create_and_replace()函數。_create_and_replace()函數是一個抽象函數,具體實現還是在LoraModel類中。
class BaseTuner(nn.Module, ABC):
r"""
A base tuner model that provides the common methods and attributes for all tuners that are injectable into a torch.nn.Module
"""
def __init__(
self,
model,
peft_config: Union[PeftConfig, dict[str, PeftConfig]],
adapter_name: str,
low_cpu_mem_usage: bool = False,
) -> None:
super().__init__()
self.model = model
self.targeted_module_names: list[str] = []
self.active_adapter: str | list[str] = adapter_name
self._pre_injection_hook(self.model, self.peft_config[adapter_name], adapter_name)
if peft_config != PeftType.XLORA or peft_config[adapter_name] != PeftType.XLORA:
self.inject_adapter(self.model, adapter_name, low_cpu_mem_usage=low_cpu_mem_usage)
# Copy the peft_config in the injected model.
self.model.peft_config = self.peft_config
_create_and_replace()函數在獲取了LoRA微調的關鍵參數r和alpha后,使用_create_new_module()函數創建新的模型架構。
def _create_and_replace(
self,
lora_config,
adapter_name,
target,
target_name,
parent,
current_key,
):
# Regexp 匹配 - 在提供的模式中查找與當前目標名稱匹配的鍵值
# Regexp matching - Find key which matches current target_name in patterns provided
r_key = get_pattern_key(lora_config.rank_pattern.keys(), current_key)
alpha_key = get_pattern_key(lora_config.alpha_pattern.keys(), current_key)
# 獲取r和alpha參數
r = lora_config.rank_pattern.get(r_key, lora_config.r)
alpha = lora_config.alpha_pattern.get(alpha_key, lora_config.lora_alpha)
kwargs = {
"r": r,
"lora_alpha": alpha,
"lora_dropout": lora_config.lora_dropout,
"fan_in_fan_out": lora_config.fan_in_fan_out,
"init_lora_weights": lora_config.init_lora_weights,
"use_rslora": lora_config.use_rslora,
"use_dora": lora_config.use_dora,
"ephemeral_gpu_offload": lora_config.runtime_config.ephemeral_gpu_offload,
"lora_bias": lora_config.lora_bias,
"loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
"loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
}
# note: AdaLoraLayer is a subclass of LoraLayer, we need to exclude it
from peft.tuners.adalora import AdaLoraLayer
if isinstance(target, LoraLayer) and not isinstance(target, AdaLoraLayer):
# 如果屬于LoraLayer或Adaloralayer,則進行更新
target.update_layer(
adapter_name,
r,
lora_alpha=alpha,
lora_dropout=lora_config.lora_dropout,
init_lora_weights=lora_config.init_lora_weights,
use_rslora=lora_config.use_rslora,
use_dora=lora_config.use_dora,
lora_bias=lora_config.lora_bias,
)
else:
# 根據LoRA關鍵參數創建新的模型
new_module = self._create_new_module(lora_config, adapter_name, target, **kwargs)
if adapter_name not in self.active_adapters:
# adding an additional adapter: it is not automatically trainable
new_module.requires_grad_(False)
self._replace_module(parent, target_name, new_module, target)
5.2.3 LoraModel的創建
_create_new_module()函數會調用分發函數進行處理,我們進入dispatch_default()函數看看究竟。
@staticmethod
def _create_new_module(lora_config, adapter_name, target, **kwargs):
# Collect dispatcher functions to decide what backend to use for the replaced LoRA layer. The order matters,
# because the first match is always used. Therefore, the default layers should be checked last.
dispatchers = []
if lora_config._custom_modules:
def dynamic_dispatch_func(target, adapter_name, lora_config, **kwargs):
new_module = None
if isinstance(target, BaseTunerLayer):
target_base_layer = target.get_base_layer()
else:
target_base_layer = target
for key, custom_cls in lora_config._custom_modules.items():
if isinstance(target_base_layer, key):
new_module = custom_cls(target, adapter_name, **kwargs)
break
return new_module
dispatchers.append(dynamic_dispatch_func)
dispatchers.extend(
[
dispatch_eetq,
dispatch_aqlm,
dispatch_awq,
dispatch_gptq,
dispatch_hqq,
dispatch_torchao,
dispatch_megatron,
dispatch_default,
]
)
new_module = None
for dispatcher in dispatchers:
new_module = dispatcher(target, adapter_name, lora_config=lora_config, **kwargs)
if new_module is not None: # first match wins
break
return new_module
從dispatch_default()函數可以看到,LoRA微調方法主要是針對Embedding、Conv1D、Conv2D、Linear層。
def dispatch_default(
target: torch.nn.Module,
adapter_name: str,
lora_config: LoraConfig,
**kwargs,
) -> Optional[torch.nn.Module]:
new_module = None
if isinstance(target, BaseTunerLayer):
target_base_layer = target.get_base_layer()
else:
target_base_layer = target
# 更新Embedding層
if isinstance(target_base_layer, torch.nn.Embedding):
embedding_kwargs = kwargs.copy()
embedding_kwargs.pop("fan_in_fan_out", None)
embedding_kwargs.update(lora_config.loftq_config)
new_module = Embedding(target, adapter_name, **embedding_kwargs)
# 更新Conv2d層
elif isinstance(target_base_layer, torch.nn.Conv2d):
kwargs.update(lora_config.loftq_config)
new_module = Conv2d(target, adapter_name, **kwargs)
# 更新Conv3d層
elif isinstance(target_base_layer, torch.nn.Conv3d):
kwargs.update(lora_config.loftq_config)
new_module = Conv3d(target, adapter_name, **kwargs)
# 更新Linear層
elif isinstance(target_base_layer, torch.nn.Linear):
kwargs.update(lora_config.loftq_config)
new_module = Linear(target, adapter_name, **kwargs)
# 更新Conv1D層
elif isinstance(target_base_layer, Conv1D):
kwargs.update(lora_config.loftq_config)
new_module = Linear(target, adapter_name, is_target_conv_1d_layer=True, **kwargs)
return new_module
5.3 調整具體模塊
我們以Linear為例進行講解。Linear類集成了nn.Module和LoreLayer類。
5.3.1 Linear
class Linear(nn.Module, LoraLayer):
# Lora implemented in a dense layer
def __init__(
self,
base_layer,
adapter_name: str,
r: int = 0,
lora_alpha: int = 1,
lora_dropout: float = 0.0,
fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
is_target_conv_1d_layer: bool = False,
init_lora_weights: Union[bool, str] = True,
use_rslora: bool = False,
use_dora: bool = False,
lora_bias: bool = False,
**kwargs,
) -> None:
super().__init__()
LoraLayer.__init__(self, base_layer, **kwargs)
self.fan_in_fan_out = fan_in_fan_out
self._active_adapter = adapter_name
self.update_layer(
adapter_name,
r,
lora_alpha=lora_alpha,
lora_dropout=lora_dropout,
init_lora_weights=init_lora_weights,
use_rslora=use_rslora,
use_dora=use_dora,
lora_bias=lora_bias,
)
self.is_target_conv_1d_layer = is_target_conv_1d_layer
LoraLayer類的初始化方法關鍵行為在于獲取可調節層(Embedding、Conv1D、Conv2D、Linear)的輸入輸出維度,方便構造新的層。
5.3.2 LoraLayer
LoraLayer類會獲取可調節層(Embedding、Conv1D、Conv2D、Linear)的輸入輸出維度,方便構造新的層。LoraLayer有如下重要函數:
- update_layer() 會作如下操作:讀取
LoRA關鍵參數r、alpha;根據Dropout參數判斷是否加入Dropout層;創建lora_A、lora_B線性層,并進行初始化; - reset_lora_parameters()函數會初始化
lora_A。 set_adapter()方法會設置可訓練參數。
class LoraLayer(BaseTunerLayer):
# All names of layers that may contain (trainable) adapter weights
adapter_layer_names = ("lora_A", "lora_B", "lora_embedding_A", "lora_embedding_B")
# All names of other parameters that may contain adapter-related parameters
other_param_names = ("r", "lora_alpha", "scaling", "lora_dropout")
def __init__(self, base_layer: nn.Module, ephemeral_gpu_offload: bool = False, **kwargs) -> None:
self.base_layer = base_layer
self.r = {}
self.lora_alpha = {}
self.scaling = {}
self.lora_dropout = nn.ModuleDict({})
self.lora_A = nn.ModuleDict({})
self.lora_B = nn.ModuleDict({})
# For Embedding layer
self.lora_embedding_A = nn.ParameterDict({})
self.lora_embedding_B = nn.ParameterDict({})
# Mark the weight as unmerged
self._disable_adapters = False
self.merged_adapters = []
self.use_dora: dict[str, bool] = {}
self.lora_bias: dict[str, bool] = {}
self.lora_magnitude_vector = torch.nn.ModuleDict() # for DoRA
self._caches: dict[str, Any] = {}
self.ephemeral_gpu_offload: bool = ephemeral_gpu_offload
self.kwargs = kwargs
base_layer = self.get_base_layer()
if isinstance(base_layer, nn.Linear):
in_features, out_features = base_layer.in_features, base_layer.out_features
elif isinstance(base_layer, nn.Conv2d):
in_features, out_features = base_layer.in_channels, base_layer.out_channels
elif isinstance(base_layer, nn.Conv3d):
in_features, out_features = base_layer.in_channels, base_layer.out_channels
elif isinstance(base_layer, nn.Embedding):
in_features, out_features = base_layer.num_embeddings, base_layer.embedding_dim
elif isinstance(base_layer, Conv1D):
in_features, out_features = (
base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
)
# 省略其它部分
self.in_features = in_features
self.out_features = out_features
def update_layer(
self,
adapter_name,
r,
lora_alpha,
lora_dropout,
init_lora_weights,
use_rslora,
use_dora: bool = False,
lora_bias: bool = False,
):
# This code works for linear layers, override for other layer types
# 讀取r、alpha參數
self.r[adapter_name] = r
self.lora_alpha[adapter_name] = lora_alpha
# 如果存在dropout參數則加入Dropout層
if lora_dropout > 0.0:
lora_dropout_layer = nn.Dropout(p=lora_dropout)
else:
lora_dropout_layer = nn.Identity()
# 在lora_dropout中加入lora_dropout_layer
self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
# Actual trainable parameters
# 實際可訓練參數,矩陣A,B
self.lora_A[adapter_name] = nn.Linear(self.in_features, r, bias=False)
self.lora_B[adapter_name] = nn.Linear(r, self.out_features, bias=lora_bias)
self.lora_bias[adapter_name] = lora_bias
if use_rslora:
self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
else:
self.scaling[adapter_name] = lora_alpha / r
# for inits that require access to the base weight, use gather_param_ctx so that the weight is gathered when using DeepSpeed
if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
with gather_params_ctx(self.get_base_layer().weight):
self.pissa_init(adapter_name, init_lora_weights)
elif isinstance(init_lora_weights, str) and init_lora_weights.lower() == "olora":
with gather_params_ctx(self.get_base_layer().weight):
self.olora_init(adapter_name)
elif init_lora_weights == "loftq":
with gather_params_ctx(self.get_base_layer().weight):
self.loftq_init(adapter_name)
elif init_lora_weights == "eva":
nn.init.zeros_(self.lora_B[adapter_name].weight)
elif init_lora_weights:
self.reset_lora_parameters(adapter_name, init_lora_weights)
# call this before dora_init
self._move_adapter_to_device_of_base_layer(adapter_name)
if use_dora:
self.dora_init(adapter_name)
self.use_dora[adapter_name] = True
else:
self.use_dora[adapter_name] = False
# 設置可訓練參數
self.set_adapter(self.active_adapters)
def reset_lora_parameters(self, adapter_name, init_lora_weights):
if adapter_name in self.lora_A.keys():
# 若init_lora_weights為true則使用kaiming初始化
if init_lora_weights is True:
# initialize A the same way as the default for nn.Linear and B to zero
nn.init.kaiming_uniform_(self.lora_A[adapter_name].weight, a=math.sqrt(5))
# 如果為gaussian則進行正態初始化
elif init_lora_weights.lower() == "gaussian":
nn.init.normal_(self.lora_A[adapter_name].weight, std=1 / self.r[adapter_name])
else:
raise ValueError(f"Unknown initialization {init_lora_weights=}")
# 對B矩陣使用全0初始化
nn.init.zeros_(self.lora_B[adapter_name].weight)
if self.lora_bias[adapter_name]:
nn.init.zeros_(self.lora_B[adapter_name].bias)
if adapter_name in self.lora_embedding_A.keys():
# Initialize A to zeros and B the same way as the default for nn.Embedding,
nn.init.zeros_(self.lora_embedding_A[adapter_name])
nn.init.normal_(self.lora_embedding_B[adapter_name])
if self.lora_bias[adapter_name]:
# embeddings are not supported at the moment, but still adding this for consistency
nn.init.zeros_(self.lora_embedding_B[adapter_name].bias)
def set_adapter(self, adapter_names: str | list[str]) -> None:
"""Set the active adapter(s).
Additionally, this function will set the specified adapters to trainable (i.e., requires_grad=True). If this is
not desired, use the following code.
```py
>>> for name, param in model_peft.named_parameters():
... if ...: # some check on name (ex. if 'lora' in name)
... param.requires_grad = False、
Args:
adapter_name (`str` or `List[str]`): Name of the adapter(s) to be activated.
"""
if isinstance(adapter_names, str):
adapter_names = [adapter_names]
# Deactivate grads on the inactive adapter and activate grads on the active adapter
for layer_name in self.adapter_layer_names:
module_dict = getattr(self, layer_name)
for key, layer in module_dict.items():
# 如果是adapter_names中需要訓練的層,則開啟梯度傳播,否則關閉
if key in adapter_names:
# Note: It is possible that not a single layer is called with requires_grad_(True) here. This may
# happen if a completely different adapter layer is being activated.
layer.requires_grad_(True)
else:
layer.requires_grad_(False)
self._active_adapter = adapter_names
5.3.3 前向傳播
Linear的forward()函數展示了LoRA模型如何與原模型推理的結果進行合并。
class Linear(nn.Module, LoraLayer):
def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
self._check_forward_args(x, *args, **kwargs)
adapter_names = kwargs.pop("adapter_names", None)
if self.disable_adapters:
if self.merged:
self.unmerge()
result = self.base_layer(x, *args, **kwargs)
elif adapter_names is not None:
result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
elif self.merged:
result = self.base_layer(x, *args, **kwargs)
else:
# 得到原始模型中的結果
result = self.base_layer(x, *args, **kwargs)
torch_result_dtype = result.dtype
for active_adapter in self.active_adapters:
if active_adapter not in self.lora_A.keys():
continue
lora_A = self.lora_A[active_adapter]
lora_B = self.lora_B[active_adapter]
dropout = self.lora_dropout[active_adapter]
scaling = self.scaling[active_adapter]
x = x.to(lora_A.weight.dtype)
if not self.use_dora[active_adapter]:
# 原始模型輸出+可訓練lora層的結果
result = result + lora_B(lora_A(dropout(x))) * scaling
else:
if isinstance(dropout, nn.Identity) or not self.training:
base_result = result
else:
x = dropout(x)
base_result = None
result = result + self.lora_magnitude_vector[active_adapter](
x,
lora_A=lora_A,
lora_B=lora_B,
scaling=scaling,
base_layer=self.get_base_layer(),
base_result=base_result,
)
result = result.to(torch_result_dtype)
return result
0x06 改進
注:下面文字以論文“Low-Rank Adaptation for Foundation Models: A Comprehensive Review”為藍本。
雖然LoRA可以在一些下游任務上實現適當的自適應性能,但與許多下游任務,諸如數學推理、編程等知識密集型任務上,與全參數微調相比,LoRA的性能仍存在差距。為了填補這一差距,許多方法被提出以進一步提高LoRA在下游任務適應性方面的表現。現有方法通常從以下幾個角度提升下游適應性能:參數效率增強;秩適應;訓練過程改進。
6.1 參數效率增強
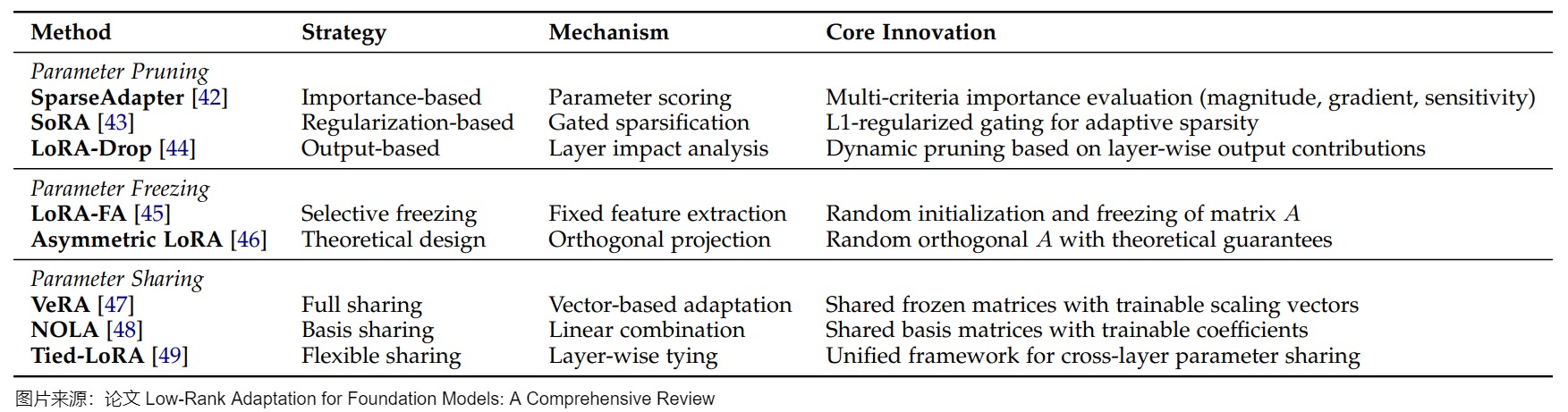
盡管 LoRA 通過其投影矩陣顯著減少了微調LLM的可調參數數量,實現了參數效率的提升,但該方法仍然需要大量的可訓練參數,而且需要昂貴的激活內存來更新低秩矩陣。例如,將 LoRA 應用于 LLaMA-270B 模型需要更新超過 1600 萬個參數。而且,隨著下游任務越來越多,lora插件的數量也會隨之增加,要進一步提高其效率成為了一個關鍵問題。當前研究主要通過四種方法來解決這一挑戰:參數分解(Parameter Decomposition)、剪枝(Parameter Pruning)、凍結(Parameter Freezing)與共享(Parameter Sharing)以及量化(Parameter Quantization)。下圖展示了這些技術的示例。
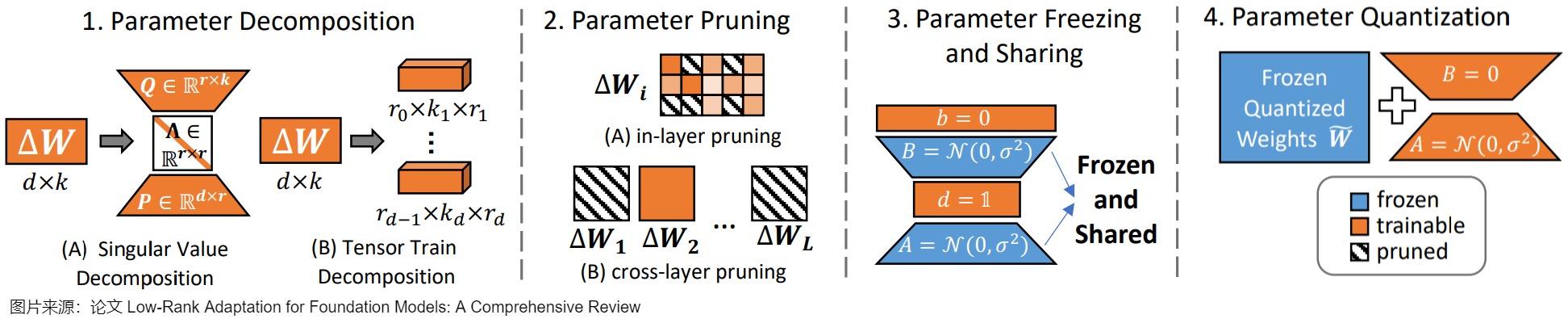
6.1.1 參數分解
參數分解方法通過將矩陣分解為更緊湊的形式來提高參數效率,同時保持任務性能。除了減少可訓練參數外,這些方法還能在微調期間實現更精細的控制。
方法
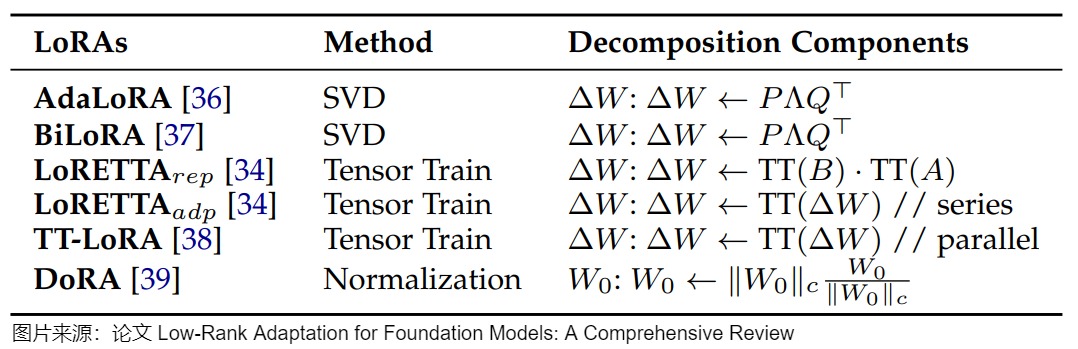
當前的方法可分為兩類主要途徑:更新矩陣分解和預訓練權重分解。這兩種方法在參數效率和微調靈活性方面都具有獨特的優勢。更新矩陣分解方法側重于分解微調期間應用的增量更新,而預訓練權重分解直接修改原始模型權重的結構,下圖提供了這些方法的詳細比較。
更新矩陣分解
在更新矩陣分解方法中,出現了兩種主要策略:
- 基于奇異值(SVD)的分解。比如,AdaLoRA 以SVD的形式參數化更新權重,然后根據重要性評分動態調整Δ W的秩,以在微調期間實現自適應參數效率;在此基礎上,BiLoRA通過兩級優化擴展了該框架,在不同的數據子集上分離奇異向量和值訓練,以減輕過度擬合。
- 基于張量列(TT)的分解。比如,LoRETTA采用TT分解,將矩陣表示為一系列低秩、小的三維張量,通常稱為核。
我們以AdaLoRA為例來看看基于奇異值分解(SVD)的方法。AdaLoRA通過正則化P和Q的正交性來近似SVD分解,然后基于新的重要性評分方法丟棄不重要的奇異值(過濾對角矩陣Λ中的元素)。即,AdaLoRA根據LoRA矩陣的奇異值作為重要程度指標,來選擇不同LoRA適配器調整秩的大小。AdaLoRA與相同秩的標準LoRA相比,兩種方法總共有相同數量的參數,但這些參數的分布不同。在標準的LoRA中,所有矩陣的秩都是相同的,而在AdaLoRA中,重要的矩陣的秩高一些,次要的矩陣的秩低一些,所以最終的參數總數是相同的。經過實驗表明AdaLoRA比標準的LoRA方法產生更好的結果,這表明在模型的部分上有更好的可訓練參數分布,這對給定的任務特別重要。
研究動機
原生 Lora 方法在每個 attention 層都引入了一個秩為 4 的矩陣,采用的是均分策略。然而,Lora 這種“均分參數”的策略顯然不是最優的。因為從直覺上說,模型中的某些矩陣比其他層更重要,應該分配更多的參數來進行調整,而有些矩陣則相對不重要,不需要過多修改。論文由此提出一個核心問題:如何根據transformer不同層、不同模塊的重要性自適應地分配參數預算,以提高微調的性能?
方案
這些重要性得分可以通過奇異值的大小或 loss 的梯度貢獻等方式來計算。通過這種方式,能夠更有針對性地調整參數。一種直觀的做法是使用 SVD(奇異值分解):每次更新 A 和 B 時,先對所有的 A 和 B 矩陣進行 SVD 分解。在每次更新時,根據奇異值的大小來動態決定哪些 rank 需要更新,哪些需要保持不變。如果某一層的矩陣的重要性較低,我們就只更新重要性高的部分,不更新低重要性的部分。然而,這種方法效率極低,因為每個訓練 step 都需要進行 SVD 分解。對于大型模型而言,頻繁對高維矩陣應用 SVD 會非常耗時。
為了解決這個問題,論文提出通過參數化 Δ 來模擬 SVD 的效果。具體做法是,使用對角矩陣 Λ 來表示奇異值,正交矩陣 ?? 和 ?? 表示 ? 的左右奇異向量。為了保證 ?? 和 ?? 的正交性,在訓練過程中增加一個正則化懲罰項。這樣,模型能夠在訓練過程中逐漸接近 SVD 分解的形式,避免了對 SVD 進行密集計算,同時提高了效率。具體參見下圖。

預訓練的權重分解
權重分解典型方案是DoRA(Weight-Decomposed Low-Rank Adaptation),其通過歸一化方法將預訓練權重分解為大小(magnitude)和方向(direction)兩個組成部分進行獨立微調,特別是可以利用LoRA有效地更新方向部分。這種兩步方法賦予DoRA比標準LoRA更大的靈活性。與LoRA傾向于均勻縮放幅度和方向不同,DoRA可以在不一定增加幅度的情況下進行細微的方向調整。DoRA即便使用更少的參數,也能超越LoRA,并且對秩選擇的敏感性較低。
研究動機
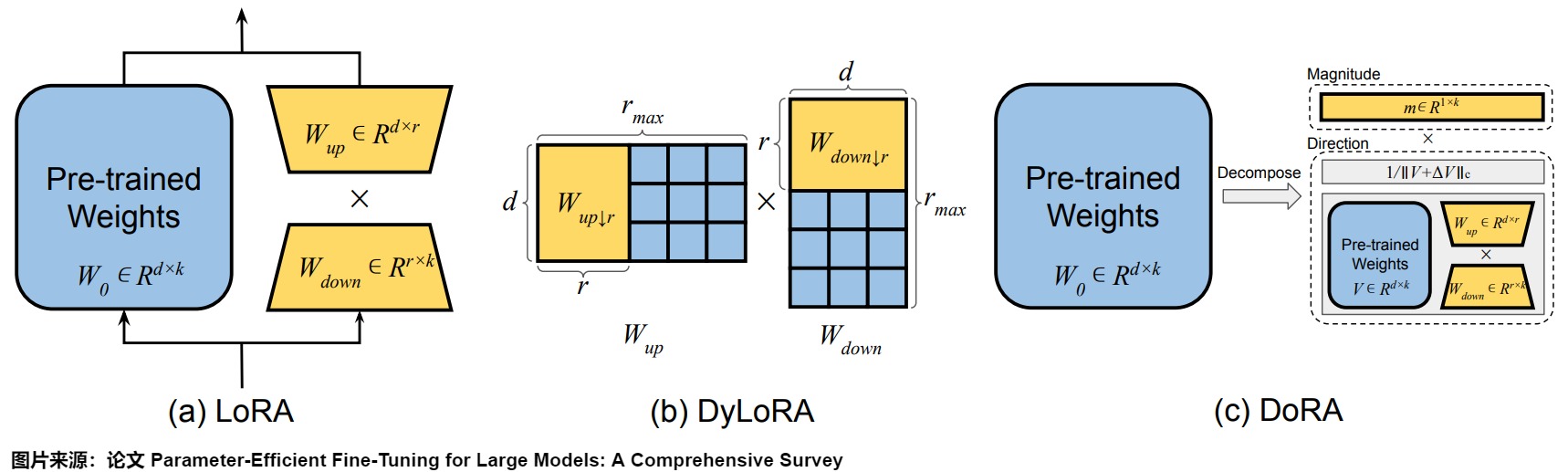
DoRA作者發現LoRA的學習更新模式和FT很不一樣,這些差異可能反映了每種方法的學習能力。
DoRA 基于這樣一個理念:任何向量都可以通過其長度(幅度)和方向(取向)來表示。論文首先引入了一種新穎的權重分解分析方法,以研究全參數微調和 Lora 微調之間在學習模式上的內在差異。具體而言,論文通過將權重矩陣分解為幅度向量m和方向矩陣V兩個獨立的部分。一旦得到了m和V,DoRA僅對方向矩陣V應用LoRA風格的低秩更新,同時允許幅度向量m單獨訓練。通過檢查 LoRA 和 FT 相對于預訓練權重在幅度和方向上的更新,DoRA 可以深入揭示它們在學習行為上的根本區別。
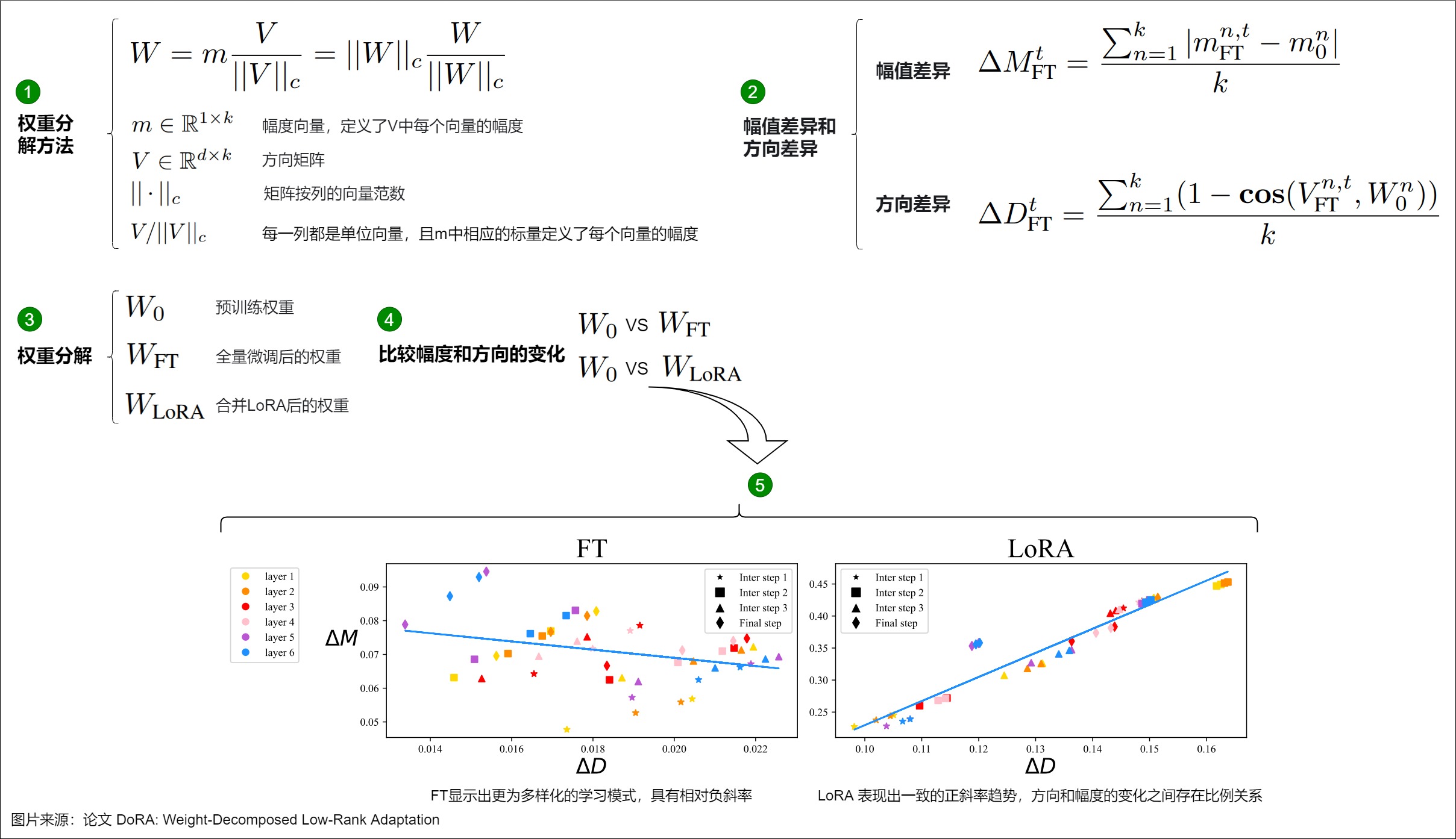
矩陣 W 的權重分解的公式可表述如下圖標號1。依據此公式對完全微調后的權重 \(W_{FT}\) 以及合并LoRA后的權重 \(W_{LoRA}\) 進行上述的分解,再與原來的權重 \(W_0\) 進行比較。例如, \(W_0\)和 \(W_{FT}\)之間的幅度和方向變化可以定義如下圖標號2。其中, \(ΔM_{FT}^t\) 和 \(ΔD_{FT}^t\)分別表示在訓練步驟 t 時, \(W_0\)和 \(W_{FT}\)之間的幅值差異和方向差異, cos?(?,?) 是余弦相似度函數。\(M_{FN}^{n,t}\)和\(M_0^n\)是各自在其幅度向量中的第 ?? 個標量,而 \(V_{FN}^{n,t}\) 和\(W_0^n\)則是 \(V_{FN}^{t}\)和\(W_0\) 中的第 n列。 \(W_0\)和 \(W_{LoRA}\)之間幅度和方向差異按照同樣方法進行計算。
論文從 FT 和 LoRA 的不同訓練步驟中選擇了四個檢查點進行分析,包括三個中間步驟和最終的檢查點,并在這些檢查點上進行權重分解分析,以確定在不同層次上 ΔM 和 ΔD 的變化。圖中下方,x軸是模型更新方向,y軸是幅度變化,圖中的散點是每一層的數據。可以看到:
- FT顯示出更為多樣化的學習模式,其訓練方式、更新的方向和幅度并沒有太大關系(或者小的負相關)。
- LoRA存在較強的正相關性,即方向和幅度的變化之間存在很強的比例關系,這可能對更精細的學習有害,因為它缺乏對更細微調整的能力。具體而言,LoRA在執行伴隨幅度顯著變化的微小方向調整或相反情況下的表現不佳,而這種能力更是FT方法的特點。
因此,論文懷疑,LoRA的這種局限性可能源于同時學習幅度和方向適應性的挑戰,這對于LoRA來說可能過于復雜,這引出了論文的方法論。
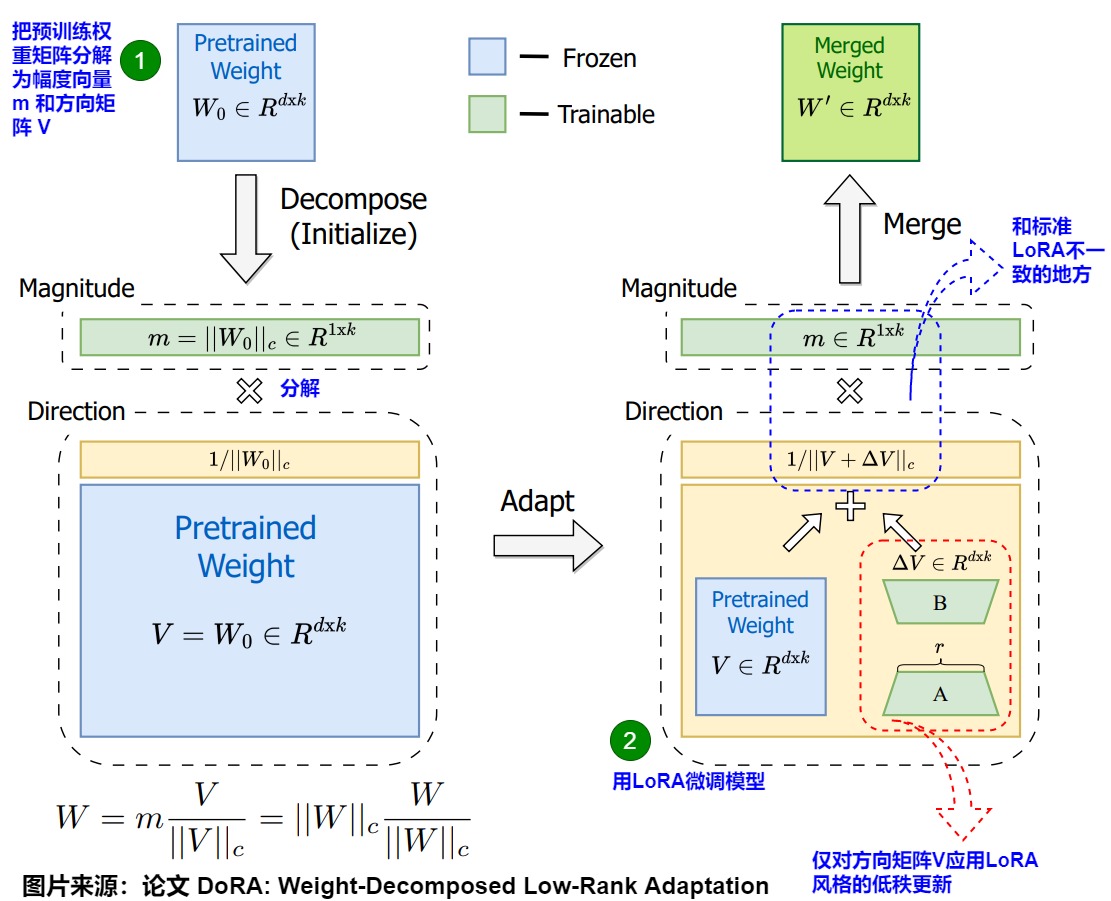
方案
根據作者對權重分解分析的見解,論文進一步引入了權重分解的低秩適應方法(DoRA)。DoRA首先將預訓練的權重分解為其幅度和方向分量,并對這兩個分量進行微調。具體參見下圖公式。

具體而言有如下微調思路。
- 首先,限制LoRA專注于方向調整,同時允許幅度分量可調,相較于LoRA在原方法中需要同時學習幅度和方向的調整,DoRA簡化了任務。對應下圖上標號1,把預訓練權重矩陣分解為幅度向量 m 和方向矩陣 V。
- 其次,由于方向分量在參數數量上較大,論文進一步通過 LoRA對其進行權重分解,使得方向更新的過程更加穩定,以實現高效微調。
因為DoRA可以更容易地將幅度和方向分量分開調整,或者用另一個的負變化來補償一個的變化。所以DoRA的方向和大小之間的關系更像微調。
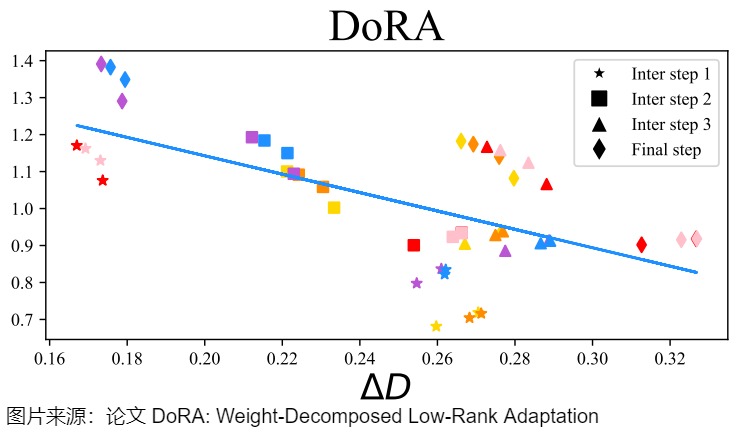
下圖展示了在與 FT 和LoRA相同的設置下,合并后的DoRA權重與\(W_0\)之間的幅度和方向差異。從DoRA和FT的 ΔD,ΔW 回歸線上,DoRA和FT表現出相同的負斜率。論文推測,FT傾向于負斜率是因為預訓練權重已經具備了適合多種下游任務的大量知識。因此,在具有足夠的學習能力時,僅通過更大幅度或方向的改變就足以進行下游適應。
論文還計算了FT、LoRA 和 DoRA 的 ΔD 和 ΔW 之間的相關性,發現 FT 和 DoRA 的相關性值分別為-0.62和-0.31,均為負相關。而LoRA則顯示為正相關,相關性值為0.83。DoRA展示了僅通過較小的幅度變化或相反的情況下進行顯著方向調整的能力,同時其學習模式更接近FT,表明其相較于LoRA具有更強的學習能力。因此,DoRA可視為LoRA的一種無成本替代方案,因為其分解的幅值和方向分量可在訓練后合并回預訓練權重,這樣不會引入額外的推理開銷。
因為DoRA可以更容易地將向量m和方向矩陣V二者分開調整,或者用另一個的負變化來補償一個的變化。所以可以DoRA的方向和大小之間的關系更像微調。
6.1.2 參數剪枝
參數剪枝技術側重于評估 LoRA 矩陣中不同參數的重要性,并刪除那些被認為不太重要的參數。這些方法可根據剪枝方式分為三類:基于重要性的剪枝、基于正則化的剪枝和基于輸出的剪枝。
-
基于重要性的剪枝:這些方法使用多個指標評估參數重要性。SparseAdapter將傳統的網絡剪枝技術應用于 LoRA 參數,通過參數幅度、梯度信息和敏感性分析來評估重要性。RoseLoRA通過基于敏感性的評分實現行/列剪枝,在保留低秩適應優勢的同時實現選擇性知識更新。LoRA-prune基于LoRA的梯度信息,聯合剪枝LoRA矩陣和大型語言模型(LLM)的參數,以優化模型結構。
-
基于正則化的剪枝:基于正則化的剪枝技術通過優化約束來引入稀疏性。SoRA在 LoRA 的下投影和上投影矩陣之間利用門控機制,采用近端梯度下降和 L1 正則化。這種方法在訓練期間實現自動稀疏化,并在訓練后消除零值元素。
-
基于輸出的剪枝:基于輸出的方法基于LoRA參數的分層影響來評估LoRA參數。LoRA-drop通過分析不同層上的\(\left \| \bigtriangleup W_ix_i \right \|^2\)的分布來評估LoRA模塊的重要性。該方法為最重要的層保留單獨的LoRA模塊,而在被認為不太重要的其它層之間共享單個LoRA。
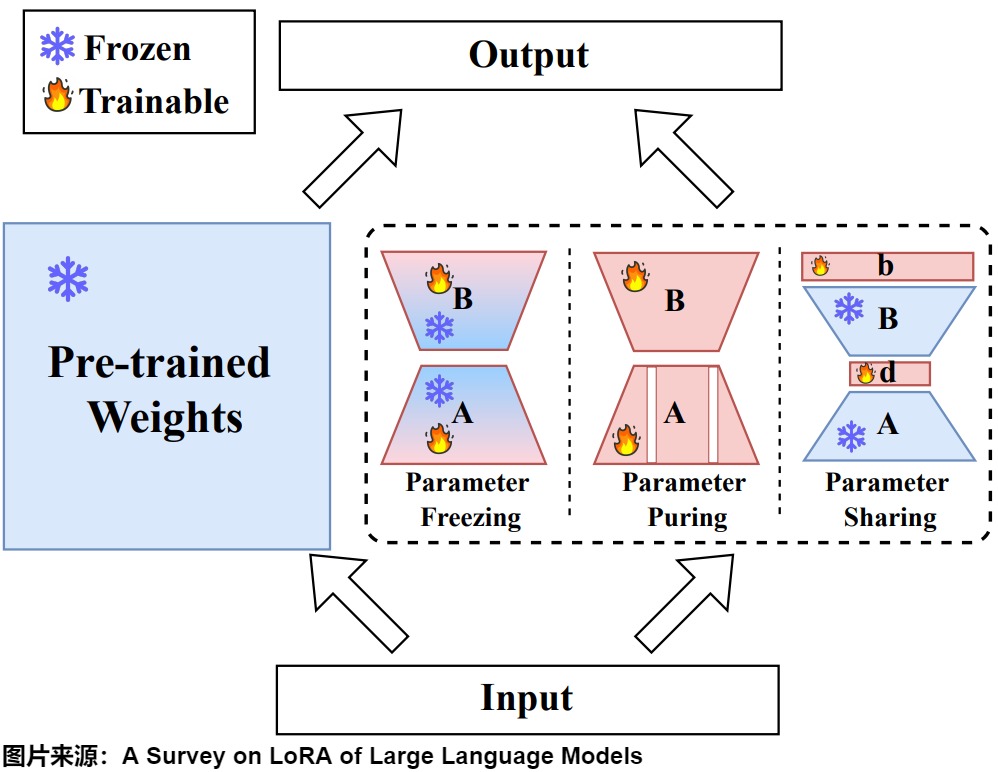
6.1.3 參數凍結與共享
參數凍結和共享技術通過矩陣凍結和跨層參數共享減少可訓練參數。它們可分為兩類:內部參數方法和外部參數方法。
- 內部參數方法在調整LoRA的部分參數的同時凍結其他參數。
- 矩陣凍結:通過在微調過程中凍結一部分LoRA參數,只更新其余的參數。研究已經揭示了矩陣A和B在適配過程中具有不對稱的作用。LoRA-FA表明,凍結隨機初始化的矩陣A而僅更新B,即可保持模型性能。LoRA-FA是LoRA與Frozen-A的縮寫,就是凍結了LoRA每一層的下投影權重,并更新上投影權重,僅訓練B矩陣。在LoRA-FA中,矩陣A在初始化后被凍結,矩陣B是在用零初始化之后進行訓練(就像在原始LoRA中一樣)。這將參數數量減半,同時具有與普通LoRA相當的性能。Asymmetric LoRA為這種方法提供了理論基礎,表明A主要作為特征提取器,而B作為特定任務的投影器。AFLoRA構建一個低秩可訓練路徑,并在訓練LoRA時逐步凍結參數。DropBP通過在反向傳播過程中隨機丟棄一些LoRA梯度計算來加速訓練過程。
- 跨層參數共享:有幾種方法探索了跨網絡層的參數共享。VeRA提出在所有層間共享一對凍結的隨機矩陣,并通過“縮放向量”進行層級適應。NOLA擴展了這一概念,將A和B表示為共享凍結基矩陣的可訓練線性組合。Tied-LoRA在保持共享矩陣可訓練的同時實現了逐層的參數綁定。VB-LoRA(Vector Bank-based LoRA)提出了一種“分割和共享/分而治之”范式,通過秩分解將LoRA的低秩分解進行分割,并基于混合模型實現全局共享。
- 額外參數方法在凍結LoRA原有參數的同時引入并調整一組額外參數。大多數方法基于奇異值分解(SVD)提出。LoRA-XS在凍結的LoRA矩陣之間添加一個小型的 r x r 權重矩陣,這些矩陣是通過對原始權重矩陣進行SVD構建的;然后在微調過程中僅調整這些 r x r 權重矩陣。類似地,BYOM-LoRA采用SVD來壓縮多任務模型的LoRA矩陣。
下圖給出了NOLA的示意圖。其動機是:LoRA面臨兩個主要限制:(1) 參數數量受限于秩分解的下界,(2) 減少的程度受模型架構和選擇的秩的影響很大。NOLA通過使用隨機生成矩陣(基)的線性組合重新參數化LoRA中的低秩矩陣,并僅優化線性混合系數。這種方法使我們能夠將可訓練參數的數量與秩的選擇和網絡架構解耦。

結合參數剪枝技術,這些方法能夠在保持適應有效性的同時顯著減少參數數量。下圖提供了這些方法的全面比較。
6.1.4 參數量化
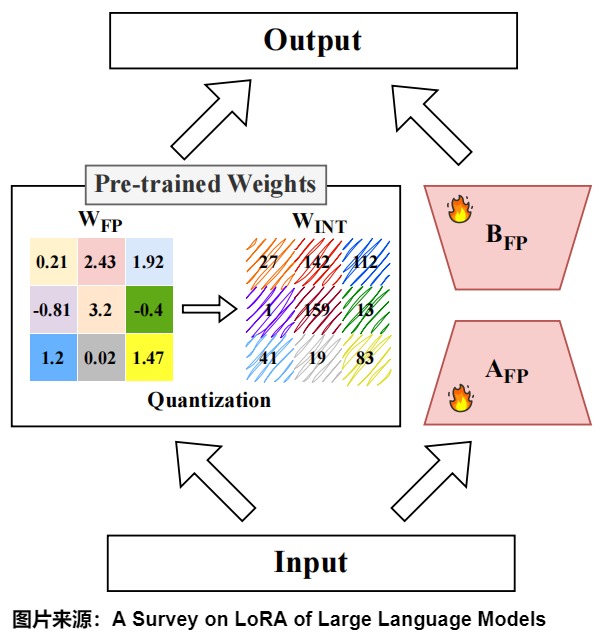
量化是指通過較低精度的數值表示來優化神經網絡復雜度,從而大大減少存儲和計算需求。在 LoRA 背景下,量化方法主要有兩個維度:量化時機和量化技術。
量化時機:量化時機指的是在微調之前、期間或之后進行量化。
- 預微調量化:預微調量化是在進行基于 LoRA 的適配之前對預訓練權重進行量化。例如,QLoRA采用 4 位 NormalFloat(NF4)量化方法。LoftQ通過解決量化高精度權重引入的差異對QLoRA進行了改進。
- 微調期間量化:微調期間量化在微調之前和整個過程中都應用量化。方法如 QA-LoRA利用分組量化在訓練期間動態調整精度,確保低秩更新和量化權重之間進行更平衡的交互。
- 后微調量化:后微調量化在微調完成后進行,主要關注用于推理的量化。LQER 利用基于低秩 SVD 的分解來最小化量化誤差,從而確保量化后的權重與原始高精度權重緊密匹配。
量化技術:針對 LoRA,已經提出了不同的量化方法,包括均勻量化、非均勻量化和混合精度量化。
- 均勻量化:均勻量化為所有權重分配相同的位寬,而不考慮其分布。QA-LoRA應用具有分組細化(group-wise refinement)的均勻量化,通過平衡精度權衡來優化內存效率和適應性。然而,對于非均勻分布的權重,均勻量化可能效果不佳,此時非均勻量化更為有效。
- 非均勻量化:QLoRA采用非均勻量化,這是專門為高斯分布設計的權重,通過在最需要的地方(靠近零)分配更多精度。該方法允許更好地表示在預訓練模型中占主導地位的較小權重。
- 混合精度量化:混合精度量化可根據權重矩陣或層動態調整位寬,從而提供更大的靈活性。諸如 LoftQ和 LQ - LoRA等方法利用混合精度來優化模型不同組件的量化。例如,LoftQ 交替量化權重矩陣的殘差并使用 SVD 來細化低秩分量。通過迭代優化低秩參數和調整量化級別,LoftQ 能夠最小化量化誤差。LQ-LoRA 在此基礎上進一步擴展,采用整數線性規劃為每個權重矩陣動態配置位寬。LQ-LoRA還引入了一種數據感知機制,該機制利用 Fisher 信息矩陣的近似值來指導量化過程。這允許LQ-LoRA以最小量化引起的損失實現權重矩陣的更精確分解。
總之,預微調量化方法(如 QLoRA 和 LoftQ)通常通過凍結預訓練權重提供更大的內存節省,而后微調方法(如 LQER)則更側重于優化推理精度。在量化技術方面,非均勻和混合精度方法(如 QLoRA、LoftQ 和 LQ - LoRA 中所見)在低比特場景下表現出優越的性能,能夠根據權重分布提供更靈活的精度分配。量化的時機和具體的量化技術在決定內存效率和模型性能之間的平衡方面都起著關鍵作用。下圖提供了所討論的量化方法的全面總結。

6.2 秩適應(Ranking Adaptation)
秩是 LoRA 中的一個關鍵參數,直接影響模型的適應性和可訓練參數的數量。原始的 LoRA 方法在所有層中采用固定的低秩,這對于不同的下游任務和模型架構可能不是最優的。另外,對于LoRA的秩,并非越高越好。過高的LoRA秩可能導致性能和效率的雙重退化。此外,在微調過程中,Transformer模型不同層的重要性可能各異,需要為每一層分配不同的秩。
為了解決這些限制,最近的工作提出了各種方法來優化 LoRA 中的秩分配,大致可分為兩個主要方面:秩細化和秩增強。下圖展示了這兩種方法。
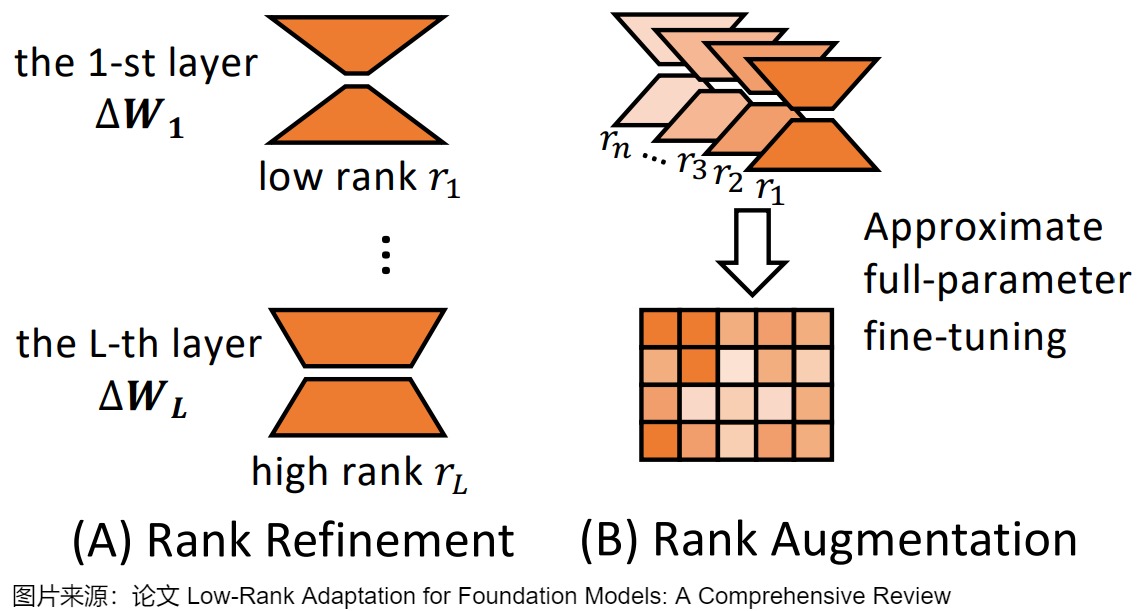
6.2.1 秩細化(Rank Refinement)
秩細化方法旨在在微調期間自適應地選擇 LoRA 模塊的秩,而不是為所有模塊分配相同的秩,從而提高模型的適應性和效率。關鍵的見解是,不同的層可能需要不同程度的適應,因此受益于不同的秩。秩細化方法可分為三種主要類型:自適應分配、啟發式策略和多秩訓練。
自適應分配(Adaptive Allocation):自適應分配方法在訓練期間根據從數據或模型參數導出的重要性指標動態調整 LoRA 模塊的秩。目前有三種方法:基于SVD的方法;基于SRD的方法;基于秩采樣的方法。
-
基于SVD的方法(SVD-based Methods)。通過奇異值分解(SVD)對矩陣進行分解并選擇性截斷其奇異值,是控制矩陣秩的有效方法。受到SVD的啟發,我們可以將LoRA參數矩陣BA分解為SVD形式,即P Lambda Q,其中P和Q是正交的,Lambda是一個非負對角矩陣。通過控制Lambda中的元素,我們可以控制BA的秩并為LoRA模塊分配秩。基于這一思路,幾種秩分配方法近似實現了BA的SVD分解,并通過過濾對角矩陣來分配秩。例如,AdaLoRA通過使用 SVD 對 LoRA 更新進行參數化,來引入一種自適應的秩分配機制。這種機制根據奇異值的大小動態修剪奇異值,使每個層能夠具有定制的秩,同時保持全局參數預算。類似地,SoRA采用可學習的門控機制來控制每個 LoRA 模塊的有效秩。為了提升稀疏性,這些門控通過L1正則化的近端梯度下降來進行優化。該方法能夠自動發現不同層的合適秩,從而提高參數效率而無需手動調整。
-
基于SRD的方法(SRD-based Methods)。然而,正交正則化給LoRA帶來了不可忽視的計算成本,降低了其效率。為了解決這個問題,一些方法省略了SVD的正交性要求,直接將矩陣分解為單個秩分量,然后通過選擇合適的分量來分配秩。DoRA(動態低秩適應)提出將LoRA參數矩陣BA分解為單秩分量,并根據啟發式重要性分數修剪這些分量。類似地,AutoLoRA也將LoRA參數矩陣BA分解為單秩分量,但它是基于元學習來修剪分量。SoRA消除了正交正則化,并通過直接控制對角矩陣來篩選P和Q的列和行(它們的組合可以視為單秩分量)。ALoRA也通過使用門控單元來篩選分量,相比之下,它基于神經架構搜索來學習門控單元。
-
基于秩采樣的方法(Rank Sampling-based Methods)。在基于SVD參數化和SRD的方法中,需要通過迭代或正交性約束來確定合適的秩,這可能帶來額外的計算負擔。秩抽樣方法避免了額外的秩搜索計算成本,使得秩分配過程更加高效。通過隨機抽樣可以靈活地適應不同的訓練條件和任務需求,并且抽樣過程簡單直觀,易于實現和集成到現有的LoRA框架中。為了避免這種額外成本,DyLoRA指出可以通過隨機采樣直接分配秩。在每個訓練步驟中,它從預定義的離散分布中采樣一個值b,并將b作為秩分配。然后,矩陣A和B被截斷到秩b。在微調過程中,只有A的第b行和B的第b列的參數是可調的,而其他參數被凍結。此外,分布可以根據用戶偏好定義。

啟發式策略(Heuristic Strategies):啟發式策略根據預定義的規則分配秩,這些規則可以來自先驗知識或經驗觀察。PRILoRA提出了一種確定性策略,其中 LoRA 模塊的秩從較低層到較高層線性增加。在遷移學習中,較高的層通常需要更多的適應性,這一啟發式算法將較高的等級分配給較高的層。
多秩訓練(Multi-Rank Training):多秩訓練方法使模型能夠在一系列秩上表現良好,在推理時提供靈活性。DyLoRA同時在多個秩上訓練 LoRA 模塊。在每個訓練迭代中,它從預定義的分布中采樣秩,使模型能夠學習在多個秩上有效地執行。這種策略在推理時無需額外訓練即可實現適應性,在具有不同計算約束的部署場景中非常有益。
6.2.2 秩增強(Rank Augmentation)
LoRA通過使用低秩矩陣來更新模型參數,雖然這有助于參數效率,但同時也限制了模型在某些知識密集型任務上的表示能力。秩增強方法旨在通過一系列低秩修改實現高秩模型更新,彌合 LoRA 與全參數微調之間的性能差距。這些方法可分為兩類:基于矩陣合并的方法和基于矩陣重采樣的方法。
基于矩陣合并的方法:基于矩陣合并的方法通過合并低秩更新矩陣來增加秩,其關鍵思想是:矩陣秩是次可加的,即對于相同大小的矩陣 M_1 和 M_2,有 \(rank ( M_1+M_2 ) <= rank ( M_1 )+ rank(M_2)\),即兩個矩陣相加的秩不會超過各自秩的和。基于這種次可加性,我們可以將多個LoRA模塊堆疊在一起,用多個低秩矩陣的和可以近似一個更高秩的矩陣,從而在不產生大量計算開銷的情況下增強捕獲復雜模式的能力。
-
ReLoRA引入了一個迭代訓練框架。這是一種合并和重新初始化 LoRA 模塊的過程,其中低秩 LoRA 模塊被訓練并定期合并到預訓練模型權重中,然后在微調過程中重新初始化這些模塊。ReLoRA 的方法相當于在微調過程中沿著微調步驟堆疊多個 LoRA 模塊,可以增加整體更新的秩。ReLoRA 有效地增加了整體秩,同時保持內存效率。
-
COLA提出了一種類似的迭代優化(合并和重新初始化)策略,其靈感來自Frank-Wolfe算法。它迭代地訓練 LoRA 模塊并將它們合并到模型中,逐步構建更高秩的適應。每個新的 LoRA 模塊最小化來自先前適配的殘差誤差,使 COLA 能夠在不增加每次迭代計算成本的情況下實現高秩表達能力。
-
MELoRA指出合并和重新初始化過程并不一定保證秩的增加,因為微調過程中的 LoRA 模塊序列可能存在重疊。為了解決這個問題,MELoRA 引入了一種并行化的秩擴充方法。核心思想是將LoRA模塊分解為更小的mini LoRA,然后并行堆疊這些mini LoRA,連接它們的輸出以形成更高秩的適應。通過組裝這些小型 LoRA 模塊,MELoRA 構建了一個等效的塊對角矩陣,其總體秩更高。
-
XGBLoRA為 LoRA 引入了梯度提升(GB)框架。它通過組合一系列Rank-1助推器(boosters/LoRA 適應)來構建最終模型,逐步改進模型的預測。利用弱學習器的 GB 原則(即從一組弱預測器構建強集成模型),XGBLoRA 克服了極低秩適應和有效性之間的困境。
基于矩陣重采樣的方法:基于矩陣重采樣的方法通過在訓練期間動態重采樣投影矩陣來實現高秩適應。基本思想是在每個訓練步驟使用低秩矩陣的同時,利用時間來積累高秩更新的效果。FLoRA將 LoRA 重新解釋為一種梯度壓縮和解壓縮機制。FLoRA觀察到LoRA在參數更新中實際上執行了一種固定的隨機投影來克服LoRA在梯度空間中的低秩限制。這種投影將梯度壓縮到低秩空間。為了打破這種限制,FLoRA建議在每次迭代中(或者定期)重新采樣LoRA 模塊中使用的投影矩陣,從而允許模型在保持參數效率的同時,能夠隨著時間的推移更充分地探索參數空間,有效地積累更高秩的適應,恢復全矩陣SGD的性能。
總之,秩適應策略通過根據不同層和任務的要求定制適應矩陣的秩來增強 LoRA 的適應性。下圖提供了關于秩細化和擴充的詳細總結。
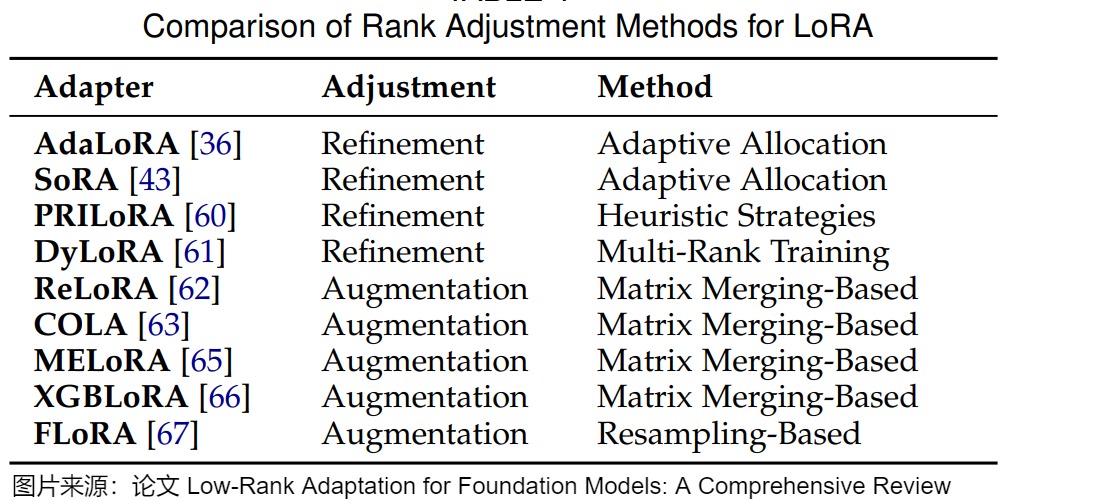
6.3 訓練過程改進
雖然 LoRA 在參數高效微調方面取得了顯著成功,但優化其訓練動態對于最大化適應性能仍然至關重要。在本節中,我們討論旨在改進訓練過程(比如提高LoRA的收斂速度和減少對超參數的敏感性)的最新進展。這方面的改進包括:初始化方法的改進以加速收斂;優化梯度更新以提高訓練的穩定性和可靠性;減少過擬合現象。
6.3.1 Co-updating LLM and LoRA
Co-updating LLM and LoRA的目的是在微調過程中更新高秩的LLM,以獲得比單獨更新LoRA更好的表示能力。
Delta-LoRA提出了一種共同更新策略,它計算兩個連續迭代的LoRA參數之間的差異,然后將這個差異應用于LLM的更新。該方法的優勢在于它能夠利用LoRA的參數效率特性,同時通過直接更新高秩的LLM來獲得更好的性能。這種方法不需要額外的內存開銷,就能夠獲得比獨立更新LoRA更好的表示能力,不僅能夠提高模型在特定下游任務上的表現,還能夠在不增加額外內存成本的情況下實現LLM的高效更新。
6.3.2 初始化改進(Initialization Improvement)
在LoRA中,參數矩陣A和B的初始化通常使用高斯噪聲和零。
有兩種簡單的方案:Init[A],將矩陣B設為零并隨機初始化矩陣A,以及Init[B],反之亦然。論文“The impact of initialization on lora finetuning dynamics”比較了這兩種方案,并通過理論分析得出Init[A]更優。研究表明,Init[A]允許使用更大的學習率而不導致不穩定,從而使學習過程更高效。然而,即使采用Init[A],這種隨機初始化方法仍會導致初始梯度較小,進而減慢收斂速度。即,如果這些低秩矩陣的初始化不當,可能會導致微調過程效率低下,甚至影響模型的下游任務適應性。
通過與預訓練權重矩陣的重要方向對齊,改進的初始化方法可以加速LoRA的收斂速度。好的初始化有助于在微調過程中保持模型的穩定性和性能,尤其是在處理新任務時。典型的改進方法如下:
- PiSSA:PiSSA(Principal Singular Values and Singular Vectors Adaptation)是一種初始化方法,它使用預訓練權重矩陣的主奇異值和奇異向量來初始化LoRA的參數。由于主奇異分量代表矩陣中最重要的方向,將初始權重與這些分量對齊可以加速收斂并提升性能。
- MiLoRA:MiLoRA(Minor Singular Components Adaptation)與PiSSA相反,它使用次要的奇異值和奇異向量進行初始化。考慮到低秩矩陣的隨機初始化可能干擾預訓練矩陣中已學習的重要特征,MiLoRA通過減少這種干擾來提高整體性能,同時適應新任務。
PiSSA
我們以PiSSA為例來進行學習。
PiSSA通過識別和微調模型內的主成分,將原始矩陣通過快速SVD分解,用兩個奇異向量和主要奇異值的乘積來初始化LoRA的AB矩陣。下圖從左到右依次為全參數微調、LoRA微調、以及PiSSA微調大模型的初始化方法。初始階段,對于相同輸入,這三種方法的輸出完全相等。但是PISSA和LoRA主要的區別是初始化方式不同:
- LoRA:使用隨機高斯分布初始化A,B初始化為零。過程中只訓練了低秩矩陣A、B。
- PISSA:同樣基于低秩特性的假設,但PISSA不是去近似???,而是直接對??進行操作。PiSSA使用SVD將??分解為兩個矩陣A和B的乘積加上一個殘差矩陣????????。A和B使用??的主奇異值和奇異向量進行初始化,而????????則使用剩余的奇異值和奇異向量初始化,并在微調過程中保持不變。也就能保證初始化時和基座模型一樣。和LoRA一樣,PISSA的訓練中也只訓練了低秩矩陣A 和 B,而????????保持凍結。
LoRA和PiSSA相比全參數微調,都節省了可訓練參數量(用橙色表示)。
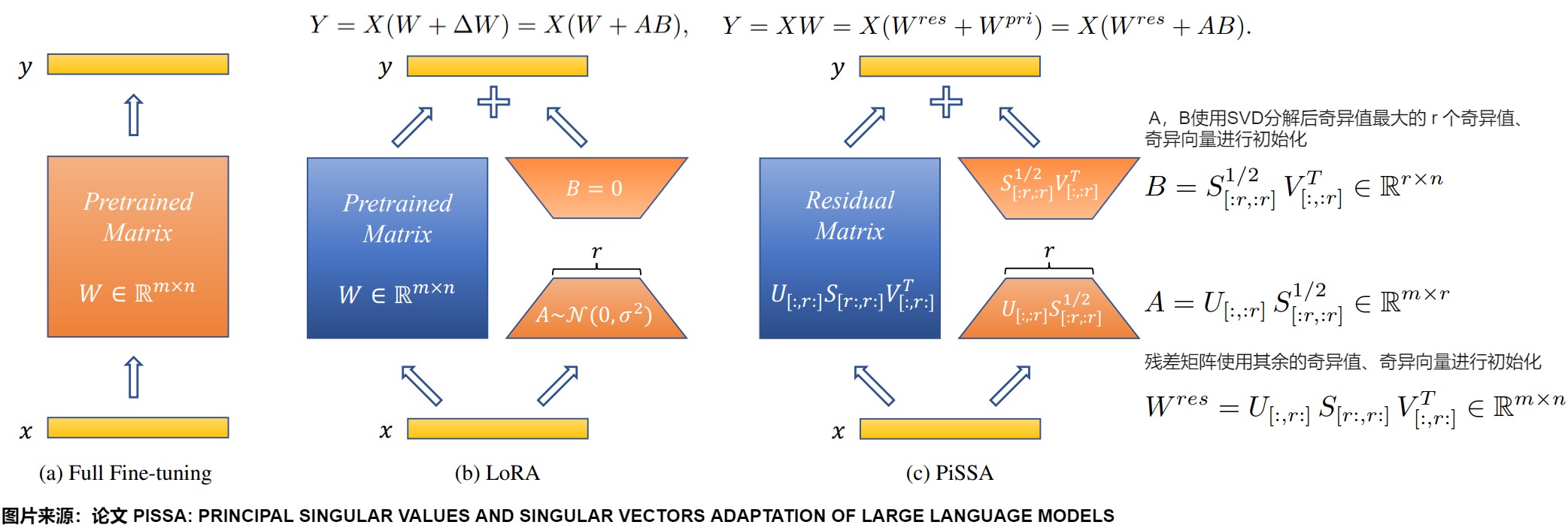
論文提出的方式很簡單,對原始矩陣進行 SVD 分解,拆開成兩部分: 主奇異值部分和殘差奇異值部分,fine tuning 主奇異值部分,frozen 殘差奇異值。具體分解如下,其中 ???????? 由奇異值小的那部分組成。????????(A 和 B)由奇異值大的部分組成,即要訓練的部分。
其實,LoRA和PiSSA的思路不同。PiSSA認為微調其實主要集中在調整奇異值較大的主成分。LoRA 論文認為Δ?? 主要是放大了 ?? 中未被強調的方向,也就是說 Lora 放大了下游任務中重要,但在預訓練中未被強調的特征部分(也就是奇異值小的部分),這與 PiSSA 的觀點是矛盾的。
- LoRA認為大模型微調前后矩陣的變化Δ??具有很低的本征秩 ?? ,因此通過A∈????×?? 和 B∈????×??相乘得到的低秩矩陣來模擬模型的變化Δ??。初始階段,使用高斯噪聲初始化 A ,使用0初始化 B ,則Δ??=AB=0, 因此保證模型初始能力沒有變化。然后微調 A 和 B 就實現了對 ?? 進行更新。但是,在微調的早期階段,梯度要么非常小,要么呈隨機分布,導致許多梯度下降步驟被浪費,LoRA 在訓練的初期往往在初始點附近徘徊,浪費大量時間。此外,不良的初始化可能會使模型陷入次優的局部最小值,影響其泛化能力。
- PiSSA不關心Δ??,而是認為??具有很低的本征秩 ?? 。因此直接對??進行奇異值分解,并用 ????????修正誤差。這種分解方法之所以有效的原因在于:主奇異值的元素遠大于殘差奇異值的元素,因此可訓練的適配器 ????????=BA 包含了原始權重矩陣 ?? 中最重要的方向。在理想情況下,訓練 ????????=BA 可以在使用較少參數的前提下,模擬微調整個模型的效果。通過直接微調模型中最關鍵的部分,PiSSA 能夠實現更快、更好的收斂。相比之下,LoRA 在初始化適配器 B 和 A 時,使用的是高斯噪聲和零值,同時保持原始權重矩陣 ?? 凍結不變。因此,在微調的早期階段,梯度要么非常小,要么呈隨機分布,導致許多梯度下降步驟被浪費。此外,不良的初始化可能會使模型陷入次優的局部最小值,影響其泛化能力。
有研究人員認為,如果任務較為通用,可能確實需要調整模型中奇異值較大的部分;但如果任務與預訓練的差異較大,僅調整奇異值大的主成分未必能夠得到最佳效果,可能更需要關注那些在預訓練中未被強調但在新任務中重要的特征。
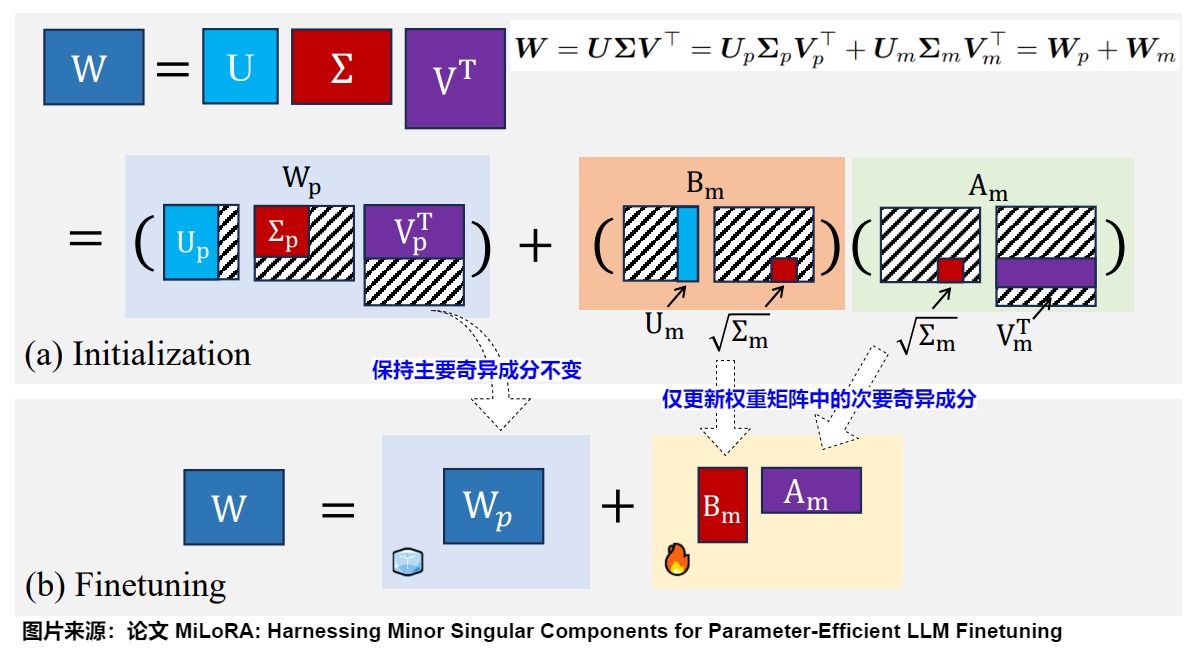
MiLoRA
與PiSSA相反,MiLoRA(Minor singular component based Low Rank Adaptation)使用次要的奇異值和奇異向量進行初始化。考慮到低秩矩陣的隨機初始化可能干擾預訓練矩陣中已學習的重要特征,MiLoRA通過減少這種干擾來提高整體性能,同時適應新任務。而PISSA主要保留奇異值進行更新。
MiLoRA的思路基于兩個觀察:
- 次要奇異成分對應于噪聲或長尾信息。
- 主要奇異成分包含重要知識,即原模型參數的核心信息。
權重矩陣的某些奇異值在整個優化過程中保持穩定,而與這些奇異值對應的子空間在整個梯度下降過程中是不變的。因此,MiLoRA的核心思想是在保持主要奇異成分不變的同時,僅更新權重矩陣中的次要奇異成分。MiLoRA通過奇異值分解(SVD)將權重矩陣分解為主要成分矩陣和次要成分矩陣。其中,主要成分對應于大的奇異值,次要成分對應于小的奇異值。MiLoRA保持主要成分(預訓練知識)不變,僅在微調過程中更新次要奇異成分。
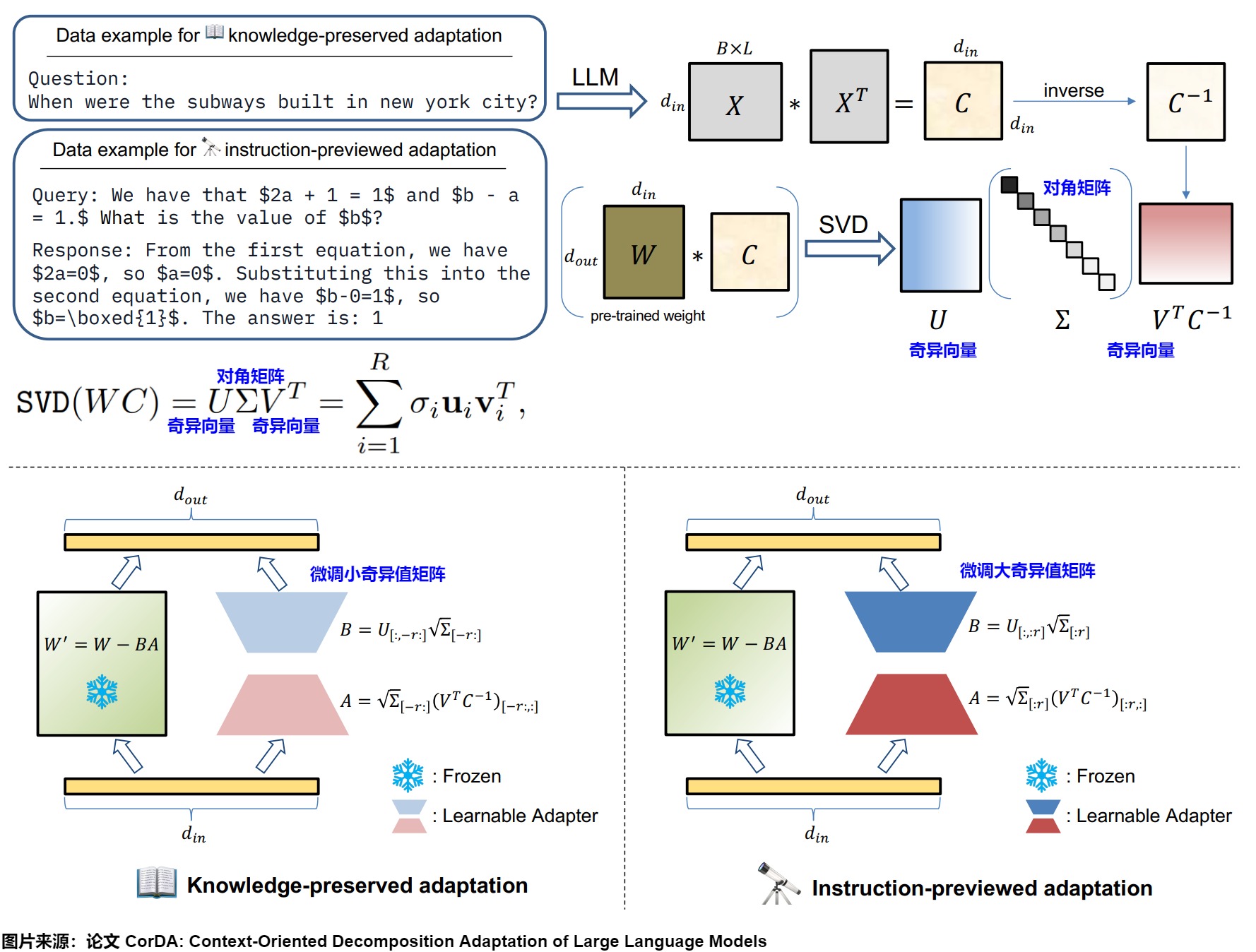
CorDA
CorDA的動機是:傳統的LoRA方法在微調過程中隨機初始化低秩矩陣,從而會有兩個問題。
-
忽略了數據上下文的重要性;
-
災難性遺忘,損失原模型參數的信息。
CorDA是上下文導向的分解適配方法。
- 首先隨機收集少量數據樣本,并假設這些樣本包含了相應任務的代表性上下文。
- 將這些樣本輸入到預訓練的LLM中,獲取每個線性層輸入激活的協方差矩陣。協方差矩陣表示的上下文能夠指導分解方向。
- 接著,對權重與協方差矩陣的乘積執行奇異值分解(SVD)來構建面向下游任務或世界知識上下文的可學習適配器。具體來說,使用輸入激活的協方差矩陣與預訓練LLM的每個線性層的權重相乘,然后進行SVD分解。
CorDA支持兩種可選模式:知識保留適配和指令預覽適配。可以根據不同的場景選擇不同的初始化策略:
- 知識保留適配的權重重構:微調最小奇異值矩陣。在這種模式下,保持凍結大奇異值相關的組件,以減少對模型已有能力的損害。這種方法適用于需要在新任務學習和保留世界知識之間找到平衡的應用場景。
- 指令預覽適配的權重重構:微調最大奇異值矩陣。在這種模式下,微調大奇異值相關的組件,以便更好地適應新任務的要求,從而提高在特定任務上的性能。這種方法適用于對特定任務的性能有較高要求,而對保留全部世界知識的要求相對較低的應用場景。
6.3.3 持續學習
遺忘
有個棘手的問題:當LLM嘗試學習多個連續任務時,它們好像有點“健忘”,容易忘記之前學到的東西,這就是我“災難性遺忘”。因此,如何在保留先前知識的基礎上增量地增強LLM,即進行持續學習,至關重要。
持續學習
LoRA 的參數高效特性允許在新任務上增量更新模型,同時減輕災難性遺忘。有幾個關鍵優勢促使在持續學習(CL)中使用 LoRA:(1)與全量微調相比降低了計算成本,(2)自然地隔離特定任務的知識,(3)可以靈活組合特定任務的適配器。現有的基于 LoRA 的持續學習方法主要有兩類:基于正則化的方法和基于集成的技術。
- 基于正則化的方法將 LoRA 更新的參數約束作為防止災難性遺忘的主要機制,側重于保留關鍵模型參數。O-LoRA 通過約束新任務更新與先前任務的子空間正交來解決災難性遺忘問題。O-LoRA 在正交子空間中增量學習新任務,同時保持先前的 LoRA 參數固定。這種方法允許有效的知識積累而無干擾。Online-LoRA提出了一種新穎的在線權重正則化策略,用于識別和鞏固重要模型參數。此外,Online-LoRA利用損失值的訓練動態來實現數據分布變化的自動識別。
- 基于集成的工作維護和組合多個特定任務的 LoRA 模塊。CoLoR 為每個任務維護單獨的 LoRA 模塊,并在推理時使用無監督方法選擇適當的模塊。CoLoR 順序訓練特定任務的 LoRA 模塊,并使用基于原型的任務識別將它們組合起來。這允許隔離任務知識,同時實現靈活組合。AM-LoRA使用多個特定任務的 LoRA 模塊與注意力機制相結合,集成來自不同任務的知識。AM-LoRA的關鍵在于設計了一個注意力機制作為知識混合模塊,以適應地集成每個LoRA的信息。通過注意力機制,AM-LoRA可以有效利用每個LoRA的獨特貢獻,同時減輕它們之間可能導致的災難性遺忘的風險。此外,AM-LoRA在學習過程中進一步引入了范數,使注意力向量更加稀疏。稀疏約束可以使模型傾向于選擇少數高度相關的LoRA,而不是集體聚合和加權所有LoRA,這可以進一步減少來自相互干擾的影響。
O-LoRA
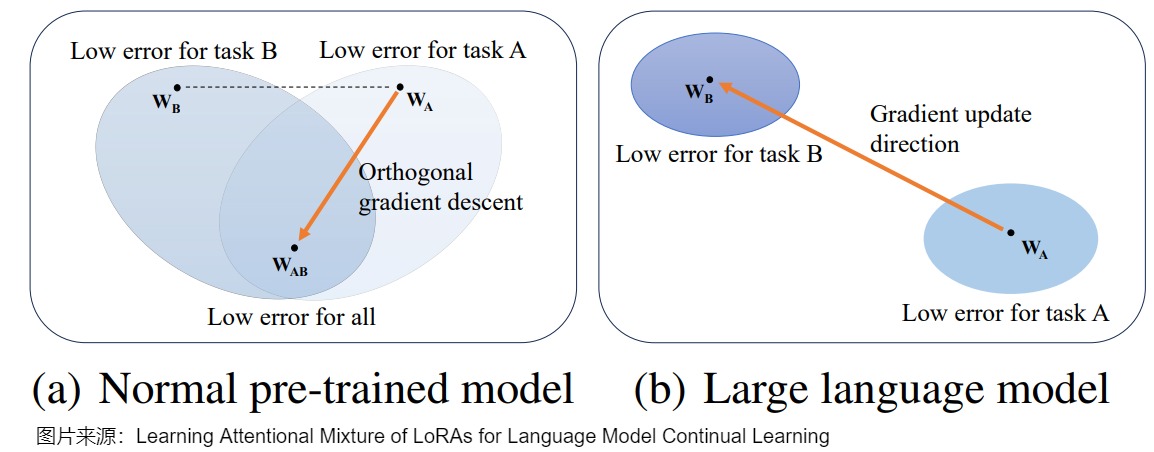
O-LoRA作者基于兩個觀察:
- 過去的方法中,所有任務都是在相同的向量空間中更新模型參數的,這樣很容易破壞過去學會的任務表示。
- LoRA的低秩假設,即模型的finetune過程往往在低秩的子空間中進行更新。所以LoRA的矩陣參數,不僅代表了對原始模型的數值更新,也捕獲了模型參數的更新方向。
O-LoRA提出了一種假設,之前任務的梯度子空間可以由LoRA參數表示,這使得模型可以在學習新任務時,逐步學習到一個新的正交子空間,從而在同時學習新任務時減輕災難性遺忘。
從參數空間的角度看,正交梯度下降的假設是基于參數空間中不同任務存在共同最優解,如下圖(a)所示。O-LoRA 在學習新任務的時候,約束其LoRA子空間與過去任務的LoRA子空間正交。子空間的正交必然會使得存在各自空間中的向量正交,從而保證了新任務的梯度更新不會對過去任務的輸出造成影響。
然而,在巨大的參數空間的LLM中,多個任務的最優參數可能非常不同,甚至不存在共同最優解。在這種情況下學習新任務時,模型參數與前一個任務的匹配程度將更低,導致災難性遺忘。即使參數收斂到共同最優解,模型也會逐漸偏離前一個任務的最優參數,導致當前參數與前一個任務參數的不匹配問題。另外,O-LoRA也限制了模型捕捉跨任務異質性的能力,從而影響了后續任務的學習。具體參見下圖(b)。
AM-LoRA
我們以AM-LoRA為例來進行分析。
微調大語言模型(LLMs)使用低秩適應(LoRA)被廣泛認為是持續學習新任務的有效方法。然而,在處理多個任務連續時,它往往會導致災難性遺忘。為此,AM-LoRA作者提出了一種持續學習方法Attentional Mixture of LoRAs(AM-LoRA),專門針對LLMs。
具體而言,AM-LoRA學習一系列任務的一系列LoRA,以持續學習來自不同任務的知識。由于原始方法需要在每個任務中調整所有參數的LoRA,因此在連續學習多個任務時,單個LoRA的改變容易導致之前任務的知識丟失。因此,作者采用增量學習方法,為每個任務學習一個獨立的LoRA,再用所有任務對應的LoRA共同構成一個任務特定的LoRA序列。
然而,僅僅凍結前任務的 LoRA 參數是不夠的。在推理過程中簡單地將所有 LoRA 特征相加將導致從過去任務中失去信息,從而降低過去任務的性能,容易導致災難性遺忘問題。AM-LoRA的關鍵在于設計了一個注意力機制作為知識混合模塊,以適應地集成每個LoRA的信息。通過注意力機制,AM-LoRA可以有效利用每個LoRA的獨特貢獻,同時減輕它們之間可能導致的災難性遺忘的風險。
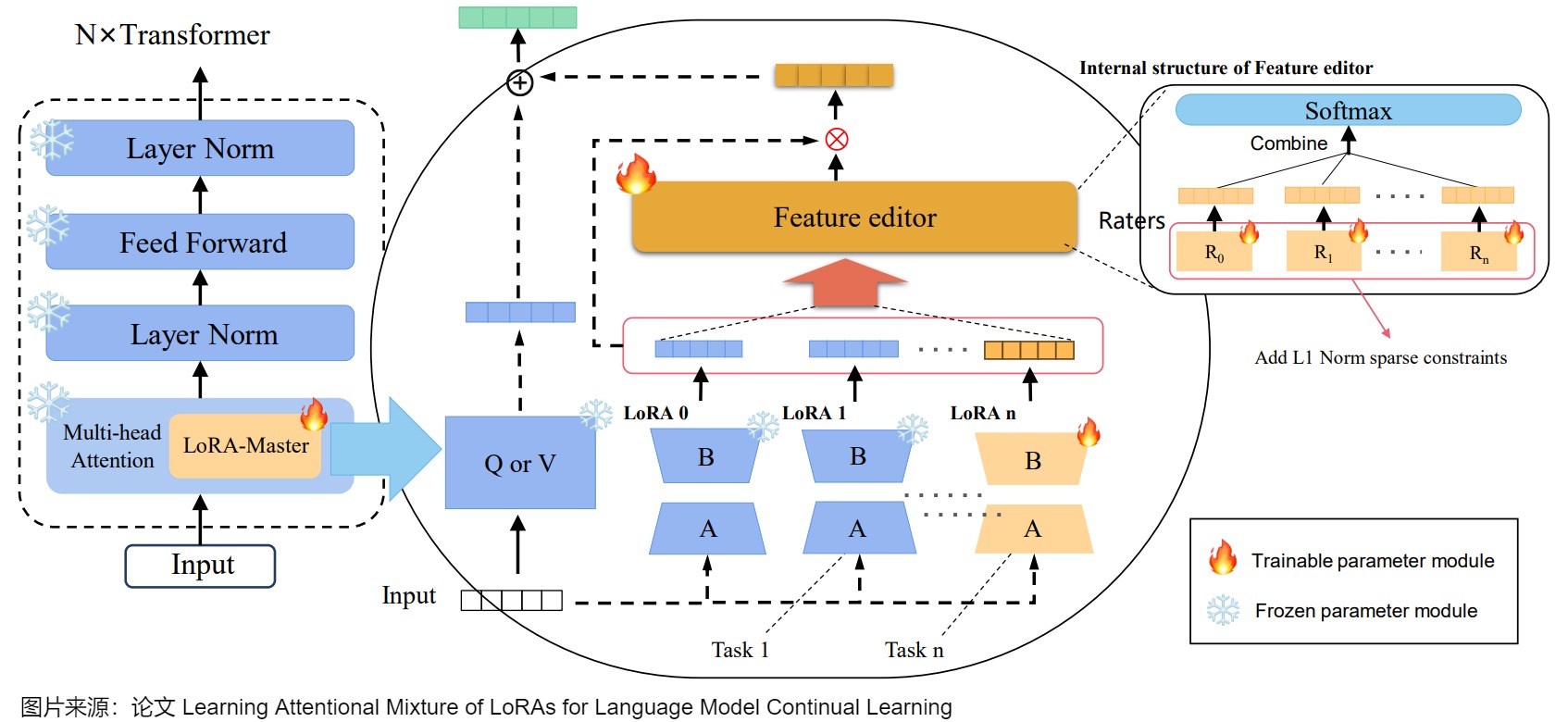
如上圖所示,AM-LoRA由兩部分組成:一個針對特定任務的LoRA矩陣序列和一個負責組合所有LoRA能力的注意力選擇器。其中,LoRA矩陣序列主要負責學習新任務知識。注意力選擇器更專注于學習如何過濾LoRA中的有用知識,以更好地處理新任務。
注意力選擇器
注意力選擇器是AM-LoRA的核心部分,它基于作者設計的用于有效整合特定任務LoRA中的知識的注意力機制。具體來說,注意力選擇器與新任務LoRA矩陣一起添加和訓練。
如上圖右側所示,將每個特定任務的LoRA輸入到注意力選擇器中,然后通過相應的密集層進行非線性變換,該密集層表示為(其中)。接下來,將轉換后的LoRA特征組合在一起并經過softmax函數。然后,在這個狀態下,每個任務的關注度分數就可以得到:

受到ResNet中的殘差連接的啟發,作者在模型中添加了一個零LoRA矩陣,允許模型在學習新任務時選擇不利用之前任務的知識。此外,它還負責在訓練LoRA的第一個任務時分配權重。
具有稀疏約束的損失函數
作者觀察到,在模型學習過程中,模型可能會保留與當前任務無關或有害的特征,導致不同任務之間的知識存在異質沖突。這將對模型的泛化性能和學習效果產生負面影響。為了解決這些問題,作者在學習過程中進一步引入了L1范數,使注意力向量更加稀疏。稀疏約束可以使模型傾向于選擇少數高度相關的LoRA,而不是集體聚合和加權所有LoRA,這可以使模型更準確地執行LoRA選擇,并減少不同任務之間的相互干擾。作者只在Attentional Selector的密集層上添加稀疏約束,這不會影響LoRA序列的學習效果。
0xFF 參考
微調效果超過LoRA還不夠,PiSSA還能減小量化誤差,超越QLoRA和LoftQ
LoRA-FA: Zhang, L., Zhang, L., Shi, S., Chu, X., & Li, B. (2023). Lora-fa: Memory-efficient low-rank tation for large language models fine-tuning. arXiv preprint arXiv:2308.03303.
[2501.00365] Low-Rank Adaptation for Foundation Models: A Comprehensive Review
A Survey on LoRA of Large Language Models
AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning
[Asymmetry in Low-Rank Adapters of Foundation Models])(https://arxiv.org/pdf/2402.16842)
Compressible Dynamics in Deep Overparameterized Low-Rank Learning & Adaptation
CorDA: Context-Oriented Decomposition Adaptation of Large Language Models
DoRA: Weight-Decomposed Low-Rank Adaptation
FLORA: Low-Rank Adapters Are Secretly Gradient Compressors
GPT4技術原理四:重整化群流作為最優輸運 王慶法 [清熙](javascript:void(0)??
https://arxiv.org/abs/2208.04848
HydraLoRA: An Asymmetric LoRA Architecture for Efficient Fine-Tuning
LLM微調系列:一篇超全的Lora綜述,7大秘籍 CourseAI
LoRA Learns Less and Forgets Less
lora 模型的運作原理是怎樣的? 一根呆毛
LoRA+: Efficient Low Rank Adaptation of Large Models
LoRA綜述來了! 浙大《大語言模型的LoRA研究》綜述 深度學習與NLP
Lora綜述:全面系統的理解lora微調 Sherlock Ma
MiLoRA: Harnessing Minor Singular Components for Parameter-Efficient LLM Finetuning
NOLA: COMPRESSING LORA USING LINEAR COMBINATION OF RANDOM BASIS
PISSA: PRINCIPAL SINGULAR VALUES AND SINGULAR VECTORS ADAPTATION OF LARGE LANGUAGE MODELS
Pushing Mixture of Experts to the Limit: Extremely Parameter Efficient MoE for Instruction Tuning
上交大高效微調全面分析|站在分解理論的肩上,見遠高效微調算法,洞察底層邏輯! 小先鋒 [AIGC 先鋒科技](javascript:void(0)??
南開大學提出AM-LoRA | LoRA家族再添一員大將,知識混合+持續學習讓LLM不再遺忘
大模型低秩適應LoRA技術全面綜述:背景、基礎、前沿、應用、挑戰 旺知識
探究大模型微調 Lora 的不同形態(上篇): AdaLora、 AsLora、 PiSSA、 DoRA
最強LoRA方法誕生 | XGBLoRA通過梯度增強逐次學習并合并一系列LoRA以完成高效微調 AI靈魂寫手
本征維度解釋了語言模型微調的有效性 Johnson7788
浙大發表的大語言模型LoRA的綜述 無影寺 [AI帝國](javascript:void(0)??
王文廣揭秘LoRA:低秩適配,大模型高效訓練的降維方法【秒懂人工智能】
AdaLoRA: Zhang, Q., Chen, M., Bukharin, A., He, P., Cheng, Y., Chen, W., & Zhao, T. (2023). Adaptive et allocation for parameter-efficient fine-tuning. arXiv preprint arXiv:2303.10512.
AGHAJANYAN, A., ZETTLEMOYER, L., AND GUPTA, S. Intrinsic dimensionality explains the effectiveness of language model finetuning. arXiv preprint arXiv:2012.13255 (2020).
Delta-LoRA: Zi, B., Qi, X., Wang, L., Wang, J., Wong, K. F., & Zhang, L. (2023). Delta-lora: Fine-tuning high-rank parameters with the delta of low-rank matrices. arXiv preprint arXiv:2309.02411.
DoRA: Liu, S. Y., Wang, C. Y., Yin, H., Molchanov, P., Wang, Y. C. F., Cheng, K. T., & Chen, M. H. (). DoRA: Weight-Decomposed Low-Rank Adaptation. arXiv preprint arXiv:2402.09353.
H. Koubbi, M. Boussard, and L. Hernandez, “The impact of lora on the emergence of clusters in transformers,” 2024.
https://arxiv.org/abs/2202.11737
https://arxiv.org/pdf/2407.05417
https://zhuanlan.zhihu.com/p/663034986
https://zhuanlan.zhihu.com/p/687583780
https://zhuanlan.zhihu.com/p/709734296
https://zhuanlan.zhihu.com/p/719438707
HU, E. J., SHEN, Y., WALLIS, P., ALLEN-ZHU, Z., LI, Y., WANG, S., WANG, L., AND CHEN, W. Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685 (2021).
INTRINSIC DIMENSIONALITY EXPLAINS THE EFFECTIVENESS OF LANGUAGE MODEL FINE-TUNING
J. Liu, J. Wu, J. Liu, and Y. Duan, “Learning attentional mixture of loras for language model continual learning,” arXiv:2409.19611, 2024.
Less is More: Extreme Gradient Boost Rank-1 Adaption for Efficient Finetuning of LLMs.
LoRA+: Hayou, S., Ghosh, N., & Yu, B. (2024). LoRA+: Efficient Low Rank Adaptation of Large Models. v preprint arXiv:2402.12354.
LoRA-drop: Zhou, H., Lu, X., Xu, W., Zhu, C., & Zhao, T. (2024). LoRA-drop: Efficient LoRA Parameter Pruning based on Output Evaluation. arXiv preprint arXiv:2402.07721.
LoRA: Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). Lora: rank adaptation of large language models. arXiv preprint arXiv:2106.09685.
Online-LoRA: Task-free Online Continual Learning via Low Rank Adaptation.
S. Malladi, A. Wettig, D. Yu, D. Chen, and S. Arora, “A kernelbased view of language model fine-tuning,” in Proceedings of the 40th ICML, vol. 202, 23–29 Jul 2023, pp. 23 610–23 641.
Sander, M. E., Ablin, P., Blondel, M., and Peyre, G. Sink- ′ formers: Transformers with doubly stochastic attention. In International Conference on Artificial Intelligence and Statistics, pp. 3515–3530. PMLR, 2022.
Thibeault, V., Allard, A. & Desrosiers, P. The low-rank hypothesis of complex systems. *Nat. Phys.* 20, 294–302 (2024). https://doi.org/10.1038/s41567-023-02303-0
VeRA: Kopiczko, D. J., Blankevoort, T., & Asano, Y. M. (2023). Vera: Vector-based random matrix tation. arXiv preprint arXiv:2310.11454.
X. Wang, T. Chen, Q. Ge, H. Xia, R. Bao, R. Zheng, Q. Zhang, T. Gui, and X. Huang, “Orthogonal subspace learning for language model continual learning,” arXiv:2310.14152, 2023.
Y. Zeng and K. Lee, “The expressive power of low-rank adaptation,” arXiv:2310.17513, 2023.
Zhu J, Greenewald K H, Nadjahi K, Ocariz Borde ′ d H S, Gabrielsson R B, Choshen L, Ghassemi M, Yurochkin M, Solomon J. Asymmetry in lowrank adapters of foundation models. arXiv preprint arXiv.2402.16842, 2024
A Rank Stabilization Scaling Factor for Fine-Tuning with LoRA
LoRA、QLoRA、LoRA+、LongRA、DoRA、MaLoRA、GaLore方案都知道嗎?值得一看!!! 簡單的機器學習
Hayou S, Ghosh N, Yu B. The impact of initialization on lora finetuning dynamics. arXiv preprint arXiv:2406.08447, 2024


 浙公網安備 33010602011771號
浙公網安備 33010602011771號