探秘Transformer系列之(21)--- MoE
探秘Transformer系列之(21)--- MoE
0x00 概要
在足夠的訓練數(shù)據(jù)下,我們可以通過增加參數(shù)和計算預算來擴大語言模型規(guī)模就可以得到更強大的模型。然而,與之相關(guān)的問題是極高的計算成本。而MoE(Mixture-of-Experts/混合專家)架構(gòu)通過條件計算,就可以在保持計算成本適度的情況下實現(xiàn)參數(shù)擴展,提供增強的模型容量和計算效率。簡單理解,MoE就是將多個專家模型混合起來形成一個新的模型。但MoE不是讓一個單一的神經(jīng)網(wǎng)絡處理所有任務,而是將工作分配給多個專門的“專家”,由一個門控網(wǎng)絡決定針對每不同輸入激活哪些專家。

注:全部文章列表在這里,估計最終在35篇左右,后續(xù)每發(fā)一篇文章,會修改此文章列表。
cnblogs 探秘Transformer系列之文章列表
0x01 前置知識
1.1 MoE出現(xiàn)的原因
MoE的出現(xiàn)有幾個主要方面原因:神經(jīng)網(wǎng)絡的稀疏性、神經(jīng)元的多語義性和計算資源的有限性。我們從中也可以看到FFN的部分劣勢。
1.1.1 神經(jīng)網(wǎng)絡的稀疏性
稀疏性是指我們可以僅使用整個系統(tǒng)的某些特定部分執(zhí)行計算。這意味著并非所有參數(shù)都會在處理每個輸入時被激活或使用,而是根據(jù)輸入的特定特征或需求,只有部分相關(guān)參數(shù)集合被調(diào)用和運行。
雖然Transformer構(gòu)建了龐大的參數(shù)網(wǎng)絡,但是它的某些層可能會非常稀疏,即某些神經(jīng)元的激活頻率會低于其他神經(jīng)元。論文“MoEfication: Transformer Feed-forward Layers are Mixtures of Experts”就指出,使用ReLU等激活函數(shù)會導致大部分的激活值都是0,這導致FFNs的激活值非常稀疏。這樣在每次預測過程中,對于用戶當前的問題來說,F(xiàn)FNs 中實際只有一小部分神經(jīng)元被激活并參與計算。而且模型的規(guī)模越大,其稀疏性也越強。大型模型在處理輸入時激活的神經(jīng)元占總體的比例更小。其實,人腦也具備類似的稀疏性。如果對于所有問題,人腦都會使用全部神經(jīng)元,恐怕人腦中的“CPU”早就燒毀了。
1.1.2 神經(jīng)網(wǎng)絡的過載性
對每個輸入,主流深度神經(jīng)網(wǎng)絡都會載入網(wǎng)絡中的所有層和神經(jīng)元,所有模型參數(shù)都會一同參與處理該輸入數(shù)據(jù)。因為上面提到的稀疏性,我們可知這意味著在處理大量參數(shù)的過程中,需要進行大量的不必要的計算。因此,網(wǎng)絡實際上對于它們所做的大多數(shù)預測來說都太大了。LLM 成為世界上最低效和最耗能的系統(tǒng)之一。
除了不受控制的消耗之外,針對每個預測運行整個模型也會對性能產(chǎn)生重要影響,參數(shù)數(shù)量的增加會導致訓練和推理過程中計算復雜度和內(nèi)存消耗的增加。在追求速度和可擴展性的實際應用中部署如此龐大的模型是一項艱巨的任務。
1.1.3 神經(jīng)元的多語義性
隨著應用場景的復雜化和細分化,垂直領(lǐng)域應用更加碎片化,人們對大模型提出了更高的要求,希望一個模型既能回答通識問題,又能解決專業(yè)領(lǐng)域問題。
但是,有研究人員發(fā)現(xiàn),神經(jīng)元具有多義性的特點。也就是說,它們不專注于一個單一的主題,而是專注于許多主題。而且重要的是,它們在語義上可能并不相關(guān)。舉個例子來說,在神經(jīng)網(wǎng)絡數(shù)十億個神經(jīng)元中的一個神經(jīng)元可能每次在輸入主題涉及“蘋果”被激活,而當輸入主題涉及“手機”時,這個神經(jīng)元也可能被激活。這不僅使神經(jīng)網(wǎng)絡難以解釋,而且也不是一個理想的情況。因為單個神經(jīng)元必須精通各種彼此幾乎毫無關(guān)系的主題。想象一下,你必須同時成為神經(jīng)科學和地質(zhì)學的專家,這將是一項艱巨的任務。
而目前不僅僅是知識范圍更加廣泛,多模態(tài)帶來的各自數(shù)據(jù)集都可能各自的數(shù)據(jù)特征完全不同,這導致神經(jīng)元很難獲取知識。更糟糕的是,學習曲線可能相互矛盾,學習一個主題的更多知識可能會影響神經(jīng)元獲取另一個主題知識的能力。
1.1.4 計算資源的有限性
模型規(guī)模是提升模型性能的關(guān)鍵因素之一。而通常來講,模型規(guī)模的擴展會導致訓練成本顯著增加,因此,計算資源的限制成為了大規(guī)模密集模型訓練的瓶頸。
因此,需要一種技術(shù)來拆分、消除或至少緩解這些問題。這就是MoE希望達到的目的。
1.2 MoE的核心理念
MoE 的基本思想是將模型的參數(shù)計數(shù)與其使用的計算量分離。而其背后的理念則是模型的不同組件(即"專家")在處理數(shù)據(jù)的不同任務或特征時具有專門化的能力。這種設計靈感來源于人類社會中的專業(yè)分工。在現(xiàn)實生活中,如果有一個包括了多個領(lǐng)域知識的復雜問題,我們通常會召集一個專家團隊共同解決復雜問題。每位專家都擁有獨特的技能。我們先拆分這個大問題到各領(lǐng)域,把不同的任務先分離出來,這樣才便于分發(fā)給不同領(lǐng)域的專家。然后讓各個領(lǐng)域的專家先逐個解決小問題,最后再把大家集合到一起來匯總結(jié)論,攻克這個任務。
MoE正是基于上述的理念,它由兩個主要部分組成:專家和門控路由機制(或者路由機制)。
- 術(shù)業(yè)有專攻。模型的不同專家(expert)擁有不同領(lǐng)域的專業(yè)知識,負責處理不同的計算任務或者數(shù)據(jù)。每個專家子網(wǎng)絡專門處理輸入數(shù)據(jù)的子集,共同完成一項任務。相較于深度學習網(wǎng)絡, MoE更像是寬度學習網(wǎng)絡。另外,MoE與集成技術(shù)的主要區(qū)別在于,對于MoE,通常只有一個或少數(shù)幾個專家模型針對每個輸入進行運算,是稀疏模型;而在集成技術(shù)中,所有模型都會對每個輸入進行運算,然后通過某種方式來綜合這些模型的輸出,這是密集模型。
- 有條件的計算。既然不同專家負責不同領(lǐng)域,怎么知道要把哪個token送去哪個expert呢?因此我們就需要對神經(jīng)網(wǎng)絡實際運行的程度擁有某種“決策權(quán)”,使得針對特定輸入,只有特定專家被激活并處理(在生成式大模型中,就是根據(jù)token token 來選擇專家的)。這部分工作就由門控機制來完成。其實,MoE的稀疏性與dropout的原理有些類似,MoE是根據(jù)任務的具體情況選擇激活一定數(shù)量的專家模型來完成這個任務,而dropout則是對神經(jīng)網(wǎng)絡中的神經(jīng)元進行隨機性失活。
通過這種范式,模型將計算與參數(shù)解耦,僅激活與特定輸入相關(guān)的專家,既保持了大規(guī)模知識庫的優(yōu)勢,又有效控制了計算成本。而且,MoE能夠在遠少于 Dense 模型所需的計算資源下進行有效的預訓練。這意味著在相同的計算預算條件下,我們可以顯著擴大模型或數(shù)據(jù)集的規(guī)模。這種可擴展且靈活的創(chuàng)新有效遵循了擴展規(guī)律,實現(xiàn)了模型容量的增長而不會導致計算需求的劇增。
0x02 發(fā)展歷史
2.1 重要節(jié)點
下圖是MoE發(fā)展歷史上的一些重要節(jié)點。

2.1.1 Adaptive mixtures of local experts
MoE的開山之作是1991年的論文“Adaptive Mixture of Local Experts"。這篇論文引入了將復雜問題分解為子問題并分配給多個專門模型的思想。這種分而治之的策略成為了 MoE 架構(gòu)的核心。
因為面對多任務學習時,多層網(wǎng)絡的各層之間通常會有強烈的干擾效應,這會導致學習過程變慢和泛化能力差。為了解決這個問題,論文提出了一種新的監(jiān)督式學習方法:由多個獨立子網(wǎng)絡(專家)組成一個系統(tǒng),每個子網(wǎng)絡獨立學習整個訓練數(shù)據(jù)集中的一個子集。模型使用一個門控網(wǎng)絡(gating network)來決定每個數(shù)據(jù)應該被哪個子網(wǎng)絡去訓練,這樣就可以減輕不同類型樣本之間的干擾。在推理時,模型將輸入同時傳遞給不同的子網(wǎng)絡和門控網(wǎng)絡,每個子網(wǎng)絡給出自己的處理結(jié)果,門控網(wǎng)絡會依據(jù)每個子網(wǎng)絡的權(quán)重來決定每個子網(wǎng)絡對當前輸入的影響程度,最終給出所需的輸出。
如何訓練這個系統(tǒng)?如何讓損失函數(shù)整合專家和門控網(wǎng)絡的輸出?論文作者作者提出了兩種思路:鼓勵競爭和鼓勵合作,具體參見下圖。

2.1.2 sparsely-gated mixture-of-experts layer
2017年,論文“Outrageously large neural networks: The sparsely-gated mixture-of-experts layer”首次將MoE引入自然語言處理領(lǐng)域,并提出了Sparse MoE(稀疏MoE)概念。和論文"Adaptive mixtures of local experts"相比,本論文 MoE 的主要區(qū)別如下:
- Sparsely-Gated:不是所有expert都會起作用,而是選擇TopK的專家進行計算,即只激活部分專家對特定輸入進行處理。這是一種條件計算,意味著只有部分專家被激活處理特定的輸入,從而可以大大降低計算量。而且,門控網(wǎng)絡依然為每個輸入同時選取多個專家,使網(wǎng)絡能夠權(quán)衡并整合各專家的貢獻,從而提升性能。這種稀疏性就是MoE可以把模型容量擴大的原因。
- token-level:相比于sample-level,此論文使用了在 token 級別進行處理,一個句子中不同的token使用不同的專家。由于其為每個輸入令牌(token)選擇對應專家的特點,該方法被稱為token選擇門控(token-choice gating)。
本論文之前的MoE中,每個專家都用于每個輸入,但是每個專家的貢獻由一個門控函數(shù)加權(quán),這是一個學習到的函數(shù),它為每個專家計算一個權(quán)重或重要性,使得所有專家的權(quán)重之和為1。由于每個專家都用于每個輸入,這種方法仍然導致一個密集激活的模型,因此沒有解決增加計算復雜度的問題。這種路由選擇算法也叫做軟性選擇路由算法(也稱為連續(xù)混合專家)。本論文使用的路由算法是硬選擇路由算法,運行只有一部分專家用于任何給定的輸入,這標志著從密集激活到稀疏模型的轉(zhuǎn)變。
另外,門控網(wǎng)絡會傾向于收斂到不均衡的狀態(tài),總是為少數(shù)專家產(chǎn)生較大的權(quán)重(相應的參數(shù)更新也會很不均衡)。因此,作者設計了額外的損失函數(shù)來促使所有專家具有同等的重要性,也首創(chuàng)了具有輔助負載平衡損失的可微分啟發(fā)式方法,通過選擇概率對專家輸出進行加權(quán),使門控過程可微分,從而能夠通過梯度優(yōu)化門控函數(shù)。這種方法隨后成為MoE領(lǐng)域的主流研究范式。
本論文也是業(yè)界第一個實施專家并行的方案。

2.1.3 GShard
2021年的論文”GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding“是第一個將MoE的思想拓展到Transformer上的工作。具體而言,GShard 將每間隔一層的FFN層替換為 MoE 結(jié)構(gòu),MoE 中的每個專家都是一個FFN(每個專家大小相同)。每個 Token 都會通過 Gating 選擇不同的專家,默認為 top2。
因為難以控制將token發(fā)給專家的概率,所以在實際操作中,可能某些expert接收到了好多token,而某些expert接收的token寥寥無幾,我們管這種現(xiàn)象叫expert負載不均。這種情況不僅不符合我們MoE的設計初衷(術(shù)業(yè)有專攻),還影響計算效率(例如引起分布式訓練中各卡通訊時的負載不均)。為了緩解“贏者通吃”問題,盡可能讓不同專家處理的token數(shù)盡量均衡,Gshard提出了以下幾種解決辦法:
- 專家容量負載:為了確保負載平衡,GShard強制每個專家處理的token數(shù)量低于某個統(tǒng)一閾值,論文將其定義為專家容量。當token選擇的兩個專家都已經(jīng)超出其容量時,該token被視為溢出token,這些token或者通過殘差連接傳遞到下一層,或被完全丟棄。
- Local group dispatching(本地組調(diào)度):將訓練批次中的所有token均勻劃分為 G 組,即每組包含 S = N/G 個token。所有組均獨立并行處理。通過這種方式,我們可以確保專家容量仍然得到執(zhí)行,并且總體負載保持平衡。
- Auxiliary loss(輔助損失):添加輔助損失函數(shù),對expert負載不均的情況做進一步懲罰。
- 隨機路由:在Top-2 gating的設計下,GShard 始終選擇排名最高的專家,但第二個專家是根據(jù)其權(quán)重比例隨機選擇的。直覺上認為在輸出是加權(quán)平均且次要權(quán)重通常較小的情況下,次要專家的貢獻可以忽略不計。
Gshard也提出了MoE跨設備分片的方法。當擴展到多個設備時,MoE 層在不同設備間共享,而其他所有層則在每個設備上復制。這樣,整個 MoE 層的計算被分散到了多個設備上,每個設備負責處理一部分計算任務。這種架構(gòu)對于大規(guī)模計算非常有效。這也解釋了為什么 MoE 可以實現(xiàn)更大模型參數(shù)、更低訓練成本。

GShard 為后續(xù)所有的 MoE 研究鋪好了路:它證明了稀疏專家是有價值的,還為后來的方案指明了“容量因子”這些關(guān)鍵概念的重要性。
2.1.4 Swith Transformer
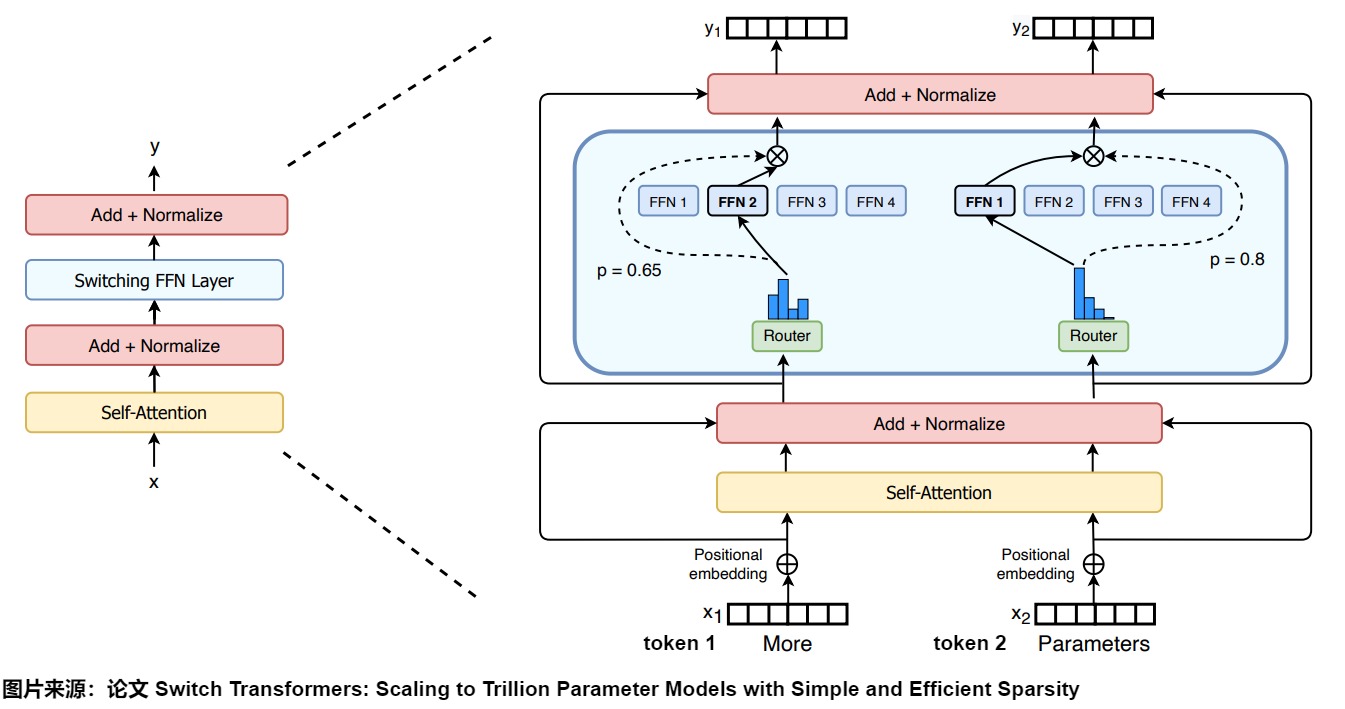
論文”Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity“用稀疏激活的混合專家層替換了Transformer塊中的FFN,同時使用簡化的門控機制使訓練更加穩(wěn)定,從而使 MoEs 成為語言建模應用更現(xiàn)實、更實用的選擇。
Switch Transformer 的指導設計原則是以簡單且計算高效的方式最大化 Transformer 模型的參數(shù)數(shù)量。在此原則指導下,論文做了一些有效努力,包括:簡化稀疏路由、使用高效稀疏路由和增強的訓練和微調(diào)技巧。Switch Transformer 作者發(fā)現(xiàn)僅使用一個專家也能保證模型的質(zhì)量。一個專家可以讓路由計算更簡單,通信量也更少;一個 Token 僅對應一個專家,計算量也更少;平均每個專家對應的 batch size 至少可以減半。因此,Switch Transformer 的門控網(wǎng)絡每次只路由到 1 個 expert,也就是每次只選取 Top1 的專家,而其他的模型都是至少 2 個專家。
2.2 詳細時間線
下圖是2017年之后的若干代表性的MoE模型的時序概覽。時間線主要根據(jù)模型的發(fā)布日期構(gòu)建。位于箭頭之上的MoE模型是開源的,而位于箭頭之下的則是專有閉源模型。來自不同領(lǐng)域的MoE模型用不同顏色標記:自然語言處理( NLP)用綠色,計算機視覺(CV)用黃色,多模態(tài)(multimodal)用粉色,推薦系統(tǒng)(RecSys)用青色。

0x03 模型結(jié)構(gòu)
MoE包括以下核心組件:
- 專家。在MoE架構(gòu)中,專家是專門針對特定任務的子模型。專家擁有不同領(lǐng)域的專業(yè)知識,負責處理不同的計算任務或者特定輸入子空間。形式上,每個專家網(wǎng)絡\(f_i\)(通常是一個linear-ReLU-linear網(wǎng)絡)由參數(shù)W來參數(shù)化,接受輸入x并生成輸出\(f_i(x; W_i)\)。
- 門控函數(shù)(也稱為路由函數(shù)或路由器):門控函數(shù)負責協(xié)調(diào)專家計算,即判定哪個輸入樣本應該由哪些專家處理,哪些專家將被激活并參與到當前的計算中。形式上,門控函數(shù)G(通常由linear-ReLU-linear-softmax網(wǎng)絡組成)由參數(shù)O來參數(shù)化,接受輸入x并產(chǎn)生輸出。
- 聚合層(Combining Layer):聚合層負責整合專家網(wǎng)絡的輸出,以形成最終的輸出結(jié)果。很多資料并沒有把聚合層單獨羅列出來。
整個結(jié)構(gòu)可以用下圖來表示。門控網(wǎng)絡輸出是一個稀疏的n維向量,\(G(x)_i\)是門控網(wǎng)絡給出的第 i 個專家的權(quán)重。\(E_i(x)\) 是第 i 個expert的輸出。那么對于在當前的輸入x,輸出就是所有 experts 的加權(quán)和。

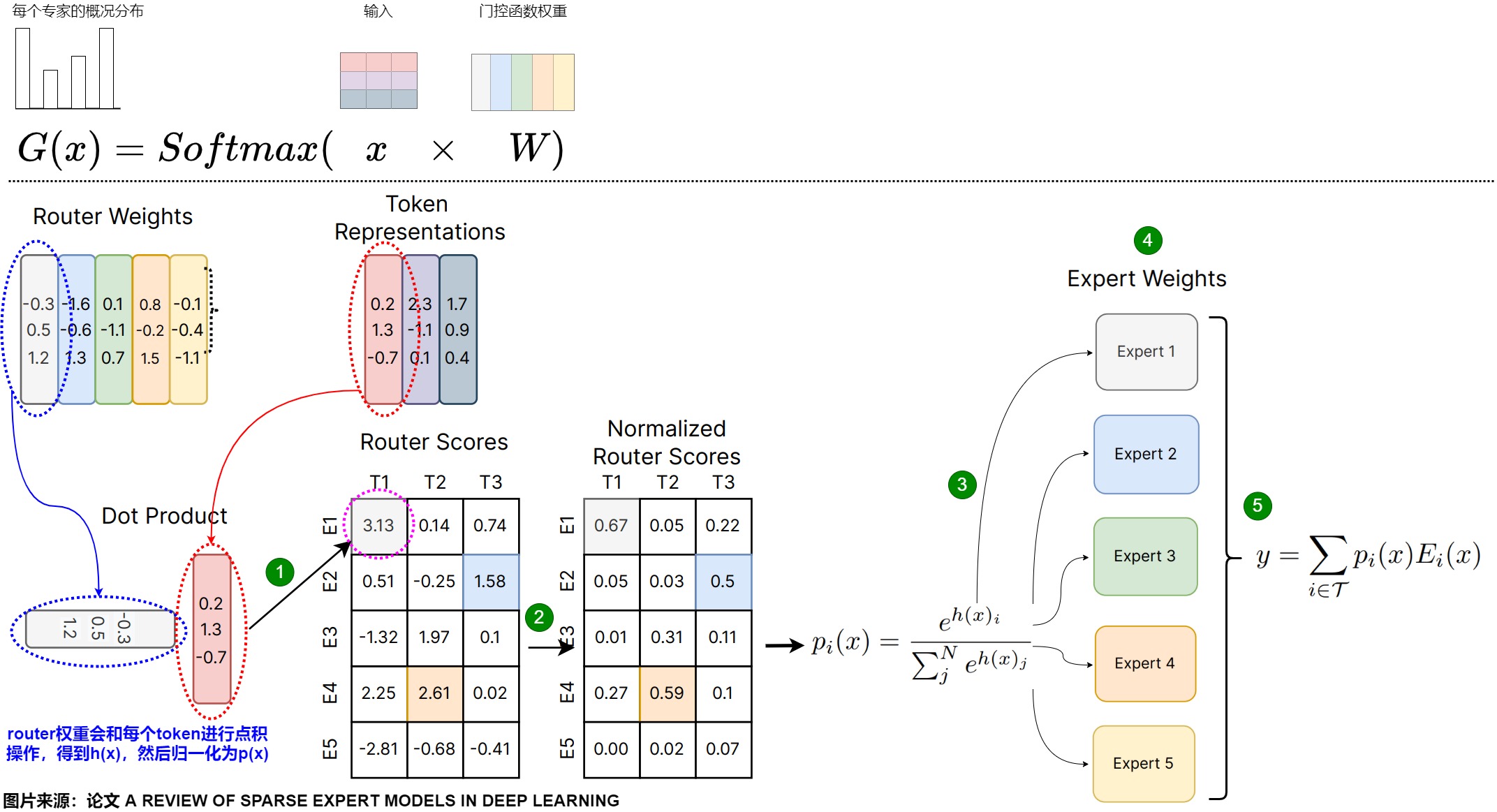
下圖給出了MoE的總體處理流程,具體是如下五步。這里每個專家和token都有顏色編碼,門控網(wǎng)絡權(quán)重(W)有每個專家的表示(顏色匹配)。為了確定路由,路由器權(quán)重對每個token embedding(x)執(zhí)行點積,以產(chǎn)生路由器得分(h(x))。然后將這些分數(shù)歸一化為1(p(x))。G使用了softmax函數(shù)。
- 將輸入token的embedding和門控網(wǎng)絡權(quán)重進行點積,得到門控分數(shù)。在語言建模的上下文中,這里每一列將表示輸入序列中的一個token。因此,每個token可以路由到不同的專家。
- 在門控分數(shù)上施加softmax將門控分數(shù)進行歸一化,得到概率。此概率表示每個專家模型對該token的貢獻程度,即在給定輸入情境下每個專家被激活的概率。或者說此概率表明專家處理傳入token的能力如何。
- 使用此概率分布作為權(quán)重來選擇最佳匹配的專家。
- 專家對輸入token進行處理。
- 專家處理之后,將每個路由器的輸出與每個選定的專家相乘,并對結(jié)果求和。
3.1 門控函數(shù)
3.1.1 條件計算
稀疏激活是 MoE 模型的關(guān)鍵部分和優(yōu)勢之一。與所有專家或參數(shù)對輸入都活躍的密集模型不同,稀疏激活確保只有一小部分專家根據(jù)輸入數(shù)據(jù)被激活。這種方法在保持性能的同時減少了計算需求,因為任何時候只有最相關(guān)的專家是活躍的。
本質(zhì)上,我們現(xiàn)在所談論的MoE 大模型是使用條件計算來強制稀疏激活(Sparse Activation)。條件計算是探討如何分離計算復雜性和計算量需求,并在其之間進行合理的權(quán)衡的理論。在此處的意思是動態(tài)開啟/關(guān)閉神經(jīng)網(wǎng)絡的部分功能。MoE 模型條件計算的核心是學習一個計算成本低的映射函數(shù),該函數(shù)確定網(wǎng)絡的哪些部分——換句話說,哪些專家可以最有效地處理給定的輸入。條件計算在大模型中通常使用路由網(wǎng)絡或者門控網(wǎng)絡來實現(xiàn)。它是判斷選擇使用哪個專家的關(guān)鍵,即在網(wǎng)絡中根據(jù)輸入數(shù)據(jù)有選擇地激活部分單元。在當前的大語言模型中,這是通過對每個 token 進行條件判斷來實現(xiàn)的。當模型輸入一個token時,路由網(wǎng)絡根據(jù)上下文和當前token,選擇合適的專家網(wǎng)絡來計算。這種選擇性激活的直接效果是加快信息在網(wǎng)絡中的傳播速度,無論是在訓練階段還是推理階段。通過條件計算或者稀疏性,大模型能夠在增加模型規(guī)模的同時,降低計算成本,實現(xiàn)了一個合適的均衡。其實大模型推理中常見的早退出機制(Early-Exit)也是一種條件計算,它允許在網(wǎng)絡的早期層級就做出決策并減少計算。
因為是條件計算,所以與具有相同參數(shù)數(shù)量的模型相比,MoE具有更快的推理速度。也因為是條件計算,所以MoE需要把所有專家系統(tǒng)完全加載到內(nèi)存中,所以需要大量顯存。
3.1.2 定義
門控網(wǎng)絡(Gating Network)的設計和實現(xiàn)是Sparsely-Gated MoE 層的核心組成部分。門控網(wǎng)絡負責為每個輸入 token 選擇一個稀疏的專家組合,這些專家將參與到當前的計算中。門控函數(shù)是一個可以執(zhí)行一系列非線性變換的網(wǎng)絡,該網(wǎng)絡對概率分布進行建模,根據(jù)概率去做出相應的選擇。門控網(wǎng)絡由學習到的參數(shù)組成,并且與網(wǎng)絡的其余部分同時進行預訓練。一個典型的門控網(wǎng)絡就是一個帶有 softmax 函數(shù)的簡單網(wǎng)絡。
假定注意力層的輸入數(shù)據(jù)形狀是 (batch_size, seq_len, embedding_size),則門控網(wǎng)絡的大小是 (token_size, expert_num),門控網(wǎng)絡的輸入形狀是 ( batch_size * seq_len, embedding_size), 輸出是 ( batch_size * seq_len, expert_num),即每個token去向每個expert的概率。比如:
gates ( batch_size * seq_len = 3, expert_num = 4):
[
[0.2, 0.4, 0.1, 0.3], # Token A 被分配到不同專家的概率
[0.1, 0.6, 0.2, 0.1], # Token B 被分配到不同專家的概率
[0.3, 0.1, 0.5, 0.1] # Token C 被分配到不同專家的概率
]
門控網(wǎng)絡會學習將輸入發(fā)送給哪個expert,softmax的輸出作為每個專家的最終使用權(quán)重。門控函數(shù)的處理流程如下:
- 計算專家分數(shù)。門控函數(shù)接收單個token的emebdding作為輸入,基于輸入數(shù)據(jù)的特征進行計算,然后輸出一組分數(shù)。這些分數(shù)表示每個專家模型對該token的貢獻程度,或者說是表明專家處理傳入token的能力如何。
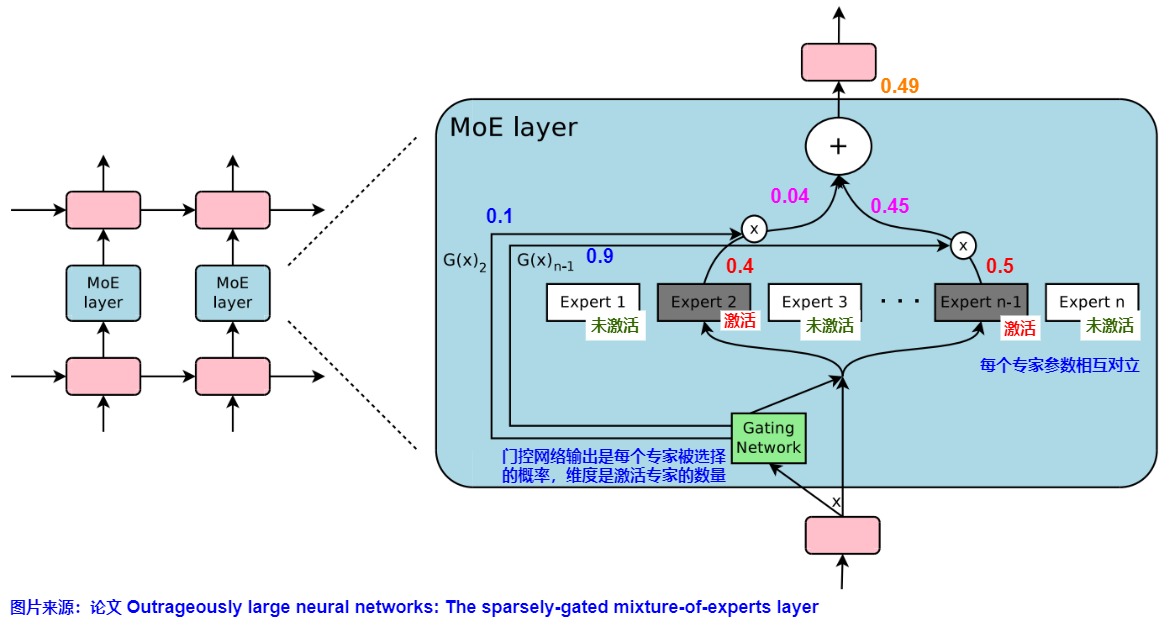
- 計算專家的概率分布。以下圖為例,門控函數(shù)使用softmax對分數(shù)進行處理,得到在給定輸入情境下每個專家被激活的概率分布。這個分布反映了輸入數(shù)據(jù)與各個專家相關(guān)性的大小,概率越高,表示該專家對于當前輸入的預測任務越重要。下圖中選擇了兩個專家,門控函數(shù)輸出的概率是0.1和0.9,說明專家1對該token貢獻是10%,專家2對該token的貢獻是90%。
- 激活專家。門控函數(shù)將每個 Token 作為輸入,并在 expert 上生成一個概率分布,以確定每個 Token 被發(fā)送給哪個 expert。根據(jù)門控輸出的概率分布,一部分專家將被選中并激活。在下圖中,如果使用top2 策略來選擇,因為其它專家的激活概率不到0.1,因此沒有被選中。專家2和專家n-1因為具有較高的激活概率,將被選中參與到后續(xù)的計算中。這意味著,只有這兩個專家的參數(shù)將被用于處理當前的輸入數(shù)據(jù)。假設專家2輸出結(jié)果值是0.4,專家n-1輸出結(jié)果值是0.5,則最終MoE返回選定專家的輸出乘以門值(選擇概率)是0.49。通過同時咨詢多個專家對給定輸入的意見,網(wǎng)絡能夠有效地權(quán)衡并整合他們的貢獻,從而提升性能。
注:在MoE模型中,雖然動態(tài)訓練門控功能是標準做法,但一些研究探索了非可訓練的token選擇門控機制(Non-trainable Token-Choice Gating)。這種機制的主要優(yōu)勢在于不需要額外的門控網(wǎng)絡參數(shù),通過特定的門控機制即可實現(xiàn)全面的負載均衡。比如,Hash Layer采用基于隨機固定門控的方式,通過對輸入token進行哈希,無需訓練門控網(wǎng)絡即可工作。人們還探索了其他更復雜的哈希函數(shù),例如通過對單獨預訓練的Transformer模型產(chǎn)生的token嵌入應用k-means聚類,或者根據(jù)訓練數(shù)據(jù)中token頻率預計算一個哈希表,將token ID映射到專家,從而確保token到專家的分配更加平衡。
3.1.3 特點
我們接下來看看門控函數(shù)的特點。
首先,門控函數(shù)不僅決定在推理過程中選擇哪些專家,還決定在訓練過程中選擇哪些專家。.這是因為只有讓每個專家在訓練期間學習到不同的信息,在推理時,才能知道哪些專家與給定的任務最相關(guān)。
其次,門控函數(shù)逐層都會選擇專家。在具有 MoE 的 LLM 的每個層級中,我們都會找到(某種程度上專業(yè)的)專家。具體參加下圖。

其實,在最微觀層面,每個神經(jīng)元就是一個專家,激活函數(shù)就起到了門控函數(shù)的作用。MoE只是把很多神經(jīng)元聚類成一個專家。
另外,"OpenMoE"和Mixtral都對門控機制進行了分析,其中提到幾個特點如下:
- 上下文無關(guān)的專精化(Context-independent Specialization)。MoE 傾向于簡單地根據(jù) token 級語義對 token 進行路由,即無論上下文如何,某些關(guān)鍵詞經(jīng)常被分配給同一位專家。因為路由規(guī)則和文本的語義主題無關(guān),這說明MoE 模型中的專家各自擅長處理不同的 token,但是專家實際可能并不專門精通某一領(lǐng)域的知識。
- 路由早期習得(Early Routing Learning)。路由在預訓練的早期就已建立,并且基本保持不變,因此 token 在整個訓練過程中始終由相同的專家處理。這或許能啟發(fā)我們設計更高效的路由機制。
- 序列尾部丟棄(Drop-towards-the-End)現(xiàn)象顯著。序列后部的token因?qū)<疫_到容量上限而更容易被丟棄。具體而言,在 MoE 模型中,為了保證負載均衡,通常會為每個專家設置其容量上限。當某個專家的容量達到上限時,該專家將不再接受新的 token 而將其丟棄(Drop)。如果我們從前往后為序列中的 tokens 分配專家,那么序列尾部的 tokens 將有更大的概率被丟棄,這在指令調(diào)優(yōu)數(shù)據(jù)集中更為嚴重。
- 位置的局部性。相鄰的token通常被路由到同一位專家,這表明token在句子中的位置會影響路由選擇,會帶來“高重復率”現(xiàn)象。這有利于減少專家負載的突發(fā)波動,但也可能導致專家被局部數(shù)據(jù)“霸占”。
因此,我們需要了解數(shù)據(jù)集的“局部規(guī)律”,因為一旦數(shù)據(jù)分布換了(比如從新聞文本轉(zhuǎn)到代碼),它原先的路由模式就可能失效。要做大規(guī)模的 MoE,就得好好考慮數(shù)據(jù)特征和專家分配之間的關(guān)系。
3.1.4 優(yōu)化
關(guān)鍵因素
現(xiàn)在MoE 大模型的整體架構(gòu)非常固定,而路由選擇則成了關(guān)鍵。路由算法可以從簡單(在張量的平均值上進行均勻選擇或分箱)到復雜。在決定特定路由算法對問題的適用性的許多因素中,以下幾個經(jīng)常被討論。
- 模型精度。MoE 模型對舍入誤差很敏感,比如 softmax 中的指數(shù)操作可能會產(chǎn)生舍入誤差,導致訓練不穩(wěn)定。 然而,簡單地裁剪(即應用硬閾值以刪除大值)門控函數(shù)輸出的logit 又可能會損害模型性能。
- 平衡負載。我們希望盡可能讓不同專家處理的token數(shù)盡量均衡。目前我們知道最簡單的解決方案是根據(jù) softmax 概率分布選擇前 k 個專家。然而,這種方法會導致訓練負載不平衡:訓練期間,大多數(shù)token都會被分發(fā)給少數(shù)專家,因此這少數(shù)專家積累了大量的輸入token,而其它專家比較空閑,這減慢了訓練速度。與此同時,許多其他專家根本沒有接受過足夠的訓練。因此需要更好的門控函數(shù),以便在所有專家之間更均勻地分配token。
- 高效。如果門控函數(shù)只能串行執(zhí)行,則很難實現(xiàn)負載均衡。假設我們有 E 個專家和N個token,則僅門函數(shù)的計算成本就至少為 O(NE)。在實際工作中,N 和 E的數(shù)量級會很大,門控函數(shù)的低效執(zhí)行將使大部分計算資源(專家)在大多數(shù)時間處于閑置狀態(tài)。因此,我們需要讓門控函數(shù)可以高效并行實現(xiàn)來利用眾多設備。
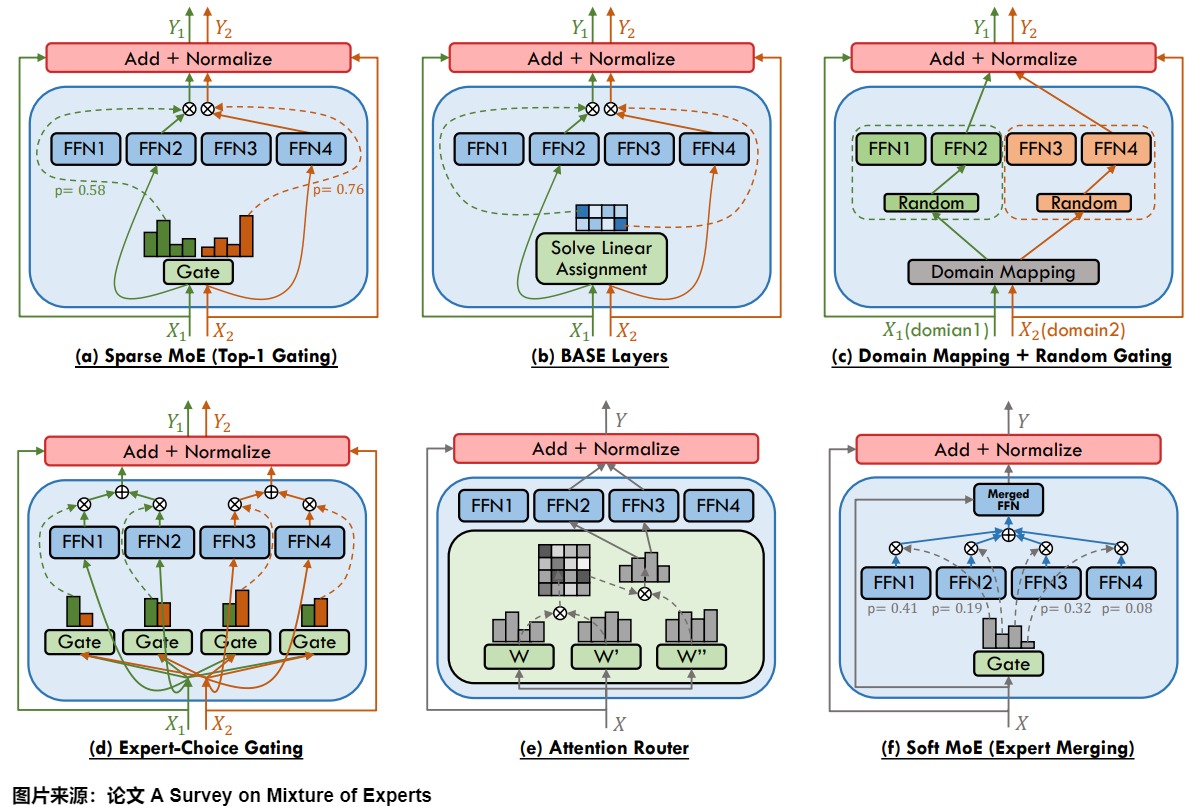
為了達成這些目標,研究人員做了不謝的努力,下圖展示了MoE模型中使用的不同門控函數(shù)。包括 (a)使用top-1門控(top-1 gating)的稀疏MoE;(b)BASE層(BASE layer),(c)組合領(lǐng)域映射與隨機門控(combining domain mapping with stochastic gating),(d)專家選擇門控(expert selection gating),(e)注意力路由器(attention router),以及(f)帶專家合并的軟MoE(soft MoE with expert merging)。這些函數(shù)可能通過各種形式的強化學習和反向傳播進行訓練,做出二元或稀疏且連續(xù)、隨機或確定性的門控決策。
改進示例
我們以論文”O(jiān)utrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer“為例,看看如何對簡單的 softmax 門控函數(shù)做升級,進而滿足需求。
softmax 函數(shù)的問題:softmax 函數(shù)會讓所有專家都會對輸入進行運算,再通過門控網(wǎng)絡的輸出進行加權(quán)求和,如果experts的數(shù)量太大,就會導致計算量非常大。因此,我們需要找到一種方法能使某些專家模型的門控網(wǎng)絡的輸出為0,這樣就沒有必要對這個專家進行相應的計算,就可以節(jié)省計算資源。
普通” top-k 路由策略可以滿足這個需求,其會根據(jù) softmax 概率分布選擇前 k 個專家。即,在Softmax函數(shù)應用于專家權(quán)重之前,執(zhí)行一個KeepTopK操作,將除前k個專家之外的所有專家的權(quán)重設置為-∞。這確保了只有前k個專家在應用Softmax后權(quán)重大于0。因此,這種MoE可以幫助我們在擴大模型規(guī)模的同時保證計算量是非線性增加的(因為每個token只用過topK個expert,不需要使用全量expert),這也是我們說MoE-layer是稀疏層的原因。
普通” top-k 路由策略有一個重要缺點是,門控網(wǎng)絡可能收斂到只激活少數(shù)專家。這是一個自我強化的問題:如果一小部分專家在早期被不成比例地選中,那么這些專家將更快地被訓練,這會導致訓練負載不平衡。而且,相對其它訓練不足的專家,這些更快訓練的專家會輸出更可靠的預測,它們將繼續(xù)被更多地選中。這種不平衡的負載意味著其他專家最終會成為名副其實的累贅。
帶噪聲的 TopK 門控 (Noisy Top-K Gating)能夠緩解這個問題,其在為每個專家預測的概率值中添加了一些高斯噪聲。在MoE模型中加入噪聲的原因主要有以下幾點:
- 提高模型的魯棒性和泛化能力。當模型在訓練或推理階段遇到不確定或嘈雜的數(shù)據(jù)時,魯棒性較強的模型更能保持穩(wěn)定的性能。
- 噪聲會增加一部分的隨機性,減少過擬合的風險。
- 加入噪聲可以實現(xiàn)不同專家之間的負載均衡。
該方案還為專家選擇添加了兩個可訓練的正則化項:最小化負載均衡損失會懲罰過度依賴任何一個專家,而最小化專家多樣性損失會獎勵對所有專家的平等利用。我們用下圖展示下上述解決思路。
- 原始處理流程如下圖標號1,其中門控函數(shù)是softmax。路由策略就是將輸入乘以權(quán)重矩陣并應用 softmax。
- 但是,這種方法并不能保證專家的選擇將是稀疏的。為了解決這個問題,我們首先對輸入進行線性變換,然后再加上一個softmax,這樣得到的是一個非稀疏的門控函數(shù)。對應下圖標號2。
- 但是這樣依然不夠,因此我們在進行softmax之前,先使用一個topk函數(shù),只保留最大的k個值,其他都設為-∞。這樣對于非TopK的部分,由于值是負無窮,這樣在經(jīng)過Softmax之后就會變成 0,不會被選中,就得到了稀疏性。在這個基礎上,我們在輸入上再加上一個高斯噪聲。此處對應下圖標號3。

隨機路由是另一種解決問題的方法,例如,在top-2 設置中的“最佳”專家是使用標準 softmax 函數(shù)選擇的,而第二個專家則是半隨機選擇的(每個專家被選中的概率與其連接的權(quán)重成正比)。因此,排名第二的專家最有可能被選中,但不再保證其肯定被選中。
另一種解決該問題的方法是根據(jù)專家容量的閾值來做調(diào)整。這種方法會設置一個閾值,該閾值定義了任何一個專家可以處理的最大token數(shù)量。還是以 Top-2的專家選擇為例,如果 top-2 中選擇的任何一個專家都已達到容量,則選擇下一個專家(Top3)來處理后續(xù)token。但是,這可能導致token溢出,即超出容量的token無法被指定專家處理。另外,也有研究提出了DSelect-k,這是一種平滑的top-k門控算法,其平滑特性優(yōu)于傳統(tǒng)的top-k方法。
3.2 專家
在 MoE 架構(gòu)中,專家是指訓練好的子網(wǎng)絡(神經(jīng)網(wǎng)絡或?qū)樱鼈儗iT處理特定的數(shù)據(jù)或任務。專家和門控機制都通過梯度下降與其他網(wǎng)絡參數(shù)一起進行聯(lián)合訓練。MoE里的“專家”是一種擬人的形象化的說法,其實,專家在本質(zhì)上是基于某種人類先驗“知識”或“策略”的“跨范疇采樣”。
3.2.1 特點
專家具備如下特點:
-
架構(gòu)。在實際應用中,一般來說,MoE 中的每個專家都是具有相同架構(gòu)的前饋神經(jīng)網(wǎng)絡。但是,我們也可以使用更復雜的體系結(jié)構(gòu)。我們甚至可以通過將每個 Experts 實現(xiàn)為另一個 MoE 來創(chuàng)建“分層”MoE 模塊。在某些情況下,并非所有 FFN 層都被 MoE 取代,例如Jamba模型具有多個 FFN和MoE 層。
![]()
-
參數(shù)子集:FFN層被分解為多個專家,每個專家實際上是FFN參數(shù)的一個子集。專家并不是對FFN的平均切分,實際上我們可以任意指定每個expert的大小,每個expert甚至可以大于原來單個FFN層,這并不會改變MoE的核心思想:對于一個token,部分專家的計算量要小于所有專家的計算量。
-
輸入分割:不同的專家會專注于不同的主題。用更專業(yè)的術(shù)語來說,輸入空間被“區(qū)域化”了(或者說更精細地劃分知識空間)。假設某個 LLM 可能收到的請求是一個“完整的知識空間”,而MoE將輸入數(shù)據(jù)根據(jù)任務類型分割成多個區(qū)域,并將每個區(qū)域的數(shù)據(jù)分配給一個或多個專家模型。
-
專注學習。每個專家模型可以專注于處理自己接受到的輸入數(shù)據(jù),學習數(shù)據(jù)中的一種特定模式或特征。由于這些專家從一開始就存在,在訓練過程中,每個專家都會在某些主題上變得更加專業(yè),而其他專家則會在其他主題上變得更加博學。例如,在圖像分類任務中,一個專家可能專門識別紋理,而另一個專家可能識別邊緣或形狀。
-
靈活擴展和組合作戰(zhàn)。在MoE范式下,只有相關(guān)的專家被激活以處理給定輸入,由于只有相關(guān)的專家被激活,因此可以減少不必要的計算(幫助我們在擴大模型規(guī)模的同時保證計算量是非線性增加的),從而加快模型的推理速度并降低運算成本。而且,MoE可以在減少計算開銷、未相應增加計算成本的情況下擴展模型的參數(shù)空間,從而受益于大量專業(yè)知識。用戶不必聘請一位“無所不知”的專家,而是組建一個擁有特定專業(yè)領(lǐng)域的團隊。這種分工有助于整個模型更高效地處理問題,因為每個專家只處理它最適合的數(shù)據(jù)類型。另外,MoE這也使得模型能夠更加靈活地適應不同的任務,因為不同的任務可能需要不同專家的組合來達到最優(yōu)的預測效果。
我們再用一個示例來看看專家學習到了什么。
從目前的研究成果來看,專家并不專攻“心理學”或“生物學”等特定領(lǐng)域。它最多只是在單詞層面學習句法信息:更具體地說,它們擅長于在特定上下文中處理特定的 tokens。專家學習的信息比整個領(lǐng)域的信息更加細粒度。因此,有時將它們稱為“專家”可能會產(chǎn)生誤導。
Mixtral 8x7B 論文中可以找到一個很好的例子,論文作者測量了所選專家在the Pile驗證數(shù)據(jù)集不同子集上的分布(token分布比例)。下圖顯示了第0、15和31層的結(jié)果(第0層和第31層分別是模型的第一層和最后一層)。論文在根據(jù)主題分配專家時沒有觀察到明顯的模式。例如,在所有層次上,ArXiv論文、生物學和哲學文檔的專家分配分布都非常相似。真有針對數(shù)學的專家的分布才略有不同。這種差異可能是數(shù)據(jù)集的合成性質(zhì)及其對自然語言的有限覆蓋的結(jié)果,在第一層和最后一層尤其明顯,其中隱藏狀態(tài)分別與輸入和輸出嵌入非常相關(guān)。這表明門控網(wǎng)絡確實表現(xiàn)出一些結(jié)構(gòu)化的句法行為。
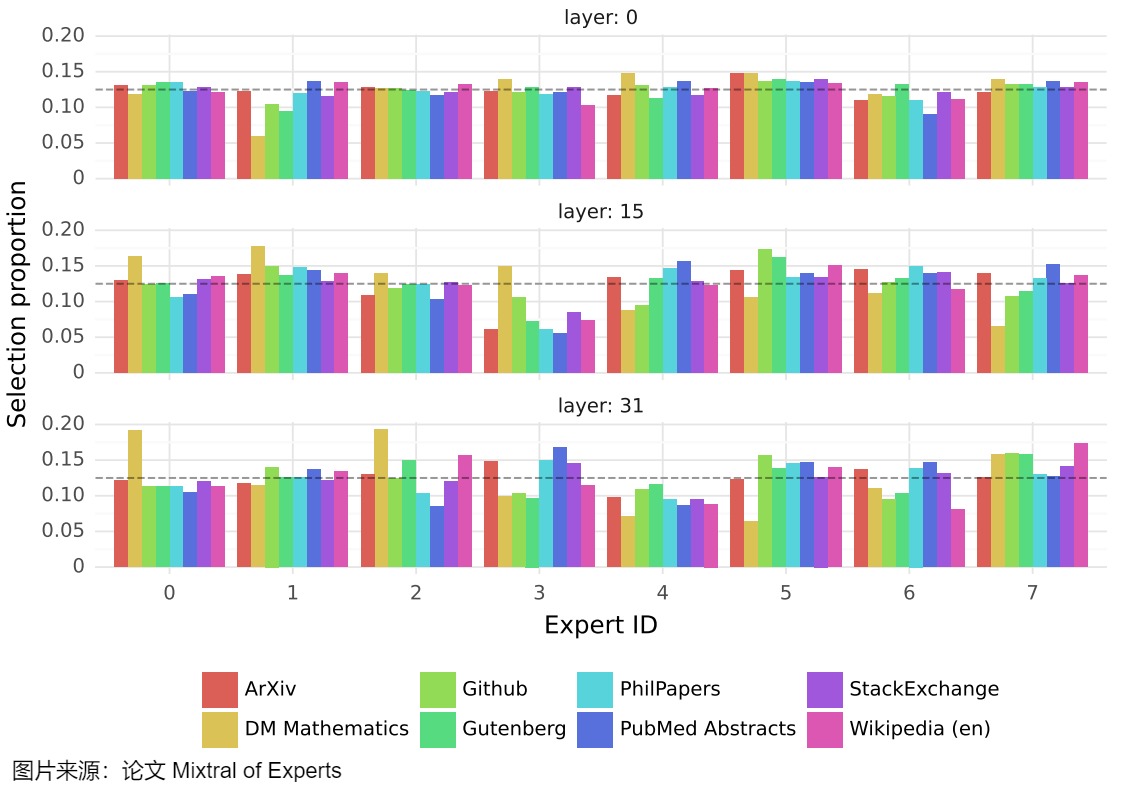
因此,盡管專家似乎沒有專業(yè)知識,但他們似乎確實被一致地用于某些類型的token。下圖顯示了來自不同領(lǐng)域(Python代碼、數(shù)學和英語)的文本示例,其中每個標記都用與其所選專家對應的背景顏色突出顯示。該圖顯示,Python中的“self”和英語中的“Question”等單詞經(jīng)常通過同一個專家傳遞,即使它們涉及多個標記。同樣,在代碼中,縮進標記總是分配給相同的專家,特別是在隱藏狀態(tài)與模型的輸入和輸出更相關(guān)的第一層和最后一層。我們還從圖中注意到,連續(xù)的token通常分配給相同的專家。事實上,論文作者確實在The Pile數(shù)據(jù)集中觀察到了一定程度的位置局部性。

因此,也有研究認為,專家提升的是記憶效果而不提升推理能力。比如論文“Mixture of Parrots: Experts improve memorization more than reasoning”研究了Mixture-of-Experts(MoE)架構(gòu)性能和推理上的理論局限性,探討了與標準密集型Transformer在記憶和推理方面的性能差異。研究發(fā)現(xiàn),隨著專家數(shù)量的增加,MoE模型在記憶任務上的表現(xiàn)提升,而在推理任務上達到飽和。論文也通過實證證明了MoE在特定記憶密集型任務上的優(yōu)越性。
另外,MoE模型實際上還提供了一種細粒度的方式來研究和理解模型內(nèi)部的工作機制。通過觀察哪些專家被激活以及它們?nèi)绾坞S著時間變化,研究人員可以更深入地洞察模型是如何學習和泛化知識,以及它是如何處理不同的輸入特征的。
3.2.2 種類
專家的網(wǎng)絡類型通常有如下幾種:
- 前饋網(wǎng)絡(Feed-Forward Network):因為FFN層比自注意力層更加稀疏,且展示出更多的領(lǐng)域特定性,所以目前大多數(shù)MoE都是FNN的替代品。比如,有研究人員發(fā)現(xiàn),大多數(shù)輸入僅激活FFN的少量神經(jīng)元,突顯了FFN的內(nèi)在稀疏性。對于同樣輸入,F(xiàn)FN層僅激活20%的專家,而自注意力層激活了80%的專家。預訓練Transformer中的模塊化涌現(xiàn)現(xiàn)象(Emergent Modularity)也揭示了神經(jīng)元激活與特定任務之間的顯著關(guān)聯(lián),支持了MoE結(jié)構(gòu)反映預訓練Transformer模塊化特性的觀點。另外,從參數(shù)量的角度我們也可以看到選擇的原因,因為隨著模型規(guī)模增長,F(xiàn)FN的計算開銷呈現(xiàn)急劇上升趨勢。例如,在擁有5400億參數(shù)的PaLM模型中,約90%的參數(shù)分布在FFN層。
- 注意力(Attention):盡管MoE研究主要集中在Transformer架構(gòu)的FFN層,也有研究人員提出了多頭注意力專家混合(Mixture of Attention Heads, MoA),將多頭注意力層與MoE結(jié)合,以提升性能并降低計算成本。MoA使用兩組專家(查詢投影和輸出投影),通過共同的門控網(wǎng)絡選擇相同的專家。為降低計算復雜度,MoA在所有注意力專家間共享\(W_K\)和\(W_V\)投影權(quán)重,專家僅在各自的查詢(\(q_tW^q_t\))和輸出投影權(quán)重(\(o_{i,t}W^O_i\))上有所區(qū)別,從而實現(xiàn)鍵(\(KW_K\))和值(\(VW_V\))序列的預計算共享。
- 其他類型。有些研究人員還探索了使用卷積神經(jīng)網(wǎng)絡(CNN)作為專家,也有將參數(shù)高效微調(diào)(PEFT)技術(shù)與MoE結(jié)合的努力,例如采用低秩適應(LoRA)作為專家。

3.2.3 位置
我們接下來看看專家如何嵌入到Transformer架構(gòu)中。下圖給出了一些實例。
- (a)展示了MoE與注意力機制中的Key和Value模塊的集成。
- (b)表示MoE在FFN中的應用。
- (c)指的是MoE在Transformer塊層級的集成,其中應用了兩組不同的專家到注意力和FFN層,分別為每個層分配專家,并通過各自的門控機制進行調(diào)控。
- (d)展示了MoE在每一層的集成,其中每個Transformer層視為一個統(tǒng)一體,門控機制協(xié)調(diào)專家之間的交互。

3.3 分類
之前的學習中,我們大致了解到了MoE有不同種類,此處我們再從最本質(zhì)的角度(門控函數(shù))來看看如何把MoE分類。門控函數(shù)是MoE架構(gòu)的核心,它負責協(xié)調(diào)專家網(wǎng)絡的參與并整合其輸出。根據(jù)輸入處理方式的不同,門控機制可分為稀疏型、稠密型和軟性三類。稀疏門控只激活部分專家,稠密門控激活所有專家,而軟性門控包括全微分方法,如輸入token合并和專家合并。三種門控函數(shù)的特點如下:
- 稀疏門控:僅激活部分專家,包括基于token選擇的top-k門控策略,以及使用輔助損失函數(shù)來促進專家間token均勻分布。
- 稠密門控:激活所有專家,在LoRA-MoE微調(diào)中表現(xiàn)出色,因為它可以有效地將多個LoRA整合到各種下游任務中。
- 軟性(soft)門控:通過token或?qū)<液喜⒌姆绞綄崿F(xiàn)完全可微性,避免了離散專家選擇的問題,例如SMEAR、Lory和Omni-SMoLA。
根據(jù)門控函數(shù)的設計,MoE層可以大致分為以下兩類:稠密MoE和稀疏MoE。
- 稠密MoE層在每次迭代中激活所有專家網(wǎng)絡\(f_1...f_N\)。稠密MoE能充分利用所有參數(shù),捕獲潛在的復雜的模式和關(guān)系,因此通常能獲得更高的預測精度,但計算開銷較大。因此這種方法在早期研究中被廣泛采用,近期有研究(EvoMoE、MoLE、LoRAMoE和DSMoE)重新探討了稠密MoE的應用。因為稀疏激活專家雖然在計算效率上有優(yōu)勢,但當總參數(shù)量相同時,往往會導致性能損失。而在LoRA-MoE微調(diào)中,由于LoRA專家的計算開銷較小,稠密激活表現(xiàn)出色。這種方法能夠有效地將多個LoRA整合到各種下游任務中,既保持了原始預訓練模型的生成能力,又維持了每個任務特定LoRA的獨特性
- 稀疏MoE層在每次前向傳遞中僅激活選定的專家子集。稀疏型MoE不是匯總所有專家的輸出,而是通過僅計算前k個專家輸出的加權(quán)和來實現(xiàn)稀疏性。稀疏激活實際上是計算需求與模型性能之間的一種權(quán)衡策略。
下圖展示了兩種MoE的特點。右側(cè)是示意圖,左側(cè)是門控函數(shù)以及負載函數(shù)。
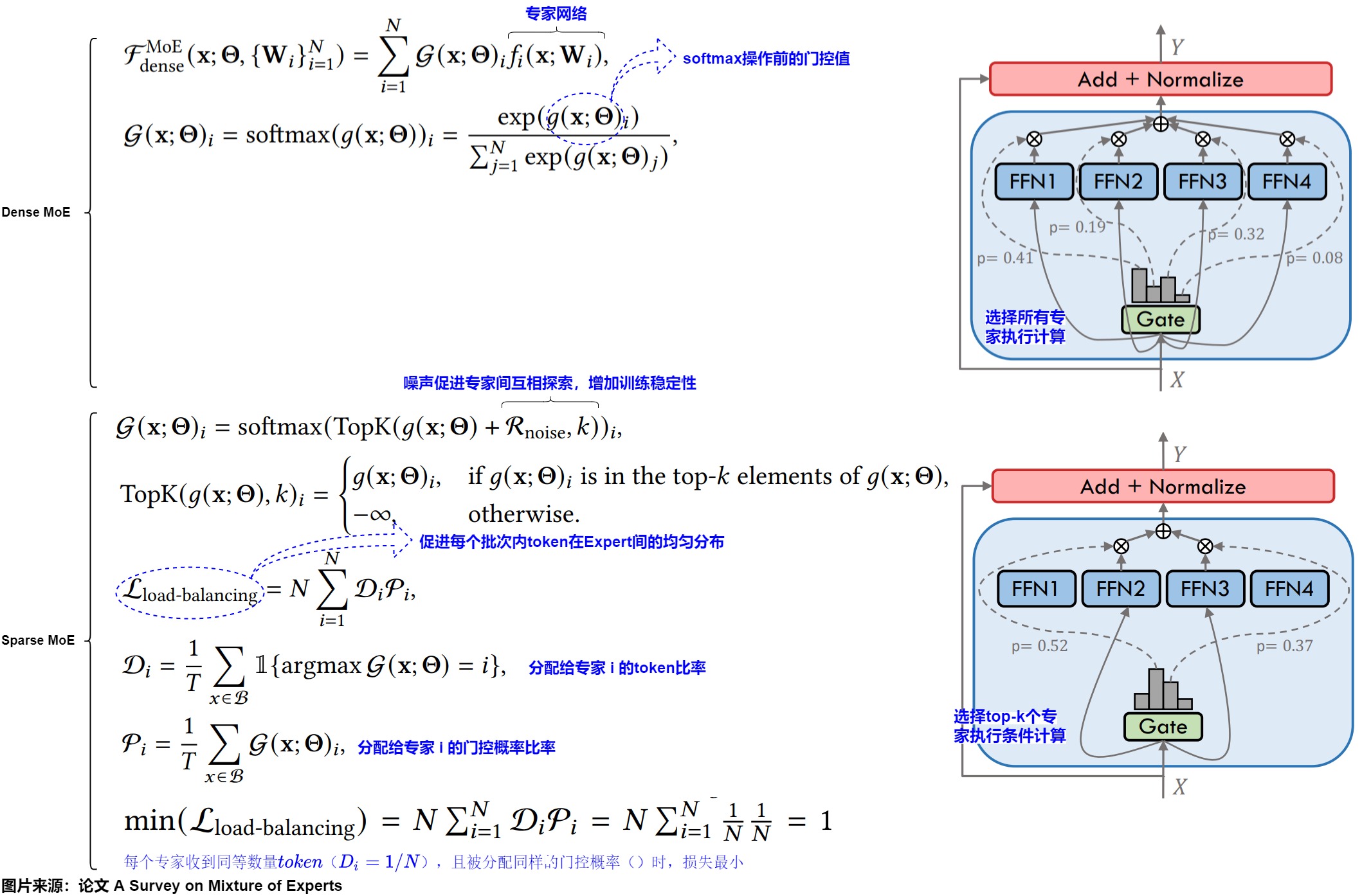
3.3.1 稠密 vs 稀疏
我們通過例子來對稠密和稀疏MoE進行比對。
以人類分工為例。稠密就是類似手工業(yè)時代的生產(chǎn)模式。在這種模式下,每個工人(即神經(jīng)元)都需要參與處理所有類型的任務,就像手工業(yè)時代的工匠需要精通產(chǎn)品制作的各個環(huán)節(jié),掌握所有的生產(chǎn)技能。這種方法雖然直觀且易于實現(xiàn),但在面對復雜多變的任務時,往往效率低下且難以擴展。稀疏MoE則是工業(yè)革命之后的分工模式:每個崗位(專家)只需要完成一部分生產(chǎn)任務。這種分工的方式大大提高了生產(chǎn)效率,推動了工業(yè)化的進程,開啟了機器大工業(yè)的時代。

3.3.2 軟性(soft)門控
論文”A Survey on Mixture of Experts“中提出軟性(soft)門控這種類型,以突出其通過門控加權(quán)合并輸入token或?qū)<襾砭徑庥嬎阈枨蟮奶攸c。為了為每個輸入token分配適當?shù)膶<遥∈栊訫oE通常需要啟發(fā)式輔助損失來確保專家參與的平衡。在涉及分布外數(shù)據(jù)的場景中,這些問題變得更加突出。與密集MoE類似,軟MoE方法通過利用所有專家處理每個輸入來保持完全的可微性,從而避免了離散專家選擇所固有的問題。
- token合并(Token Merging):Soft MoE摒棄了傳統(tǒng)的稀疏和離散門控機制,采用軟分配策略來合并token。該方法計算所有token的加權(quán)平均值,權(quán)重取決于token和專家的關(guān)系,然后用相應專家處理每個加權(quán)平均結(jié)果。然而,token合并使其難以應用于自回歸解碼器,因為在推理時無法獲取用于加權(quán)平均的未來token。
- 專家合并(Expert Merging):SMEAR框架通過加權(quán)平均合并所有專家參數(shù)來避免離散門控。SMEAR的作者認為,傳統(tǒng)稀疏MoE模型難以匹敵參數(shù)量相當?shù)某砻苣P突蚴褂梅菍W習啟發(fā)式門控函數(shù)的模型,可能是由于非可微、離散門控決策的訓練模塊中存在梯度估計偏差。SMEAR通過單個合并專家處理輸入token,既不顯著增加計算成本,又支持標準梯度訓練。
3.4 比對
論文“A Uniffed View for Attention and MoE”把注意力機制和MoE做了比對。Attention 結(jié)構(gòu)的作用其實就是使用加權(quán)和的形式來聚合不同 token 的信息。MoE 其實是通過線性投影來學習一個 Router, 基于 Router 來聚合不同 expert 的信息. 本質(zhì)上來說, router 的輸出經(jīng)過 top-k+softmax 來學習一個加權(quán)求和的權(quán)重, 最終聚合不同 token 的信息。
兩者的相似之處:
- 都使用了 softmax 來歸一化權(quán)重,本質(zhì)上也是希望學習穩(wěn)定。
- 本質(zhì)都是對新特征的加權(quán)和。
- 都是動態(tài)權(quán)重, 根據(jù)輸入來自適應地聚合信息。
二者的區(qū)別在于
- Attention 是聚合不同 token 的信息,MoE 是聚合不同地 Expert。
- Attention 會用上所有 token (Softmax 結(jié)果為正數(shù),故所有 token 都會用上);MoE 是一種稀疏選擇,只會選擇部分結(jié)果。
Attention和MoE都是學習一個權(quán)重來聚合信息,可以總結(jié)到如下圖標號3所示,f是權(quán)重, g 是學習到的新特征。具體如下圖。

從計算機體系結(jié)構(gòu)的視角來看也有啟發(fā)。注意力機制(含F(xiàn)FN)類似把所有上下文都放在內(nèi)存中。MoE則可以理解為頁表系統(tǒng),需要的時候才把專家對應的頁表放到內(nèi)存中。
0x04 計算流程
4.1 算法
下圖是top-k門控函數(shù)算法的偽代碼,具體流程如下。
- 給定輸入x,使用門控函數(shù)計算出得分score = G(x)。
- 選出前k的分數(shù)對應的索引。
- 遍歷索引,使用索引對應的專家來進行計算,得到推理結(jié)果。
- 使用分數(shù)作為權(quán)重對專家計算的結(jié)果值進行修正。
- 綜合這k個專家的結(jié)果作為最終推理結(jié)果。

4.2 流程
MoE的整個計算過程如下圖所示:
- Routing。Routing也叫“experts selection”或者稀疏性激活,本質(zhì)上是對門控函數(shù)的使用,是MoE的核心理念。Routing是一個對輸入進行多分類的鑒別過程,目的是確定最適合處理輸入的專家模型。在語言模型的應用中,當輸入token通過MoE層時,Token通過和Router的權(quán)重矩陣相乘得到一個Expert Indices(決策矩陣)和一個概率張量,即索引和概率:
- Expert indices是expert-to-token映射,用于指示每個token被分配給了哪個expert。即張量中第i個值代表本token應該分配到第i個專家。
- Probabilities張量是分配置信度的概率,其中第i個值代表這個專家對于該token最終結(jié)果的權(quán)重。
- Permutation(排列/置換)。根據(jù)路由決策(expert-to-token映射)將Token分配給對應的專家。其間可能會依據(jù)專家的容量對token進行丟棄操作。
- Computation。專家依據(jù)分配到的經(jīng)過Permutation重排序的tokens進行計算。通過使每個專家專注于執(zhí)行特定任務,這一方法實現(xiàn)了計算的高效性。這種方式允許模型對不同類型的輸入數(shù)據(jù)進行個性化處理,提高了整體效率和性能。每個專家網(wǎng)絡并行處理其分配到的token,計算輸出。這一步涉及到塊稀疏矩陣乘法,其中輸入矩陣 ??″ 與專家網(wǎng)絡的權(quán)重矩陣相乘。設 ?? 為專家網(wǎng)絡的權(quán)重矩陣,則專家網(wǎng)絡的輸出可以表示為: ??=??″×?? ,其中 ?? 為所有專家網(wǎng)絡輸出的匯總結(jié)果。
- Un-Permutation。收集專家的計算結(jié)果。這是Permutation的逆運算,目的是為了將從各個experts收集到的處理后的tokens組合成一個完整的序列,這個序列保持了原始tokens的順序。即,將每個專家網(wǎng)絡的輸出根據(jù)原始的token順序重新排列。設 ?? 為所有專家網(wǎng)絡輸出的匯總結(jié)果,則反排列操作可以表示為: ??′=scatter(??,??????????????) ,其中 ??′ 為最終的模型輸出, scatter 操作根據(jù) ?????????????? 中的索引將 ?? 中的輸出重新排列以匹配原始的token順序。接著使用Routing步驟生成的分配置信度概率對結(jié)果進行縮放(加權(quán)求和),以得到最終的模型輸出,然后將這個結(jié)果繼續(xù)向下游處理。

因為Permutation相對復雜,我們接下來仔細分析。
4.3 Permutation
Permutation的主要作用是:
- 分發(fā)token。Permutation會依據(jù)Expert Indices構(gòu)建本地的置換Token位置的后的臨時矩陣(將輸入Token根據(jù)路由結(jié)果重新排列),這樣可以把屬于每個專家的token分別放在一起,然后把tokens送給對應的專家。使得每個專家網(wǎng)絡可以并行處理其分配到的token,以確保模型可以充分利用GPU的并行計算能力。比如上圖中,“the”和“jumped”應該分配給專家1,所以就把它們放在一起。“quick”和“fox"都應該被發(fā)送給專家2,所以把它們也放在一起。
- 維持token和expert的順序。因為一個batch里有很多token,我們將這些token發(fā)往不同的expert做計算后,專家輸出結(jié)果的順序肯定是打亂的,所以需要通過一種方式追蹤順序,把token permute回正常的位置再輸入下一層網(wǎng)絡。通過構(gòu)建的矩陣,Permutation在計算時,就可以維護住這種順序。
- 負載均衡。Permutation可以實現(xiàn)輸入數(shù)據(jù)在不同專家之間的合理分配,以平衡各個專家的計算負載。不同的輸入樣本可能對不同專家的計算資源需求不同。通過對輸入樣本進行置換,使得每個專家能夠相對均勻地接收到需要處理的樣本,避免某些專家過度使用而其他專家閑置的情況。
- 增加多樣性。Permutation可以增加模型對輸入數(shù)據(jù)處理的多樣性。因為不同的置換順序可能會導致不同專家組合對數(shù)據(jù)進行處理,從而挖掘出數(shù)據(jù)的不同特征。
從代數(shù)的角度來看,MoE計算實際上是對token進行一次置換群的操作:\(P \ concat(Experts) \ P^{-1}\)。P(permutation操作)為一個進行Token位置置換的稀疏矩陣,實際上也構(gòu)成了代數(shù)上的一個置換群的結(jié)構(gòu),\(P^{-1}\)需要對Token進行還原,保證原有的Token順序輸出到下一層。MoE實現(xiàn)的本質(zhì)問題是:基于Permutation矩陣后構(gòu)建的稀疏矩陣乘法如何進行并行。
4.4 實現(xiàn)
4.4.1 Mistral Inference
我們首先用https://github.com/mistralai/mistral-src來學習,此代碼相對簡單易懂。其中,gate是門控函數(shù),在使用時會用配置如下:gate=nn.Linear(dim, moe.num_experts, bias=False)。
假設我們定義了4個專家,路由取前2名專家,即num_experts=4, num_experts_per_tok=2,同時詞嵌入大小為32。MoE接收注意力層的輸出作為輸入X,即將輸入從(batch_size,sequence_length,input_dim)的形狀[2, 4, 32]投影到對應于(batch_size,sequence_length,num_experts)的形狀[2, 4, 4],其中num_experts即expert=4。然后通過torch.topk 將張量轉(zhuǎn)換為[2, 4, 2]。torch.topk返回的selected_experts可以理解為對于每個token選中的兩個專家的序號索引。

具體代碼如下。
import dataclasses
from typing import List
import torch
import torch.nn.functional as F
from simple_parsing.helpers import Serializable
from torch import nn
@dataclasses.dataclass
class MoeArgs(Serializable):
num_experts: int # 專家數(shù)量
num_experts_per_tok: int # 每一個token被分配給幾個專家
# gate=nn.Linear(dim, moe.num_experts, bias=False)
class MoeLayer(nn.Module):
def __init__(self, experts: List[nn.Module], gate: nn.Module, moe_args: MoeArgs):
super().__init__()
assert len(experts) > 0
self.experts = nn.ModuleList(experts)
self.gate = gate
self.args = moe_args
def forward(self, inputs: torch.Tensor) -> torch.Tensor:
gate_logits = self.gate(inputs) # 通過門控網(wǎng)絡獲得各個專家的logits
# 取出topk(k=2)專家的權(quán)重以及專家索引
weights, selected_experts = torch.topk(gate_logits, self.args.num_experts_per_tok)
#使用softmax來歸一化權(quán)重
weights = F.softmax(weights, dim=1, dtype=torch.float).to(inputs.dtype)
# 創(chuàng)建形狀和x一致,初始值為0的矩陣,用來存儲每個expert的輸出
results = torch.zeros_like(inputs)
for i, expert in enumerate(self.experts): #遍歷每一個專家
# selected_experts == i 得到的是一個矩陣,行為token的idx,列為專家的idx
batch_idx, nth_expert = torch.where(selected_experts == i)
# 每一個token的結(jié)果都是由2個專家的結(jié)果進行加權(quán)求和得到的
# 利用None來增加維度,新增維度大小為1,有幾個None就會增加幾個維度。
results[batch_idx] += weights[batch_idx, nth_expert, None] * expert(inputs[batch_idx])
return results
使用代碼如下,可以看到,門控網(wǎng)絡就是nn.Linear的實例,而專家網(wǎng)絡是FeedForward的實例。
class FeedForward(nn.Module):
def __init__(self, args: TransformerArgs):
super().__init__()
self.w1 = nn.Linear(args.dim, args.hidden_dim, bias=False)
self.w2 = nn.Linear(args.hidden_dim, args.dim, bias=False)
self.w3 = nn.Linear(args.dim, args.hidden_dim, bias=False)
def forward(self, x) -> torch.Tensor:
return self.w2(nn.functional.silu(self.w1(x)) * self.w3(x))
class TransformerBlock(nn.Module):
def __init__(self, args: TransformerArgs):
super().__init__()
self.n_heads = args.n_heads
self.dim = args.dim
self.attention = Attention(args)
self.feed_forward = MoeLayer(
experts=[FeedForward(args=args) for _ in range(args.moe.num_experts)],
gate=nn.Linear(args.dim, args.moe.num_experts, bias=False),
moe_args=args.moe,
)
self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps)
self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps)
self.args = args
def forward(
self,
x: torch.Tensor,
freqs_cis: torch.Tensor,
positions: torch.Tensor,
mask: Optional[torch.Tensor],
) -> torch.Tensor:
r = self.attention.forward(self.attention_norm(x), freqs_cis, positions, mask)
h = x + r
r = self.feed_forward.forward(self.ffn_norm(h))
out = h + r
return out
4.4.2 Mixtral 8x7B
我們在用Mixtral 8x7B來學習,此實現(xiàn)更加復雜。代碼來源:transformers/src/transformers/models/mixtral
下面是MoE層的代碼。此處要重點介紹下代碼中的掩碼矩陣。因為在MoE中,并不是所有的輸入都要經(jīng)過所有的專家。通常只有一部分輸入經(jīng)過特定的專家進行處理。因此使用掩碼矩陣來決定決定哪些輸入token與哪些專家進行交互。掩碼矩陣的使用有多種可能,比如對于一個輸入batch,掩碼矩陣可以:
- 指定每個輸入樣本是由專家 1 處理,還是專家 2 處理,或者專家 3 處理,或者是其中幾個專家的組合來處理。
- 也可以當掩碼矩陣中的某個元素為 1,表示對應的token和專家之間有連接(即該專家會處理這個輸入),0則表示沒有連接。
- 也可以結(jié)合專家容量用到填充上。
另外,在訓練過程中,Mask 矩陣還用于正確地計算和更新專家的參數(shù)。因為只有與輸入有連接的專家才應該對這個輸入的損失產(chǎn)生貢獻,通過 Mask 矩陣可以準確地計算每個專家的梯度,從而正確地更新專家的參數(shù),避免錯誤地更新那些沒有處理特定輸入的專家的參數(shù)。
class MixtralSparseMoeBlock(nn.Module):
"""
This implementation is
strictly equivalent to standard MoE with full capacity (no
dropped tokens). It's faster since it formulates MoE operations
in terms of block-sparse operations to accomodate imbalanced
assignments of tokens to experts, whereas standard MoE either
(1) drop tokens at the cost of reduced performance or (2) set
capacity factor to number of experts and thus waste computation
and memory on padding.
"""
def __init__(self, config):
# 初始化了MoE層中使用到的各個部分參數(shù)
super().__init__()
self.hidden_dim = config.hidden_size
self.ffn_dim = config.intermediate_size
# 設置專家數(shù)量
self.num_experts = config.num_local_experts
# 設置要選擇的topk專家數(shù)量
self.top_k = config.num_experts_per_tok
# gating
# 初始化線性層作為門控機制
self.gate = nn.Linear(self.hidden_dim, self.num_experts, bias=False)
# 創(chuàng)建專家網(wǎng)絡的列表,每個專家是一個 MixtralBlockSparseTop2MLP 實例
self.experts = nn.ModuleList([MixtralBlockSparseTop2MLP(config) for _ in range(self.num_experts)])
# Jitter parameters
self.jitter_noise = config.router_jitter_noise
def forward(self, hidden_states: torch.Tensor) -> torch.Tensor:
""" """
# 將注意力模塊的輸出隱狀態(tài)hidden_states作為專家模塊的輸入。
batch_size, sequence_length, hidden_dim = hidden_states.shape
if self.training and self.jitter_noise > 0:
hidden_states *= torch.empty_like(hidden_states).uniform_(1.0 - self.jitter_noise, 1.0 + self.jitter_noise)
# 原有hidden_states形狀為[batch_size, sequence_length, hidden_dim],為方便計算,將batch_size和sequence_length合并,重構(gòu)為一個形狀為(batch * sequence_length, n_experts)的二維張量。而且,后續(xù)計算不是樣本維度,而是token維度,這樣更清晰
hidden_states = hidden_states.view(-1, hidden_dim)
# 將hidden_states導入門控網(wǎng)絡中,輸出一個路由邏輯用于后續(xù)專家分配
# 計算每個專家的分數(shù),router_logits的形狀為[batch_size * sequence_length, n_experts]
router_logits = self.gate(hidden_states)
# 計算專家經(jīng)過softmax之后的概率,最后選取top k個專家用于輸出(在dim=1進行softmax處理,即對應路由邏輯中的n_experts以及hidden_states中的hidden_dim)
routing_weights = F.softmax(router_logits, dim=1, dtype=torch.float)
# 通過門控函數(shù)獲得分數(shù)最高的 top_k 和門控權(quán)重和專家索引
# selected_experts和router_weight的形狀都是 (b * s, top_k)
routing_weights, selected_experts = torch.topk(routing_weights, self.top_k, dim=-1)
# 最后對專家權(quán)重進行歸一化,確保權(quán)重之和為1,并且將權(quán)重的類別和輸入統(tǒng)一
routing_weights /= routing_weights.sum(dim=-1, keepdim=True)
# we cast back to the input dtype
routing_weights = routing_weights.to(hidden_states.dtype)
# 將token導入對應的專家網(wǎng)絡中進行前向傳播得到輸出
final_hidden_states = torch.zeros( # 初始化全零矩陣,后續(xù)疊加為最終結(jié)果
(batch_size * sequence_length, hidden_dim), dtype=hidden_states.dtype, device=hidden_states.device
)
# One hot encode the selected experts to create an expert mask
# this will be used to easily index which expert is going to be sollicitated
# 生成專家掩碼,具體是根據(jù)專家網(wǎng)絡的總數(shù)量構(gòu)建一個one_hot編碼,根據(jù)輸入token所分配的專家網(wǎng)絡,將one_hot編碼中對應的專家網(wǎng)絡索引由0變?yōu)?,據(jù)此來索引給定的專家網(wǎng)絡,掩碼原始形狀是是 (b * s, top_k, expert_number),permute之后形狀是(expert_number, top_k, b * s)
expert_mask = torch.nn.functional.one_hot(selected_experts, num_classes=self.num_experts).permute(2, 1, 0)
# Loop over all available experts in the model and perform the computation on each expert
# 在循環(huán)中依次通過各個專家網(wǎng)絡處理每個輸入token
for expert_idx in range(self.num_experts):
#依次取出專家網(wǎng)絡
expert_layer = self.experts[expert_idx]
# expert_mask[expert_idx] shape 是 (top_k, b * s)
# idx 和 top_x 都是一維張量
# idx 的值是 0 或 1, 表示這個token認為當前專家是 top1 還是 top2
# top_x 的值是 token 在展平之后的 batch*seq_len 個token中的位置索引
idx, top_x = torch.where(expert_mask[expert_idx])
# Index the correct hidden states and compute the expert hidden state for
# the current expert. We need to make sure to multiply the output hidden
# states by `routing_weights` on the corresponding tokens (top-1 and top-2)
# 找出當前專家網(wǎng)絡應該處理的,對應第top_x個token所對應的隱向量hidden_states
# hidden_states 的形狀是 (b * s, hidden_dim)
current_state = hidden_states[None, top_x].reshape(-1, hidden_dim)
# 將hidden_states傳入到專家網(wǎng)絡當中進行處理
# router_weights的形狀是 (b * s, top_k)
current_hidden_states = expert_layer(current_state) * routing_weights[top_x, idx, None]
# However `index_add_` only support torch tensors for indexing so we'll use
# the `top_x` tensor here.
# 將輸出存入之前定義的張量當中
final_hidden_states.index_add_(0, top_x, current_hidden_states.to(hidden_states.dtype))
# 將計算完成的輸出形狀還原為之前的形狀 (b * s, expert_number)
final_hidden_states = final_hidden_states.reshape(batch_size, sequence_length, hidden_dim)
return final_hidden_states, router_logits
專家網(wǎng)絡的代碼如下,Mixtral 8x7B使用了一個三層的MLP來作為MoE中的專家網(wǎng)絡。MLP中的三個全連接層均參與了前向傳播,最后對全連接層的輸出和專家網(wǎng)絡的輸出進行加權(quán)得到最終的輸出。此處與Mixtral of Experts代碼的不同在于把激活函數(shù)用配置項來表示,這樣更靈活,比如hidden_act="silu"。
class MixtralBlockSparseTop2MLP(nn.Module):
def __init__(self, config: MixtralConfig):
super().__init__()
self.ffn_dim = config.intermediate_size
self.hidden_dim = config.hidden_size
self.w1 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)
self.w2 = nn.Linear(self.ffn_dim, self.hidden_dim, bias=False)
self.w3 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)
self.act_fn = ACT2FN[config.hidden_act]
def forward(self, hidden_states):
current_hidden_states = self.act_fn(self.w1(hidden_states)) * self.w3(hidden_states)
current_hidden_states = self.w2(current_hidden_states)
return current_hidden_states
4.5 參數(shù)量
MoE 之所以有趣,很大一部分原因在于其計算要求。由于在給定時間內(nèi)只使用專家的一個子集,因此我們可以訪問比正在使用的更多的參數(shù)。但是如何計算MoE的參數(shù)量以及內(nèi)存占用?
當前MoE 大模型有兩種“署名”方法,各有優(yōu)劣。
- 類似“8x22B”這樣的名稱。這表示模型有8個專家,每個專家有22B 參數(shù)。優(yōu)勢是清晰的給出了專家個數(shù)和規(guī)模,劣勢是容易讓大家誤認為模型一共只有8x22B這么多參數(shù)。
- 類似”57BA14B”這樣的名稱。表示總參數(shù)規(guī)模一共57B,每次推理激活參數(shù)14B。但不清楚里面有多少專家,每個專家的大小。
因此,有研究人員建議使用如下方式來對MoE模型進行標記:總參數(shù)量-激活參數(shù)量-普通專家數(shù)量-激活專家數(shù)量-共享專家數(shù)量,我們接下來解釋下。
-
總參數(shù)量。實際上專家只是模型的一部分,還有注意力層、embedding層,LM Head、門控網(wǎng)絡等模塊。總參數(shù)量通常被稱為稀疏參數(shù)量,可以理解為模型容量的衡量標準,也是在推理時需要多大的顯存 VRAM 的參考數(shù)值,因為模型的所有參數(shù)都必須加載到顯存/內(nèi)存中。
-
激活參數(shù)量。實際上用于處理單個token的參數(shù)數(shù)量,因為該token只通過一些專家塊但不通過其他專家塊,即在推理時,我們只使用了部分專家,所以激活的參數(shù)比較少。該指標可以理解為模型推理時計算成本的衡量標準。換句話說,MoE 模型需要更多的 VRAM 來加載整個模型(包括所有專家),但因為推理時只用到了部分專家,因此MoE在推理過程中的激活的參數(shù)較少、運行速度更快。
-
普通專家數(shù)量-激活專家數(shù)量-共享專家數(shù)量。這個依據(jù)不同MoE的實現(xiàn)不同而不同。因為有的MoE沒有共享專家,只有專家。假如每一個Transformer層有64個普通專家和一個共享專家,激活專家數(shù)量為8,則推理時會從64個普通專家中選擇8個專家進行激活。該層推理時主要加載的參數(shù)為:激活專家數(shù) * 專家大小 + 共享專家數(shù) * 專家大小 + 注意力層大小 + 門控函數(shù)大小。
另外,即使每個輸入只使用一部分參數(shù),所有專家的完整參數(shù)集通常也需要加載到內(nèi)存中,這可能會增加推理過程中的整體內(nèi)存占用。
4.6 計算量
在推理的實際計算時,每個 Token 都會經(jīng)門控網(wǎng)絡來選擇 1 個或多個 Expert,然后執(zhí)行類似 FFN 的計算。我們可以參考論文“Scaling Laws for Fine-Grained Mixture of Experts”給出的MoE計算量的公式,具體指標如下:
-
G(Granularity) :粒度,也就是將一個完整的 FFN 切分為多少個細粒度的專家,比如一個 FFN 可以切分為 8 個小專家,每個專家的參數(shù)量為原始 FFN 的 1/8。
-
E(Expansion rate) :膨脹率,即所有專家的參數(shù)量擴展為單個標準 FFN 參數(shù)量的多少倍。比如,G=8,總共 64 個細粒度專家,則這里的 E=64/8=8,相當于有 8 個同標準規(guī)模的 FFN。該指標可以理解為MoE參數(shù)總數(shù)是其激活參數(shù)的比例。
-
D:token數(shù)目。
-
cf:表示除 Router 之外的計算量與參數(shù)量的比值,論文中設置為 6。對于每個token,線性層的一個活躍參數(shù)的FLOPs是6。操作分解如下:
- 在前向傳播過程中,使用2個操作(單次乘法和單次加法)來計算輸入和線性投影的矩陣乘法。
- 在反向傳播過程中,使用2個操作來計算輸入的梯度
- 在反向傳播過程中,使用2個操作來計算線性層權(quán)重的梯度。
-
cr:表示 Router 的計算量與參數(shù)量的比值,對于比較簡單的 Router,通常為 6-20。具體拆解如下:
- 在前向傳播過程中,使用2個操作來根據(jù)輸入和“路由線性層”計算專家logits。
- 在反向傳播過程中,使用2個操作來計算“路由線性層”關(guān)于輸入的梯度。
- 在反向傳播過程中,使用2個操作來計算“路由線性層”關(guān)于線性層的梯度,
- 在前向傳播過程中,使用2個操作將輸入token路由到選定的專家。
- 在前向傳播過程中,使用2個操作將專家的輸出路由回選定的token,并將這些輸出乘以路由分數(shù)。
- 在反向傳播過程中,使用2個操作將梯度從輸出token路由回到專家。
- 在反向傳播過程中,使用2個操作將梯度從專家路由到輸入token。
與cf的FLOP計算類似,cr的FLOP也是成對的,因為每次乘法后都是加法(用于累加輸出或梯度)。

由于 Router 的計算量通常很小,常常可以忽略。如果不考慮 Router 引入的計算量,由于上述每個 Expert 實際上與非 MoE 模型的 FFN 一樣,因此也可以用同樣的方式推導出訓練時每個 Token 的計算量依然為 C=6ND,只不過這里的 N 不再是整個模型的參數(shù)量,而是每個 Token 激活的參數(shù)量。
0x05 并行計算
MOE Transformer layer的并行方式一般如下:
- 非專家部分(注意力機制)采用張量并行和數(shù)據(jù)并行;
- 專家部分采用專家并行和張量并行;
5.1 通訊需求
我們首先看看MoE計算中的通訊需求。
5.1.1 單token
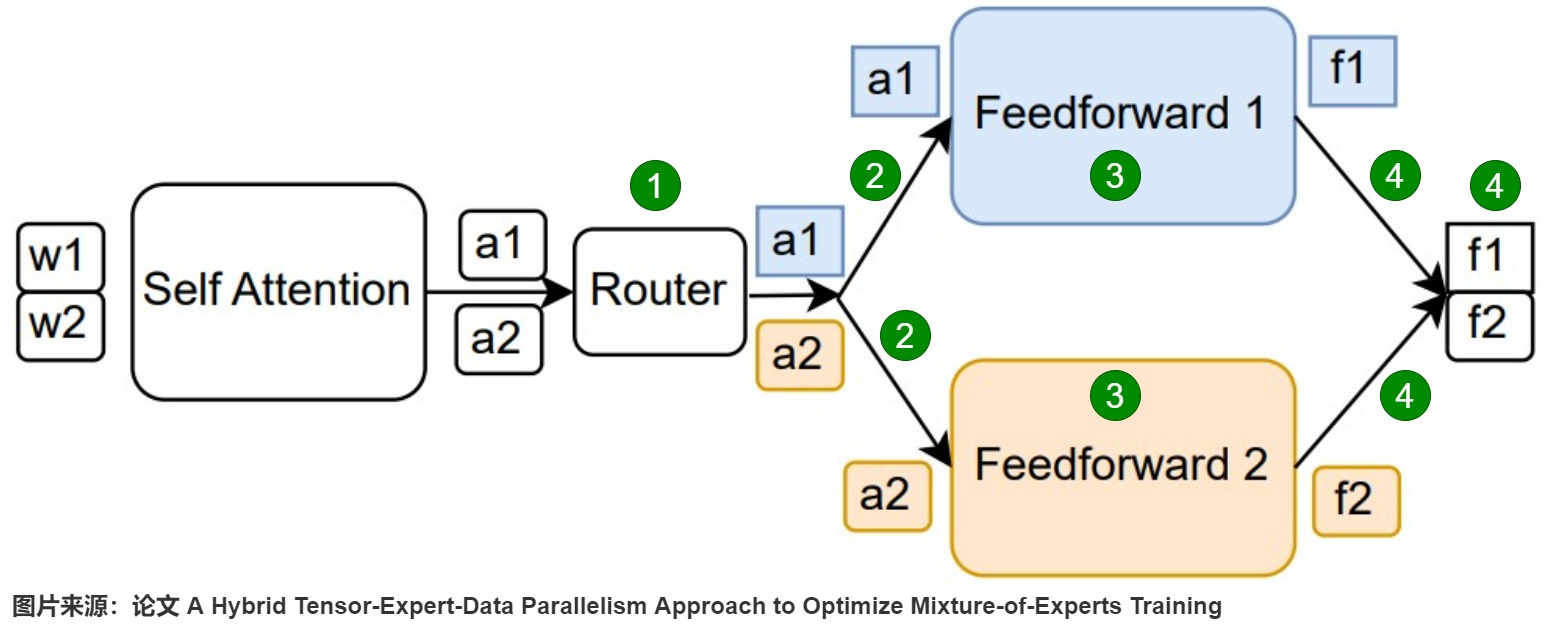
下圖是一個MOE結(jié)構(gòu)的Transformer layer的計算過程,其中:
- w1/w2表示自注意力模塊的輸入;
- a1/a2表示自注意力模塊的輸出,F(xiàn)FN的輸入;
- f1/f2表示FFN的輸出;
具體分為五步:1) 整理,2)發(fā)送,3)計算,4)原路返還,5) 加權(quán)求和。其中第2,第4步存在通信需求。
5.1.2 多token
上述是針對每個token單獨操作,所以看起來很簡單。但要知道,我們通常是同時處理一個batch的所有token,所以上述操作,無論是傳輸還是計算,都要針對矩陣做改變。此外,我們也不知道對于單個token,它選擇的k個專家到底在哪些卡上。因此,MoE的實現(xiàn)就復雜在整理和傳輸之上。
實際中的通信操作如下圖所示,在專家并行模式下,專家層的前后會分別引入 All-to-All 通信操作。前一個 All-to-All 用于將每個 Worker 上的 Token 按照 Router 后對應的專家發(fā)送到專家所在的 GPU,也叫 All-to-All Dispatch;后一個 All-to-All 用于將專家計算后的 Token 重新按照原來的方式排列,也叫 All-to-All Combine。可以看出來這里有兩步通信需求:
- 把token發(fā)給專家(對于下圖標號1)。需要把token按照expert-to-token映射序列發(fā)給對應的GPU。
- 收集k個計算結(jié)果(對于下圖標號2)。需要對token進行還原,保證按照原有的token順序輸出到下一層。

上面提到了兩個概念:專家并行和All-to-All通信,我們分別來分析下。
5.2 專家并行
在面對龐大而復雜的模型時,如何高效利用計算資源、提升訓練速度,一直是研究者們關(guān)注的焦點。傳統(tǒng)的做法通常是通過數(shù)據(jù)并行和模型并行的方式來進行加速計算,但這種方式在處理MoE模型時不是很適合,因為MoE 的特點是工作負載的稀疏性和動態(tài)性。因此,研究人員提出了專家并行(expert parallelism),通過分發(fā)切分后token(dispatching partitioned local tokens)并限制專家容量的負載均衡,來實現(xiàn)并行門控和專家計算。目前,專家并行已成為促進MoE模型高效擴展的基本策略。
5.2.1 定義
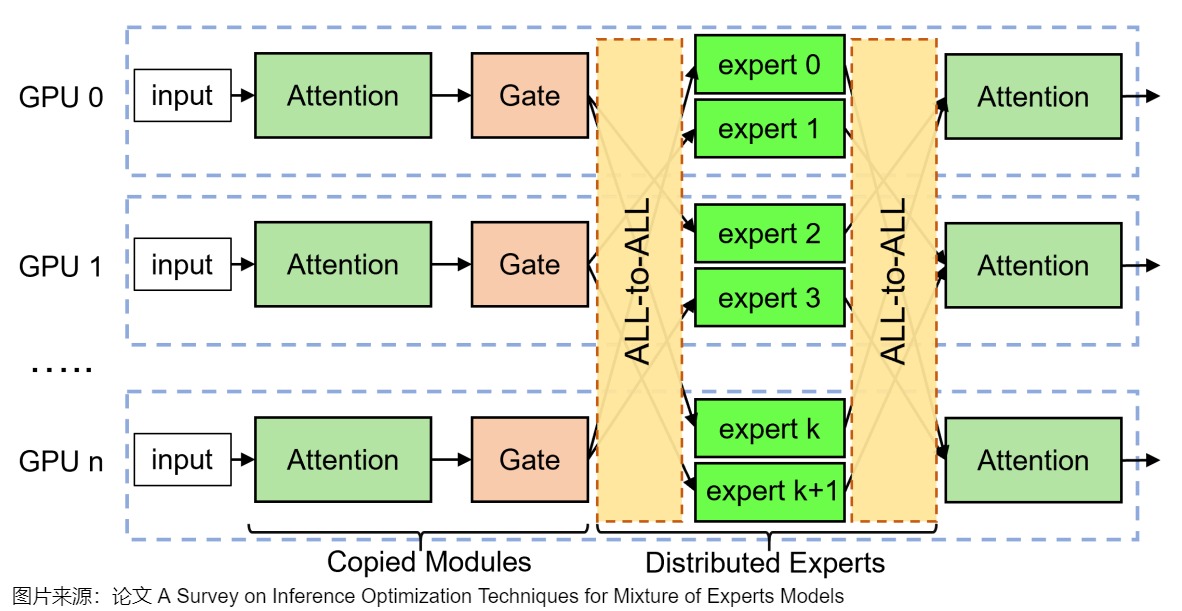
專家并行在本質(zhì)上是一種模型并行方法,但也可以看作是數(shù)據(jù)并行的擴展。專家并行的思路是將MoE層中不同的專家分配到不同的計算設備上,每個設備負責存儲和計算部分專家,而所有非專家層則在設備間復制。專家并行的流程包括以下幾個順序操作:門控路由、輸入編碼、All-to-All dispatch、專家計算、All-to-All combine和輸出解碼。
- 每個 EP rank 上只包含一部分 expert,而每個 EP rank 上的 token(即 token 對應的hidden state) 會根據(jù) 門控路由的結(jié)果分發(fā)到其他 EP rank 上的 expert。
- 和數(shù)據(jù)并行方案類似,每一張卡的輸入是一個完整的任務,需要在每張卡任務的Batch和序列維度進行掩碼,拆解為不同的子任務。因此,專家并行采用輸入編碼(input encode)將發(fā)往給同一專家的輸入令牌(token)聚合到一個連續(xù)的內(nèi)存空間中,這一空間由門控路由token-expert映射決定,該操作就是permutation。
- 隨后,每個設備會根據(jù)MoE模型的路由規(guī)則,使用All-to-All dispatch將輸入token(各自的任務)發(fā)送到相應專家所在的設備上。
- 經(jīng)過專家的本地計算后,逆過程(All-to-All combine和輸出解碼)會根據(jù)門控索引來恢復原始的數(shù)據(jù)布局,將結(jié)果返回到原設備,這樣就在每張卡上還原為完整的任務。
因為專家們被精心地分散部署于各個節(jié)點之上,但每個節(jié)點所承擔的任務卻有所不同。每個節(jié)點都擁有獨特的專家資源,并且數(shù)據(jù)也被巧妙地分割,確保在所有節(jié)點之間實現(xiàn)均衡分配,使得計算資源得到了更加充分的利用。
注:為了達到計算設備所需的最佳利用率和吞吐量,通用矩陣乘法(GEMM)的輸入大小需要足夠大。
5.2.2 歷史
業(yè)界鼻祖
論文”O(jiān)utrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer“第一個用到了專家并行方案,論文給出的描述是:”Mixing Data Parallelism and Model Parallelism“。
論文遇到的問題如下。在現(xiàn)代CPU和GPU上,需要使用大的batch size來提高計算效率,這樣可以分攤參數(shù)加載和更新的開銷。如果門控網(wǎng)絡為每個示例從n個專家中選擇k個,那么假設一個batch中有b個樣本,每個專家都會收到\(\frac{kb}{n} \ll b\)個樣本。如果專家數(shù)量增加,這會導致原始(native)MoE實現(xiàn)的效率很低,即平均到每個 Expert 上的樣本會遠小于 b,這種方式很不利于模型的擴展。解決這個batch收縮(shrinking batch)問題的辦法是使原始batch盡可能大。然而,batch大小往往受到存儲前向和方向傳播激活所需內(nèi)存的限制。
為了解決這個問題,論文采用以下技術(shù)來增加batch size。論文讓不同的batch同步運行,這樣它們可以組合起來為MoE使用。論文根據(jù)傳統(tǒng)的數(shù)據(jù)并行方案那樣來分配模型中其它常規(guī)層和門控網(wǎng)絡,但是每個專家只保留一個共享的拷貝。MoE層的每個專家都會收到一個由所有數(shù)據(jù)并行輸入batch中相關(guān)樣本的組合。同一組設備既可以作為數(shù)據(jù)并行副本(其它常規(guī)層和門控網(wǎng)絡),也可以作為模型并行分片(每個設備承載專家集合中的部分專家)。如果模型分布在d個設備上,每個設備處理一批大小為b的數(shù)據(jù),則每個專家都會收到一批數(shù)量大約是\(\frac{kbd}{n}\)個樣本。因此,我們實現(xiàn)了專家batch size的d倍增大。

Gshard
Gshard則完善了MoE跨設備分片的方法。當擴展到多個設備時,MoE 層在不同設備間共享,而其他所有層則在每個設備上復制。這樣,整個 MoE 層的計算被分散到了多個設備上,每個設備負責處理一部分計算任務。這種架構(gòu)對于大規(guī)模計算非常有效。Gshard讓人們真正意識到,只要把層和 token 智能拆分并均衡地分配給各個專家,訓練幾百億甚至上千億參數(shù)的模型是可以做到的。

Switch Transformers
Switch Transformers 應該是第一個顯式提出來專家并行概念的論文。論文作者試圖平衡每個令牌的FLOPS和模型參數(shù)之間的關(guān)系。因為如果用原生MoE實現(xiàn),當擴大專家數(shù)量時,我們雖然會增加參數(shù)的數(shù)量,并不會改變每個令牌的FLOP。為了增加FLOP,我們還必須增加\(d_{ff}\)的維度(這會增加參數(shù),但會導致速度較慢)。這導致我們需要進行一系列的平衡:當增加\(d_{ff}\)時,每個core的內(nèi)存將耗盡,這就需要增加m。但由于core的數(shù)量是固定為N,并且N=n×m,我們必須減少n,這又迫使使用較小的批處理大小(以便保持每個核心的令牌常數(shù))。因此論文采用了專家并行。
注:假定N是core的總數(shù),n是數(shù)據(jù)并行度,m是模型并行度,E是專家數(shù),C是專家容量。
小結(jié)
專家并行首先將experts分散保存到不同的設備上,然后將走同一數(shù)據(jù)流路徑(data path)的輸入tokens組合在一起構(gòu)成token group(這些tokens選擇了同樣的expert),隨后讓不同的token groups(不同的data path)同時做并行計算。
在非專家并行方案中,如果專家數(shù)目越多,則每個激活專家受到的batch size會越小。而專家并行讓每個專家收到的batch size與專家并行數(shù)成正比。只要 batch size 大小(d*b,d個設備,每個設備處理一批大小為b的數(shù)據(jù)) 隨著專家數(shù)的增加而增加,就可以保證每個專家收到的樣本數(shù)為常數(shù),對顯存和帶寬的需求也就基本是常數(shù),這樣就減少了訪存開銷(data access)并最大化利用了內(nèi)存帶寬。
5.2.3 協(xié)同
隨著模型規(guī)模的增加,往往需要結(jié)合各種分布式并行策略。包括數(shù)據(jù)并行(Data Parallel,DP)、模型并行(Model Parallel,MP,或者稱為 Tensor Parallel,TP)和專家并行(Expert Parallel,EP)。下圖給出了專家并行和其它并行方式結(jié)合的樣例。因為不同專家被分配到不同的設備上,所以很好的解決了顯存開銷問題。而且,使用 EP 不會減少數(shù)據(jù)并行的數(shù)量,因為每個 EP 處理不同的數(shù)據(jù)。另外,因為 EP 和 TP 對通信的要求都很高,所以一般不會讓 EP 和 TP 跨機。
一般情況下,單個expert不會被拆分(EP only),但有時為了達到更好的性能,我們會使用更多的設備,其數(shù)量甚至會比expert數(shù)量還多,這種情況下還可以做expert-slicing,也就是把expert本身(MLP)做tensor-slicing并在多個設備上實現(xiàn)張量并行,這就是EP + TP。如果單個expert做tp切割,數(shù)據(jù)過單個expert后的輸出結(jié)果一定會在同個ep_tp_group內(nèi)做AllReduce。
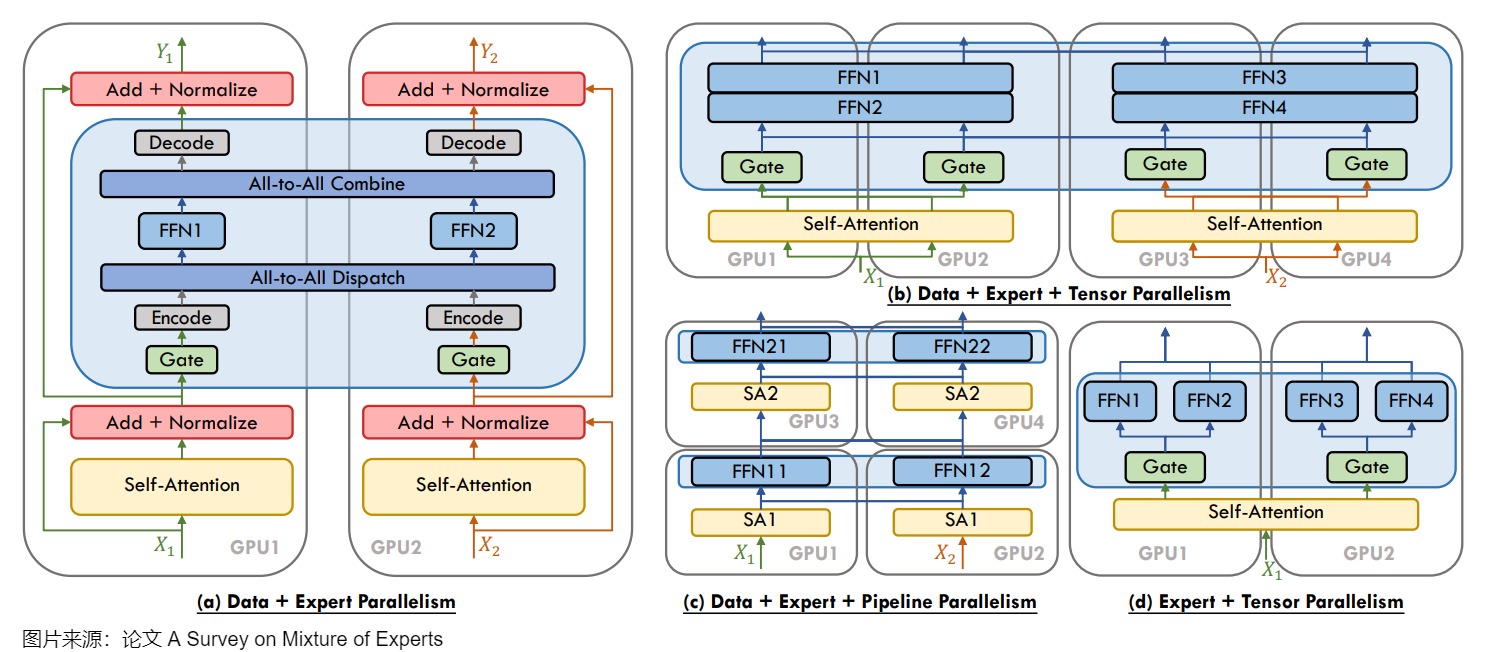
分布式并行策略的選擇影響計算效率、通信開銷、內(nèi)存占用之間的復雜相互作用,這可能受到不同硬件配置的影響。因此,實際應用中的部署策略需要在多個方面進行精細的權(quán)衡,并為特定的使用場景量身定制設計。
5.2.4 如何切分
下圖是從模型參數(shù)切分和數(shù)據(jù)切分的角度(只考慮 FFN 層)來比較幾種并行策略。
每個4×4的虛線網(wǎng)格代表16個core,陰影方塊是該core上包含的數(shù)據(jù)(模型權(quán)重或一批令牌)。第一行:說明模型權(quán)重如何在core之間分配。陰影方塊的大小標識了FFN層中不同的權(quán)重矩陣大小,每種顏色都標識了一個唯一的權(quán)重矩陣。第二行:說明數(shù)據(jù)batch如何在core之間分割。不同顏色代表不同令牌。每種策略的模型權(quán)重和數(shù)據(jù)張量分割如下。
- 第一列:數(shù)據(jù)并行。上方表明所有設備(1-16)都有相同、全部的模型參數(shù)。下方表明每個設備只有一個數(shù)據(jù)分片,且不重復,共 16 個數(shù)據(jù)分片。
- 第二列:模型并行。上方表明所有設備(1-16)都只有模型參數(shù)的一部分,共 16 個分片。下方表明所有設備使用共同的一份數(shù)據(jù)。
- 第三列:模型并行+數(shù)據(jù)并行,設備分為 4 組(1-4,5-8,9-12,13-16)。上方表明每組(4 個設備)都有完整的模型參數(shù)副本,但是每組內(nèi)的設備只有參數(shù)的一部分。下方表明數(shù)據(jù)分為 4 個切片,每組(4 個設備)對應一個數(shù)據(jù)切片。
- 第四列:專家并行+數(shù)據(jù)并行,設備分為 16 組(1-16)。上方表明每一個設備都有不同的專家,共 16 個專家。下方表明每個設備都有不同的數(shù)據(jù)分片(Token),共 16 個數(shù)據(jù)分片,一個專家對應一個分片。
- 第五列:專家并行+模型并行+數(shù)據(jù)并行,有 4 組設備(1-4,5-8,9-12,13-16)。上方表明有 4 個專家,每個專家分布在對應的 4 個設備上,比如綠色專家分布在 5,6,7,8 設備上。下方表明有 4 個數(shù)據(jù)分片,每組設備(每個專家)對應一個數(shù)據(jù)分片,一組里的 4 個設備共享一份數(shù)據(jù)分片。

5.2.5 優(yōu)勢
EP主要優(yōu)勢如下:
- 大大減小了模型參數(shù)冗余,節(jié)省出大量的顯存空間,為大batchsize提供顯存空間基礎。
- 消除了畸形矩陣的運算,增加AI值,解決bandwidth bound問題;
- 單卡的通信量不受整個實例的batchsize的影響,為大batchsize提供高效通信基礎;
- 通過節(jié)省出的顯存帶來的大batch,可以將各個節(jié)點打滿,實現(xiàn)稀疏模型到稠密模型的轉(zhuǎn)化;
我們再對第一點做下解析。因為雖然MoE一次推理的激活權(quán)值只較少,但是依然需要將所有參數(shù)都載入內(nèi)存,這些參數(shù)沒有參與計算但是占用了大量的顯存,導致batchsize很難打高。EP方案種,每張卡至少一個Expert,在保證足夠大的batchsize和負載均衡的條件下,每一張卡的所有expert都處于一個完全激活的狀態(tài),消除了memory bound的問題,或者說把一個稀疏模型轉(zhuǎn)化為一個稠密模型,也可以發(fā)揮出GPU的算力。
當然EP也有存在的問題,最大的問題可能是部署實例減少,且單部署實例故障概率增加,加上多卡之間的通信同步會大大增加出錯的概率,最終導致整個系統(tǒng)的穩(wěn)定性和可用性面臨比較大的挑戰(zhàn)。
5.3 All-to-All通信
可能我們會直觀的認為,哪個Token通過Router決定了那個Expert,那么就直接通過NVLINK內(nèi)存拷貝或者RDMA發(fā)送過去就好了,為什么需要AlltoAll的通信范式呢?我們仔細分析下。
5.3.1 困境
假設我們有2張顯卡,4個專家。專家平均分布在2個顯卡上,每個顯卡上2個專家。在數(shù)據(jù)并行的場景下,每個顯卡有自己獨立的一個batch,在MoE層以外的地方,各個設備獨立計算。一旦到了MoE層,數(shù)據(jù)在顯卡間需要分發(fā)。因為當前設備上的某個token,它所需要的專家,可能坐落在其它設備上。
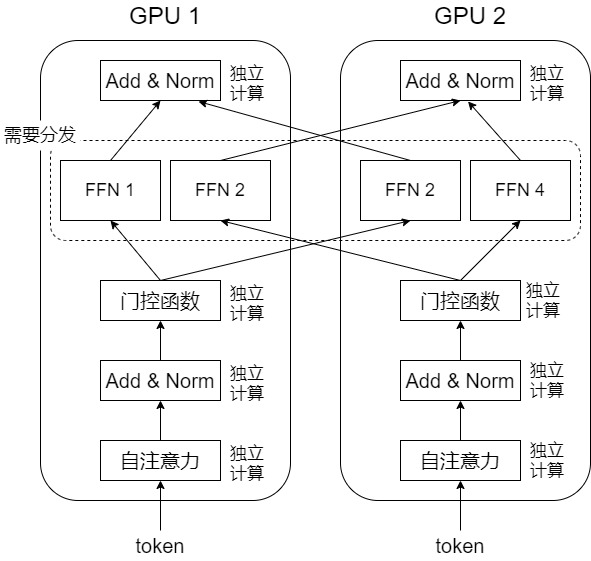
在MoE層,每張顯卡需要傳輸哪些token給其它顯卡呢?一種方法是,每張顯卡把自己所有的a個token都發(fā)給其它顯卡。每個顯卡的每個專家都獲得了2a個token。然而,對于每個專家,它實際只需要處理這2a個token中的部分token。因此,需要有一個機制讓每個專家從自己獲得的2a的token中找到自己應該處理的a/2個token,計算完成后,還需要把這a/2個token原路返回,還原成原來的形狀。
我們看看這個機制。假設每個專家最多可以處理 p 個token,每個顯卡有兩個專家,則每個顯卡最多處理 2p 個token。在傳輸前,每張卡把這些token整合成一個形狀為 (2,p) 的張量,因為有兩張顯卡(本顯卡也要發(fā)給自己),所以實際上每個顯卡要:
- 整理出來形狀為 (2, 2, p) 的張量,這是每個顯卡要傳給其它每個顯卡的數(shù)據(jù)。假如每個token維度是m,則張量實際形狀是 (2, 2, p, m) 。
- 對于第 1 個顯卡,它自己保留 (?,0,?,?) ,然后把 (?,1,?,?) 傳輸給第 2 個顯卡。第 2 個顯卡保留 (?,1,?,?) ,把 (?,0,?,?) 發(fā)給第 1 個顯卡。因此,每個顯卡拿到的張量形狀還是 (2, 2, p, m) 。
- 每個卡會發(fā)給每個專家形狀為 (2, p, m) 的張量。
實際上,在集合通信中已經(jīng)有了這個通信機制,這就是All-to-All通信。
5.3.2 All-to-All
在此通訊模式中,每個進程向每個其他進程發(fā)消息的一部分,最后每個進程擁有各個進程消息的一部分。All-to-All的作用相當于分布式轉(zhuǎn)置Transpose操作。具體如下圖所示。可以看到,GPU0把自己收到的4個綠色的塊分配給了全部4個GPU 。

我們結(jié)合MoE來看看。我們需要通過All-to-All通訊將token發(fā)去指定的expert做計算,再通過All-to-All通訊將計算結(jié)果返回。假設我們有一個4張卡的GPU集群。下圖標號1描繪了首次做All-to-All(All-to-All Dispatch)的過程,這個過程的目的是將token發(fā)去對應的expert上進行計算。對比一下左側(cè)圖和中間圖的數(shù)據(jù)塊排布,你會發(fā)現(xiàn)All-to-All就相當于做了一次矩陣轉(zhuǎn)置。因此通過All-to-All,我們就讓數(shù)據(jù)塊去到了它對應的位置:A0、B0、C0和D0去GPU0,A1、B1、C1和D1去GPU1,以此類推。而為了實現(xiàn)這種轉(zhuǎn)置,我們必須提前token做分塊排序,讓它按照要去的專家位置排好。標號2描繪了第二次做All-to-All(All-to-All Combine)的過程,這個過程的目的是將MoE算完的token再返回給各卡,原理和上述一致。

在 All-to-All Dispatch 操作之前準備好 All-to-All 輸入的過程叫輸入編碼,即需要對本GPU上的 local token 按照路由結(jié)果進行 permute/group,將發(fā)往同一個專家的 token 進行分組。隨后,這些 token 通過 All-to-All Dispatch 通信發(fā)送到對應的 expert rank(每個 EP rank 上只包含一部分 expert)。
在 All-to-All Combine 操作之后需要解包 All-to-All 的輸出,組織為原始的順序,這叫輸出解碼。大多數(shù)流行的DL框架利用NCCL的點對點(P2P)API來實現(xiàn)線性 All-to-All 算法,參見下圖左側(cè)。下圖右側(cè)是用python實現(xiàn)的輸入編碼。

5.4 分布式計算過程
5.4.1 多種范式結(jié)合
有了All-to-All的支撐,我們看看TP、DP和EP互相結(jié)合的MoE分布式計算過程,其中并行劃分為:Transformer layer在四張GPU卡上并行,TensorParallel=2,DataParallel=2,ExpertParallel=2。張量并行組(GPU0和GPU1)在處理token 1和token 2,而張量并行組(GPU 2和GPU 3)處理token 3和token 4。整體計算過程分為7步。
-
步驟1:每個GPU首先計算屬于它們自己的的自注意力塊的分區(qū)。{GPU0,GPU1}與{GPU2,GPU3}之間是數(shù)據(jù)并行。
-
步驟2:在每個自注意力塊的張量并行組內(nèi),每個GPU都會執(zhí)行All-Reduce操作(對張量并行的部分和進行規(guī)約)來聚合它們各自token的完整輸出激活(a1、a2、a3和a4)。這一步是聚合自注意力塊的張量并行輸出。
-
步驟3:每個GPU對于自己的本地token執(zhí)行MoE路由功能。
-
步驟4:根據(jù)路由結(jié)果,將token發(fā)送到對應的專家。我們假設路由函數(shù)將令牌1和3映射到專家1,且將令牌2和4映射到專家2。于是執(zhí)行如下操作。在專家并行組中執(zhí)行一個All-to-All通信操作,根據(jù)路由函數(shù)決定的映射來路由令牌。讓我們看看GPU 0和2組成的專家并行組。在GPU 0上,令牌1已映射到專家1,令牌2已映射到專家2。因此,我們希望GPU 0保留a1,并將a2發(fā)送到容納專家2的GPU2。類似地,在GPU 2上,我們希望保留a4并將a3發(fā)送到GPU 0。
-
步驟5:專家計算。在All-to-All通信操作完成之后,每個專家分塊在自己所在的GPU進行計算。
-
步驟6:在FFN的張量并行組內(nèi)執(zhí)行All-reduce操作來聚合完整輸出。這一步是聚合FFN的張量并行輸出。
-
步驟7:All-to-All通信,回到數(shù)據(jù)并行;執(zhí)行All-to-All通信操作(實際是第一個All-to-All的逆操作),將令牌帶回它們的原始GPU。

5.4.2 通信復雜度
TP vs EP

如上圖左邊所示,TP的基本思路是將模型參數(shù)切分到多個 GPU 進行計算。面對參數(shù)量大幅增大但計算量不變的MoE架構(gòu),TP 方案暴露出兩大核心問題:通信會成為瓶頸,內(nèi)存也會逐漸成為瓶頸,
通訊會成為瓶頸
隨著TP size的增大,通訊會逐漸成為瓶頸。假設每次推理一個batch里一共有 S 個token,hidden dimension是 D,那么對于TP每一個MoE層每個GPU需要發(fā)送 \(2SD\) 大小的數(shù)據(jù),通訊量并不會隨著TP size的增大而降低。
TP的部署方式使得每個GPU上都需要AllReduce來聚合所有input tokens的activation,無論是Self-Attention還是MLP都是對Reduce維度的劃分,而reduce維度的劃分,無論劃分多少份,都是不會改變結(jié)果矩陣的大小的。那么TP中的AllReduce的通信量會隨著整個部署實例batch size的增大而增大,并且即使增大TP并行度,其通信量也不會變小。這是因為TP技術(shù)是源自稠密模型的設計范式。
內(nèi)存會成為瓶頸
由于TP劃分的是權(quán)重,對同一個實例里的每一張卡都有相同的輸入,所以TP的整體通信量是和當前實例的batch-size成正比的,且不受TP劃分粒度的增加而減少。整個實例增大batchsize,那么對于實例內(nèi)的每一張卡都需要增加batchsize。這極大限制了推理的batch size。
有限的batch size使得每次推理時,每個專家分到的token數(shù)量極其有限,使得專家的計算從compute-bound變?yōu)榱薽emory-bound,大大降低了GPU的利用率。同時由于專家負載的不均衡性,較小的batch size甚至可能會導致單次推理時只有部分專家被激活。然而,TP 方案要求所有 GPU 加載全部專家的參數(shù),即使某些專家未參與計算,也會占用顯存資源。
EP的作用
TP很難增大推理的batch size,使得專家部分計算遇到內(nèi)存瓶頸(memory-bound),TP也幾乎不可能進行大規(guī)模模型并行擴展,來增加單個部署實例的batchsize。因此,面對超大參數(shù)量 MoE 模型以及大規(guī)模推理場景,傳統(tǒng) TP 方案有著巨大的本質(zhì)上的局限性。
EP 方案為大規(guī)模 MoE 推理提供了一種全新的并行思路,能夠有效解決 TP 方案的兩大核心問題。
在通信開銷方面,EP 采用 All-to-all 原語進行數(shù)據(jù)交換。在EP size增大的情況下,EP能大幅降低計算相同數(shù)量token的情況下單個GPU的通訊開銷。同樣以一個batch一共包含 ?? 個token為例,假設每個token需要選擇top-?? 的專家,以及專家之間負載平衡的話,那么每個GPU在token分發(fā)(dispatch)和重組(combine)兩個階段各需要發(fā)送\(\frac{K \cdot S}{M}\cdot D\)大小的數(shù)據(jù),其中M是EP size。考慮dispatch和combine兩階段的通訊,當\(\frac{K}{M}?1\) 時,EP的通訊開銷會遠低于TP。
EP同時使得每個GPU可以計算不同的input data,而不需要像TP一樣在每個GPU上處理相同的token并聚合 activation,EP可以極大的擴展batch size,使得每個專家都能分到足夠數(shù)量的token,解決memory access的bottleneck。
通訊復雜度對比
下圖給出了各個并行范式的通訊復雜度對比。

在專家并行(expert parallelism)中,每個MoE層在前向和反向傳播階段中,一共需要進行四次 All-to-All 通信,這會產(chǎn)生顯著的開銷,甚至成為效率的主要制約因素。這種通信的效率取決于多個因素,包括通道帶寬的異質(zhì)性、網(wǎng)絡拓撲結(jié)構(gòu)和集體通信算法。此外,MoE固有的負載不均衡可能通過引發(fā)同步延遲來加劇這些低效。為了優(yōu)化節(jié)點內(nèi)高帶寬和節(jié)點間低帶寬的使用,研究人員做了很多努力,比如:
- 最小化網(wǎng)絡流量并利用高帶寬連接。比如引入分層 All-to-All 、拓撲感知的路由策略、利用專家親和性來進行分配等。
- 考慮到通信和計算的并發(fā)性,把流水線并行和專家并行集成,以此協(xié)調(diào) All-to-All 通信和專家計算的重疊。也有研究人員利用GPU的大規(guī)模并行性和GPU發(fā)起的通信,將計算與依賴的集合通信進行融合。或者將通信依賴關(guān)系進行解耦來通信與計算之間的重疊。
5.4.3 代碼示例
不同框架對MoE并行的相關(guān)概念不同,這恐怕是從事人工智能或者機器學習工作的人最苦惱的地方:模糊且有爭議的定義。所以我們選取兩個框架來看看。
DeepSpeed-Megatron
此處參考了 圖解大模型訓練系列之:DeepSpeed-Megatron MoE并行訓練(源碼解讀篇) 猛猿 的精彩文章。
首先,我們給出一些背景知識。world size代表將要參與訓練的進程數(shù)(或者計算設備數(shù)),每個進程都會被分配一個rank,該rank是一個介于0和world size-1之間的數(shù)字,該數(shù)字在作業(yè)中是唯一的。它作為進程標識符,并用于代替地址,將張量發(fā)送到指定的rank(進程)。
DeepSeed-Megatron中,假設每個MoE層有若干個專家(統(tǒng)稱其為一套專家),現(xiàn)在我們想把這一套專家分布排列到若干GPU上。我們可以先定好要用幾塊GPU裝下一套專家(EP),進而我們就能確認全局上共有多少套專家副本在跑(DP)。假設一共8張GPU,則:
- ep_world_size = 4:表示我們希望用4塊GPU裝下一套完整的專家。ep_group = 8 / ep_world_size = 8 /4 = 2,即一共2個專家組。我們需要在每個專家組內(nèi)做All-to-All通信,將token發(fā)送去對應的專家。
- ep_dp_world_size = 2:MoE層的數(shù)據(jù)并行的大小。例如下圖中[g0, g8]上都維護著e0,所以它們構(gòu)成一個ep_dp_group。這個group的作用是當我們在計算bwd時,它們之間是需要做梯度的allreduce通訊的,構(gòu)成ep_dp_group的條件不僅是e相同,還需要每個e接受到的的batch數(shù)據(jù)不同。
即,在FWD中,ep_group進行all2all通訊,將token發(fā)去對應的專家做計算,并將計算結(jié)果取回。
在BWD中,ep_dp_group進行AllReduce通訊梯度,用于更新對應的專家的參數(shù)。
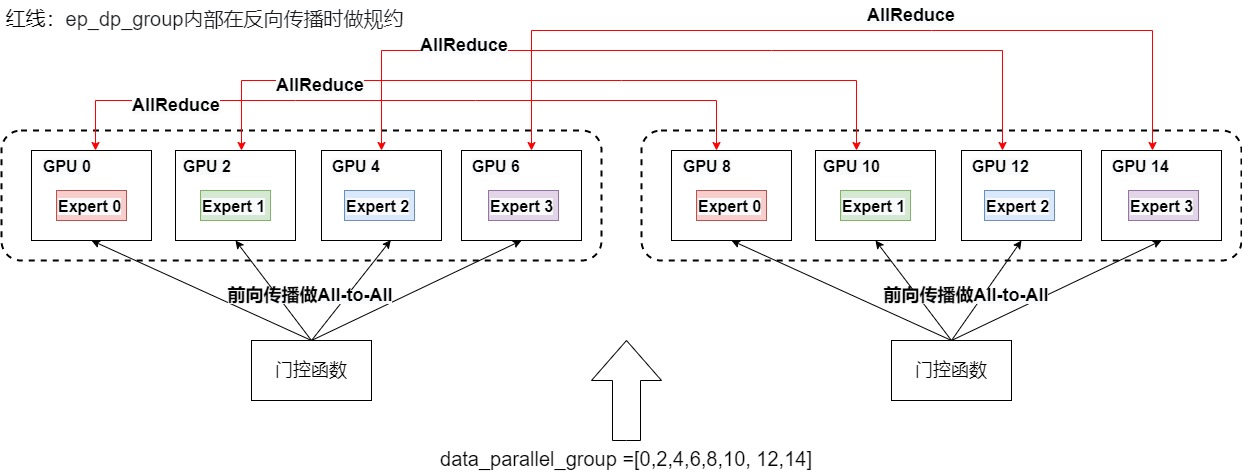
我們來看看源碼中的示例函數(shù)。
def _get_expert_parallel_ranks(world_size,
tensor_parallel_size_,
expert_parallel_size_,
pipeline_parallel_size_=1,
use_data_before_expert_parallel_=False):
"""Generate expert parallel and expert data parallel group ranks list.
Example - E + M + D parallel
world_size = 16
model_degree = 2
expert_degree = 4 # number of experts in same group
mp_group = [0, 1], [2,3], [4,5] ...
data_parallel_group =[0,2,4,6,8,10, 12,14], [1,3,5,7,9,11,13,15]
expert_parallel_group = [0,2,4,6], [8,10,12,14] [1,3,5,7], [9,11,13,15]
expert_data_parallel_group = [0,8],[2,10],[4,12],[6,14], [1,9],[3,11],[5,13],[7,15]
Args:
world_size (int): Distributed world size.
tensor_parallel_size_ (int): Tensor parallel group size.
expert_parallel_size_ (int): Expert parallel group size.
pipeline_parallel_size_ (int): Pipeline parallel group size
use_data_before_expert_parallel_ (bool): Use the D + E instead of E + D topology
Returns:
Expert parallel group ranks and Expert data parallel group ranks list.
"""
_ensure_divisibility(world_size, tensor_parallel_size_ * pipeline_parallel_size_)
#
dp_world_size = world_size // (tensor_parallel_size_ * pipeline_parallel_size_)
_ensure_divisibility(dp_world_size, expert_parallel_size_)
# Generate data parallel groups
data_parallel_groups = []
dp_group_size = tensor_parallel_size_
pp_stride = world_size // pipeline_parallel_size_
if use_data_before_expert_parallel_:
dp_stride = world_size // expert_parallel_size_ // tensor_parallel_size_ // pipeline_parallel_size_
for pp_stage_start in range(0, world_size, pp_stride):
pp_stage_next = pp_stage_start + pp_stride
for i in range(dp_group_size):
data_parallel_groups.append(list())
for ds in range(dp_stride):
# [0, 4, 8, 12, 16, 20, 24, 28, 2, 6, 10, 14, 18, 22, 26, 30]
# [1, 5, 9, 13, 17, 21, 25, 29, 3, 7, 11, 15, 19, 23, 27, 31]
data_parallel_groups[-1].extend(
list(
range(pp_stage_start + i + ds * tensor_parallel_size_, pp_stage_next,
dp_stride * tensor_parallel_size_)))
else:
for pp_stage_start in range(0, world_size, pp_stride):
pp_stage_next = pp_stage_start + pp_stride
for i in range(dp_group_size):
data_parallel_groups.append(list(range(pp_stage_start + i, pp_stage_next, dp_group_size)))
expert_parallel_groups = []
expert_data_parallel_groups = []
for dp_ranks in data_parallel_groups:
# partition of expert parallel groups, e.g. [0,2,4,6], [8,10,12,14]
part_ep_groups = []
for i in range(0, dp_world_size, expert_parallel_size_):
part_ep_groups.append(dp_ranks[i:i + expert_parallel_size_])
expert_parallel_groups.extend(part_ep_groups)
# zip part_ep_groups get expert data parallel ranks, e.g [0,8],[2,10],[4,12],[6,14]
for expert_dp_ranks in zip(*part_ep_groups):
expert_data_parallel_groups.append(list(expert_dp_ranks))
return expert_parallel_groups, expert_data_parallel_groups
下圖展示了一個MoE層的整體架構(gòu)。
- 首先,我們定義好了單個expert模型架構(gòu)(ParallelMLP)
- 然后,鑒于一張卡上可能不止維護1個expert(num_local_experts = num_experts // ep_world_size),我們需要定義這張卡上expert的集合Experts(nn.ModuleList,見代碼細節(jié))
- 再次,我們需要一個TopKGate策略,來幫助token選擇expert。
- 最后,將以上內(nèi)容組裝成一個MOELayer。
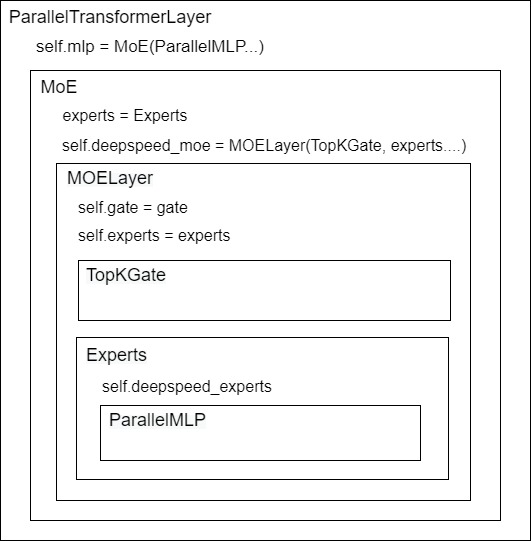
下面是ParallelTransformerLayer的定義。
class ParallelTransformerLayer(MegatronModule):
"""A single transformer layer.
Transformer layer takes input with size [s, b, h] and returns an
output of the same size.
"""
def __init__(self, config,
layer_number, layer_type=LayerType.encoder,
self_attn_mask_type=AttnMaskType.padding,
drop_path_rate=0., num_experts=1):
# retriever=None):
args = get_args()
super(ParallelTransformerLayer, self).__init__()
self.layer_number = layer_number
self.layer_type = layer_type
# MLP
self.num_experts = num_experts
if args.num_experts_switch is not None:
self.mlp = SwitchMLP(config) # Megatron-LM's MoE
else:
if self.num_experts <= 1: # dense, not MoE
self.mlp = ParallelMLP(config)
else: # DeepSpeed's MoE
enable_expert_tensor_parallelism = args.enable_expert_tensor_parallelism
self.mlp = MoE(args.hidden_size,
# 定義單個專家
ParallelMLP(config, moe=True, enable_expert_tensor_parallelism=enable_expert_tensor_parallelism),
num_experts=self.num_experts, # 每層專家數(shù)
ep_size=args.moe_expert_parallel_size, # ep_world_size
k=args.topk,
use_residual=(args.mlp_type == 'residual'),
capacity_factor=args.moe_train_capacity_factor,
eval_capacity_factor=args.moe_eval_capacity_factor,
min_capacity=args.moe_min_capacity,
drop_tokens=args.moe_token_dropping, # 是否需要做溢出處理
use_tutel=args.use_tutel,
enable_expert_tensor_parallelism=enable_expert_tensor_parallelism,
top2_2nd_expert_sampling=args.moe_top2_2nd_expert_sampling)
MoE代碼位于from deepspeed.moe.layer import MoE,具體如下。
class MoE(nn.Module):
"""Initialize an MoE layer.
Arguments:
hidden_size (int): token embedding.
expert (nn.Module): 專家 (e.g., MLP, torch.linear),此處使用ParallMLP
num_experts (int, optional): 每層專家數(shù)
ep_size (int, optional): default=1, 專家并行中的rank數(shù),或者說ep_world_size,即用ep_size張卡容納全部專家
k (int, optional): default=1, top-k gating value, only supports k=1 or k=2.
capacity_factor (float, optional): default=1.0, 訓練時的容量因子
eval_capacity_factor (float, optional): default=1.0, eval時的容量因子
min_capacity (int, optional): default=4, 每個專家最小的容量值.
use_residual (bool, optional): default=False, 該層是否是一個residual expert層 (https://arxiv.org/abs/2201.05596) layer.c
noisy_gate_policy (str, optional): default=None, 加噪策略.
drop_tokens (bool, optional): default=True, whether to drop tokens - (setting to False is equivalent to infinite capacity).
use_rts (bool, optional): default=True, whether to use Random Token Selection.
use_tutel (bool, optional): default=False, whether to use Tutel optimizations (if installed).
enable_expert_tensor_parallelism (bool, optional): default=False, # 是否對專家進行TP切分
top2_2nd_expert_sampling (bool, optional): default=True, whether to perform sampling for 2nd expert
"""
def __init__(self,
hidden_size: int,
expert: nn.Module,
num_experts: int = 1,
ep_size: int = 1,
k: int = 1,
capacity_factor: float = 1.0,
eval_capacity_factor: float = 1.0,
min_capacity: int = 4,
use_residual: bool = False,
noisy_gate_policy: Optional[str] = None,
drop_tokens: bool = True,
use_rts: bool = True,
use_tutel: bool = False,
enable_expert_tensor_parallelism: bool = False,
top2_2nd_expert_sampling: bool = True) -> None:
super(MoE, self).__init__()
self.use_residual = use_residual
self.enable_expert_tensor_parallelism = enable_expert_tensor_parallelism
self.ep_size = ep_size
self.expert_group_name = f"ep_size_{self.ep_size}"
self.num_experts = num_experts
self.num_local_experts = num_experts // self.ep_size # 單塊GPU上需存放的專家數(shù)量
# 定義一個MoE層上所有的專家
experts = Experts(expert, self.num_local_experts, self.expert_group_name)
# 定義MoE層
self.deepspeed_moe = MOELayer(TopKGate(hidden_size, num_experts, k, capacity_factor, eval_capacity_factor,min_capacity, noisy_gate_policy, drop_tokens, use_rts, None,top2_2nd_expert_sampling), experts, self.expert_group_name, self.ep_size, self.num_local_experts, use_tutel=use_tutel)
if self.use_residual:
self.mlp = expert
# coefficient is used for weighted sum of the output of expert and mlp
self.coefficient = nn.Linear(hidden_size, 2)
def set_deepspeed_parallelism(self, use_data_before_expert_parallel_: bool = False) -> None:
# 專家分布相關(guān)設置
self._create_process_groups(
use_data_before_expert_parallel_=use_data_before_expert_parallel_)
def _create_process_groups(self, use_data_before_expert_parallel_: bool = False) -> None:
# 專家分布相關(guān)設
# Create process group for a layer if needed
if self.expert_group_name not in groups._get_expert_parallel_group_dict():
# 按EP + DP方式設置專家并行相關(guān)組
if (groups.mpu is None) or (not self.enable_expert_tensor_parallelism):
# Condition 1 - no groups.mpu means no tensor parallelism
# Condition 2 - disabling expert tensor parallelism on purpose
groups._create_expert_and_data_parallel(
self.ep_size, use_data_before_expert_parallel_=use_data_before_expert_parallel_)
else:
# 使用EP + DP + TP方式設置專家并行相關(guān)組
# expert tensor parallelism is enabled
groups.
_create_expert_data_and_model_parallel(
self.ep_size, mpu=groups.mpu, use_data_before_expert_parallel_=use_data_before_expert_parallel_)
# Set the group handle for the MOELayer (deepspeed_moe) object
# 為當前進程所屬的MoE層設置ep_group,樣就可以在ep_group內(nèi)做All-to-All通訊,如果不設置ep_group,默認對所有GPU卡(ep_world_size)做All-to-All通信
self.deepspeed_moe._set_ep_group(
groups._get_expert_parallel_group(self.expert_group_name))
def forward(self,
hidden_states: torch.Tensor,
used_token: Optional[torch.Tensor] = None) -> Tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
""" MoE forward
Arguments:
hidden_states (Tensor): input to the layer
used_token (Tensor, optional): default: None, mask only used tokens
Returns:
A tuple including output, gate loss, and expert count.
* output (Tensor): output of the model
* l_aux (Tensor): gate loss value
* exp_counts (Tensor): expert count
"""
output = self.deepspeed_moe(hidden_states, used_token)
if self.use_residual:
# Residual MoE
output_mlp = self.mlp(hidden_states)
if isinstance(output_mlp, tuple):
output_mlp = output_mlp[0] # Ignore the bias term for now
coef = self.coefficient(hidden_states)
coef = F.softmax(coef, dim=-1)
output = output * coef[..., 0:1] + output_mlp * coef[..., 1:]
return output, self.deepspeed_moe.l_aux, self.deepspeed_moe.exp_counts
deepspeed在MOELayer的實現(xiàn)如下。
class MOELayer(Base):
"""MOELayer module which implements MixtureOfExperts as described in Gshard_.
::
gate = TopKGate(model_dim, num_experts)
moe = MOELayer(gate, expert)
output = moe(input)
l_aux = moe.l_aux
.. Gshard_: https://arxiv.org/pdf/2006.16668.pdf
Args:
gate (torch.nn.Module):
gate network
expert (torch.nn.Module):
expert network
"""
def __init__(self,
gate: Module,
experts: Module,
ep_group_name,
ep_size,
num_local_experts: int,
use_tutel: bool = False) -> None:
super().__init__()
self.gate = gate # TopKGate類,用來決定token的分發(fā)策略
self.experts = experts # 當前進程所屬的GPU上維護的所有專家,nn.ModuleList[ParallelMLP()]
self.ep_group = None # 當前進程所屬的ep_group,為None時表示所有GPU構(gòu)成一個ep_group
self.ep_size = ep_size # 當前進程所屬的ep_group的ep_world_size,即GPU卡數(shù)
self.ep_group_name = ep_group_name # 當前進程所屬的ep_group的名字
self.num_local_experts = num_local_experts # 當前進程所屬的GPU上所維護的專家數(shù)量,即為self.experts中維護的專家s數(shù)量
self.use_tutel = use_tutel and TUTEL_INSTALLED and gate.k == 1 # 是否使用tutel做路由優(yōu)化
def _set_ep_group(self, ep_group):
self.ep_group = ep_group
self.gate._set_ep_group(ep_group)
def forward(self, *input: Tensor, **kwargs: Any) -> Tensor:
"""
*號:傳入的input是一個tuple,一般是一個二元組
input[0]是做計算的batch數(shù)據(jù),其形狀為(seq_len, batch_size, embedding_size),embedding_size就是d_model
input[1]是掩碼數(shù)據(jù),其尺寸為(seq_len * batch_size),可以在計算MoE結(jié)果時,對某些token做掩碼,使其不參與計算
"""
# Implement Algorithm 2 from GShard paper.
d_model = input[0].shape[-1]
# Initial implementation -> Reshape into S tokens by dropping sequence dimension.
# Reshape into G groups so that each group can distribute tokens equally
# group_size = kwargs['group_size'] if 'group_size' in kwargs.keys() else 1
# reshaped_input尺寸為(seq_len * batch_size, token_embedding_size)
reshaped_input = input[0].reshape(-1, d_model)
if self.use_tutel: # 使用Tutel做路由優(yōu)化
self.l_aux, C, E, indices_, locations_, gates_, self.exp_counts = self.gate(reshaped_input, input[1], True)
S, M = reshaped_input.size(0), reshaped_input.size(1)
if not hasattr(self, '_tutel_dispatcher'):
self._tutel_dispatcher = tutel_moe.fast_dispatcher(E, C, M, dispatch_dtype=reshaped_input.dtype)
self._tutel_dispatcher.update(indices_, locations_, gates_, capacity=C)
dispatched_input = self._tutel_dispatcher.encode(reshaped_input)
else:
# 使用自定義的Gshard gate來確定token的分發(fā)策略
# gate:TopKGate類,l_aux: 輔助損失函數(shù)值
# combine_weights: 尺寸為(seq_len * batch_size, expert_num, capacity),表示對每個token(總共seq_len * capacity個)而言,它對每個專家(總共expert_num個)的weight,這個weight按照該token在專家buffer中的位置(總共capacity個token)存放,不是目標位置的地方則用0填充
# dispatch_mask:相當于combine_weights.bool(),combine_weights為0的地方設為False,為1的地方設為True。dispatch_mask后續(xù)將被用在zero padding
self.l_aux, combine_weights, dispatch_mask, self.exp_counts = self.gate(reshaped_input, input[1])
# 將輸入數(shù)據(jù)按照專家的順序排好,并做zero padding,
# dispatched_input: 尺寸為(expert_num, capacity, token_embedding_size),表示每個專家的buffer下要處理的token_embedding
dispatched_input = einsum("sec,sm->ecm", dispatch_mask.type_as(input[0]), reshaped_input)
tensor_model_world_size = bwc_tensor_model_parallel_world_size(groups.mpu)
# 當expert不采用tp切分,而non-MoE部分采用tp切分時,為避免數(shù)據(jù)重復發(fā)送,需要對同一個tp組內(nèi)的tokens做去重
if tensor_model_world_size > 1:
# If the non-expert is tensor-parallel,
# Whether expert is tensor-parallel or not , it will create
# duplicate tokens on the tensor-parallel ranks.
# drop duplicate tokens also doubles up as a communication
# optimization as we are reducing the all-to-all communication volume.
# 1: for not tensor-parallel expert,drop duplicate tokens to ensure
# both correctness and reduce all-to-all communication.
# 2: for tensor-parallel expert,drop duplicate tokens to reduce all-to-all
# communication volume,before expert execution, it is necessary to perform
# an allgather to ensure correctness,
dispatched_input = drop_tokens(dispatched_input, dim=1)
# 第一次All2All:將token發(fā)給對應的expert,dispatched_input尺寸為(expert_num, capacity, token_embedding_size),又可以寫成(ep_world_size * num_local_experts, capacity, token_embedding_size)。
dispatched_input = _AllToAll.apply(self.ep_group, dispatched_input)
if tensor_model_world_size > 1 and groups._get_expert_model_parallel_world_size() > 1:
# if both expert and non-expert are tensor-parallel
# the dropped duplicate tokens need to be gathered on each
# tensor parallel rank again to ensure correctness
dispatched_input = gather_tokens(dispatched_input, dim=1)
# Re-shape after all-to-all: ecm -> gecm(g是ep_world_size,e是num_local_experts)
# 在將dispatched_input正式喂給expert前,把它reshape成(ep_world_size, num_local_experts, capacity, token_embedding_size)
dispatched_input = dispatched_input.reshape(self.ep_size, self.num_local_experts, -1, d_model)
# 將token喂給expert計算,expert_output尺寸為(ep_world_size, num_local_experts, capacity, token_embedding_size)
expert_output = self.experts(dispatched_input)
# Re-shape before drop_tokens: gecm -> ecm
# expert_output的形狀是(ep_world_size * num_local_experts, capacity, token_embedding_size)。
expert_output = expert_output.reshape(self.ep_size * self.num_local_experts, -1, d_model)
if tensor_model_world_size > 1 and groups._get_expert_model_parallel_world_size() > 1:
# if both expert and non-expert are tensor-parallel
# drop duplicate tokens to ensure both correctness
# and reduce all-to-all communication.
expert_output = drop_tokens(expert_output, dim=1)
# 第二次All2All,將算好的token返回給產(chǎn)出它的GPU, expert_output為(ep_world_size * num_local_experts, C, M),即此時這張卡上維護的token過MoE的結(jié)果,是由它從ep_group(ep_world_size)內(nèi)所有expert(num_local_experts)的結(jié)果匯總而來
expert_output = _AllToAll.apply(self.ep_group, expert_output)
# 如果之前在tp組內(nèi)做過數(shù)據(jù)去重處理,這里要把數(shù)據(jù)all-gather回來
if tensor_model_world_size > 1:
# the dropped duplicate tokens need to be gathered on each
# tensor parallel rank again for the tensor-parallel
# non-expert of the next layer.
expert_output = gather_tokens(expert_output, dim=1)
# 使用combine_weights進行加權(quán)計算
if self.use_tutel:
combined_output = self._tutel_dispatcher.decode(expert_output.view(E * C, M))
else:
combined_output = einsum("sec,ecm->sm", combine_weights.type_as(input[0]), expert_output)
# 最終輸出a尺寸為:(seq_len, batch_size, token_embedding_size)
a = combined_output.reshape(input[0].shape)
return a
門控函數(shù)定義如下。
class TopKGate(Module):
"""Gate module which implements Top2Gating as described in Gshard_.
::
gate = TopKGate(model_dim, num_experts)
l_aux, combine_weights, dispatch_mask = gate(input)
.. Gshard_: https://arxiv.org/pdf/2006.16668.pdf
Args:
model_dim (int):
size of model embedding dimension
num_experts (int):
number of experts in model
"""
wg: torch.nn.Linear
def __init__(self,
model_dim: int,
num_experts: int,
k: int = 1,
capacity_factor: float = 1.0,
eval_capacity_factor: float = 1.0,
min_capacity: int = 8,
noisy_gate_policy: Optional[str] = None,
drop_tokens: bool = True,
use_rts: bool = True,
ep_group: Union[torch.distributed.ProcessGroup, None] = None,
top2_2nd_expert_sampling: bool = True) -> None:
super().__init__()
self.wg = torch.nn.Linear(model_dim, num_experts, bias=False)
self.ep_group = ep_group
self.k = k
self.capacity_factor = capacity_factor
self.eval_capacity_factor = eval_capacity_factor
self.min_capacity = min_capacity
self.noisy_gate_policy = noisy_gate_policy
self.timers = SynchronizedWallClockTimer()
self.wall_clock_breakdown = False
self.gate_time = 0.0
self.drop_tokens = drop_tokens
self.use_rts = use_rts
self.top2_2nd_expert_sampling = top2_2nd_expert_sampling
def _set_ep_group(self, ep_group):
self.ep_group = ep_group
def forward(self,
input: torch.Tensor,
used_token: torch.Tensor = None,
use_tutel: bool = False) -> Tuple[Tensor, Tensor, Tensor]:
input_fp32 = input.float()
# input jittering
if self.noisy_gate_policy == 'Jitter' and self.training:
input_fp32 = multiplicative_jitter(input_fp32, device=input.device)
logits = torch.nn.functional.linear(input_fp32, weight=self.wg.weight.float(), bias=None)
if self.k == 1:
gate_output = top1gating(logits, self.capacity_factor if self.training else self.eval_capacity_factor, self.min_capacity, used_token, self.noisy_gate_policy if self.training else None, self.drop_tokens, self.use_rts, self.ep_group, use_tutel)
elif self.k == 2:
gate_output = top2gating(logits, self.capacity_factor if self.training else self.eval_capacity_factor, self.min_capacity, self.drop_tokens, self.ep_group, self.top2_2nd_expert_sampling)
else:
gate_output = topkgating(logits, self.k, self.capacity_factor if self.training else self.eval_capacity_factor, self.min_capacity, self.drop_tokens, self.ep_group)
return gate_output
Experts的定義如下,其定義一個MoE層上所有的Expert。
class Experts(nn.Module):
def __init__(self, expert: nn.Module, num_local_experts: int = 1, expert_group_name: Optional[str] = None) -> None:
super(Experts, self).__init__()
self.deepspeed_experts = nn.ModuleList([copy.deepcopy(expert) for _ in range(num_local_experts)])
self.num_local_experts = num_local_experts # 每塊GPU上共num_local_experts個expert
for expert in self.deepspeed_experts:
for param in expert.parameters():
param.allreduce = False
param.group_name = expert_group_name
def forward(self, inputs: torch.Tensor) -> torch.Tensor:
"""
inputs尺寸:(ep_world_size, num_local_experts, capacity, token_embedding_size)
在分發(fā)去experts前,每張卡上的輸出結(jié)果為(ep_world_size * num_local_experts, capacity, token_embedding_size)
對于All2All通訊可以理解為,對于ep_group內(nèi)的每張卡,都將數(shù)據(jù)沿著ep_world_size * num_local_experts維度切成ep_world_size塊后,再進行通訊。目的是保證每張卡上的數(shù)據(jù)塊數(shù)量 = ep_world_size,這樣All2All通訊才不會出錯,因此發(fā)送完畢后,每張卡上的數(shù)據(jù)可以又表示為(ep_world_size * num_local_experts, capacity, token_embedding_size)
進一步在正式把數(shù)據(jù)喂給這張卡上維護的experts前,我們可以把數(shù)據(jù)reshape成(ep_world_size, num_local_experts, capacity, token_embedding_size)的形式。即沿著num_local_experts維度將數(shù)據(jù)切分為num_local_experts個chunck,則一個chunk對應一個local_expert,再次實現(xiàn)了token 和local expert間一一對應的關(guān)系
"""
# chunks: 沿著num_local_expert維度切分inputs,方便各塊input喂給該GPU上對應的各個expert
chunks = inputs.chunk(self.num_local_experts, dim=1)
expert_outputs: List[torch.Tensor] = []
for chunk, expert in zip(chunks, self.deepspeed_experts):
# out尺寸:(ep_world_size, capacity, token_embedding_size)
out = expert(chunk)
if isinstance(out, tuple):
out = out[0] # Ignore the bias term for now
expert_outputs += [out]
# concat后最終out尺寸: (ep_world_size, num_local_experts, capacity, token_embedding_size)
return torch.cat(expert_outputs, dim=1)
專家定義如下。
class ParallelMLP(MegatronModule):
"""MLP.
MLP will take the input with h hidden state, project it to 4*h
hidden dimension, perform nonlinear transformation, and project the
state back into h hidden dimension.
"""
def __init__(self, config, moe=False, enable_expert_tensor_parallelism=False):
super(ParallelMLP, self).__init__()
args = get_args()
self.add_bias = config.add_bias_linear
ffn_hidden_size = config.ffn_hidden_size
if config.gated_linear_unit:
ffn_hidden_size *= 2
# Project to 4h. If using swiglu double the output width, see https://arxiv.org/pdf/2002.05202.pdf
# self.dense_h_to_4h:Wi,尺寸大小(h, 4h/tp_world_size)
self.dense_h_to_4h = tensor_parallel.ColumnParallelLinear(
config.hidden_size,
ffn_hidden_size,
config=config,
init_method=config.init_method,
bias=self.add_bias,
gather_output=False,
skip_bias_add=True,
moe=moe,
enable_expert_tensor_parallelism=enable_expert_tensor_parallelism
)
self.bias_gelu_fusion = False
self.activation_func = None
self.swiglu = args.swiglu
if args.openai_gelu:
self.activation_func = openai_gelu
elif args.onnx_safe:
self.activation_func = erf_gelu
elif args.swiglu:
def swiglu(x):
x = torch.chunk(x, 2, dim=-1)
return F.silu(x[0]) * x[1]
self.activation_func = swiglu
elif args.squared_relu:
def squared_relu(x):
return torch.pow(F.relu(x), 2)
self.activation_func = squared_relu
else:
self.bias_gelu_fusion = args.bias_gelu_fusion
self.activation_func = F.gelu
# Project back to h.
# self.dense_4h_to_h, Wo, 尺寸大小為(4h/tp_world_size, h)
self.dense_4h_to_h = tensor_parallel.RowParallelLinear(
config.ffn_hidden_size,
config.hidden_size,
config=config,
init_method=config.output_layer_init_method,
bias=self.add_bias,
input_is_parallel=True,
moe=moe,
enable_expert_tensor_parallelism=enable_expert_tensor_parallelism
)
def forward(self, hidden_states):
# [s, b, 4hp]
# 輸入數(shù)據(jù)過Wi層,如果做TP切分,則尺寸為[s, b, 4h/tp_word_size]
intermediate_parallel, bias_parallel = self.dense_h_to_4h(hidden_states)
if self.bias_gelu_fusion:
# DeepSpeed FLOPS profiler temporarily substitues functions like F.gelu to calculate the throughput
intermediate_parallel = bias_gelu_impl(intermediate_parallel, bias_parallel)
else:
if bias_parallel is not None:
intermediate_parallel = intermediate_parallel + bias_parallel
intermediate_parallel = self.activation_func(intermediate_parallel)
# [s, b, h]
# Wi層輸出數(shù)據(jù)過Wo層,如果對expert采取tp切分,這里的輸出需要在tp_group內(nèi)做AllReduce
output, output_bias = self.dense_4h_to_h(intermediate_parallel)
return output, output_bias
FastMoE
我們使用 FastMoE 作為示例,看看如何實現(xiàn)分布式操作。 這里的代碼比較顯式。
論文”FASTMOE: A FAST MIXTURE-OF-EXPERT TRAINING SYSTEM“提出了 FastMoE,這是一個基于 Pytorch 的分布式 MoE 訓練系統(tǒng)。該系統(tǒng)支持將不同的專家放置在多個節(jié)點上的多個 GPU 中,從而實現(xiàn)專家數(shù)量和 GPU 數(shù)量線性增加。
FastMoE 支持將專家分布在多個節(jié)點的多個 Worker 上,并且將不同 Worker 之間的數(shù)據(jù)通信隱藏起來,模型開發(fā)人員不用考慮。此外,在分布式 MoE 系統(tǒng)中的一個主要挑戰(zhàn)為:動態(tài)路由導致分配給不同專家的輸入樣本數(shù)可能存在很大的差異。作者的方案為:在 Worker 之間交換實際的數(shù)據(jù)之前,先在 Worker 之間交換大小信息,Worker 根據(jù)相應信息分配 Buffer,然后傳輸真實的數(shù)據(jù)。
FastMoE 將所有輸入樣本一起 Batching 后發(fā)給同一個專家。由于數(shù)據(jù)表示的限制,F(xiàn)astMoE 使用專門開發(fā)的 CUDA Kernel 進行內(nèi)存移動,以減少開銷。如下圖所示,給定每個樣本要進入的索引(Gating 輸出),通過 Scatter 操作將所有樣本按照對應順序進行排布,執(zhí)行完專家計算之后,再按照相反的 Gather 操作進行復原。

MoE代碼如下,關(guān)鍵函數(shù)是_fmoe_general_global_forward()函數(shù),該函數(shù)會完成MoE的關(guān)鍵計算步驟。
class FMoE(nn.Module):
r"""
A general moe implementation that supports an arbitrary module as the
expert.
* `num_expert` stands for the number of experts on **each** worker.
* `world_size` stands for the total number of workers that contains
different experts.
* `slice_group` can be a torch's communication group, indicating that
specific model parallel is applied across the group, and workers in the
group hold the same copy of input feature, and requires the same copy of
the output. For each worker, FMoE only computes the output of a certain
slice of the input batch, and will all-gather the outputs after
computation.
* `mp_group` is a deprecated alias of `slice_group`
* `moe_group` stands for the group of process that performs expert
parallelism. The default value `None` means all processes. See the
parallelism document for more details of the groups.
* `top_k` stands for the number of experts each token is going to.
* `gate` is a gate class which can found in `fmoe.gates`.
* `expert` can be specified as a module class, it is used to generate
`num_expert` expert modules.
* `gate_bias` is only valid for naive_gate and its subclasses, it means
whether to add bias to the gate module.
"""
def __init__(
self,
num_expert=32,
d_model=1024,
world_size=1,
mp_group=None, # being deprecated
slice_group=None,
moe_group=None,
top_k=2,
gate=NaiveGate,
expert=None,
gate_hook=None,
mask=None,
mask_dict=None,
gate_bias=True,
):
super().__init__()
self.num_expert = num_expert
self.d_model = d_model
self.world_size = world_size
self.slice_group = slice_group
if mp_group is not None:
self.slice_group = mp_group
if self.slice_group is None:
self.slice_size = 1
self.slice_rank = 0
else:
self.slice_size = self.slice_group.size()
self.slice_rank = self.slice_group.rank()
self.top_k = top_k
if type(expert) is list:
self.experts = nn.ModuleList([e(d_model) for e in expert])
self.experts_fused = False
self.num_expert = num_expert = len(expert)
elif expert is not None:
self.experts = nn.ModuleList([expert(d_model) for _ in range(num_expert)])
self.experts_fused = False
else:
self.experts_fused = True
if issubclass(gate, NaiveGate):
self.gate = gate(d_model, num_expert, world_size, top_k, gate_bias=gate_bias)
else:
self.gate = gate(d_model, num_expert, world_size, top_k)
self.gate_hook = gate_hook
self.mask = mask
self.mask_dict = mask_dict
self.moe_group = moe_group
def expert_fn(self, inp, fwd_expert_count):
r"""
The default expert function which either calls the experts as a whole
or as separate experts.
"""
if self.experts_fused:
return self.experts(inp, fwd_expert_count)
if isinstance(fwd_expert_count, torch.Tensor):
fwd_expert_count_cpu = fwd_expert_count.cpu().numpy()
outputs = []
base_idx = 0
for i in range(self.num_expert):
batch_size = fwd_expert_count_cpu[i]
inp_slice = inp[base_idx : base_idx + batch_size]
outputs.append(self.experts[i](inp_slice, torch.tensor([fwd_expert_count[i]])))
base_idx += batch_size
return torch.cat(outputs, dim=0)
def expert_fn_single(self, inp, fwd_expert_count, idx):
r"""
forward single expert for smart scheduling.
"""
output = self.experts[idx](inp, fwd_expert_count)
return output
def mark_parallel_comm(self, expert_dp_comm="none"):
r"""
Automatically mark the data parallel comms of the parameters within the
module. This can be typically called at the end of the __init__ function
in child classes.
"""
if self.experts is not None:
comm = expert_dp_comm
if isinstance(self.experts, list):
for e in self.experts:
mark_module_parallel_comm(e, comm)
else:
mark_module_parallel_comm(self.experts, comm)
mark_module_parallel_comm(self.gate, "gate")
def forward(self, moe_inp):
r"""
The FMoE module first computes gate output, and then conduct MoE forward
according to the gate. The score of the selected gate given by the
expert is multiplied to the experts' output tensors as a weight.
"""
moe_inp_batch_size = tree.flatten(
tree.map_structure(lambda tensor: tensor.shape[0], moe_inp)
)
if self.world_size > 1:
def ensure_comm_func(tensor):
ensure_comm(tensor, self.moe_group)
tree.map_structure(ensure_comm_func, moe_inp)
if self.slice_size > 1:
def slice_func(tensor):
return Slice.apply(
tensor, self.slice_rank, self.slice_size, self.slice_group
)
moe_inp = tree.map_structure(slice_func, moe_inp)
gate_top_k_idx, gate_score = self.gate(moe_inp)
if self.gate_hook is not None:
self.gate_hook(gate_top_k_idx, gate_score, None)
# delete masked tensors
if self.mask is not None and self.mask_dict is not None:
# TODO: to fix
def delete_mask_func(tensor):
# to: (BxL') x d_model
tensor = tensor[mask == 0, :]
return tensor
mask = self.mask.view(-1)
moe_inp = tree.map_structure(delete_mask_func, moe_inp)
gate_top_k_idx = gate_top_k_idx[mask == 0, :]
fwd = _fmoe_general_global_forward(
moe_inp, gate_top_k_idx, self.expert_fn_single if fmoe_faster_schedule else self.expert_fn,
self.num_expert, self.world_size,
experts=self.experts
)
# recover deleted tensors
if self.mask is not None and self.mask_dict is not None:
def recover_func(tensor):
# to: (BxL') x top_k x dim
dim = tensor.shape[-1]
tensor = tensor.view(-1, self.top_k, dim)
# to: (BxL) x top_k x d_model
x = torch.zeros(
mask.shape[0],
self.top_k,
dim,
device=tensor.device,
dtype=tensor.dtype,
)
# recover
x[mask == 0] = tensor
for k, v in self.mask_dict.items():
x[mask == k] = v
return x
moe_outp = tree.map_structure(recover_func, fwd)
else:
def view_func(tensor):
dim = tensor.shape[-1]
tensor = tensor.view(-1, self.top_k, dim)
return tensor
moe_outp = tree.map_structure(view_func, fwd)
gate_score = gate_score.view(-1, 1, self.top_k)
def bmm_func(tensor):
dim = tensor.shape[-1]
tensor = torch.bmm(gate_score, tensor).reshape(-1, dim)
return tensor
moe_outp = tree.map_structure(bmm_func, moe_outp)
if self.slice_size > 1:
def all_gather_func(tensor):
return AllGather.apply(
tensor, self.slice_rank, self.slice_size, self.slice_group
)
moe_outp = tree.map_structure(all_gather_func, moe_outp)
moe_outp_batch_size = tree.flatten(
tree.map_structure(lambda tensor: tensor.shape[0], moe_outp)
)
return moe_outp
_fmoe_general_global_forward()函數(shù)的代碼如下。
def prepare_forward(gate, num_expert, world_size):
r"""
Prepare necessary information from gate output for MoE computation.
Args:
gate: a 1-d Long Tensor representing the target expert of each input
sample.
num_expert: number of experts on each worker.
world_size: number of workers that hold different experts.
comm: the communicator of all workers in the expert-parallel group.
"""
pos, local_expert_count, global_expert_count = count_by_gate(gate,
num_expert, world_size)
with torch.no_grad():
fwd_expert_count = global_expert_count.view(world_size,
num_expert).sum(dim=0)
fwd_batch_size = int(fwd_expert_count.sum().item())
return (
pos,
local_expert_count.cpu(),
global_expert_count.cpu(),
fwd_expert_count.cpu(),
fwd_batch_size,
)
def _fmoe_general_global_forward(inp, gate, expert_fn, num_expert, world_size, **kwargs):
r"""
A private function that performs the following steps to complete the MoE
computation.
* Count the number of tokens from each worker to each expert.
* Send the features to their target position so that input features to each
expert are contiguous in memory.
* Perform the forward computation of the experts using `expert_fn`
* Gather the output features of experts back, and reorder them as sentences.
Intermediate results like expert counts are hidden from users by this
function.
"""
(
pos,
local_expert_count,
global_expert_count,
fwd_expert_count,
fwd_batch_size,
) = prepare_forward(gate, num_expert, world_size) # 獲得專家index信息
topk = 1
if len(gate.shape) == 2:
topk = gate.shape[1]
def scatter_func(tensor): # All-to-All dispatch
return MOEScatter.apply(
tensor,
torch.div(pos, topk, rounding_mode='floor'),
local_expert_count,
global_expert_count,
fwd_batch_size,
world_size,
)
x = tree.map_structure(scatter_func, inp)
x = expert_fn(x, fwd_expert_count) # 專家處理
out_batch_size = tree.flatten(inp)[0].shape[0]
if len(gate.shape) == 2:
out_batch_size *= gate.shape[1]
def gather_func(tensor): # All-to-All combine,返回給對應的rank
return MOEGather.apply(
tensor,
pos,
local_expert_count,
global_expert_count,
out_batch_size,
world_size,
)
outp = tree.map_structure(gather_func, x)
return outp
訓練時的步進函數(shù),可以看到torch.distributed.all_reduce的使用。
def patch_forward_step(forward_step_func, Megatron_Version="v2.2"):
r"""
Patch model's forward_step_func to support balance loss
"""
from megatron.mpu import is_pipeline_last_stage
from megatron.mpu import get_tensor_model_parallel_group
from megatron import get_args
if not get_args().balance_strategy:
return forward_step_func
def forward_step_with_balance_loss_v2_2(data_iterator, model, input_tensor):
args = get_args()
output = forward_step_func(data_iterator, model, input_tensor)
if not is_pipeline_last_stage() or not args.balance_strategy:
return output
while hasattr(model, 'module'):
model = model.module
loss_list = [l.mlp.gate.get_loss(clear=False).view(1)
for l in model.language_model.transformer.layers
if l.mlp.gate.has_loss]
if len(loss_list) == 0:
return output
loss_name = args.balance_strategy + "_loss"
(loss, state_dict), bal_loss = (
output,
torch.cat(loss_list).mean() * args.balance_loss_weight
)
# avarage across moe group
moe_group = get_tensor_model_parallel_group()
world_size = torch.distributed.get_world_size(group=moe_group)
averaged_bal_loss = bal_loss.clone().detach()
torch.distributed.all_reduce(averaged_bal_loss, group=moe_group)
averaged_bal_loss /= world_size
loss += bal_loss
state_dict[loss_name] = averaged_bal_loss
return loss, state_dict
0xFF 參考
一個關(guān)于MoE的猜想 渣B zartbot
SwitchHead:使用專家混合模型注意力加速 Transformer
LLM MOE的進化之路,從普通簡化 MOE,到 sparse moe,再到 deepseek 使用的 share_expert sparse moe chaofa用代碼打點醬油
Mixture of Parrots: Experts improve memorization more than reasoning
Scaling Laws for Fine-Grained Mixture of Experts
https://arxiv.org/pdf/2402.07871
大規(guī)模分布式 AI 模型訓練系列—專家并行 AI閑談
DeepSeek-R1模型架構(gòu)深度解讀(三)弄懂DeepSeekMoE AI算法之道 [AI算法之道](javascript:void(0)??
詳細談談DeepSeek MoE相關(guān)的技術(shù)發(fā)展 渣B [zartbot](javascript:void(0)??
DeepSpeed-MoE: Advancing Mixture-of-Experts Inference and Training to Power Next-Generation AI Scale
SGLang的Expert Parallel特性解讀 BBuf [GiantPandaCV]
圖解大模型訓練系列之:DeepSpeed-Megatron MoE并行訓練(源碼解讀篇) 猛猿
圖解大模型訓練系列之:DeepSpeed-Megatron MoE并行訓練(原理篇) 猛猿
簡單理解DeepSpeed-MoE專家模型和all2all通訊 voodoo
重新思考 MoE 王慶法 [清熙]
Moe模型的對比:Mixtral, Qwen2-MoE, DeepSeek-v3 Alex [算法狗]
混合專家模型Mixtral-8x7B模型挖坑指北 孟繁續(xù) [青稞AI]
A Uniffed View for Attention and MoE
統(tǒng)一視角看 Attention 與 MoE Taki
關(guān)于Deepseek采用EP推理方式的一些思考 楊鵬程
首篇MoE工作-Adaptive mixtures of local experts(1991) uihcgniw
【IDPT論文解讀】Adaptive Mixtures of Local Experts - 多系統(tǒng)融合 JaPay
Deepseek-MOE架構(gòu)圖解(V1->V2->V3) 假如給我一只AI



 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號