探秘Transformer系列之(19)----FlashAttention V2 及升級版本
探秘Transformer系列之(19)----FlashAttention V2 及升級版本
0x00 概述
FlashAttention利用了GPU內存的非對稱層次結構,將內存消耗降至線性(而非二次方),并相較于優化基線實現了2到4倍的運行速度提升。然而,該技術的速度依然沒有達到優化矩陣乘法(GEMM)操作的速度,前向傳播的計算吞吐量僅達到理論最大浮點運算速率(FLOPs/s)的30-50%,而反向傳播只能達到25-35%。這種低效率是由于GPU上不同線程塊之間的負載分配不佳,導致低占用率或不必要的共享內存讀/寫。
因此,原作者對FlashAttention進行了升級,得到了V2版本。而其它研究人員也在V1和V2之上發揮自己的聰明才智,進行了優化和發展。
0x01 FlashAttention V2
1.1 動機
作者發現在GPU的不同線程塊和warp的不合理的work分區是導致計算低效的一個主要原因。為了解決這個問題,FlashAttention 2設計了更好的worker分區方案。充分的利用并行化和高效的work分解提高計算利用率。
1.2 方案
FlashAttention 2 的優化點主要包括以下,其中第二和第三點都可以歸結為在cuda gemm層面的優化。
- 減少冗余計算。減少非矩陣乘法運算(non-matmul)的FLOPs,增加Tensor Cores的運算比例。
- 序列長度維度的并行。在不同線程塊之間把并行化做到單個頭級別,在序列長度的維度上對前向傳播和反向傳播做并行化。該方法在輸入序列很長(此時batch size通常很小)的情況下增加了GPU利用率。即使對于單個head,也在不同的thread block之間進行并行計算。
- 調整Warp Partitioning(分區)策略,分散負載,減少通信。在一個attention計算塊內,將工作分配在一個單個線程塊的不同warp上,來減少數據交換和共享內存讀寫。
減少冗余計算
為什么要減少非矩陣乘法運算(non-matmul)計算?這是因為矩陣乘法可以在現代硬件上被高效實現。
在深度學習中通常會使用矩陣乘法運算來進行前向傳播和反向傳播。為了迎合加速需求,硬件廠商定制了矩陣乘法(GEMM)的專用計算單元;而有了專用計算單元后,軟件算法的設計實現又在朝這個方向靠攏,兩者互相影響。然而,并不是所有的運算都可以被表示成矩陣乘法的形式,如加法、乘法、除法等就是在矩陣乘法之外的操作。雖然這些非矩陣乘法運算的FLOPs要比矩陣乘法低,但是由于其沒有針對性加速,所以其計算吞吐要遠低于矩陣乘法運算。因此需要想辦法在GPU上避免非矩陣運算。減少了非矩陣乘法的FLOPs。
減少冗余計算和交換循環順序是通過調整算法結構來完成的,主要是消除了原先頻繁的rescale操作。
增加并行
FlashAttention V1在batch size和head維度施加了并行化,即每個head被分配了一個線程塊,一共batch_size * head_num 個線程塊進行并行。但是由于內存限制,在處理長序列輸入時,人們通常會減小batch size和head數量,這樣就降低了并行化程度。
因此,FlashAttention V2還在序列長度這一維度上進行并行化,即將V1中Q的循環也修改為使用多個線程塊來并行操作,這樣總的線程塊有所增加,就提高了 GPU 的利用率。具體來說,V2 通過增加 num_m_block 的概念,將 Q 矩陣在序列長度方向上進一步劃分為多個小塊,每一塊由不同的 block 來處理。而且,每個 block 可以獨立地計算它所負責的輸出部分,減少了不同 block 之間的依賴和通信開銷。
序列并行的目的就是如何更好地劃分線程塊。
調整Warp Partitioning策略
FlashAttention V1使用是split-K策略,在該策略中,所有warp將中間結果寫入共享內存進行同步,然后將中間結果相加,這些共享內存讀取會拖慢前向傳播的計算。
FlashAttention V2使用更好的Warp Partitioning(分區)策略,在每個線程塊內部來分散warps之間的工作負載,進而減少通過共享內存的通信。
從本質上來說,調整warps工作負載策略是在線程塊內部進行優化。
1.3 算法
FlashAttention V2 算法主要優化點是調換了外層和內層循環的順序。把Q循環挪到了最外層,把KV移到了內循環。

具體如下。
- 和V1相比,V2的第3行和第6行調換了外層和內層循環的順序。把Q循環挪到了最外層,把KV移到了內循環。
- 第8行會計算分塊 \(S_i^{(i)}\)。
- 第9行會更新三個中間變量。
- \(m_i^{(j)}\) 表示截止到當前分塊 \(S_i^{(j)}\)(包含當前分塊)為止的rowmax;
- \(\tilde P_i^{(j)}\)表示使用當前每行最大值計算歸一化前的 \(P_i^{(i)}\) ;
- \(l_i^{(j)}\) 表示截止到當前分塊 \(S_i^{(j)}\) (包含當前分塊為止)的rowsum;
- 第10行會計算O。\(O_i^{(i)}\) 表示截止到當前分塊\(S_i^{(i)}\)(包含當前分塊)止計算出的O值。由第9和第10行知,當我們固定Q循環KV時,我們每個分塊都是用當前最新的rowmax和rowsum計算的,同理對應的 \(O_i^{(i)}\)也是用當前最新的rowmax和rowsum計算的。這樣當我們遍歷完所有的KV時,得到的 \(O_i^{(i)}\) 就等于最終全局的結果。
- 第12行的\(diag(l_i^{(j)})^{?1}\)會對O進行統一的歸一化操作。在內循環中沒有做歸一化,而是統一放到外循環來做,這樣可以減少非矩陣運算。
- 第13行會計算中間變量 \(L_i=m_i^{(T_c)} + log(l_i^{(T_c)})\)。并且在第15行回寫到HBM中。因為從HBM上讀取\(l_i\),\(m_i\) 會消耗讀寫,所以我們不希望再存每一Q分塊對應的 \(m_i\)和 \(l_i\)。但是在反向傳播中,我們依然需要 \(l_i\),\(m_i\) 來做 \(S_i^{(i)}\) 和\(P_i^{(i)}\) 的重計算(用鏈式求導法則來計算dQ,dK,dV,需要如此操作)。所以在V2中,我們只存儲 \(L_i=m_i^{(T_c)} + log(l_i^{(T_c)})\) ,然后通過\(L_i\)來計算\(P_i^{(i)}=exp(S_{ij}-L_i)\)。這樣可以節省HBM讀寫操作。L是log-sum-exp的縮寫。
減少冗余計算
FlashAttention V2 算法通過減少中間縮放的次數減少了冗余計算。
原始Softmax
原始softmax為了數值穩定性(因為指數增長太快,數值會過大甚至溢出),會減去最大值,這樣帶來的代價就是要對token遍歷3次。
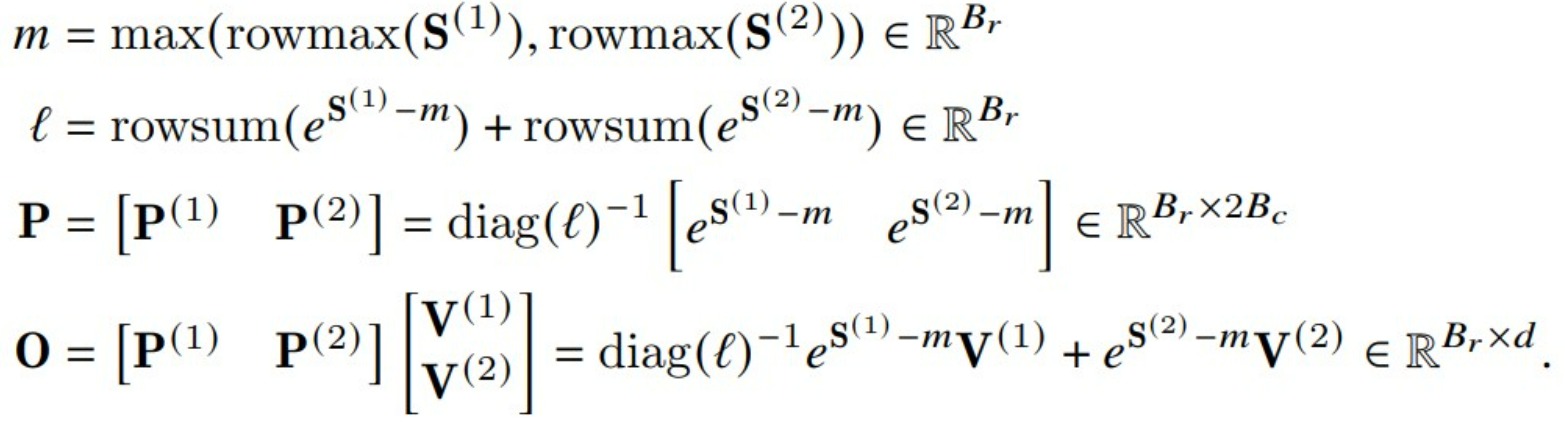
FlashAttention V1
FlashAttention V1計算O的操作如下所示。
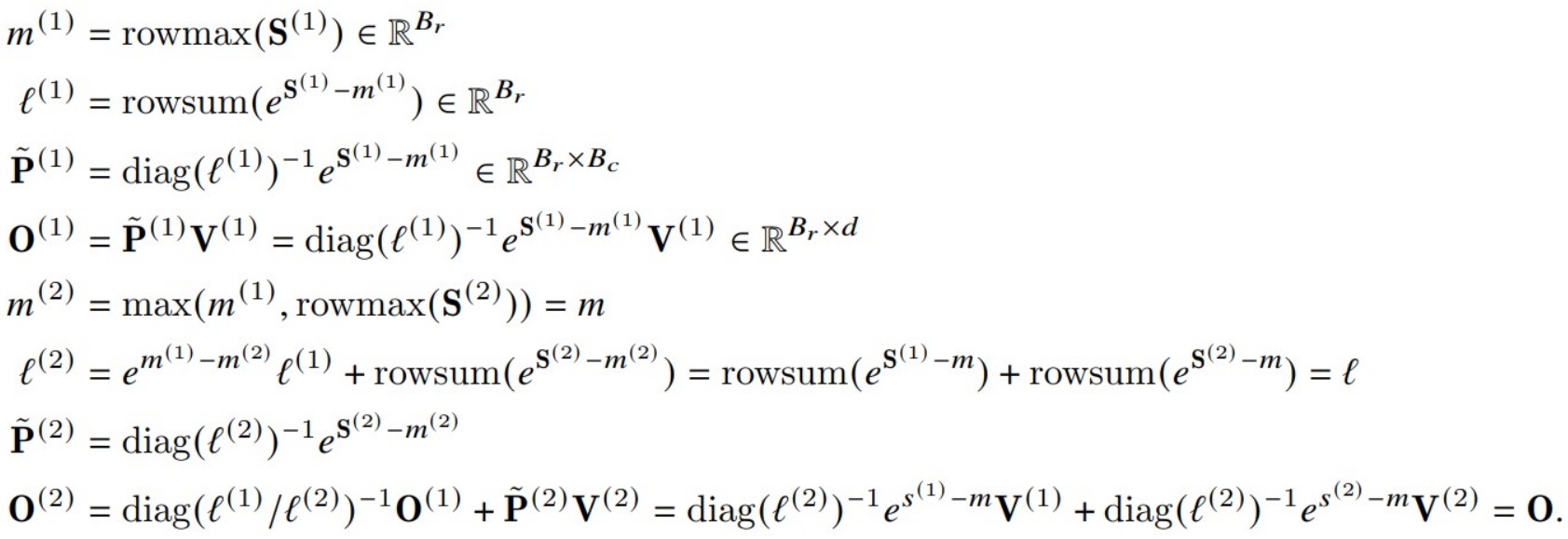
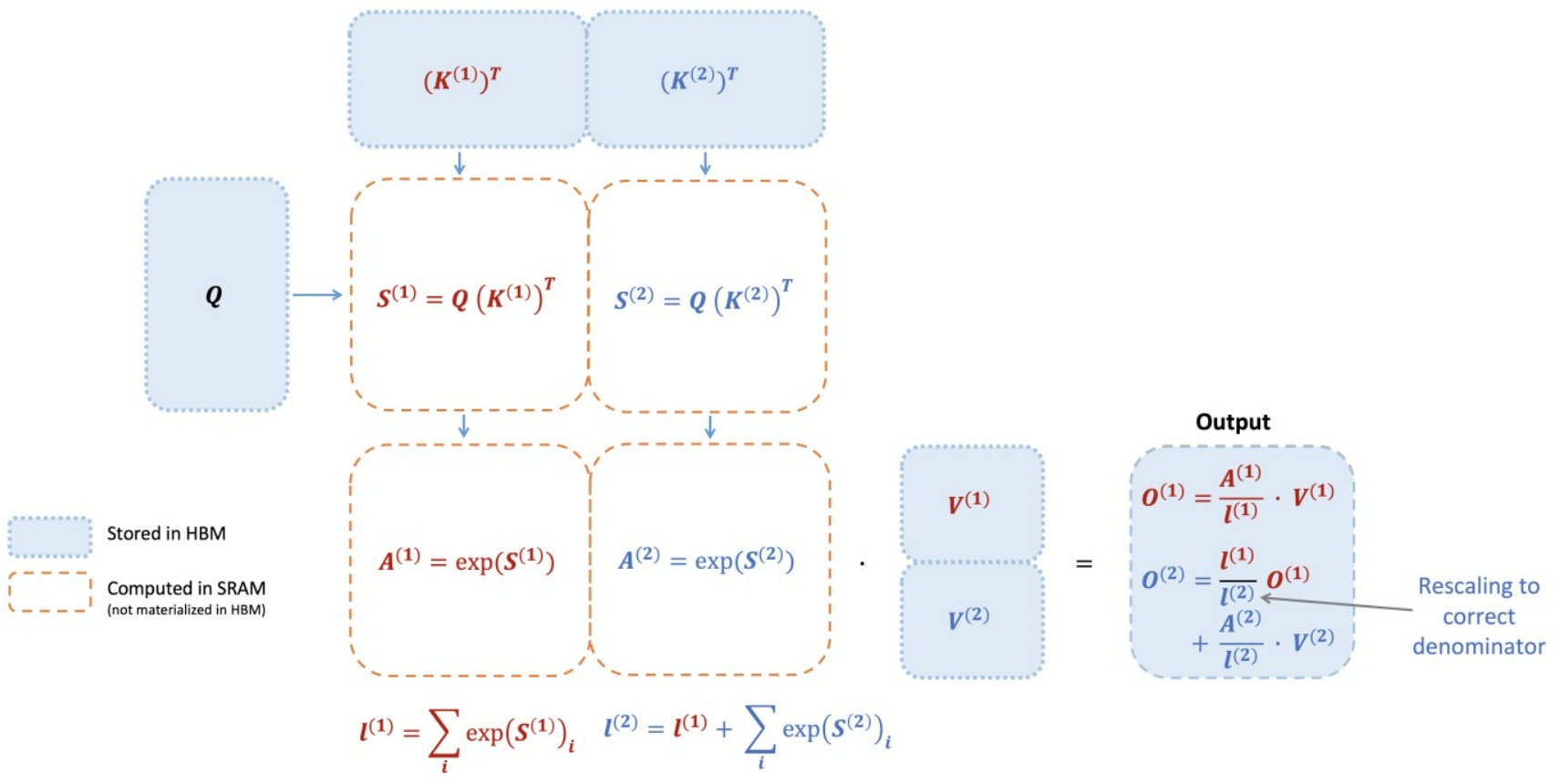
下圖展示了FlashAttention如何使用online softmax進行分塊計算。
FlashAttention V2
FlashAttention V2則修改為如下。
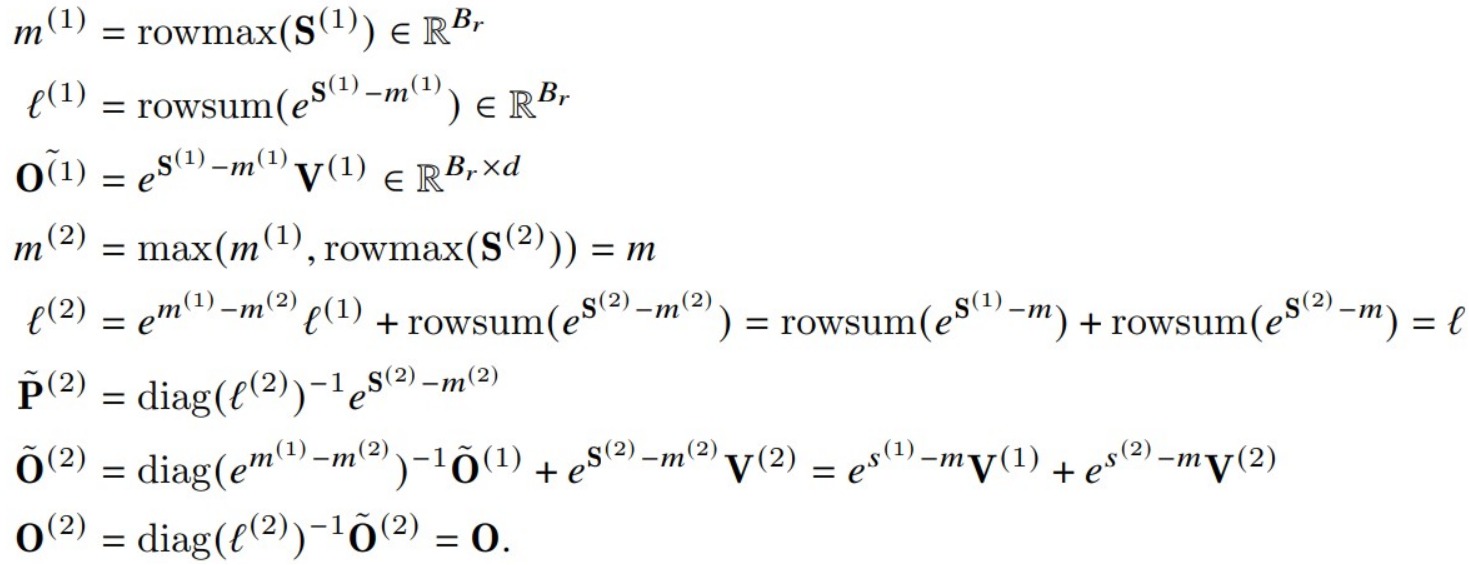
我們把V1和V2放在一起比較可以更好的看出區別。
- V1算法會在內循環中迭代地對前序值用rescale進行修正,即每個block的每次迭代都需要執行rescale操作,這涉及到除法運算。
- V2算法則把rescale操作從內循環轉移到外循環中,這種rescale操作被延后到循環的最后才執行一次,每次計算可以減少一次除法運算。即:
- 在內循環中,計算\(O^{(1)}\)時刪除了\(diag(l^{(1)})^{-1}\)操作,只是對\(O^{(1)}\)的分子進行修正;在計算\(O^{(2)}\)時刪除了\(diag(l^{(2)})^{-1}\)操作。
- 在內循環結束后,在外循環中統一執行一次rescale修正,得到最終值。這樣每次內循環計算可以減少一次除法(非矩陣乘法運算)運算。V2只要在每次迭代中確保分子部分\(O^{(1)}\)和\(O^{(2)}\)被scale為正確值、以及可以計算出最終的分母部分 \(?^{(2)}\),就可以得到和V1同樣的效果。

交換循環順序
GPU特點
在詳細介紹FlashAttention v2的并行策略之前,需要簡單回顧一下GPU的基本工作原理。
從硬件層面上看,GPU適合并行任務的原因是因為GPU通常含有大量計算單元。雖然GPU的單個計算單元通常不如CPU強大,但大量的計算單元可以同時完成并行任務。SM(Streaming multiprocessors)就是GPU中真正的物理計算單元,在A100中一共有108個SM。為了提高計算吞吐量,需要盡可能保證在每個時刻有較多的SM同時在參與計算。
從軟件層面上看,GPU依靠線程完成計算工作。GPU有大量線程,這些線程按照線程塊的形式進行管理。比如每個線程塊包括128個線程,這些線程塊被調度到SM上進行計算。
為了更好的協作,在每個線程塊又劃分成多個warp。warps 是NVIDIA GPU并行計算的基本單元(線程實際調度的最小單位)。一個Warp通常包含32個線程,它們同時執行相同的指令,但對不同的數據進行操作。在GPU執行指令時,通常以Warps為單位進行調度,這可以充分利用GPU的并行處理能力。同一個warp中的所有線程可以協作完成矩陣乘法。但是如果共享變量不在一個線程塊內,則意味著要往共享內存上寫更多的中間結果。
FlashAttention V1
我們首先從并行化角度看看V1版本的一些特點。
首先,前置條件是:如果我們把O看作一個矩陣,那么從矩陣角度理解,V1版本的外循環 j 對應的是O矩陣的列,內循環 i 對應的是 O 矩陣的行。
其次,目前內外循環的配置會導致需要把整個外循環操作放在一個線程塊內,這是因為:
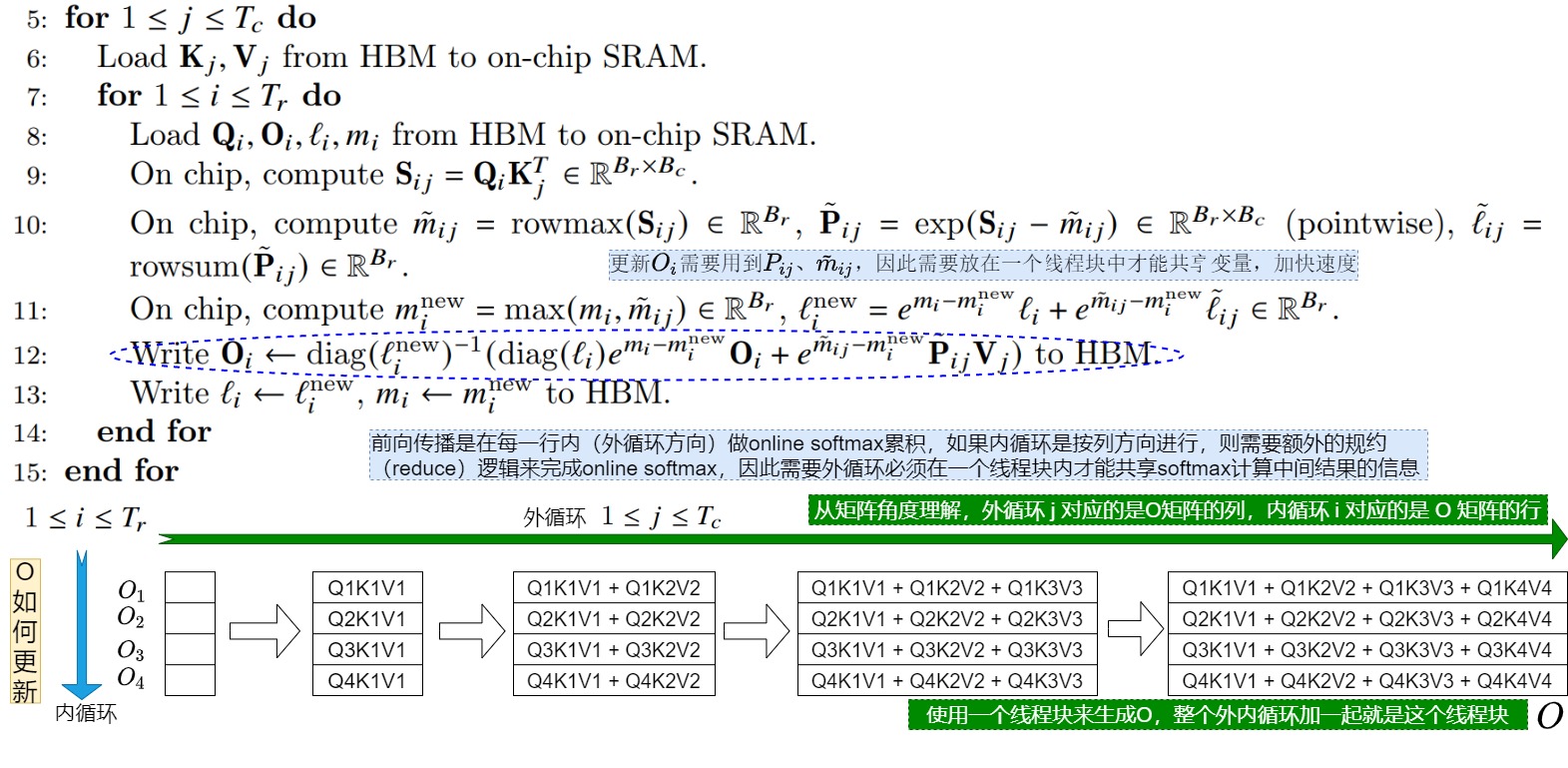
- 前向傳播時,我們需要在每一行內按列(外循環方向)來做online softmax累積,更新\(O_i\)需要用到$ P_{ij}\(、\)\tilde m_{ij}\(,而\) P_{ij}\(、\)\tilde m_{ij}$是在內循環中計算出來。
- 內循環按行方向進行迭代,和online softmax的在每一行上按列方向操作有沖突,需要額外的規約(reduce)邏輯來完成online softmax。
理想狀態下,V1應該把整個外循環操作放在一個線程塊內才能共享softmax計算中間結果的信息,加快速度。如果整個外循環操作不在同一個線程塊內,這些中間結果信息就要放在共享內存中,或者需要額外的通信操作。比如cross thread block reduce。
第三,目前內外循環的配置會導致內外循環有依賴。這是因為更新\(O_i\)需要用到\(V_j\),而V1的兩重循環中會先在外層循環加載K, V,然后內層循環再加載Q。這就會導致內層循環每次計算的只是\(O_i\)的一部分,且每次內循環的迭代都需要對\(O_i\)進行全局內存的讀寫。
綜上所述,V1只能在batch_size和headnum維度以線程塊為粒度做并行,當序列比較長,batch size比較小時,V1的效率就大幅下降。具體也可以參見下圖,在FlashAttention v1中使用一個線程塊(thread block)來生成下圖中的結果O,或者可以理解為,整個內外循環加起來是一個線程塊。
FlashAttention V2
由V1的分析可知,不應該讓內循環放在softmax規約的維度。另外,在Attention的計算中,不同query的Attention計算是完全獨立的。輸出結果O1僅和Q1相關,與Q2、Q3、Q4均無邏輯依賴關系,應該可以并行。
因此,FA2對于前向傳播調整了循環的順序,先load Q,再load K, V。
我們來分析下調整順序帶來的影響。
- 外循環可以增加并行度。交換了Q loop順序到最外層之后,\(Q*K^T\)在“行”方向的seqlen上天然可以并行,外循環的每個迭代計算之間沒有任何依賴。可以把這一維度的并行度從串行迭代改成并行的線程塊,即把不同query塊的注意力計算發送給不同的線程塊來并行執行,這些線程塊之間不需要通信。
- 內循環可以減少操作。
- 對比FA1,內循環不需要每次存取 O_i,?_i,m_i到HBM,從而減少了IO操作,耗時也隨之減少。
- online softmax是在每一行上按列進行累積,和內循環的迭代方向一致,所以不需要額外的規約邏輯。
因此,V2可以對batch_size,num_heads,seq_len三層循環以thread block為粒度并行切分,對于seq_len,可以理解為外循環被切成了\(T_r\)個并行塊。這些thread block之間是不需要通信的,從而顯著增加GPU的吞吐。
如下圖所示,在FlashAttention v1中使用一個thread block來生成下圖中的結果O;但是在FlashAttention v2中一個thread block僅負責生成圖示中結果O的一個子集,也就是圖下方中的每一行(O1, O2...)。在單個線程塊中會迭代地對(Q1,K1,V1),(Q1,K2,V2),(Q1,K3,V3),(Q1, K4, V4)數據進行tiling化的attention運算,將結果累積至O1中,迭代中的O1值是中間結果值,而最后一輪迭代后O1即為真實結果值。這也符合attention是加權平均和的語義解釋,可以理解為,O1是Q1的更深語義空間的加權平均和表示。
這樣多個thread block可以并行地生成O2,O3,O4部分從而增大算法整體并行度,提高了GPU利用率。

反向傳播遵循同樣的原理,沒有把inner loop放在softmax規約的維度,因此反向傳播的循環依然和V1相同,外層循環先load K,V, 內層循環再load Q,但是在seq length(“列”方向)上增加了一維并行度。具體分析如下。
在BWD的過程中主要是求 \(dV_j\) \(dK_j\), \(dQ_i\) (為了求它們還需要求中間結果 \(dS_{ij}\), \(dP_{ij}\) ),我們來總結一下這些梯度都需要沿著哪些方向AllReduce:
- \(dV_j\) :沿著i方向做AllReduce,也就是需要每行的結果加總。
- \(dK_j\) :沿著i方向做AllReduce,也就是需要每行的結果加總。
- \(dQ_i\) : 沿著j方向做AllReduce,也就是需要每列的結果加總。
- \(dS_{ij}\), \(dP_{ij}\) :只與當前i,j相關。
如果還是保持Q內循環,KV外循環,相當于固定行,遍歷列,那么在這些梯度中,只有 \(dQ_i\) 從中受益了。但是KV梯度要往HBM上寫中間結果,總體占用顯存和顯存操作都大。因為KV的數據量比Q大,所以只能做權衡,犧牲Q,讓KV進入內循環(S和P的計算不受循環變動影響)。
反向傳播具體算法如下。

序列并行
在寫CUDA代碼時,我們需要確定總共需要分配多少個block。對于FlashAttention來說,會在每個block中做注意力計算。因為計算注意力時,batch、head之間是數據獨立的,因此如何劃分塊要看Q、K、V之間的數據依賴關系是否可以支持并行。
- 因為存在數據依賴關系,所以V1對batch_size,num_heads兩個維度來劃分線程塊。一共有
batch_size * num_heads個block,每個block負責計算O矩陣的一部分。具體設置grid代碼舉例如下:dim3 grid(params.b, params.h)。 - 因為Qi需要和全量的K和V計算,所以V2對batch_size,num_heads,seq_len三個維度來劃分線程塊。一共有
batch_size * num_heads * num_m_block個block,每個block負責計算矩陣O的一部分。num_m_block是沿著Q矩陣行方向做的切分,每份維護了若干個token。具體設置grid代碼舉例如下。
if (params.num_splits == 1) {
dim3 grid(params.b, params.h, params.num_splits);
kernel<<<grid, Kernel_traits::THREADS, smem_size_dq_dk_dv, stream>>>(params);
} else {
dim3 grid_dot(params.b, params.h, (params.seqlen_q + 128 - 1) / 128);
fmha_bwd_dot_do_o_kernel<Kernel_traits><<<grid_dot, Kernel_traits::THREADS, 0, stream>>>(params);
int num_splits = params.seqlen_k / blocksize_c; // seqlen_k is divisible by blocksize_c
dim3 grid(params.b, params.h, num_splits);
kernel_seqparallel<<<grid, Kernel_traits::THREADS, smem_size_dq_dk_dv, stream>>>(params);
}
增加序列并行的目的是為了更好的利用SM,讓SM打滿。當batch_size和num_heads都比較大時,block也比較多,此時SM利用率比較高。但是如果我們的數據seq_len比較長,此時往往對應著較小的batch_size和num_heads,此時就會有閑置的SM。而為了解決這個問題,V2就引入在Q的seq_len上的劃分。
FlashAttention V1
FlashAttention V1在batch和heads兩個維度上進行了并行化。
- 對于單個序列來說,FlashAttention v1的并行計算主要在注意力頭之間。在一次前向計算過程中,同一自注意力計算中的注意力頭可以并行計算。
- 同一batch中的數據也是并行處理的。
所以FlashAttention v1的并行實際在兩個維度同時進行:batch和注意力頭。需要thread block的數量等于batch size × number of heads。每個block被調到到一個SM上運行,A100一共有108個streaming multiprocessors。當塊數量很大,就會有更多的SM在并行計算,整體的吞吐量自然也就會比較高,可以充分利用GPU資源。
但是在處理長序列輸入時,由于內存限制,通常會減小batch size和注意力頭的數量,這樣并行化程度就降低了。因為如果batch size和注意力頭的數量設置太大,就會OOM。因此,對于長上下文的場景來說由于能組的batch比較小或者注意力頭比較少。單卡上的batch size通常變得非常小,因此實際可以并行的attention head數量可能遠遠少于SM數量,導致系統整體吞吐量較低。
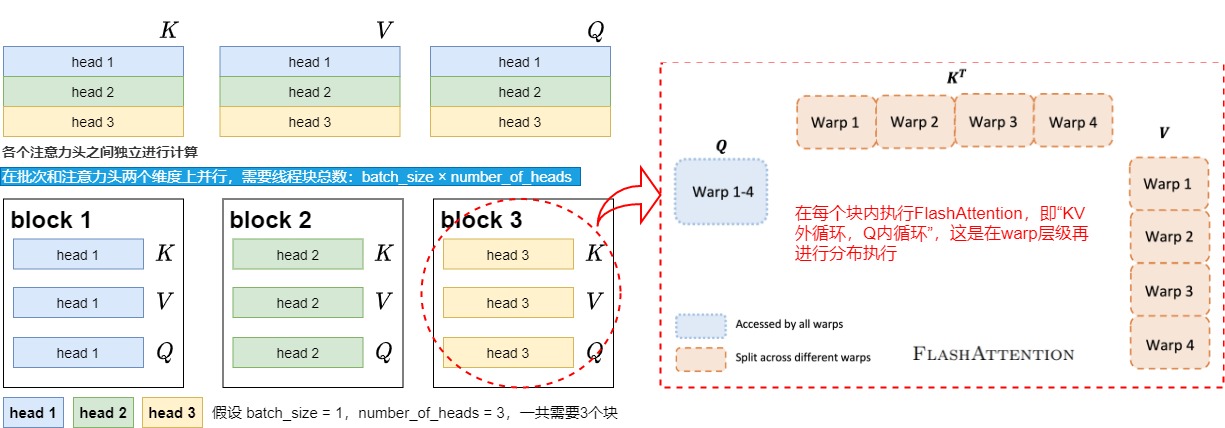
V1的線程塊分布如下圖所示。
假設batch_size = 1,num_heads = 3,我們用不同的顏色來表示不同的注意力頭。我們知道在Multihead Attention中,各個注意力頭是可以獨立進行計算的,在計算完畢后將結果拼接起來即可。所以我們將1個注意力頭劃分給1個block,這樣就能實現block間的并行計算。而每個block內就能執行V1中的"KV外循環,Q內循環”的過程了。這個過程是由block的再下級warp level層面進行組織,由thread實行計算的。最終,每個block只要在計算完畢后把結果寫入自己所維護的O的對應位置即可。
FlashAttention V2
FlashAttention v1的并行策略導致輸入序列較長時,會因batch size較小而導致整體可并行的線程塊數遠少于SM數量。因此需要思考除了在batch和attention head維度之外,還能在哪些維度進行并行。所以FlashAttention v2實際上在FlashAttention v1的并行策略基礎上,增加了在序列長度這一維度上的并行操作。這其實也是內外循環置換這個總體思想的配套改進措施。
前向傳播劃分
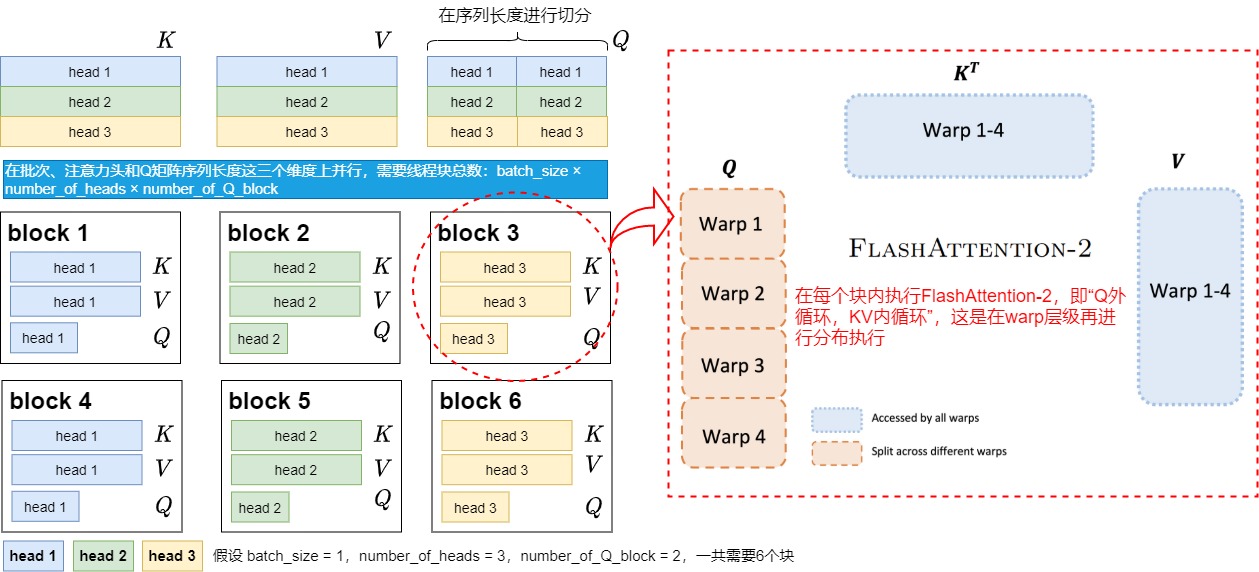
現在我們繼續假設batch_size = 1,num_heads = 3。與V1不同的是,我們在Q的seq_len維度上也做了切分,將其分成2份,即num_m_block = 2。所以現在我們共有1x2x3 = 6個block在跑。這些block之間的運算也是獨立的,因為:
- head的計算是獨立的,所以各種顏色的block互不干擾
- 采用Q做外循環,KV做內循環時,行與行之間的block是獨立的,因此不同行的block互相不干擾。
每個block從Q上加載對應位置的切塊,同時從KV上加載對應head的切塊,計算出自己所維護的那部分O,然后寫入O的對應位置。
劃分區別
因為V2中FWD和BWD的內外循環不一致,所以thread block的劃分也會有所不同。
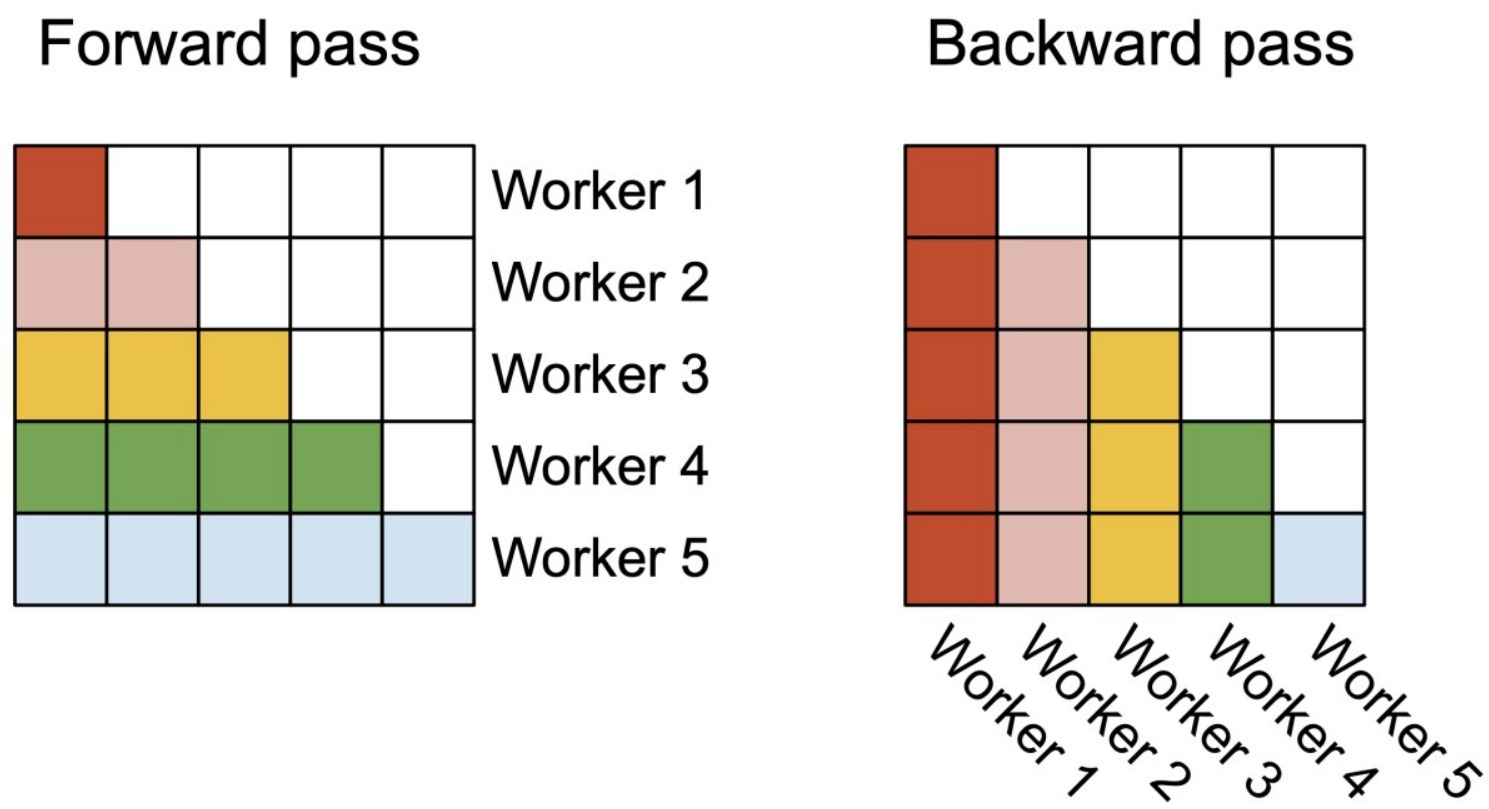
圖中的整個大方框表示輸出矩陣,worker表示thread block,不同的thread block用不同顏色表示,白色代表因為mask操作而免于計算。
- 前向傳播:每一行對應一個worker,它表示O矩陣的每一行都是由一個thread block計算出來的(假設num_heads = 1)。
- 反向傳播:每一列對應一個worker,這是因為BWD中我們是KV做外循環,Q做內循環,這種情況下dK, dV都是按行累加的,而dQ是按列累加的,少數服從多數,因此這里thread_block是按 \(K^T\) 的列劃分的。
其它可能性
- 為什么V1不做序列并行?其實無論是FA1還是FA2其實都可以做,從代碼中看,在V1后期的版本中,也出現了seq維度的并行。雖然V1也引進過seq parallel,但是它的grid組織形式是(batch_size, num_heads, num_m_blocks),而V2的組織形式是(num_m_blocks, batch_size, num_heads),這種順序調換的意義是什么呢?這樣的調換是為了提升L2 cache hit rate。對于同一列的block,它們讀的是KV的相同部分,因此同一列block在讀取數據時,有很大概率可以直接從L2 cache上讀到自己要的數據(別的block之前取過的)。
- 為什么只對Q的seq_len做了切分,而不對KV的seq_len做切分?答案是,一般來說,在Q seq length上拆block并行對于GPU occupancy已經夠了。除非你認為SM真得打不滿,否則盡量不要在KV維度上做切分,因為如此一來,不同的block之間是沒法獨立計算的(比如對于O的某一行,它的各個部分來自不同的block,為了得到全局的softmax結果,這些block的結果還需要匯總做一次計算),會額外帶來通信開銷。其實,在V2的cutlass實現中,確實也提供了對KV的seq_len做切分的方法。
另外,FlashAttention V2在訓練和推理prefill的時候計算并行度均比較高,因為query_num比較大,另外還有head_num和batch_size。但是在推理decode階段就不適合,因為此時query_num為1,單純batch_size * head_num的值就很小了,所以推理的時候沒有使用FlashAttention V2。
調整warps間工作負載
說完了thread block的并行,再來看一個block內的warp怎么分配工作的,此處是優化thread blocks內部warp級別的工作模式,盡量減少warp間的通訊和讀取shared memory的次數。
矩陣乘法本身是可分塊計算的。所以我們可以充分利用多個warps的計算能力來對矩陣進行分塊處理,從而加快整體計算速度。每一個thread block負責某個分塊的一個attention head的計算。在每個thread block中,threads又會被組織為多個warps,每個warp中的threads可以協同完成矩陣乘法計算。Work Partitioning主要針對的是對warp的組織優化。不管是V1還是V2,在Ampere架構下,每個block內進一步被劃分為4個warp,在Hopper架構下則是8個warp。
左圖表示V1,右圖表示V2。
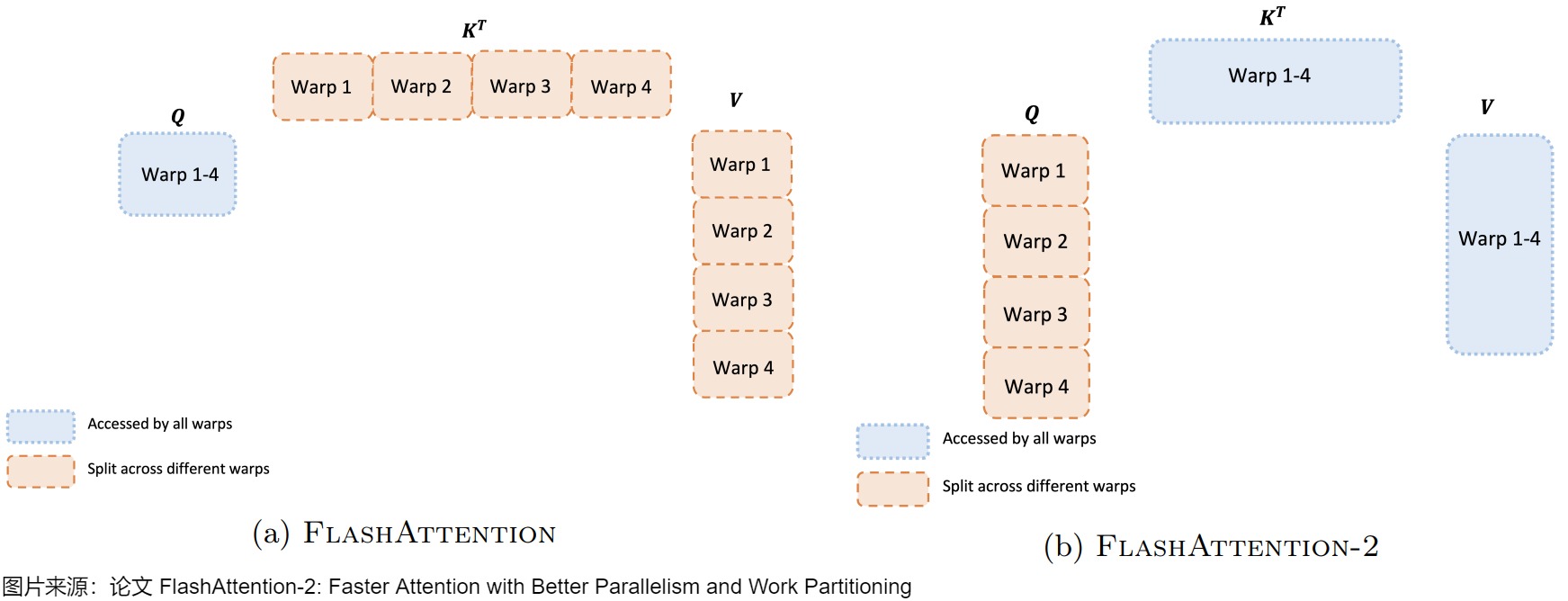
FlashAttention V1
flash attention1的forward計算中,對于每一個block,是將\(K,V\)切分到4個不同的warps上,但是將\(Q\)保持為對所有的4個warps是可見的。作者把這個計算方法稱之為'split-K'。
每個warp都從shared memory上讀取相同的Q塊以及自己所負責計算的KV塊。每個warp計算自己的 $QK^T $,然后再和被分割的V相乘。對于同一個Q需要所有KV都計算過才能出結果,而每個warp只是計算出了列方向上的結果,這些列方向上的結果必須匯總起來,才能得到最終O矩陣行方向上的對應結果。所以,每個warp需要把自己算出來的中間結果寫到shared memory上,再由一個warp(例如warp1)進行統一的整合。這就是各個warp間需要通訊的原因。需要寫中間結果,所以影響了計算效率。另外,內外循環的依賴也導致了V1無法進行并行操作,只能把外循環整體作為一個線程塊執行,warp內部也是串行操作。
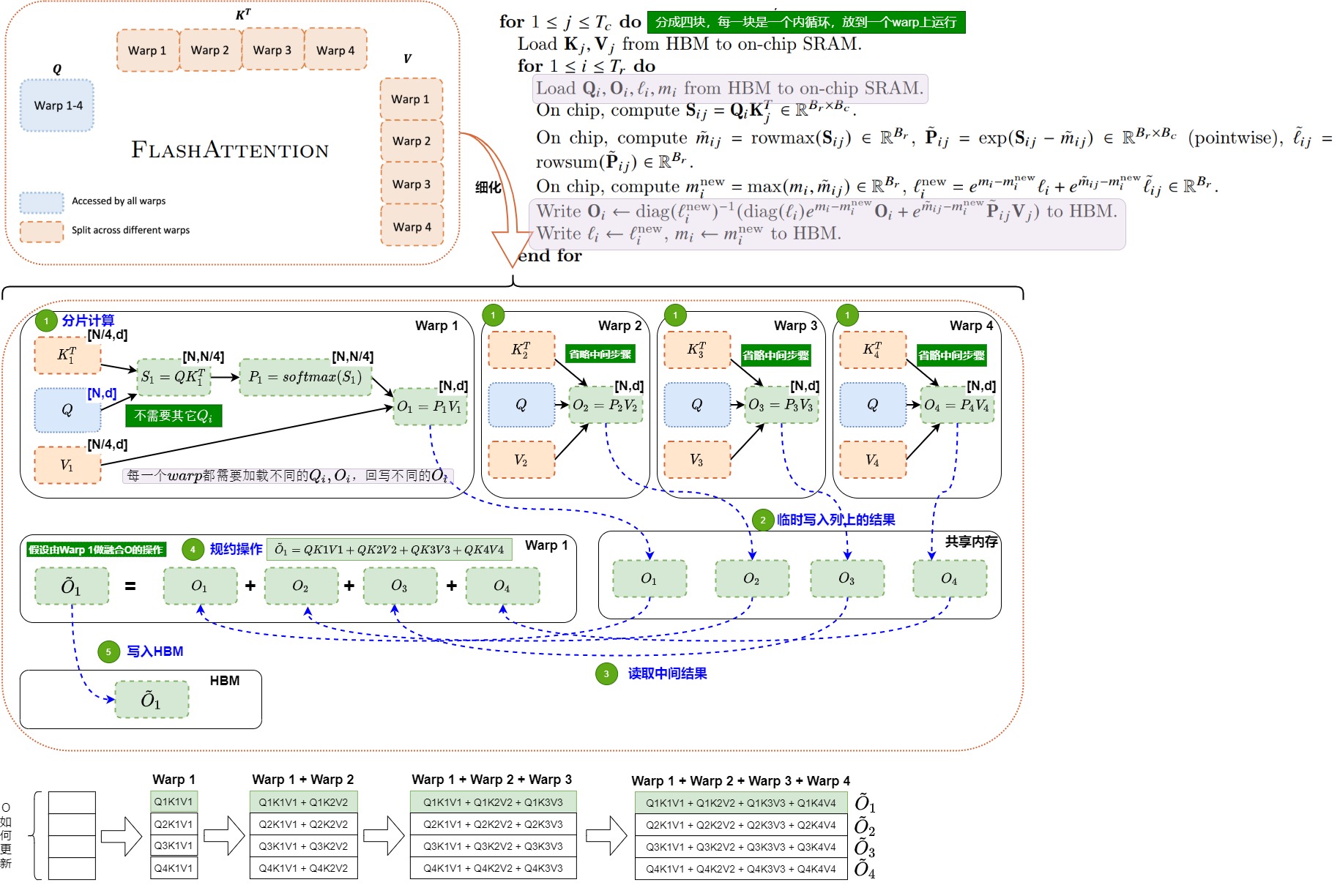
FlashAttention V2
Flash Attention 1這樣分塊的缺點是:因為而且fwd的目的是沿著行方向計算softmax,行方向信息最后要匯總的,所以需要把中間結果寫回SRAM,然后調用耗時的Synchronize后進行相加操作。內存操作就會減慢計算。為了克服這個缺點,v2則使用的是split-Q策略,這樣在每個warp計算\(QK^\top\)后,結果只需要對應的V分片即可得到O的對應分片,而無需進行warps間的通信,減少了中間共享內存讀寫。
關于這樣修改為什么會減少shared memory的讀寫以提高性能,paper的原文是這么說的:

V2實現中,在Q維度上按warp進行切分,每個warp都從shared memory上讀取相同的KV塊以及自己所負責計算的Q塊。Q維度上的切分是互相獨立的(行方向上的計算是完全獨立的)。對于確定的 Q token,對應的序列維K的所有結果都在一個 warp內,即:一個local softmax的所有計算元素都在一個quarter warp內。即每個warp最后只需要跟分割后的V相乘得到對應的分塊輸出結果,然后把自己計算出的結果寫到O的對應位置即可。這樣softmax的計算以及后面 \(P \times VT\) 的計算,都在一個warp內。因為并減少了額外的加法以及它對應的讀寫操作,所以warp間不需要再做通訊。同時不需要在內循環中進行HBM寫入(改為更低頻的外循環寫入,因為內循環一輪直接就計算完成了,不需要跨外循環同步),減少了I/O開銷。
不過這種warp并行方式在V2的BWD過程中就有缺陷了:由于bwd中dK和dV是在行方向上的AllReduce,所以這種切分方式會導致warp間需要通訊。
1.4 Causal Mask處理
V2還有一個針對Causal Masking(因果掩碼)的簡單優化。在對LLM進行自回歸訓練時,通常需要使用一個Mask作用于Attention Score矩陣,來保證每個token不會attend到它之后的token。
FlashAttention 本身基于分塊計算,因此如果某個分塊需要被完全mask,那么可以直接跳過該分塊,而無需進行任何計算。所以計算過程就存在Early Exit的可能。也就是,存在mask全為0的block以及索引滿足某些條件的block,可以不需要計算直接返回。具體來說可以根據row和column的index大小可以分為三種類型:
- column_index < row_index,此時整個塊都需要進行計算\(Softmax(QK^T)\),無需causal mask。
- column_index > row_index,此時整個塊都可以skip,不需要進行計算\(QK^T\),無需causal mask。
- column_index = row_index,需要應用causal mask對塊內數據進行處理后再計算,即\(Softmax(Mask(QK^T))\),可避免部分運算。
具體論文部分摘錄如下。

1.5 MQA/GQA
在FlashAttention中,也支持MQA和GQA。對于MQA和GQA的情形,FlashAttention采用Indexing的方式,而不是直接復制多份KV Head的內容到顯存然后再進行計算。而是通過傳入KV/KV Head索引到Kernel中,然后計算內存地址,直接從內存中讀取KV。

1.6 總結
比較
我們首先把V1和V2進行系統性比較。

計算量
FlashAttention v2 的優勢在于少了原來每一步的乘法和除法。其縮減操作的思路具體如下。
假設我們一個向量x,并將其“一切為二”進行分塊得到兩個子向量。
當都計算完兩個子向量后,為了將子向量\(x_2\)的 softmax 更新至全局,需要對它進行分母替換:即將局部的EXP求和項升級為全局。而替換的邏輯是乘上原來的分母\(l_2\),然后再除以新的全局EXP求和項\(l_{all}^{new}\)。這一步更新完后也就得到\(x_2\)最終的 softmax。如果我們對向量x 進行一分為二,而是一分為三。此時,\(x_2\)的 softmax 在由本次更新后,在后續還會再更新一次:當\(x_3\)處理完之后。此時對于\(x_2\)的 softmax ,我們又要乘以\(l_{all}^{new}\) (上一次的全局EXP求和項),并除以此時新的全局EXP求和項。
回過頭再來看,就會發現其實沒有必要去除以\(l_2\),因為下一次更新由需要乘以一個\(l_2\)來抵消分母。同理,如果 \(x_2\) 之后還有分塊,那么我們也無需除以此時的\(l_{all}^{new}\),因為下一次更新時又會乘以一個 \(l_{all}^{new}\) 來抵消。
所以我們其實可以在每一次分塊計算完畢后不去除以此時的EXP求和項,只需要等到最后去直接除以最終的 \(l_{all}^{new}\)即可。其本質是在每一次迭代過程中,不再除以EXP求和項。因為不除以EXP求和項了,所以也就無需對EXP求和項進行更新。直到處理完最后一個分塊后,直接用此時的全局EXP求和項來做分母即可。
IO
調整循環順序后,對比FA1,內循環不需要每次讀寫\(o_i, l_i, m_i\)到HBM,從而減少了IO-Accesses,耗時也會隨之減少。
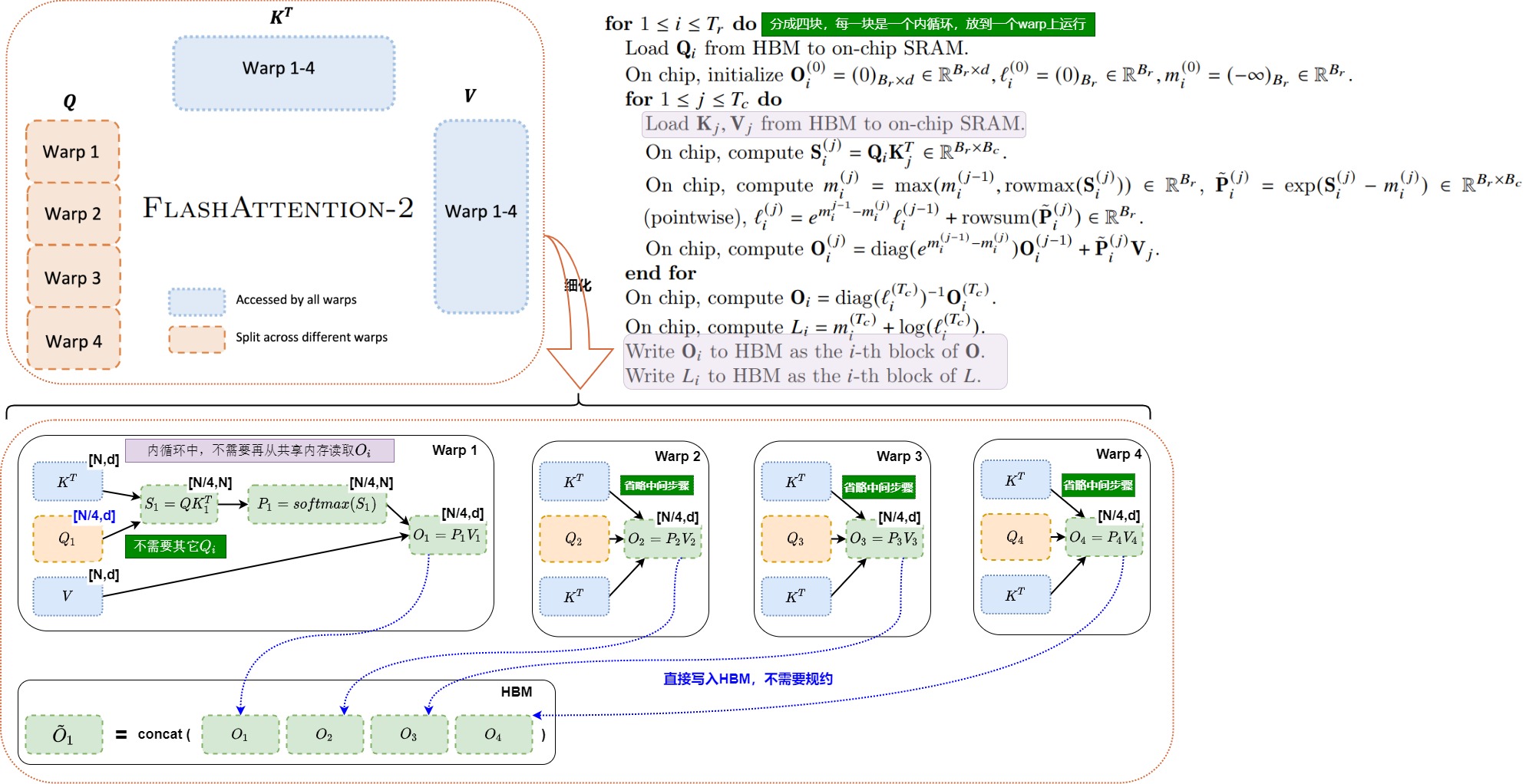
V2總體
我們再用一個V2的整體圖作為總結。
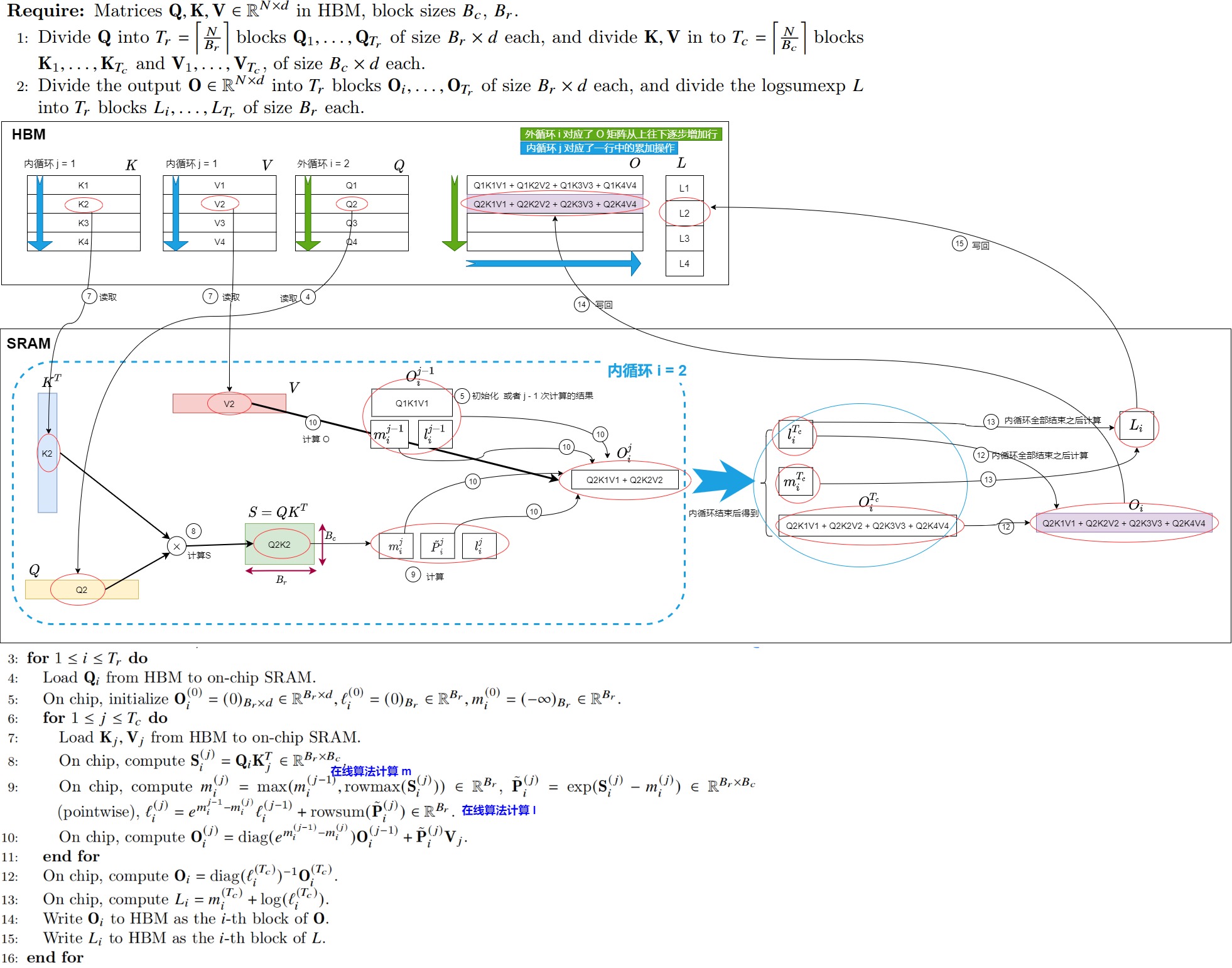
1.7 問題
FlashAttention-2 使用online softmax 技術來將單個查詢塊的注意力計算分割成工作塊。每個工作塊包括一個鍵塊和一個相應的值塊,并且這些工作塊按順序到達,以更新給定查詢塊的注意力輸出。FlashAttention-2 為每個傳入的工作塊計算在線 softmax,重新調整從前一個工作塊獲得的中間輸出,并將其與當前工作塊的部分輸出結合起來,以獲得最新的更新輸出。然而,這種精確計算注意力的方法在其順序性上受到限制,在解碼階段特別是在需要遍歷大量鍵/值塊的情況下,會導致計算速度較慢。
1.8 實現
此處我們用V2的實現來進行學習。
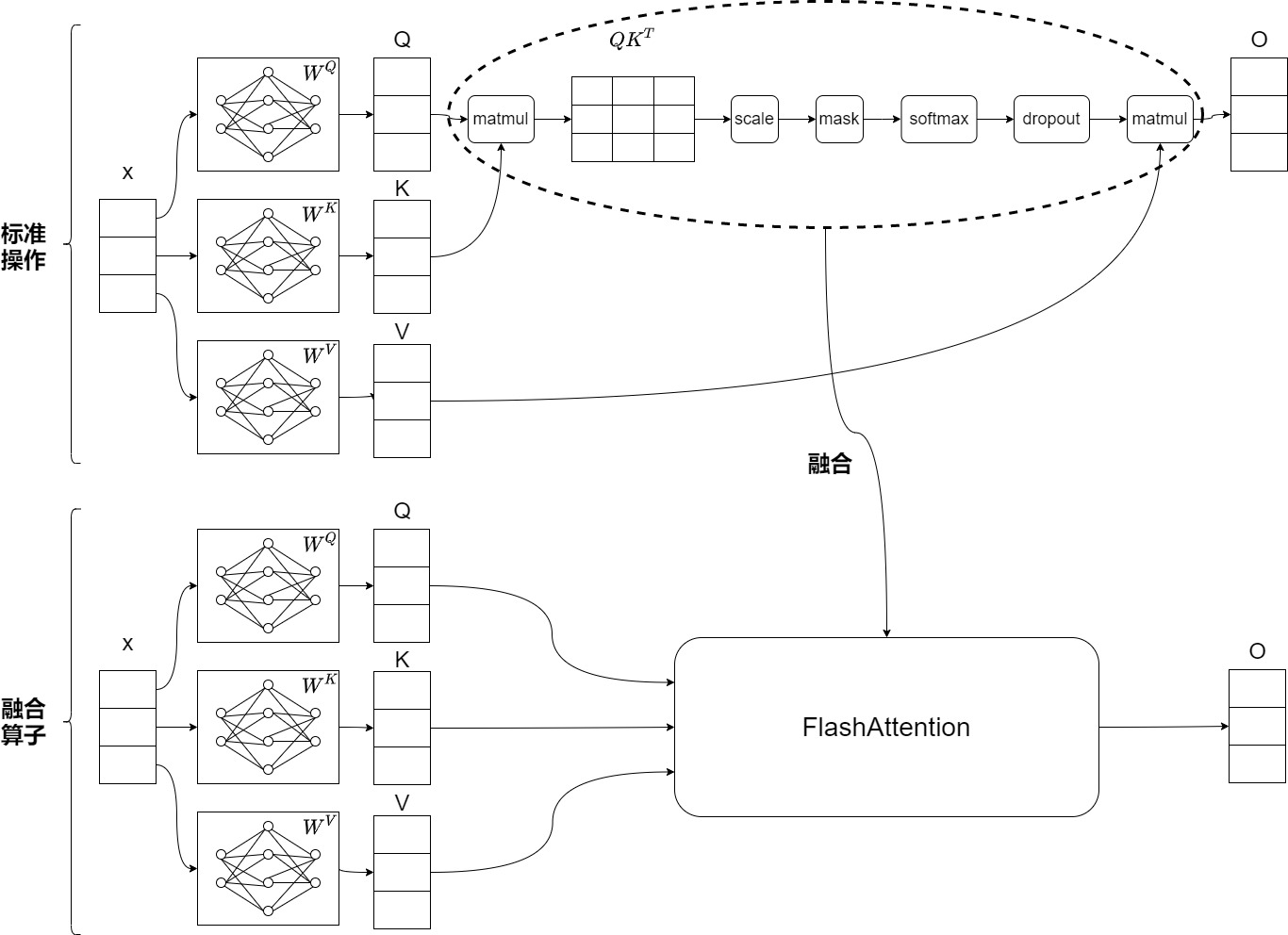
融合算子
最終,FlashAttention可以用一個kernel來執行注意力的操作:從HBM中加載輸入數據,在SRAM中執行所有的計算操作(矩陣乘法,mask,softmax,dropout,矩陣乘法),再將計算結果寫回到HBM中。通過kernel融合將多個操作融合為一個操作,不需要保留中的S和P矩陣,避免了反復地從HBM中讀寫數據。
Triton實現
菲爾-蒂勒特(Phil Tillet)在 Triton實現中首次提出并實現了交換循環順序(行塊上的外循環和列塊上的內循環,而非最初 FlashAttention 論文中的相反順序)以及序列長度維度上的并行化等想法。
注:FlashAttention V1算法在 k v 的維度上做外循環,在 q 的維度上做內循環。而在triton的代碼實現中,則采用了在 q 的維度上做外循環,在 k v 的維度上做內循環。
V2中調換了循環順序,使outer loop每個迭代計算沒有依賴,可以發送給不同的thread block并行執行,也就是可以對batch* head* sequence三層循環以thread block為粒度并行切分,從而顯著增加GPU的吞吐。反向遵循同樣的原理:不要把inner loop放在softmax規約的維度,因此正向反向的循環順序是不同的。
基本思路
FlashAttention V2的計算流程如下, Q按inner loop順序分別和K, V分開進行計算得到partial sum, 最后將partial sum累加,得到和Q形狀一樣的輸出。偽碼描述為。
flash_attention_2():
# outter loop
parallel do q[NUM_BLOCK_M]:
# inner loop
for i in range(NUM_BLOCK_N):
qk = q @ k[i].T
score = online_softmax(qk)
out += score @ v[i]
rescale(out)
對應到代碼,基本思路為:_attention實現并行、發射算子。_att_fwd找到本線程應該存取的數據,_attn_fwd_inner負責實際計算注意力。
線程模型
單線程的注意力計算做如下操作: q[seqlen, headdim] @ k[seqlen, headdim].T @ v[seqlen, headdim]
多線性的注意力計算需要從q的維度切分,每個線程負責Block_M個token的單頭注意力計算([Block_M, headdim])。即如果輸入的形狀為[bs, head, seqlen, headdim],則總線程數為bs x head x seqlen/Block_M。在bs x head維度和seqlen維度都并行。
class _attention
_attention利用 torch.autograd.Function 實現 Flash Attention 的自定義算子。
class _attention(torch.autograd.Function):
@staticmethod
def forward(ctx, q, k, v, causal, sm_scale):
# shape constraints
# q k v 的 shape 是 [B, H, S, D],因此數組-1是最后一個維度,就是D_HEAD,頭的維度。
Lq, Lk, Lv = q.shape[-1], k.shape[-1], v.shape[-1]
assert Lq == Lk and Lk == Lv
assert Lk in {16, 32, 64, 128}
# 初始化輸出
o = torch.empty_like(q)
# 設置q在S維度上的切分,即Q分塊的粒度。每個塊需要處理q塊的形狀為 [1, 1, BLOCK_M, D]
BLOCK_M = 128 # BLOCK SIZE of Q、O Matrix
# 設置關于內循環時,K、V塊在S維度上的長度,即,KV的分塊計算的粒度
BLOCK_N = 64 if Lk <= 64 else 32 # TILE SIZE of K、V Matrix
# num_stages 是關于 A100 中新的異步數據拷貝特性的設置,可以粗略地理解為 prefetch 的深度,緩存多少份數據在buffer里
num_stages = 4 if Lk <= 64 else 3
# 每個kernel所需要的 warp數量是4,線程數是 4 x 32
num_warps = 4
stage = 3 if causal else 1
# Tuning for H100
if torch.cuda.get_device_capability()[0] == 9:
num_warps = 8
num_stages = 7 if Lk >= 64 else 3
# 劃分二維網格,共有 triton.cdiv(q.shape[2], BLOCK_M)*q.shape[0]*q.shape[1]個塊
grid = (triton.cdiv(q.shape[2], BLOCK_M), q.shape[0] * q.shape[1], 1)
# 存下S矩陣每行的最大值,用于用于反向傳播使用
M = torch.empty((q.shape[0], q.shape[1], q.shape[2]), device=q.device, dtype=torch.float32)
_attn_fwd[grid](
q, k, v, sm_scale, M, o, #
q.stride(0), q.stride(1), q.stride(2), q.stride(3), #
k.stride(0), k.stride(1), k.stride(2), k.stride(3), #
v.stride(0), v.stride(1), v.stride(2), v.stride(3), #
o.stride(0), o.stride(1), o.stride(2), o.stride(3), #
q.shape[0], q.shape[1], #
N_CTX=q.shape[2], #
BLOCK_M=BLOCK_M, #
BLOCK_N=BLOCK_N, #
BLOCK_DMODEL=Lk, # head size
STAGE=stage, #
num_warps=num_warps, # _attn_fwd函數被分成了4個warp
num_stages=num_stages #
)
ctx.save_for_backward(q, k, v, o, M)
ctx.grid = grid
ctx.sm_scale = sm_scale
ctx.BLOCK_DMODEL = Lk
ctx.causal = causal
return o
@staticmethod
def backward(ctx, do):
q, k, v, o, M = ctx.saved_tensors
assert do.is_contiguous()
assert q.stride() == k.stride() == v.stride() == o.stride() == do.stride()
dq = torch.empty_like(q)
dk = torch.empty_like(k)
dv = torch.empty_like(v)
BATCH, N_HEAD, N_CTX = q.shape[:3]
PRE_BLOCK = 128
NUM_WARPS, NUM_STAGES = 4, 5
BLOCK_M1, BLOCK_N1, BLOCK_M2, BLOCK_N2 = 32, 128, 128, 32
BLK_SLICE_FACTOR = 2
RCP_LN2 = 1.4426950408889634 # = 1.0 / ln(2)
arg_k = k
arg_k = arg_k * (ctx.sm_scale * RCP_LN2)
PRE_BLOCK = 128
assert N_CTX % PRE_BLOCK == 0
pre_grid = (N_CTX // PRE_BLOCK, BATCH * N_HEAD)
delta = torch.empty_like(M)
_attn_bwd_preprocess[pre_grid](
o, do, #
delta, #
BATCH, N_HEAD, N_CTX, #
BLOCK_M=PRE_BLOCK, D_HEAD=ctx.BLOCK_DMODEL #
)
grid = (N_CTX // BLOCK_N1, 1, BATCH * N_HEAD)
_attn_bwd[grid](
q, arg_k, v, ctx.sm_scale, do, dq, dk, dv, #
M, delta, #
q.stride(0), q.stride(1), q.stride(2), q.stride(3), #
N_HEAD, N_CTX, #
BLOCK_M1=BLOCK_M1, BLOCK_N1=BLOCK_N1, #
BLOCK_M2=BLOCK_M2, BLOCK_N2=BLOCK_N2, #
BLK_SLICE_FACTOR=BLK_SLICE_FACTOR, #
BLOCK_DMODEL=ctx.BLOCK_DMODEL, #
num_warps=NUM_WARPS, #
num_stages=NUM_STAGES #
)
return dq, dk, dv, None, None
可以這么調用_attention()類。Z,H,N_CTX,D_head分別是batch, head, sequence length, head dimension,如此看來,batch, head, sequence length已經融合到q,k,v里面了。
q = torch.empty((Z, H, N_CTX, D_HEAD), dtype=dtype, device="cuda").normal_(mean=0.1, std=0.2).requires_grad_()
k = torch.empty((Z, H, N_CTX, D_HEAD), dtype=dtype, device="cuda").normal_(mean=0.4, std=0.2).requires_grad_()
v = torch.empty((Z, H, N_CTX, D_HEAD), dtype=dtype, device="cuda").normal_(mean=0.3, std=0.2).requires_grad_()
_attn_fwd
_attn_fwd是Triton中的一個內核函數,用于將一個批次的輸入Q、K、V矩陣與權重矩陣相乘,然后執行 softmax 操作。此內核函數通過計算每個位置的加權和,并將其存儲在輸出矩陣中來實現self-attention操作。在計算期間,每個線程塊處理一個輸入矩陣行的一部分,并將其存儲在共享內存中,以便在處理其他行時可以重用該數據。這段代碼的邏輯是這樣的:
- 根據當前程序的索引和輸入矩陣的行跨度(即每行占用的字節數),計算出輸入矩陣中當前行的起始指針。
- 根據塊大小(即每個程序處理的列數),創建一個偏移量數組,表示每個程序要訪問的輸入元素的索引。注意塊大小是大于等于列數的最小2的冪,所以可以保證每行可以被一個塊完全處理。
- 根據偏移量和掩碼(用于過濾掉超出列數的偏移量),從輸入指針中加載當前行的元素到寄存器中,并減去當前行的最大值,以提高數值穩定性。
- 對減去最大值后的元素進行指數運算,并在給定軸上求和,得到分母。然后將分子除以分母,得到softmax輸出。
- 根據偏移量和掩碼(用于過濾掉超出列數的偏移量),將softmax輸出從寄存器中存儲到輸出指針中。
這樣,每個程序都可以并行地處理輸入矩陣的一部分,并將結果寫入輸出矩陣中。這種方式可以提高內存訪問和計算的效率和并行度。
具體代碼如下。
"""
# Another trick we can use is to ask the compiler to use more threads per row by
# increasing the number of warps (`num_warps`) over which each row is distributed.
# You will see in the next tutorial how to auto-tune this value in a more natural
# way so you don't have to come up with manual heuristics yourself.
"""
@triton.jit
def _attn_fwd(Q, K, V, sm_scale, M, Out, #
stride_qz, stride_qh, stride_qm, stride_qk, # stride_qz就是batch,使用它就能在batch上并行
stride_kz, stride_kh, stride_kn, stride_kk, # k和n與v相反
stride_vz, stride_vh, stride_vk, stride_vn, # k和n與k相反
stride_oz, stride_oh, stride_om, stride_on, #
Z, H, #
N_CTX: tl.constexpr, #
BLOCK_M: tl.constexpr, #
BLOCK_DMODEL: tl.constexpr, #
BLOCK_N: tl.constexpr, #
STAGE: tl.constexpr #
):
# 目的是知道本線程塊應該操作什么數據
# program_id是外層循環中線程塊的id,線程塊包括warp組線程。start_m就是線程塊的grid第一維度坐標,借此可以獲取本線程塊在 q 的 S 維度上的指針位置 start_m * BLOCK_M。
start_m = tl.program_id(0) # 對應論文算法的外層循環,即Q矩陣的第幾個塊
# 獲取本線程塊的grid的第二維度坐標。第二維度的數量等于 Z * H,因此使用它可以確定在第幾個 batch 的第幾個 head。此處用Z表示B維度
# 下面三行依據內層循環對應的線程索引知道本線程在qkv上應該在的offset
off_hz = tl.program_id(1)
off_z = off_hz // H # batch 的 offset
off_h = off_hz % H # head 的 offset
# 獲取當前 head 的 shape 為 [S, D] tensor 的 offset
# 使用 stride_qz來對batch并行,使用stride_qh在head上并行,就是對batch, head在線程角度進行并行
qvk_offset = off_z.to(tl.int64) * stride_qz + off_h.to(tl.int64) * stride_qh
# 根據當前程序的索引和輸入矩陣的行跨度(即每行占用的字節數),計算出輸入矩陣中當前行的起始指針
# 創建一個 block 指針指向對應 [S, D] tensor 里的 [start_m * BLOCK_M:(start_m + 1) * BLOCK_M, D] BLOCK_DMODEL=D,即第 start_m 個 block 加載 Q 的一個子 tensor [BLOCK_M, BLOCK_DMODEL]
# 以行的方式訪問則使用 order=(1, 0)
Q_block_ptr = tl.make_block_ptr( # 構建一個指針
base=Q + qvk_offset, # 找到在輸入矩陣中的起始位置
shape=(N_CTX, BLOCK_DMODEL),
strides=(stride_qm, stride_qk),
offsets=(start_m * BLOCK_M, 0), # Q在外層,和算法一致
block_shape=(BLOCK_M, BLOCK_DMODEL),
order=(1, 0),
)
v_order: tl.constexpr = (0, 1) if V.dtype.element_ty == tl.float8e5 else (1, 0)
V_block_ptr = tl.make_block_ptr(
base=V + qvk_offset,
shape=(N_CTX, BLOCK_DMODEL),
strides=(stride_vk, stride_vn),
offsets=(0, 0),
block_shape=(BLOCK_N, BLOCK_DMODEL),
order=v_order,
)
# k 需要進行一個轉置
K_block_ptr = tl.make_block_ptr(
base=K + qvk_offset,
shape=(BLOCK_DMODEL, N_CTX),
strides=(stride_kk, stride_kn),
offsets=(0, 0),
block_shape=(BLOCK_DMODEL, BLOCK_N),
order=(0, 1), # 轉置
)
O_block_ptr = tl.make_block_ptr(
base=Out + qvk_offset,
shape=(N_CTX, BLOCK_DMODEL),
strides=(stride_om, stride_on),
offsets=(start_m * BLOCK_M, 0), # 外層循環,利用start_m(外層循環對應的線程索引)知道本線程在q上的offset
block_shape=(BLOCK_M, BLOCK_DMODEL),
order=(1, 0),
)
# initialize offsets
# tl.arange函數,用于創建一個從0到指定值的連續整數序列,類似于Python中的range函數。
offs_m = start_m * BLOCK_M + tl.arange(0, BLOCK_M)
offs_n = tl.arange(0, BLOCK_N)
# initialize pointer to m and l
m_i = tl.zeros([BLOCK_M], dtype=tl.float32) - float("inf") # 初始化為負無窮
l_i = tl.zeros([BLOCK_M], dtype=tl.float32) + 1.0
acc = tl.zeros([BLOCK_M, BLOCK_DMODEL], dtype=tl.float32) # 向量o
# load scales
qk_scale = sm_scale
qk_scale *= 1.44269504 # 1/log(2)
# load q: it will stay in SRAM throughout
# 對于每個 block 需要整個 q 的子 tensor [BLOCK_M, BLOCK_DMODEL] 全程參與
q = tl.load(Q_block_ptr)
# stage 1: off-band
# For causal = True, STAGE = 3 and _attn_fwd_inner gets 1 as its STAGE
# For causal = False, STAGE = 1, and _attn_fwd_inner gets 3 as its STAGE
if STAGE & 1:
acc, l_i, m_i = _attn_fwd_inner(acc, l_i, m_i, q, K_block_ptr, V_block_ptr, #
start_m, qk_scale, #
BLOCK_M, BLOCK_DMODEL, BLOCK_N, #
4 - STAGE, offs_m, offs_n, N_CTX, V.dtype.element_ty == tl.float8e5 #
)
# stage 2: on-band
if STAGE & 2:
# barrier makes it easier for compielr to schedule the
# two loops independently
tl.debug_barrier()
acc, l_i, m_i = _attn_fwd_inner(acc, l_i, m_i, q, K_block_ptr, V_block_ptr, #
start_m, qk_scale, #
BLOCK_M, BLOCK_DMODEL, BLOCK_N, #
2, offs_m, offs_n, N_CTX, V.dtype.element_ty == tl.float8e5 #
)
# 后處理
# 算法流程第13步
m_i += tl.math.log2(l_i)
# 算法流程第12步
acc = acc / l_i[:, None]
m_ptrs = M + off_hz * N_CTX + offs_m
# 將結果寫回
# 算法流程第15步
tl.store(m_ptrs, m_i)
# 算法流程第14步
tl.store(O_block_ptr, acc.to(Out.type.element_ty))
_attn_fwd_inner
_attn_fwd_inner()函數是具體執行注意力操作的地方。首先,第 start_m 個 block 加載 Q 的一個子 tensor [BLOCK_M, BLOCK_DMODEL],依次跟 K 的 N_k 個子 tensor [BLOCK_DMODEL, BLOCK_N] 相乘,其中 N_k x BLOCK_N = start_m x BLOCK_M,這里面跟 K 的子 tensor 得到結果 [BLOCK_M, BLOCK_N] 后,再與對應 V 的子 tensor [BLOCK_N, BLOCK_DMODEL] 相乘得到 O 的 子 tensor [BLOCK_M, BLOCK_DMODEL],由于要循環 N_k 次,所以最后 O 的結果是 N_k 個疊加的結果。可知第 start_m 個 block 得到 Q 和 K 所有子 tensor 相乘的結果拼接之后,實際形狀為 [BLOCK_M, start_m x BLOCK_M]。
具體代碼如下,按照按照V2流程來標注。
@triton.jit
def _attn_fwd_inner(acc, l_i, m_i, q, #
K_block_ptr, V_block_ptr, #
start_m, qk_scale, #
BLOCK_M: tl.constexpr, BLOCK_DMODEL: tl.constexpr, BLOCK_N: tl.constexpr, #
STAGE: tl.constexpr, offs_m: tl.constexpr, offs_n: tl.constexpr, #
N_CTX: tl.constexpr):
# range of values handled by this stage
if STAGE == 1:
lo, hi = 0, start_m * BLOCK_M
elif STAGE == 2:
lo, hi = start_m * BLOCK_M, (start_m + 1) * BLOCK_M
lo = tl.multiple_of(lo, BLOCK_M)
# causal = False
else:
lo, hi = 0, N_CTX
# 調整 block 指針的起始 offsets
K_block_ptr = tl.advance(K_block_ptr, (0, lo))
V_block_ptr = tl.advance(V_block_ptr, (lo, 0))
# loop over k, v and update accumulator
# 第一階段從 0, start_m * BLOCK_M
# 算法流程第6步,執行內循環
for start_n in range(lo, hi, BLOCK_N): # 對應的內層循環
start_n = tl.multiple_of(start_n, BLOCK_N)
#實際執行QK^T @ V
# -- compute score=QK^T ----
# k [BLOCK_DMODEL, BLOCK_N]
# 算法流程第7步,load Kj, Vj到SRAM
k = tl.load(K_block_ptr)
# qk [BLOCK_M, BLOCK_N]
qk = tl.zeros([BLOCK_M, BLOCK_N], dtype=tl.float32)
# 算法流程第8步
qk += tl.dot(q, k)
# 算法流程第9步
if STAGE == 2:
# 第二階段去除小三角形對結果的影響
mask = offs_m[:, None] >= (start_n + offs_n[None, :])
qk = qk * qk_scale + tl.where(mask, 0, -1.0e6)
m_ij = tl.maximum(m_i, tl.max(qk, 1)) # 最大的m, 最后一個維度(行向量)的最大值構成的向量
qk -= m_ij[:, None]
else:
# 統計當前的 m_ij
m_ij = tl.maximum(m_i, tl.max(qk, 1) * qk_scale) # 最大的m
qk = qk * qk_scale - m_ij[:, None]
p = tl.math.exp2(qk) # 計算exp
# 統計當前的 l_ij
l_ij = tl.sum(p, 1) # 最后一個維度的求和
# -- update m_i and l_i
# 計算當前的修正因子 alpha
alpha = tl.math.exp2(m_i - m_ij)
# 修正當前的 l_i
l_i = l_i * alpha + l_ij
# 算法流程第10步
# -- update output accumulator --
# 對 O 子 tensor 的累加結果進行修正
acc = acc * alpha[:, None]
# update acc
# 算法流程第7步,load Kj, Vj到SRAM
v = tl.load(V_block_ptr)
# score @V
acc += tl.dot(p.to(tl.float16), v)
# update m_i
m_i = m_ij
# 調整 K 和 V 的指針
V_block_ptr = tl.advance(V_block_ptr, (BLOCK_N, 0))
K_block_ptr = tl.advance(K_block_ptr, (0, BLOCK_N))
return acc, l_i, m_i
0x02 Flash-Decoding
雖然 FlashAttention-2 比 FlashAttention 實現了 2 倍的加速,但是因為它們忽略了注意機制在解碼階段與解碼階段的不同行為,所以僅在解碼的預填充階段才能發揮效果。在decoding 階段會嚴重浪費GPU核心。而且由于缺乏對張量并行的支持,Vanilla FlashAttention-2也無法適應多GPU場景。
而當代大型語言模型需要一個能夠在多GPU場景中良好擴展的注意力機制,這樣才可以對越來越長的上下文長度提供有效支持。為了提高 attention 在推理階段的計算速度,FlashAttention作者提出了 FlashDecoding,其博客地址:[https://crfm.stanford.edu/2023/10/12/flashdecoding.html]。Flash-Decoding 主要是針對LLM推理的加速,面對Q的seq length=1的情況,在K/V方向做了block并行,來提高GPU Utilization從而達到加速的目的。Flash-Decoding在 batch_size 較小和序列長度較大時有著明顯的加速效果,且性能對序列長度的增加并不敏感。
2.1 現狀
在LLM的推理過程本質上包括兩個不同的計算階段。
- 第一階段是提示計算階段(有時稱為預填充階段)。在此階段,來自輸入提示的所有token都經過模型的前向傳播以生成第一個輸出token。 此階段計算量較大,需要較高的 FLOPS/s。
- 第二階段是解碼階段(有時稱為Token 生成階段)。該階段以自回歸方式開始,每個后續token都是根據前一個token的前向傳播結果,以及序列中先前的KV-Cache來生成的。 隨著上下文長度的增加,這個緩存的上下文可能會很長。如此長的上下文長度的順序處理使得解碼階段變慢,而且受內存帶寬和容量限制。
下圖總結了自注意力涉及的三個操作,以及解碼和預填充階段涉及的相應維度。
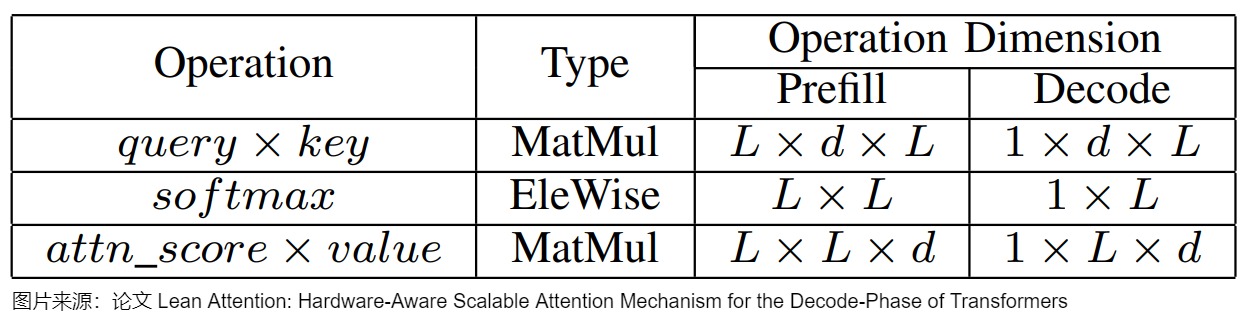
雖然研究人員已經提出了KV-Cache和 FlashAttention 等機制,來滿足LLM的低延遲需求。 然而,這些技術并不能根據推理過程中不同階段在計算上的不同性質來進行處理。
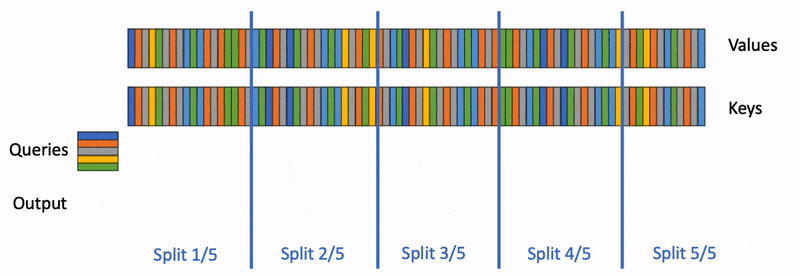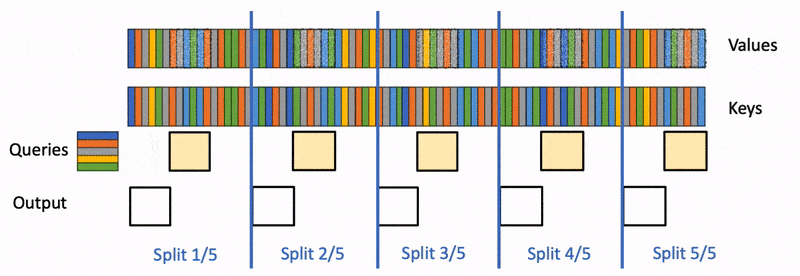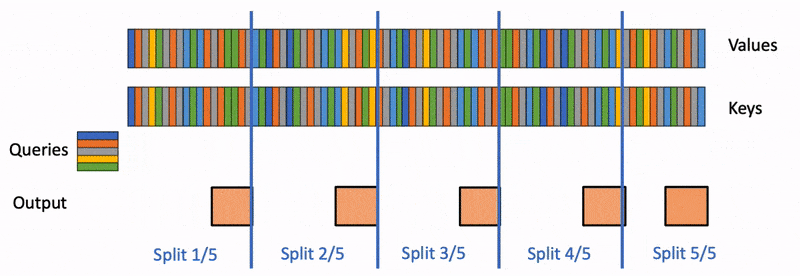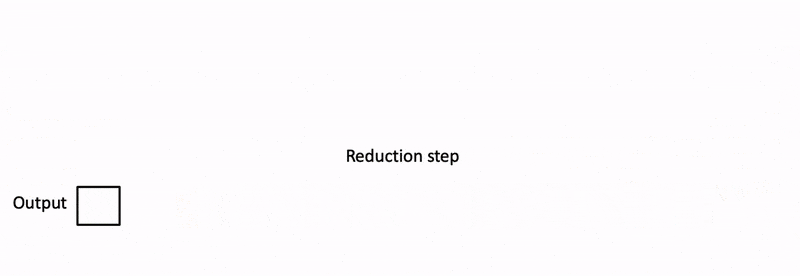
FlashAttention V2 前向傳播會在Q的seqlen維度以及batch_size維度做并行。從下圖可以看到,對于當前的Q的分塊Queries,forward pass會在thread block中,逐個遍歷所有的K, V分塊,計算逐個分塊的局部Attention輸出。每個局部的Attention輸出,會在thread block內部遍歷的過程中,隨著每一次迭代,根據當前次迭代的值進行scale,一直到沿著K,V的迭代完成后,就獲得了最終正確的Output。

這種方式對于訓練時期的前向傳播是有效的,因為因為訓練時,seqlen或bs會比較大,GPU資源能夠被有效地利用。但是推理的Generation階段是逐token生成,每次推理實際的queries token數為1,已經無法通過queries進行并行了。特別是如果bs還比較小,會導致GPU資源無法得到有效的利用。即,如果batch size小于 GPU 上流處理器(SM)的數量(A100 GPU 上有 108 個 SM),那么 atttention 操作只能使用一小部分 GPU!尤其是在使用較長的上下文時。
2.2 方案
于是針對這種情況,FlashAttention作者開發了FlashDecoding,對推理階段的forward進行優化。基本的思路其實也很直觀:既然在推理場景decode階段,query_num = 1和可能過小的batch size會導致block數量不夠,那么是否可以不去考慮query增加block,而考慮在key和vlaue的維度去增加block?
按照此思路,Flash-Decoding 在 FlashAttention V2對 batch size 和 query length 并行的基礎上增加了一個新的并行化維度:keys/values 的序列長度。這種新的并發性減少了延遲,同時增加了硬件占用率,但需要額外的最終規約成本。
Flash Decoding主要包含以下三個步驟:
- 將K/V切分成更小的塊,這樣可以支持后續的并發。因為不需要在物理上分開,所以此處數據分塊不涉及GPU操作。鍵/值塊依然是完整鍵/值張量的視圖。
- 并行啟動這些K/V塊。在這些K/V塊上使用標準FlashAttention并行計算query與每個塊的注意力。對于每個塊的每行(因為一行是一個特征維度),Flash Decoding會記錄一個額外的標量:注意力值的 log-sum-exp。
- 最后,利用內積中的加法可交換性,通過對所有拆分塊的計算結果進行歸約,結合 log-sum-exp 調整各個塊的貢獻,計算出最終的結果。
我們只需要對第2步和第3步執行單獨的kernels。雖然最終的reduction操作會引入一些額外的計算,但在總體上,Flash-Decoding通過增加并行化的方式取得了更高的效率。
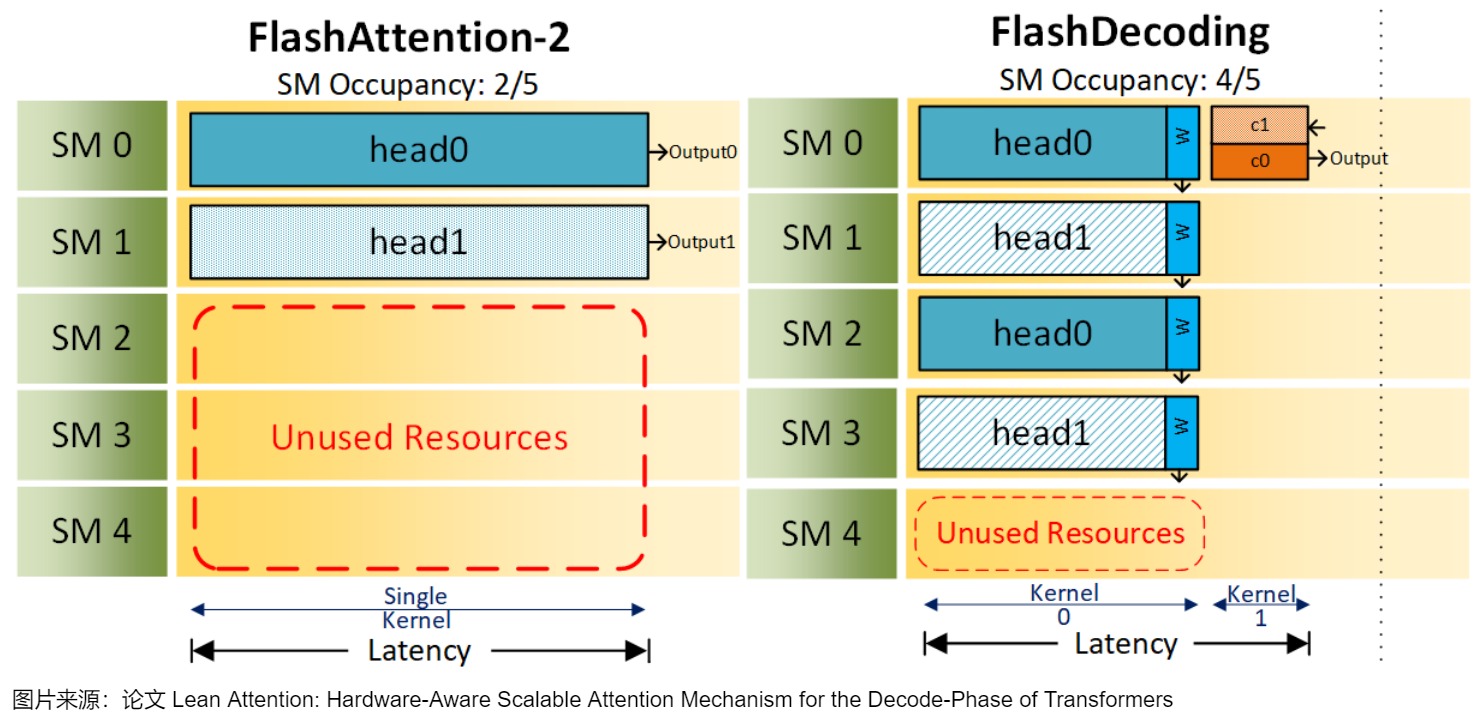
我們以一張圖來對Flash-Decoding和FlashAttention V2進行對比。圖中假設有2個head,一個batch,5個SM。1個block只能做相同的事情,如,只能單獨計算head1或者head0,不能同時計算head0和head1。batch為1的時候,FlashAttention2就只能分配2個block,FlashDecoding 則能分配4個block。
2.3 討論
FlashAttention對batch size和query length進行了并行化加速,Flash-Decoding在此基礎上增加了一個新的并行化維度:keys/values的序列長度。即使batch size很小,但只要上下文足夠長,它就可以充分利用GPU。與FlashAttention類似,Flash-Decoding幾乎不用額外存儲大量數據到全局內存中,從而減少了內存開銷。
FlashDecoding有如下2個可能不高效的地方。
- 需要啟動2次的kernel,第一次kernel是每個block算query和部分key和部分value的部分attention結果,第二次kernel主要是對第一次的部分attention結果進行校正reduce。
- 第一次計算的時候,序列維度的并行度是固定的,長序列和短序列使用的block數量是一樣多的,這就導致長序列計算的慢,短序列計算的快。
FlashDecoding++(作者并非Tri Dao)基于FlashDecoding進行了修改,通過近似softmax中的全局最大值來消除同步成本,以避免最終重新縮放。FlashDecoding++在FlashDecoding的內部循環中避免了計算中間局部softmax,一旦算法可以確定所有部分指數和(partial exponential sums),就會計算最終全局softmax。此外,FlashDecoding++使用雙緩沖來隱藏內存訪問延遲。
盡管有這些改進,FlashDecoding和FlashDecoding++ 依然是一種非最優的負載平衡策略。它需要啟動額外的reduce核心,因此受到內核啟動開銷,以及隨著問題規模增加而增加的減少或修正開銷的影響。
0x03 Flash-Mask
隨著人工智能技術的迅猛發展,以 Transformer 為代表的大模型在自然語言處理、計算機視覺和多模態應用中展現出了非凡的能力。在這些大模型中,注意力(Attention)機制是一個關鍵環節。為了在大模型訓練任務中確定哪些 Query-Key token 之間需要進行有效的 Attention 計算,業界通常使用注意力掩碼(Attention Mask)。然而,目前的注意力掩碼通常采用二維稠密矩陣表示,這導致了一些問題。一方面,這種表示方法引入了大量冗余計算,因為許多無效 token 的 Attention 仍需計算;另一方面,另一方面因其巨大的存儲占用導致難以實現長序列場景的高效訓練,難以進行高效訓練。
雖然業界已有 FlashAttention 等針對特定注意力掩碼的計算加速方法,但其支持的注意力掩碼模式有限,難以滿足大模型訓練任務對靈活注意力掩碼的需求。為了解決上述問題,飛槳獨創 FlashMask 技術,提出了列式稀疏的注意力掩碼表示方法,支持靈活多樣的注意力掩碼模式,這樣可以降低存儲復雜度,并在此基礎上實現了高效的算子 Kernel,其線性訪存復雜度 O(N),這極大的加速了大模型訓練效率,尤其是長序列場景下的訓練效率。
3.1 動機
FLASHMASK可以理解為是對FA的一個擴展。FA旨在解決傳統注意力機制在處理長句子時面臨的計算和內存需求呈平方階增長的問題。這種增長對于 Transformer 模型在任意一個硬件上來說都是一個重大挑戰,尤其是長句子的LLM訓練中。具體點講,FA通過 IO 感知的內存優化減少了注意力延遲,并消除了對 \(O(N^2)\) 的內存依賴。然而,在上述訓練場景下,FA的不足有二:
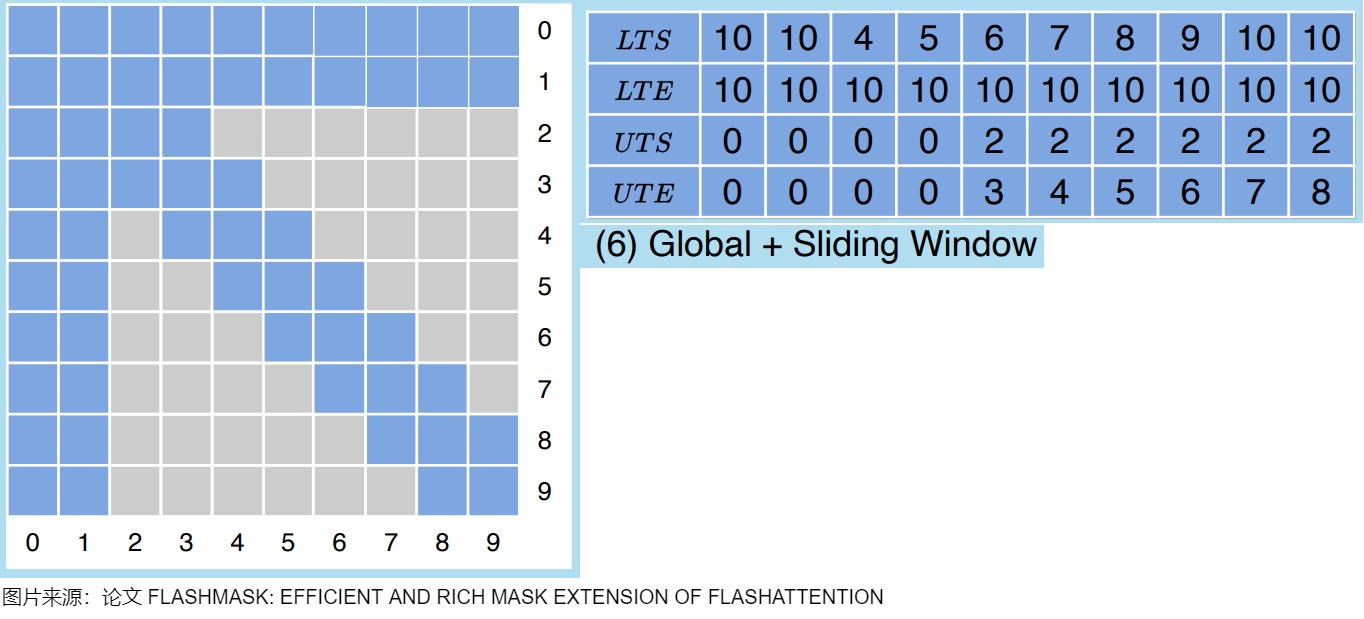
- 對某些attention mask類型的原生支持有限,并不天然地適應更復雜的mask需求,如下圖上方粉色區域,FlashAttention 只能支持如純因果掩碼(Causal)、滑動窗口掩碼(Sliding Window)、因果文檔掩碼(Causal Document Mask)和文檔掩碼(Document Mask)等幾種固定形式的掩碼。然而,實際訓練任務中使用的注意力掩碼形式往往豐富多變,當前技術難以滿足大模型不同訓練任務對注意力掩碼靈活性的要求。
- 以往的方法使用稠密mask矩陣,這會導致 \(O(N^2)\) 的訪存增長,從而效率不高,導致支持的最大上下文長度有限。
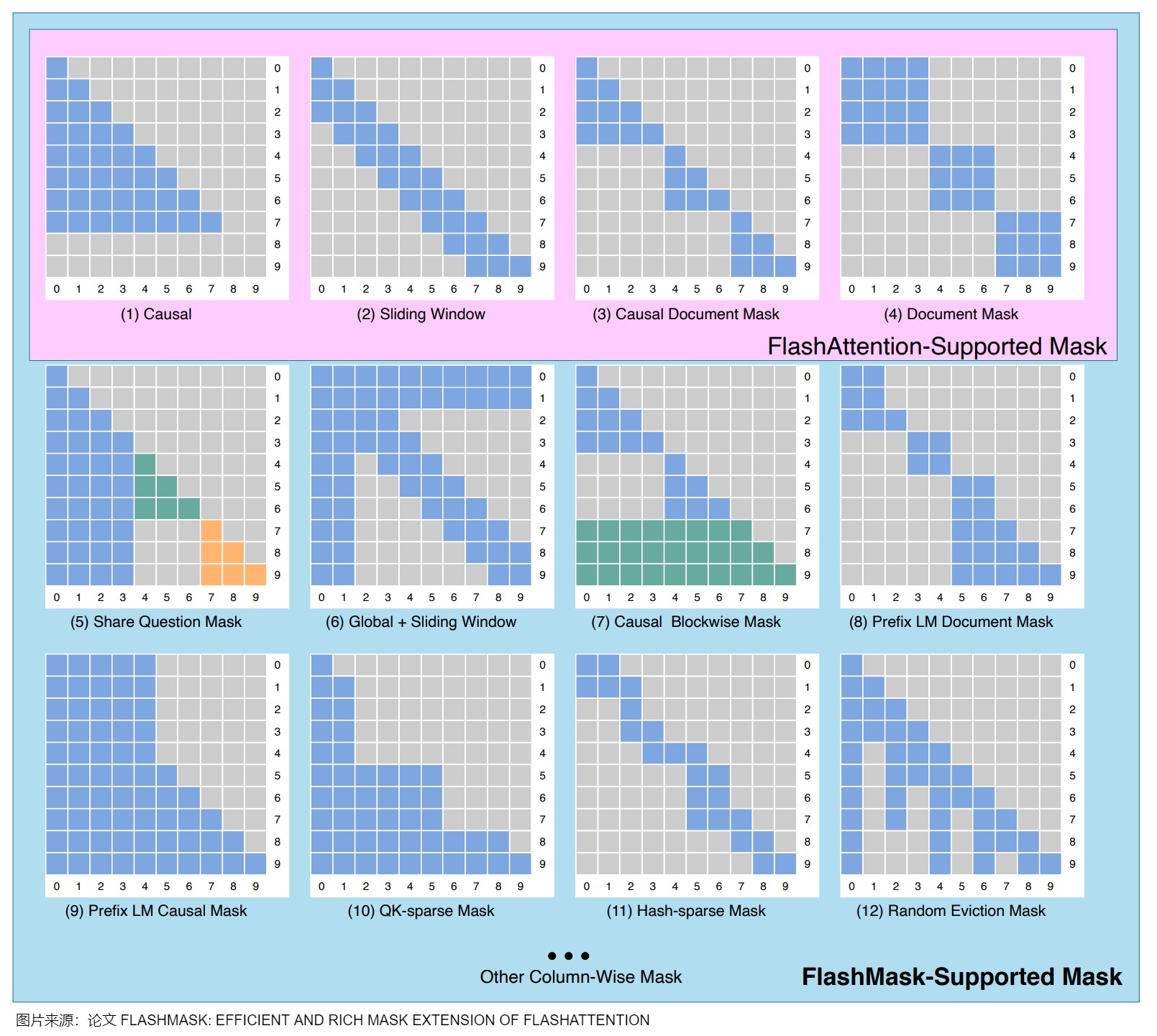
3.2 思路
FlashMask 的核心發現是,在大模型常見的注意力掩碼模式中,Query-Key token 的掩碼模式具有一定的連續性。具體而言,對于每一個 Key token,無效注意力計算的 Query token 是相鄰排列的。也就是說,在上圖的二維掩碼矩陣中,當Query token 和 Key token 相互作用時,是沿列方向連續分布的。基于這一洞察,FlashMask 巧妙地將二維稠密掩碼矩陣轉換為一維的行索引區間,從而實現更為緊湊的表示形式,并顯著降低了存儲需求。我們可以公式化表示為:
其中 N 為 Key 的序列長度,\(M_j\)為二維的稠密掩碼矩陣的第 j 列,為連續的行索引區間,表示這些連續 Query token 是被 mask 掉,置為無效 Attention 計算。
為了高效處理因果和雙向注意力場景中的復雜掩碼模式,FlashMask 提出了一種新穎的列式稀疏表示方法。以對角線為區分,它使用四個一維向量來表示掩碼:
- 下三角起始行索引(Lower Triangular Start,簡稱 LTS)。
- 下三角結束行索引(Lower Triangular End,簡稱 LTE)。
- 上三角起始行索引(Upper Triangular Start,簡稱 UTS)。
- 上三角結束行索引(Upper Triangular End,簡稱 UTE)。
其中下三角被 mask 掉的行索引區間使用[??????, ??????)表示,上三角被 mask 掉的行索引區間使用 [??????, ??????)表示。
熟悉稀疏矩陣的朋友都知道,表示稀疏矩陣通常用幾個一維數組或向量就可以表示,無需用二維tensor,這也是稀疏化的重要收益來源。同理,FlashMask 也是相同的思想,用4個向量表示k矩陣每一個token在左下角和右上角對應的哪些q token被mask了。FlashMask把mask分為兩個區域,一個左下角,一個右上角,LT開頭的描述左下角的masked情況,UT表示右上角的masked情況,拿(6)舉例如下,q有10個token,k也有10個token,針對每個k維度的token,我們來計算對應q維度token的masked情況,比如對于5號token,灰色部分有下圖紅圈部分,所以[LTS,LTE)=[7,10),[UTS,UTE)=[2,4)。
3.3 算法
FlashMask 將列式掩碼表示方法集成到 FlashAttention-2算法中,增強了其對注意力掩碼的支持能力。在 FlashAttention Kernel 的分塊計算基礎上,FlashMask 利用上述的 LTS 等掩碼向量,來判斷當前分塊的掩碼類型:
- 完全掩碼塊:此類塊的所有元素均被掩碼,計算時可直接跳過。
- 部分掩碼塊:此類塊僅部分元素被掩碼,因此需要對該塊進行逐元素的掩碼處理。
- 未掩碼塊:此類塊中的所有元素均未被掩碼,可以簡化計算過程,無需額外的掩碼操作。
通過這種分類處理,FlashMask 顯著提升了計算效率,如下圖所示。
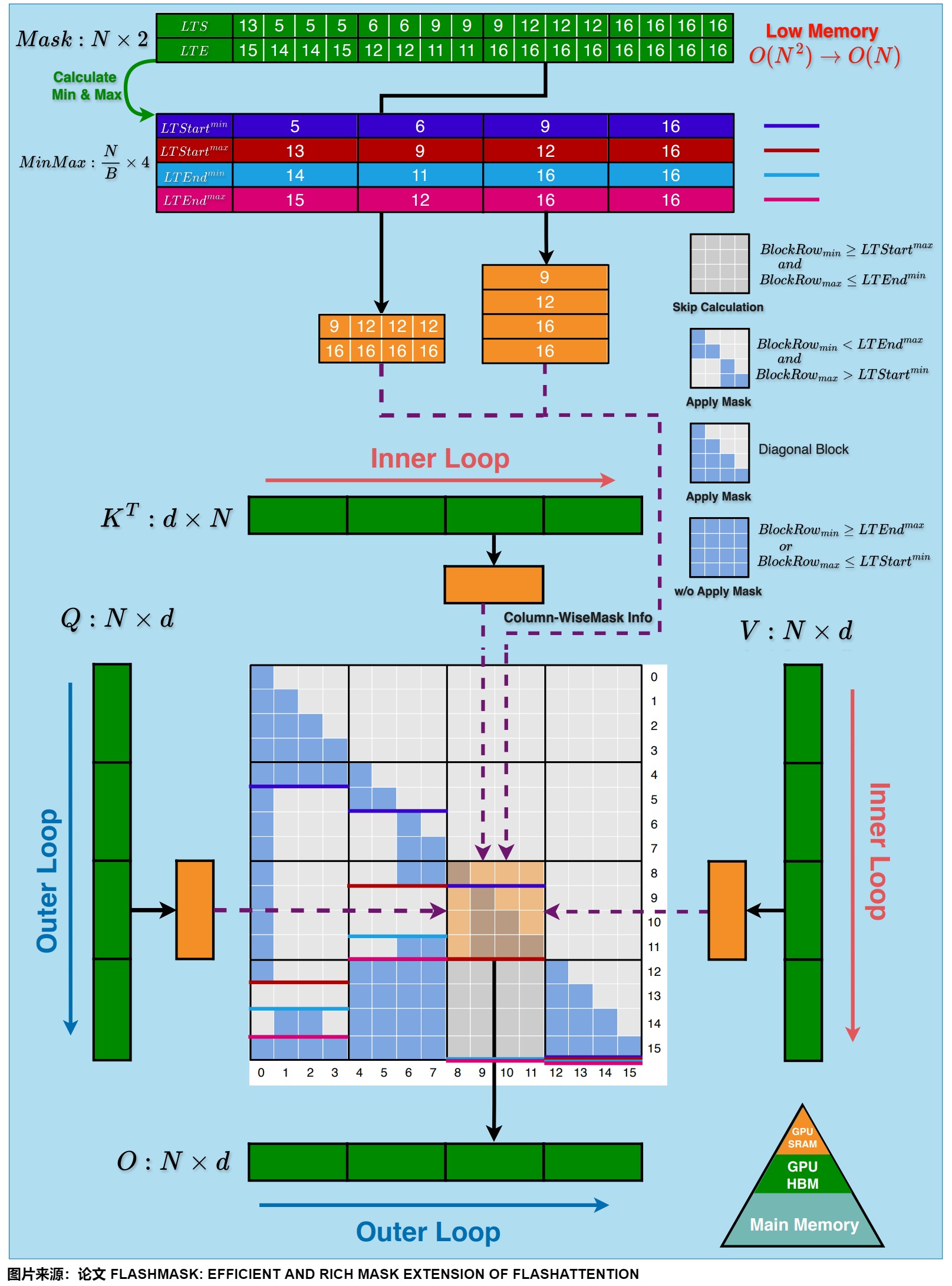
下圖的算法詳細描述了 FlashMask 擴展 FlashAttention-2的前向計算過程,其中淺藍色陰影部分表示 FlashMask 新增的計算步驟。

0x04 FlashAttention-3
FlashAttention作者又推出了V3,其特點是:
- 更高效的 GPU 利用率。針對H100 GPU 推出了WGMMA(翹曲矩陣乘法累加)功能,比A100吞吐量高3倍。針對H100 GPU 的TMA(張量記憶加速器)功能,可加速全局內存和共享內存之間的數據傳輸,負責所有索引計算和越界預測。這樣可以釋放寄存器,增加圖塊大小和效率的寶貴資源。
- 以更低的精度獲得更好的性能。FlashAttention-3 可以在保持精度的同時處理較低精度的數字 (FP8),具體而言,FlashAttention-3 利用QuIP: 2-Bit Quantization of Large Language Models With Guarantees技術,通過非相干處理減少量化誤差,即將查詢和鍵與隨機正交矩陣相乘,以“分散”異常值并減少量化誤差。
- 能夠在 LLM 中使用更長的上下文。通過加速注意力機制,FlashAttention-3 使 AI 模型能夠更有效地處理更長的文本片段。這可以使應用程序能夠理解和生成更長、更復雜的內容,而不會減慢速度。
因為其主要是和硬件相關,我們不做深入介紹,有興趣的讀者可以自行深入研究。
0xFF 參考
(Beta) Implementing High-Performance Transformers with Scaled Dot Product Attention (SDPA)
[ 大模型訓練 ] FlashAttention v1、v2 - 最清晰的公式推導 && 算法講解 Alan小分享
[1805.02867] Online normalizer calculation for softmax (arxiv.org) Maxim Milakov and Natalia Gimelshein. Online normalizer calculation for softmax. CoRR, abs/1805.02867, 2018.
[Attention優化][2w字]??原理&圖解: 從Online-Softmax到FlashAttention V1/V2/V3 DefTruth
[Attention優化][萬字]??TensorRT 9.2 MHA/Myelin Optimize vs FlashAttention-2 profile DefTruth
[FlashAttention][2w字]??原理&圖解: 從Online-Softmax到FlashAttention-1/2/FlashDecoding/FlashDecoding++ DefTruth
Antinomi:FlashAttention核心邏輯以及V1 V2差異總結
Flash Attention on INTEL GPU 毛毛雨
Flash Attention V2 的 Triton 官方示例學習[forward] 來自L77星云
flash attention論文及源碼學習 KIDGINBROOK
FlashAttention v2論文溫故 進擊的Killua
FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-precision
FlashAttention:加速計算,節省顯存, IO感知的精確注意力 回旋托馬斯x
FlashAttention圖解(如何加速Attention) Austin
FlashAttention核心邏輯以及V1 V2差異總結 Antinomi
From Online Softmax to FlashAttention by Zihao Ye
From Online Softmax to FlashAttention
LLM 推理加速技術—— Flash Attention 的算子融合方法 sudit
NLP(十七):從 FlashAttention 到 PagedAttention, 如何進一步優化 Attention 性能 紫氣東來
ops(7):self-attention 的 CUDA 實現及優化 (上) 紫氣東來
ops(8):self-attention 的 CUDA 實現及優化 (下) 紫氣東來
Scaled Dot Product Attention (SDPA) 在 CPU 上的 性能優化 Mingfei
【手撕LLM-FlashAttention2】只因For循環優化的太美 小冬瓜AIGC
【手撕LLM-FlashAttention】從softmax說起,保姆級超長文!! 小冬瓜AIGC
一心二用的Online Softmax TaurusMoon
萬字長文詳解FlashAttention v1/v2 Civ
萬字長文詳解FlashAttention v1/v2 Civ
使用cutlass cute復現flash attention 66RING
回旋托馬斯x:FlashAttention:加速計算,節省顯存, IO感知的精確注意力
圖解大模型計算加速系列:Flash Attention V2,從原理到并行計算 猛猿
圖解大模型計算加速系列:FlashAttention V1,從硬件到計算邏輯 猛猿
大模型訓練加速之FlashAttention系列:爆款工作背后的產品觀 方佳瑞
學習Flash Attention和Flash Decoding的一些思考與疑惑 稻殼特溯
序列并行DeepSpeed-FPDT 手抓餅熊 [大模型新視界](javascript:void(0)??
我的 Transformer 加速筆記(一):FlashAttention 篇 delin
手撕Flash Attention!原理解析及代碼實現 晚安湯姆布利多
線性Attention的探索:Attention必須有個Softmax嗎? By 蘇劍林
細嚼慢咽地學習FlashAttention2-舉例子1 迷途小書僮
通透理解FlashAttention與FlashAttention2:讓大模型上下文長度突破32K的技術之一 v_JULY_v
降低Transformer復雜度O(N^2)的方法匯總(一) Civ
降低Transformer復雜度O(N^2)的方法匯總(二) Civ
A Case Study in CUDA Kernel Fusion: Implementing FlashAttention-2 on NVIDIA Hopper Architecture using the CUTLASS Library[5]
Andrew Kerr. Gtc 2020: developing cuda kernels to push tensor cores to the absolute limit on nvidia a100. May 2020.
FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning. https://arxiv.org/abs/2307.08691
FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness[2]
FlashMask: Efficient and Rich Mask Extension of FlashAttention. https://arxiv.org/abs/2410.01359
FlexAttention: The Flexibility of PyTorch with the Performance of FlashAttention. https://pytorch.org/blog/flexattention/
From Online Softmax to FlashAttention(@http://cs.washington.edu)
From Online Softmax to FlashAttention. https://courses.cs.washington.edu/courses/cse599m/23sp/notes/flashattn.pdf
Maxim Milakov and Natalia Gimelshein. Online normalizer calculation for softmax. CoRR, abs/1805.02867, 2018.
Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism.[6]
Self-attention Does Not Need O(n^2) Memory. https://arxiv.org/abs/2112.05682
The I/O Complexity of Attention, or How Optimal is Flash Attention?[4]
Tri Dao, Daniel Y. Fu, Stefano Ermon, Atri Rudra, and Christopher Ré. Flashattention: fast and memory- efficient exact attention with io-awareness. CoRR, abs/2205.14135, 2022.
晚安湯姆布利多](https://www.zhihu.com/people/Rancho2508)
從Coding視角出發推導Ring Attention和FlashAttentionV2前向過程 楊鵬程
結合代碼聊聊FlashAttentionV3前向過程的原理 楊鵬程
聊聊CUDA編程中線程劃分和數據分塊 之 PagedAttention(V1/V2)分析 楊鵬程
[DefTruth:Attention優化]??FFPA(Split-D): FA2無限HeadDim擴展,2x↑?? vs SDPA EA


 浙公網安備 33010602011771號
浙公網安備 33010602011771號