探秘Transformer系列之（17）--- RoPE

從零開始解析Transformer，目標是：(1) 解析Transformer如何運作，以及為何如此運作，讓新同學可以入門；(2) 力爭融入一些比較新的或者有特色的論文或者理念，讓老鳥也可以有所收獲。

探秘Transformer系列之（17）--- RoPE

文章總表

全部文章列表在這里探秘Transformer系列之文章列表，后續每發一篇文章，會修改這里。

0x00 概述

RoPE編碼來自蘇神的工作Roformer, 它是目前LLM中廣受歡迎使用的PE編碼方式之一。

Transformer論文使用了Sinusoidal位置編碼，其是加性編碼，即詞嵌入與編碼位置相加。每個位置的嵌入向量是固定的，不考慮其與其他位置的關系。Sinusoidal位置編碼希望引入相對位置關系（任意位置的位置編碼都可以表達為一個已知位置的位置編碼的關于距離的線性組合），但不是很成功，模型只能在一定程度上感知相對位置。位置編碼常見的改進思路是以三角式位置編碼公式為基礎，調整自注意力計算偏置。而RoPE拋棄了位置編碼常見的改進思路，即以三角式位置編碼公式為基礎，通過旋轉矩陣、復數乘法、歐拉公式等技巧，既能以自注意力矩陣偏置的形式，反映兩個token的相對位置信息，又能拆解到特征序列上，通過直接編碼token的絕對位置實現，兼顧絕對位置編碼和相對位置編碼的優勢。

RoPE沒有修改Attention的結構，反而像絕對位置編碼一樣在輸入層做文章，對輸入向量直接進行改造，即對兩個輸入token形成的Query和Key向量做一個旋轉變換，使得變換后的Query和Key帶有位置信息，進一步使得Attention的內積操作不需要做任何更改就能自動感知到相對位置信息。換句話說，RoPR的出發點和策略是相對位置編碼思想，但是實現方式卻用的是絕對位置編碼。

0x01 總體思路

我們首先看看對于三角函數編碼的修改思路或者痛點，具有兩點。

在前面章節的分析中，我們已經知道attention層的計算( $??_??^????_{??+Δ??}$ ）會破壞掉輸入層位置編碼的優良性質，那么我們自然而然會想到：如果直接在attention層中融入位置信息，也就是直接把位置編碼作用于 $??_??^????_{??+Δ??}$，這樣不就能維持位置編碼優良性質不變嘛。
三角函數編碼是將位置信息直接添加到 token 嵌入中。有人認為這樣其實是在用位置信息污染語義信息，應該嘗試在不修改規范的情況下對信息進行編碼。

因此我們先回顧下注意力機制。

1.1 注意力機制回顧

注意力機制的關鍵之處在于通過向量的內積得到了自注意力矩陣元素 $A_{m,n}$。比如，計算第 m 個詞嵌入向量 $x_m$ 對應的自注意力輸出結果，就是$q_m$和其他所有的$k_n$都會計算一個注意力分數，再將注意力分數乘以對應的$v_n$，然后求和得到輸出向量$o_m$。具體公式展開如下：

\[q_m = x_mW^Q \\k_n =x_nW^K \\v_n = x_nW^V \\a_{m,n} =\frac{exp(\frac{q_m^Tk_n}{\sqrt d})}{\sum ^N _{j=1}exp(\frac{q_m^Tk_j}{\sqrt d})}\\o_m = \sum ^N _{n=1} a_{m,n}v_n \]

1.2 思路分析

從上面公式可以看到，一個 token 對另一個 token 的影響是由 $QK^T$ 點積來決定的，或者說，注意力分數其實就是兩個特征向量之間的內積。這是我們應該關注位置編碼的地方。因此我們來看看點積的表示：$\vec{a}\vec{b} = |\vec{a}|\vec{b}|cos\theta$，從中有兩點洞察：

可以通過增加或減小兩個向量之間的夾角來調整兩個向量的點積結果。
旋轉對向量的范數完全沒有影響，這個范數也許可以編碼 token 的語義信息。

因此只需要在進入注意力機制之前，對Query和Key向量進行絕對位置編碼改造即可，跟Value沒有關系。這樣就可以把位置編碼的信息直接引入 $??_??^????_??$ 中，這也就意味著，我們希望根據|n-m|的結果，給這個內積計算一定的懲罰：

當|n-m|較小時，我們希望拉進近$??_??,??_??$的距離。
當|n-m|較大時，我們希望拉遠$??_??,??_??$的距離。

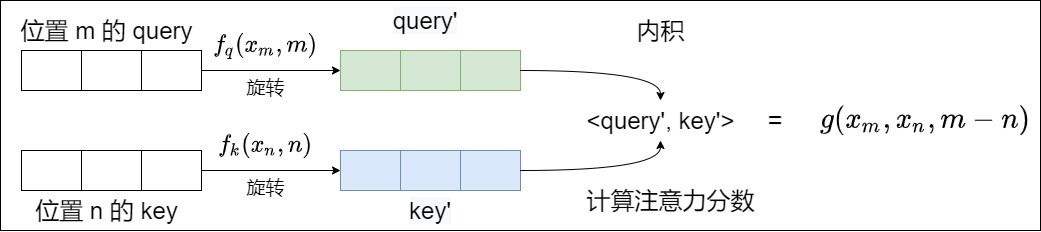
我們來看看論文中展示如何尋找到解決方案的。RoPE的出發點是“通過絕對位置編碼的方式實現相對位置編碼”，即編碼時使用絕對位置，但是其點積結果反應相對位置。從數學角度就是找到合適的位置編碼函數 f，使得如下公式成立。

\[f(q,m)^Tf(k,n) = g(q,k,m-n) \]

用通俗語言來解讀，就是對m位置的q和n位置的k進行加工，使得加工后的$qk^T$在計算注意力分數時，會隱含m-n這個相對位置信息。我們再用論文的公式來進一步解釋。RoPE希望把 $??_??$ 和 $??_??$ 的內積操作，編碼成一個函數g，g的自變量包括兩個token $??_??$ 和 $??_n$ 以及其相對位置m-n。?? 表示 $??_??$ 和 $??_??$ 進行內積操作。

\[\langle f_q(x_m,m), f_k(x_n,n) \rangle = g(x_m, x_n, m-n) \]

因為函數g的性質，所以 $??_??$ 和 $??_??$ 的內積也會蘊含相對位置m-n。然后使得當兩個詞相對位置近時(m-n小)，內積可以大一點。兩個詞相對位置遠的時候(m-n大)，內積可以小一點。這樣就在不對注意力結構進行改造的前提下，將顯式的相對位置信息融入自注意力計算中，使得Attention內積能夠自動感知到相對位置信息，達到了以絕對位置編碼的形式實現相對位置編碼的目的。

注意，這里只有 $f_q(x_m,m), f_k(x_n,n)$是需要求解的函數。而對于 g，我們要求是表達式中有 $x_m, x_n, m-n$，也可以說是$q_m, k_n$的內積會受相對位置 ????? 影響。

1.3 結果展示

我們再看看RoPE是否滿足了“通過絕對位置編碼的方式實現相對位置編碼”。

注入絕對位置信息。對于t位置的$q_t$和 s位置的$k_s$，RoPE首先將$q_t$和 $k_s$在特征維度方向上兩兩維度一組，每兩個維度構成一個復數，對應復平面中的一個向量。然后將這些向量與復數旋轉矩陣的對應位置相乘，通過將一個向量旋轉某個角度來為這個向量注入絕對位置信息。即，給位置為m的向量$q_m$乘上矩陣$R_m$，給位置為n的向量$k_n$乘上矩陣$R_n$，分別得到新的位置向量。

\[f(q,m) = R_mq = \begin{pmatrix} cos m\theta & -sin m\theta \\ sin m\theta & cos m\theta \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \end{pmatrix} \\ f(k,n) = R_nk = \begin{pmatrix}cos n\theta & -sin n\theta \\sin n\theta & cos n\theta\end{pmatrix} \begin{pmatrix} k_0 \\ k_1 \end{pmatrix} \]
得到相對位置信息。用變換后的Q,K序列做注意力計算，通過公式展開后，就可以在注意力計算中得到相對位置信息。$(R_mq_m)^T(R_nk_n) = q_m^TR_m^TR_nk_n = q_m^TR_{n-m}k_n$。即位置為m的向量q和位置為n的向量k可以通過點積來計算二者的注意力分數，即旋轉前的注意力分數與旋轉后的注意力分數的差值僅與相對位置有關。

簡略證明如下。假設$R_n$是旋轉矩陣。

\[q_m = x_mW_qR(m\theta) \\ k_n = x_nW_kR(n\theta) \\ q_mk_n^T = x_mW_qR(m\theta)R(n\theta)^TW_k^Tx_n^T \\ = x_mW_qR(m\theta)R(-n\theta)W_k^Tx_n^T \\ =x_mW_qR((m-n)\theta)W_k^Tx_n^T \\ =g(x_m,x_n,m-n) \]

即

\[(qR_m)(kR_n)^T = qR_mR_n^Tk^T = qR_{m-n}k^T \]

$R_m$是一個正交矩陣，它不會改變向量的模長，因此通常來說它不會改變原模型的穩定性。

1.4 問題

我們目前有幾個問題值得思考。

論文中提到了函數f()，f()是怎么實現的？
為什么這樣轉換可以嵌入Token的位置信息？
這樣轉換為啥具有外推性？為啥說與三角函數PE思想有相似？

0x02 原理推導

下面就是要找到一個改造函數f，使得這個恒等變換g成立。我們依據RoFormer論文思路來繼續分析。

2.1 f()函數

首先，把“給輸入詞嵌入添加位置信息，然后轉換為q、k、V” 這個過程定義為函數f()，得到如下公式：

\[q_m = f_q(x_m, m) \\k_n = f_k(x_n,n) \\v_n = f_v(x_n,n) \\a_{m,n} =\frac{exp(\frac{q_m^Tk_n}{\sqrt d})}{\sum ^N _{j=1}exp(\frac{q_m^Tk_j}{\sqrt d})}\\o_m = \sum ^N _{n=1} a_{m,n}v_n \]

其次，我們對公式中的標記做深入分析。

$x_m$，$x_n$ ：輸入中所在位置分別為m,n的二維行向量，即未加入位置編碼的原始詞向量，并非是word embedding，則是token embedding。
$q_m$：第m個token對應的詞向量$x_m$集成位置信息m之后，轉換出來的query向量。
$k_n$：第n個token對應的詞向量$x_n$集成位置信息n之后，轉換出來的key向量。
$v_n$：第n個token對應的詞向量$x_n$集成位置信息n之后，轉換出來的value向量。
$f()$：給x向量加上位置信息，變成 q, k, v 的函數。基于 transformer 的位置編碼方法都是著重于構造一個合適的 $f_{q,k,v}$ 。

可以看到，RoPE算法的關鍵就是如何構建這個轉換函數f()，該f()在給詞向量引入絕對位置信息的同時，讓$q_mk_n^T$中也具備相對位置信息。我們接下來就看看這個f()的來龍去脈。

2.2 目標

本節我們用反推方式來進行分析。

首先來看看f()期望達成的目標。我們希望對于$q_mk_n^T = f_q(x_m, m)(f_k(x_n, n))^T$來說，雖然這個計算的輸入是向量$x_m$和$x_n$，以及絕對位置m和n，但是我們希望這個計算的結果只依賴于向量$x_m$和$x_n$本身，以及向量$x_m$和$x_n$之間的相對距離（m-n），而不依賴其絕對位置m和n。

其次，為了更方便的推導，接下來引入一個函數g()來進行演繹。我們希望$q_mk_n^T = f_q(x_m, m)(f_k(x_n, n))^T= g(x_m,x_n,m-n)$，最終推導的g函數公式里面只有相對距離，沒有絕對位置m和n。即，假定 query 向量 $q_m$和 key 向量$k_n$之間的內積操作可以被一個函數 g 表示，該函數 g 的輸入是詞嵌入向量 $x_m$，$x_n$和它們之間的相對位置 m - n：

\[<f_q(x_m,m),f_k(x_n,n)>\ = \ g(x_m,x_n,m-n) \]

g 可以理解為一個核函數，讓本來直接通過f()的運算（"語義信息加上絕對位置信息"結果的點積），變成用g來解釋（語義信息加上相對位置信息）。后續我們可以看到，g是通過極坐標（把相對距離轉換成為角度）來解釋點積。具體如下圖所示。

引入 g 函數只是為了方便推導，本質目標還是尋找一個f函數，即希望可以找到一個具有良好性質的f()函數，將顯式的相對位置依賴性納入自注意公式中，即找到一種q、k向量的編碼方式f()，使得編碼后的$q_m$和$k_n$的點積可以由 $x_m, x_n$ 和 m - n 表示出來（點積可以用詞向量加上相對位置信息表示）。

2.3 推導

既然知道目標，我們就一步一步來推導f()。

先忽略f()中輸入參數中的絕對位置參數，假設f()函數就是簡單的把原始token embedding返回。此處f()將$W^K, W^Q, W^V$的權重矩陣操作過程也包含進去了。

\[q_m = f_q(x_m, m) = x_m \\k_n = f_k(x_n, n) = x_n \\v_n = f_v(x_n, n) = x_n \]

我們看看如何給上面的初版f()函數逐步增加功能。

調整視角

我們要調整視角來看。

從二維向量到復數

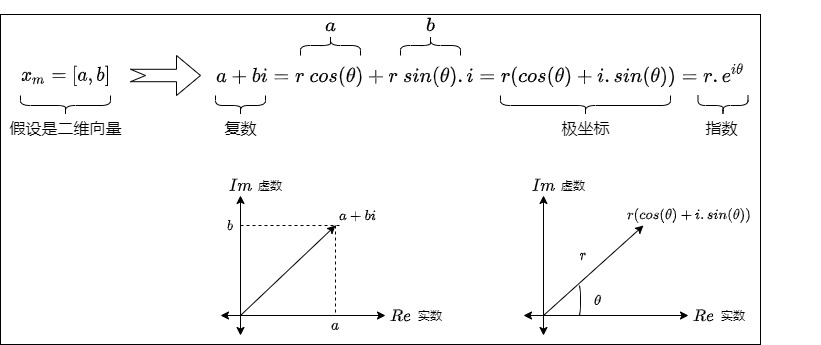
簡單起見，我們先假設$x_m$,$x_n$是二維行向量，即先假設輸入向量是二維的。比如$x_m$是[a,b]。既然是二維，而一個復數等價于復平面上一個二維向量，那么我們可以將它當作復數來考慮。于是我們把$x_m$轉換為$a+bi$。為何引入復數？這是因為平面旋轉雖然用矩陣看起來很直觀，但用復數表示更優雅。

從復數到極坐標

歐拉公式建立了指數函數，三角函數和復數之間的橋梁，一些三角函數用指數形式很容易解決和理解。比如，x表示任意實數，e是自然對數的底數，i是復數中的虛數單位，則依據歐拉公式有:

\[e^{ix} = cosx + i\ sinx \]

該表達式的意義是：為實部為cosx，虛部為sinx的一個復數可以表示成為一個指數形式。

依據歐拉公式，我們可以把二維向量的復數進而用極坐標來表示。$$a + bi = r\ cos(\theta) + r \ sin(\theta) . i = r(cos(\theta) + i.sin(\theta)) = r . e^{i \theta}$$。這里：

$cos(\theta) + i.sin(\theta)$ 是通過復平面的坐標來描述單位圓上的點。當 θ 從 0 到 2π 變化時，復數 $??^{????} $描述了單位圓的完整一圈。
$e^{i\theta}$是通過單位圓的圓周運動來描述單位圓上的點。通過復數的指數形式，我們可以將復數看作是復平面上圍繞原點旋轉的單位向量。
對于 $r\cdot e^{i\theta}$，r是語義，$\theta$是位置。

三個表現形式表達了同樣的信息：將二維向量逆時針旋轉角度$\theta$。即，一個二維向量$(x_{even}, x_{odd})$可以當成復數$x_{even} + i·x_{odd}$，然后乘上$e^{i\theta}$就能實現旋轉。這樣復雜的旋轉從復數角度來看就是單純地給相位加個角度。

因此，$x_m$和$x_n$是可以用極坐標來表示的，即用角度+長度來表示，這樣就可以把位置信息和語義信息分離開。

下一步思路

所以，我們下面要分成兩條路線來看看從指數形式如何思考。

如何給f()函數加上絕對位置信息？這是極坐標轉換的結果。
f()函數如何交互才能夠把相對位置信息變成相對位置信息？這是棣莫弗公式完成的功效。

然后再把這兩個路線合并起來。

引入絕對位置信息

依據歐拉公式，一個復數乘以$e^{i\theta}$等價于其對應的二維向量逆時針旋轉 $\theta$角度；也就是乘以旋轉矩陣。為何RoPE要旋轉旋轉操作呢？其它映射難道不行嘛？比如用線性變化把原來不同位置上的embedding向量分別映射到新的向量空間。其實主要是因為旋轉是一種不會破壞原來向量幾何特性的線性變換。長度不變，夾角不變，這對注意力用點積來衡量相似度特別有用。

旋轉矩陣

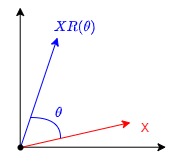
我們先簡單復習一下旋轉矩陣（Rotation matrix）。在二維空間中，存在一個旋轉矩陣 $R(\theta)$ ，當一個二維向量左乘旋轉矩陣時，該向量即可實現弧度為 $\theta$的逆時針旋轉操作。旋轉矩陣就是，別的向量乘以它，就可以改變向量的方向，但不改變大小和手性。

\[R(\theta) = \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix} \]

物理意義是：$XR(\theta)$是對X進行逆時針旋轉$\theta$。具體證明如下。

\[X = \rho(cos\phi,sin\phi)\\ XR(\theta) = \rho(cos\phi,sin\phi) \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix} \\ = \rho(cos\phi cos\theta - sin\phi sin\theta,cos\phi sin\theta + sin\phi cos\theta)\\ =\rho(cos(\phi + \theta),sin(\phi + \theta)) \]

也可以參見下圖。

旋轉矩陣幾個主要特性如下：

保持模長：旋轉不會改變向量的模長（長度），這對于點積計算中的數值穩定性至關重要。
保持相對角度：旋轉不會影響對兩個向量的夾角。如果向量 ??1和 ??2在空間中的夾角為 ??，那么經過旋轉后，夾角仍然是 ??。這對于注意力機制中通過點積衡量相似性尤其重要。
自然嵌入相對位置關系：旋轉引入的角度差 $Δ??=??_{??,??}???_{??,??}$隱含了位置 ??和 ??的距離 ?????，這種關系直接體現在點積的結果中。

旋轉矩陣還有兩個性質也需要留意。

正交性：旋轉矩陣的轉置等于其逆矩陣。$R(\theta)^T = R(-\theta)$
可加性：先繞角度$\theta_1$旋轉，再繞角度$\theta_2$旋轉，則相當于繞角度$\theta_1 + \theta_2$旋轉，即$R(\theta_1)R(\theta_2) = R(\theta_1 + \theta_2)$。

絕對位置編碼

旋轉矩陣的性質恰恰滿足了我們編碼絕對位置信息的要求。把token embedding繞原點旋轉一定的角度之后，且這個選擇的角度與絕對位置數值相關（比如是$m\theta$），我們就在嵌入向量中引入了角度信息，也就把絕對位置引入了f()函數。具體如下圖所示。$R_m$是一個旋轉矩陣，f()函數表示在保持向量模長的同時，將其逆時針旋轉$m\theta$，這意味著只要將向量旋轉某個角度，就可以實現對該向量添加對應的絕對位置信息。

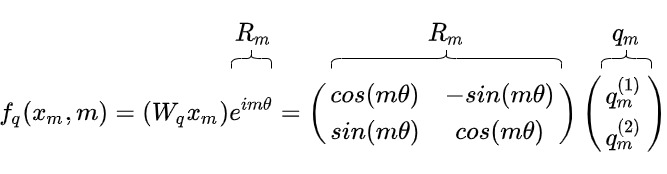
我們再進一步解釋：

?? 是一個非零的常數，$q_??^{(1)}$ 是q向量的第一維度，m是位置。
給 $q_m$乘這個旋轉矩陣，從幾何意義來看，就是給逆$q_m$時針旋轉其索引的 ?? 倍數。該操作只改變方向，不會改變q的模長。

舉例如下：

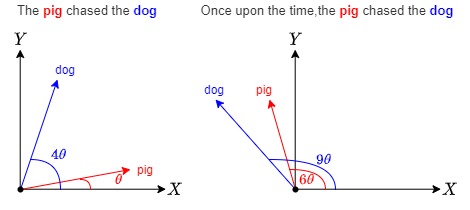
dog：單詞dog在第0位，不進行旋轉
The dog：單詞dog在第1位，旋轉角度θ
The pig chased the dog：單詞dog在第4位，旋轉角度4θ
Once upon the time, the ping chased the dong：單詞dong在第9位，旋轉角度為9θ.

找到相對位置信息

到目前位置，f()擁有了如下功能：在用復數和指數視角下，通過給向量乘以一個和絕對位置信息有關的旋轉矩陣，給向量注入了絕對位置信息，得到了新的$q_m$和$k_n$。我們再看看f()這個功能是否好用，即是否可以依據絕對位置信息來導出相對位置信息。

找到交互

我們先看看在目前視角（復數和指數）下如何進行交互。這個基礎是棣莫弗公式：兩個復數相乘可以轉成用極坐標表達的旋轉半徑相乘，再變成旋轉角度的相加。假設$\alpha,\beta$是$x_m,x_n$的弧度表示。‘則交互如下。

\[(a+bi)(c+di) = r1(cos(\alpha ) + i\ sin(\alpha ))\times r2(cos(\beta) + i\ sin(\beta)) = r1 \times r2 \times (cos(\alpha + \beta) + i\ sin(\alpha + \beta)) \]

找到內積

但是，我們的目標是$q_mk_n^T$，這是內積，并非相乘。我們繼續研究會發現，依據復數乘法性質，一個復數A（a+bi）的共軛乘以另外一個復數B（c+di），結果的實部等于A和B的內積，結果的虛部等于A和B的外積。即，第一個復數的共軛乘以第二個復數的運算，正好符合內外積運算的要求，內積取實部，外積取虛部。

\[(a-bi)(c+di) = (ac+bd)+(ad-bc)i\\ ac+bd是內積\\ ad-bc是外積 \]

注：

復數z的坐標表示為z=a+bi，其中a是復數的實部，b是復述的虛部，z的共軛復數是a-bi，即實部不變，虛部取相反數。
兩個復數相乘直接展開相乘即可，z1=a+bi，z2=c+di，則z1×z2=(ac-bd)+(bc+ad)i。

把位置信息融入內積

接下來看看如何把絕對位置信息融入到內積，變成相對位置信息。下面公式中，<>表示內積計算，? 是共軛復數，R[?] 表示 ? 的實部，右端的乘法是普通的復數乘法。公式的意思就是說：如果把二維向量當復數看待時，兩個二維向量的內積等于一個復數與另一個復數的共軛的乘積的實部。

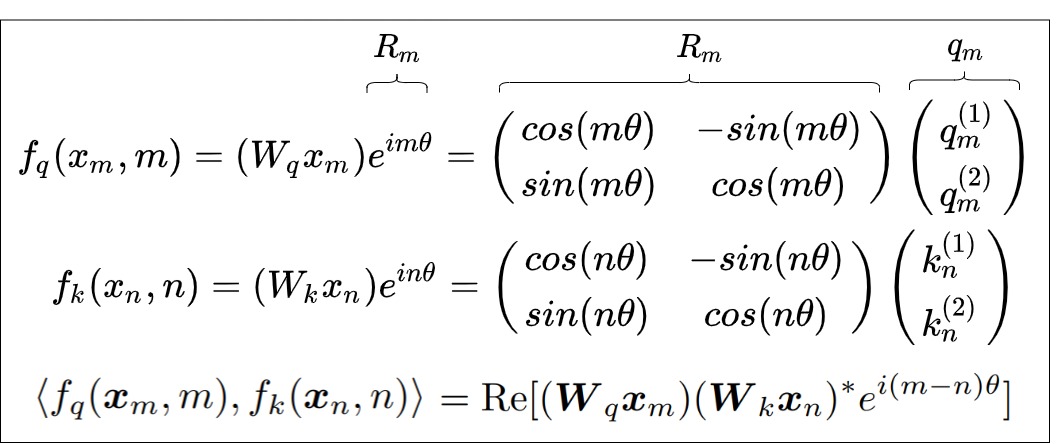
小結

我們總結推導步驟如下圖：

先將$x_m$，$x_n$轉化為對應的復數形式$x_m$，$x_n$，也可以表達成極坐標形式；
應用旋轉變換，得到新的復數形式$x_m$,$x_n$。具體是將$x_m$,$x_n$分別乘以$e^{imθ}$,$e^{inθ}$，變成$x_me^{imθ}$,$x_ne^{inθ}$，那么就相當于給$x_m$, $x_n$,配上了絕對位置編碼（顯式地依賴絕對位置m,n），即得到了$q_m$,$k_n$。即，對$x_m$施加復數乘法后的結果向量$q_m$,$k_n$，就是$x_m$經過矩陣旋轉之后的向量。
通過復數操作來計算 query 和 key 之間的內積，得到自注意力的計算結果。具體而言，因為$q_m$,$k_n$已經是復數，我們將$q_m$的共軛乘以$k_n$，將結果取實部，就得到了RoPE編碼后的自注意力矩陣元素 $A_{m,n}$。$<(W_qx_m)e^{im\theta},(W_kx_n)e^{in\theta}> = Re[(x_me^{im\theta})(x_ne^{in\theta})^*] = Re[x_mx_n*ei^{(m-n)\theta}]$，我們會發現，內積只依賴于相對位置m?n，這就巧妙地利用到復數的幅角相加性質來將絕對位置與相對位置融合在一起了。

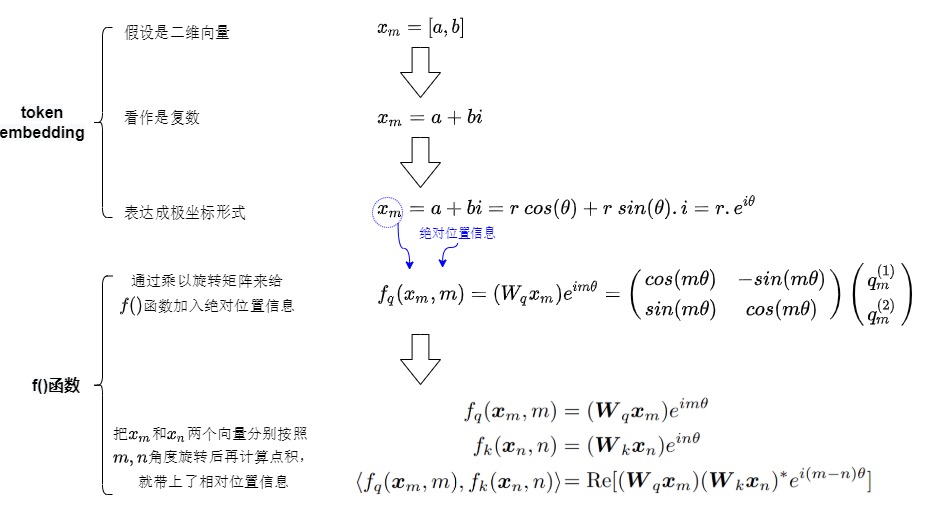
$x_m$和$x_n$兩個向量一開始只有絕對位置信息，把$x_m$和$x_n$兩個向量分別按照m,n角度進行旋轉之后，再來計算點積（讓絕對位置信息做交互），向量內積就自動帶上了相對位置信息。

2.4 正式定義

既然推導完畢，我們來正式看看f()和g()函數的解讀，也就是把上面的推導再詳細梳理下。

f()引入絕對信息

f()定義如下，可以理解為f()的作用是把兩個輸入參數（絕對位置信息m和詞信息$x_m$）分開放在極坐標的兩部分，分別經由以長度和角度來表示。

\[f_q(x_m,m) = (W_qx_m)e^{im\theta} \]

我們來仔細推導下。

首先，$W_q$ 是二維矩陣，$x_m$是二維向量，$W_qx_m$相乘的結果也是二維向量$q_m$。

\[W_qx_m = \begin{pmatrix} W_q^{(11)} & W_q^{(12)} \\ W_q^{(21)} & W_q^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix} = \begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix} = q_m \]

然后，把$q_m$解讀為復數形式，這樣可以后續更好的處理，即通過復數乘法來執行旋轉操作。

\[q_m = [q_m^{(1)},q_m^{(2)}] = q_m^{(1)} + i \ q_m^{(2)} \]

將$e^{im\theta}$也用復數表示。$e^{i\theta}$表示以單位圓上，幅度為$m\theta$為終點的向量。$e^{im\theta} = cos(m\theta) + i\ sin(m\theta)$。

因此，

\[f_q(x_m,m) = (W_qx_m)e^{im\theta} = q_me^{im\theta} \]

就是兩個復數相乘

\[f_q(x_m,m) = (W_qx_m)e^{im\theta} = q_me^{im\theta} = (q_m^{(1)} + i \ q_m^{(2)} )\ \times \ (cos(m\theta) + i\ sin(m\theta)) = \\(q_m^{(1)} cos(m\theta) - q_m^{(2)} sin(m\theta)) + i \ (q_m^{(2)}cos(m\theta) + q_m^{(1)}sin(m\theta)) \]

接下來，重新將f(x) 表達為實數向量形式

這其實就是query向量乘以一個旋轉矩陣$R_m$，即把位置信息加入了進來，但是把絕對位置信息和詞信息抽離開。放在極坐標的兩部分。

\[f_q(x_m,m) = (W_qx_m)e^{im\theta} \\ = q_me^{im\theta} = (q_m^{(1)} + i \ q_m^{(2)} )\ * \ (cos(m\theta) + i\ sin(m\theta)) \\ = [q_m^{(1)} cos(m\theta) - q_m^{(2)} sin(m\theta) , q_m^{(2)}cos(m\theta) + q_m^{(1)}sin(m\theta)] \\ = \begin{pmatrix} cos(m\theta) & -sin(m\theta) \\ sin(m\theta) & cos(m\theta) \end{pmatrix} \begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix} \\ = R_mq_m \]

具體參見下圖。

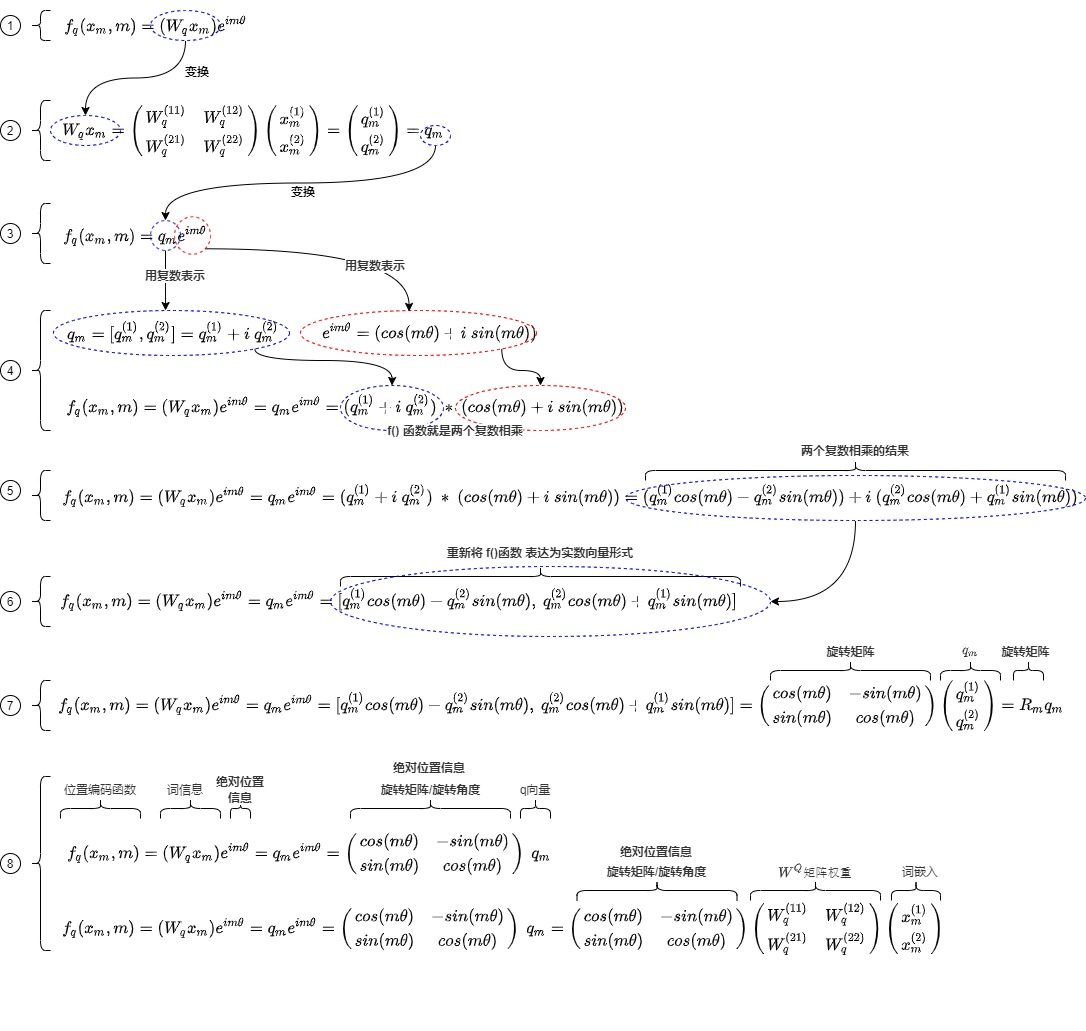
以上推導了f()函數的作用是把絕對位置信息加入到了詞嵌入中，我們來看看f()的點積如何引入相對位置信息，即，用g()來論證我們構造的f()是正確的。

g()函數驗證相對信息

我們希望驗證的是：得到f函數之后，我們經由f()函數構造了query 向量$q_m$ 和 key 向量$k_n$，兩個向量之間的內積操作可以被一個函數 g 表示，該函數 g 的輸入是詞嵌入向量 $x_m$、$x_n$和它們之間的相對位置 m - n。這樣就證明f()的有效性：通過絕對位置信息來表達相對位置信息。位置信息是高維向量，用極坐標表示位置信息，相對位置 m - n 在極坐標中就是他們的夾角（即從m旋轉一定角度到n），這樣就把位置信息變成了角度信息。

用數學公式表達如下。

已知

\[q_m = f_q(x_m,m) = (W_qx_m)e^{im\theta} \\ k_n = f_k(x_n,n) = (W_kx_n)e^{in\theta} \\ g(x_m,x_n,m-n) = Re[(W_qx_m)(W_kx_n)^* e^{i(m-n)\theta}] \]

要論證

\[\langle f_q(x_m,m),f_k(x_n,n)\rangle = g(x_m,x_n,m-n) = Re[(W_qx_m)(W_kx_n)^* e^{i(m-n)\theta}] \]

Re[x]表示一個復數x的實部，$(W_kx_n)^*$表示復數$W_kx_n$的共軛。

接下來證明 $ \langle f_q(x_m,m),f_k(x_n,n)\rangle = Re[(W_qx_m)(W_kx_n)^* e^{i(m-n)\theta}] $左右相等即可。

右面等式

先推導Re[]內部的信息。

\[W_qx_m = q_m = q_m^{(1)} + i \ q_m^{(2)} \\ W_kx_n = k_n = k_n^{(1)} + i \ k_n^{(2)} \\ (W_kx_n)^* = k_n^* = k_n^{(1)} - i \ k_n^{(2)} \\ e^{i(m-n)\theta} = cos((m-n)\theta) + i \ sin((m-n)\theta) \]

繼續推導

\[g(x_m,x_n,m-n) = Re[(W_qx_m)(W_kx_n)^* e^{i(m-n)\theta}] \\ = Re[(q_m^{(1)} + i \ q_m^{(2)})(k_n^{(1)} + i \ k_n^{(2)})(cos((m-n)\theta) + i \ sin((m-n)\theta))] \\ = (q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})cos((m-n)\theta) - (q_m^{(2)}k_n^{(1)} + q_m^{(1)}k_n^{(2)})sin((m-n)\theta) \]

用圖例表示如下。

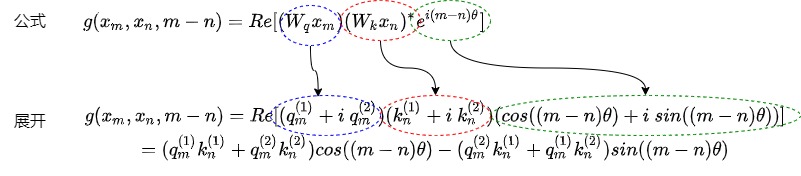
左邊等式

左邊等式展開如下。

\[f_q(x_m,m) = (W_qx_m)e^{im\theta} =[q_m^{(1)} cos(m\theta) - q_m^{(2)} sin(m\theta) , \ q_m^{(2)}cos(m\theta) + q_m^{(1)}sin(m\theta)] \\ f_k(x_n,n) = (W_kx_n)e^{in\theta} =[k_n^{(1)} cos(n\theta) - k_n^{(2)} sin(n\theta) , \ k_n^{(2)}cos(n\theta) + k_n^{(1)}sin(n\theta)] \\ <f_q(x_m,m),f_k(x_n,n) >\\= (q_m^{(1)} cos(m\theta) - q_m^{(2)} sin(m\theta))(k_n^{(1)} cos(n\theta) - k_n^{(2)} sin(n\theta)) + (q_m^{(2)}cos(m\theta) + q_m^{(1)}sin(m\theta))(k_n^{(2)}cos(n\theta) + k_n^{(1)}sin(n\theta)) \\ = (q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})cos((m-n)\theta) - (q_m^{(2)}k_n^{(1)} + q_m^{(1)}k_n^{(2)})sin((m-n)\theta) \\ = \begin{pmatrix} q_m^{(1)} & q_m^{(2)} \end{pmatrix} \begin{pmatrix} cos((m-n)\theta) & -sin((m-n)\theta) \\ sin((m-n)\theta) & cos((m-n)\theta) \end{pmatrix} \begin{pmatrix} k_n^{(1)} \\ k_n^{(2)} \end{pmatrix} \]

可以看到等式左右是相等的。具體也可以如下圖所示。

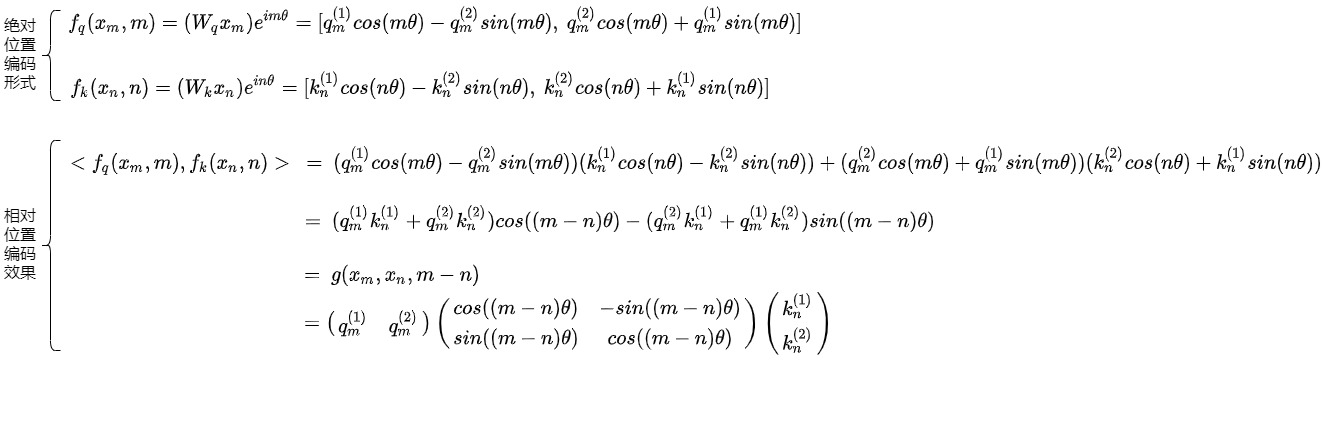
因此，RoPE 完成了其預期的目的。

添加絕對位置信息。添加絕對位置編碼是通過使用旋轉矩陣來完成的，即通過一個基于位置的旋轉矩陣將每個位置的嵌入旋轉到一個新的位置。
得到相對位置信息。可以使得兩個token的編碼，經過內積變換（self-attn）后，得到的結果，受它們位置的差值，即相對位置影響。即將顯式的相對位置依賴性納入自注意公式中。$q_m$和$k_n$之間的內積僅由$q_m$和$k_n$，距離$|i-j|$的值決定。

高維度

迄今為止，我們討論的是二維向量，而位置編碼通常是高維向量，這種情況下我們如何處理？RoPE 沒有嘗試在一個旋轉操作中編碼所有位置信息，而是將同一維度內的組件配對并旋轉它們（否則混合使用 x 和 y 偏移量信息）。通過獨立處理每個維度，RoPE 保持了空間的自然結構，而且可以根據需要推廣到任意多個維度。

我們仔細分析以下。

首先，我們看看如何用對角陣在正交的子空間上施加不同的行變換，假設有兩個方陣A，B，設$X=(X^1,X^2)$，則變化如下。

\[(X^1,X^2)\begin{pmatrix} A & 0 \\ 0 & B \end{pmatrix} = (X^1A,X^2B) \]

其次，內積滿足線性疊加性，任意偶數維的RoPE都可以表示為二維情形的拼接。

于是我們可以把每個向量（Key或者Query）兩維度一組切分，分成元素對${(q^1,q^2),(q^3,q^4),...}$，每對都解釋為二維向量。這樣就把原始的空間切分為一個個獨立正交的二維子空間。然后RoPE以角度$\theta_i$對每個二維向量（維度對$(q_i,q_{i+1})$）在每個子空間上面分別進行獨立的旋轉，其他的子空間不動。旋轉角的取值與三角式位置編碼相同，即采樣頻率 $\theta$ 乘上token下標（$m\theta_i = m \times base^{-2i/d}$）。旋轉完再做內積，將所有切分拼接，就得到了含有位置信息的特征向量。

因為每一組都滿足一個函數g（帶有相對關系m-n），最后他們相加，也一定會滿足g函數。

\[\begin{pmatrix} cos(m\theta_1) & -sin(m\theta_1) & 0 & 0 & ... & 0 & 0\\ sin(m\theta_1) & cos(m\theta_1)& 0 & 0 &... & 0 & 0 \\ 0 & 0 & cos(m\theta_2) & -sin(m\theta_2) & ... & 0 & 0 \\ 0 & 0 & sin(m\theta_2) & cos(m\theta_2) & ... & 0 & 0 \\ 0 & 0 &0 & 0 & ... & 0 & 0 \\ . & . &. & . & .\ \ & . & . \\ . & . &. & . & \ .\ & . & . \\ . & . &. & . & \ \ . & . & . \\ 0 & 0 &0 & 0 & ... & cos(m\theta_{d/2}) & -sin(m\theta_{d/2}) \\ 0 & 0 &0 & 0 & ... & sin(m\theta_{d/2}) & cos(m\theta_{d/2}) \\ \end{pmatrix} \begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \\ q_m^{(3)} \\ q_m^{(4)} \\ .\\ .\\ .\\ q_m^{(d-1)} \\ q_m^{(d)} \end{pmatrix} \]

這里 $\theta_i=10000^{?2i/d}$ ，??=0,1,2,...,??/2?1，沿用了 Transformer 最早的 Sinusoidal 位置編碼的方案。因為每個位置旋轉的角度不一樣， $??_?? $從0到d/2-1是單調遞減的，頻率是遞減的過程，所以它可以帶來一定的遠程衰減性。

如果加入$x_m$和$W_{q,k}$，則具體如下：

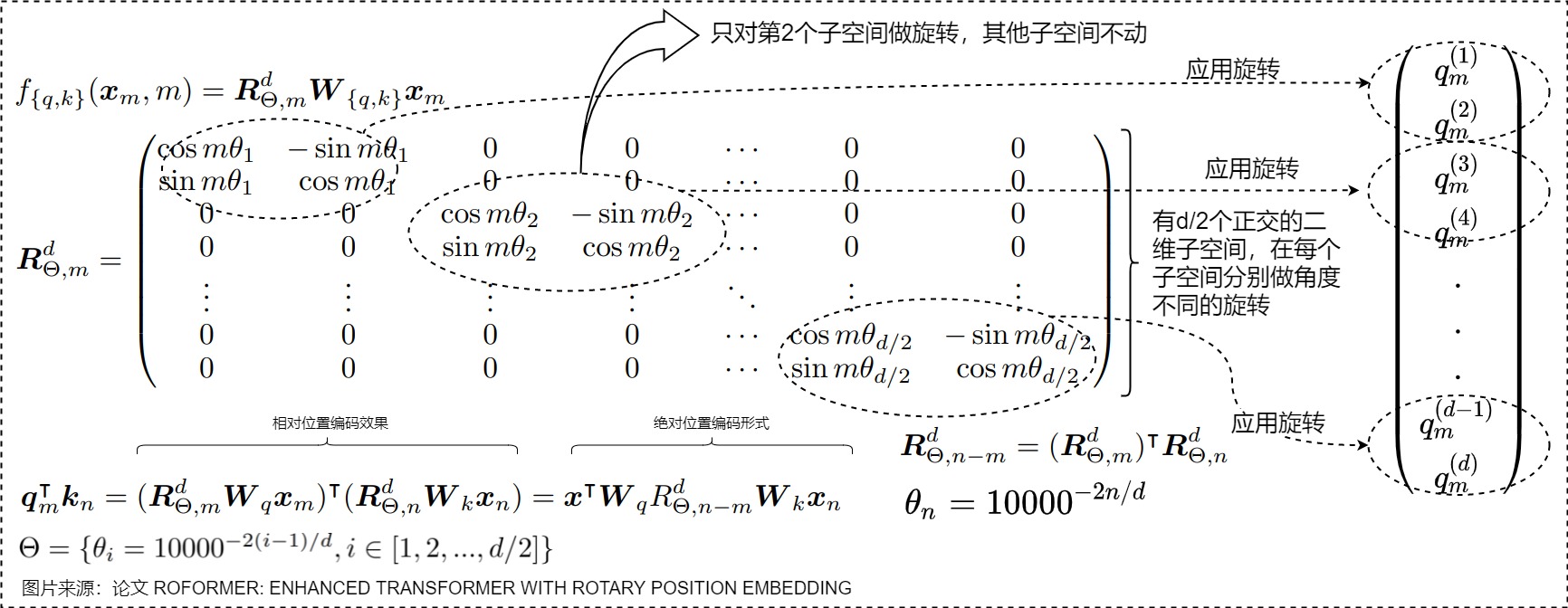
$??^d_{??,??}$ 是一個正交矩陣，它不會改變向量的模長，因此通常來說它不會改變原模型的穩定性。另外，因為$R_m$的稀疏性，直接用矩陣乘法實現會很浪費算力，所以在實踐中推薦使用如下圖所示的計算方式。其中$\bigotimes$是逐位對應相乘。

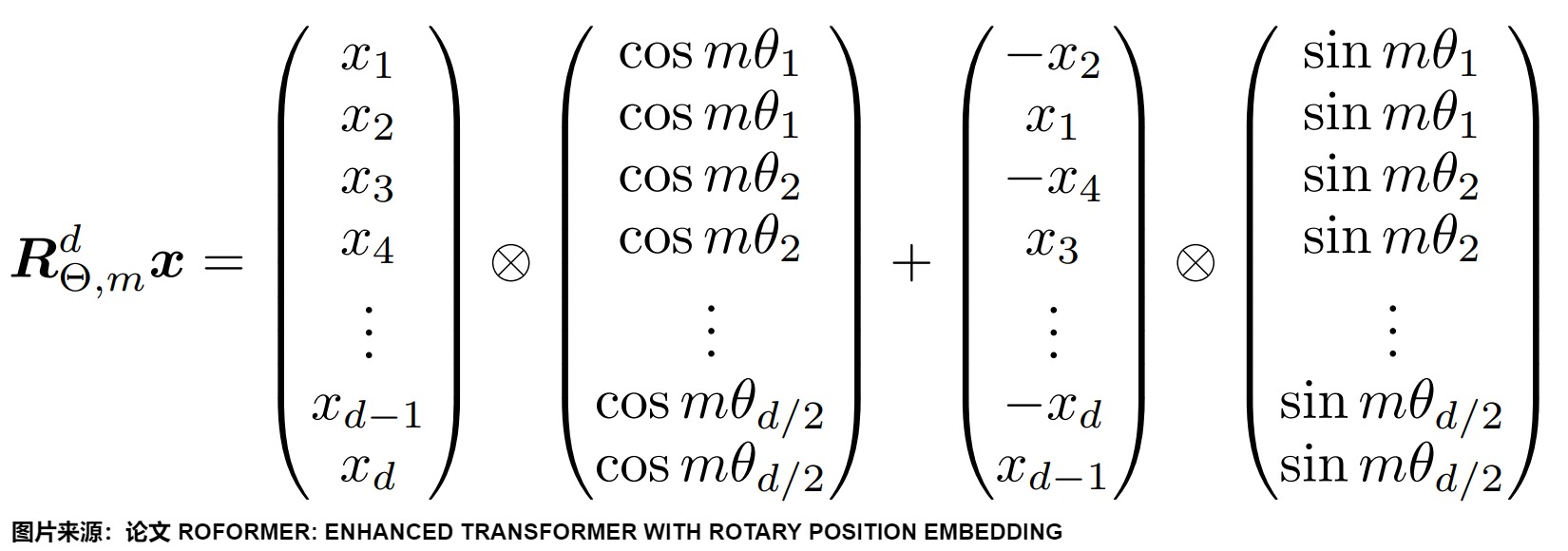
可以看出RoPE形式上和Sinusoidal位置編碼有點相似，只不過Sinusoidal位置編碼是加性的，而RoPE可以視為乘性編碼，即給位置 m 的 Query 高維向量 $q_m$ 乘上矩陣 $R_m$。這對應著向量在各個子維度上的旋轉，所以叫做旋轉位置編碼。因為在獨立的二維子空間做不同角度的旋轉。你可以將其想象成一個逆時針的時鐘系統，帶有時針分針秒針還有更細粒度的針。靠前的 pair 表示的粒度越大。或者說，RoPE通過不同頻率的三角函數有效區分了長程和短程。

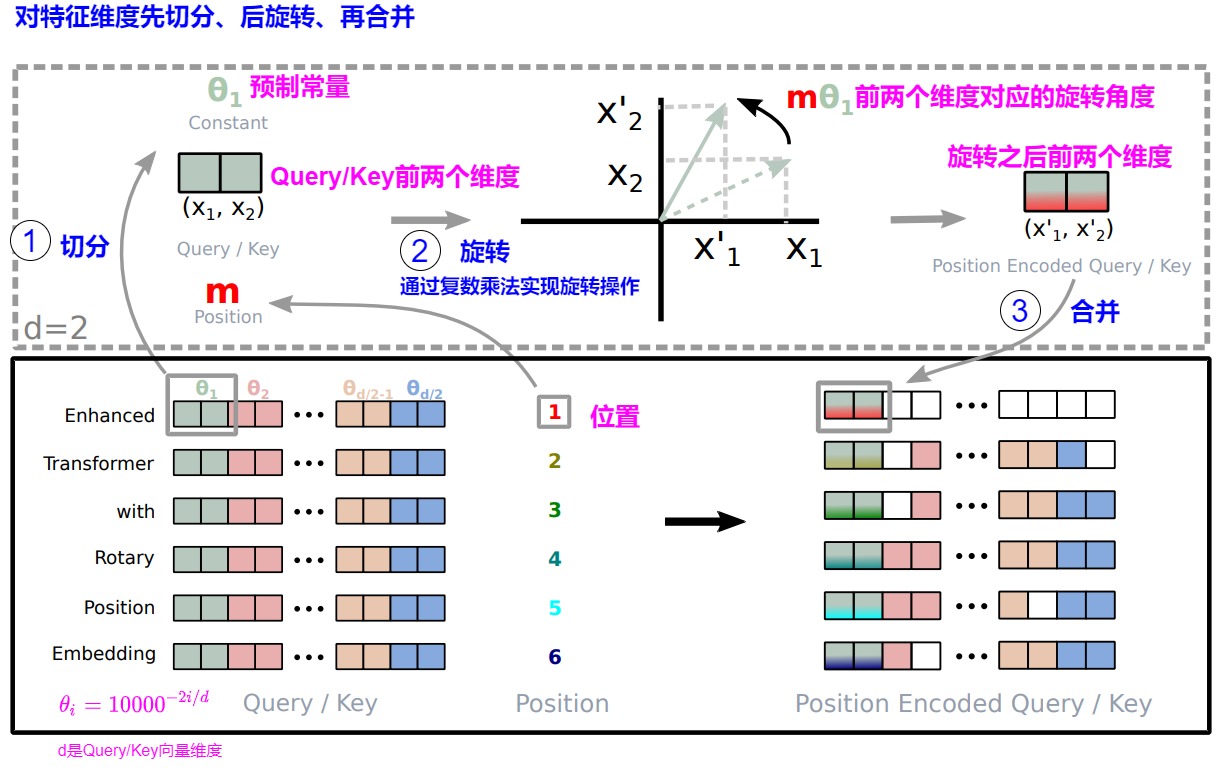
我們再使用論文的圖進行闡釋。

對于位置為m的d維q向量，我們將單詞的詞向量大小設定為2的倍數，即按照維度兩兩一組切分，每對都解釋成為一個二維向量。
第i組（即向量中的2i，2i+1元素）的旋轉角度為$mθ_i$，$θ_i$與i以及詞向量的hidden size有關，是一個這是一個從1漸變到接近于0的函數，因此，前面維度的????旋轉的更快，后面的旋轉的更慢。
然后對切分后的每個二維向量旋轉。
旋轉完成后將所有切分拼接，就得到了含有位置信息的特征向量。

2.5 總結

正弦位置編碼其實就是一種想要通過絕對位置編碼表達相對位置的位置編碼。但是由于投影矩陣的存在，這種能力被破壞了。這樣，雖然原始transformer中的正弦位置編碼實際上沒有起到它應有的效果。

RoPE的思想和正弦位置編碼有一定相似性，都嘗試在編碼過程中將相對位置信息考慮進去、位置變換的過程都利用三角函數轉換公式、在二維平面上進行位置轉換和旋轉形式一致。

兩者不同的是：

三角函數PE是直接計算每個絕對位置向量后，在輸入時把絕對位置向量與Token向量相加。或者說，是采用相加的形式將位置編碼融入到詞向量中。
RoPE是在投影之后，注意力計算前做旋轉。即RoPE可以看成是將三角函數PE計算的位置向量分別與輸入經過三個權重矩陣的query、key后的矩陣進行一個轉換操作。是將原始query、key向量改造成一個帶有位置信息的新向量，位置信息由參數m和θ進行表征，其中m為token在句子中的位置，θ的下標和向量中各元素的位置直接相關。

注意，不能在投影前旋轉，因為那樣就無法合并m-n了。可能就是因為在投影之后做旋轉，所以RoPE才避免出現了正弦位置編碼的問題。另外，在RoPE中采用的是類似哈達馬積的乘積形式。
由于三角函數的性質，導致三角函數PE本身就具備表達相對距離的能力，而RoPE位置編碼本身不能表達相對距離，需要結合Attention的內積才能激發相對距離的表達能力。

或者說，相對于三角函數PE，RoPE更深入將位置信息嵌入到模型結構中。從形式上看它有點像乘性的絕對位置編碼，通過在q,k中施行該位置編碼，那么效果就等價于相對位置編碼。而如果還需要顯式的絕對位置信息，則可以同時在v上也施行這種位置編碼。

在蘇神的文章Transformer升級之路：12、無限外推的ReRoPE？中指出：RoPE 形式上是一種絕對位置編碼，但實際上給 Attention 帶來的是相對位置信息，即如下的Toeplitz矩陣。這種形式的bias讓我們想起了ALiBi，它并沒有作用在 embedding 上，而是直接作用在了 Attention 上，通過這種構造方式既實現了遠程衰減，又實現了位置的相對關系。

\[\left(\begin{array}{ccccccccc} 0 & & & & & & & & \\ 1 & 0 & & & & & & & \\ 2 & 1 & 0 & & & & & & \\ 3 & 2 & 1 & 0 & & & & & \\ \ddots & 3 & 2 & 1 & 0 & & & & \\ \ddots & \ddots & 3 & 2 & 1 & 0 & & & \\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & & \\ L-2 & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \\ L-1 & L-2 & \ddots & \ddots & \ddots & 3 & 2 & 1 & 0 \end{array}\right) \\ \]

總的來說，RoPE通過絕對位置的操作，可以達到絕對位置的效果，也能達到相對位置的效果。這樣一來，我們得到了一種融絕對位置與相對位置于一體的位置編碼方案。

最后總結結合 RoPE 的 self-attention 操作的流程如下：

首先，對于 token 序列中的每個詞嵌入向量，都計算其對應的 query 和 key 向量;
然后在得到 query 和 key 向量的基礎上，對每個 token 位置都計算對應的旋轉位置編碼；
接著對每個 token 位置的 query 和 key 向量的元素按照兩兩一組應用旋轉變換；
最后再計算 query 和 key 之間的內積得到 self-attention 的計算結果。計算內積后，絕對位置信息不復存在，僅留下相對位置信息。

此外，RoPE 僅應用于查詢（Query）和鍵（Key）的嵌入，不適用于值（Value）的嵌入。

0x03 性質

本節來學習RoPE的一些主要特性以及業界思考。

3.1 相關性

旋轉編碼 RoPE 有如下特點：

計算$qk^T$點積時，保留了詞語的相對位置信息（不會因詞語的絕對位置發生改變），這樣可以有效地保持位置信息的相對關系。
相鄰位置的編碼之間有一定的相似性，即便在旋轉后，相鄰的位置仍然會有相似的嵌入。而距離較遠的編碼之間有一定的差異性。這樣可以增強模型對位置信息的感知和利用。
語義相似的Token平均來說獲得更多的注意力。即，當 k和q相近時，不管它們的相對距離n-m多大，其注意力 $q^TR_{n-m}k$平均都應該更大，至少要比隨機的兩個token更大。

3.2 周期性

因為旋轉一圈的弧度是$2\pi$ ，所以RoPE中的向量旋轉就像時鐘一樣，每組分量的旋轉都具有周期性。因為每組分量的旋轉弧度都隨著位置索引的增加而線性增加，所以越靠后的分組，它的正弦函數的周期越大、頻率越低，它的旋轉速度越慢。整體頻率可以對應到低頻，以及高頻上。

所以我們接下來就有一個問題：隨著位置的增大，旋轉角度是否會重復？具體解答如下。

在任意第k個子空間，只要$\theta_k$公式中不含有$\pi$，那么就不會出現周期性重復。
如果每個子空間都不會出現周期性重復，整體更不會重復。

3.3 $\beta$進制

蘇神認為RoPE是β進制編碼，原文如下。

位置n的旋轉位置編碼（RoPE），本質上就是數字n的β進制編碼！

對于一個10進制的數字n，如果希望得到其的β進制表示的（從右往左數）第m位數字，方法是

\[?\frac{n}{β^{m-1}}?mod\ β \]

也就是先除以$β^{k-1}$次方，然后求模（余數）。而RoPE可以改寫為

\[[cos(\frac{n}{β^0}),sin(\frac{n}{β^0}),cos(\frac{n}{β^1}),sin(\frac{n}{β^1}),?,cos(\frac{n}{β^{d/2-1}}),sin(\frac{n}{β^{d/2-1}}] \]

其中，$β=10000^{2/d}$。模運算的最重要特性是周期性，cos,sin剛好也是周期函數。所以，除掉取整函數這個無關緊要的差異外，RoPE（或者說Sinusoidal位置編碼）其實就是數字n的β進制編碼！

3.4 對稱性

對照三角函數編碼性質，對于RoPE編碼，位置m的token A對于位置n的Token B的注意力影響，和位置為2n-m上的token C對于Token B的注意力影響一樣。尤其當位置m的Token與位置2n-m的Token相同時，有如下表達式

\[g(x_m,x_n,m-n)=g(x_n,x_{2n-m},n-(2n-m)) \]

這證明RoPE編碼也是符合對稱性，沒有學習到方向的差異。

3.5 頻域

$\theta$的大小決定了對應維度的單調性，也賦予了這些維度上的參數不同的學習傾向。$\theta$ 就對應到了傅里葉變換中的頻率這一概念。$\theta$ 較大時，注意力計算結果僅在相對距離 t?s 較小時保持一致的單調性，之后陷入波動，本質上就是高頻信號； $\theta$ 較小時，注意力計算結果能在相對距離 t?s 較大時仍然能保持一致的單調性，波動較為平緩，本質上就是低頻信號。

論文“SCALING LAWS OF ROPE-BASE"指出，如果用$q_tk_s$表示 s 位置的token對 t 位置token的語義相似度，$q_tk_s$是一個二維時域信號，有 t,s 兩個時域維度。語義相似度 $q_tk_s$ 就是由不同頻域維度上的語義相似度分量$q_t^{(n)}k_s^{(n)}$組合而成的，每個維度對應一個頻段 $\theta_n$ ，高頻分量對應局部語義影響，低頻分量對應長上下文語義影響。從頻域到時域，最樸素的轉換方式就是傅里葉逆變換，通過$e^{i(s-t)\theta_n}$將不同頻段的分量組合。由于是為了獲取 s 位置對 t 位置的位置信息，所以變換對象是 $q_t^{(1)}k_s^{(1)}...q_t^{(d)}k_s^{(d)}$，變換的目標維度是原始二維時域的對角線方向，即 s?t 方向。

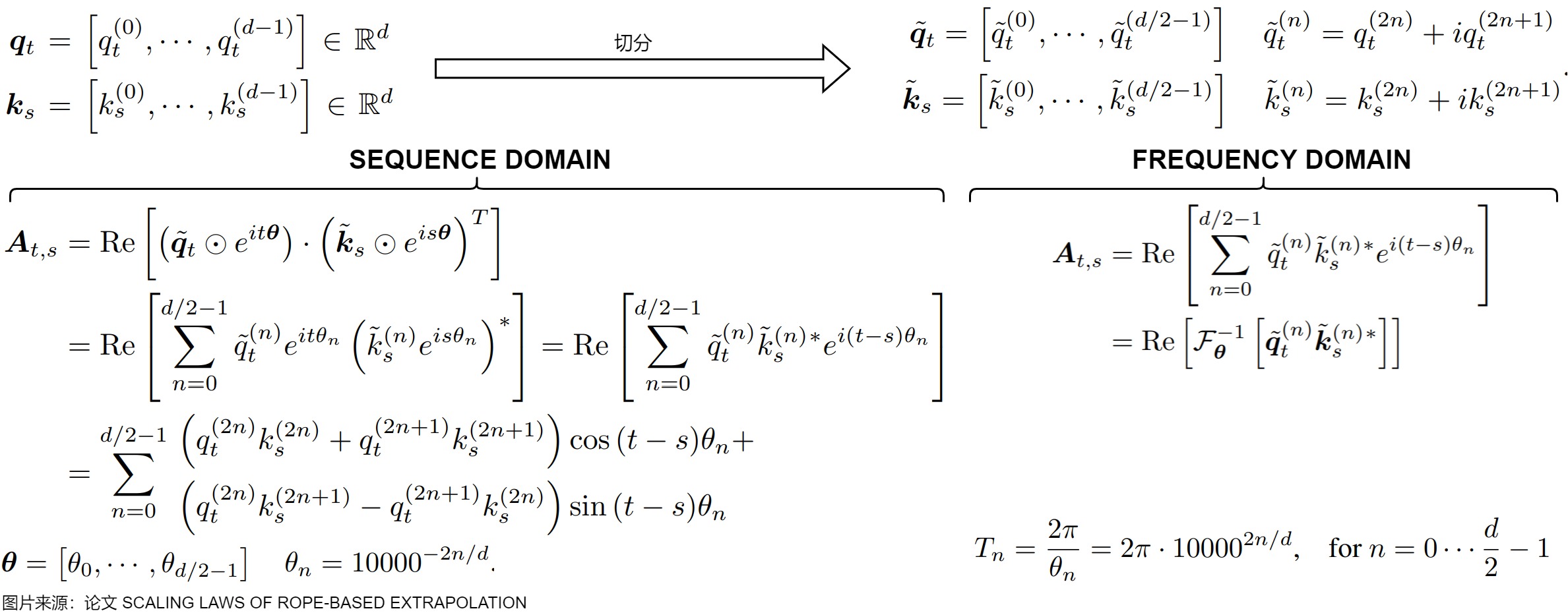
論文“Round and Round We Go! What makes Rotary Positional Encodings useful?”也揭示了RoPE不同頻率成分在模型學習中的作用：高頻用于位置注意力，低頻用于語義注意力。

我們可以計算出每個維度的ROPE對應的波長（Wavelength）是$\lambda_d = \frac{2\pi}{\theta_d} = 2????^{\frac{2d}{|D|}}$，，其中 |D| 是維度的總數，b是base。波長描述了嵌入在該維度上完成一次完整旋轉（2π）所需的標記數量。波長與RoPE嵌入的頻率有關，且在不同維度上可能有所不同。

當給定一個長度L，有的維度會出現周期比L更長，可以假設，當出現這個情況的時候，所有的位置都能獲得一個唯一的編碼，也就是絕對位置都保留了下來。反之，周期比較短的維度只能保留相對位置信息。

3.6 高頻低頻

RoPE中，向量旋轉就像時鐘一樣，因為旋轉一圈的弧度是$2\pi$，所以每組分量的旋轉都具有周期性。RoPE以角度$\theta_i$對每個二維向量（維度對$(q_i,q_{i+1})$）分別進行旋轉，旋轉角的取值與三角式位置編碼相同，即采樣頻率 $\theta$ 乘上token下標（$m\theta_i = m \times base^{-2i/d}$），旋轉完將所有切分拼接，就得到了含有位置信息的特征向量。這里 $\theta_i=10000^{?2i/d}$ ，沿用了 Transformer 最早的 Sinusoidal 位置編碼的方案。它可以帶來一定的遠程衰減性。每個位置旋轉的角度不一樣。

\[\begin{pmatrix}cos(m\theta_1) & -sin(m\theta_1) & 0 & 0 & ... & 0 & 0\\sin(m\theta_1) & cos(m\theta_1)& 0 & 0 &... & 0 & 0 \\0 & 0 & cos(m\theta_2) & -sin(m\theta_2) & ... & 0 & 0 \\0 & 0 & sin(m\theta_2) & cos(m\theta_2) & ... & 0 & 0 \\0 & 0 &0 & 0 & ... & 0 & 0 \\. & . &. & . & .\ \ & . & . \\. & . &. & . & \ .\ & . & . \\. & . &. & . & \ \ . & . & . \\0 & 0 &0 & 0 & ... & cos(m\theta_{d/2}) & -sin(m\theta_{d/2}) \\0 & 0 &0 & 0 & ... & sin(m\theta_{d/2}) & cos(m\theta_{d/2}) \\\end{pmatrix} \begin{pmatrix}q_m^{(1)} \\q_m^{(2)} \\q_m^{(3)} \\q_m^{(4)} \\.\\.\\.\\q_m^{(d-1)} \\q_m^{(d)}\end{pmatrix} \]

在周期函數中，如$sin(\omega x)$ ，$\omega$ 越大，頻率越大。在RoPE中，$\omega$隨維度變量 k 增加,$b^{-2k/d}$減小，從而頻率降低。

\[sin(\frac{p}{b^\frac{2k}w0obha2h00}),cos(\frac{p}{b^\frac{2k}w0obha2h00}) \]

我們可得：位置編碼的低維對應高頻，高維對應低頻。對于每組分量，它的旋轉弧度隨著位置索引的增加而線性增加。越靠后的分組，它的旋轉速度越慢，正弦函數的周期越大、頻率越低。

高頻：是RoPE的位置向量，i 比較小（前面的維度）， ???? 較大的時候，周期短，頻率高。
低頻: 是RoPE的位置向量，i 比較小（后面的維度），???? 較小的時候，周期長，頻率低。

NTK-RoPE、YaRN的作者Bowen Peng認為：高頻學習到的是局部的相對距離，低頻學習到的是遠程的絕對距離。高頻低頻兩者都很重要，它們之間更像是一種層次的關系；用進制類別來看，低頻對應的就是高位，如果只保留低位而去掉高位，那么結果就相當于求模（余數），無法準確表達出位置信息來。

3.7 遠程衰減

遠程衰減基于一個很樸素的假設：相對距離越遠，則彼此之間的關聯度越低，依賴度越低。如果位置編碼具有遠程衰減特性，則可以讓位置相近的Token平均來說獲得更多的注意力。

表現

RoPE也呈現出遠程衰減的性質，具體表現為：對于兩個詞向量，若它們之間的距離越近，則它們的內積分數越高，反之則越低。即，位置 m 的 Query 向量 $q_m$ 與位置 n 的 Key 向量 $k_n$ 相對距離越遠（ |n?m| 越大）， $(R_mq_m)^T(R_nk_n))$ 越小。從下圖可以看到，隨著相對距離的變大，內積結果有衰減趨勢。

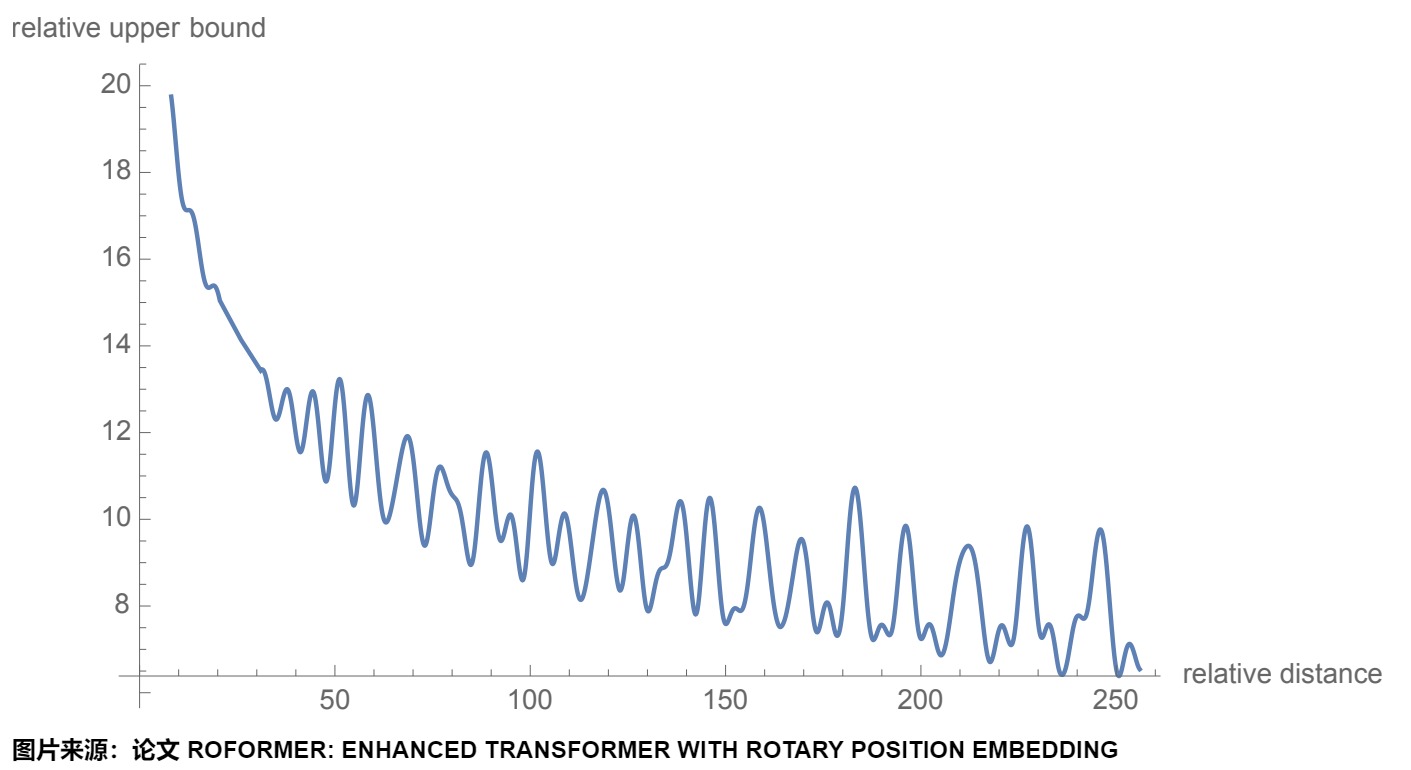
從圖上也可以看出，在衰減曲線后期會產生很大波動，產生了U形狀的注意力模式。對比圖如下。

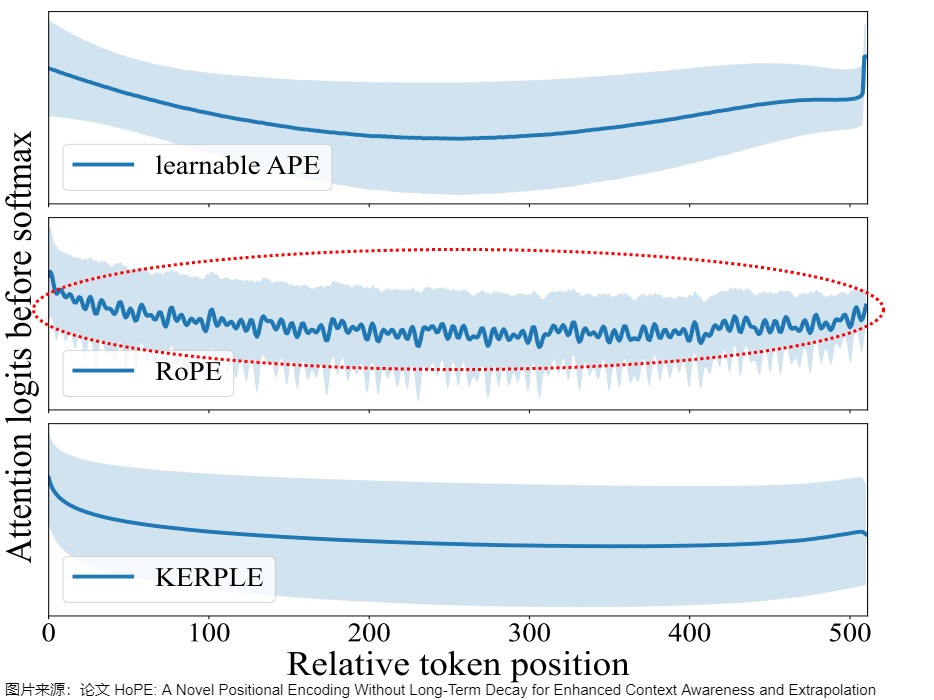
論文”HoPE: A Novel Positional Encoding Without Long-Term Decay for Enhanced Context Awareness and Extrapolation"對此進行了細致的分析，發現在RoPE中，U形狀的注意力模式是由特定學習到的組件（learned components）造成的，這些組件也是限制RoPE表達能力和外推能力的關鍵因素。具體參見下圖。

(a) 表示將RoPE分解為組件（Comps）進行分析（見圖上紅圈方程式）。上部子圖顯示了每個組件對整體注意力邏輯的貢獻。我們用紅色突出顯示了一些具有突出模式（patterns）的組件，即“激活”組件，用藍色突出顯示了低頻組件。下部子圖展示了整體注意力邏輯，以及“激活”組件的組合效應。
(b) 給出了訓練期間RoPE不同組件的方差（VAF）。
(c) 揭示了外推中的OOD現象是由“激活”組件引起的。兩個上部的子圖顯示了第一層的注意模式，下部的子圖則顯示了后續層的異常模式。

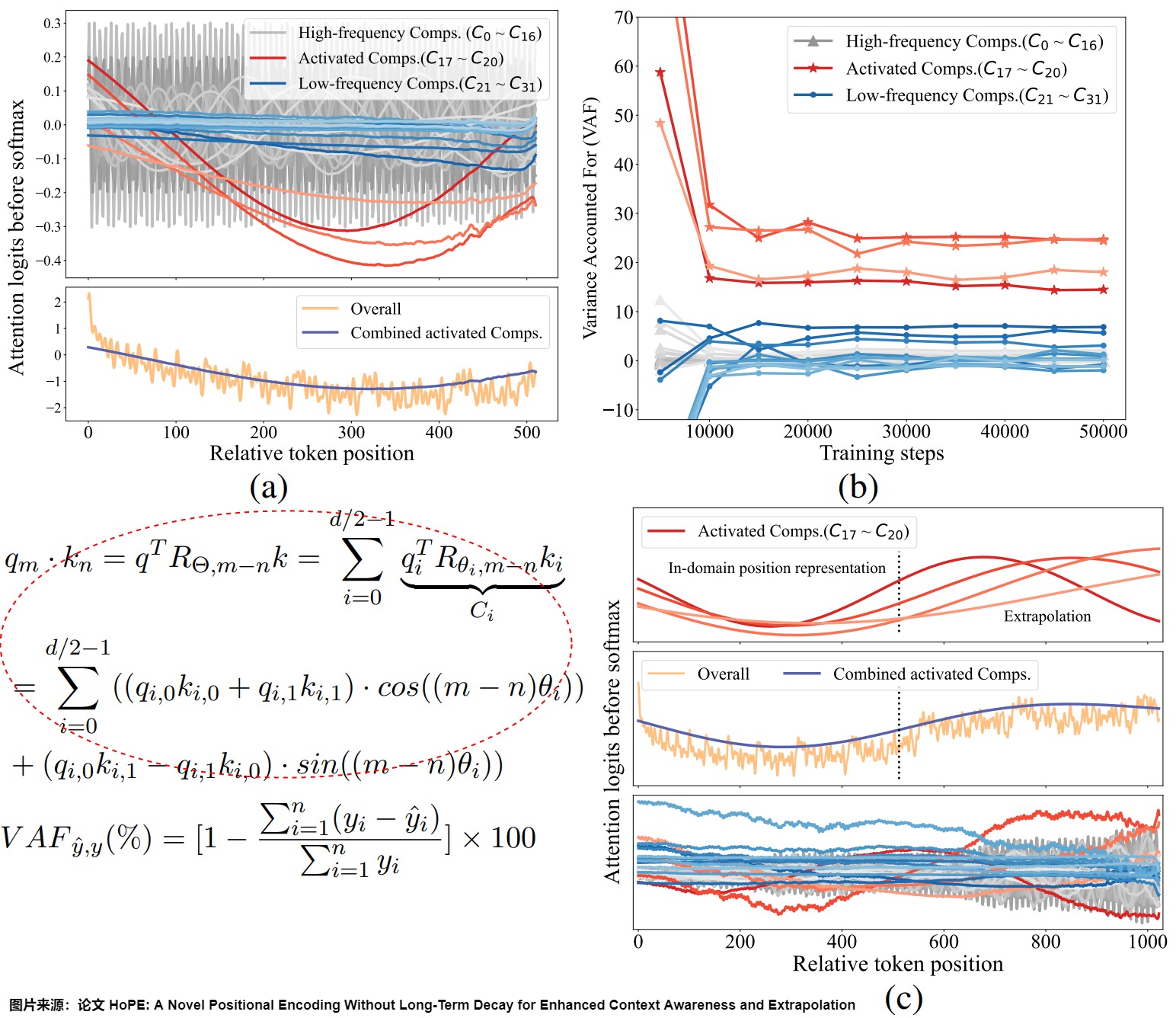
基于這些發現，該論文提出了一種新的位置編碼方法——High-frequency rotary Position Encoding（HoPE）。HoPE通過去除RoPE中的位置依賴組件，保留高頻信號，從而理論上也打破了長期衰減的原則。

能否設計不振蕩的位置編碼？很難，位置編碼函數如果不振蕩，那么往往缺乏足夠的容量去編碼足夠多的位置信息，也就是某種意義上來說，位置編碼函數的復雜性本身也是編碼位置的要求。

論證

我們接下來對遠程衰減進行論證。

首先，我們用論文中的推導來看，具體參見下圖。

其次，有研究人員認為下面公式為RoPE的主要功能項。Transformer位置編碼（意義）河畔草lxr

\[C_{RoPE}(t-s) = \frac{1}{d/2}\sum_{n=1}^{d/2}cos(s-t)\theta_n \\ \ \theta_n = 10000^{-2n/d} \]

$C_{RoPE}(t?s)$ 大致隨相對距離 t?s 呈現單調減的關系。但是整體偏置的單調減并不意味著每個維度偏置的單調減： $\theta_n$ 的大小決定了維度 2n?1,2n 的單調性，也賦予了這些維度上的參數不同的學習傾向：

n 較小時， $\theta_n$ 較大，趨向于1，僅在相對距離 t?s 較小時保持一致的單調性，之后陷入波動，誘導對應維度刻畫較近的位置信息；
n 較大時， $\theta_n$ 較小，趨向于0，能相對距離 t?s 較大時仍然保持一致的單調性，誘導對應維度刻畫較遠的位置信息。

反過來，不同相對位置的語義信息也會反映在不同的特征維度上：

在相對距離 t?s 較小時，所有維度的偏置都接近于1，對應自注意力分布更加關注相鄰位置的信息；
在相對距離 t?s 較大時，多數維度有正有負相互抵消，只有部分維度的偏置較大，如果兩個token對應維度的語義特征高度重合則會予以部分強調，否對應自注意力分布趨近于0。這也正是相對偏置的一大優勢，即對相對距離較遠的語義關聯，沒有給予絕對的懲罰，而是給予相對的過濾：雖然通過整體偏置抑制較遠距離的信息，但是仍然允許某些特征維度上的語義匯集到自注意力計算中。

基數

對于$\theta_n = 10000^{-2n/d}$，10000這個數決定了 ?? 的大小，我們稱其為基數（base）。base的不同取值會影響注意力遠程衰減的程度。因為“隨距離衰減”是外推的關鍵，所以base的性質與大模型的長度外推息息相關，如NTK-Aware Scaled RoPE、NTK-by-parts、Dynamic NTK等長度外推方法，本質上都是通過改變base，從而影響每個位置對應的旋轉角度，進而影響模型的位置編碼信息，最終達到長度外推的目的。

由于 RoPE 中的 attention 值除了 q,k 本身外，僅和$ R_{n-m} $因子相關，下面考察$ R_{n-m} $ 因子的特點

\[\begin{aligned} \left\langle\boldsymbol{p}_{\mathrm{m}}, \boldsymbol{p}_{\mathrm{n}}\right\rangle & =\operatorname{Re}\left[\mathrm{e}^{\mathrm{i}(\mathrm{m}-\mathrm{n}) \theta_0}+\mathrm{e}^{\mathrm{i}(\mathrm{m}-\mathrm{n}) \theta_1}+\cdots+\mathrm{e}^{\mathrm{i}(\mathrm{m}-\mathrm{n}) \theta*{\mathrmw0obha2h00 / 2-1}}\right] \ & =\frac{\mathrmw0obha2h00}{2} \cdot \operatorname{Re}\left[\sum*{\mathrm{i}=0}^{\mathrmw0obha2h00 / 2-1} \mathrm{e}^{\mathrm{i}(\mathrm{m}-\mathrm{n}) 10000^{-\mathrm{i} / \mathrmw0obha2h00 / 2)}} \frac{1}{\mathrm{~d} / 2}\right] \ & \approx \frac{\mathrmw0obha2h00}{2} \cdot \operatorname{Re}\left[\int_0^1 \mathrm{e}^{\mathrm{i}(\mathrm{m}-\mathrm{n}) \cdot 10000^{-\mathrm{t}} \mathrm{dt}}\right] \end{aligned} \ \]

那么問題就變成了積分 $\int_0^1 \mathrm{e}^{\mathrm{i}(\mathrm{m}-\mathrm{n}) \cdot 10000^{-\mathrm{t}} }\mathrm{dt} $的漸進估計問題，通過一下函數計算積分值與位置距離的關系就可以分析出不同 base 值的影響。

base=1，完全失去遠程衰減特性。
base 越小，衰減得越快且幅度也更大。太小的base會破壞注意力遠程衰減的性質，例如base=10或100時，注意力分數不再隨著相對位置的增大呈現出震蕩下降的趨勢。
base 越大，衰減得越慢且幅度也越小。這也是為什么訓練更長的窗口，要把base改大的原因。所以現在業界的主流做法都是窗口變長后，base也要跟著變大做適配。蘋果就在其模型中用了很大的基數。輸入序列越長，base就需要越大，讓未充分訓練過的窗口強行衰減變慢，本身也是降低崩的概率的一種方式。

平滑性

另外，embedding維度和衰減曲線的平滑程度成正相關，維度越高，衰減曲線越平滑。外推性的基本前提是函數的“光滑性”。外推性就是局部推斷整體，它依賴的就是給定函數的高階光滑性（高階導數存在且有界）。但是三角函數編碼或RoPE不具備這種性質。它們是一系列正余弦函數的組合，這算是關于位置編碼k的高頻振蕩函數，而不是直線或者漸近趨于直線之類的函數，所以基于它的模型往往外推行為難以預估。

3.8 外推

盡管RoPE可以理論上可以編碼任意長度的絕對位置信息，并且通過旋轉矩陣（三角計算）來生成超過預訓練長度的位置編碼，并且RoPE也具有遠程衰減特性（“隨距離衰減”是外推的關鍵）。RoPE仍然存在外推問題（length extrapolation problem），即對于基于RoPE的大語言模型，測試長度超過訓練長度之后，模型的效果會有顯著的崩壞，具體表現為語言建模困惑度急劇攀升。遠程衰減屬性導致在更長文的外推中，RoPE編碼的作用影響也在衰減，效果在逐步變差。

我們將在后面專門寫一篇來做具體分析。

0x04 實現

4.1 基礎Torch知識

torch.outer

torch.outer(a, b) 計算兩個 1D 向量 a 和 b 的外積，生成一個二維矩陣，其中每個元素的計算方式為：result[i,j]=??[i]×??[j]。即，result矩陣的第 i 行、第 j 列的元素等于向量 a 的第 i 個元素與向量 b 的第 j 個元素的乘積。

外積（outer product）是指兩個向量 a 和 b 通過外積操作生成的矩陣：??=?????。其中 ????? 生成一個矩陣，行數等于向量 ?? 的元素數，列數等于向量 ??的元素數。

torch.matmul

當輸入張量的維度大于 2 時，torch.matmul將執行批量矩陣乘法。

torch.polar

torch.polar()函數會構造一個復數張量，用法是torch.polar(abs, angle, *, out=None) → Tensor。其元素是極坐標對應的笛卡爾坐標，絕對值為 abs，角度為 angle。 out=abs?cos(angle)+abs?sin(angle)?j。

torch.repeat_interleave

torch.repeat_interleave()函數會返回一個具有與輸入相同維度的重復張量。

torch.view_as_complex

把一個tensor轉為復數形式，要求這個tensor的最后一個維度形狀為2。

torch.view_as_real

把復數tensor變回實數，可以看做是是剛才操作的逆變換。

4.2 在Transformer中的位置

不同于原始 Transformer 的絕對位置編碼，RoPE位于多頭注意力機制的內部，直接作用于每個頭完成變換的query和key，而且每個頭使用相同的RoPE（RoPE的輸入參數只有位置和維度，跟頭無關），這也意味著在 transformer中的每一層都要加入RoPE。

4.3 llama3

lama中對RoPE的實現采用復數的公式來計算$f_q(x_m,m) = (W_qx_m)e^{im\theta}$。該方式速度較快，但不方便后續修改。

具體而言，是把每個向量（Key或者Query）兩維度一組切分，分成元素對${(q^1,q^2),(q^3,q^4),...}$，每對都解釋為二維向量。然后RoPE以角度$\theta_i$對每個二維向量（維度對$(q_i,q_{i+1})$）分別進行旋轉，旋轉角的取值與三角式位置編碼相同，即采樣頻率 $\theta$ 乘上token下標（$m\theta_i = m \times base^{-2i/d}$），旋轉完將所有切分拼接，就得到了含有位置信息的特征向量。

\[\begin{pmatrix}cos(m\theta_1) & -sin(m\theta_1) & 0 & 0 & ... & 0 & 0\\sin(m\theta_1) & cos(m\theta_1)& 0 & 0 &... & 0 & 0 \\0 & 0 & cos(m\theta_2) & -sin(m\theta_2) & ... & 0 & 0 \\0 & 0 & sin(m\theta_2) & cos(m\theta_2) & ... & 0 & 0 \\0 & 0 &0 & 0 & ... & 0 & 0 \\. & . &. & . & .\ \ & . & . \\. & . &. & . & \ .\ & . & . \\. & . &. & . & \ \ . & . & . \\0 & 0 &0 & 0 & ... & cos(m\theta_{d/2}) & -sin(m\theta_{d/2}) \\0 & 0 &0 & 0 & ... & sin(m\theta_{d/2}) & cos(m\theta_{d/2}) \\\end{pmatrix} \begin{pmatrix}q_m^{(1)} \\q_m^{(2)} \\q_m^{(3)} \\q_m^{(4)} \\.\\.\\.\\q_m^{(d-1)} \\q_m^{(d)}\end{pmatrix} \]

這里 $\theta_i=10000^{?2i/d}$ ，沿用了 Transformer 最早的 Sinusoidal 位置編碼的方案。它可以帶來一定的遠程衰減性。每個位置旋轉的角度不一樣。

總體

其總體代碼和公式對應如下圖所示。

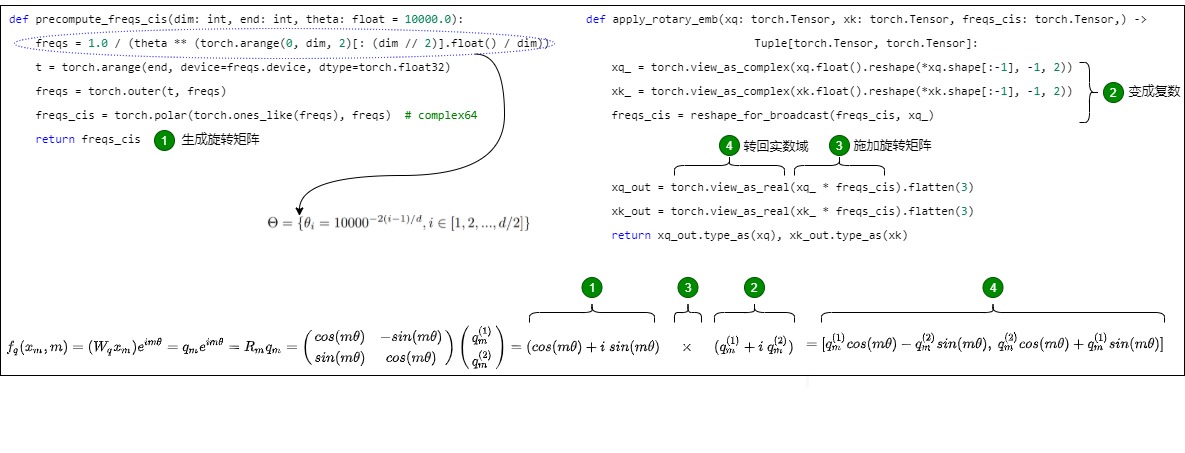
在實現 RoPE 算法之前，需要注意：為了方便代碼實現，在進行旋轉之前，需要將旋轉矩陣轉換為極坐標形式，嵌入向量（q、k）需要轉換為復數形式。完成旋轉后，旋轉后的嵌入需要轉換回實數形式，以便進行注意力計算。

準備旋轉矩陣

precompute_freqs_cis()函數會生成旋轉矩陣，即給定維度預計算頻率θ。θ 完全由 Q、K、V 的向量長度 d 決定。位置 m 對應我們的 query 長度，實際代碼中由 max_position_embeddings 參數決定，可以理解為模型支持的最長 query 的長度，因此 max 有了，m 的范圍也就有了。結合上面的信息，針對一個固定了最長 query 長度 m 和向量維度 d 的 LLM，我們可以提前將其對應的旋轉變換矩陣構造完成。

freqs = torch.outer(t, freqs)的矩陣如下。

\[freqs =\begin{bmatrix} 1\theta _1 & 1\theta_2 & 1\theta_3 & ... & 1\theta_{d/2-1} & 1\theta_{d/2}\\ 2\theta_1 & 2\theta_{2} & 2\theta_{3} & ... & 2\theta_{d/2-1} & 2\theta_{d/2}\\ \vdots & \vdots & \vdots &\ddots & \vdots & \vdots \\ \vdots& \vdots& \vdots & \vdots & \vdots & \vdots\\ m\theta_{1} & m\theta_{2} & m\theta_{3} & ... & m\theta_{d/2-1} &m\theta_{d/2} \\ \end{bmatrix} \]

結合這個 Rd 的變換矩陣，分別執行 cos 和 sin，便可以得到我們計算所需的全位置全維度的變換矩陣。

torch.polar之后的 freqs 如下。

\[freqs =\begin{bmatrix} cos(\theta_1)+i \cdot sin(\theta_1) & cos(\theta_2)+i \cdot sin(\theta_2) & ... & cos(\theta_{d/2})+i \cdot sin(\theta_{d/2})\\ cos(2\theta_1)+i \cdot sin(2\theta_1) & cos(2\theta_2)+i \cdot sin(2\theta_2) & ... & cos(2\theta_{d/2})+i \cdot sin(2\theta_{d/2})\\ \vdots & \vdots &\ddots & \vdots & \\ cos(m\theta_1)+i \cdot sin(m\theta_1) & cos(m\theta_2)+i \cdot sin(m\theta_2) & ... & cos(m\theta_{d/2})+i \cdot sin(m\theta_{d/2}) \end{bmatrix} \]

具體代碼如下。

# 生成旋轉矩陣
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    # 根據維度 d 生成旋轉角度θ向量。計算詞向量元素兩兩分組之后，每組元素對應的旋轉角度 θ_i，由于是將向量兩兩旋轉應用 RoPE，所以共有 dim/2 個 θ。θ 完全由 Q、K、V 的向量長度 dim 決定
    # freqs 長度是 dim/2，一半的維度。2表示是偶數這里 θ 完全由 Q、K、V 的向量長度 d 決定，即 dim維度，取0，2，4...等維度
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) 
    # 生成 token 序列索引 t = [0, 1,..., seq_len-1]，即拿到所有位置對應的ID，就是論文中常說的m或者n
    t = torch.arange(end, device=freqs.device, dtype=torch.float32)
    # 計算m * θ。將旋轉角度和 `token` 位置索引相乘，即求向量的外積，結果是一個矩陣，該矩陣包含了每個位置和每個維度對應的旋轉角度，即每個元素代表位置t在第i維上的旋轉角度（頻率）
    freqs = torch.outer(t, freqs) # freqs的形狀是 [seq_len, dim // 2]，具體參見上面公式。
    
    # 將上一步的結果寫成復數的形式??^{??????},模是1，幅角是freqs。freqs_cis的大小為(seqlen, dim//2)
    # 假設 freqs = [x, y]，則 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]    
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis

precompute_freqs_cis()函數用如下方式進行調用。

class Transformer(nn.Module):
    def __init__(self, params: ModelArgs):
        super().__init__()
        self.params = params
        self.vocab_size = params.vocab_size
        self.n_layers = params.n_layers

        self.tok_embeddings = VocabParallelEmbedding(
            params.vocab_size, params.dim, init_method=lambda x: x
        )

        self.layers = torch.nn.ModuleList()
        for layer_id in range(params.n_layers):
            self.layers.append(TransformerBlock(layer_id, params))

        self.norm = RMSNorm(params.dim, eps=params.norm_eps)
        self.output = ColumnParallelLinear(
            params.dim, params.vocab_size, bias=False, init_method=lambda x: x
        )

        # 預先計算出來選擇矩陣，乘以2是為了動態擴展
        self.freqs_cis = precompute_freqs_cis(
            params.dim // params.n_heads,
            params.max_seq_len * 2,
            params.rope_theta,
        )

實現

apply_rotary_emb()方法用于將 cos、sin 的旋轉矩陣應用到原始的 query 和 key 向量上，這樣在 Attention 內積時，就會為 query 和 key 引入位置信息。

# 為了匹配q和k，需要對角度進行擴展  
# freqs_cis維度是[seq len, dim/2]
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    # 需要確保形狀和x的形狀匹配，即是(x.shape[1]=seq len, x.shape[-1]=dim/2)
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    # x的第二維和最后一維保留，其他維度置為1
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape) # [1,S,1,head_dim//2] 

def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    """
    作用: 將q,k向量分別與旋轉向量相乘,得到旋轉后的q,k向量q/k_rotated
    輸入: 
    x_q(torch.Tensor): 實際上是權重 W_q * 詞嵌入向量值, 來自上一個線性層的輸出, 形狀為 [batch_size, seq_len, n_heads, head_dim]或者[batch_size, seq_len, dim]
    x_k(torch.Tensor): 實際上是權重 W_k * 詞嵌入向量值, 來自上一個線性層的輸出, 形狀為 [batch_size, seq_len, n_heads, head_dim]或者[batch_size, seq_len, dim]
    freqs_cis (torch.Tensor): 頻率復數張量, 形狀為 [max_seq_len, head_dim]
    輸出: 施加了旋轉編碼后的q和k
    """    

    # 實數域張量轉為復數域張量。將一個大小為n的向量xq_兩兩組合形成復數來計算，需要增加維度，把最后一維變成2，即把最后一維的兩個實數作為一個復數的實部和虛部來構建一個復數。 
    # 計算過程q:[batch_size,atten_heads,seq_len,atten_dim]->q_complex:[b,a_h,s,a_d//2,2]->[b,a_h,s,a_d//2]->[b,a_h,s,a_d//2,2]
    # [:-1]意思是從第一維到倒數第二維；*是為了展開列表；-1, 2表示把最后一維展開成兩維：x/2和2，即最后一維是2； 
    # xq_.shape = [batch_size,atten_heads,seq_len,atten_dim//2,2]，如果不考慮多頭，則是[batch_size, seq_len, dim // 2, 2]
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2)) # 復數形式張量
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2)) # 復數形式張量
    
    # freqs_cis 的形狀必須與 xq 和 xk 相匹配，因此我們需要將 freqs_cis 的形狀從 [max_seq_len, head_dim] 調整為 [1, max_seq_len, 1, head_dim]。即，旋轉矩陣（freqs_cis）的維度在序列長度（seq_len，維度 1）和頭部維度（head_dim，維度 3）上需要與嵌入的維度一致。  
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    
    # 通過復數乘法實現向量旋轉操作，然后將結果轉回實數域。這是幅度不變，角度變換的操作，即把結果恢復成原來的樣子，將第三維之后壓平，也就是(atten_dim//2,2)->(atten_dim)。位置編碼只和向量的序列位置還有向量本身有關，和batch以及注意力頭無關，所以只用關注第二維和第四維
    # xq_out.shape = [batch_size, seq_len, dim]
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk) # 又是實數了

調用

Transformer會調用Transformer層進行RoPE操作。

class Transformer(nn.Module):
    
    @torch.inference_mode()
    def forward(self, tokens: torch.Tensor, start_pos: int):
        _bsz, seqlen = tokens.shape
        h = self.tok_embeddings(tokens)
        self.freqs_cis = self.freqs_cis.to(h.device)
        freqs_cis = self.freqs_cis[start_pos : start_pos + seqlen]

        mask = None
        if seqlen > 1:
            mask = torch.full((seqlen, seqlen), float("-inf"), device=tokens.device)

            mask = torch.triu(mask, diagonal=1)

            # When performing key-value caching, we compute the attention scores
            # only for the new sequence. Thus, the matrix of scores is of size
            # (seqlen, cache_len + seqlen), and the only masked entries are (i, j) for
            # j > cache_len + i, since row i corresponds to token cache_len + i.
            mask = torch.hstack(
                [torch.zeros((seqlen, start_pos), device=tokens.device), mask]
            ).type_as(h)

        for layer in self.layers:
            h = layer(h, start_pos, freqs_cis, mask)
        h = self.norm(h)
        output = self.output(h).float()
        return output

TransformerBlock會直接調用到Attention的forward函數。

class TransformerBlock(nn.Module):
    def __init__(self, layer_id: int, args: ModelArgs):
        super().__init__()
        self.n_heads = args.n_heads
        self.dim = args.dim
        self.head_dim = args.dim // args.n_heads
        self.attention = Attention(args)
        self.feed_forward = FeedForward(
            dim=args.dim,
            hidden_dim=4 * args.dim,
            multiple_of=args.multiple_of,
            ffn_dim_multiplier=args.ffn_dim_multiplier,
        )
        self.layer_id = layer_id
        self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps)
        self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps)

    def forward(
        self,
        x: torch.Tensor,
        start_pos: int,
        freqs_cis: torch.Tensor,
        mask: Optional[torch.Tensor],
    ):
        h = x + self.attention(self.attention_norm(x), start_pos, freqs_cis, mask)
        out = h + self.feed_forward(self.ffn_norm(h))
        return out

Attention會做如下操作。

def forward(
    self,
    x: torch.Tensor,
    start_pos: int,
    freqs_cis: torch.Tensor,
    mask: Optional[torch.Tensor],
):
    bsz, seqlen, _ = x.shape
    xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)

    xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
    xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
    xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)

    # attention 操作之前，應用旋轉位置編碼
    xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)

    self.cache_k = self.cache_k.to(xq)
    self.cache_v = self.cache_v.to(xq)

    self.cache_k[:bsz, start_pos : start_pos + seqlen] = xk
    self.cache_v[:bsz, start_pos : start_pos + seqlen] = xv

    keys = self.cache_k[:bsz, : start_pos + seqlen]
    values = self.cache_v[:bsz, : start_pos + seqlen]

    # repeat k/v heads if n_kv_heads < n_heads
    keys = repeat_kv(
        keys, self.n_rep
    )  # (bs, cache_len + seqlen, n_local_heads, head_dim)
    values = repeat_kv(
        values, self.n_rep
    )  # (bs, cache_len + seqlen, n_local_heads, head_dim)

    # Q/K/V 對應維度為 [bsz, seq_len, num_heads, head_dim]，transpose 將 seq_len 和 num_heads 的維度調換了，得到的 states 維度為 [bsz, num_heads, seq_len, head_dim]。這個變換是為了將 seq_len x head_dim = 4096 x 8 挪到一起，方便后面的 ? 對位相乘。
    xq = xq.transpose(1, 2)  # (bs, n_local_heads, seqlen, head_dim)
    keys = keys.transpose(1, 2)  # (bs, n_local_heads, cache_len + seqlen, head_dim)
    values = values.transpose(
        1, 2
    )  # (bs, n_local_heads, cache_len + seqlen, head_dim)
    scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim)
    if mask is not None:
        scores = scores + mask  # (bs, n_local_heads, seqlen, cache_len + seqlen)
    scores = F.softmax(scores.float(), dim=-1).type_as(xq)
    output = torch.matmul(scores, values)  # (bs, n_local_heads, seqlen, head_dim)
    output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
    return self.wo(output)

4.4 rotate_half

rotate_half是RoPE中經常使用的方法，我們專門來分析下。rotate_half() 的作用是將輸入張量x的一半隱藏維度進行旋轉，即進行語義向量復數化，實現向量乘以虛數i，等價于向量逆時針旋轉90度。

\[f_q(x_m,m) = (W_1x_m)(cos(m\theta) + isin(m\theta)) \]

上述式子繼續推導，合并cos和sin就可以發現，$q_t$旋轉后的結果就是$q_t$乘上cos，再加上$q_t$翻轉維度并取反一維后乘上sin的結果，因此程序里實現叫rotate_half。

\[\begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix} = cos(m\theta)\begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix} + sin(m\theta)\begin{pmatrix} -q_m^{(2)} \\ q_m^{(1)} \end{pmatrix} \]

rotate_half其實有兩種實現方式。我們首先看看其中一種。具體來說，它將輸入張量的后半部分（劃為虛部）取負，然后與前半部分（劃為實部）拼接，從而實現旋轉操作。其流程如下：

?分割張量?：假設輸入張量x的形狀為[batch_size, num_attention_heads, seq_len, head_size]，函數首先將張量x分割成兩部分：x1和x2。x1包含前半部分，x2包含后半部分。
?旋轉操作?：將x2取負，然后將x2與x1拼接在一起。這樣，原始張量的后半部分被旋轉到了前半部分的位置，實現了旋轉效果。
?拼接?：最后，將取負后的x2與x1在最后一個維度上拼接，形成最終的旋轉位置嵌入張量。

具體代碼對應如下。

# 后半部分和前半部分進行了交換，并且將后半部分的符號取反。
# 這個函數很好理解，就是將原始向量從中間劈開分為 A、B 兩份，然后拼接為 [-B, A] 的狀態：比如 [q0,q1,q2,q3,q4,q5,q6,q7] -> [-q4,-q5,-q6,-q7,q0,q1,q2,q3]
def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    # 前64個embedding位置 x=[batch_size, num_heads, seq_len, emb_size] => [batch_size, num_heads, seq_len, emb_size/2]
    x1 = x[..., : x.shape[-1] // 2] 
    # 后64個embedding位置 x=[batch_size, num_heads, seq_len, emb_size] => [batch_size, num_heads, seq_len, emb_size/2]
    x2 = x[..., x.shape[-1] // 2 :] 
    # 后64embedding位置取負號，和前64embedding位置拼接
    return torch.cat((-x2, x1), dim=-1)

def apply_rotary_pos_emb(q, k, cos, sin, position_ids=None, unsqueeze_dim=1):
    cos = cos.unsqueeze(unsqueeze_dim)
    sin = sin.unsqueeze(unsqueeze_dim)
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

將 rotate_half() 代入到 apply_rotary_pos_emb()，以 q=[x1,x2] 為例：

q_embed = [x1, x2] * cos + [-x2, x1] * sin = [x1 * cos - x2 * sin, x2 * cos + x1 * sin]

具體參見下圖。這里的負號，對應和角公式中的負號。計算旋角 $m\theta$ 的過程此處省略。

然而，上面的代碼是HuggingFace的Transformer庫的實現，和RoPE論文公式有些許差異，具體為元素位置排列上的差異，在論文中q0的結果是q0和q1這一對元素經過三角函數變換而成的，但是在實際公式中q0是由q0和$q_{d/2+1}$這一對形成的。

HuggingFace：$[-q_4,-q_5,-q_6,-q_7,q_0,q_1,q_2,q_3]$
論文：$[-q_1, q_0, -q_2, q_3,....q_{n-1}, q_{n-2}]$

具體近似如下。

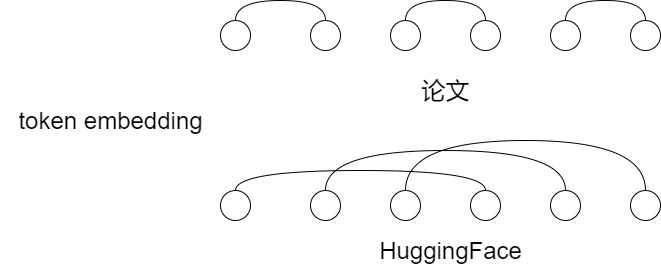
其實，這涉及到兩個對特征維度進行切分的不同的實現。

按照RoPE論文的思路，就是GPT-J style。實現過程中對特征向量的奇偶維度進行rotate_half操作，相鄰兩維度一組（ ⊙ 表示對應位相乘，對 $k_s$ 的操作相同）。

由于對奇偶維度旋轉需要將維度兩兩交錯，實現較為復雜，后來的研究人員提出，直接將特征維度一切二，這種實現方式稱為GPT-NeoX style，實現過程中對特征向量的前后各半進行rotate_half操作。GPT-J style 和 GPT-NeoX style 是等價的，可以互相轉化的：GPT-J style中的奇數維度對應GPT-NeoX style的前一半維度，GPT-J style中的偶數維度對應GPT-NeoX style的后一半維度。將GPT-J style的奇數維度抽出來整體拼接在偶數維度之前，就會得到GPT-NeoX style的結果。

兩種實現方式只是對應的R矩陣不同，最終都可以實現絕對位置實現相對位置編碼的目的。對最終的結果沒有影響。因為RoPE對原始向量的改造本質上是以一對元素為單位經過旋轉矩陣運算，將所有對的結果進行拼接的過程，而到底是選擇連續的元素作為一對，還是其他的挑選方式都是可以的，只要是embedding維度為偶數，且挑選的策略為不重復的一對，最終Attention的內積結果都能感知到相對位置信息，因為Attention滿足內積線性疊加性，至于誰和誰一組進行疊加并不重要。

GPT-J sytle

是和原始論文和博客一樣，使用的相鄰兩個為一組。

\[\begin{bmatrix}q_m^{(1)} \\q_m^{(2)} \\q_m^{(3)} \\q_m^{(4)} \\{\vdots}\\q_m^{(d-1)} \\q_m^{(d)} \\\end{bmatrix} = \begin{bmatrix}cos(m\theta_1) \\cos(m\theta_1) \\cos(m\theta_2) \\cos(m\theta_2) \\{\vdots}\\cos(m\theta_{d/2}) \\cos(m\theta_{d/2}) \\\end{bmatrix} \otimes\begin{bmatrix}q_m^{(1)} \\q_m^{(2)} \\q_m^{(3)} \\q_m^{(4)} \\{\vdots}\\q_m^{(d-1)} \\q_m^{(d)} \\\end{bmatrix}+ \begin{bmatrix}sin(m\theta_1) \\sin(m\theta_1) \\sin(m\theta_2) \\sin(m\theta_2) \\{\vdots}\\sin(m\theta_{d/2}) \\sin(m\theta_{d/2}) \\\end{bmatrix} \otimes\begin{bmatrix}-q_m^{(2)} \\q_m^{(1)} \\-q_m^{(4)} \\q_m^{(3)} \\{\vdots}\\-q_m^{(d)} \\q_m^{(d-1)} \\\end{bmatrix} \]

GPT-NeoX style

不是相鄰兩個元素為一組，而是 ??0 和 $??_{??/2?1}$ 為一組。

\[\begin{bmatrix} q_m^{(1)} \\ q_m^{(2)} \\ {\vdots}\\ q_m^{(d/2)} \\ q_m^{(d/2+1)} \\ {\vdots}\\ q_m^{(d)}\\ \end{bmatrix} = \begin{bmatrix} cos(m\theta_1) \\ cos(m\theta_2) \\ {\vdots}\\ cos(m\theta_{d/2}) \\ cos(m\theta_1) \\ cos(m\theta_2) \\ {\vdots}\\ cos(m\theta_{d/2}) \\ \end{bmatrix} \otimes \begin{bmatrix} q_m^{(1)} \\ q_m^{(2)} \\ {\vdots}\\ q_m^{(d/2)} \\ q_m^{(d/2+1)} \\ {\vdots}\\ q_m^{(d)}\\ \end{bmatrix} + \begin{bmatrix} sin(m\theta_1) \\ sin(m\theta_2) \\ {\vdots}\\ sin(m\theta_{d/2}) \\ sin(m\theta_1) \\ sin(m\theta_2) \\ {\vdots}\\ sin(m\theta_{d/2}) \\ \end{bmatrix} \otimes \begin{bmatrix} -q_m^{(d/2+1)} \\ {\vdots}\\ -q_m^{(d)} \\ q_m^{(1)} \\ q_m^{(2)} \\ {\vdots}\\ q_m^{(d/2)} \\ \end{bmatrix} \]

在FlashAttention的源碼中就實現了GPT-J sytle 和 GPT-NeoX style的RoPE。

https://github.com/Dao-AILab/flash-attention/blob/main/flash_attn/layers/rotary.py

def rotate_half(x, interleaved=False):
    if not interleaved:
        x1, x2 = x.chunk(2, dim=-1)
        return torch.cat((-x2, x1), dim=-1)
    else:
        x1, x2 = x[..., ::2], x[..., 1::2]
        return rearrange(torch.stack((-x2, x1), dim=-1), '... d two -> ... (d two)', two=2)

def apply_rotary_emb_torch(x, cos, sin, interleaved=False):
    """
    x: (batch_size, seqlen, nheads, headdim)
    cos, sin: (seqlen, rotary_dim / 2)
    """
    ro_dim = cos.shape[-1] * 2
    assert ro_dim <= x.shape[-1]
    cos = repeat(cos, 's d -> s 1 (2 d)')
    sin = repeat(sin, 's d -> s 1 (2 d)')
    return torch.cat([x[..., :ro_dim] * cos + rotate_half(x[..., :ro_dim], interleaved) * sin, x[..., ro_dim:]], dim=-1)