探秘Transformer系列之(16)--- 資源占用
探秘Transformer系列之(16)--- 資源占用
文章總表
全部文章列表在這里 探秘Transformer系列之文章列表,后續每發一篇文章,會修改這里。
0x00 概述
對于標準 Transformer 模型,不管是 Encoder Only 的 Bert 系列模型,還是 Decoder Only 的 GPT 系列模型,同配置下參數量和計算量都是類似的。其中的一個關鍵點是:標準 Transformer block(層)輸入、輸出以及中間 Hidden Dim 保持不變,始終是 Token Embedding 的 Hidden Dim,所有的 Transformer Block 都非常規整。
如下圖所示,Encoder主要參數都來自幾個矩陣乘的 Weight 矩陣,其中 d 表示 Token Embedding 的 Hidden Dim,l 表示 Token 數,h 表示 MHA 中的 Head 個數,\(d_{FFN}\) 表示 FFN 層中間升維后的 Dim。其主要幾個模塊的參數量如下。
- MHA:\(W_Q,W_K,W_V\) 的大小都是 d x d。當然這里也可以從 h 個 Head 的角度去看,則每個 Head 的 \(W_Q,W_K,W_V\) 為 d x d/h。在 MHA 的最后還有一個矩陣乘操作,對應的 \(W_{out}\) 維度依然為 d x d。所以MHA處權重矩陣的參數量是 \(3d \times d + d \times d\)。
- FFN:標準 Transformer 的 FFN 中有兩個 Linear 層(先升維再降維),對應權重矩陣 \(W_1\) 和$ W_2$ 的大小都是 \(d_{FFN}\) x d,并且標準的 \(d_{FFN}\) 為 4d,也就是說 FFN 處兩個權重矩陣的參數量為 8d x d。
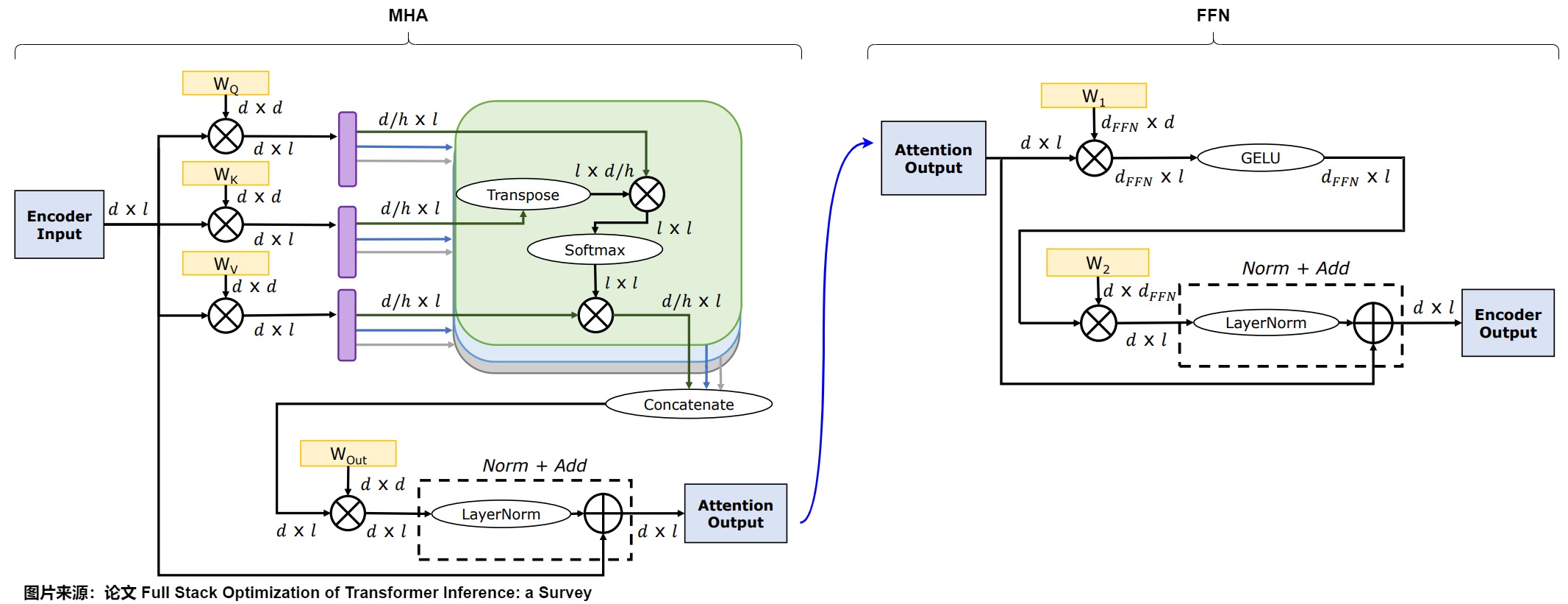
綜上,在標準的 Transformer 模型或者 LLaMA 系列(MHA)中,如果忽略詞表、Embedding、LayerNorm 等參數后,總參數量為(所有 Transformer Block): \(N = n_{layer} \times (n_{mha}+ n_{ffn}) = n_{layer} \times (3d \times d + d \times d + 8d \times d) = 12 \times n_{layer} \times d \times d\)
注意:本章參考了多篇論文,其中對術語的定義各不相同,因為模型結構也不同,所以計算結果與其它資料可能也有差異。
0x01 背景知識
1.1 數據類型
深度學習中用的數值類型命名規范一般為TypeNum,比如Int64、Float32、Double64。
- Type:有Int,Float,Double等。
- Num: 一般是 8,16,32,64,128,表示該類型所占據的比特數目。
常用的數值類型如下圖所示。
| 類型 | 大小(字節數) |
|---|---|
| int4 | 0.5 |
| int8 | 1 |
| int16 | 2 |
| int32 | 4 |
| int64 | 8 |
| float32 | 4 |
| float16 | 2 |
1.2 進制&換算
我們先拋出一個問題:1B參數對應多少G顯存?B和G都代表十億(1000M或1024M),但這是兩個不同的度量維度。
數字進制
B是英美常用的進制單位,比如:
-
1K = 1000,一千;
-
1M = 1000 K,百萬;
-
1B = 1000 M,十億;
可以看出來,這個進制單位以 1000 為進制。以 Qwen-7B 為例,7B 的意思就是 這個 LLM 的 模型參數有 70億 個 參數。
存儲度量
G是計算機內存/磁盤存儲的度量,基本單位是字節,進制是 1024。單位依次是:KB / MB / GB / TB。平時說顯存有多少G/M是說有多少G/M個字節(byte),1個字節=8比特(bit)。舉例來說:有一個1000x1000的 矩陣,float32,那么占用的顯存差不多就是1000x1000x4 Byte = 4MB。
換算
可以看出來,\(1B=10^9 byte \approx 1GB\),1B和1G的大小基本一致,所以我們記作B和G相等。但是,1B模型參數對應多少G內存和參數的精度有關。如果是全精度訓練(fp32),一個參數對應32比特,也就是4個字節,參數換算到顯存的時候要乘4,也就是1B模型參數對應4G顯存。如果是fp16或者bf16就是乘2,1B模型參數對應2G顯存。具體如下表所示。
| 數據類型 | 每1B參數需要占用內存 |
|---|---|
| fp32 | 4G |
| fp16/bf16 | 2G |
| int8 | 1G |
| int4 | 0.5G |
1.3 參數顯存占用
有參數的模塊才會占用顯存。這部份的顯存占用和輸入無關,模型加載完成之后就會占用。一般的卷積層都會占用顯存,而我們經常使用的激活層Relu沒有參數,所以不會占用緩存。
有參數的層
常見的有參數的模塊主要包括:
- 卷積層,通常的conv2d。
- 全連接層,也就是Linear層。
- BatchNorm層。
- Embedding層。
無參數的層
常見的無參數的模塊主要包括:
- 多數的激活層,比如Sigmoid/ReLU。
- 池化層。
- Dropout。
所需資源
我們可以用如下公式來計算神經網絡的顯存占用:顯存占用 = 模型顯存占用 + 輸入輸出相關的顯存
模型顯存占用是模型中與輸入無關的顯存占用,主要包括:
- 模型權重參數。
- 梯度(一般是參數量的1倍)。
- 優化器的動量(和具體優化器密切相關,比如普通SGD沒有動量,momentum-SGD動量與梯度一樣,Adam優化器動量數量是梯度的兩倍)。
輸入輸出相關的顯存占用主要如下:
- batch_size × 每個樣本的顯存占用。
- 每一層的feature map,需要保存激活來進行反向傳播。
因為 反向傳播 / Adam-優化 / Transformer架構 等因素,一般來說,訓練需要的顯存,是 同樣規模推理 的 3-4倍。
1.4 計算量
上文提到Transformer的計算復雜度是 $O(dN^2) $。大 O 表示法關注的是計算量級與輸入規模之間的關系,并不是具體的計算量。具體計算量通常用FLOPs體現。這里簡單列舉一些比較常見的單位:
- FLOPs :floating point of operations的縮寫,是浮點運算次數,一般特指乘加運算次數,理解為計算量,可以用來衡量算法/模型復雜度。
- 一個GFLOPS(gigaFLOPS)= 每秒十億(=10^9)次的浮點運算
- 一個TFLOPS(teraFLOPS) = 每秒一萬億(=10^12)次的浮點運算
0x02 Transformer參數量
以Decoder only模型為例,其主要包括 3 個部分:embedding,decoder,head。最主要部分是decoder,其由若干個decoder-layer組成,每個decoder-layer又分為兩部分:MHA和FFN。我們接下來逐一看看這些模塊的參數量。
2.1 術語
我們先給出本節使用的術語。
| Symbol | Meaning |
|---|---|
| \(d\) | 模型的詞嵌入大小(The model size / hidden state dimension / positional encoding size) |
| \(h\) | 注意力頭個數 |
| \(s\) | 文本總長度(prompt+解碼器輸出) |
| \(b\) | 數據batch size(批大小) |
| \(l\) | Transformer層數 |
| \(v\) | 詞表大小 |
2.2 embedding層
embedding層的輸入形狀是[b,s,v],輸出形狀是[b,s,d],參數量為\(v \times d\)。如果采用可訓練式的位置編碼,會有一些可訓練模型參數,但是其數量比較少。如果采用相對位置編碼,例如RoPE和ALiBi,則不包含可訓練的模型參數。因此我們忽略位置編碼的參數。
2.3 Transformer層
Transformer模型由 l 個相同的層組成,每個層主要分為兩部分:MHA和FFN。因為多頭只是邏輯上切分,物理上沒有增加模塊,因此后續討論中省略多頭(某些論文中如果討論多頭相關,我們會以論文為準),而又因為Decoder only模型使用的是自注意力,因此接下來我們認為 Q、K、V、O的維度相等。
MHA
MHA中包含四個權重矩陣\(W^Q,W^K,W^V,W^O\)以及偏置(某些模型可能沒有偏置)。4個權重矩陣的形狀為 [\(d\),\(d\)],4個偏置的形狀為 [\(d\)],其中 \(d = h \times d_{head}\)。因此,多頭注意力層參數量為:\(4\times (d \times d + d) = 4d^2 + 4d\)。
FFN
FFN包括兩個線性層。
- 第一層將原有的維度映射到4倍原維度大小,即從\(d\)映射到4\(d\)。權重矩陣形狀是[d, 4d],偏置形狀是[4d]。參數量為:\(d\times 4d + 4d\)
- 第二層從4倍維度降維回原始維度。即從4\(d\)映射到\(d\)。權重矩陣形狀是[4d, d],偏置形狀是[d]。參數量為: \(4d\times d + d\)
最終FFN的參數是:\(8d^2 + 5d\)。
LayerNorm
對于Layer Norm來說,其縮放參數 \(\gamma\)與平移參數 \(beta\) 維度都為 \(d\),因此參數量是 \(2 \times d\)。因為MHA和FFN都有LayerNorm,因此總參數量是\(4 \times d\)。
小結
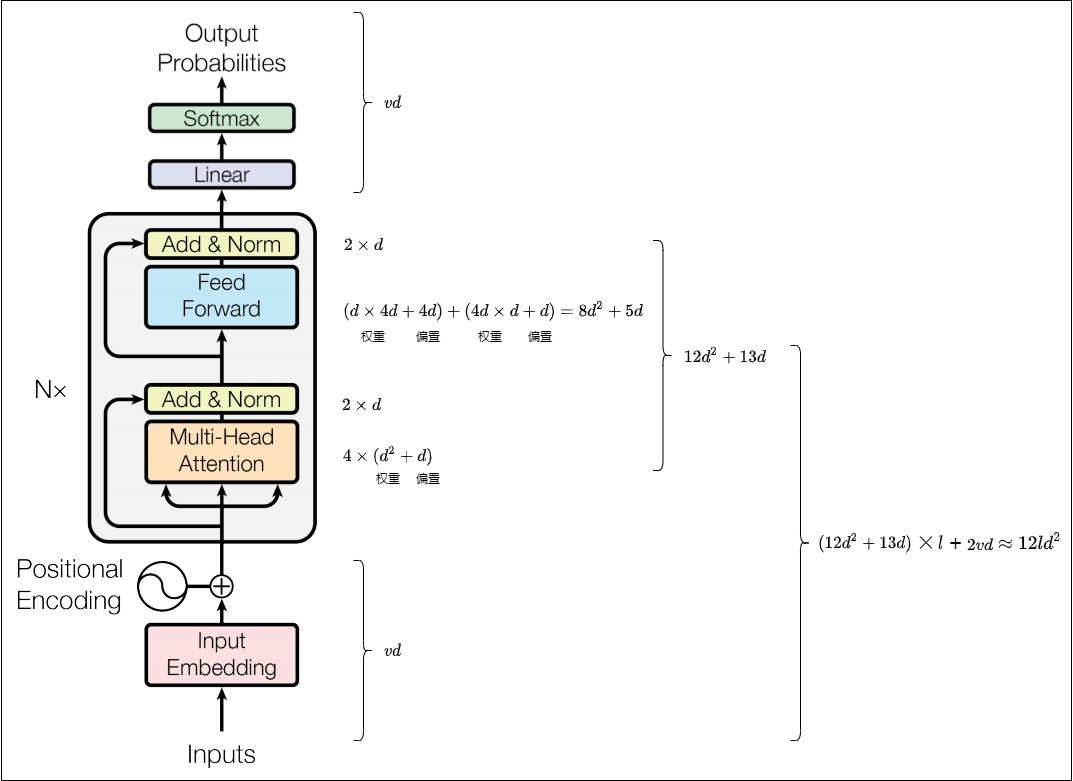
綜上,單個Transformer層的參數量是:\(12d^2 + 13d\)。
2.4 lm_head
lm_head是自然語言處理模型中的一個組件,主要作用是將模型的輸出(通常是經過Transformer編碼器處理后的隱藏狀態)轉換成預測下一個詞的概率分布。
Head與embedding的參數量相同。如果是tied embedding(即,head權重矩陣與詞嵌入矩陣是參數共享的),則兩者公用一個參數。
2.5 最終參數量
最終,l 層transformer模型的可訓練模型參數量為\(l(12d^2 + 13d) + 2vd\) 。當d較大時,可以忽略一次項,模型參數量近似為\(12ld^2\) 。
2.6 LLaMA3
我們再用LLaMA3來看看在工業界落地中的一些特殊之處。
SwiGLU
LLaMA 等模型在 FFN 中會使用 SwiGLU 激活,這也就導致其會額外多了一個權重矩陣。LLaMA論文中提到,使用 SwiGLU 后將 dFFN 從 4d 降低到了 8d/3。這樣 3 個權重矩陣的參數量還是 8d,總的參數量依然可以使用 \(12 \times n_{layer}\times d\times d\)來 預估。
GQA
前面公式對應的是 MHA(Multi Head Attention),這也是 LLaMA-1 系列模型的標準實現。不過,LLaMA-2 的 30B 和 70B 模型以及 LLaMA-3 的全部模型都開始使用 GQA(Grouped Query Attention)。使用 GQA 時,多個 注意力頭會共享一個 Key 和 Value,此時\(W^K,W^V\)的大小會變為 d x d/g,其中 g 表示每 g 個 Head 共享相同的 Key 和 Value。LLaMA 2論文提到,為了保持使用 GQA 和使用 MHA 的總參數量保持不變,對于 GQA 模型,LLaMA 2會將 FFN Dim 維度乘以 1.3。
經過上述調整之后,LLaMA 3 不再是標準的 Transformer Block,此時使用 \(N=12d^2\) 來預估參數量已經不太準確。但依舊可以將其按照(\(W^Q,W^O\))(\(W^K,W^V\)),$W_{FFN} $和 \(W_{emb}\) 4 個部分來統計。比如,對于 LLaMA 3 模型,我們可以按照下述方式估計其參數量:\(N = n_{layer} \times (2d^2 + 2d \times d \times kv/h + 3d \times d_{FFN})+2 \times Vocab \times d\)。
0x03 Transformer顯存占用
3.1 訓練
在訓練神經網絡的過程中,占用顯存的大頭主要分為四部分:模型參數、前向計算過程中產生的中間激活、后向傳播計算得到的梯度、優化器狀態。后面幾個的數量可能比模型參數更大,因此對模型內存的需求量也更大。
訓練大模型時經常采用AdamW優化器,并用混合精度訓練來加速訓練,我們基于這個前提分析顯存占用。在一次訓練迭代中,每個可訓練模型參數需要保存這個參數本身、參數對應的梯度以及優化器對這個參數的兩個狀態(Adam中的一階動量和二階動量)。設模型參數量為 Φ ,那么梯度的元素數量為 Φ ,AdamW優化器的元素數量為 2Φ 。在混合精度訓練中,會使用半精度來進行前向與反向傳播計算,優化器更新模型參數時會使用單精度進行狀態、梯度以及參數的更新。所以一個參數在訓練時占用的空間為正向傳播時使用半精度和反向傳播時使用單精度所占用的空間之和。因此,使用AdamW優化器和混合精度訓練來訓練時候,針對每個可訓練模型參數,訓練階段會占用 (2+4)+(2+4)+(4+4)=20bytes 。參數量為 Φ 的大模型,模型參數、梯度和優化器狀態占用的顯存大小為 20Φ bytes 。

模型參數、梯度與優化器狀態的空間占用已經計算完了,接下來就是在前向傳播時的中間激活部分的空間占用。我們將在后續小節進行分析。
模型的訓練包含 Forward 和 Backward 過程。Backward 過程實際上包含兩部分,一部分是對輸入的梯度(鏈式法則),一部分是對權重的梯度。其實這兩部分主要的計算量都是矩陣乘法,并且大小與 Forward中的大小一致,因此往往會直接近似 Backward 的計算量為 Forward 的 2 倍。
3.2 推理
推理階段通常比訓練階段要求更低的顯存,因為不涉及梯度計算和參數更新等大量計算。少了梯度、優化器狀態和中間激活,模型推理階段占用的顯存要遠小于訓練階段。
如果使用KV cache來加速推理過程,KV cache也需要占用顯存,KV cache占用的顯存下文會詳細介紹,此處忽略。此外,輸入數據也需要放到GPU上,還有一些中間結果(推理過程中的中間結果用完會盡快釋放掉),不過這部分占用的顯存是很小的,也可以忽略。
最終,推理階段的主要顯存占用為模型的參數,模型參數內存 = n × p。n是模型參數總量,p是每個參數占用的字節數。如果使用半精度進行推理的話,一個參數占用2bytes空間,那么模型在推理時的顯存占用約為:
以下是計算模型推理時所需顯存的一些關鍵因素:
-
模型結構: 模型的結構包括層數、每層的神經元數量、卷積核大小等。較深的模型通常需要更多的顯存,因為每一層都會產生中間計算結果。
-
輸入數據: 推理時所需的顯存與輸入數據的尺寸有關。更大尺寸的輸入數據會占用更多的顯存。
-
批處理大小 BatchSize: 批處理大小是指一次推理中處理的樣本數量。較大的批處理大小可能會增加顯存使用,因為需要同時存儲多個樣本的計算結果。
-
數據類型: 使用的數據類型(如單精度浮點數、半精度浮點數)也會影響顯存需求。較低精度的數據類型通常會減少顯存需求。
-
中間計算: 在模型的推理過程中,可能會產生一些中間計算結果,這些中間結果也會占用一定的顯存。
3.3 激活
訓練中的激活(activations)指的是:前向傳播過程中計算得到的,并在反向傳播過程中需要用到的所有張量。這里的激活不包含模型參數和優化器狀態,但包含了dropout操作需要用到的mask矩陣。
在一次訓練迭代中,模型參數(或梯度)占用的顯存大小只與模型參數量和參數數據類型有關,與輸入數據的大小是沒有關系的。優化器狀態占用的顯存大小也是一樣,與優化器類型有關,與模型參數量有關,但與輸入數據的大小無關。而中間激活值與輸入數據的大小(批次大小 b 和序列長度 s )是成正相關的,隨著批次大小 b 和序列長度 s 的增大,中間激活占用的顯存會同步增大。當我們訓練神經網絡遇到顯存不足OOM(Out Of Memory)問題時,通常會嘗試減小批次大小來避免顯存不足的問題,這種方式減少的其實是中間激活占用的顯存,而不是模型參數、梯度和優化器的顯存。
我們接下來以論文“Reducing Activation Recomputation in Large Transformer Models”中的Megatron為例,分步來計算一下中間激活的顯存占用。
架構
下圖就是Megatron的架構。
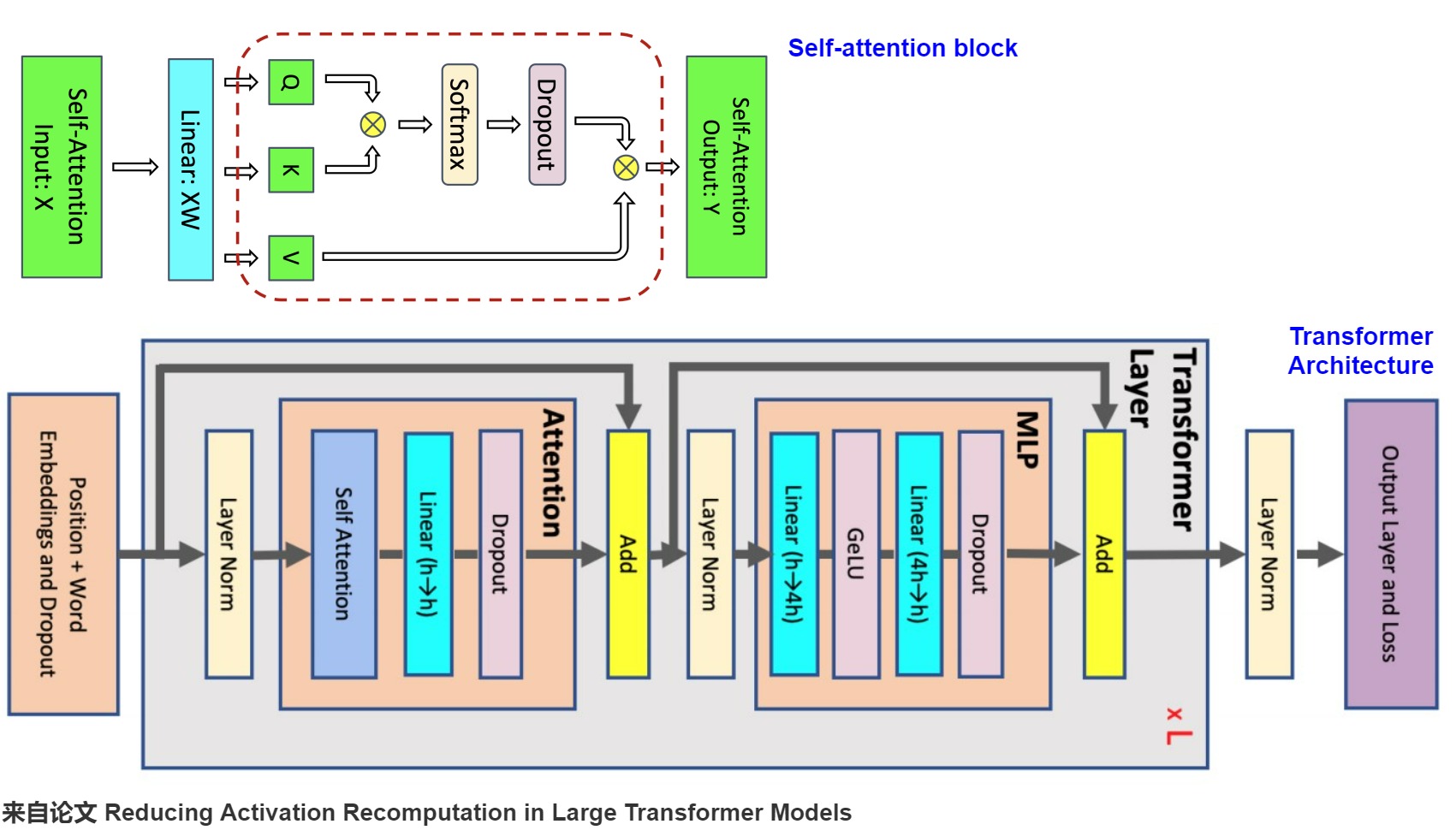
其代碼如下所示。其中指定了core_attention就是submodules.core_attention,linear_proj就是submodules.linear_proj。
class Attention(MegatronModule, ABC):
"""Attention layer abstract class.
This layer only contains common modules required for the "self attn" and
"cross attn" specializations.
"""
def __init__(
self,
config: TransformerConfig,
submodules: Union[SelfAttentionSubmodules, CrossAttentionSubmodules],
layer_number: int,
attn_mask_type: AttnMaskType,
attention_type: str,
):
super().__init__(config=config)
self.config = config
self.layer_number = layer_number
self.attn_mask_type = attn_mask_type
self.attention_type = attention_type
# For normal attention without groups, num_query_groups == num_attention_heads,
# so these two will be the same
self.query_projection_size = self.config.kv_channels * self.config.num_attention_heads
self.kv_projection_size = self.config.kv_channels * self.config.num_query_groups
# Per attention head and per partition values.
world_size = parallel_state.get_tensor_model_parallel_world_size()
self.hidden_size_per_attention_head = divide(
self.query_projection_size, self.config.num_attention_heads
)
self.num_attention_heads_per_partition = divide(self.config.num_attention_heads, world_size)
self.num_query_groups_per_partition = divide(self.config.num_query_groups, world_size)
self.core_attention = build_module(
submodules.core_attention,
config=self.config,
layer_number=self.layer_number,
attn_mask_type=self.attn_mask_type,
attention_type=self.attention_type,
)
self.checkpoint_core_attention = self.config.recompute_granularity == 'selective'
# Output.
self.linear_proj = build_module(
submodules.linear_proj,
self.query_projection_size,
self.config.hidden_size,
config=self.config,
init_method=self.config.output_layer_init_method,
bias=self.config.add_bias_linear,
input_is_parallel=True,
skip_bias_add=True,
is_expert=False,
tp_comm_buffer_name='proj',
)
def forward(
self,
hidden_states,
attention_mask,
key_value_states=None,
inference_params=None,
rotary_pos_emb=None,
packed_seq_params=None,
):
# hidden_states: [sq, b, h]
# For self attention we just duplicate the rotary_pos_emb if it isn't already
if rotary_pos_emb is not None and not isinstance(rotary_pos_emb, tuple):
rotary_pos_emb = (rotary_pos_emb,) * 2
# =====================
# Query, Key, and Value
# =====================
# Get the query, key and value tensors based on the type of attention -
# self or cross attn.
query, key, value = self.get_query_key_value_tensors(hidden_states, key_value_states)
# ===================================================
# Adjust key, value, and rotary_pos_emb for inference
# ===================================================
key, value, rotary_pos_emb, attn_mask_type = self._adjust_key_value_for_inference(
inference_params, key, value, rotary_pos_emb
)
if packed_seq_params is not None:
query = query.squeeze(1)
key = key.squeeze(1)
value = value.squeeze(1)
# ================================================
# relative positional embedding (rotary embedding)
# ================================================
if rotary_pos_emb is not None:
q_pos_emb, k_pos_emb = rotary_pos_emb
if packed_seq_params is not None:
cu_seqlens_q = packed_seq_params.cu_seqlens_q
cu_seqlens_kv = packed_seq_params.cu_seqlens_kv
else:
cu_seqlens_q = cu_seqlens_kv = None
query = apply_rotary_pos_emb(
query, q_pos_emb, config=self.config, cu_seqlens=cu_seqlens_q
)
key = apply_rotary_pos_emb(key, k_pos_emb, config=self.config, cu_seqlens=cu_seqlens_kv)
# TODO, can apply positional embedding to value_layer so it has
# absolute positional embedding.
# otherwise, only relative positional embedding takes effect
# value_layer = apply_rotary_pos_emb(value_layer, k_pos_emb)
# ==================================
# core attention computation
# ==================================
if self.checkpoint_core_attention and self.training:
core_attn_out = self._checkpointed_attention_forward(
query,
key,
value,
attention_mask,
attn_mask_type=attn_mask_type,
packed_seq_params=packed_seq_params,
)
else:
core_attn_out = self.core_attention(
query,
key,
value,
attention_mask,
attn_mask_type=attn_mask_type,
packed_seq_params=packed_seq_params,
)
if packed_seq_params is not None:
# reshape to same output shape as unpacked case
# (t, np, hn) -> (t, b=1, h=np*hn)
# t is the pack size = sum (sq_i)
# note that batch is a dummy dimension in the packed case
core_attn_out = core_attn_out.reshape(core_attn_out.size(0), 1, -1)
# =================
# Output. [sq, b, h]
# =================
output, bias = self.linear_proj(core_attn_out) # 這里是線性層
return output, bias
最終注意力代碼是:
class DotProductAttention(MegatronModule):
"""
Region where selective activation recomputation is applied.
This region is memory intensive but less compute intensive which
makes activation checkpointing more efficient for LLMs (20B+).
See Reducing Activation Recomputation in Large Transformer Models:
https://arxiv.org/abs/2205.05198 for more details.
We use the following notation:
h: hidden size
n: number of attention heads
p: number of tensor model parallel partitions
b: batch size
s: sequence length
"""
def __init__(
self,
config: TransformerConfig,
layer_number: int,
attn_mask_type: AttnMaskType,
attention_type: str,
attention_dropout: float = None,
):
super().__init__(config=config)
self.config: TransformerConfig = config
assert (
self.config.context_parallel_size == 1
), "Context parallelism is only supported by TEDotProductAttention!"
assert (
self.config.window_size is None
), "Sliding Window Attention is only supported by TEDotProductAttention!"
self.layer_number = max(1, layer_number)
self.attn_mask_type = attn_mask_type
self.attention_type = attention_type # unused for now
projection_size = self.config.kv_channels * self.config.num_attention_heads
# Per attention head and per partition values.
world_size = parallel_state.get_tensor_model_parallel_world_size()
self.hidden_size_per_partition = divide(projection_size, world_size)
self.hidden_size_per_attention_head = divide(projection_size, config.num_attention_heads)
self.num_attention_heads_per_partition = divide(self.config.num_attention_heads, world_size)
self.num_query_groups_per_partition = divide(self.config.num_query_groups, world_size)
coeff = None
self.norm_factor = math.sqrt(self.hidden_size_per_attention_head)
if self.config.apply_query_key_layer_scaling:
coeff = self.layer_number
self.norm_factor *= coeff
self.scale_mask_softmax = FusedScaleMaskSoftmax(
input_in_fp16=self.config.fp16,
input_in_bf16=self.config.bf16,
attn_mask_type=self.attn_mask_type,
scaled_masked_softmax_fusion=self.config.masked_softmax_fusion,
mask_func=attention_mask_func,
softmax_in_fp32=self.config.attention_softmax_in_fp32,
scale=coeff,
)
# Dropout. Note that for a single iteration, this layer will generate
# different outputs on different number of parallel partitions but
# on average it should not be partition dependent.
self.attention_dropout = torch.nn.Dropout(
self.config.attention_dropout if attention_dropout is None else attention_dropout
)
def forward(
self,
query: Tensor,
key: Tensor,
value: Tensor,
attention_mask: Tensor,
attn_mask_type: AttnMaskType = None,
packed_seq_params: Optional[PackedSeqParams] = None,
):
assert packed_seq_params is None, (
"Packed sequence is not supported by DotProductAttention."
"Please use TEDotProductAttention instead."
)
# ===================================
# Raw attention scores. [b, n/p, s, s]
# ===================================
# expand the key and value [sk, b, ng, hn] -> [sk, b, np, hn]
# This is a noop for normal attention where ng == np. When using group query attention this
# creates a view that has the keys and values virtually repeated along their dimension to
# match the number of queries.
# attn_mask_type is not used.
if self.num_attention_heads_per_partition // self.num_query_groups_per_partition > 1:
key = key.repeat_interleave(
self.num_attention_heads_per_partition // self.num_query_groups_per_partition, dim=2
)
value = value.repeat_interleave(
self.num_attention_heads_per_partition // self.num_query_groups_per_partition, dim=2
)
# [b, np, sq, sk]
output_size = (query.size(1), query.size(2), query.size(0), key.size(0))
# [sq, b, np, hn] -> [sq, b * np, hn]
# This will be a simple view when doing normal attention, but in group query attention
# the key and value tensors are repeated to match the queries so you can't use
# simple strides to extract the queries.
query = query.reshape(output_size[2], output_size[0] * output_size[1], -1)
# [sk, b, np, hn] -> [sk, b * np, hn]
key = key.view(output_size[3], output_size[0] * output_size[1], -1)
# preallocting input tensor: [b * np, sq, sk]
matmul_input_buffer = parallel_state.get_global_memory_buffer().get_tensor(
(output_size[0] * output_size[1], output_size[2], output_size[3]), query.dtype, "mpu"
)
# Raw attention scores. [b * np, sq, sk]
matmul_result = torch.baddbmm(
matmul_input_buffer,
query.transpose(0, 1), # [b * np, sq, hn]
key.transpose(0, 1).transpose(1, 2), # [b * np, hn, sk]
beta=0.0,
alpha=(1.0 / self.norm_factor),
)
# change view to [b, np, sq, sk]
attention_scores = matmul_result.view(*output_size)
# ===========================
# Attention probs and dropout ----------------- 在這里有softmax的dropout
# ===========================
# attention scores and attention mask [b, np, sq, sk]
attention_probs: Tensor = self.scale_mask_softmax(attention_scores, attention_mask)
# This is actually dropping out entire tokens to attend to, which might
# seem a bit unusual, but is taken from the original Transformer paper.
if not self.config.sequence_parallel:
with tensor_parallel.get_cuda_rng_tracker().fork():
attention_probs = self.attention_dropout(attention_probs)
else:
attention_probs = self.attention_dropout(attention_probs)
# =========================
# Context layer. [sq, b, hp]
# =========================
# value -> context layer.
# [sk, b, np, hn] --> [b, np, sq, hn]
# context layer shape: [b, np, sq, hn]
output_size = (value.size(1), value.size(2), query.size(0), value.size(3))
# change view [sk, b * np, hn]
value = value.view(value.size(0), output_size[0] * output_size[1], -1)
# change view [b * np, sq, sk]
attention_probs = attention_probs.view(output_size[0] * output_size[1], output_size[2], -1)
# matmul: [b * np, sq, hn]
context = torch.bmm(attention_probs, value.transpose(0, 1))
# change view [b, np, sq, hn]
context = context.view(*output_size)
# [b, np, sq, hn] --> [sq, b, np, hn]
context = context.permute(2, 0, 1, 3).contiguous()
# [sq, b, np, hn] --> [sq, b, hp]
new_context_shape = context.size()[:-2] + (self.hidden_size_per_partition,)
context = context.view(*new_context_shape)
return context
術語說明
我們首先看看論文中的術語。
- a是 transformer 模型中注意力頭 (attention heads) 的個數。
- b為每個GPU的batch size;
- h是每個 transformer 層的隱含維度
- L為Transformer的層數;
- p為流水線并行的并行機器數;
- s為句子的長度,即序列中詞元的個數
- t為張量并行的并行機器數;
- v為詞典的大小;
我們假設激活數據類型為 fp16。
數據量
每個Transformer層由一個注意力和一個MLP構成,中間還有兩個LayerNorm。下面,我們來推導存儲每個元素的激活所需的內存。在下面的分析中需要注意幾點:
- 單位是bytes,而不是元素個數。
- 大模型在訓練過程中通常采用混合精度訓練,因此,在分析中間激活的顯存占用時,我們假設中間激活值是以float16或bfloat16數據格式來保存的,每個元素占了2個bytes。唯一例外的是,dropout操作的mask矩陣,每個元素只占1個bytes。
- 在分析中間激活的顯存占用時,只考慮激活占用顯存的大頭,忽略掉一些小的buffers。比如,對于layer normalization,計算梯度時需要用到層的輸入、輸入的均值 和方差 。輸入包含了 bs? 個元素,而輸入的均值和方差分別包含了 bs 個元素。由于 ? 通常是比較大的(千數量級),有 bs??bs 。因此,對于layer normalization,中間激活近似估計為 bs? ,而不是 bs?+2bs 。
注意力塊
注意力塊的激活如下。
| 保存內容 | 操作 | 激活大小 | 所屬模塊 | 保存原因 |
|---|---|---|---|---|
| X | Query (Q), Key (K), Value (V) 相關的矩陣乘法 | 2bsh | self attention | 保存Q/K/V共同的輸入X |
| Q、K | \(QK^T\) 矩陣乘法 | 4bsh | self attention | 保存 \(QK^T\) 矩陣乘法的輸入 |
| \(QK^T\) | Softmax | \(2 bas^2\) | self attention | 保存Softmax 的輸入,形狀是 [b, a, s, s] |
| Mask | Softmax dropout | \(bas^2\) | self attention | 保存Softmax dropout 的mask,形狀和\(QK^T\)相同,一個byte即可 |
| V | 注意力計算 | 2bsh | self attention | 保存\(softmax(\frac{QK^T}{\sqrt d})V\)的輸入V |
| Score | 注意力計算 | \(2 bas^2\) | self attention | 保存\(softmax(\frac{QK^T}{\sqrt d})V\)的輸入\(softmax(\frac{QK^T}{\sqrt d})\) |
| Linear | 計算輸出映射 | 2bsh | linear projection | 輸入映射需要保存其輸入 |
| Mask | attention dropout | bsh | attention dropout | 24內dropout需要保存mask矩陣,一個byte即可 |
| 總計 | \(11bsh + 5bas^2\) |
我們回顧一下MHA的計算邏輯如下:
上述表格中的各個計算解釋如下。
-
輸入X。X被用來計算Q、K、V。X的形狀是[b,s,h],元素個數是bsh,FP16占據兩個byte,所以顯存為2bsh。
-
中間激活 Q、K。這兩者被用來計算\(QK^T\)。Q、K的形狀都是[b,s,h],元素類型是FP16,兩者占據顯存大小是4bsh。
-
中間激活\(QK^T\)。\(QK^T\)是softmax的輸入,元素類型是FP16,占據顯存大小是\(2bs^2a\)。a是注意力頭數目。
Q的形狀是[b,a,s,h/a],\(K^T\)形狀是[b,a,h/a,s]。\(QK^T\)形狀是[b,a,s,s]。計算公式如下:\(score=softmax(QK^T/\sqrt d_k)\)
-
dropout用到的mask矩陣。softmax操作完成之后,會進行dropout操作。需要保存一個mask矩陣,mask矩陣的形狀與\(QK^T\)相同,類型是int,占據顯存是\(bs^2a\)。
-
score權重矩陣和V。這兩者被用來計算Z。
- softmax和dropout結束之后,得到了score權重矩陣,大小是2\(bs^2a\)。
- V的形狀都是[b,s,h],元素類型是FP16,占據顯存大小是2bsh。
-
計算輸出映射以及一個dropout操作。輸入映射需要保存其輸入,大小為 2bsh ;dropout需要保存mask矩陣,大小為 bsh 。二者占用顯存大小合計為 3bsh。
因此,將上述中間激活相加得到self-attention塊的中間激活占用顯存大小為 \(11bsh + 5bas^2\)
MLP
FFN的兩個線性層以2sbh和8sbh的大小存儲它們的輸入。GeLU非線性還需要其大小為8sbh的輸入用于反向傳播。最后,dropout將其掩碼存儲為sbh大小。總的來說,MLP塊需要19sbh字節的存儲空間。
| 模塊 | 動作 | 激活大小 |
|---|---|---|
| linear 1 | 第一個線性層需要保存其輸入 | 2 bsh |
| GeLU | 激活函數需要保存其輸入 | 8 bsh |
| linear 2 | 第二個線性層需要保存其輸入 | 8 bsh |
| dropout | 最后有一個dropout操作,需要保存mask矩陣 | bsh |
| 總計 | 19sbh |
我們回顧一下MHA的計算邏輯如下:
上述的各個計算如下。
-
第一個線性層需要保存其輸入,占用顯存大小為 2bsh 。
-
激活函數需要保存其輸入,占用顯存大小為 8bsh 。
-
第二個線性層需要保存其輸入,占用顯存大小為 8bsh。
-
最后有一個dropout操作,需要保存mask矩陣,占用顯存大小為bsh 。
因此,對于MLP塊,需要保存的中間激活值為 19bsh 。
LayerNorm
另外,self-attention塊和MLP塊分別對應了一個layer normalization。每個layer norm需要保存其輸入,大小為 2sbh。2個layer norm需要保存的中間激活為 4sbh。
總結
綜上,每個transformer層需要保存的中間激活占用顯存大小為\(34bsh + 5bas^2\)。對于 l 層transformer模型,還有embedding層、最后的LayerNorm和輸出層。當隱藏維度 ? 比較大,層數l 較深時,這部分的中間激活是很少的,可以忽略。因此,對于 l 層transformer模型,中間激活占用的顯存大小可以近似為 \((34bsh + 5bas^2)\times l\)。
作為對比,下圖是哈佛代碼中解碼器對應的激活情況,里面有各個張量的形狀。
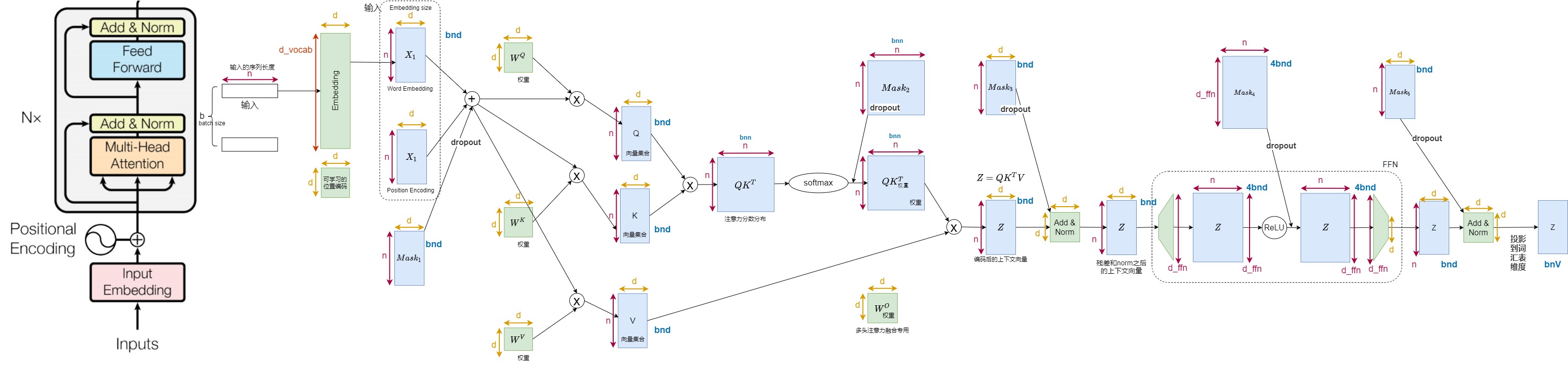
有研究指出,13B 的 LLM 推理時,每個 token 大約消耗 1MB 的顯存。
另外,對于計算量和顯存量,我們也很容易見到不同的計算結果,這基本是因為計算原則不同,比如:梯度可能是FP16存儲,參數可能是FP32存儲,是否采用重計算等等。
并行
實際工作中,LLM總是以各種并行策略進行訓練或者推理,激活又各不相同。下圖是各種并行策略下,每個Transfromer層的激活大小(bytes)。
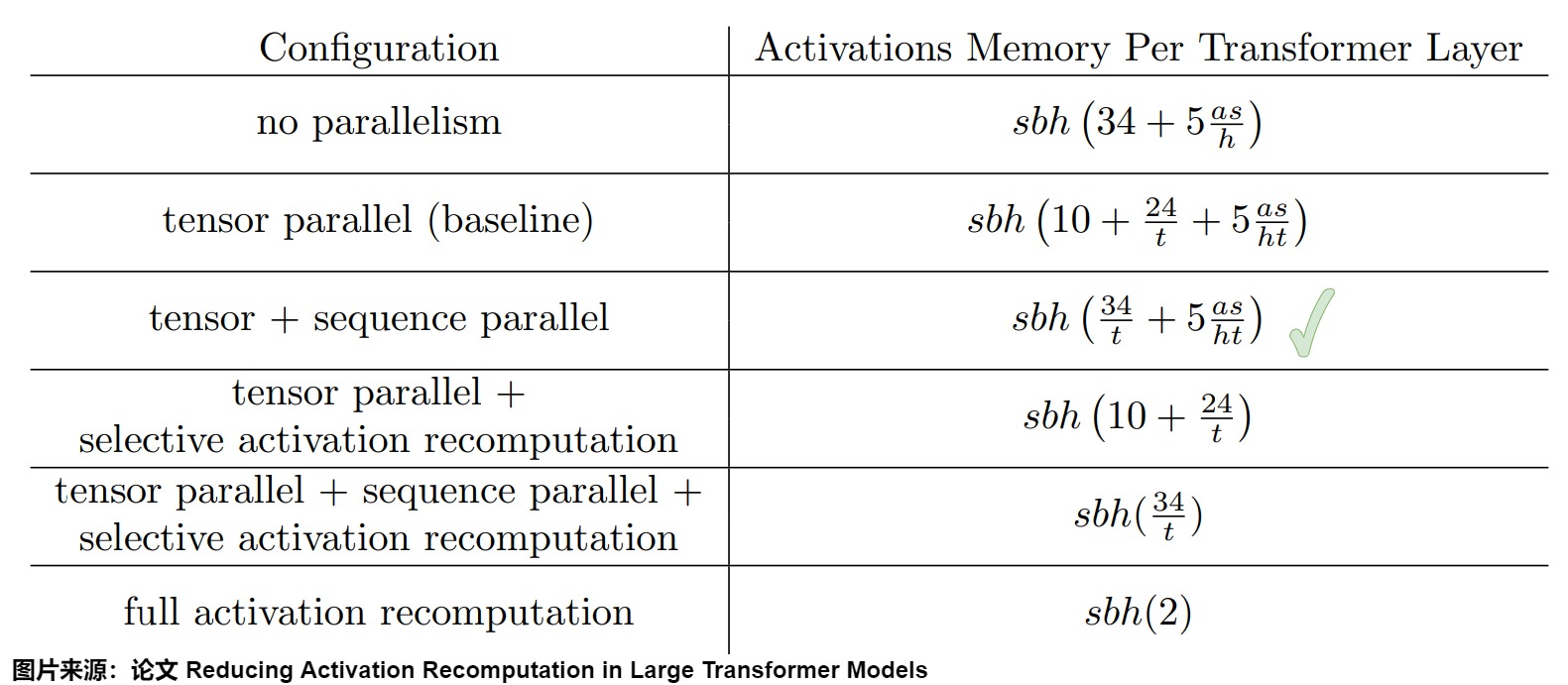
我們再來看看并行策略下,對于 l 層transformer模型,embedding層、最后的LayerNorm和輸出層所輸出的激活。
-
位置和單詞嵌入不需要為反向傳播存儲任何大量的激活。但是dropout需要存儲。嵌入層中的dropout也會沿著序列維度進行并行(sequence parallelism)。因此,它的存儲將占據sbhp/t大小。請注意,系數p是因為流水線并行中,我們需要存儲p個microbatches(微批次)。
-
輸出層之前的Layer Norm也使用序列并行(sequence parallelism),因此需要2sbh/t存儲。輸出層會投影到詞匯表維度,這需要存儲大小為2sbh/t的輸入。最后,交叉熵損失(cross entropy loss)需要存儲以32位浮點進行計算的logit,因此需要4sbv/t的存儲空間。請注意,由于我們只考慮流水線第一階段的激活,因此上述激活,即總共4sbh/t(1+v/h),僅在沒有流水線并行(p=1)的情況下才會考慮在內。
-
輸入嵌入、最后一個LayerNorm和輸出層而產生的總共額外內存為:
![]()
0x04 Transformer計算量
廣義上,當處理一個 token 時,模型執行兩種類型的操作:注意力計算和矩陣-向量乘法。
- MHA(紅框):\(W_Q\),\(W_K\),\(W_V\) 對應的計算量都為 2 x (d x d x l),其中 2 表示一個乘法和一個加法。
- MHA(藍框):\(W_{out}\) 對應的計算量為 2 x (d x d x l)。
- MHA Attention(綠色圓角方塊):計算量是2 x (l x d/h x l + l x d/h x l) x h = 4 x d x l x l。如果是 Decoder(LLM),由于 Causal Mask 的存在,此處的計算量應該減半,也就是 2 x d x l x l。
- FFN(綠框):W1 和 W2 對應的計算量為 $2 \times (d_{FFN} \times d \times l) $和 \(2\times (d \times _{FFN} \times l)\)。LLaMA 的 SwiGLU 類似。
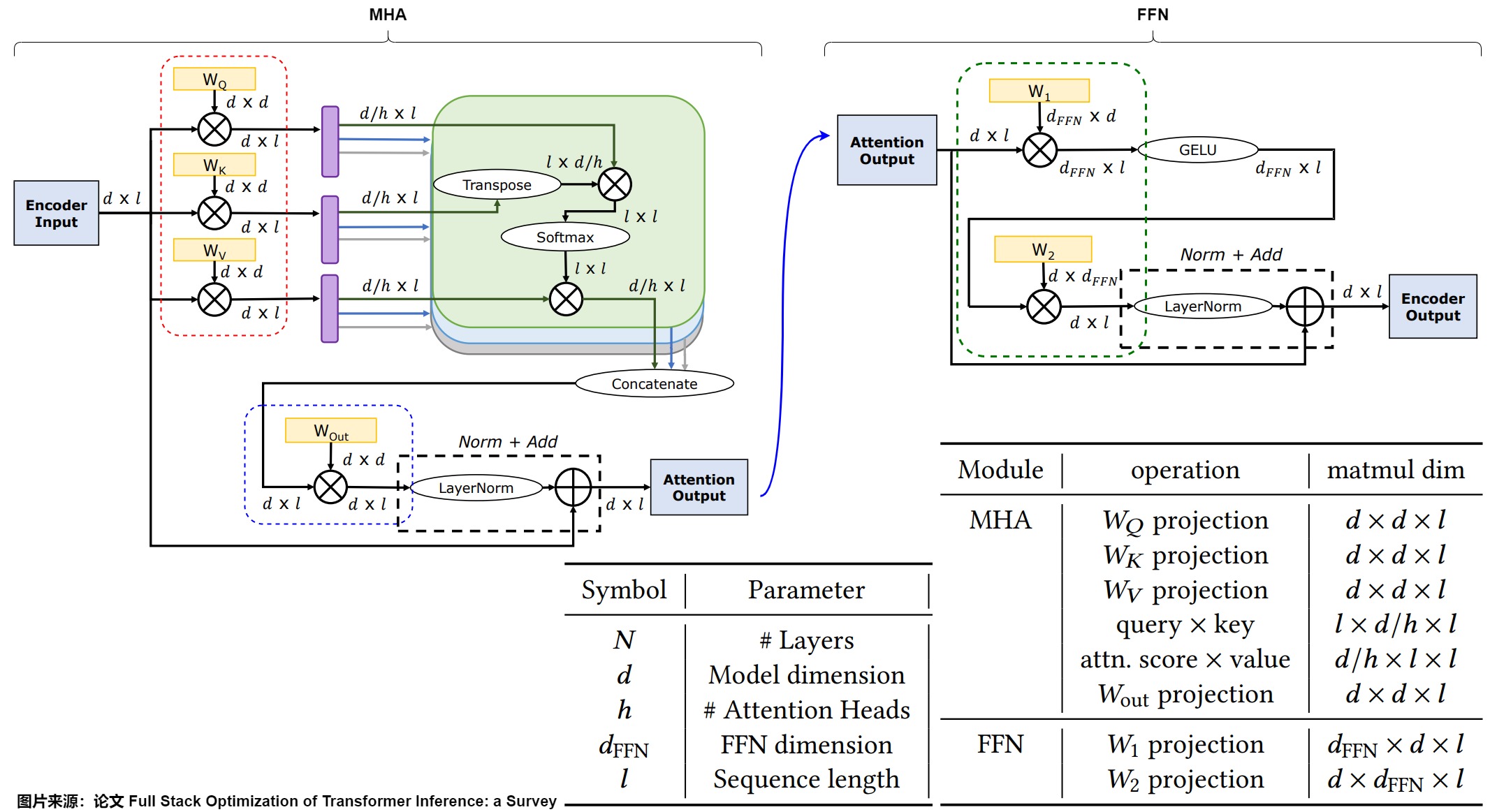
我們后續也按照megatron論文的術語進行分析,忽略多頭,即頭數為1。
4.1 矩陣乘法
在decode階段,則主要是矩陣-向量乘法。一個大矩陣乘以一個向量,得到另一個向量。
因此我們首先看看矩陣乘法的計算特點。人們定義算術強度(Arithmetic Intensity)為FLOP : I/O。當將一個\(N\times M\)矩陣與一個\(M\times P\)矩陣相乘以產生一個\(N\times P\)矩陣時,矩陣-向量乘法對每個矩陣元素執行一次乘加運算。FLOP(浮點操作,即計算量)為\(2M\times P \times N\),I/O(從GPU內存傳輸到GPU寄存器的數據傳輸)計數為\(M\times N + M \times P + N \times P\) 。
4.2 前向傳播計算量
Embedding
Embedding操作的輸入是[b,s]。在實際計算的矩陣-向量乘法中,embedding操作并不會使用這整個embedding大矩陣,每個 token 只讀取這個矩陣中的一行,就是查表操作。最終輸出張量變成[b,s,h]。因此計算量相對很小,后面我們將忽略這部分。
MHA
在標準的Transformer計算中,假設\(Q,K,V \in R^{s\times h}\),則計算如下(省略了\(\sqrt h\))。N是序列長度,h是維度。
- 獲取注意力分數 :$ S = QK^T \in R^{s \times s}$。對每個 query 向量,都計算它與所有位置的 key 向量之間的點積。
- 獲取注意力權重:$ P = softmax(S) \in R^{s \times s}$。即歸一化得到的一組標量。
- 計算最終輸出:\(O = PV \in R^{s \times h}\)。使用注意力權重,對所有之前的 value 向量進行加權求和來計算一個向量o。
因此我們可以知道,計算S和O是主要的部分。
計算Q、K、V
單個矩陣乘法是:[b, s, h] x [h, h] 得到 [b, s, h],因此其計算量是\(2bsh^2\)。三個矩陣的計算量是 \(3 \times 2 bsh^2 = 6 bsh^2\)
QK^T
在這個階段,針對每個query元素,注意力計算會對每個鍵元素執行一次乘加操作以計算點積。總體操作為:[b, s, h] x [b, h, s] = [b, s, s] ,其計算量是:\(2bs^2h\)
softmax 函數不會改變輸入矩陣的維度,即 [??,??]→[s,s],native softmax 的 FLOPs 為 (4/5)sh。因為比較小,所以可以忽略。縮放 \(\sqrt d\) 是逐元素操作,也可以忽略。
乘以V
乘以V(attention over values)階段會對每個值元素執行一次乘加操作以計算加權和。總體操作為: [b, s, s] x [b, s, h] = [b, s, h],計算量是:\(2bs^2h\)。
線性映射
線性映射(post-attention linear projection)這一步是與\(W^O\)的多頭融合,矩陣乘法的輸入和輸出形狀為 [b,s,?]×[?,?]→[b,s,?] 。計算量為 \(2bs?^2\) 。
MLP
這一步涉及兩個操作。
-
第一個線性層,矩陣乘法的輸入和輸出形狀為 [b,s,?]×[?,4?]→[b,s,4?] 。計算量為 \(8bs?^2\) 。
-
第二個線性層,矩陣乘法的輸入和輸出形狀為 [b,s,4?]×[4?,?]→[b,s,?] 。計算量為 \(8bs?^2\) 。
LayerNorm
LayerNorm 操作是逐元素進行的,因此不存在通用的公式來。LayerNorm 層的兩個權重都是一個長度為 ? 的向量,FLOPs 可以預估為: 2?,但通常忽略不計。
單層layer
將上述計算量相加,得到前向傳播階段中每個transformer層的計算量大約為 $24bs?2+4bs2? $,可以發現:
-
參數量和計算量跟head數量無關,head劃分更多是通過特征子空間劃分提高精度,而不是為了節省參數量或者計算量。
-
回憶參數量是\(12lh^2\),所以在給定固定序列長度的情況下,計算量也隨著參數的數量增加而線性增加。
-
計算復雜度隨著序列長度的增加呈二次方增加的趨勢。
| Attention | 計算量 | FFN | 計算量 |
|---|---|---|---|
| 計算Q、K、V | \(6 bsh^2\) | 第一個線性層 | \(8 bs?^2\) |
| QK^T | \(2 bs^2h\) | 第二個線性層 | \(8 bs?^2\) |
| 乘以V | \(2 bs^2h\) | ||
| 線性映射 | \(2 bs?^2\) |
4.3 綜合思考
模型的訓練包含前向傳播和反向傳播過程。上述只是主要考慮到前向傳播階段中,Transformer的計算量。我們接下來結合反向傳播來綜合考慮。反向傳播過程實際上包含兩部分,一部分是對輸入的梯度的計算,一部分是對權重的梯度。其實這兩部分主要的計算量都是矩陣乘法,并且大小與 前向傳播中的計算量大小一致,因此往往會直接把反向傳播的計算量近似為前向傳播的 2 倍。
反向傳播
我們把反向傳播加進來繼續分析。
單層
單個Transformer層的計算量現在如下:
- 前向傳播所需要的浮點數運算:\(24 bs?^2 + 4 bs^2?\)。
- 對于backward,對于神經網絡中的權重和輸入需要計算梯度,因此反向傳播需要2倍FLOPs。
- 如果使用activation checkpointing:在backward的時候,每一層需要額外的計算forward。
所以每層需要的總浮點數計算為\(4×(24 bs?^2 + 4 bs^2?)=96bs?^2(1+s/6?)\)。
logits
另一個耗費計算量的部分是logits的計算:將隱藏向量映射為詞表大小,得到每個 token 對應的 logits 向量。矩陣乘法的輸入和輸出形狀為 [b,s,?]×[?,V]→[b,s,V] 。矩陣乘法的輸入和輸出形狀為: [??,?]×[?,??]?>[s,V]。
因此前向傳播需要 2bs?V ,反向傳播需要 4bs?V ,總體需要 6bs?V 的計算量。
總體計算量
Megatron-LM的經典論文 "Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM"給出了一個計算標準Transformer-decoder結構浮點數運算的公式。對于一個 l 層的transformer模型,輸入形狀為 [b,s] 時,其計算量如下。
-
單次推理,前向傳播所需要的浮點數運算:\(l\times(24bs?^2+4bs^2?)+2bs?V\)
-
單次訓練,前向后向傳播需要浮點運算為:
如果沒有如果使用activation checkpointing,則是
在Megatron-Deepspeed的代碼里,我們也能看到用這個公式來計算TFLOPS(每秒所執行的浮點運算次數,floating-point operations per second):
# General TFLOPs formula (borrowed from Equation 3 in Section 5.1 of
# https://arxiv.org/pdf/2104.04473.pdf).
# The factor of 4 is when used with activation check-pointing,
# otherwise it will be 3, but for 200B model, activation check-pointing will always be on.
checkpoint_activations_factor = 4 if args.checkpoint_activations else 3
# GLU activations double the hidden states in the upscaling feed-forward in each transformer layer
# This leads to 16bsh^2 instead of 8bsh^2 per first feed-forward layer in MLP, thus we increase the coefficient by 8.
# Refer to https://github.com/bigscience-workshop/Megatron-DeepSpeed/pull/283#issue-1260805063 for more details.
coefficient = 32 if args.glu_activation else 24
flops_per_iteration = (coefficient * checkpoint_activations_factor * batch_size * seq_len * num_layers * (hidden_size**2)) * (1. + (seq_len / (6. * hidden_size)) + (vocab_size / (16. * num_layers * hidden_size)))
tflops = flops_per_iteration / (elapsed_time_per_iteration * args.world_size * (10**12))
4.4 計算特點
與參數量的關系
我們先給出結論:計算量主要和模型參數和token數相關。假設數據集中總共包含 D 個 Token,模型參數量為N,則對于序列不是特別長的場景,所有 Token Forward的計算量可以近似為2ND。
單次推理
單次推理時候,計算量和參數量的關系如下:
因為單次推理時輸入的token數為bs,因此可以近似認為,在一次前向傳播中,對于每個token,每個模型參數需要進行2次浮點運算(一次乘法,一次加法)。即從單個 Token 單個矩陣乘的視角,可以近似認為,單次推理時(只包含正向傳播)的計算量就是參數量的 2 倍,就是每個 token 過一遍所有參數的計算量。
一次迭代訓練包含了前向傳播和后向傳播,后向傳播的計算量是前向傳播的 2 倍。因此,即一次迭代訓練中,對于每個 token 和 每個模型參數,需要進行 6 次浮點數運算。
在論文"Scaling Laws for Neural Language Model"中也有類似的計算公式,具體如下圖所示。
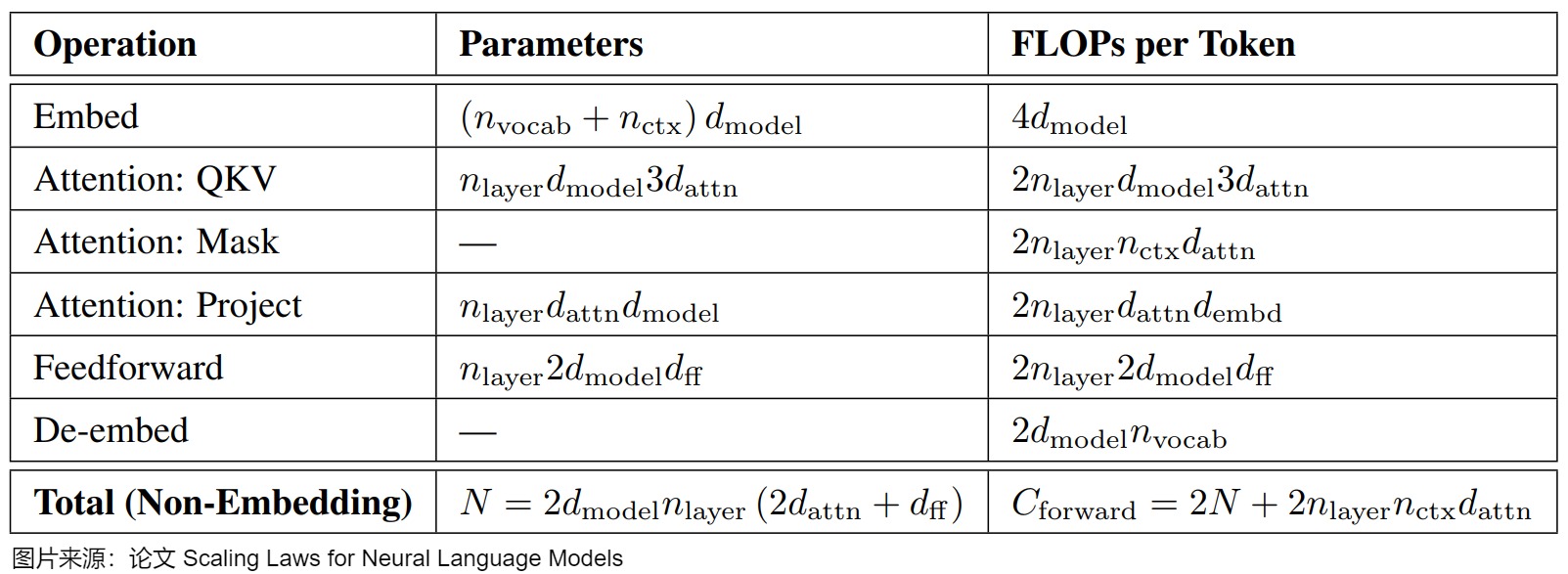
單次訓練
一次訓練迭代包含了前向傳播和后向傳播,因為反向傳播計算量是前向傳播的2倍,所以單次訓練,對于每個token,每個模型參數需要進行6次浮點運算。訓練總算力(Flops)= 6 * 模型的參數量 * 訓練數據的 token 數。這就是所有訓練數據過一遍訓練所需的算力。如果需要訓練需要多少時長,則可以近似使用下面公式:
帶寬受限
算力并不能說明一切,模型還需要訪問 GPU 內存,內存帶寬也可能成為瓶頸。因為需要把參數從內存里面讀出來吧?內存訪問量 = 參數數量 * 2 bytes。針對內存帶寬部分,大語言模型中的計算具備一些鮮明的特點。我們一一進行分析。
注意力計算
在大語言模型推理中,注意力計算是訪存密集型的,其耗時受限于硬件的訪存帶寬,而非運算速度。
對于矩陣乘法算子,其特點如下。
- 參數量太大會導致矩陣乘法算子成為訪存密集型。當輸入的數據不夠多,運算量不夠大的時候,這些算子會因為參數訪存過多而受限于訪存帶寬。
- 計算量將隨著Batchsize增長而快速增加。當Batchsize小于16時,我們可以認為矩陣乘法算子為訪存密集型的。只有當Batchsize充分大時,矩陣乘法算子才會變成計算密集型的,它們的性質會隨著Batchsize變化而變化。
FFN計算
對于FFN算子,在大多數端側應用中,我們都是以Batchsize=1的方式去調用大語言模型,此時網絡中大部分的計算量和訪存量都集中在FFN中。大語言模型整體的運算-訪存比極低,整個網絡都將是訪存密集的,其運行耗時完全受限于訪存帶寬而非硬件算力。
KV Cache的影響
KV Cache是對注意力優化的重要途經。它本質上是文本中每個之前位置的 key 向量和 value 向量的集合。這項技術的出現大大縮減了Self Attention的計算量。這使得在KV Cache技術出現后,可以把推理流程分為prefill和decode階段(我們會在后文詳細分析)。下圖就是decode階段對應的圖例。概括地說,其中包含了兩種算子:
- 自注意力(Self-Attention,黃色標出)涉及矩陣-矩陣乘法。
- 密集投影(Dense Projection,綠色標出)涉及向量-矩陣乘法。
Self Attention算子的計算特點非常顯著:這是一個運算訪存比接近1:1的訪存密集型算子。對其訪存量和計算量進行理論估計,可得發現,其內存訪問量和計算量的復雜度都是\(O(batch\ size \times sequence\ length \times hidden \ dimension)\)。作為對比,對MatMul和FeedForward(都是矩陣乘法算子)做類似的估計,可得結論:其內存訪問量和計算量的復雜度都是\(O(batch\ size \times hidden \ dimension)\)。
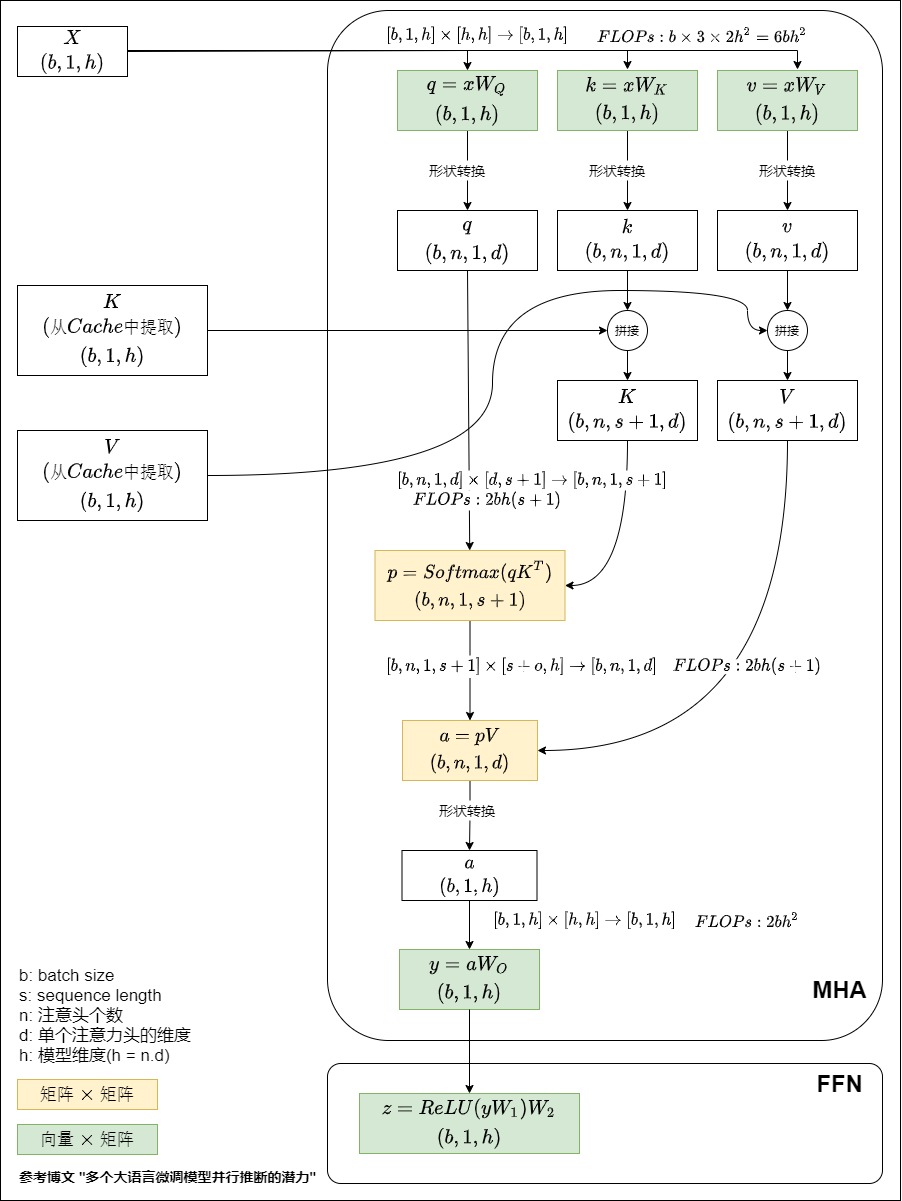
prefill
MHA 塊的 FLOPs: \(8sh^2 + 4s^2h\)。FFN的是\(16sh^2\)。
decode
MHA 層每一輪解碼的 FLOPs: \(8h^2 + 4(s+1)h\)。FFN的是\(16h^2\)。
總體
而在輸入數據形狀為 [??,??]的情況下,一次訓練/推理:
prefill 階段每輪總計算量:\(??×(24l?^2??+4l???^2)+2???????)=24l?^2????+4l?????^2+2???????\)
decode 階段每輪總計算量:\(??×(8l?^2+4l?(??+1)+16l?^2)+2?????=24l?^2??+4l???(??+1)+2???????\)
kv cache 節省了多少計算量
對于上下文長度 s,不使用 kv cache d的 self-attention 的總計算量復雜度為:總計算量:\(??(??^3?)\),使用后的總計算量近似為 \(??(??^2?)\)。計算量節省比率:
計算復雜度從 \(??(??^3?)\) 降低到 \(??(??^2?)\),即使用 kv cache 可節省約 ?? 倍的計算量。當 ??較大時,1/s接近于 0。輸出 tokens 數越多,計算量節省越可觀。
0x05 優化方向
自回歸大語言模型在運行效率上面最大的缺陷是解碼過程是串行和變長的,并行計算和內存帶寬資源無法得到高效利用,進而也導致了內存的管理和回收問題。針對此情形,工業界已經出現了不少的系統優化方案,這些上面每種技術手段都可以大幅度地提升模型推理的速度、性能。
5.1 基于注意力機制來修改外推技術
博文“How Do Language Models put Attention Weights over Long Context“中提到,不同層的注意力分布有顯著差異:
- 起始層主要是詞嵌入和詞嵌入的一層層混合,注意力分布大致均勻。
- 中間層的注意力模式變得更加復雜,大部分概率質量集中在初始標記(注意力匯聚)和最近的/最后標記(近期偏見)上。
- 最后層則可以看到所有的注意力模式。
從上面可以看出,也就是說,中間層大部分都是“V形”注意力分布,意味著中間層很多的token其實作用不大。因此可以考慮針對不同的層來通過減少token的方式來加速推理,增加外推能力。
我們接下來就看看如何基于注意力機制來增加外推能力。
| 名稱 | 主要思想 |
|---|---|
| StreamLLM | 在組裝KV-Cache的時,包括所有頭部的token(Sink模式),同時引入Window Attention機制來提高計算效率。 |
| LM-Infinite | 采用V-shaped注意力機制。因為中間token注意力分布較少,因此引入Λ形注意力掩碼,也設置一個距離上限來限制“有效距離”。同時可以選擇性地關注中間的具有最大的注意力logits的k個tokens。 |
| SirLLM | 通過度量Token的熵和一個記憶衰減機制來篩選關鍵短語。熵值高的token被認為包含更多的信息。記憶衰減機制是:將token熵緩存中的每個熵值乘以一個小于1的衰減比率。隨著時間的推移,較早的信息會逐漸被遺忘,而最近的關鍵信息則被保留。 |
| Sparase-Q | 令牌通常只關注序列的一小部分。如果能有效地預測哪些令牌將獲得高注意力分數,就可以僅存儲高分令牌的鍵值,從而提高內存帶寬效率。因此提出一種壓縮思想,通過估計最大注意力分數來選擇r個分量,然后確定top-k的key向量和value向量。 |
| Dynamic Memory Compression | DMC在預訓練的LLMs上進行微調來學習壓縮策略,然后在推理時對關鍵值緩存進行在線壓縮。DMC引入了決策變量α和重要性變量ω,這些變量在每個時間步驟決定是將當前的key和value表示追加到緩存中,還是與緩存中的頂部元素進行加權平均。 |
| Infini-attention | 將壓縮記憶(compressive memory)整合到標準的注意力機制中,并在單個 Transformer 塊中構建了掩蔽局部注意力(masked local attention)和長期線性注意力(long-term linear attention)機制。 |
| LongLoRA | 引入Shifted Sparse Attention對模型進行微調以此對上下文長度進行拓展。經過Shifted Sparse Attention微調的模型在推理時保留了原始的標準自注意力架構。這意味著在推理階段,模型可以使用未修改的注意力機制,從而使得大部分現有的優化和基礎設施可以重用。 |
| self-extend Attention | 使用簡單的floor division操作將未見過的大的相對位置映射到預訓練期間遇到的相對位置。為了解決長距離依賴和鄰近依賴的問題,Self Extend引入了雙層注意力機制:分組注意力(Grouped Attention)和鄰近注意力(Neighbor Attention)。 |
| Dual Chunk Attention | 通過將長序列的注意力計算分解為基于塊的模塊,使得模型能夠有效地捕獲同一塊內(Intra-Chunk)和不同塊間(Inter-Chunk)的相對位置信息。然后將內部塊、跨塊和連續塊的注意力輸出合并,得到最終的輸出表示。這一表示考慮了序列中的局部和全局信息,從而使得模型能夠有效地處理長序列。 |
5.2 基于Memory機制外推技術
基于Memory機制的外推技術其實沿用的還是壓縮思想,借助外部存儲將歷史信息存儲,然后使用最近的token進行查詢獲取一些歷史上重要的token。
| 名稱 | 主要思想 |
|---|---|
| InfLLM | 通過構建一個額外的上下文記憶模塊來讓存儲遠離當前處理位置的上下文信息,并設計了一個高效的機制來查找與當前處理的標記相關的單元,以便在注意力計算中使用。 |
| Recurrent Memory Transformer (RMT) | 通過結合循環神經網絡(RNN)的循環機制和Transformer模型的記憶增強能力來實現上下文拓展。RMT在Transformer模型的基礎上引入了一個記憶機制,該機制由一組可訓練的實值向量(稱為記憶標記)組成。這些記憶向量可以存儲和處理局部和全局信息,并通過循環機制在長序列的不同段之間傳遞信息。 |
0xFF 參考
Contiguous Batching/Inflight Batching
Full Stack Transformer Inference Optimization Season 2: Deploying Long-Context Models Yao Fu Paper version
How Do Language Models put Attention Weights over Long Context Yao Fu
HunYuan MoE:聊一聊 LLM 參數量、計算量和 MFU 等 AI閑談
llm 參數量-計算量-顯存占用分析 Zhang
LLM 大模型訓練-推理顯存占用分析 chaofa用代碼打點醬油
Notion – The all-in-one workspace for your notes, tasks, wikis, and databases.
OpenPPL-LLM | OpenPPL之大語言模型推理引擎來啦 OpenPPL
Towards 100x Speedup: Full Stack Transformer Inference Optimization Yao Fu
Transformer 數據估計- 顯存占用 Bruce 仗劍走天涯
分析transformer模型的參數量、計算量、中間激活、KV cache 回旋托馬斯x
剖析GPT推斷中的批處理效應 Lequn Chen || abcdabcd987
多個大語言微調模型并行推斷的潛力 Lequn Chen || abcdabcd987
大模型推理瓶頸及極限理論值分析 喜歡卷卷的瓦力
激活內存:模型推理需要多少內存 魏新宇 [大魏分享]



 浙公網安備 33010602011771號
浙公網安備 33010602011771號