探秘Transformer之（8）--- 位置編碼

從零開始解析Transformer，目標是：(1) 解析Transformer如何運作，以及為何如此運作，讓新同學可以入門；(2) 力爭融入一些比較新的或者有特色的論文或者理念，讓老鳥也可以有所收獲。

探秘Transformer之（8）--- 位置編碼

探秘Transformer之（8）--- 位置編碼

0x00 概述

位置編碼（Positional Embedding）是一種用于處理序列數據的技術，被用來表示輸入序列中的單詞位置。在Transformer 實現中起到了舉足輕重的作用。Transformer 需要關注每個輸入詞的兩個信息：該詞的含義和它在序列中的位置。位置編碼可以針對這兩個關注點做關鍵的補充。

針對“輸入詞的含義”這個關注點，Transformer通過嵌入層對詞的含義進行編碼，位置編碼可以在此之上注入位置相關的先驗知識，比如："相近的token應該具有相近的Embedding"、“相對位置比絕對位置更重要”、“遠距離的相對位置可以不用那么準確”、“越遠的相對位置越模糊”、“越近的Token越重要”和”越遠的Token平均而言越不重要“等。
針對“輸入詞在序列中的位置”這個關注點，Transformer通過位置編碼層表示該詞的位置。在序列數據中，單詞的順序和位置對于語義的理解非常重要。傳統的詞向量表示只考慮了單詞的語義信息，而沒有考慮單詞的位置，而注意力機制又有置換不變性的弊端。于是，位置編碼為每個單詞分配一個唯一的位置向量，這樣可以將單詞的位置信息融入到模型的表示中，進而克服注意力機制的置換不變性，使得模型在處理序列數據時更好地理解單詞的上下文和關系。

最終，Transformer 通過結合這兩個層的輸出來完成兩種不同的信息編碼。

注：在深度學習中，一般將學習出來的編碼稱之為embedding，有將位置信息"嵌入" 到某個向量空間的意思。例如Bert的位置向量就是學習得到，所以稱為"Position Embedding"。而原始Transformers模型中位置向量的思路是通過規則（三角函數）直接計算出來，不涉及學習過程，被稱為Position Encoding。

0x01 問題

1.1 詞序的重要性

無論何種語言，其語句都是一種時序型數據，即每個詞都是位置相關的（position-wise）。句子中詞的順序和位置決定了句子的實際語義。單詞相同但順序不同可能會導致句子的語義發生變化。比如下面兩個句子的意義就完全不同。

從北京到上海。
從上海到北京。

歷史上還有經典的曾國藩例子：如果寫“臣屢戰屢敗”，結果可能是曾國藩被拖出去斬首。如果寫“臣屢敗屢戰”，結果曾國藩是忠勇無雙有賞賜。

因此，自然語言文本信息的處理是一個具有先后順序的序列任務，位置信息對于理解語言是相當重要的，學習不到順序信息，那么模型效果將會大打折扣，因此需在模型中引入某種表達位置的機制。

1.2 Transformer架構的缺陷

位置不變性

Transformer模型拋棄了RNN、CNN作為序列學習的基本模型，完全采用注意力機制取而代之。對于一個輸入句子，其單詞不再是順序輸入，而是一次性輸入一個序列中的所有詞，依靠純粹的自注意力機制來捕獲詞之間的聯系，直接對這個序列整體進行特征變換。

注意力操作是一種全局操作，可以捕捉句子中較長的依賴關系。比如，Transformer可以讓序列中每兩個元素$x_t$，$x_s$都能無視其絕對位置$t$，$s$和相對位置$t-s$而進行信息交換，從而計算輸入序列中的每個元素與整個序列的注意力權重。或者說，序列中位置信息是以常數形式進行變換，這樣才能夠防止長時信息丟失和遺忘問題。

\[q_t = W^Qx_t\ \ k_t=W^Kx_t\ \ v_t = W^Vx_t \\ q_s = W^Qx_st\ \ k_s=W^Kx_s\ \ v_s = W^Vx_s \\ A_{t,s}=q_t^Tk_s=x_t^T(W^Q)^TW^Kx_s \ \ \alpha_{t,s}=softmax(\frac{A_{t,s}}{\sqrt d}) = \frac{e^{\frac{q_t^Tk_s}{\sqrt d}}}{\sum_s e^{\frac{q_t^Tk_s}{\sqrt d}}}\\ encoder : h_t = \sum^T_{s=1} \alpha_{t,s}v_s \\ decoder : h_t = \sum^t_{s=1} \alpha_{t,s}v_s \]

然而，如果考慮到位置關系，則Transformer的優勢就變成了劣勢，因為Transformer本身來說是沒有位置或者順序的概念的，它具有位置不變性（ORDER INVARIANCE）或者說置換不變性（Permutation Invariance）。

置換不變性的意思是：詞與詞的位置隨意變動，并不會導致這些詞的注意力權重產生變化，注意力層的整個結果維持不變。即，無論位置如何變化，每一個詞向量計算結果和位置變化之前完全一致，僅僅是詞向量在輸出矩陣的排列隨著詞和詞位置互換而對應調整了一下。我們假設目前沒有加入位置編碼，則對于自注意力的計算公式$A=softmax(QK^T)V$來說，有如下例子。如果q是“我”，無論句子是“我愛你”還是“你愛我”，其注意力輸出都是完全一致的。這說明在沒有位置序列信息的情況下，改變詞語順序的句子實際語義是不一樣的，但是注意力輸出相同，無法準確建模。

import torch
import torch.nn.functional as F
d = 8 # 詞嵌入維度
l = 3 # 句子長度
q = torch.randn(1,d) # 我
k = torch.randn(l,d) # 我愛你
v = torch.randn(l,d) # 我愛你

orig_attn = F.softmax(q@k.transpose(1,0),dim=1)@v

# 調轉位置
k_shift = k[[2,1,0],:] # 你愛我
v_shift = v[[2,1,0],:] # 你愛我
shift_attn = F.softmax(q@k_shift.transpose(1,0),dim=1)@v_shift

print('我愛你:',orig_attn)
print('你愛我:',shift_attn)

證明

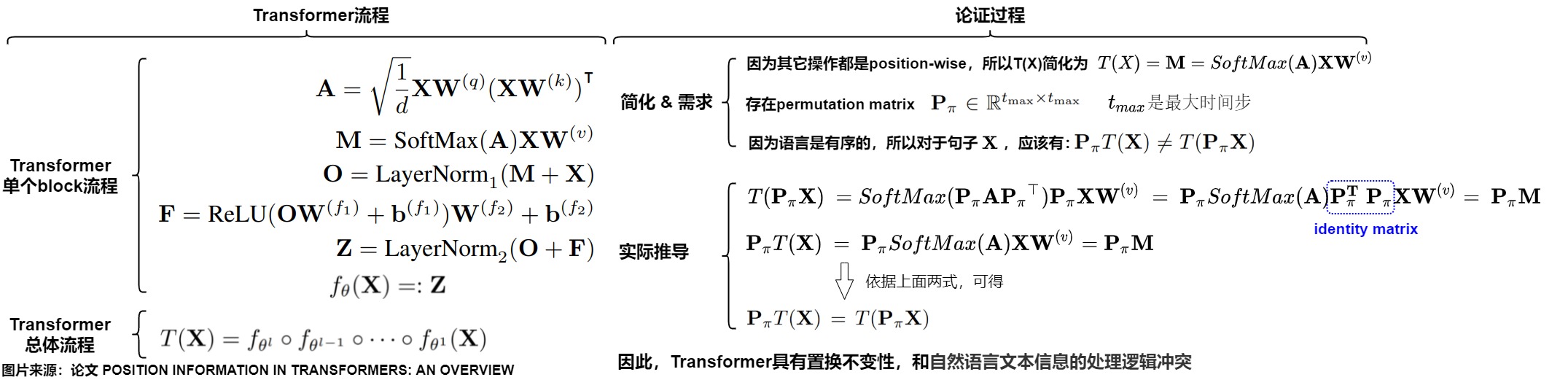
我們接下來證明下位置不變性。在 Transformer-NoPE 架構中，Embedding 層和 FFN 層都是point-wise（逐點式），均與位置或者說順序無關，只有注意力模塊與位置相關。我們只需要關注注意力機制是否為置換等價或者順序不變。

假設有置換矩陣$\mathbf{P_\pi}$, 則$\mathbf{P_\pi X}$ 是將$\mathbf{X}$的行依據$\pi$重新排列的結果（可以理解為把K，V按行打亂順序，相當于把句子中的語序打亂），注意，$\mathbf{P_\pi}$只作用于$\mathbf{X}$的行，不改變列的順序。我們看看把$\mathbf{P_\pi X}$輸入注意力機制的運行邏輯中，是否會影響其運行結果。

查詢矩陣的變化

原來的查詢矩陣是：

\[\mathbf{Q =XW^{(q)}} \\ \mathbf{K =XW^{(k)}} \]

則置換后的查詢矩陣也要發生變化，即：

\[Q' = \mathbf{P_{\pi}XW^{(q)}} = \mathbf{P_{\pi}Q}\\ K' = \mathbf{P_{\pi}XW^{(k)}} = \mathbf{P_{\pi}K} \]

注意力矩陣的變化

原來的注意力計算公式是：

\[\mathbf{A} = \frac{1}{\sqrt d} \mathbf{QK}^\top \]

則置換后的注意力計算也要發生變化，即：

\[\mathbf{A}' = \frac{1}{\sqrt d} \mathbf{Q'(K')}^\top \\ = \frac{1}{\sqrt d}({\mathbf{P_{\pi}Q)(P_{\pi}K)}}^\top \\ = \frac{1}{\sqrt d}\mathbf{P_{\pi}QK}^\top P_{\pi}^\top \\ = \mathbf{P_{\pi}}\mathbf{A} P_{\pi}^\top \\ \]

注意力分數的變化

原來的注意力分數的計算公式是：

\[SoftMax(A)_i = \frac{e^{A_i}}{\sum_j e^{A_j}} \]

則置換后的注意力分數的計算也要發生變化，即

\[SoftMax(A’)_i = \frac{e^{(\mathbf{P_{\pi}}\mathbf{A} \mathbf{P_{\pi}}^\top)_i}}{\sum_j e^{(\mathbf{P_{\pi}}\mathbf{A} \mathbf{P_{\pi}}^\top)_j}} \]

因為置換矩陣只是排列的行，而Softmax的操作是行獨立的，實際上對行和列進行重新排列并不會改變Softmax的結果，因此有：

\[SoftMax(\mathbf{P_{\pi}}\mathbf{A} \mathbf{P_{\pi}}^\top) = \mathbf{P_{\pi}}SoftMax(\mathbf{A}) \mathbf{P_{\pi}}^\top \]

最終結果

我們把上述變化綜合起來，最終推導如下所示：無論句子順序如何，其注意力計算結果完全一致。即假設$x_s$，$x_t$分別代表第s和第t個輸入單詞，則有$T(...,x_s,..., x_t, ...) = T(...,x_t,..., x_s, ...)$，T函數天然滿足恒等式T(x,y)=T(y,x)，無法區分輸入的是$x,y$還是$y,x$。

后果

因此，在未加入位置信息的情況下，Transformer存在兩個問題。

第一個問題是模型不能捕捉序列的順序。

沒有位置信息的自注意力模型頂多是一個非常精妙的“類詞袋模型“，即模型把序列看成是一個集合，既然是集合，那么模型把輸入序列的每一個單詞都同等看待，自然就沒有位置信息，那么隱狀態就和時序無關。某個單詞如果在不同的位置出現多次，其每次計算出的注意力加權求和結果都完全一致。

比如位置 j 的token最終的注意力輸出如下。可以看到，因為位置信息是以常數形式進行變換，所以計算公式中沒有任何位置信息的描述，只有求和算子，這就是類詞袋模型。

\[z_j = \sum _{i=0}^n softmax(\frac{q_j^T.k_i}{\sqrt d})v_i \]

而且，給定一個句子，最終的這個句子的詞嵌入組合只來源于句子中所有單詞的特征，和句子中單詞的排序沒有任何關系，即丟失了詞之間的位置信息。輸入元素位置的變動不會對注意力結果產生影響，從而只要集合中包含的元素是確定的，輸出結果就是確定的。

然而，這顯然和語言、代碼、語音等序列的內在特征相違背：一句話打亂單詞順序后，所表達的意思、單詞指代或修飾的對象、甚至單詞對應的語義，可能都會隨之改變。舉個例子。將[我，愛，你]和[你，愛，我] 都輸入Transformer，這個類詞袋模型給出的句子表征會完全一致。而我們期望的是：“愛”這個詞的詞向量，在“我愛你”和“我你愛”這兩個句子中，經過神經網絡計算應該得到不同的輸出，因為我們的輸入中，“愛”這個詞在句子中的位置實際上已經發生了變化，我們輸入的是兩個不同的句子，一個詞在兩個不同的句子中，應該是不同的向量表示，但是神經網絡無法捕捉到這個變化。

                                 [ [0.3, 0.5, 0.1, 0.4]
[我，愛，你]  => Transformer =>    [0.1, -0.6, -0.2, 0.3], 
                                 [0.3, 0.5, 0.3, -0.1] ]

                                 [ [0.3, 0.5, 0.1, 0.4]
[你，愛，我]  => Transformer =>     [0.1, -0.6, -0.2, 0.3], 
                                   [0.3, 0.5, 0.3, -0.1] ]

第二個問題是單詞間的權重和位置無關。

無論 t 和 s 所處的位置如何變化，它們之間的注意力權重 $A_{t,s}$ 均不會發生變化，也就是位置無關。然而，這又和語言的特性相違背：多數的時候，離得越近的單詞相關性可能越高，我們希望它們之間的的注意力權重更大；離得很遠的兩個單詞可能毫無關系，我們希望其注意力權重更小。

1.3 解決思路

既然Transformer中的自注意力機制無法捕捉輸入元素序列的順序，因此我們需要對位置關系進行建模，把單詞的順序合并到Transformer架構中，從而打破這種置換不變性，于是Transformer作者提出了 Position Embedding 的方法，也就是“位置向量”或者說”位置編碼“。

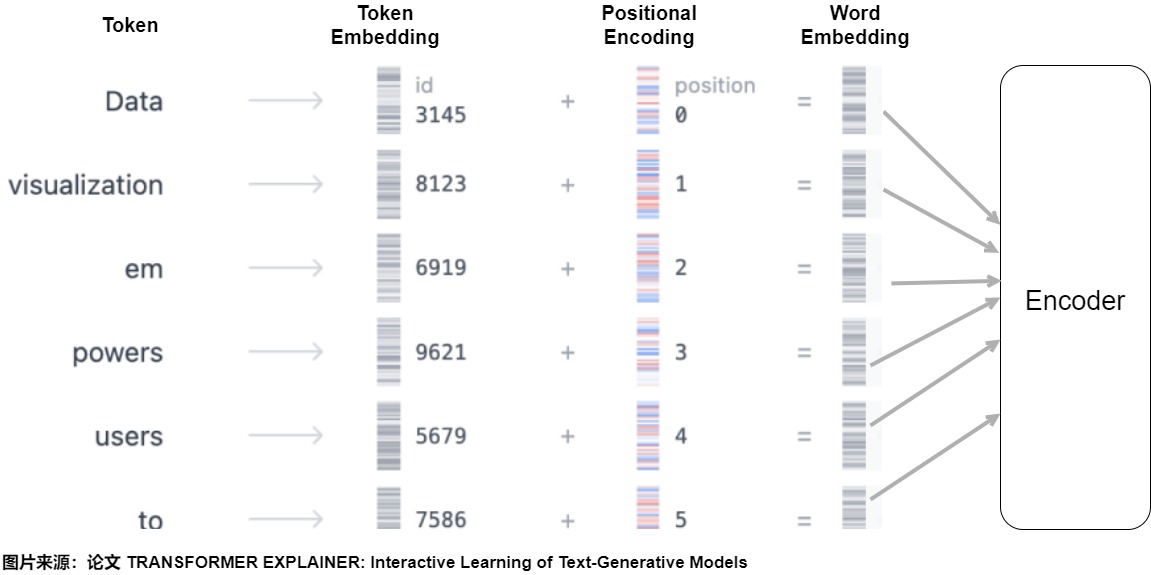
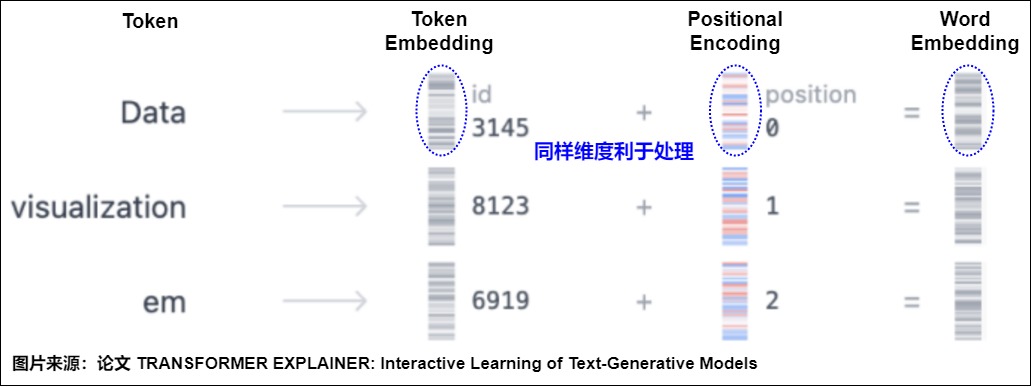
位置編碼的作用就是給每個位置都加上一個唯一的位置編碼向量，即將詞序信息向量化。對于輸入的每個單詞，每個單詞都有對應的向量 (與位置無關)。為了給每個位置都加上一個唯一的位置編碼向量碼，需要使用另一個具有相同維度的向量，其中每個向量唯一地代表句子中的一個位置。然后通過將詞嵌入與其相應的位置嵌入求和來形成 Transformer 層的輸入，即輸入模型的整個Embedding是Word Embedding與Positional Embedding直接相加之后的結果。模型會將這個結果矩陣作為輸入提供給后續層。

這樣給每個詞都引入了其在句子中特定位置的信息，類似$T(..., x_s,..., x_t, ...) = T(...,x_s+p_s,..., x_t+p_t, ...)$。注意力機制就可以分辨出不同位置的詞，從而模型不但知道注意力要聚焦在哪個單詞上面，還要知道單詞之間的互相距離有多遠，在計算注意力得分時就可以考慮兩個元素之間的相對位置。模型也就具備了處理序列問題的能力。后面無論每個輸入向量學習到了什么信息，都能夠通過位置向量回溯到模型中的具體位置，也就為后面的輸出提供了可參考的依據。

1.4 應具備的性質

論文"A Length-Extrapolatable Transformer"論文中提到了了transformers位置建模的三條設計原則：具備位置敏感性；針對位置平移具備魯棒性；可以外推。原文摘錄如下：

First, a Transformer should be sensitive to order. Otherwise, it will degenerate into a bag-of-word model which confuses the whole meaning.

Then, position translation can’t hurt the representation a lot especially combing with the proper attention-mask operations.

After that, a good sequence model needs to deal with any input length.

論文"On Position Embeddings in BERT"則指出，Position Embedding是為了位置的時序特點進行建模。基于此，該論文提出Position Embedding應該具有三個特性：平移不變性（translation invariance，兩個位置的關系只與相對位置有關）、單調性（monotonicity，隨著距離的增大而衰減），對稱性（ symmetry，兩個位置的關系是對稱的，i,j和i,j相同）。原文摘錄如下：

Informally, as positions are originally positive integers, one may expect position vectors in vector space to have the following properties: 1) neighboring positions are embedded closer than faraway ones; 2) distances of two arbitrary m-offset position vectors are identical; 3) the metric (distance) itself is symmetric.

Property 1. Monotonicity: The proximity of embedded positions decreases when positions are further apart.

Property 2. Translation invariance: The proximity of embedded positions are translation invariant.

Property 3. Symmetry: The proximity of embedded positions is symmetric

我們順著這些展開，詳細看看一個良好的位置編碼應該具備的性質，理想情況下，位置編碼應滿足以下標準：

唯一性/確定性。每個位置都需要一個無論序列長度如何，都保持一致的編碼，即無論當前序列的長度是 10 還是 10,000，位置 5 處的標記都應該具有相同的編碼。而且，該位置編碼必須是確定性的，即每個位置都有唯一的編碼（或者盡量不同），這樣才能體現同一個token在不同位置的區別，確保模型對位置有分辨能力。另外，如果位置編碼能從一個確定的過程中產生，那將是最理想的。這樣，模型就能有效地學習編碼方案背后的機制。
有界性：編碼范圍是有界的，值要在一定的范圍內不會過大導致溢出。因為位置信息本身就是矯正量，不應該隨著句子加長，位置編碼的數字就無限增大，那樣容易對單詞的本體語義向量造成影響。
相對性：對模型來說，真正重要的往往不是絕對位置，而是token之間的相對位置。所以我們期望位置編碼即可以表達絕對位置信息（表示同一個單詞在序列之中不同位置的區別，即token在序列之中的絕對位置），也可以表達相對位置信息（如果有一組詞無論在什么位置都不會發生詞義的變化，則我們認為這組詞的實際含義與絕對位置沒有關系）。
單調性或者說距離衰減性：位置編碼的最大意義就是給模型提供位置語義相關性。而位置相關性應該隨相對位置距離增大而減少，并且是單調衰減關系。具體就是距離近的相關性高，距離遠的相關性低。距離衰減性相當于軟的窗口注意力。這符合人類自然語言的習慣，即相近的文字關聯性更強，位置相近的Token平均來說應該獲得更多的注意力，而距離比較遠的Token平均獲得更少的注意力。單調性也可以等同為一個卷積神經網絡，在做信息聚合的時候會優先考慮局部信息。距離越近的元素則會被考慮的越多。
平移不變性：任何位置之間的相對距離在不同長度的句子中應該是一致的。具體來說是，兩個位置的關系只與相對位置有關，與序列長度無關。在任何長度不同的序列中，相同位置的Token之間的相對位置/距離保持一致（體現Token位置之間差異的不變性）。比如長度10和長度100的句子中，第1個單詞和第5個單詞之間的距離應該相同。即，如果兩個token在句子1中的相對距離為k，在句子2中的相對距離也是k，那么這兩個句子中，兩個token之間的相關性應該是一致的，也就是attention_sample1(token1, token2) = attention_sample2(token1, token2)。
線性關系。位置之間的關系在數學上應該是簡單的，或者說存在線性關系。如果知道位置 p 的編碼，那么計算位置 p+k 的編碼就應該很簡單，這樣模型就能更容易地學習位置模式。
多維度：隨著多模態模型成為常態，位置編碼方案應該能夠自然地拓展至多個維度，從 1D 擴展到 nD。這將使模型能夠使用圖像或腦部掃描這樣的數據，它們分別是 2D 和 4D 的。
外推性或者說泛化性：位置編碼可泛化到比訓練中遇到的序列更長的序列上。為了提高模型在現實世界中的實用性，它們應該在訓練分布之外泛化。因此，編碼方案需要有足夠的適應性，以處理意想不到的輸入長度，同時又不違反任何其他理想特性。具體說就是編碼系統不受句子長短的影響（即適用于任意文本長度），在訓練沒有見到的樣本上，沒有見過的長度上也能表現不錯。化未見為已見，化分布外為分布內。
周期性：這個性質是出于實現上的考慮。因為要求是相對且有界，所以容易聯想到一個性質 —— 周期性，這樣更遠距離的值可以和較近距離的值相同，從而有一定的外推性。
結合語義信息。在涉及長上下文理解和搜索的任務中，注意力機制應該優先考慮語義相似性，而不是被與位置編碼相關的信息所掩蓋，因為在較長距離上位置編碼的相關性可能較低。因此，PE 應該結合語義和位置信息，確保語義信息不受位置距離的過度影響。

0x02 編碼方案演化

既然知道了理想位置編碼的屬性，我們就來嘗試從無到有一步一步設計和迭代位置編碼方案，并且比對各種方案和期望性質之間的差距。Positional encoding有一些想象+實驗+論證的意味，或者說，在 LLM 引入位置信息更像是構建特征工程，這里特征對應的信息就是位置。

為了更好的說明，我們先給出哈佛代碼。這就是Transformer論文中的方式。函數的總體目標是計算每個維度（每一列）的相關位置信息。因此需要：

初始化一個形狀為 (max_len, 1) 的絕對位置矩陣position。對應代碼中的position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1) 。在position中，詞匯的絕對位置用它的索引表示。絕對位置矩陣初始化之后，接下來就是考慮如何將這些位置信息加入到位置編碼矩陣中。因此，需要將形狀為 (max_len, 1) 的絕對位置矩陣，變換成(max_len, d_model) 形狀，然后覆蓋初始位置編碼矩陣。這就需要構建一個轉換矩陣 div_term。
構建轉換矩陣div_term 就對應代碼中的 div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))，具體操作為。
- 將自然數的絕對位置編碼縮放成足夠小的數字 10000 ^ (2i / d_model)，這樣有助于在之后的梯度下降過程中更快的收斂。
- 用 torch.exp()函數來構建一個形狀為(1, d_model) 變換矩陣div_term，用于縮放不同位置的正弦和余弦函數。div_term是256維的張量，即公式里面sin和cos括號中的內容。和原始論文不同，哈佛代碼通過e和ln進行了變換，這樣速度會快一些。
- div_term具體如下：
  
  \[{div\_term}_i = 10000^{-\frac{i}{d_{model}}} \]
使用position和div_term構建位置編碼pe，計算每個維度（每一列）的相關位置信息。具體是使用正弦torch.sin(position * div_term)和余弦函數torch.cos(position * div_term)來生成位置編碼，位置編碼是一個d_model維的向量，對于這個向量的每一個維度，如果這個維度為偶數，則用正弦函數進行編碼，如果這個維度為奇數，則用余弦函數編碼。
使用unsqueeze(0)在第一個維度添加一個維度batch_size，以便進行批處理。

代碼中的幾個注意點如下：

Transformer模型的輸入X：[batch_size, max_len, d_model]，是batch_size個句子的編碼。位置編碼是對一條句子中所有word的位置進行編碼，并且由于我們對位置編碼后要加到X上，因此，一個位置的編碼的維度與一個word編碼的維度相同，都是d_model。這樣，一條句子的位置就編碼為[max_len, d_model]維度的張量，batch_size條句子的位置編碼就是[batch_size, max_len, d_model]維度的張量。
代碼div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))使用等價的指數+對數運算，其原因是為了確保數值穩定性和計算效率。一方面，當d_model較大時，直接使用冪運算會導致10000 ^ (2i / d_model) 變得非常小，以至于在數值計算中產生下溢。通過將其轉換為指數和對數運算，這樣可以在計算過程中保持更好的數值范圍，從而避免這種情況。另一方面，在許多計算設備和庫中，指數和對數運算的實現通常比冪運算更快。
調用 Module.register_buffer 函數。register_buffer通常用于保存一些模型參數之外的值，比如在 BatchNorm 中的 running_mean，它不是模型的參數，但是模型也會修改它，而且在預測的時候也要使用它。在此處，pe 是一個提前計算好的常量，在前向傳播時候要用到它。因此register_buffer()函數會把 pe保存下來。

具體代碼如下。

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        """
        d_model: 詞嵌入維度
        max_len: 序列的最大長度
        dropout: 置0比率
        
        PE(pos, 2i)     = sin(pos/pow(10000, 2*i/d_model)), (0<= i <= d_model)
        PE(pos, 2i + 1) = cos(pos/pow(10000, (2*i)/d_model)),
        PE(p+k, 2i) = PE(p, 2i)PE(k, 2i+1) + PE(p, 2i+1)PE(k, 2i)
        sin(a+b) = sin(a)cos(b) + cos(a)sin(b)   
        
        注: 序列上不同位置上token的同一個維度i上，才具有線性關系
        """
        
        # 初始化一個全0位置矩陣，矩陣的大小是max_len x d_model，后續計算的位置編碼會存儲在pe中
        pe = torch.zeros(max_len, d_model) 
        
        """
        初始化一個絕對位置矩陣position, 在這里，詞匯的絕對位置用它的索引表示，具體操作是：
        1. 使用arange方法獲得一個連續自然數向量（0到max_len-1的整數序列）。
        2. 使用unsqueeze方法拓展向量維度使其成為矩陣，目的是為了和div_term進行計算
        假設max_len是500，則 position是tensor([[0,1,2,...,499]])，形狀是torch.Size([500, 1])
        """
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1) 
        """
        構建一個1xd_model形狀的變換矩陣div_term，具體操作是：
        1. 將自然數的絕對位置編碼縮放成足夠小的數字 10000 ^ (2i / d_model)，這樣有助于在之后的梯度下降過程中更快的收斂。
        2. 用 torch.exp()函數來構建一個形狀為(1, d_model) 變換矩陣div_term，用于縮放不同位置的正弦和余弦函數。div_term是256維的張量，即公式里面sin和cos括號中的內容。和原始論文不同，此處通過e和ln進行了變換，這樣速度會快一些。
        """
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        
        """
        使用position和div_term共同構建位置編碼pe，計算每個維度（每一列）的相關位置信息
        具體是使用正弦和余弦函數生成位置編碼，d_model的偶數索引使用正弦函數；奇數索引使用余弦函數
        此時pe形狀是[max_len,d_model]
        """
        pe[:, 0::2] = torch.sin(position * div_term) 
        pe[:, 1::2] = torch.cos(position * div_term)
        
        # 在第一個維度添加一個維度batch_size，以便進行批處理
        pe = pe.unsqueeze(0).transpose(0, 1) 
        # 此時pe形狀是[1,max_len,d_model]
        self.register_buffer("pe", pe) # 將pe注冊為緩沖區，以便在不同設備之間傳輸模型時保持其狀態
        
    def forward(self, x):
        """
        forward函數的參數是x, 表示文本序列的詞嵌入表示。
        目的是返回Embedding + PositionEncoding
        """
        # 在位置矩陣中取與輸入序列長度相等的前x.size(1)行，然后和Token Embedding相加，因為默認max_len一般太大了，所以要進行與輸入張量的適配。
        # 這里需要注意的一點便是，在輸入x的維度中，batch_size是第1個維度，seq_len是第2個維度，size(1)實際獲取的是第2個維度。
        # 因為不需要進行梯度求解的，因此把requires_grad設置成false。
        x = x + self.pe[:, : x.size(1)].requires_grad_(False)
        # 返回最后得到的結果并進行dropout操作
        return self.dropout(x)

2.1 整型數字位置編碼

我們首先想到的方法是將 token 位置的整數值添加到 token 嵌入的每個分量中，即為每個時間步按一定步長線性分配一個數字。比如第i個位置token的位置編碼就是i。i 的取值范圍為 0→L，其中 L 是當前序列的長度。數學映射為 f(x) = x。比如：“我喜歡蘋果”，其位置編碼就是：

\[我\ 0 \\ 喜 \ 1 \\ 歡 \ 2 \\ 蘋 \ 3\\ 果 \ 4 \]

我們把哈佛代碼修改如下，這里把詞維度的所有索引都變成了位置數值。

max_len = 5
d_model = 4
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
pe[:, 0::2] = position
pe[:, 1::2] = position
print(pe)

輸出為：

tensor([[0., 0., 0., 0.],
        [1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.],
        [4., 4., 4., 4.]])

這種方案的優點是：實施簡單、計算速度快。但是有幾個缺點：

位置編碼數值無界（單調遞增），容易造成編碼數值過大。這樣又帶來幾個問題：
- 不能很好地處理長序列的輸入。假如對句子序列長度沒有限制，那么句子最后一個字的位置編碼比第一個字的位置編碼要大很多。即如果句子有1000個字，最后一個字的位置編碼是999，比第一個字的位置編碼0要大很多。數字越大就說明這個位置的權重越大，這與序列的真實權重不一定符合。
- 位置編碼會干擾模型。位置編碼和token的embedding會相加再傳給attention，如果word embedding的范圍比較小，則位置編碼會給相加的結果造成很大干擾。比如：最后一個字的embedding是0.5，但是其位置編碼是999，則0.5 + 999之后， 0.5的影響力會被極度消弱，數值會有傾斜，這意味著信噪比非常低，模型很難從位置信息中分離出語義信息。模型的效果會被干擾。另外也會導致模型的權重存在很大的數字，影響訓練的穩定性（比如導致梯度消失）。
缺少泛化能力。位置編碼是依據固定長度來計算的，而模型在推理時可能遇到比訓練時更長的序列，這意味著如果序列太長，位置編碼可能會失效。模型處理不好本方案訓練時沒見過的位置。比如，訓練時候最長序列是1000，但是推理時候序列超出了1000，則難以泛化。
難以和注意力機制融合。目前的位置關系是通過如下方法進行表達：$f(m-n) = f(m)-f(n) = m-n$，但是這個 f(x) 函數不好與自注意力機制結合，因為向量之間做內積乘法，減法顯然無法接受。而且，因為self-attention層中的參數是用序列長度無關方法訓練出來的，引入序列長度相關的任何參數都會導致參數目標的異化。

我們接下來分為兩支來看看如何解決上述問題。一個是嘗試減法之外的機制（乘法表示）。一個是如何解決位置編碼數值無界問題（歸一化）。

2.2 乘法表示

既然減法很難和注意力融合，而內積的方式限定了我們的計算方式只能為乘法，那我們來嘗試乘法的性質構建距離函數 f(x)，看看是否可以表達距離關系，比如如下公式：

\[f(m-n)=f(m) \times f(n) \]

這樣的問題在于乘法有交換律，無法區分位置先后，比如：

\[f(m-n)=f(m) \times f(n) = f(n)\times f(m) = f(n-m) \]

會造成”從北京去上海“和”從上海去北京“無法區分的問題。因此我們需要細化對 f(x) 的需求，使得 f(x) 不僅需要滿足:

\[f(m-n) = f(m) \times f(n) \]

還需要不滿足交換律：

\[f(m-n)=f(m) \times f(n) \neq f(n)\times f(m) = f(n-m) \]

我們來看看向量乘法。對于位置 m、n 的 token，V(m)、V(n) 對應其位置向量，結果發現向量點積乘法也滿足交換律，因此也不合適。

\[f(m-n) = V(m)\times V(n) = V(n)\times V(m) = f(n-m) \]

我們再看看矩陣乘法，發現矩陣 $R_m \times R_n$ 相乘不滿足交換律，即：

\[R^T_m\times R_n \neq R^T_n \times R_m \]

因此矩陣的乘法性質滿足我們上面不斷嚴苛的條件，順利進入我們的視野。這為后續分析RoPE打下了基礎。

2.3 歸一化

為了解決整型值帶來的位置編碼數值無界問題，我們決定試試把位置編碼限制在一定值域范圍內，最簡單的思路就是用句子長度來對位置編碼進行歸一化到[0,1]之間，即Position Encoding = position / (seq_len)，這樣就得到了一個等差數列。

代碼修改為：

max_len = 5
d_model = 4
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
pe[:, 0::2] = position / max_len
pe[:, 1::2] = position / max_len
print(pe)

輸出是：

tensor([[0.0000, 0.0000, 0.0000, 0.0000],
        [0.2000, 0.2000, 0.2000, 0.2000],
        [0.4000, 0.4000, 0.4000, 0.4000],
        [0.6000, 0.6000, 0.6000, 0.6000],
        [0.8000, 0.8000, 0.8000, 0.8000]])

這樣雖然解決了上述問題，但是又有了新的問題：對于長度不同的序列，這種歸一化方法會導致問題。

原因是：長度不同的序列的歸一化方式不一致。因為不同句子的序列長度可能不同，因此不同長度的位置編碼的步長是不同的。這就會導致在不同的句子中同一位置就會有不同的位置編碼，這反過來會混淆我們的模型，不是我們希望的。因為位置信息之中，最關鍵的就是相對位置信息，如果使用本例方式，則長文本的相對次序關系會被削弱。在較短的文本中相鄰的兩個字的位置編碼的差異與長文本中的相鄰兩個字的位置編碼可能存在數量級上的差異。我們以如下兩個句子為例：

不逢北國之秋，已將近十余年了。
北國的槐樹，也是一種能使人聯想起秋來的點綴。

兩個句子中，”北國“都是相鄰的，按照相關性的要求，在任何長度不同的序列中，相同位置的Token之間的相對位置/距離應該保持一致（體現Token位置之間差異的不變性），然而本方案卻無法滿足。第一個句子之中，PE(北) = 2/13，PE(國)=3/13。PE(北)-PE(國)=1/13。第二個句子之中，PE(北) = 0/20，PE(國)=1/20。PE(北)-PE(國)=1/20。其原因就是因為無法找到一個歸一化的標準。

我們再回到代碼來佐證，可以看到，上面示例中，每個token之間距離是0.2。如果把max_len修改為10，則得到如下，每個token之間距離是0.1。

tensor([[0.0000, 0.0000, 0.0000, 0.0000],
        [0.1000, 0.1000, 0.1000, 0.1000],
        [0.2000, 0.2000, 0.2000, 0.2000],
        [0.3000, 0.3000, 0.3000, 0.3000],
        [0.4000, 0.4000, 0.4000, 0.4000],
        [0.5000, 0.5000, 0.5000, 0.5000],
        [0.6000, 0.6000, 0.6000, 0.6000],
        [0.7000, 0.7000, 0.7000, 0.7000],
        [0.8000, 0.8000, 0.8000, 0.8000],
        [0.9000, 0.9000, 0.9000, 0.9000]])

2.4 二進制位置編碼

有沒有更好的方法來確保我們的數字介于 0 和 1 之間呢？如果我們認真思考一段時間，也許會想到將十進制數轉換為二進制數。因此，我們將位置編碼轉換為二進制表示法，并將二進制值（可能已歸一化）與嵌入維度相匹配，而不是將我們的（可能已歸一化的）整數位置添加到嵌入的每個分量中。

比如，我們將感興趣的位置（2）轉換為二進制表示（0010），且限定在$d_{model}$之內，則可以和Embedding直接相加。具體是將每一位添加到 token 嵌入的相應維度中。最小有效位（LSB）將在每個后續標記的 0 和 1 之間循環，而最大有效位（MSB）將每 $2^{n-1}$ 個 token 循環一次，其中 n 是位數。讀者可以在下圖中看到如何把0—15通過二進制編碼，得到不同索引的位置編碼向量。

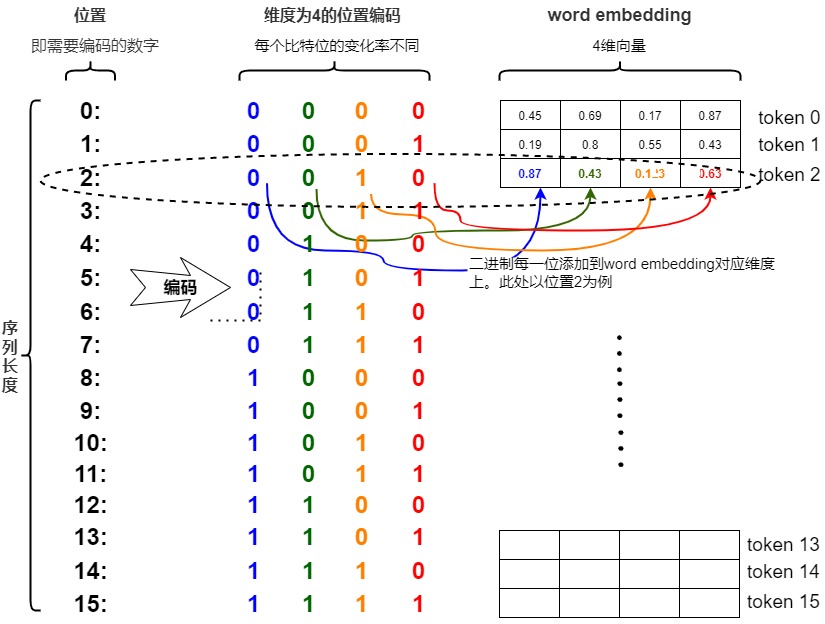
現在所有的值都是有界的（位于0，1之間），且transformer中的$d_{model}$本來就足夠大，基本可以把我們要的每一個位置都編碼出來了。

雖然看上去不錯，但是二進制編碼依然存在缺點：這樣編碼出來的位置向量處在一個離散的空間中，沒法表示浮點型。而且不同位置間的變化是不連續的，所以輸出會”跳躍“。而神經網絡的優化過程喜歡平滑、連續和可預測的變化。其實，二進制位置編碼就有了多維位置編碼的影子。而神經網絡恰好擅長處理高維數據。如果覺得二進制數字的跨度過小，想進一步增加數字的跨度，我們還可以進一步增大進制的基數，如使用6進制、8進制甚至16進制，這樣也可以進一步減少輸入的維度，又沒有縮小相鄰數字的差距（歸一化的缺點）。如果我們將二進制編碼變為連續的高進制版本，就可以建模0—10萬甚至百萬的位置編碼。

2.5 需求拓展

我們先做個小結，迄今為止我們位置編碼方案的成果是：我們已經解決了數值范圍的問題，得到了在不同序列長度上保持一致的唯一編碼。但是問題依然存在：

浮點數的世界中使用二進制值是對空間的浪費，因此我們需要一個有界又連續的周期函數。
前面的幾種方法也可以看作是類詞表方法，即建立一個長度為L的詞表，按照詞表的長度分配位置編碼。或者也可以認為是單調函數方法，此方法的特點是：追求token在序列之中的絕對位置，使得后續token的位置編碼都大于前面的token的位置編碼。

因此，我們需要考慮下，是否可以把構建重心從絕對位置調整為相對位置？即構建一個函數f，其輸入是token的絕對位置信息，輸出是token的相對位置信息。

\[相對位置信息 = f(絕對位置信息) \]

比如：“我喜歡蘋果”，如果把“歡”的位置編碼設置為0，其他token的位置編碼為該token和“歡”之間的距離，負數表示在“歡”字前面。其位置編碼就是：

\[\begin{aligned} &我\ &{-2} \\&喜 \ &{-1} \\&歡 \ &0 \\&蘋 \ &1\\&果 \ &2 \end{aligned} \]

通過使用相對位置，就可以知道token之間距離遠近。注意：相對位置編碼需要線性相關。

那么我們接下來的目標就明確了，需要尋找取值范圍是有界、平滑、連續且可以表示相對位置的函數。如果把比特位看成維度，則最好各個維度的頻率不同，低維度頻率變化快，高維度頻率變化慢。正弦函數sin就可以滿足這一點。事實上，正弦函數也能表示出二進制那樣的交替，隨著正弦函數頻率的降低，也可以達到上圖紅色位到橙色位交替頻率的變化，具體特點如下：

不同維度用不同頻率的sin組合。通過調整三角函數的頻率，我們可以實現這種低位到高位的變化。
因為每個維度是用t除以維度index，所以每個維度變化的周期和index相關，即維度的周期不同。
波長如果變長，數據變換就會變慢，符合低位變化快、高位變化慢的情況。

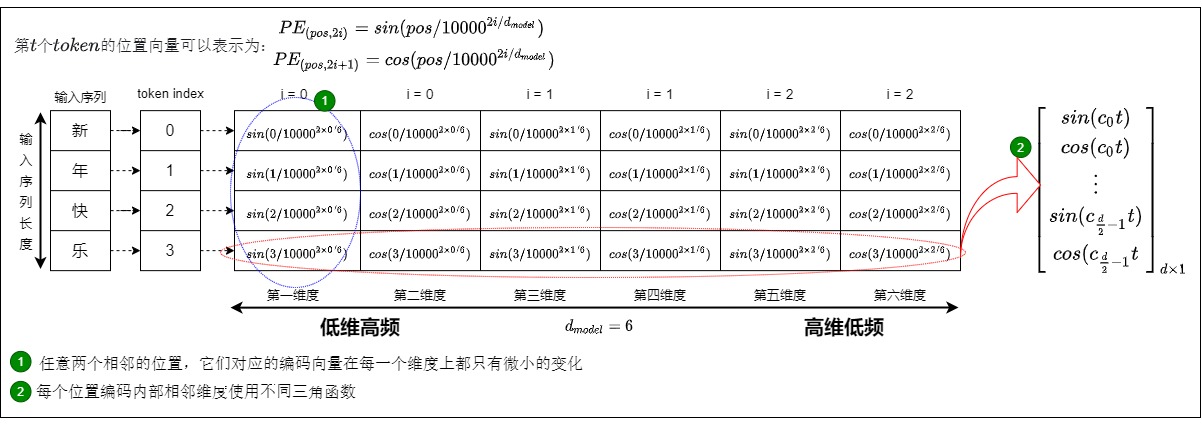
于是，我們可以考慮把位置向量當中的每一個元素（對應一個維度）都用一個sin函數來表示，則第t個token的位置向量可以表示為：

\[PE_t = [sin(\frac{t}{1}),sin(\frac{t}{2}),sin(\frac{t}{3})...,sin(\frac{t}{i}),..., sin(\frac{t}{d_{model}})] \]

我們還可以通過頻率index來控制sin函數的波長，頻率不斷減小，則波長不斷變大，此時sin函數對t的變動越不敏感。這樣可以使得編碼向量在任意維度上都能保持唯一性，即不同位置在同一個維度上不會有相同的值。這是由正弦和余弦函數的周期性和相位差保證的，即對于任意兩個不同的位置，它們對應的編碼向量在每一個維度上都不相等。假定

\[PE_t = [sin(\frac{t}{2^0}),sin(\frac{t}{2^1}),sin(\frac{t}{2^3})...,sin(\frac{t}{2^{i-1}}),..., sin(\frac{t}{2^{d_{model}-1}})] \]

第一個維度sin函數周期是完整2pi, 第二維度是4pi，依次類推，越往后，維度增加值變化的頻率依次變慢。于是我們就引入三角位置編碼。

2.6 三角函數編碼

性質

我們首先介紹幾個和位置編碼相關的三角函數的性質。

三角恒等式

三角恒等式是關于三角函數的一些已證明的恒等式，比如有兩角和差、二倍角公式、三倍角公式等。對于位置編碼最重要的是和差公式：依據兩個角度自身的正弦和余弦可以計算出它們的和與差的正弦和余弦。

\[cos(α+β)=cosα·cosβ-sinα·sinβ \\ cos(α-β)=cosα·cosβ+sinα·sinβ \\ sin(α±β)=sinα·cosβ±cosα·sinβ \\ \]

周期性

在數學中，周期函數是指經過一個確定的周期之后，數值皆能重復的函數。對于實數或者整數函數來說，周期性意味著按照一定的間隔重復一個特定部分就可以繪制出完整的函數圖。如果在函數 ??中所有的位置 x 都滿足:??(??+??)=??(??)，那么，??就是周期為 ??的周期函數。

三角函數正弦函數與余弦函數都是常見的周期函數，其周期為 2π，即 ????????=??????(??+2??)。這意味著正弦函數的圖像會在水平方向上每隔2π的長度重復一次。這個周期性是正弦函數的基本特性之一，也是其在多個領域應用的基礎。

波長

在物理學中，波形的頻率表示每秒內完成的周期數，而波長（wavelength）表示波形重復的距離。正弦函數的波長是指正弦波完成一個完整周期所需要的距離或時間。sin函數的波長與它的頻率和周期有關，頻率指一秒內周期的數量，周期指一個波所需的時間。因此，波長等于速度乘以周期。

。在公式上，正弦函數通常表示為：??=sin?(????+??)。其中：

?? 是輸出值。
??是輸入變量，通常代表時間或空間。
?? 是波數（wave number），它與波長 ?? 的關系是 ??=2????。
??是相位偏移。

因此，波長 ?? 的計算公式為：??=2??。對于RoPE而言 $??_??=2??/??_??$

定義

三角函數式位置編碼（也稱為Sinusoidal位置編碼）是Transformer原始論文提出來的位置編碼方案，這種編碼方案基于無參數的固定式三角函數來計算編碼向量（通過sin和cos函數的線性變換來提供給模型的位置信息），這樣就用絕對位置編碼來捕捉不同位置之間的相對關系，其定義如下：

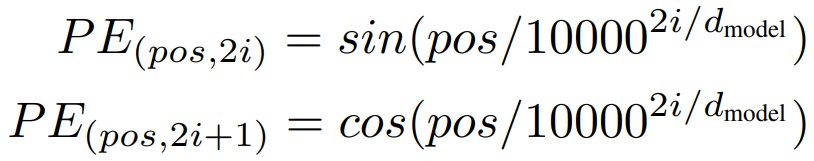
轉換成具體代碼如下：

PE(pos,2i) = sin(pos / 10000^(2i/d_model))
PE(pos,2i+1) = cos(pos / 10000^(2i/d_model))

編碼方式

Transformer作者嘗試了兩種編碼方法（學習和公式）。

從數據中學習：學習式是“learned and fixed”，即“Postional Embedding”。位置向量是在訓練過程中從數據中學習到的，它只能表征有限長度內的位置，無法對任意位置進行建模。
正弦函數：公式方法是Position Encoding，此方法使用正弦函數為每個位置構建唯一的嵌入。算出來的可以接受更長的序列長度而不必受訓練的干擾.

兩種方法取得的效果都差不多。因為通過公式來計算更簡單、參數量也更小，所以Transformer作者選擇了第二種。

公式解讀

以下是關于公式的一些說明:

$d_{model}$是詞向量維度。在論文中是直接將詞嵌入向量和位置編碼進行相加，所以我們需要讓位置編碼的維數和詞嵌入向量的維數相等。
pos是位置索引，表示此token在序列之中的位置，即單詞在序列中的位置，設句子長度為L，那么pos取值范圍是0~L-1。比如第一個token位置就是0。
i 表示位置向量的維度索引，2i 表示偶數的維度，2i+1 表示奇數維度，例如$d_{model}$ 為512，則i的取值范圍是0~255。
10000：定義的超參數標量，這是Transformer作者所使用的值。
$PE_{(pos,i)}$表示某個token的位置編碼，位置編碼不是單獨某個數字，而是一個$d_{model}$維度向量。其可以由位置索引pos和維度索引i計算得到。即正弦這一類的參數式位置編碼中涉及兩個概念：一個是距離，另一個是維度。因為結合了這兩個概念，所以可以保證在一定范圍內位置編碼的唯一性：
- 不同pos的同一維度特征對應的正弦值或者余弦值也會不一樣，這樣會導致不同位置的pos的位置編碼變得唯一。
- 同一pos的不同維度所對應的數值也不一樣。
同一個token中不同維度的特征信息，可以用sin和cos的方式計算，即使用不同頻率的正弦、余弦函數生成。每個分量上是sin，cos輪流交替的，一對相鄰的偶數和奇數分量形成一對，該對的三角函數輸入相同。可以認為是輸入x的嵌入維度上，依次加上不同頻段的正余弦波。
- 位置嵌入函數的周期從2??到10000*2??變化，而每個位置在embedding dimension維度上都會得到不同周期的sin和cos函數的取值組合。維度 i 的周期為 $??=????????^{??/??}?2??$，其中0 <= i < d，因此周期T的范圍是 ??∈[2??,?????????2??]。
- sin和cos公式表達的含義是在偶數的位置使用sin函數計算，在奇數的位置使用cos函數計算。每對奇數和偶數拼成一組，例如0,1一組，2,3一組，分別用上面的sin和cos函數做處理。
- 每組內sin和cos函數共享一個頻率，不同組函數的頻率不同（低維用高頻，高維用低頻），從而產生不同的周期性變化。這有點傅里葉頻譜變換的味道，希望用若干組cos和sin函數來代表不同的特征維度(類比頻率)。
- 第k組的頻率$f_k=2\pi \cdot 10000^{2k/d}$，其中$k=1,...,d/2$。這樣就在embedding dimension維度上隨著維度序號增大，周期變化會越來越慢。
- 所有pos相同維度上的三角函數相同（偶數都是sin，奇數都是cos），差別僅是pos值不同，因此三角函數輸入的分母相同，差異在分子。
位置編碼將詞的位置信息表征為向量，該向量由詞位置和分量位置共同確定。對輸入padding的位置采用全0向量作為位置編碼。
位置編碼矩陣所有句子共享，因此不同句子中相同位置的字/詞的位置編碼的結果相同。

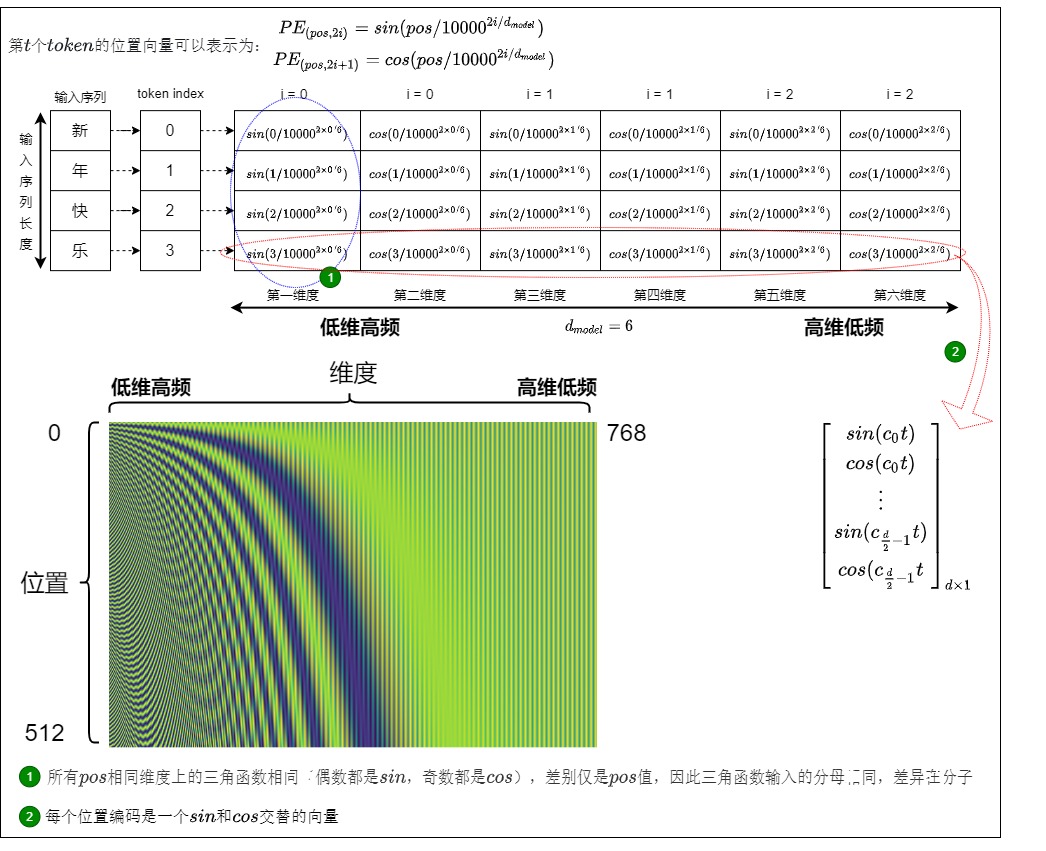
具體樣例

三角函數式位置編碼的具體樣例如下圖所示，位置編碼層的輸出是一個矩陣，矩陣的每一行表示一個 token 的位置編碼向量，每個位置編碼是一個sin和cos交替的向量（$d_{model}$可以被2整除）。其中$c_i = 1/10000^{2i/d_{model}}$

\[PE_{pos} = \begin{bmatrix} sin(c_0t) \\ cos(c_0t) \\ {\vdots}\\ sin(c_{\fracw0obha2h00{2}-1}t) \\ cos(c_{\fracw0obha2h00{2}-1}t \\ \end{bmatrix}_{d\times 1} \]

具體如下圖所示。

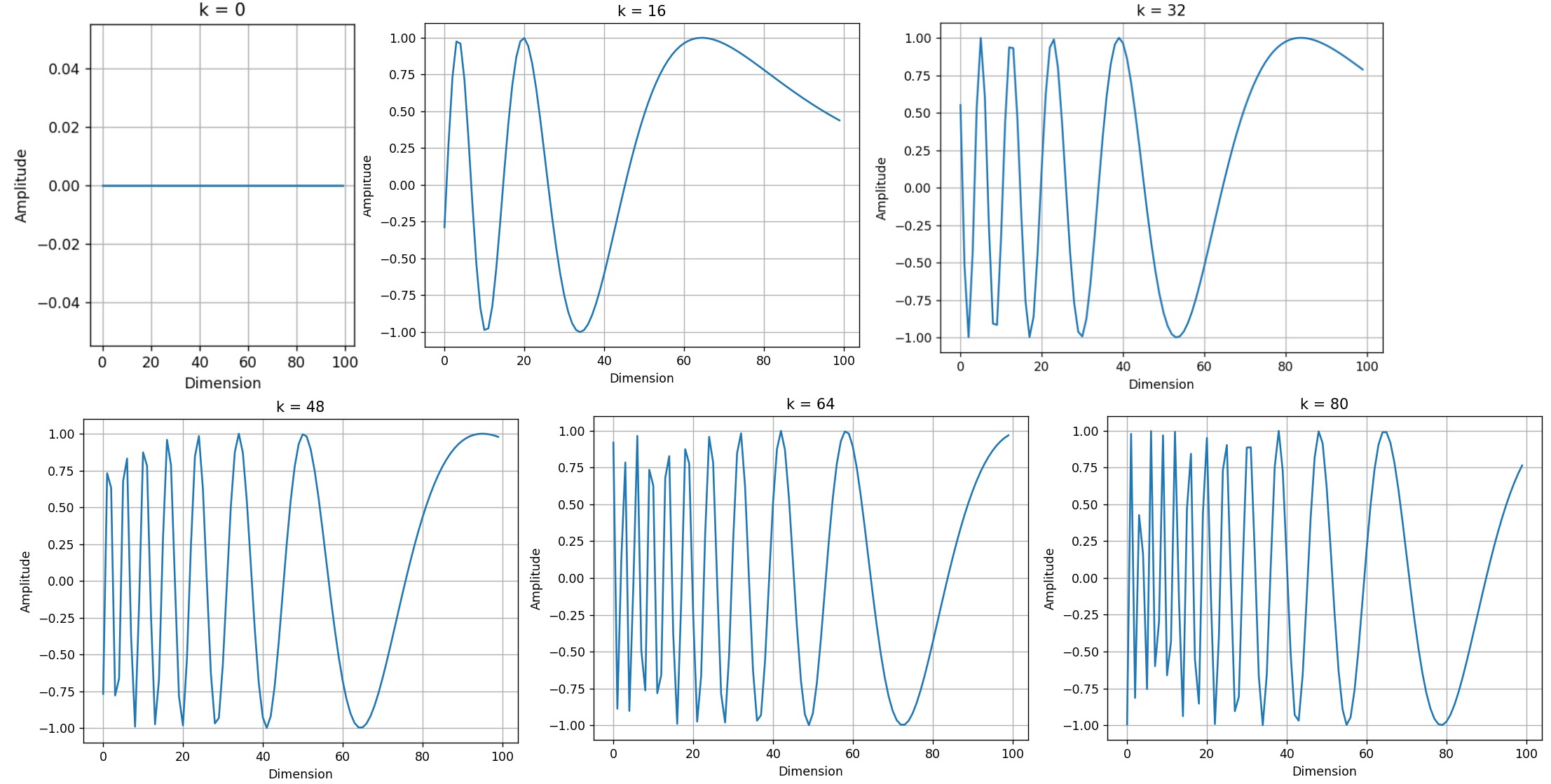
我們再設定n=10,000和d=512，看看不同位置的正弦波。

def plotSinusoid(k, d=512, n=10000):
    x = np.arange(0, 100, 1)
    denominator = np.power(n, 2*x/d)
    y = np.sin(k/denominator)
    plt.plot(x, y)
    plt.title('k = ' + str(k))
 
fig = plt.figure(figsize=(15, 4))    
for i in range(4):
    plt.subplot(141 + i)
    plotSinusoid(i*4)

可以看出，每個位置 ?? 都對應一個不同的正弦波，它將該位置編碼為一個向量。對于固定的嵌入維度 ??，波長是通過以下公式確定的：$????=2????^{2??/??}$，而且，正弦波的波長隨著嵌入維度 ?? 的增長呈幾何級數變化。

優點

簡單來說，Transformer基于正余弦的位置編碼用維度控制頻率，用位置控制相位。就是對不同維度使用不同頻率（隨特征維度變化，低維用高頻，高維用低頻）的正/余弦函數進而生成不同位置的高維位置向量。

正弦位置編碼有幾個明顯的優點：

簡單且可解釋。
采用公式生成，避免了訓練得到的位置向量固定長度的尷尬。
- 位置編碼是根據絕對位置計算的，而且是固定的，這意味著模型在訓練和測試時使用相同的位置編碼，保持一致性。
- 編碼值不依賴于文本的長度。
有值域范圍限制，其優點如下：
- 采用sin-cos位置編碼保證了位置向量值在-1~1之間，穩定可控。除了第一行以外，位置矩陣的所有值都是三角函數sin，cos的結果，因此所有位置和各分量上的結果都是介于-1到1之間的，使得位置編碼值固定在一個區間內不會太大或者太小，從而使得位置編碼和詞原始embedding相加存在可行性。而且，導出的位置編碼與input_embedding相加不會使得結果偏離過大而對詞義產生破壞。
- cos, sin函數的值域在[-1, 1]之間，且是周期性的，非常適合用在神經網絡中的初始化賦值中。
可以泛化到未見過的數據、以及易于擴展。
- 模型可以接受不同長度的輸入。
- 三角函數有顯式的生成規律，具有一定外推性。由于位置編碼是基于三角函數計算的，使 PE 能夠處理比訓練時見過的序列更長的輸入。假設訓練集里面最長的句子是有 20 個單詞，突然來了一個長度為 21 的句子，則使用公式計算的方法可以計算出第 21 位的 Embedding。
- 位置向量的值是有界的，且位于連續空間中。模型在處理位置向量時更容易泛化，即更好處理長度和訓練數據分布不一致的序列（sin函數本身的性質）
可以反應相對位置信息.
- 能通過三角函數關系表達2個位置的相對關系，這樣能夠體現詞匯在不同位置的區別（特別是同一詞匯在不同位置的區別）。
- 不同位置之間的位置向量是正弦和余弦函數的周期函數。這使得不同位置之間的位置向量能夠保持一定的相似性，從而幫助模型更好地理解位置信息并捕捉到序列中的順序關系。可以讓模型容易地計算出相對位置，對于固定長度的間距 k，PE(pos+k) 可以用 PE(pos) 計算得到。因為 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。

0x03 三角函數編碼思路分析

前面我們講述了理想情況下位置編碼應滿足的性質。因為三角函數編碼是Transformer論證采用的方案，所以我們用這些性質來驗證三角函數編碼的設計思路。

3.1 作者的話

Transformer為什么要使用正弦位置編碼？論文作者表示是因為正弦位置編碼可以表達相對位置，而且可以外推到訓練之外的長度。原文如下。

因為作者并沒有解釋設計思路，所以我們需要在接下來繼續探究。下面幾個小節之間彼此有糾纏。比如討論多維度時候會默認使用三角函數。討論三角函數時候會使用多維度進行討論。這是雙生花，一個硬幣的兩面。

3.2 為何要多維度

把token在序列中的位置記為pos，把向量的某一維度記為i，我們需要為pos的向量的每個數設置一個實數數值，該數值要滿足如下性質：

同一個pos的不同維度i的數值要各不相同。
不同向量的同一個維度的數值要依據pos不同而不同，且編碼規則要滿足相對關系，即$f(pos+1)-f(pos)=f(pos)-f(pos-1)$。

Sinusoidal位置編碼恰恰可以滿足上面的條件。我們用如下代碼生成圖例，假定句子長度是512，詞向量維度是768。Positional Encoding是定義在位置-維度平面上的二元函數。

import numpy as np
import math
from matplotlib import image

seq_len = 512
dimension = 768
data = np.zeros((seq_len, dimension))

for pos in range(seq_len):
   for i in range(dimension):
      if i % 2 == 0:
          data[pos,i] = math.sin(pos / math.pow(10000, i / dimension))
      else:
          data[pos,i] = math.cos(pos / math.pow(10000, (i-1) / dimension))

image.imsave('Sinusoidal.png', data)

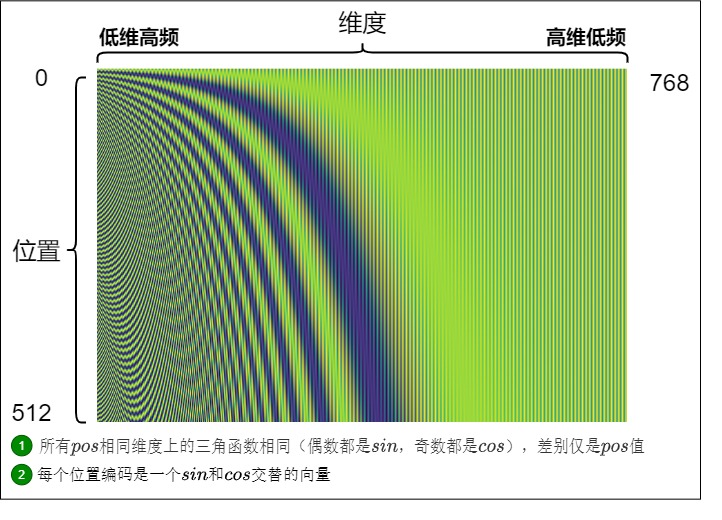
Sinusoidal位置編碼與維度分量的關系如下圖所示，可以發現：

每個分量都具有周期性，是正弦或余弦函數。
越靠后的分量(i 越大)，波長越長，頻率越低。

這樣，每個位置在embedding dimension維度上都會得到不同周期的sin和cos函數的取值組合，每一維度上都包含了一定的位置信息，而各個位置字符的編碼值又各不相同。從而產生獨一的紋理位置信息，模型從而學到位置之間的依賴關系和自然語言的時序特性。

了解了這些基本的特性后，接下來就需要討論更加深層次的問題。我們來看看為何要用一個向量來表達位置信息，具體來說，向量有如下幾點優勢：

利用處理。
避免重復。
增加差異性，能夠對位置不同進行差異化刻畫，區分特征維度。

利于處理

如何將positional encoding融合到自注意力算法中？具體有兩個方案：直接改輸入矩陣 X ，或者改self-attention的算法。顯然改輸入矩陣更直觀和方便。

確定修改輸入矩陣后，我們再考慮到位置信息作用在input embedding上。比起用單一的值，更好的方案是用一個和input embedding維度一樣的向量來表示位置。只要讓positional encoding生成的positional embedding和token embedding一樣長，就能直接相加獲得與原來相同大小的新輸入矩陣，不需要修改self-attention算法。

避免重復

接下來我們看看為何為向量的每個維度設置一個周期。

我們先假設使用sin函數來生成位置編碼。因為正弦圖像是具有周期性的，如果各個維度使用同一sin函數，比如$PE(pos)=sin(pos)$。因為可能會出現不同的位置是一個值的情況，那么維度之間就會出現相關性，就不能有效的使用全部的高維度空間作為編碼空間，也就失去了位置編碼的意義，因為如何讓不同詞之間分開才是位置編碼的目的。

因此不能直接使用pos，我們可以加入一個alpha參數來調控位置函數的波長。

\[PE(pos) = sin(\frac{pos}{\alpha}) \]

如前文所述，token的embedding維度是$d_{model}$，則位置編碼的維度也是$d_{model}$，那么這個$d_{model}$維度向量的不同維度上可以采用不同的$\alpha$ 。假設$\alpha$就設定為維度的index，即，

\[PE_t = sin(\frac{t}{i}) \]

我們得到如下公式。這一行代表第t個token的位置編碼$PE_t$，行中的第i個元素就是$PE_t$中的第i個維度的元素。這樣每個維度sin函數的周期不同，就會降低重復的幾率。

\[PE_t = [sin(\frac{t}{1}),sin(\frac{t}{2}),sin(\frac{t}{3})...,sin(\frac{t}{i}),..., sin(\frac{t}{d_{model}})] \]

我們再來討論下調控參數（或者叫做底數）$\alpha$的取值。實際上，Transformer位置編碼中的分母 $10000^{2i/d_{model}}$就是$\alpha$，我們可以通過α來調節函數周期。

$\alpha$ 如果比較小，$pos/\alpha$則容易很大，會導致函數的頻率偏大，引起波長偏短，周期偏小，這樣很容易進入下一個周期，從而出現不同t下的位置向量可能出現重合的情況，在長文本中還是可能會有一些不同位置的字符的編碼一樣（一個較小的t和一個較大的t代表的向量可能會重合）。因此需要拉長波長（三角函數周期）來確保不同位置的向量不發生碰撞，這就要把所有的頻率都設成一個非常小的值，就是取較大的$\alpha$來減少重復幾率。
$\alpha$ 如果比較大，位置向量能表示的序列就越長，這是大底數的好處。但是 $\alpha$如果過大，意味著周期越大，在-1到+1的范圍內向量的取值越密集，則相鄰token的位置編碼差異較小，向量幾乎重合。這對后續的Self-Attention模塊來說是不利的，因為它需要經歷更多的訓練次數才能準確地找到每個位置的信息，或者說，才能準確地區分不同的位置。而且，長序列需要長編碼。但這樣又會增加計算量，特別是長編碼會影響模型的訓練時間。所以，底數并非是越大越好。

所以，$\alpha$的取值要定在一個合適的范圍。我們進一步細化，把分母改寫為$\alpha ^{2i/d_{model}}$，這樣更加清晰。對于$\alpha$，Transformer作者取了一個實驗上的經驗數值10000。使用 10000 很可能就是確保循環周期足夠大，以便編碼足夠長的文本。

區分特征維度

引入多個維度之后就會在高維的表示空間對位置編碼以及token的語義做進一步細分，不止是按照一個一個詞來分，而是按照詞和詞嵌入的特征來分，讓不同維度刻畫不同特征，在不同維度表示單一位置的不同信息，體現位置的差異性。比如高頻分量對應局部語義影響，低頻分量對應長上下文語義影響。在不同維度上用不同的函數，能夠進一步增強這種差異性。這樣不僅不同詞之間分開了，同一個詞不同的特征之間也能區分出來。

除此之外，從模型可解釋性出發，位置編碼，尤其是包含相對偏置的編碼方案，為特征向量$ q_t,k_s$ 的不同維度賦予了不同的實際含義。增加了Transformer架構的可解釋性。

3.3 為何要多種頻率

位置編碼存儲的是一個包含各頻率的正弦和余弦對，但是為什么用包含各多種頻率的三角函數？其實，此問題和上一個問題有一定關聯，因此放在一起分析。多種頻率有幾個好處：

可以使得不同位置的編碼向量之間有一定的規律性（這是由正弦和余弦函數的連續性和單調性來保證的）。比如相鄰位置之間的差異較小，而距離較遠的位置之間的差異較大，即：
- 對于任意兩個相鄰的位置，它們對應的編碼向量在每一個維度上都只有微小的變化。
- 對于任意兩個距離較遠的位置，它們對應的編碼向量在每一個維度上都有較大的差異。
可以使得編碼向量在任意維度上都能保持唯一性，即，對于任意兩個不同的位置，它們對應的編碼向量在這些維度上不會完全相等（這是由正弦和余弦函數的周期性和相位差保證的）。注：接下來會對周期性做嚴格分析。
和時鐘系統有點類似，時針分針秒針分別表示不同粒度的時間。這里則用不同的顆粒度來捕獲更細粒度的位置信息。

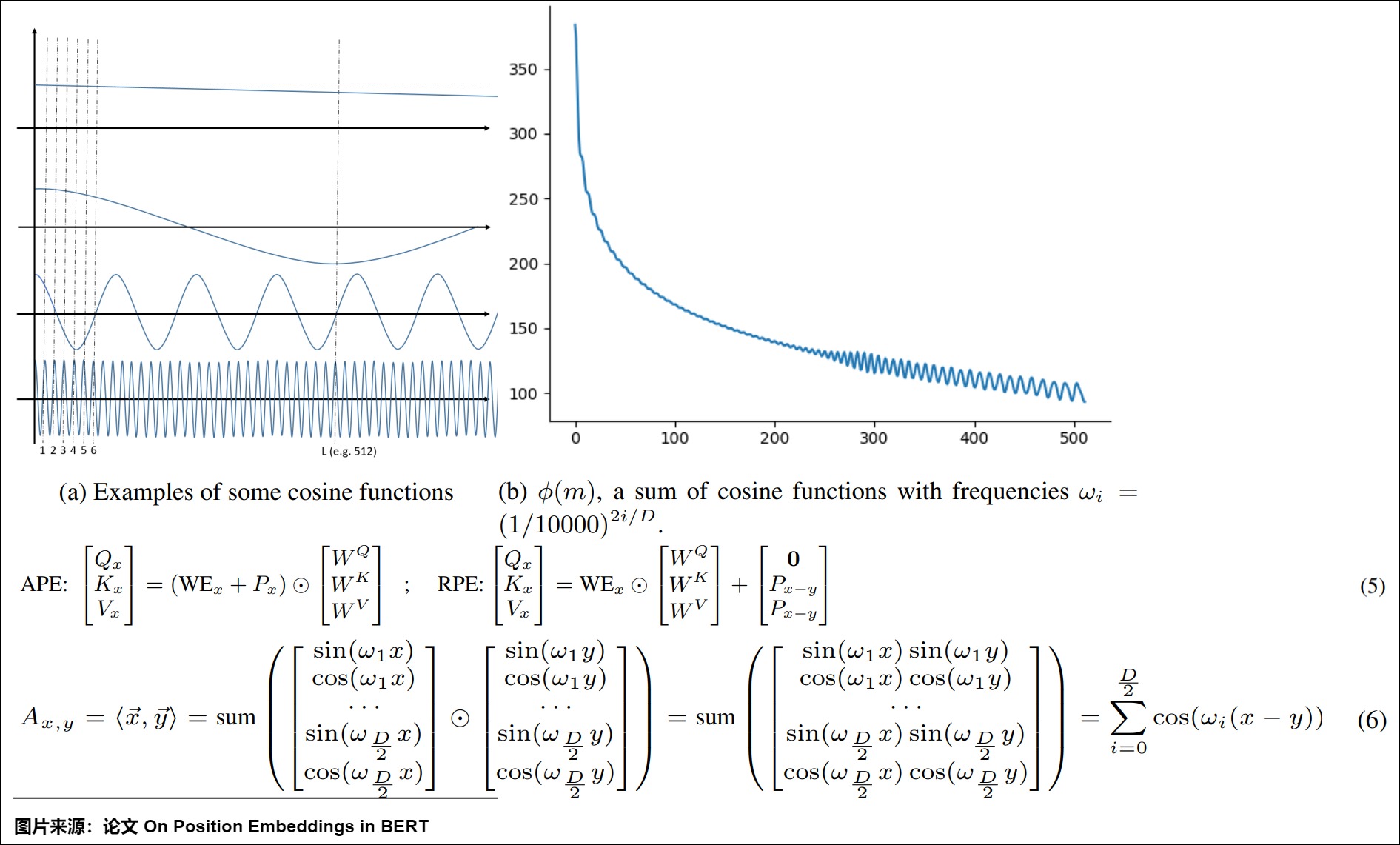
這種模式可以自適應地調整頻率以滿足不同的功能。比如上圖(b)， $\phi(m)$是單個頻率的多個余弦函數之和，它決定了任意兩個m距離位置向量之間的接近度，這里m是增加趨勢。如(a)所示，每個頻率可以發揮不同的作用：

極小的頻率對公式中的整體單詞表示（$WE_x+P_x$）幾乎沒有影響，因為它使這種位置嵌入隨著位置的增加而幾乎相同。
一些較小的頻率（$ω_i<\frac{\Pi}{L}$）可能有利于保證單調性（隨著距離的增大而衰減）。
一些更大的頻率會促進局部參與機制，因為如果$ω_i$足夠大，方程6中的cos函數在開始時會急劇下降。
一些大頻率（$ω_i>\Pi$）將是整體模式的平滑因子，因為它會隨機地對所有位置施加偏差。

3.4 為何同時使用cos，sin

同時使用cos，sin的主要原因是：

讓相近位置的單詞更容易區分。如果兩個詞距離很近，則其攜帶信息其實是類似的，這樣如果兩個詞轉換為向量，則其在向量空間內就會距離很近，容易互相影響。如"I love reading books"，reading和books它們一起出現的概率是較大的（對應于離得近的詞）。因此，語義相近的單詞一定要在位置上可以很容易的區分出來。為了讓兩個相鄰的維度產生差異，對位置不同進行差異化刻畫，Transformer在偶數維度用正弦，奇數維度用余弦。
sin/cos交替可以讓周期變得更長。
sin/cos交替可以讓模型很容易地計算出相對位置。對于固定長度的間距 k，PE(pos+k) 可以用 PE(pos) 計算得到。因為 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)，即sin(x+k)和cos(x+k)都可以用二者表示出來。

另外，知乎上有帖子也對“是否一定設置奇偶下標 2i 和 2i+1”展開了討論。討論中提到 tensor2tensor 的最初版本只是簡單地分了兩段（前 256 維使用 sin，后 256 維使用 cos)，并且tensor2tensor的作者解釋是因為后面的全連接層可以幫助重排坐標，所以sin 和 cos 這個交錯形式沒有特別的意義，我們可以按照任意的方式重排它。相關代碼如下：

 return tf.concat([tf.sin(scaled_time), tf.cos(scaled_time)], axis=1)
// PE(pos, 0:channels/2) = sin(scaled_time)
// PE(pos, channels/2:)  = cos(scaled_time)

tensor2tensor作者回復引用如下：

I think this does not matter, since there is a fully connected layer after the encoding is added (and before) and it can permute the coordinates.

3.5 表示絕對位置

接下來我們看看為何三角函數可以表示絕對位置，其實，這也是對三角函數優點的解讀。

結論

我們先說結論，使用多個周期不同的周期函數組成的多維度編碼和遞增序列編碼其實是可以等價的。這也就回答了為什么周期函數能夠引入位置信息。實際上，只要能找到多個周期不同但特征相同（例如余弦函數的波形都是相同的，這就是特征相同）的函數，理論上都可以用來做positional encoding。

解讀

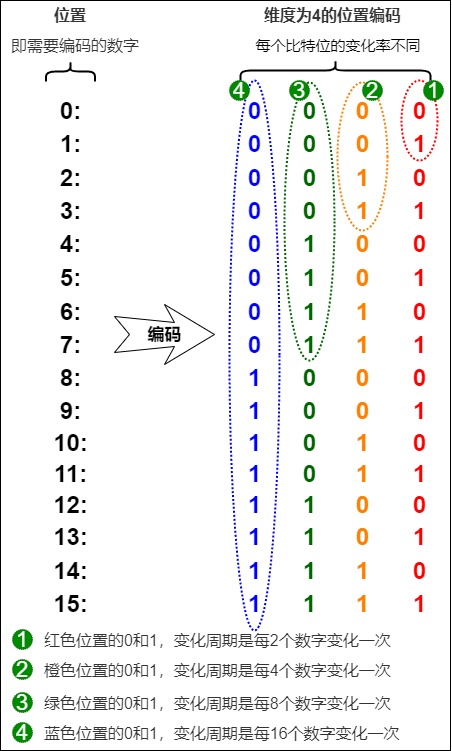
我們使用網上傳播非常廣的例子作為樣例。因為轉換進制可以理解為使用多維數據來表示相同含義，所以我們可以用二進制位置編碼法來代替三角函數編碼。如下圖，假設有一個序列有16個token，且embedding size為4，我們就能用二進制編碼法得出每個token的positional embedding，而且可以發現如下規律。

不同位置上的數字交替變化。每一列上的數字都是0，1交替變化。
每個維度（也就是每一列）其實都是有周期的，但是不同列上周期變換的規律不同。每個比特位的變化率是不一樣的，越低位的變化越快，最后一位數字每次都會0、1交替；倒數第二位置上兩個交替一次，以此類推。即紅色位置0和1每個數字會變化一次，而橙色位，每2個數字才會變化一次。即，第i列上的周期為$2^i$個數據交替一次。

這其實也在一定層度上回答了為什么周期函數能夠引入位置信息。而三角函數編碼中正余弦的交替在某種意義上等價于位置的二進制表示的alternating bits。

周期性

我們接下來看看周期性會不會重復。

首先，我們采用網上同樣經典的鐘表例子，來看看鐘表視角下的高維旋轉。一塊鐘表有三根針：

秒針：走得最快。
分針：走得中等。
時針：走得最慢。

這三個頻率各不相等的圓周運動就構成了時刻。當兩塊表擺在你面前時，即使走得最快的秒針重合了，但是如果走得較慢的分針和時針不一樣，他們照樣能代表不同的時刻。

正弦編碼的公式就定義了一個“鐘表”，“鐘表”有d/2根指針，d就是編碼的長度，i表示指針的序號。指針的位置可以唯一地由一對正余弦值表示，即(sinθ,cosθ)，其中θ是指針與水平方向的夾角。不同指針的頻率不同，第0根指針的頻率是1，最后一根指針的頻率是1/10000。相鄰兩個指針的頻率呈一個固定的倍數關系，即中間的指針按等比數列的規律排列。很顯然，不同的位置編碼唯一對應“鐘表”的“一個時間點”。我們知道，鐘表是有周期的，12小時一個周期。正弦編碼也有周期，如果選擇得當，就會即表達了位置信息，也具備一定的外推性。

其次，我們看看在正弦編碼中如何選擇才能保證任意一個子空間內，位置編碼都是唯一的，從而避免重復。

注：i 表達位置在序列中的獨特性，由底數決定每個子空間的不同，子空間內部由sin，cos來區分。

三角函數的性質如下：

(sinx, cosx)組成的向量對的周期是$4\pi$
假設在第k個子空間內，i,j位置發生了重復，那么存在整數m，使得$j\theta_k - i\theta_k=4m\pi$，那么$\theta_k=\frac{4m\pi}{j-i}$
在任意第k個子空間內，只要$\theta_k$公式中不含有$\pi$，則旋轉角度序列$\{{i\theta_k}\}_i$都不會出現周期性重復。

\[PE(pos, 2i)=sin(pos/10000^{2i/d_{model}}) \\ PE(pos, 2i+1)=cos?(pos/10000^{2i/d_{model}}) \]

因此，在設置合適的??值的前提下，每個位置都能取到唯一的位置編碼，這體現了位置編碼的絕對性。

最后，我們看看周期內的一些特殊節點。記$B=10000^{1/d}$，那么$\theta_k=\frac{1}{B^{k-1}}$是一個等比數列，其周期如下。

	0	$1/B$	$1/B^2$	...	$1/B^{d-1}$
周期	$2\pi$	$2B\pi$	$2B^2\pi$	...	$2B^{d-1}\pi$

在這個過程當中，有三個節點非常的關鍵，分別是$\pi$/2, $\pi$, 2$\pi$。

只有當cos/sin內部的取值在訓練階段遍歷0到$\pi$/2，模型才會意識到cos為負、sin不單調；
只有當cos/sin內部的取值達到$\pi$，模型才會意識到cos不單調、sin為負；
只有當cos/sin內部的取值達到2$\pi$，模型才能感知到所有的可能的cos/sin取值，進而可能意識到每個維度位置編碼的周期性表示（真正意識到周期性表示可能需要在訓練長度范圍內經歷一輪以上的周期）。

3.6 表示相對位置

相對語義的重要性

語義應該是和相對位置更加有關，而不是絕對位置，即i和j之間的語義相似性計算應該依賴向量還有相對距離，而不依賴其絕對位置。

\[Q_iK^T_j = g(X_i, X_j, i-j) \]

之前我們對三角函數位置編碼的推演如下：

\[PE_t = [sin(\frac{t}{1}),sin(\frac{t}{2}),sin(\frac{t}{3})...,sin(\frac{t}{i}),..., sin(\frac{t}{d_{model}})] \]

PE形式只用sin()還沒有解決相對性，如果能夠實現任意位置的編碼只需通過一個相對值的變換即能轉換到距離當前同樣相對值的位置編碼表示的形式，則這種編碼方式才可實現相對性的特性。所以我們對位置向量再提出一個要求，不同的位置向量是可以通過線性轉換得到的。這樣，我們不僅能表示一個token的絕對位置，還可以表示一個token的相對位置。這就需要cos函數的加入。此處其實也是部分回答了如下問題：為何用sin和cos交替來表示位置？

結論

我們也先說結論。所以三角式位置編碼作為一種絕對位置編碼，也包含了一定相對位置信息，即三角函數式位置編碼可以用絕對位置編碼來捕捉不同位置之間的相對關系。其原因是因為三角函數有如下性質：

\[sin(α+β)=sinαcosβ+cosαsinβ \\ cos(α+β)=cosαcosβ-sinαsinβ \]

這說明sin-cos位置編碼具有表達相對位置的能力，即位置$\alpha + \beta$向量可以表達為位置$\alpha$向量和位置$\beta$ 向量的組合。因此可以得到兩個結論：

兩個位置編碼的點積僅取決于偏移量（相對位置），即兩個位置編碼的點積值可以反映出兩個位置編碼間的距離。
給定距離，任意位置的位置編碼都可以表達為一個已知位置的位置編碼的關于距離的線性組合。

證明

結論1是：時間步p和時間步p+k的位置編碼的內積，即 $PE_p . PE_{p+k}$ 是與p無關，只與k有關的定值。也就是說，任意兩個相距k個時間步的位置編碼向量的內積都是相同的，這就相當于內積蘊含了兩個時間步之間相對位置關系的信息。

首先，下面是點積的計算。可以看到，兩個位置向量的內積只和相對位置 ?? 有關。

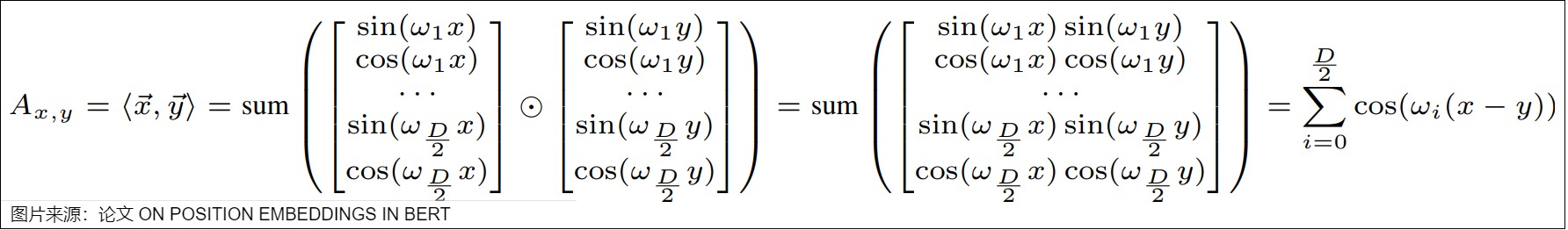
其次，具體證明過程如下，這里$c_i$是$\frac{1}{10000^{\frac{2i}{d_{model}}}}$，其中，d 表示位置嵌入的維度

\[c_i = \frac{1}{10000^{\frac{2i}{d_{model}}}} \]

公式中用到了三角變換公式：

\[cos(x-y)=sin(x)sin(y) + cos(x)cos(y) \]

結論2是：相隔 k 個詞的兩個位置 pos 和 pos+k 的位置編碼是由 k 的位置編碼定義的一個線性變換，即$PE_{pos+k}$可以表示成$PE_{pos}$的線性函數。具體證明如下。

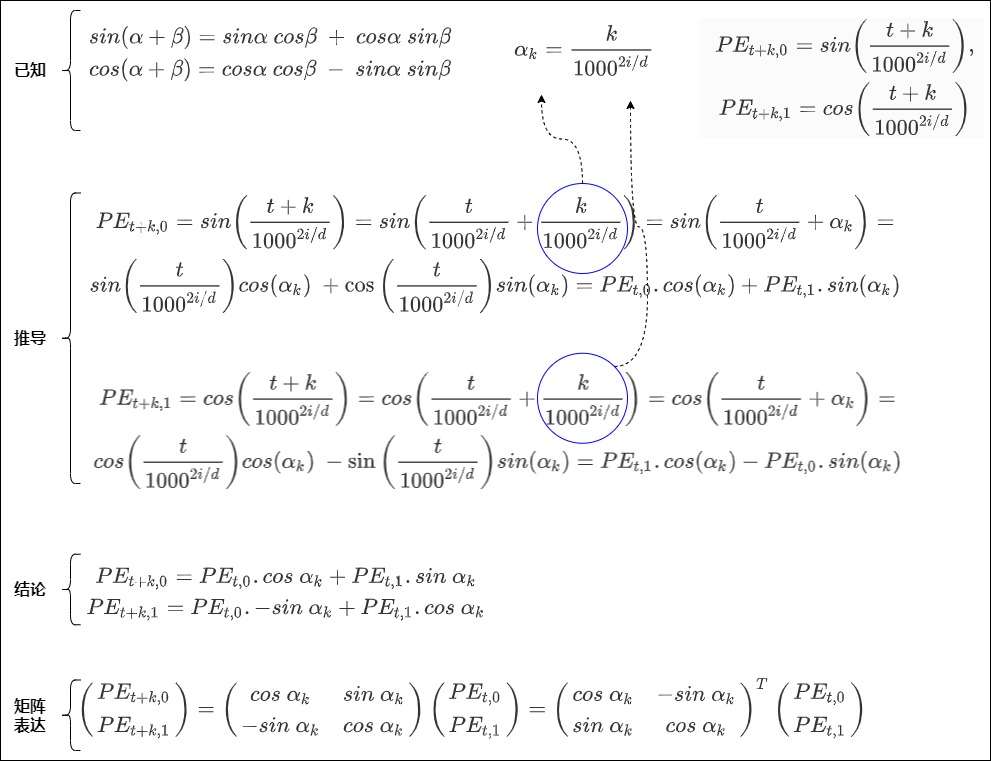
首先做簡化，把pos用t來表示，把 $d_{model}$用d表示，使用1000。這樣在三角式位置編碼中，位置 t 對應的位置向量在偶數位和奇數位的值分別為：

\[PE_{t,2i} = sin\bigg(\frac{t}{1000^{2i/d}}\bigg), \\PE_{t,2i+1} = cos\bigg(\frac{t}{1000^{2i/d}}\bigg) \]

已知三角恒等式如下：

\[sin(\alpha + \beta) = sin \alpha\ cos\beta\ + \ cos\alpha \ sin\beta \\ cos(\alpha + \beta) = cos \alpha\ cos\beta\ - \ sin\alpha \ sin\beta \]

假設位置編碼的維度是2，即i=0的情況。有

\[PE_{t+k,0} = sin\bigg(\frac{t+k}{1000^{2i/d}}\bigg), \\ PE_{t+k,1} = cos\bigg(\frac{t+k}{1000^{2i/d}}\bigg) \]

假設

\[\alpha_k =\frac{k}{1000^{2i/d}} \]

得到

\[PE_{t+k,0} = sin\bigg(\frac{t+k}{1000^{2i/d}}\bigg) = sin\bigg(\frac{t}{1000^{2i/d}} + \frac{k}{1000^{2i/d}}\bigg) = sin\bigg(\frac{t}{1000^{2i/d}} + \alpha_k\bigg) = \\ sin\bigg(\frac{t}{1000^{2i/d}}\bigg)cos(\alpha_k) \ + \cos\bigg(\frac{t}{1000^{2i/d}}\bigg)sin(\alpha_k) = PE_{t,0} . cos(\alpha_k) + PE_{t,1}.sin(\alpha_k)\\ \]

以及

\[PE_{t+k,1} = cos\bigg(\frac{t+k}{1000^{2i/d}}\bigg) = cos\bigg(\frac{t}{1000^{2i/d}} + \frac{k}{1000^{2i/d}}\bigg) = cos\bigg(\frac{t}{1000^{2i/d}} + \alpha_k\bigg) = \\ cos\bigg(\frac{t}{1000^{2i/d}}\bigg)cos(\alpha_k) \ - \sin\bigg(\frac{t}{1000^{2i/d}}\bigg)sin(\alpha_k) = PE_{t,1} . cos(\alpha_k) - PE_{t,0}.sin(\alpha_k)\\ \]

即

\[PE_{t+k,0} = PE_{t,0} . cos\ \alpha_k + PE_{t,1}.sin\ \alpha_k\\PE_{t+k,1} = PE_{t,0}.-sin\ \alpha_k + PE_{t,1} . cos\ \alpha_k \]

因為任何變換三角函數參數的運算T都必須是某種旋轉，而旋轉可以通過對（余弦，正弦）對來應用線性變化完成。所以我們用矩陣來把上面公式重新表示，得到。

\[\begin{bmatrix} PE_{t+k,0} \\ PE_{t+k,1} \end{bmatrix} = \begin{bmatrix} cos\ \alpha_k & sin\ \alpha_k \\-sin\ \alpha_k & cos\ \alpha_k \end{bmatrix} \begin{bmatrix} PE_{t,0} \\ PE_{t,1} \end{bmatrix} = \begin{bmatrix} cos\ \alpha_k & -sin\ \alpha_k \\sin\ \alpha_k & cos\ \alpha_k \end{bmatrix}^T \begin{bmatrix} PE_{t,0} \\ PE_{t,1} \end{bmatrix} \]

這說明$PE_{t+k}$ 可以分解為一個“與相對距離k有關的矩陣”和$PE_t$的乘積。假定這個“與相對距離k有關的矩陣”為$R_k$，則有 $PE_{t+k} = R^T_k . PE_t$，進一步可以得到

\[PE_{t+k_1+k_2} = R^T_{k_1} R^T_{k_2}PE_t \]

即有 $R_{k_1+k_2} = R_{k_1}R_{k_2}$。

另外依據 $-sin\ \alpha_k = sin\ -\alpha_k$和$cos\ \alpha_k = cos \ - \alpha_k$，可以得到 $R_{k_1} = R^T_{-k_1}$，進一步有

\[R_{k_2-k_1}=R^T_{k_1}R_{k_2} \]

證明完成。我們再用一張圖片總結如下：

或者我們進一步來拓展。

\[因為 \ \alpha_k =\frac{k}{1000^{2i/d}} \\這就是 PE_k \]

因此得到

\[PE_{t+k,2i} = PE_{t,2i} \times PE_{k,2i+1} + PE_{t,2i+1} \times PE_{k,2i} \\ PE_{t+k,2i+1} = PE_{t,2i+1} \times PE_{k,2i+1} - PE_{t,2i} \times PE_{k,2i} \\ \]

因為相對距離k是常數，因此 $PE_{k,2i}$和$PE_{k,2i+1}$是常數。，分別簡寫為 u, v 可得下式：

\[\begin{bmatrix} PE_{t+k,2i} \\ PE_{t+k,2i+1} \end{bmatrix} = \begin{bmatrix} v & u \\-u & v \end{bmatrix} \begin{bmatrix} PE_{t,2i} \\ PE_{t,2i+1} \end{bmatrix} \]

$PE_{t+k}$可以表示為$PE_t$ 的線性變換表示。作者希望借助上述絕對位置的編碼公式，讓模型能夠學習到相對位置信息。我們繼續拓展上面圖得到如下。

3.7 旋轉

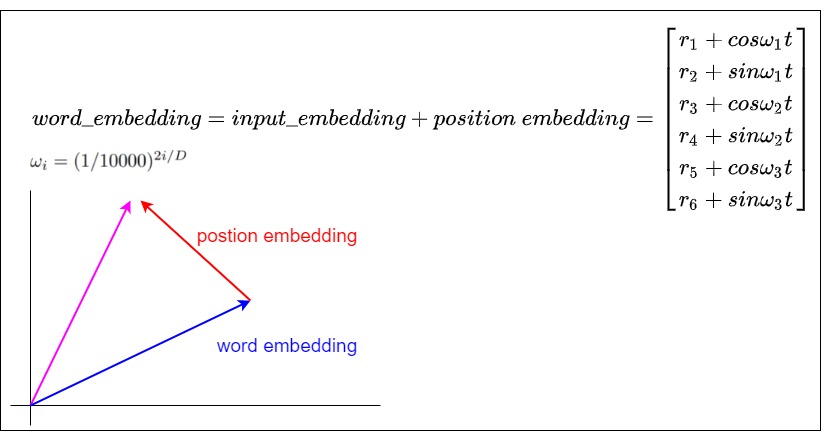
從一個角度來看，$PE_{t+k}$是$PE_t$按照順時針旋轉得到的。公式就是根據向量的下標兩兩配對，分成多組，每一組的二維向量根據位置信息進行順時針旋轉，旋轉的角度跟相對位置是線性關系。證明如下。

從另一個角度來看，三角函數式位置編碼其實就是以旋轉的方式給詞向量注入位置信息。如果我們是用加法將詞向量和位置向量合在一起，也相當于是在原始的詞向量上施加一個平移。

3.8 為何是相加

此問題是：為什么位置編碼是和詞嵌入相加而不是將二者拼接起來？關于此問題也有很多討論和分析。我們具體學習下。

解釋1：無論拼接還是相加，最終都要經過多頭注意力的各個頭入口處的線性變換，進行特征重新組合與降維，其實每一維都變成了之前所有維向量的線性組合。而拼接會導致維度增加，需要再經過一個線性變換降低維度，這樣會擴大參數空間，占用內存增加，而且不易擬合。和拼接相比，相加是先做線性變換后融合，可以節約模型參數。
解釋2：相加，在一定程度上保持了token和position這兩個embedding空間的獨立性，體現的是一種特征交叉；拼接會讓2個embedding空間被融合成了一個統一的大embedding空間，這時候再做線性變換只是相當于降維或者說池化。其實在數學上是等價的，用哪種方案都行。

0x04 三角函數編碼的特性

我們已經知道了三角函數編碼的一些優秀特性。

在設置合適的??值的前提下，每個位置都能取到唯一的位置編碼（絕對性）。
一個位置編碼可以由另一個位置編碼旋轉而來（相對性）。

我們接下來看看三角函數編碼的一些其它特性。

4.1 無向性

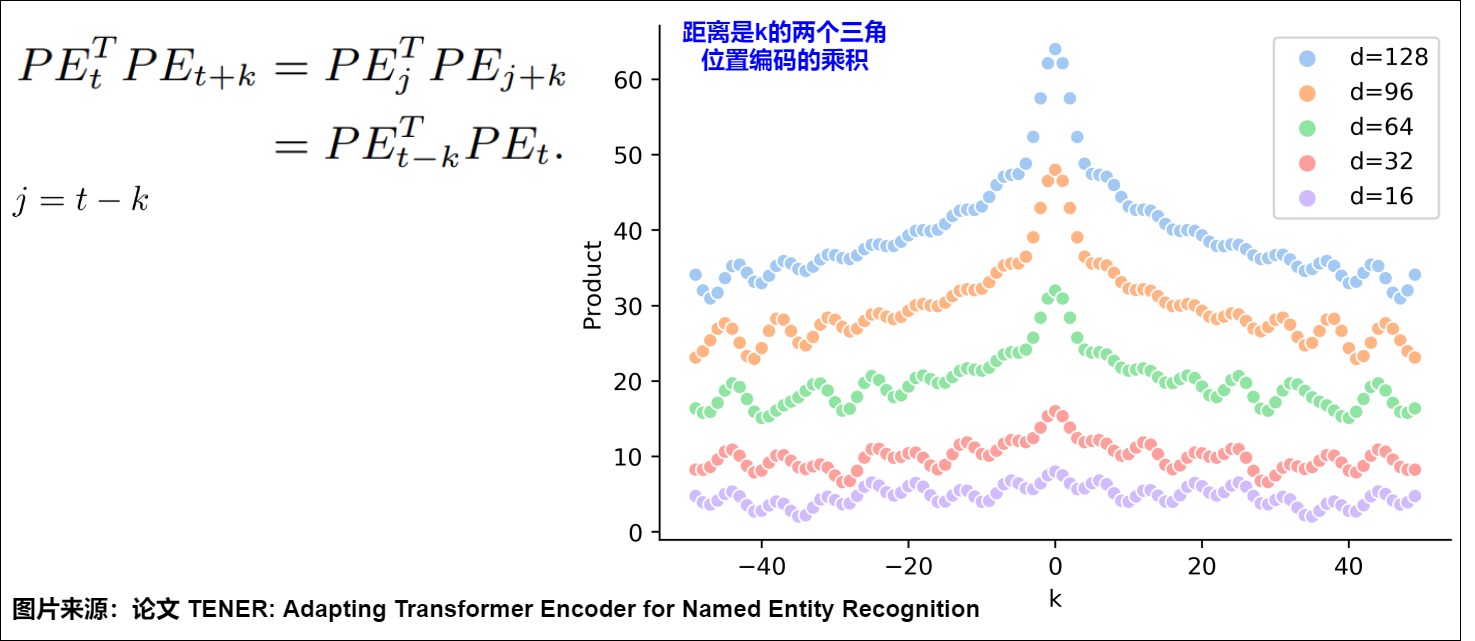
正弦位置編碼的一個特性是：相鄰時間步之間的距離是對稱的，并隨時間衰減。這說明三角函數位置編碼無法學習到方向。其原因是因為兩個token之間的距離只和相對距離k有關，和位置t或者j無關，所以位置t->t+k之間的距離，和位置j->j+k之間的距離是相等的。具體如下圖所示，圖上一些基礎信息如下：

橫軸表示 Δ。
縱軸表示固定某個 $????_??$ 的情況下，改變 Δ 后得到的 $????_??$ 和 $????_??+Δ??$ 的內積。
d表示不同的hidden_size。

我們可以看到 $????_??^???????_{??+Δ??}$ 的變動趨勢為：

在固定某個??????的情況下，兩個位置編碼的內積具有對稱性。
在固定某個??????的情況下，兩個位置編碼的內積具有遠程衰減性，即兩個位置編碼相距越遠，點積值越小，但是不具備單調性。

這說明位置向量的點積雖然可以反映相對距離，但因為點積的結果是對稱的，它并沒有學習到位置的方向性。

4.2 遠距離衰減性

遠程衰減性（Distant Decay）是指位置編碼應能捕獲到序列中位置信息和長距離依賴關系（相隔較遠的單詞之間的關系）。具體來說就是：

當兩個位置相隔較遠時，它們的編碼相差較大，相似度較低，這有助于模型區分這些位置，更好地理解和區分序列中的詞序關系。
而當兩個位置相隔較近時，它們的相似度較高，這有助于模型理解它們之間的關系。

遠程衰減的先驗是：文本是離散時序數據，我們通常會假設文字之間距離越近相關性越強。即位置相近的Token平均來說獲得更多的注意力，而距離比較遠的Token平均獲得更少的注意力。在此先驗條件下，良好的震蕩曲線應該具備如下特點：可以在無限長度下保持連續單調衰減；衰減曲線是非線性的，近距離衰減變化迅速，遠距離衰減平緩；在衰減過程中，盡可能少震蕩。其實，位置編碼對自注意力的局部化可以想象成從全自注意力到卷積的過渡：如何沒有位置編碼，隨意讓token的語義無視相對距離交互，就會讓序列失去順序信息的同時，以無關語義干擾token特征的刻畫；如果位置編碼自注意力局部化過于顯著，則Transformer模塊刻畫token特征時只能看到鄰近位置token，那就和CNN沒什么區別了。因此如何設計好位置編碼隨相對距離的下降曲線就顯得尤為重要。

在使用正弦和余弦函數的位置編碼方法中，不同位置的詞的位置編碼是通過正弦和余弦函數生成的。這種方法可以捕獲到不同位置之間的關系，并且具有良好的遠程衰減性。在設置合適的??值的前提下，兩個位置編碼的內積大小可以反應位置的遠近，內積越小，距離越遠（衰減性）。具體如上圖所示，隨著相對距離的增加，位置向量的內積結果會逐漸降低，即會存在遠程衰減。

但是我們也發現，在長距離下，衰減性并非預期單調下降，而是包括兩種震蕩：一種是局部窗口內的震蕩，一種是隨距離收斂到一定波動范圍。其帶來的影響是使得位置編碼更傾向于捕捉局部信息，限制了遠程交互的影響。這種特性對短序列有效，但對長序列可能受限，即造成 Sinusoidal 位置編碼外推性一般。另外，這些震蕩將會放大建模誤差，這也是其中一個長文本難訓的原因。

4.3 外推性

長度外推能力（extrapolation，也稱length extrapolation）：如果模型在不經微調的情況下，在超過訓練長度的文本上測試，依然能較好的維持其訓練效果，我們就稱該模型具有長度外推能力。相反，如果大模型由于訓練和預測時輸入的長度不一致，導致模型泛化能力下降，我們就說模型的外推性存在問題。如何讓位置編碼在保證分布內表現的前提下，提升其外推表現，是設計位置編碼的一個重要權衡。因為Sinusoidal位置編碼中的正弦余弦函數具備如下特點，所以理論上也具備一定長度外推的能力。

有顯式的生成規律。
周期性。
可以表達相對位置。因為$\sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta $ , $\cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$ ，這表明位置 $\alpha + \beta$ 的向量可以表示成位置 $\alpha$ 和位置 $\beta$ 的向量組合，提供了位置拓展的可能性。
內積具備遠程衰減的特性。

問題

然而實際上，三角函數編碼在外推性上的表現不甚理想。部分是因為，sin和cos是高頻振蕩函數，不是直線或者漸近趨于直線類的函數，往往外推行為難以預估。

論文”TENER: Adapting Transformer Encoder for Named Entity Recognition“對這個問題做了精彩的實驗和分析。為了更詳細探究這個問題，論文假設：

$??_??$,$??_{??+Δ??}$ 分別為兩個不同位置的原始token向量，其尺寸為(hidden_size, 1)
$????_??$,$????_{??+Δ??}$ 分別為兩個不同位置的原始PE向量，其尺寸為(hidden_size, 1)
$??_??$,$??_??$ 分別為尺寸為(hidden_size, hidden_size)的Q、K矩陣

應用了sinusoidal位置編碼的q和k點積如下：

\[??_??^?????_{??+Δ??}=[??_???(????+????_??)]^??[??_???(??_{??+Δ??}+????_{??+Δ??})]=[??_??^????_??^??+????_??^????_??^??][??_????_{??+Δ??}+??_??????_{??+Δ??}] \]

從中我們不難發現，經過attention層后，位置編碼真正起作用的不再是 $????_??^??????_{??+Δ??}$ 這兩個位置變量都相關的部，而是引入了線性變化后的 $????_??^????_??^????_??????_{??+Δ??}$ 。那么在引入這種線性變化后，位置編碼還能保持上述所說的絕對性、相對性和遠距離衰減性這種優良性值嗎？論文用實驗的方式來細看這一點。由于 $??_??^????_??$ 本質上可以合成一種線性變化，所以我們可以隨機初始化一個線性矩陣W來代替它。從下圖我們可以看出看固定住某個t之后，變動 Δ 的點積結果。

淺藍色代表：兩個不同位置sinusoidal位置編碼的點積$????_??^???????_{??+Δ??}$，確實有很好的遠程衰減，可以反映出兩個位置編碼間的距離。
黃色和綠色代表：引入兩個隨機初始化的線性變化的矩陣的點積。PE矩陣乘以W權重矩陣之后，沒有明顯規律了。表明引入線性變化后，$????_??^???????_{??+Δ??}$變成了$????_??^??W????_{??+Δ??}$，原始位置編碼的優良性質（遠程衰減性等）都受到了極大程度的破壞，其內積所反映的距離因素效果就被破壞。

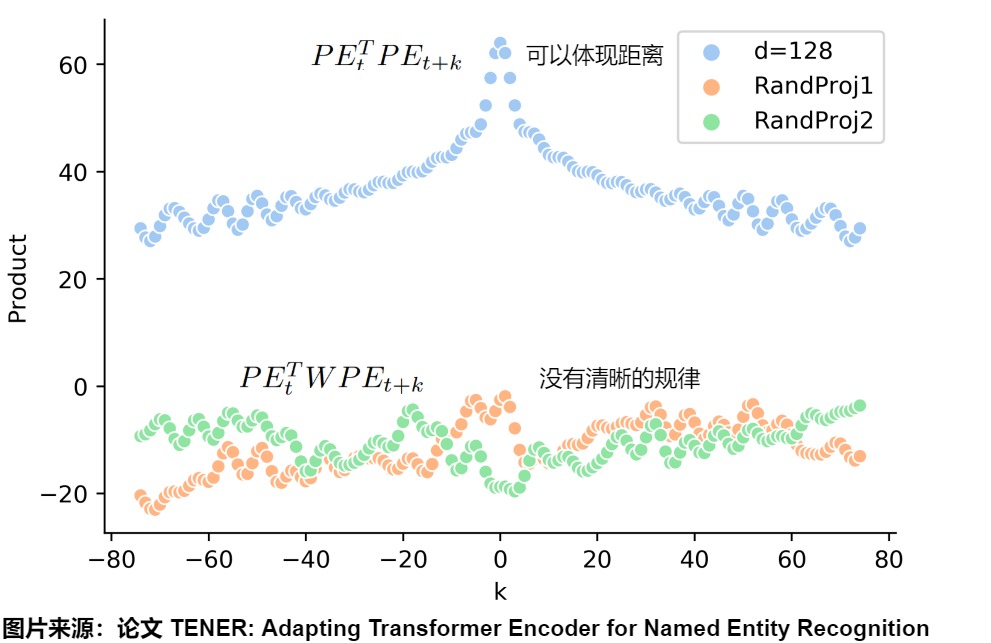
其原因在于：最初Transformers的位置編碼巧妙的引入周期性變化的三角函數公式保證其值有界性，同時三角函數的加減變化的公式也滿足了相對性。但這種相對位置信息僅僅包含在位置編碼內部。當word embedding（位置編碼和輸入層的token相加）進入自注意力內部時，情況就發生了變化，此時，真正起作用的不是兩個位置編碼的乘積，位置編碼還要乘上兩個投影矩陣，而引入這個投影矩陣后，位置信息會被損壞，丟失了遠程衰減這個性質。

蘇神在其博客中也說到。$cos(q_i,k_j)$的訓練不充分是Attention無法長度外推的主要原因。

第 i 個token與第 j 個token的相關性打分由內積完成：$s(j|i)=q_i?k_j=∥qi∥∥kj∥cos(q_i,k_j)$。第二個等號，我們從幾何意義出發，將它分解為了各自模長與夾角余弦的乘積。如果模長不變，$cos(q_i,k_j)$變小，則意味著相距較遠的兩個位置編碼的內積越小，即內積可以用于反饋兩個位置向量在絕對位置上的遠近。

為了提高某個位置j的相對重要性，模型有兩個選擇：

增大模長∥kj∥；
增大$cos(q_i,k_j)$，即縮小$q_i,k_j$的夾角大小。

然而，由于“維度災難”的存在，在高維空間中顯著地改變夾角大小相對來說沒有那么容易，所以模型會優先選擇通過增大模長來完成，這導致的直接后果是：$cos(q_i,k_j)$的訓練可能并不充分。被訓練過的$q_i,k_j$的夾角只是一個有限的集合，而進行長度外推時，它要面對一個更大的集合，從而無法進行正確的預測。

論證

sinusoidal位置編碼是在輸入x的嵌入維度上，依次加上不同頻段的正余弦波。這樣，兩個sinusoidal位置編碼的點積結果中存在若干正余弦波的疊加，這可以表示token間的相對位置。

下面假設t,s這兩個詞。$W^T_Q$和$W_K^T$是權重矩陣，$x_t$和$x_s$是詞嵌入，$p_t$和$p_s$是第t, 第s個位置的位置向量。我們希望$p_t^Tp_s$是$g(i-j)$。即是相對位置相關。從下圖來看。

(a)是詞的內容信息，是兩個詞的相關性，和位置向量和位置編碼沒關系。
(b)和(c)是詞和位置的相關性，都只有一個位置的向量，是關于絕對位置編碼的信息，所以也不包含相對位置信息。
(d)同時包含$p_t$和$p_s$，是最有可能包含相對位置信息的，可以借此得到兩個位置的相關性。

按照Vanilla Transformer的位置編碼方法，如果沒有$W_Q$和$W_K$，那么，(d)只包含相對位置信息。但是，最終計算注意力分數的公式中，得到的是經過參數矩陣映射后的正余弦波組合，并非是正余弦波組合。中間加入一個“不可知”的線性變換以后，就沒有相對位置信息了，即兩者的點積無法反映方向性，導致缺少單調性。

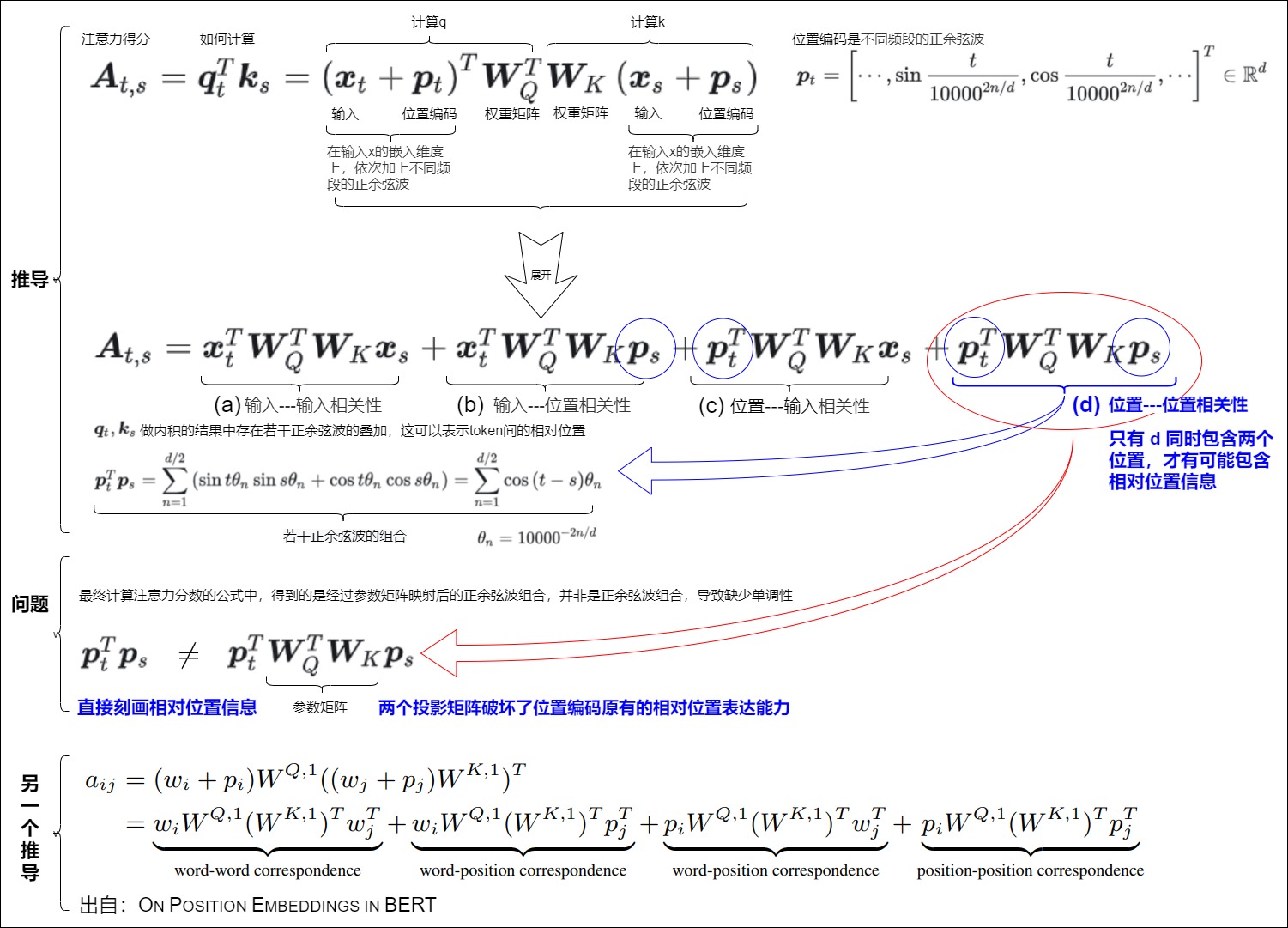
這樣，雖然原始transformer中的正弦位置編碼其實就是一種想要通過絕對位置編碼表達相對位置的位置編碼，從而希望正弦位置嵌入能夠推斷出比所看到的更長的序列。但是研究人員隨后發現，正弦APE很難外推。

因此，人們提出了各種APEs和RPEs，以增強正弦位置編碼，從而增強Transformer的外推。后續我們會分析這些方案如何在刻畫序列內部不同位置間的相對距離、控制自注意力矩陣不同位置的偏置大小的基礎上，去左右模型的參數學習過程與最終效果。

0x05 NoPE

位置編碼是Transformer模型的一個關鍵部分，它使模型能夠處理序列數據，捕捉到元素之間的順序關系。盡管存在一些限制，但它的引入是實現高效并行處理的重要步驟。然而位置編碼似乎像是個臨時的救火隊長或者說權宜之計。因此有人認為位置編碼不那么重要，尤其是Decoder-only模型基于Causal Attention，而Causal Attention本身不具備置換不變性，所以它原則上似乎不需要位置編碼（NoPE）。當然也有研究人員認為即便是Decoder-only模型，也需要PE。我們接下來看看這些觀點。

5.1 不需要

已經有研究證明，無位置編碼（NoPE）的 Transformer 已經被證明在自回歸語言模型任務上和 Transformer+RoPE 效果相當，這些任務包括。

因果關系自回歸模型：在自回歸模型（如GPT系列）中，因果注意力機制（causal attention mechanism）通過限制每個元素只能與之前的元素進行交互，從而隱含地引入了位置信息。盡管顯式的位置編碼可以提高模型性能，但一些研究表明，即使沒有顯式位置編碼，這類模型也能夠學習到一定的位置信息。
特定的非序列任務：對于一些不依賴于元素順序的任務，如某些類型的圖像分類，位置編碼可能不是必需的，因為模型的目標可能更多地側重于提取全局特征而非理解元素間的順序關系，加上位置編碼甚至可能還會導致性能下降。

具體可以參見。

Haviv, A., Ram, O., Press, O., Izsak, P., & Levy, O. (2022). Transformer Language Models without Positional Encodings Still Learn Positional Information. (EMNLP 2022).

Chi, T.C., Fan, T.H., Chen, L.W., Rudnicky, A., & Ramadge, P. (2023). Latent Positional Information is in the Self-Attention Variance of Transformer Language Models Without Positional Embeddings. (ACL 2023)

Kazemnejad, A., Padhi, I., Natesan Ramamurthy, K., Das, P., & Reddy, S. (2023). The Impact of Positional Encoding on Length Generalization in Transformers. (NeurIPS 2023).

論文“Length Generalization of Causal Transformers without Position Encoding”也提出了適用于 NoPE 的長度泛化方法。該論文討論了無位置編碼（NoPE）模型的長度泛化性問題。作者發現，通過簡單的注意力縮放（引入 SoftMax 溫度超參讓注意力強制集中）就能顯著提升 NoPE 的長度泛化能力，但是對 RoPE 沒有顯著效果。論文認為，NoPE 去除了顯式位置編碼的干擾，直擊模型內部的位置信息表示。

5.2 需要

下面引用蘇劍林大神的結論：NoPE對于長文本可能會存在位置分辨率不足、效率較低、注意力彌散等問題，所以即便是Decoder-only模型，我們仍需要給它補充上額外的位置編碼（特別是相對位置編碼），以完善上述種種不足之處。

NoPE主要是通過hidden state向量的方差來表達位置信息的。“Causal + NoPE”實際上是將位置信息隱藏在了??的分量方差之中，或者等價地，隱藏在??的$l_2$范數中。它相當于說????是由某個不帶位置信息的向量????乘上某個跟位置??相關的標量函數??(??)得到，這又意味著：

NoPE實現的是類似于乘性的絕對位置編碼，并且它只是將位置信息壓縮到單個標量中，所以這是一種非常弱的位置編碼
單個標量能表示的信息有限，當輸入長度增加時，位置編碼會越來越緊湊以至于難以區分，比如極簡例子有$p(n)～\frac{1}{\sqrt n}$，當n??足夠大時$\frac{1}{\sqrt n}$與$\frac{1}{\sqrt {n+1}}$幾乎不可分辨，也就是沒法區分位置??與??+1；
主流的觀點認為相對位置編碼更適合自然語言，既然NoPE實現的是絕對位置編碼，所以效率上自然不如再給模型額外補充上相對位置編碼；
NoPE既沒有給模型添加諸如遠程衰減之類的先驗，看上去也沒有賦予模型學習到這種先驗的能力，當輸入長度足夠大可能就會出現注意力不集中的問題。