數據結構和算法學習日志-第八章:樹
第八章 樹
思維導圖:

第八章 第一節:樹的定義和樹的存儲結構
1.樹的定義和樹的存儲結構
1.1 樹的定義
1.1.1 定義
樹(Tree)是n(n>=0)個節點的有限集。當n=0時稱為空樹。在任意一棵非空樹中:
有且僅有一個特定的被稱為根(Root)的節點
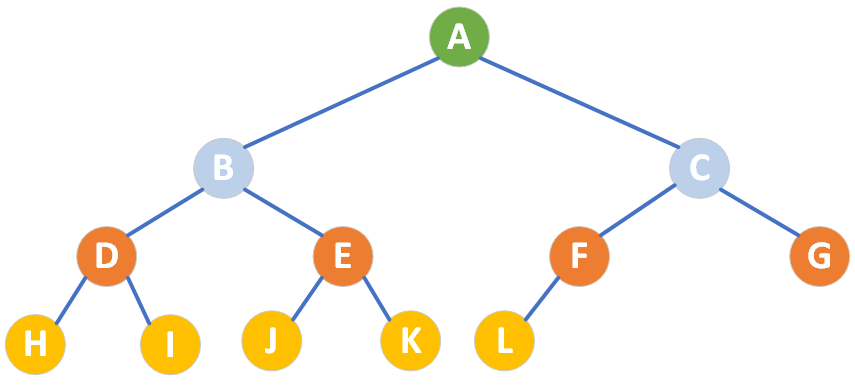
當n>1時,其余節點可分為m(m>0)個互不相交的有限集T1、T2、……、Tm,其中每個集合本身又是一棵樹,并且稱為根的子樹(SubTree),如下圖所示:

對于上面這棵樹而言,A是它的根節點,左側橙色部分和右側黃色部分分別是這棵樹的兩個子樹,而分別在以B、C為根節點的子樹中還有子樹,所以我們可以說樹是遞歸定義的,樹的特性對于它們的子樹以及子樹的子樹而言同樣是適用的。
對于樹的定義有3點需要特別強調一下:
層次結構:樹具有根節點、子節點和葉節點,呈現出一種分層的結構。
無環性:樹是一種無環結構,即0任意兩個節點之間只有唯一的一條路徑。
單一根節點:樹只有一個根節點,從根節點可以訪問樹中的所有其他節點。
1.2 節點的關系和分類
對于一棵樹而言,里邊有一些常用概念是需要大家掌握的:
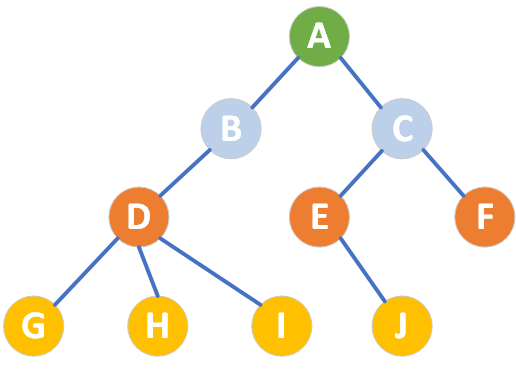
節點(Node):樹中的每個元素稱為節點,即圖中的A、B、C、...、H、I、J。
根節點(Root Node):樹的頂層節點,沒有父節點,即圖中的節點A。
父節點(Parent Node):直接連接某個節點的上層節點。比如:
B、C節點的父節點為根節點A
E、F節點的父節點為節點C
G、H、I節點的父節點為根節點D
子節點(Child Node):由某個節點直接連接的下層節點。比如:
A節點的子節點為節點B、C
C節點的子節點為節點E、F
D節點的子節點為節點G、H、I
子孫節點:以某節點為根的子樹中的任意節點都是該節點的子孫
葉子節點(Leaf Node):沒有子節點的節點。圖中的G、H、I、J就是葉子節點。
兄弟節點(Sibling Nodes):具有相同父節點的節點。
堂兄弟節點:在樹中的層次相同,但是父節點不同。舉例:
節點D和節點E、F互為堂兄弟節點
節點G、H、I和節點、J互為堂兄弟節點
層次(Level):從根開始定義,根為第一層,根的孩子為第二層,以此類推。圖中相同顏色的節點表示相同的層次,從根節點向下一共四層。
路徑(Path):從一個節點到另一個節點所經過的節點序列。
高度(Height):節點到葉節點的最長路徑長度。
從根節點到葉子節點得到的高度就是樹的高度
根節點A到葉子節點F的高度是3,到葉子節點G、H、I、J的高度是4,所以根節點的高度是4,樹的高度也是4
深度(Depth):節點到根節點的路徑長度。比如:
從AE深度為3,從AH深度為4
子樹(Subtree):由一個節點及其所有后代節點組成的樹。
度(Degree):節點的子節點數量,樹的度是所有節點度的最大值。
葉子節點的度為0
樹的度是樹內各個節點度的最大值
節點E的度為1,節點A的度為2,節點D的度為3,樹的度為3
有序樹/無序樹:如果樹以及它的子樹中所有子節點從左至右是有次序的,不能互換的,此時將這棵樹稱為有序樹,否則稱為無序樹。
森林(Forest):m(m>=0)棵互不相交的樹的集合。
線性表與樹結構有很多地方是不同的,下表是關于二者的對比:

溫馨提示:上表中所說的雙親(Parent)就是當前節點的父節點,只有一個而不是兩個。
2. 樹的存儲結構
關于數到存儲結構和線性表一樣有兩種:線性存儲和鏈式存儲。先看順序存儲結構,如果是線性表可以用一段連續的存儲單元一對一的進行數據元素的存儲,對于樹這種一對多的結構應該如何進行存儲呢?
在數據結構中,樹的表示法有多種,常見的包括雙親表示法、孩子表示法和孩子兄弟表示法。每種表示法都有其優點和適用的場景。下面詳細介紹這些表示法。
2.1 雙親表示法
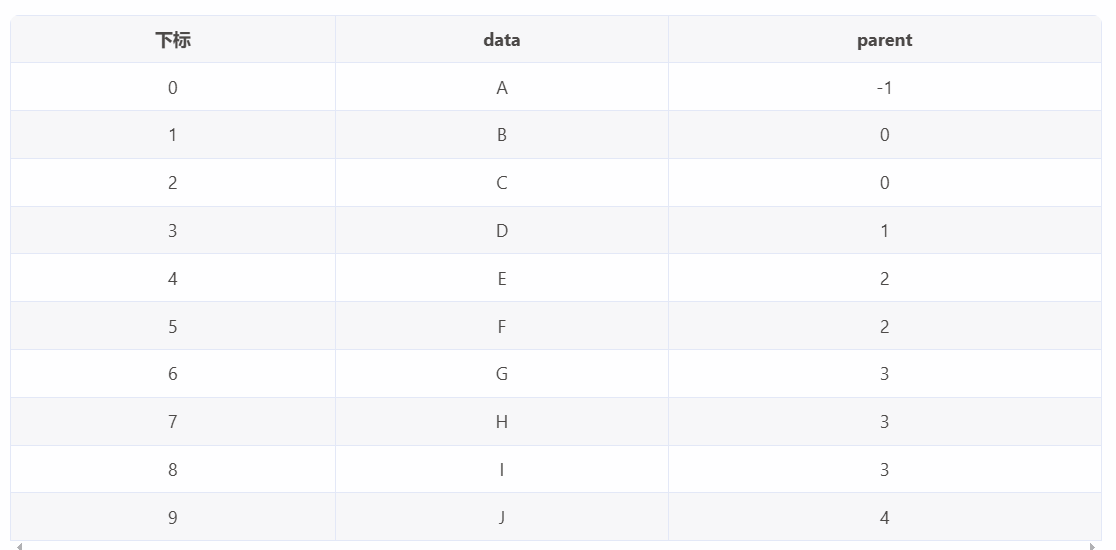
雙親表示法是一種用數組來表示樹的方法,在存儲樹節點的時候,在每個節點中附設一個指示器指示其雙親節點在數組中的位置。
基于上面的描述,我們需要定義出這樣的一個樹節點結構(假設節點存儲的數據是整形):
typedef struct TreeNode {
int value; // 節點的值
int parent; // 父節點的索引
} TreeNode;
data:節點存儲的數據
parent:父節點在數組中的位置,根節點沒有父節點,用 -1 表示
我們可以通過一個表格來直觀的描述一下節點在數組中的關系:

我們來看一段示例代碼:
#include <stdio.h>
#include <stdlib.h>
// 定義樹節點結構
typedef struct TreeNode {
int value; // 節點的值
int parent; // 父節點的索引
} TreeNode;
// 添加節點的函數
void addNode(TreeNode** tree, int* size, int value, int parentIndex) {
// 動態調整內存,增加一個節點的空間,所以是(*size + 1)
TreeNode* temp = realloc(*tree, (*size + 1) * sizeof(TreeNode));
//realloc 是 C 語言中用于調整已分配內存大小的函數。它的主要作用是可以擴展或縮小已經分配的內存塊。
if (temp == NULL) {
printf("realloc failed \n");
exit(1); // 返回錯誤代碼,表示內存分配失敗
}
*tree = temp; // 更新樹指針
(*tree)[*size].value = value; // 設置新節點的值
(*tree)[*size].parent = parentIndex; // 設置新節點的父節點索引
(*size)++; // 增加樹的大小
}
int main() {
TreeNode* tree = NULL; // 初始化樹指針為 NULL
int size = 0; // 初始化樹的大小為 0
// 創建根節點,根節點的父節點索引為 -1
addNode(&tree, &size, 1, -1); // 索引 0
addNode(&tree, &size, 2, 0); // 索引 1
addNode(&tree, &size, 3, 0); // 索引 2
addNode(&tree, &size, 4, 1); // 索引 3
addNode(&tree, &size, 5, 1); // 索引 4
// 輸出樹的結構
for (int i = 0; i < size; ++i) {
printf("Node value: %d", tree[i].value); // 輸出當前節點的值
if (tree[i].parent != -1) {
// 如果不是根節點,輸出其父節點的值
printf(", Parent value: %d\n", tree[tree[i].parent].value);
}
else {
// 如果是根節點,輸出提示信息
printf(", This is the root node.\n");
}
}
// 釋放動態分配的內存
free(tree);
return 0; // 程序結束
}
輸出的結果如下:
Node value: 1, This is the root node.
Node value: 2, Parent value: 1
Node value: 3, Parent value: 1
Node value: 4, Parent value: 2
Node value: 5, Parent value: 2
通過測試輸出的日志信息可知,我們可以快速的通過每個節點中的parent域找到它們的父節點(也就是雙親節點),時間復雜度為O(1)。但是如果我們想知道當前節點的子節點是誰,就需要遍歷整棵樹才能得到結果。
如果我們對上面的TreeNode結構進行優化給它添加用于描述孩子節點位置的成員就可以快速找到當前節點的子節點了:
struct TreeNode
{
int data;
int parent;
int child1;
int child2;
...
...
...
};
但是此時問題來了,對于一棵樹中的節點而言,我怎么知道它有多少個子節點呢?如果child成員定義的太多會浪費存儲空間,如果定義的太少就不能存儲所有的子節點信息。這該如何是好呢?
2.2 孩子表示法
孩子表示法是一種為每個節點存儲其所有子節點的表示方法,在存儲的時候可以使用數組也可以使用鏈表。
孩子表示法中,每個節點都有一個指針列表或數組,指向它的所有子節點。我們可以使用 std::vector 來存儲子節點指針。關于節點結構可以這樣定義:
// 定義樹的節點結構
typedef struct TreeNode {
int value; // 節點的值
struct TreeNode** children; // 指向子節點的指針數組
int childCount; // 子節點數量
} TreeNode;
value:節點的值,可以根據實際需求修改為其他數據類型
children:子節點列表,存儲的是當前節點所有的子節點
如果想要根據上面的樹節點結構構造這樣一棵樹,代碼應該怎么寫呢?

#include <stdio.h>
#include <stdlib.h>
// 定義樹的節點結構
typedef struct TreeNode {
int value; // 節點的值
struct TreeNode** children; // 指向子節點的指針數組
int childCount; // 子節點數量
} TreeNode;
// 創建新節點的函數
TreeNode* createNode(int val) {
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode)); // 動態分配內存
if (!node) { // 檢查內存分配是否成功
fprintf(stderr, "Memory allocation failed\n");
exit(EXIT_FAILURE); // 失敗則退出程序
}
node->value = val; // 設置節點值
node->children = NULL; // 初始化子節點指針為 NULL
node->childCount = 0; // 初始化子節點計數為 0
return node; // 返回新創建的節點
}
// 添加子節點的函數
void addChild(TreeNode* parent, TreeNode* child) {
parent->childCount++; // 增加子節點計數
// 重新分配內存以容納新的子節點
TreeNode** temp = (TreeNode**)realloc(parent->children,
parent->childCount * sizeof(TreeNode*));
if (!temp) { // 檢查內存重新分配是否成功
fprintf(stderr, "Memory allocation failed\n");
exit(EXIT_FAILURE); // 失敗則退出程序
}
parent->children = temp; // 更新父節點的子節點指針
parent->children[parent->childCount - 1] = child; // 將新子節點添加到數組中
}
// 遞歸打印樹的結構
void printTree(TreeNode* node, int level) {
if (!node) return; // 如果節點為空,返回
// 打印當前節點的值,前面加上縮進
for (int i = 0; i < level; i++) {
printf(" "); // 根據層級打印縮進
}
printf("Node value: %d\n", node->value); // 打印節點值
// 遞歸打印每個子節點
for (int i = 0; i < node->childCount; i++) {
printTree(node->children[i], level + 1);
}
}
// 釋放樹的內存
void freeTree(TreeNode* node) {
if (!node) return; // 如果節點為空,返回
// 遞歸釋放每個子節點的內存
for (int i = 0; i < node->childCount; i++) {
freeTree(node->children[i]);
}
free(node->children); // 釋放子節點指針數組的內存
free(node); // 釋放當前節點的內存
}
int main() {
// 創建樹的節點
TreeNode* root = createNode(1);
TreeNode* child1 = createNode(2);
TreeNode* child2 = createNode(3);
TreeNode* child3 = createNode(4);
TreeNode* child4 = createNode(5);
TreeNode* child5 = createNode(6);
TreeNode* child6 = createNode(7);
TreeNode* child7 = createNode(8);
// 構建樹結構
addChild(root, child1); // 將 child1 添加為 root 的子節點
addChild(root, child2); // 將 child2 添加為 root 的子節點
addChild(root, child3); // 將 child3 添加為 root 的子節點
addChild(child2, child4); // 將 child4 添加為 child2 的子節點
addChild(child2, child5); // 將 child5 添加為 child2 的子節點
addChild(child1, child6); // 將 child6 添加為 child1 的子節點
addChild(child3, child7); // 將 child7 添加為 child3 的子節點
// 打印樹結構
printTree(root, 0); // 從根節點開始打印
// 釋放內存
freeTree(root); // 釋放整棵樹的內存
return 0; // 程序結束
}
在上面的程序中先創建了若干個樹節點,然后通過 addChild 函數將子節點添加到了父節點對應的vector容器中,通過這種方式能夠非常輕松的基于父節點找到它所有的子節點,但是想要通過子節點訪問其父節點就變得麻煩了。那么有沒有一種方法既可以快速的通過子節點訪問到它的父節點并且能夠通過父節點快速訪問到它的所有的子節點呢?
當然有,就是孩子雙親表示法,也就是在孩子表示法的節點基礎上再添加一個指向雙親的數據域:
struct TreeNode
{
int value;
TreeNode* parent;
std::vector<TreeNode*> children;
};
value:節點的值,可以根據實際需求修改為其他數據類型
parent:記錄當前節點的父節點的位置(地址)。
children:子節點列表,存儲的是當前節點所有的子節點
做了這樣的修改之后,可以在程序中再添加一個setParent方法,用于給各個節點設置父節點(根節點的父節點可以指定為 nullptr),代碼比較簡單,此處就略過了,可以自己私下寫一寫。
2.3 孩子兄弟表示法
在孩子兄弟表示法中,樹被轉化為了一種特殊的樹,我們可以做這樣的約定:每個節點的左側子節點表示該節點的第一個子節點,而右側子節點表示該節點的下一個兄弟節點。也就是說在內存中這棵樹的存儲結構和實際的邏輯結構是不一樣的。
根據描述我們可以定義這樣的一個樹節點:
// 定義樹節點結構體
typedef struct TreeNode {
int value; // 節點的值
struct TreeNode* firstChild; // 指向第一個子節點
struct TreeNode* nextSibling; // 指向下一個兄弟節點
} TreeNode;
value:節點的值,可以根據實際需求修改為其他數據類型
firstChild:指向第一個子節點(地址)
nextSibling:指向下一個兄弟節點(地址)

如果想要在內存中存儲這樣的一棵樹,我們需要使用孩子兄弟表示法對其進行轉換可以得到下面這個圖:
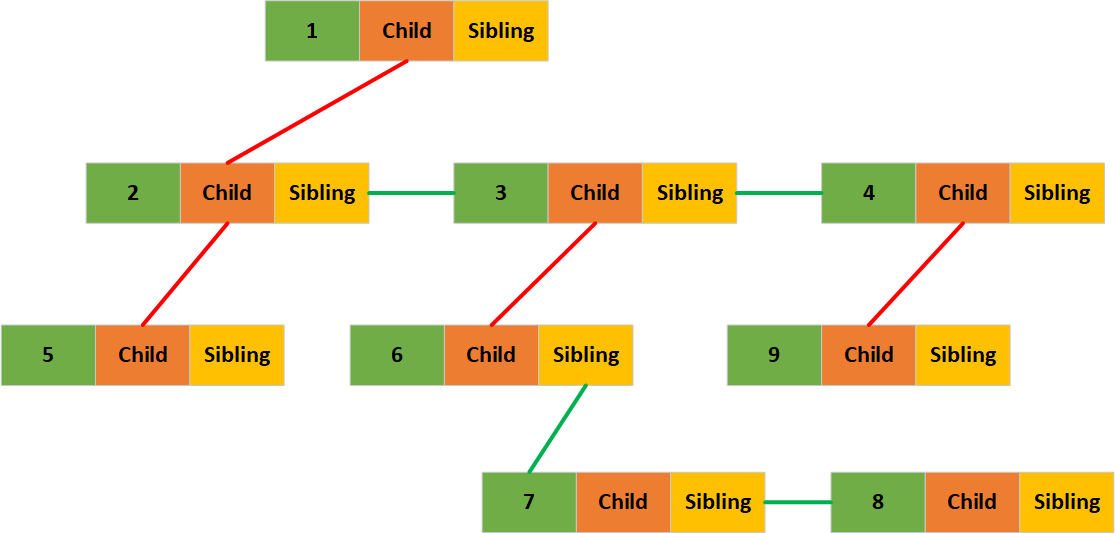
在上面的圖中紅色線表示節點之間的關系為父子,綠色的線表示節點之間的關系為兄弟,但是這樣看起來似乎還是不太直觀,我們來換一種畫法:

圖中的左側節點(橙色)表示和父節點之間原來的實際關系為父子,右側節點(黃色)表示節點和父節點之間原來的實際關系為兄弟。可見內存中存儲的樹結構和實際的樹結構已經完全不一樣了,但是樹節點中存儲的屬性,我們完全可以把原來的樹還原出來。
示例C++代碼如下:
#include <stdio.h>
#include <stdlib.h>
// 定義樹節點結構體
typedef struct TreeNode {
int value; // 節點的值
struct TreeNode* firstChild; // 指向第一個子節點
struct TreeNode* nextSibling; // 指向下一個兄弟節點
} TreeNode;
// 創建新的樹節點
TreeNode* createNode(int val) {
// 分配內存并檢查是否成功
TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
if (!newNode) { // 檢查內存分配是否成功
fprintf(stderr, "Memory allocation failed\n");
exit(EXIT_FAILURE); // 失敗則退出程序
}
newNode->value = val; // 設置節點的值
newNode->firstChild = NULL; // 初始化第一個子節點為 NULL
newNode->nextSibling = NULL; // 初始化下一個兄弟節點為 NULL
return newNode; // 返回新創建的節點
}
// 添加子節點的函數
void addChild(TreeNode* parent, TreeNode* child) {
// 如果父節點沒有子節點,則將新節點設置為第一個子節點
if (!parent->firstChild) {
parent->firstChild = child;
}
else {
// 否則,找到最后一個兄弟節點,并將新節點添加到最后
TreeNode* sibling = parent->firstChild;
while (sibling->nextSibling) {
sibling = sibling->nextSibling; // 遍歷到最后一個兄弟節點
}
sibling->nextSibling = child; // 將新節點添加為最后一個兄弟
}
}
// 打印樹的函數
void printTree(TreeNode* node) {
if (node == NULL) return; // 如果節點為空,直接返回
// 打印當前節點的值
printf("當前節點為: %d", node->value);
if (node->firstChild) {
// 如果當前節點有子節點,打印子節點的值
printf(", %d的子節點為: ", node->value);
printf("%d", node->firstChild->value);
TreeNode* sibling = node->firstChild->nextSibling; // 獲取第一個子節點的下一個兄弟
while (sibling) {
printf(", %d", sibling->value); // 打印所有兄弟節點的值
sibling = sibling->nextSibling; // 繼續遍歷兄弟節點
}
}
else {
// 如果沒有子節點,輸出相應信息
printf(", %d沒有子節點!", node->value);
}
printf("\n"); // 換行輸出
// 遞歸打印子節點和下一個兄弟節點
printTree(node->firstChild);
printTree(node->nextSibling);
}
// 釋放樹的內存
void freeTree(TreeNode* node) {
if (node == NULL) return; // 如果節點為空,直接返回
// 遞歸釋放子節點
freeTree(node->firstChild);
// 遞歸釋放下一個兄弟節點
freeTree(node->nextSibling);
free(node); // 釋放當前節點的內存
}
int main() {
// 創建節點
TreeNode* root = createNode(1); // 根節點
TreeNode* child1 = createNode(2); // 第一個子節點
TreeNode* child2 = createNode(3); // 第二個子節點
TreeNode* child3 = createNode(4); // 第三個子節點
TreeNode* child1_1 = createNode(5); // 第一個子節點的子節點
TreeNode* child2_1 = createNode(6); // 第二個子節點的子節點
TreeNode* child2_2 = createNode(7); // 第二個子節點的子節點
TreeNode* child2_3 = createNode(8); // 第二個子節點的子節點
TreeNode* child3_1 = createNode(9); // 第三個子節點的子節點
// 構建樹
addChild(root, child1); // 將 child1 添加為 root 的子節點
addChild(root, child2); // 將 child2 添加為 root 的子節點
addChild(root, child3); // 將 child3 添加為 root 的子節點
addChild(child1, child1_1); // 將 child1_1 添加為 child1 的子節點
addChild(child2, child2_1); // 將 child2_1 添加為 child2 的子節點
addChild(child2, child2_2); // 將 child2_2 添加為 child2 的子節點
addChild(child2, child2_3); // 將 child2_3 添加為 child2 的子節點
addChild(child3, child3_1); // 將 child3_1 添加為 child3 的子節點
// 打印樹結構
printTree(root);
// 釋放內存
freeTree(root);
return 0; // 程序結束
}
程序輸出的結果如下:
當前節點為: 1, 1的子節點為: 2, 3, 4
當前節點為: 2, 2的子節點為: 5
當前節點為: 5, 5沒有子節點!
當前節點為: 3, 3的子節點為: 6, 7, 8
當前節點為: 6, 6沒有子節點!
當前節點為: 7, 7沒有子節點!
當前節點為: 8, 8沒有子節點!
當前節點為: 4, 4的子節點為: 9
當前節點為: 9, 9沒有子節點!
``
在程序中構建的樹和上面的例子是一樣的,我們是是通過孩子兄弟表示法進行了存儲,并且在打印的時候又還原了這棵樹,通過對比可以確認結果是沒問題的。
孩子兄弟表示法就是充分利用了二叉樹的特性和算法來處理一棵非二叉樹,那么,什么樣的樹可以被稱之為二叉樹呢?
第八章 第二節:二叉樹以及它的形態、性質、存儲結構和遍歷
1. 二叉樹
?二叉樹是一種樹形數據結構,其中每個節點最多有兩個子節點,分別稱為?左子節點和?右子節點。二叉樹由一個根節點和兩棵互不相交的子樹組成,這兩棵子樹分別稱為根的左子樹和右子樹。二叉樹的定義可以遞歸地描述:二叉樹是一個有限的節點集合,這個集合可以是空集(即沒有節點),或者由一個根節點和兩棵互不相交的二叉樹組成。?

1.1 二叉樹的特點和形態
二叉樹有三個特點依次是:
每個節點最多有兩棵子樹,所以二叉樹中不存在度大于2的節點
左子樹和右子樹是有順序的,次序不能顛倒,也就是說二叉樹是有序樹
即使樹中某節點只有一棵子樹,也要區分它是左子樹還是右子樹
基于以上描述,我們對二叉樹的形態做了歸納,一共有五種形態,分別是:
空二叉樹
只有一個根節點
根節點只有左子樹
根節點只有右子樹
根節點既有左子樹,又有右子樹
以上五種形態應該是比較容易理解的,如果加大難度,大家可以思考一下,如果是有三個節點的二叉樹,它一共有幾種形態呢?

是的,一共有五種形態,上圖中第一種和第二種二叉樹比較特殊,它們只有左子樹或者只有右子樹,和線性表已經無異了。
1.2 特殊的二叉樹
斜樹
斜樹顧名思義一定要是斜的,它一共有兩種形態,就是上圖中的1和2。
所有節點都只有左子樹的二叉樹叫左斜樹
所有節點都只有右子樹的二叉樹叫右斜樹
斜樹有很明顯的特點,就是每一層都只有一個節點,節點的個數與二叉樹的深度相同。
通過上圖可以看到,不論是左斜樹還是右斜樹和線性表的的結構是完全相同的,我們可以這樣理解:線性表結構是樹的一種極特殊的表現形式。
滿二叉樹
滿二叉樹就是一棵完美的二叉樹,也就是在一顆二叉樹中所有分支節點都存在左子樹和右子樹,并且所有的葉子都在同一層。
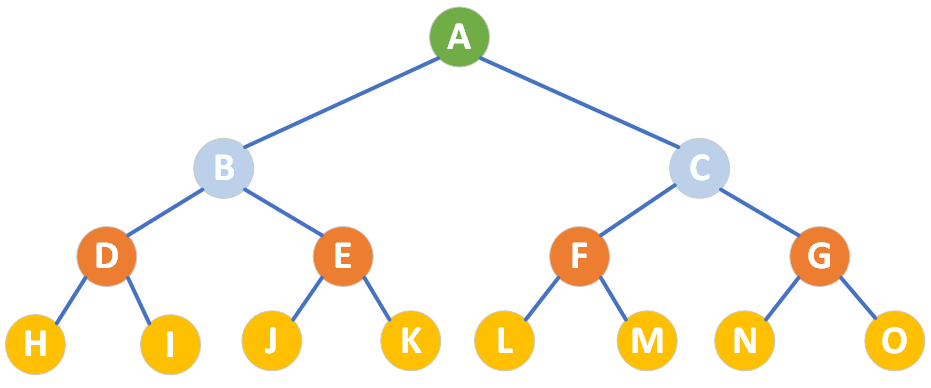
上圖為大家展示的就是一棵滿二叉樹。滿二叉樹有三個特點:
葉子節點只能出現在最下層
所有的非葉子節點的度一定都是 2
在同樣深度的二叉樹中,滿二叉樹的節點個數最多,葉子數量最多
完全二叉樹
完全二叉樹是滿二叉樹的簡配版本,對于深度為k的二叉樹,如果其節點個數為n,且每個節點都與深度為k的滿二叉樹中編號從1到n的節點一一對應,那么這棵二叉樹就是完全二叉樹。

具體來說,完全二叉樹除了最后一層外,每一層上的節點數都達到了最大值,而在最后一層上,節點是連續缺少的,也就是只缺少右邊的若干節點。滿二叉樹一定是一棵完全二叉樹,但完全二叉樹不一定是滿二叉樹。
對于完全二叉樹而言,有以下五個特點:
葉子節點只能出現在最下面兩層
最下層的葉子一定集中在左側部分連續位置
倒數第二層如有葉子節點,一定都在右部連續位置
如果節點度為1,那么該節點一定只有左孩子,不存在只有右子樹的情況
同樣節點數的二叉樹,完全二叉樹深度最小
基于完全二叉樹這種結構特點,使得在查找和訪問節點時,可以通過簡單的數組索引或類似機制快速定位到任何節點,從而提高了數據處理的效率。?
2. 二叉樹的性質
二叉樹有一些需要理解并且記住的特性,以便我們更好的使用它。
性質1:二叉樹的第 i 層上至多有 2i-1(i≥1)個節點 。
第1層是根節點,只有一個,2i-1 = 20 = 1。
第2層最多有兩個節點,22-1 = 21 = 2。
第3層最多有四個節點,23-1 = 22 = 4。
第4層最多有八個節點,24-1 = 23 = 8。
性質2:深度為 k 的二叉樹中至多含有 2k-1 個節點(k≥1) 。
如果只有1層,只有一個根節點,至多有1個節點,2k-1 = 21-1 = 1
如果有2層,最多的節點數為 1+2 = 2k-1 = 22-1 = 3
如果有3層,最多的節點數為 1+2+4 = 2k-1 = 23-1 = 7
如果有4層,最多的節點數為 1+2+4+8 = 2k-1 = 24-1 = 15
性質3:若在任意一棵二叉樹中,葉子節點有 n0 個,度為2的節點有 n2個,則 n0=n2+1 。
在上圖中度為2的節點數為5,葉子節點數量為6,滿足 n0=n2+1
在上圖中去掉節點L,度為2的節點數為5,葉子節點數量為6,滿足 n0=n2+1
在上圖中去掉節點K、L,度為2的節點數為4,葉子節點數量為5,滿足 n0=n2+1
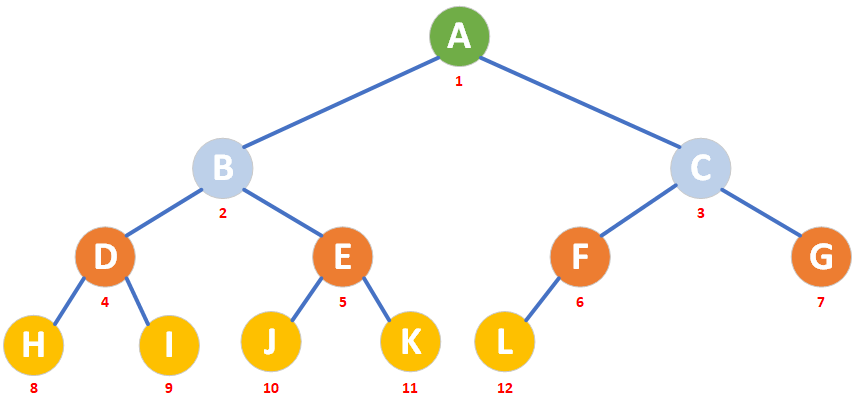
性質4:具有n個節點的完全二叉樹的深度為 ?log2n?+1(? ? 表示向下取整)。
如上圖所示,完全二叉樹有12個節點,深度為:?log212?+1 = 3+1 = 4
如果在上圖基礎上再增加4個節點,深度為:?log216?+1 = 4+1 = 5
性質5:若對一棵有 n 個節點的完全二叉樹的節點按層序進行編號(從第1層到第 ?log2n?+1層,每層從左到右),那么,對于編號為i(1≤i≤n)的節點:
當i=1時,該節點為根,它無雙親節點 。
當i>1時,該節點的雙親節點的編號為i/2 。
對于上圖而言,編號為7(G)的節點,其父節點為 3(C)
對于上圖而言,編號為5(E)的節點,其父節點為 2(B)
對于上圖而言,編號為11(K)的節點,其父節點為 5(E)
若2i≤n,則有編號為2i的左節點,否則沒有左節點 。
上圖中的G(7)、H(8)、I(9)、J(10)、K(11)、L(12) 乘以2 > n(12),它們沒有左節點
上圖中的A(1)、B(2)、C(3)、D(4)、E(5)、F(6) 乘以2 ≤ n(12),它們有左節點
若2i+1≤n,則有編號為2i+1的右節點,否則沒有右節點。
上圖中的節點F,2*(F)+1 = 13 > n(12),它沒有右節點
上圖中的A(1)、B(2)、C(3)、D(4)、E(5) 乘以2 + 1 < n(12),它們有右節點
3. 二叉樹的存儲結構
3.1 順序存儲
二叉樹的順序存儲結構就是用一維數組存儲二叉樹中的節點,并且通過數組是下標來描述節點之間的邏輯關系,比如雙親和孩子的關系,左右兄弟的關系等。下面通過一棵完全二叉樹為大家舉例說明:
如果從數組的1號位置開始存儲數據,二叉樹的節點在數組的位置應該是這樣的:

假設父節點位置為 i,左孩子位置為 2i,右孩子位置為 2i+1
假設左孩子節點位置為 i,右兄弟位置為 i+1,父節點位置為 i/2
假設右孩子節點位置為 i,左兄弟位置為 i-1,父節點位置為 i/2
如果從數組的0號位置開始存儲數據,二叉樹的節點在數組的位置應該是這樣的:

假設父節點位置為 i,左孩子位置為 2i+1,右孩子位置為 2i+2
假設左孩子節點位置為 i,右兄弟位置為 i+1,父節點位置為 (i-1)/2
假設右孩子節點位置為 i,左兄弟位置為 i-1,父節點位置為 (i-1)/2
如果存儲的二叉樹不是完全二叉樹,此時在數組中應該如何存儲二叉樹的節點呢?

在上面這棵二叉樹中有很多節點缺失了,為了看起來更直觀,我們使用灰色將其畫了出來,在存儲這棵普通的二叉樹的時候有兩種方式:
將A、B、C、F、G、L按順序依次存儲到數組中
使用完全二叉樹的方式來存儲這棵普通的二叉樹數據
通過認真分析考慮之后,相信大家選擇的都是后者,只有通過這種方式才能通過父節點找到左右孩子節點或者通過左右孩子節點找到它們的父節點。

通過上面的表可以清晰的看到使用順序存儲的方式存儲二叉樹會造成內存的浪費,尤其是當二叉樹變成一棵右斜樹的時候,浪費的內存空間是最多的。所以順序存儲結構一般只用于存儲完全二叉樹。
3.2 鏈式存儲
既然順序存儲結果有弊端,我們在來看一下鏈式存儲結果能不能彌補這個缺陷。由于二叉樹每個節點最多只有兩個孩子,所以為每個樹節點設計一個數據域和兩個指針域,通過這種方式組成的鏈表我們稱其為二叉鏈表。
typedef struct BinaryTreeNode {
char data; // 節點存儲的數據
struct BinaryTreeNode* left; // 指向左子樹的指針
struct BinaryTreeNode* right; // 指向右子樹的指針
} BTreeNode;
data:存儲節點數據,可以根據實際需求指定它的類型。
lchild:存儲左側孩子節點的地址。
rchild:存儲右側孩子節點的地址。

可以看到通過鏈式存儲的方式存儲二叉樹不存在內存浪費的問題,它適用于任何形式的二叉樹。使用二叉鏈表可以快速的通過父節點訪問它的左右孩子節點,但是想要通過孩子節點訪問父節點就比較麻煩了,解決方案也比較簡單我們可以給鏈表節點再添加一個指針域,讓它指向當前節點的父節點:
struct TreeNode
{
int data;
TreeNode* lchild;
TreeNode* rchild;
TreeNode* parent;
};
data:存儲節點數據,可以根據實際需求指定它的類型。
lchild:存儲左側孩子節點的地址。
rchild:存儲右側孩子節點的地址。
parent:存儲雙親節點(父節點)的地址。
通過這種節點組成的鏈表我們將其稱之為三叉鏈表。
4. 二叉樹的遍歷
4.1 二叉樹的遍歷方法
二叉樹的遍歷是指從根節點出發,按照某種次序依次訪問二叉樹中的所有節點,使得每個節點被訪問一次并且僅被訪問一次。
二叉樹的次序遍歷不同于線性結構,線性結構比較簡單通過循序從頭到尾進行訪問即可。由于樹節點之間不存在唯一的前驅和后繼關系,在訪問一個節點之后,下一個被訪問的節點就面臨著不同的選擇,選擇不同,被訪問到的節點的順序也不一樣。
由于樹的遞歸定義的,所以樹的遍歷一般也是通過遞歸的方式實現,通過遞歸的方式對樹進行遍歷一共有三種方式:
前序遍歷:先訪問根節點,然后前序遍歷左子樹,最后前序遍歷右子樹
中序遍歷:中序遍歷左子樹,然后訪問根節點,最后中序遍歷右子樹
后序遍歷:后序遍歷左子樹,然后后序遍歷右子樹,最后訪問根節點
通過三種遍歷方式的定義可知,前、中、后其實是相對于根節點而言的,并且二叉樹的左子樹和右子樹的遍歷也是遞歸的,同樣遵循前序、中序、后序的規則,在遍歷過程中如果樹為空,直接返回,遞歸結束。

4.2.1前序遍歷
了解了前序遍歷的規則之后,我們來分析一下上面這棵二叉樹通過前序遍歷之后節點的訪問順序是什么?
先訪問根節點A
然后遍歷左子樹
訪問根節點B
遍歷以B為根節點的左子樹,遍歷以D為根節點的左子樹
訪問根節點D,訪問左子樹G,訪問右子樹H
最后遍歷右子樹
訪問根節點C
遍歷以C為根節點的左子樹,遍歷以E為根節點的左子樹
訪問根節點E,訪問左子樹 nullptr,訪問右子樹I
遍歷以C為根節點的右子樹,訪問根節點F
所以通過前序遍歷的方式,樹節點的訪問順序為:A、B、D、G、H、C、E、I、F

4.2.2中序遍歷
還是這棵樹,如果換成中序遍歷,節點的訪問順序就不一樣了,我們來根據遍歷的規則分析一下:
先遍歷左子樹
遍歷以B為根節點的左子樹,遍歷以D為根節點的左子樹
訪問左葉子節點G,訪問根節點D,訪問右葉子節點H
訪問根節點的左孩子節點B
然后訪問根節點A
最后遍歷右子樹
遍歷以C為根節點的左子樹,遍歷以E為根節點的左子樹
訪問左葉子節點nullptr,訪問根節點E,訪問右葉子節點I
訪問根節點C,遍歷右子樹,訪問根節點F
所以通過中序遍歷的方式,二叉樹節點的訪問順序為:G、D、H、B、A、E、I、C、F

4.2.3后序遍歷
如果使用遍歷的方式遍歷這棵樹,得到的遍歷順序又會發生變化,其順序為:
先遍歷左子樹
遍歷以B為根節點的左子樹,遍歷以D為根節點的左子樹
訪問左葉子節點G,訪問右葉子節點H,訪問根節點D
遍歷以B為根節點的右子樹為 nullptr,訪問根節點B
然后遍歷右子樹
遍歷以C為根節點的左子樹,遍歷以E為根節點的左子樹
訪問左葉子節點nullptr,訪問右葉子節點I,訪問根節點E
遍歷右子樹,訪問根節點F,訪問根節點C
最后訪問根節點A
所以通過后序遍歷的方式,二叉樹節點的訪問順序為:G、H、D、B、I、E、F、C、A

4.2 二叉樹的創建和遍歷
4.2.1直接構建二叉樹
想要構建一棵二叉樹最簡單的方式就是創建若干個節點,然后按照父子、兄弟關系把它們通過指針連接到一起,代碼如下:
int main()
{
// 創建二叉樹
TreeNode* root = new TreeNode(1);
TreeNode* node1 = new TreeNode(2);
TreeNode* node2 = new TreeNode(3);
TreeNode* node3 = new TreeNode(4);
TreeNode* node4 = new TreeNode(5);
TreeNode* node5 = new TreeNode(6);
TreeNode* node6 = new TreeNode(7);
root->left = node1;
root->right = node2;
node1->left = node3;
node1->right = node4;
node2->left = node5;
node2->right = node6;
cout << "先序遍歷: ";
// preOrderTraversal(root);
cout << endl;
cout << "中序遍歷: ";
// inOrderTraversal(root);
cout << endl;
cout << "后序遍歷: ";
// postOrderTraversal(root);
cout << endl;
delete root;
delete node1;
delete node2;
delete node3;
delete node4;
delete node5;
delete node6;
return 0;
}
這種創建二叉樹的方法特點是簡單,但是不夠靈活。
4.2.2通過終端輸入構建二叉樹
如果想要靈活地創建出一個二叉樹,可以讓用戶通過終端輸入的方式指定出節點的值以及節點和節點之間的關系,但是有一個細節需要進行處理,就是某些節點沒有左孩子或者右孩子。因此,我們可以做這樣的一個約定:如果節點的左孩子或者右孩子為空,那么在輸入的時候就使用 # 來表示。

準備工作做好之后,我們就可以生成一棵二叉樹了,假設二叉樹的節點值是一個字符,對應的代碼實現如下:
/ 創建先序樹
void createPreOrderTree(BTreeNode** root) {
char ch;
scanf_s(" %c", &ch, 1); // 使用 scanf_s
if (ch == '#') { // '#' 表示空節點
*root = NULL;
}
else {
*root = (BTreeNode*)malloc(sizeof(BTreeNode)); // 分配內存
if (*root == NULL) {
fprintf(stderr, "內存分配失敗\n");
exit(1);
}
(*root)->data = ch; // 設置節點值
createPreOrderTree(&(*root)->left); // 遞歸創建左子樹
createPreOrderTree(&(*root)->right); // 遞歸創建右子樹
}
}
上面的代碼中是通過先序的方式創建了一棵二叉樹,即:先創建根節點,然后創建左子樹,最后創建右子樹。
如果想要通過中序或者后序的方式創建一棵二叉樹,其實也非常簡單,只需要對代碼做很小的改動:
// 創建中序樹
void createInOrderTree(BTreeNode** root) {
char ch;
scanf_s(" %c", &ch, 1); // 使用 scanf_s
if (ch == '#') { // '#' 表示空節點
*root = NULL;
}
else {
*root = (BTreeNode*)malloc(sizeof(BTreeNode)); // 分配內存
if (*root == NULL) {
fprintf(stderr, "內存分配失敗\n");
exit(1);
}
createInOrderTree(&(*root)->left); // 遞歸創建左子樹
(*root)->data = ch; // 設置節點值
createInOrderTree(&(*root)->right); // 遞歸創建右子樹
}
}
// 創建后序樹
void createPostOrderTree(BTreeNode** root) {
char ch;
scanf_s(" %c", &ch, 1); // 使用 scanf_s
if (ch == '#') { // '#' 表示空節點
*root = NULL;
}
else {
*root = (BTreeNode*)malloc(sizeof(BTreeNode)); // 分配內存
if (*root == NULL) {
fprintf(stderr, "內存分配失敗\n");
exit(1);
}
createPostOrderTree(&(*root)->left); // 遞歸創建左子樹
createPostOrderTree(&(*root)->right); // 遞歸創建右子樹
(*root)->data = ch; // 設置節點值
}
}
現在我們已經可以根據意愿創建出一棵屬于自己的二叉樹,接下來就是對其進行遍歷了。
4.2.3遍歷二叉樹
根據前面的講解我們已經知道了遍歷二叉樹有三種方式,并且它們是遞歸的,在代碼編寫過程中我們要注意遞歸結束的條件即當前為空樹的時候,想明白這些之后對應的代碼實現就非常簡單了:
#include <stdio.h>
#include <stdlib.h>
// 定義二叉樹節點
typedef struct BinaryTreeNode {
char data; // 節點存儲的數據
struct BinaryTreeNode* left; // 指向左子樹的指針
struct BinaryTreeNode* right; // 指向右子樹的指針
} BTreeNode;
// 創建先序樹
void createPreOrderTree(BTreeNode** root) {
char ch;
scanf_s(" %c", &ch, 1); // 使用 scanf_s
if (ch == '#') { // '#' 表示空節點
*root = NULL;
}
else {
*root = (BTreeNode*)malloc(sizeof(BTreeNode)); // 分配內存
if (*root == NULL) {
fprintf(stderr, "內存分配失敗\n");
exit(1);
}
(*root)->data = ch; // 設置節點值
createPreOrderTree(&(*root)->left); // 遞歸創建左子樹
createPreOrderTree(&(*root)->right); // 遞歸創建右子樹
}
}
// 創建中序樹
void createInOrderTree(BTreeNode** root) {
char ch;
scanf_s(" %c", &ch, 1); // 使用 scanf_s
if (ch == '#') { // '#' 表示空節點
*root = NULL;
}
else {
*root = (BTreeNode*)malloc(sizeof(BTreeNode)); // 分配內存
if (*root == NULL) {
fprintf(stderr, "內存分配失敗\n");
exit(1);
}
createInOrderTree(&(*root)->left); // 遞歸創建左子樹
(*root)->data = ch; // 設置節點值
createInOrderTree(&(*root)->right); // 遞歸創建右子樹
}
}
// 創建后序樹
void createPostOrderTree(BTreeNode** root) {
char ch;
scanf_s(" %c", &ch, 1); // 使用 scanf_s
if (ch == '#') { // '#' 表示空節點
*root = NULL;
}
else {
*root = (BTreeNode*)malloc(sizeof(BTreeNode)); // 分配內存
if (*root == NULL) {
fprintf(stderr, "內存分配失敗\n");
exit(1);
}
createPostOrderTree(&(*root)->left); // 遞歸創建左子樹
createPostOrderTree(&(*root)->right); // 遞歸創建右子樹
(*root)->data = ch; // 設置節點值
}
}
// 先序遍歷
void preOrderTraversal(BTreeNode* root) {
if (root) {
printf("%c ", root->data); // 訪問當前節點
preOrderTraversal(root->left); // 遍歷左子樹
preOrderTraversal(root->right); // 遍歷右子樹
}
}
// 中序遍歷
void inOrderTraversal(BTreeNode* root) {
if (root) {
inOrderTraversal(root->left); // 遍歷左子樹
printf("%c ", root->data); // 訪問當前節點
inOrderTraversal(root->right); // 遍歷右子樹
}
}
// 后序遍歷
void postOrderTraversal(BTreeNode* root) {
if (root) {
postOrderTraversal(root->left); // 遍歷左子樹
postOrderTraversal(root->right); // 遍歷右子樹
printf("%c ", root->data); // 訪問當前節點
}
}
// 釋放樹的內存
void freeTree(BTreeNode* root) {
if (root) {
freeTree(root->left); // 釋放左子樹
freeTree(root->right); // 釋放右子樹
free(root); // 釋放當前節點
}
}
int main() {
printf("前序輸入二叉樹(必須按照二叉樹的結構進行輸入,#代表空:)\n");
BTreeNode* root = NULL; // 初始化根節點為 NULL
createPreOrderTree(&root); // 創建先序樹
printf("先序遍歷: ");
preOrderTraversal(root); // 先序遍歷
printf("\n");
printf("中序遍歷: ");
inOrderTraversal(root); // 中序遍歷
printf("\n");
printf("后序遍歷: ");
postOrderTraversal(root); // 后序遍歷
printf("\n");
// 釋放分配的內存
freeTree(root);
return 0;
}
通過上面的三個遍歷函數可以看到,函數體內部的代碼是極其相似的,只是訪問根節點的時機不同罷了,左右子樹都是先遍歷左子樹再遍歷右子樹,對于子樹的遍歷也是相同的規則,因此使用遞歸是遍歷二叉樹最簡單的一種處理方式。
4.2.4釋放樹節點
因為在上面的代碼中二叉樹的節點是動態創建的,所以在程序的最后還需要釋放節點資源,關于釋放的順序應該是先釋放子節點然后釋放父節點,所以對應的遍歷方式應該是后序遍歷。最后,基于這種方式我們就可以通過遞歸的方式釋放整棵二叉樹。
對應的代碼如下:
// 釋放樹的內存
void freeTree(BTreeNode* root) {
if (root) {
freeTree(root->left); // 釋放左子樹
freeTree(root->right); // 釋放右子樹
free(root); // 釋放當前節點
}
}
最后再次給大家強調一下,不論是使用先序遍歷、中序遍歷還是后序遍歷的方式創建二叉樹,在釋放資源的時候一定使用的是后續遍歷的方式,也就是從下往上,這一點相信大家能夠想明白。


 浙公網安備 33010602011771號
浙公網安備 33010602011771號