個人簡介

本人就讀于浙江某大學，大學期間有 ACM 集訓經歷。

因為是24考研考生，有認真考慮浙大，想著可以抵機試分數而報了名。

考試

體驗感極差。

先說前提：我們學校周末不對學生開放某教學樓= =

因為不想考試被打擾，我在這棟教學樓想辦法找了一間空教室作為考試地點。

第一題忘記是啥了，反正是道 easy 題，估計20min之內就拿下了20分。

第二題是模擬題，我寫了一百來行，正在調的時候（此時大概過去了1h）突然教室的門被打開了，有幾個學生進來說他們借了這間教室開班會，大概半小時之后就開始了，我只能先離開這里再另外找地方。本來考試的要求是考試范圍之內兩米不能有人，也肯定不能說話，我同時打破了這兩條規定，心想不會被浙大拉進黑名單吧，心態直接就崩掉了。我這次考試叫上了我一個室友，以備不時之需，沒想到真用上了，室友提醒我先呼叫監考老師再行動，接通之后我向監考老師說明了情況，監考老師倒是對我這邊的情況非常寬容，說我可以去找下一個考試的地方，不過要快一點，我室友就拿第二機位 手機 一直拍著我去找地方。由于這棟樓并沒有空教室開放，我們最后跑到了頂樓六樓，我坐在樓梯間考完了整場考試。

坐在樓梯間的時候，我不好拿鼠標，就只用了電腦的觸控板，debug時對我來說真的很不方便，第二題寫的代碼又長，我debug了很久，過樣例后一交，只有18分，被扣掉了七分。

這時候只有不到一個半小時了，我于是趕緊看下一題，所幸第三題很簡單，就是統計一下圖中點的入度、出度，我大概10min之內AC了這道題，獲得25分。

第四題的簡化題意如下：給你一棵樹的中序遍歷和后序遍歷序列，你需要求出這棵樹的輪廓，再判斷它是不是愛心型的。

思路其實很簡單，首先根據中序、后序遍歷求出這棵樹的結構；然后dfs求樹的輪廓；最后判斷愛心（輪廓上的點的高度先下降，再上升，再下降，再上升）。

但我在考場上并沒有寫出這道題。首先是我有點盲目自信，疏于復習，數據結構的知識（尤其是樹）我已經忘記了一些，根據中序、后序遍歷的序列求樹的結構我并沒有清晰的思路，只能在考場現推；其次就是我此時的心態已經完全炸裂了，根本靜不下心來思考任何有深度的問題，我記得考場上的我知道手算要怎么算，但是轉化成代碼的時候，我卡在了一個子序列的區間范圍的問題上，直到短時間內我覺得做出這題是無望了，就放棄了這道題，去看第二題模擬題。然而第二題我看來看去找不到錯誤，手造的數據都是可以通過的，我就有些沒轍。就這樣坐牢到考試結束。 T T

體會

我也算花錢買教訓了，這場考試提醒了我該復習數據結構了。

還有 什么煞筆學校周末竟然不對學生開放教室。。我真的很無語

下次如果有這樣的考試，還是得走正規流程借教室吧，或者干脆訂個鐘點房算了。被打擾到真的真的很心梗，崩潰就在一瞬間

第四題題解

我的做法上面已經說過了，就是首先根據中序、后序遍歷求出這棵樹的結構；然后dfs求樹的輪廓；最后判斷愛心（輪廓上的點的高度先下降，再上升，再下降，再上升）。

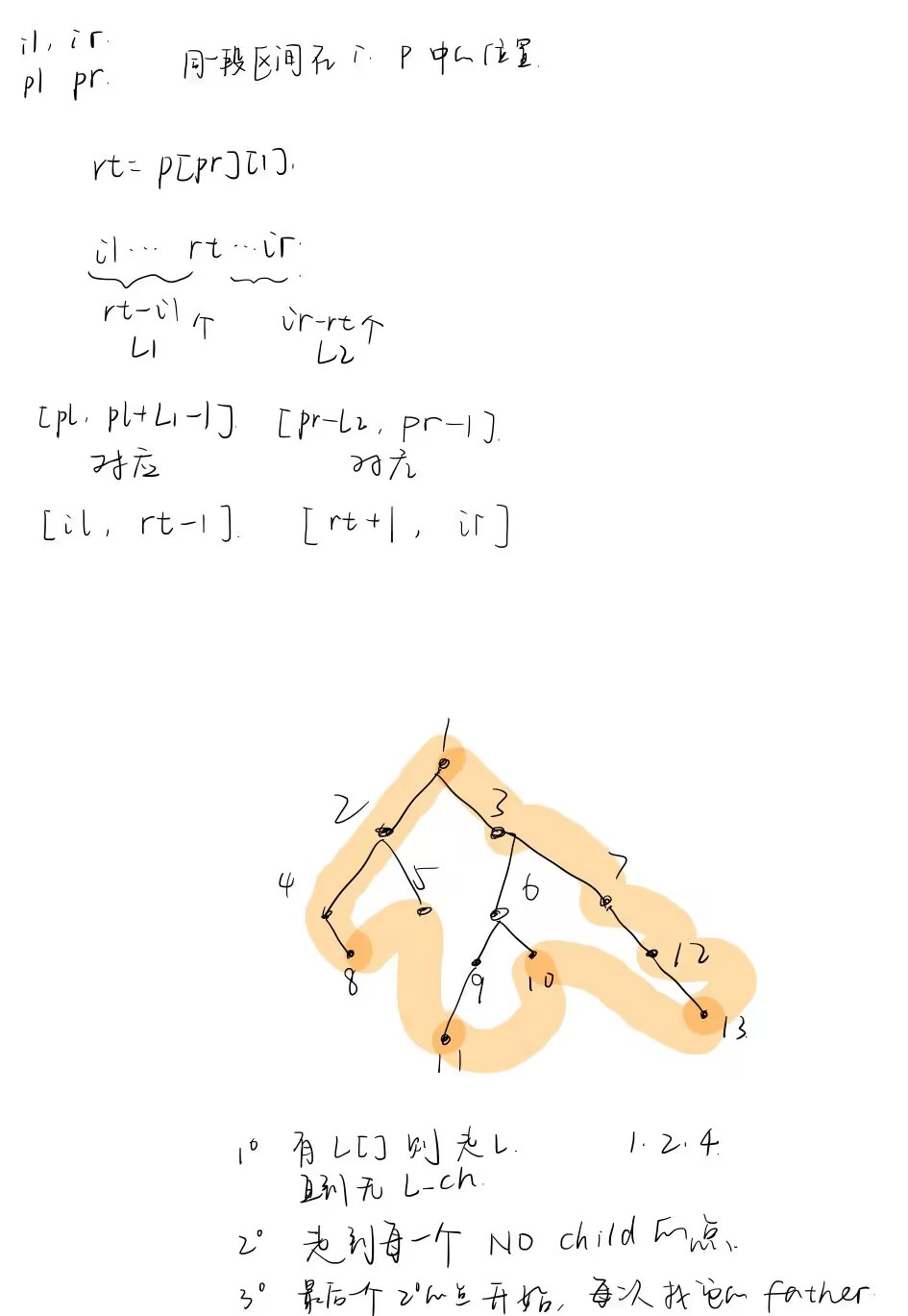
求樹的結構

// il ir 和 pl pr 分別是中序、后序遍歷序列中子序列的左右區間
// build函數的作用是找到每個當前的子樹root的左右兒子，記在L[root], R[root]里，遞歸求出整棵樹的結構
int build(int il, int ir, int pl, int pr) {
    if(il > ir || pl > pr) return -1;
    int root = P[pr];  // value
    int rt = p[root][0];  // pos
    int L1 = rt - il, L2 = ir - rt;
    L[root] = build(il, rt - 1, pl, pl + L1 - 1);
    R[root] = build(rt + 1, ir, pr - L2, pr - 1);
    return root;
}

求樹的輪廓

我的想法是分步。首先第一部分是只要當前結點有左兒子，就把這個左兒子push_back進ans；第二部分是所有沒有兒子的結點；第三部分是從最后一個第二部分的點開始，把它的爸爸依次push進答案

// 寫了2個dfs，寫一個應該也行的
void dfs(int rt, int fa) {  // 先序
    // cout << rt << ' ' ;
    if(rt == -1) return;
    d[rt] = d[fa] + 1;
    father[rt] = fa;
    if(link && L[rt] != -1 && R[rt] != -1) {link = 0;}
    dfs(L[rt], rt);
    dfs(R[rt], rt);
    return;
}

void dfs2(int rt) {
    if(rt == -1) return;
    if(State == 1) {
        if(L[rt] != -1) {
            vis[L[rt]] = 1;
            ans.push_back(L[rt]);
        }
        else State = 2;
    }
    if(State == 2) {
        if(L[rt] == -1 && R[rt] == -1 && !vis[rt]) {
            vis[rt] = 1;
            ans.push_back(rt);
        }
    }
    dfs2(L[rt]);
    dfs2(R[rt]);
}

判斷愛心

這就要根據之前dfs求出的點的深度來進行。

bool check() {   // 輪廓的 depth 先 + 再 - 再 + 再 -
    if(link) return 0; 
    int depth = d[ans[0]];
    int state = 1;
    for(int i = 1; i < ans.size(); i++) {
        if(state == 1 || state == 3) {
            if(d[ans[i]] < depth) state = ((state == 1) ? 2 : 4); 
        }
        else if(state == 2 || state == 4) {
            if(d[ans[i]] > depth) state = ((state == 1) ? 2 : 4); 
        }
        depth = d[ans[i]];
    }
    return (state == 4);
}

最后放一下整個的代碼吧，也不知道對不對，求問哪里能提交？？？

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int L[N], R[N], I[N], P[N], p[N][2], d[N];
int root, father[N], State;
bool link, vis[N];
vector<int> ans;

int build(int il, int ir, int pl, int pr) {
    if(il > ir || pl > pr) return -1;
    int root = P[pr];  // value
    int rt = p[root][0];  // pos
    int L1 = rt - il, L2 = ir - rt;
    L[root] = build(il, rt - 1, pl, pl + L1 - 1);
    R[root] = build(rt + 1, ir, pr - L2, pr - 1);
    return root;
}

void dfs(int rt, int fa) {  // 先序
    // cout << rt << ' ' ;
    if(rt == -1) return;
    d[rt] = d[fa] + 1;
    father[rt] = fa;
    if(link && L[rt] != -1 && R[rt] != -1) {link = 0;}
    dfs(L[rt], rt);
    dfs(R[rt], rt);
    return;
}

void dfs2(int rt) {
    if(rt == -1) return;
    if(State == 1) {
        if(L[rt] != -1) {
            vis[L[rt]] = 1;
            ans.push_back(L[rt]);
        }
        else State = 2;
    }
    if(State == 2) {
        if(L[rt] == -1 && R[rt] == -1 && !vis[rt]) {
            vis[rt] = 1;
            ans.push_back(rt);
        }
    }
    dfs2(L[rt]);
    dfs2(R[rt]);
}

bool check() {   // 輪廓的 depth 先 + 再 - 再 + 再 -
    if(link) return 0; 
    int depth = d[ans[0]];
    int state = 1;
    for(int i = 1; i < ans.size(); i++) {
        if(state == 1 || state == 3) {
            if(d[ans[i]] < depth) state = ((state == 1) ? 2 : 4); 
        }
        else if(state == 2 || state == 4) {
            if(d[ans[i]] > depth) state = ((state == 1) ? 2 : 4); 
        }
        depth = d[ans[i]];
    }
    return (state == 4);
}

void print() {
    for(auto i : ans) {
        printf("%d ", i); 
        // cout << i << ' ' << d[i] << endl;
    }puts("");
}

int main() {
    cin >> n;
    for(int i = 1; i <= n; i++) {
        scanf("%d", &I[i]);
        p[I[i]][0] = i;
    }
    for(int i = 1; i <= n; i++) {
        scanf("%d", &P[i]);
        p[P[i]][1] = i;
    }
    root = build(1, n, 1, n);
    // cout << "root:" << root << endl;
    link = 1;
    d[root] = 1; 
    dfs(root, 0); 

    State = 1; vis[root] = 1; ans.push_back(root); 
    dfs2(root);

    int tem = ans.back();
    while(1) {
        tem = father[tem];
        if(vis[tem]) break;
        ans.push_back(tem);
    }

    if(check()) {
        puts("Yes");
    }
    else puts("No");
    print();
    return 0;
}