前綴和筆記

• 前綴和是一種重要的預處理，能大大降低查詢的時間復雜度。可以簡單理解為“數列的前 \(n\) 項的和”。

• C++ 標準庫中實現了前綴和函數 std::partial_sum，定義于頭文件 <numeric> 中。

一維前綴和

簡介

一維前綴和顧名思義

就是一維的前綴和

前綴和是什么呢？

前綴和就是到目前為止全部的和是多少

一維就是單純的一串數

他的前綴和就成了一維前綴和

舉例

\(1\space2\space3\space4\space5\space6\)

他的前綴和依次就是 \(1\space3\space6\space10\space15\space21\)

\(i\) 位置上的前綴和就是從第一個數到第 \(i\) 個數全部數的和

這樣就很顯然的知道了什么是一維前綴和了吧？

例題

P1115 最大子段和 - 洛谷

輸入 #1

7
2 -4 3 -1 2 -4 3

輸出 #1

4

參考代碼：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 200010;
int a[maxn],s[maxn];
int n;
int main(){
	cin>>n;
	for (int i = 1;i <= n ; i ++ )  cin>>a[i];
	for (int i = 1; i <= n ; i ++ ) {
		s[i]=s[i-1]+a[i];
	}
	int ans = -2e9 ,mn = s[0];
	for (int r = 1; r <= n ; r ++ ) {
			ans = max(ans,s[r]-mn);
			mn = min(mn,s[r]);
	}
	cout<<ans<<endl;
    return 0;
}

二維前綴和

簡介

二維前綴和顧名思義

就是二維的前綴和

二維很顯然了

有 \(x\) 軸和 \(y\) 軸也就是一個面

這很顯然

那二維前綴和中一個 \(f[i][j]\) 表示的意思就是

以 \((1,1)\) 為左上角以 \((i,j)\) 為右下角這個矩陣里面數的和

如圖

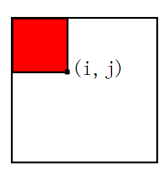
\(f[i][j]\)表示的就是圖中紅色的部分

二維前綴和求矩陣元素和

二維前綴和可以用來干什么呢？

一維前綴和你可以用來 \(O(1)\) 求某個點的值

那么類比一下

二維前綴和也是可以用來求某個矩陣的值的

但是怎么來求呢？

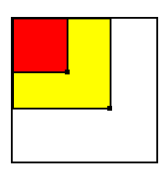
就如圖中

知道了兩個點的位置和他們的二維前綴和

圖中紅色是左上角的那個點的二維前綴和

紅色+黃色部分是右下角的那個點的二維前綴和

是不是可以用這個來求出他們之間的矩陣的和呢？

也就是這一部分：

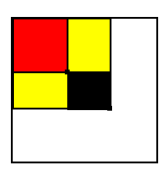
圖中黑色的部分就是我們要求的那個矩陣和

是不是可以通過某些奇怪的方法求出黑色部分是多少？

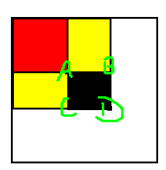
• \(D\) 點表示的二維前綴和值是紅色部分+兩個黃色部分+黑色部分

• \(A\) 點表示的是紅色部分

• \(B\) 點表示的是上面的黃色部分+紅色部分

• \(C\) 點表示的是下面的黃色部分+紅色部分

這里面只有 \(D\) 的前綴和里面包括黑色部分

只要減去 \(D\) 里面的哪兩個黃色部分和紅色部分是不是就剩下了我們要求的黑色部分了？

那怎么減去呢？

可以這樣：\(D-B-C+A\)

這就是二維前綴和最重要的部分了

化成二維數組的形式就是這樣的

為什么上文成立

繼續看上面那張圖

由 \(D-B-C+A\) 到方程式這個很顯然所以就不多說了

只要證明出 \(D-B-C+A\) 是正確的那就沒有問題了

這個可以化成：

紅色部分+上面的黃色部分+下面的黃色部分+黑色部分-上面的黃色部分-紅色部分-下面的黃色部分-紅色部分+紅色部分

這樣是不是很巧妙的就只剩下了黑色部分

所以成立

二維前綴和怎么求

這個可以類比上面求矩陣的思想

只是這個矩陣的右下角是 \((i,j)\) ，左上角也是
\((i,j)\)

就是一個 \(1\times1\) 的矩陣

所以也是很好求的

但是上面是已知 \(D,A,B,C\) 求黑色部分

這里你只知道 \(A,B,C\) 和黑色部分

因為是一個 \(1\times1\) 的矩陣嘛

所以黑色部分就只有一個元素也就是 \((i,j)\) 坐標上的那個元素值

所以就可以個加法變減法，減法變加法一個性質的

通過 \(A,B,C\) 和黑色部分來求出 \(D\)

• \(D\) 點表示的二維前綴和值是紅色部分+兩個黃色部分+黑色部分
• \(A\) 點表示的是紅色部分
• \(B\) 點表示的是上面的黃色部分+紅色部分
• \(C\) 點表示的是下面的黃色部分+紅色部分

所以 \(D\) 就可以等于 \(B+C-D\space+\) 黑色部分:

上面的黃色部分+紅色部分+下面的黃色部分+紅色部分-紅色部分+黑色部分
=上面的黃色部分+紅色部分+下面的黃色部分+黑色部分

剛好等于 \(D\),方程式為

例題

P1387 最大正方形 - 洛谷

在一個 \(n\times m\) 的只包含 \(0\) 和 \(1\) 的矩陣里找出一個不包含 \(0\) 的最大正方形，輸出邊長。

輸入 #1

4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1

輸出 #1

2

參考代碼：

#include <algorithm>
#include <iostream>
using namespace std;
int a[103][103];
int b[103][103];  // 前綴和數組，相當于上文的 f[]
int main() {
  int n, m;
  cin >> n >> m;

  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      cin >> a[i][j];
      b[i][j] =
          b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1] + a[i][j];  // 求前綴和
    }
  }

  int ans = 1;

  int l = 2;
  while (l <= min(n, m)) {  //判斷條件
    for (int i = l; i <= n; i++) {
      for (int j = l; j <= m; j++) {
        if (b[i][j] - b[i - l][j] - b[i][j - l] + b[i - l][j - l] == l * l) {
          ans = max(ans, l);  //在這里統計答案
        }
      }
    }
    l++;
  }

  cout << ans << endl;
  return 0;
}

作業

P1719 最大加權矩形 - 洛谷

求最大矩陣和

輸入 #1

4
0 -2 -7 0
 9 2 -6 2
-4 1 -4 1 
-1 8  0 -2

輸出 #1

15

輸出 #1解釋

9  2
-4  1
-1  8

\(ACcode:\)

#include<bits/stdc++.h>
using namespace std;
const int maxn = 500;
int a[maxn][maxn],s[maxn][maxn],p[maxn];
int n;
int getarea(int p[]) {
	int mn = min(p[1],0),sum = p[1],mx=-2e9;
	for (int i = 2; i <= n ; i ++ ) {
		sum+=p[i];
		mx=max(mx,sum-mn);
		mn=min(mn,sum);
	}
	return mx;
}
int main(){
	cin>>n;
	for (int i = 1; i <= n ; i ++ ) {
		for (int j = 1; j <= n ; j ++ ) {
			cin>>a[i][j];
			s[i][j]=s[i-1][j]+a[i][j];
		}
	}
	int ans = -2e9;
	for (int d = 1; d <= n ; d ++ ){
		for (int i = d ; i <= n ; i ++ ) {
			
			for (int j = 1 ; j <= n ; j ++ ) p[j] = s[i][j]-s[i-d][j];//構造一維的情況 
			ans=max(ans,getarea(p));
		}
	}
	cout<<ans<<endl;
    return 0;
}