CSP-S模擬40/煉石計劃NOIP模擬賽第五套
歇宰遷main:
大大大大大家好我我我是肝· \(HZOI\) 爆零大玉·硬化,今今今今今天我又雙叒叕爆零啦【大悲】。我的 \(S\) 組怎么辦啊么辦啊么辦啊么辦啊么辦啊么辦啊么辦啊么辦啊么辦啊!!!
徒



戈
《醫學》
ドクター?キドリです
愛?爆破ッテロ
簡単になれば
埋まった マター マター
ドクター?キドリです
愛想良いかも
朦朧オオトも 埋めた メタ メタ
何処にも無いから寢ていたら
壊れて泣いてるユメを診たんだよ
次期には噓に診えてクルゥ
カオが→鈍器になっちゃうヨ
偽が→権利を取ったんだ
無くなってほしい煩悩が
ドウヤラ生き延びてしまった
生き延びてしまったんだ
足が→タガメになっちゃうヨ
噓が→動機になったんだ
疑ってほしい本能を
ドウヤラ本心だと思った
本心だと思ったんだ
クチョォ
ドクター?キドリです
全部辭めろよ
アティチュードが
感動物に屆く猛毒
損得の得の方ダケ
回った 割った 割った
カオが→鈍器になっちゃうヨ
偽が→権利を取ったんだ
無くなってほしい煩悩が
ドウヤラ生き延びてしまった
生き延びてしまったんだ
音が→機能になってしまう
人が→偽りに集まる
塞がってしまえよ耳
ドウヤラ屆いて居ない診たい
屆いて居ない診たいネ゛
クチョォ
T1 公約數神廟
喵。
題目描述:
自己發明。
土地私有制使得賢者成為謎語人,全職神喵不是群居動物,若 \(i\leq j\) 且 兩者的 \(_{Gong^{產_{黨}}}\) 大于一,那么你可以從神喵 \(i\) 走到神喵 \(j\) ,不管世界上有多少 \(_{共_{Chan_黨}}\),神喵自己都能走到自己, \(0\) 沒有\(共_{產^{Dang}}\)。
Solve:
先說賽時罷:
首先我們可以發現我們不會。于是我們先觀察數據范圍發現 \(a_i\) 只有 \(1000\) 這啟發我們先篩個質數:
const int cnt = 168, pr[] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997};
對不起!
然后暴力地分解質因數:
for(register int i = 1; i <= n; i ++){
a[i] = r();
int hh = a[i];
for(register int j = 1; hh > 1; j ++){
if(hh % pr[j] == 0){
while(hh % pr[j] == 0){
hh /= pr[j];
}
}
}
}
太劣了!
之后我們發現如果左右端點兩個數的 \(gcd\) 大于一就一定可行,于是特判輸出屎 \(Shi\) 。
真沒治!
但是還有一種情況就是這樣的:
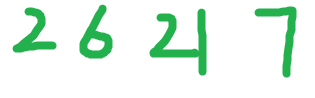
二通過六和二十一可以到與它沒有共同質因數的七。
于是我們發現可以把所有有共同質因數的點都連上邊。

炸炸炸炸炸炸炸!
于是我們每次拆到一個質因數都只和上一次剛剛出現那個質因數的位置連有向邊。

會不會炸!
不知道,讓我們拿出智慧的計算器,摁一下,發現一千以內的數最多有四個不相同的質因數,于是最多建出 \(4×(n-1)\) 條邊,炸不了。
這么好!
但是每次詢問跑一遍電風扇 \(DFS\) 是 \(O(n)\) 的,不過可以得到前 \(80pts\) 了。
你要不看看樣例過了嗎!
沒有。
我們驚奇地發現:我們剛剛的操作建了整整零條邊!按理來說應該只有自己到自己的地方是 \(Shi\) 口牙,為什么還有一個呢?
零與其它不為零的數的最大公約數在本題竟然等于那個數!!!
那我難道要讓零跟每個點都連條邊嗎?
炸炸炸炸炸炸炸!
這是賽時,我想不到正解的前綴和,但是直接跑太劣了,加邊太爆炸了,于是為了維護 \([x,y]\) 區間是否存在 \(0\) ,我自以為是地寫了一棵線段樹。
人傻常數大,全部都爆炸!
于是我用的其實是 \(bool\) ,然后就是很高興,沒寫假。
然后每次暴力 \(DFS\) 時清空 \(v\) 數組太唐了于是改成了記時間戳。
然后呢?
然后自己發明了兩個小樣例給自己 \(Hack\) 了。
1:
5 2
1 0 1 0 1
1 5
2 4
Expect:
Fou
Fou
2:
5 1
1 0 3 0 1
2 4
Expect:
Shi
壞了少特判!
于是我就特判了兩頭是一的/兩頭是零且中間沒比一大的是 \(Fou\) ,兩頭是零且中間有比一大的是 \(Shi\) 。
對不起注意力太差了沒發現只有一頭是一也是 \(Fou\)
之后其實如果加上沒發現的特判就能 \(AC\) 了,時間復雜度其實不會算,但是應該最壞最壞能到 \(O(n~q~logn)\) ,自帶多少常數不會算,肯定跑不滿,大抵是數據水可過罷。
《不使用快讀快寫/關閉流同步,僅使用 \(scanf\) 跑得嚴格快于 \(admin\) 的碼》
啊啊啊我為什么少個特判啊啊啊啊啊啊啊啊!!!
Code:
想看卡常點這里
#include <bits/stdc++.h>
using namespace std;
#define lson (root << 1)
#define rson (root << 1 | 1)
#define mid ((l + r) >> 1)
const short cnt = 168, pr[] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997};
const int _ = 100010;
short a[_];
int x, y, nw, n, q, bfr[1001], to[_ << 2], nxt[_ << 2], h[_], tot, v[_];
bool t[_ << 2];
struct hhh{
int x, y;
};
inline short gcd(short x, short y){
return y ? gcd(y, x % y) : x;
}
inline int r(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}
inline void add(int x, int y){
to[++ tot] = y;
nxt[tot] = h[x];
h[x] = tot;
return ;
}
inline bool zhao(int s, int t){
if(s == t){
return 1;
}
if(s > t || v[s] == nw){
return 0;
}
v[s] = nw;
for(int i = h[s]; i; i = nxt[i]){
int hhh = to[i];
if(zhao(hhh, t)){
return 1;
}
}
return 0;
}
inline void update(int root, int l, int r, int p, int v){
if(l == r){
t[root] = v;
return ;
}
if(p <= mid){
update(lson, l, mid, p, v);
}
else{
update(rson, mid + 1, r, p, v);
}
t[root] |= t[lson] | t[rson];
return ;
}
inline bool query(int root, int l, int r, int x, int y){
if(l >= x && r <= y){
return t[root];
}
bool as = 0;
if(x <= mid){
as |= query(lson, l, mid, x, y);
}
if(y > mid){
as |= query(rson, mid + 1, r, x, y);
}
return as;
}
int main(){
freopen("gcd.in", "r", stdin);
freopen("gcd.out", "w", stdout);
n = r(), q = r();
for(register int i = 1; i <= n; i ++){
a[i] = r();
short hh = a[i];
if(! hh){
update(1, 1, n, i, 1);
continue;
}
for(register int j = 1; hh > 1; j ++){
if(hh % pr[j] == 0){
while(hh % pr[j] == 0){
hh /= pr[j];
}
if(bfr[pr[j]]){
add(bfr[pr[j]], i);
}
bfr[pr[j]] = i;
}
}
}
for(register int i = 1; i <= q; i ++){
nw ++;
x = r(), y = r();
register short miao = gcd(a[x], a[y]);
if(x == y){
putchar('S'), putchar('h'), putchar('i'), putchar('\n');
continue;
}
else if(miao > 1){
putchar('S'), putchar('h'), putchar('i'), putchar('\n');
continue;
}
else if(a[x] == 1 || a[y] == 1){
putchar('F'), putchar('o'), putchar('u'), putchar('\n');
continue;
}
else if(! a[x] && ! a[y]){
bool f = 0;
for(int j = x; j < y; j ++){
if(a[j] > 1){
f = 1;
break;
}
}
f ? (putchar('S'), putchar('h'), putchar('i'), putchar('\n')) : (putchar('F'), putchar('o'), putchar('u'), putchar('\n'));
continue;
}
else if(query(1, 1, n, x, y)){
putchar('S'), putchar('h'), putchar('i'), putchar('\n');
continue;
}
else{
zhao(x, y) ? (putchar('S'), putchar('h'), putchar('i'), putchar('\n')) : (putchar('F'), putchar('o'), putchar('u'), putchar('\n'));
}
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define lson (root << 1)
#define rson (root << 1 | 1)
#define mid ((l + r) >> 1)
const short cnt = 168, pr[] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997};
const int _ = 100010;
short a[_];
int x, y, nw, n, q, bfr[1001], to[_ << 2], nxt[_ << 2], h[_], tot, v[_];
bool t[_ << 2];
struct hhh{
int x, y;
};
inline short gcd(short x, short y){
return y ? gcd(y, x % y) : x;
}
inline int r(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}
inline void add(int x, int y){
to[++ tot] = y;
nxt[tot] = h[x];
h[x] = tot;
return ;
}
inline bool zhao(int s, int t){
if(s == t){
return 1;
}
if(s > t || v[s] == nw){
return 0;
}
v[s] = nw;
for(int i = h[s]; i; i = nxt[i]){
int hhh = to[i];
if(zhao(hhh, t)){
return 1;
}
}
return 0;
}
inline void update(int root, int l, int r, int p, int v){
if(l == r){
t[root] = v;
return ;
}
if(p <= mid){
update(lson, l, mid, p, v);
}
else{
update(rson, mid + 1, r, p, v);
}
t[root] |= t[lson] | t[rson];
return ;
}
inline bool query(int root, int l, int r, int x, int y){
if(l >= x && r <= y){
return t[root];
}
bool as = 0;
if(x <= mid){
as |= query(lson, l, mid, x, y);
}
if(y > mid){
as |= query(rson, mid + 1, r, x, y);
}
return as;
}
int main(){
freopen("gcd.in", "r", stdin);
freopen("gcd.out", "w", stdout);
scanf("%d%d", & n, & q);
for(register int i = 1; i <= n; i ++){
scanf("%d", & a[i]);
short hh = a[i];
if(! hh){
update(1, 1, n, i, 1);
continue;
}
for(register int j = 1; hh > 1; j ++){
if(hh % pr[j] == 0){
while(hh % pr[j] == 0){
hh /= pr[j];
}
if(bfr[pr[j]]){
add(bfr[pr[j]], i);
}
bfr[pr[j]] = i;
}
}
}
for(register int i = 1; i <= q; i ++){
nw ++;
scanf("%d%d", & x, & y);
register short miao = gcd(a[x], a[y]);
if(x == y){
printf("Shi\n");
continue;
}
else if(miao > 1){
printf("Shi\n");
continue;
}
else if(a[x] == 1 || a[y] == 1){
printf("Fou\n");
continue;
}
else if(! a[x] && ! a[y]){
bool f = 0;
for(int j = x; j < y; j ++){
if(a[j] > 1){
f = 1;
break;
}
}
f ? (printf("Shi\n")) : (printf("Fou\n"));
continue;
}
else if(query(1, 1, n, x, y)){
printf("Shi\n");
continue;
}
else{
zhao(x, y) ? (printf("Shi\n")) : (printf("Fou\n"));
}
}
return 0;
}
T2 棧法師
我討厭模擬,我看著就覺得惡心。
Solve:
一些人:
根據題意,我們需要按不降序砍死他們,但是我們必須把他們轉移到一個棧里才能用彈棧的方式砍死。
我們可以這樣搞:






我 \(C_{a}o\) 了粘完才發現是個藏頭的東西(啊啊啊啊啊啊大大大大大大大大大哥別殺我!!!)
這樣的東西是平凡的,直接模擬一下就可以了。
再看這群人:

我們還是這樣殺:




我們發現了一個可怕的事情——
我們殺不了他了:

于是只能新開一個棧來中轉:



終于殺完啦!
于是我們直接模擬 \(k=1\) 的情況,如果不行那么 \(k\) 就等于二。(這不廢話)
把彈出的數都放入棧法杖 A 中,棧法杖 B 僅作為中轉,設下一個要輸出的數為 \(x\):
若 \(x\) 還在序列 \(a\) 中,則一直進行 \((1, 1)\) 操作直到 \(x\) 進入棧法杖 A,然后進行一次 \((2, 1)\) 操作將其輸出;操作次數 = 當前序列 \(a\) 長度 - \(x\) 初始位置 + 1。
否則 \(x\) 在棧法杖 A 中,進行 \((3, 1, 2)\) 操作直到 \(x\) 是棧頂,進行一次 \((2, 1)\) 操作將其輸出,然后進行 \((3, 2, 1)\) 操作清空棧法杖 B;操作次數 = 當前 \(A\) 棧 size - \(x\) 初始位置之后 \(<x\) 元素數量 - 1。
\(x\) 初始位置之后 \(<x\) 元素數量" 可以使用樹狀數組預處理。
總復雜度 \(O(n\log n)\)。
Code:
#include <bits/stdc++.h>
#define lowbit(x) (x & (- x))
const int _ = 100005;
int t, b[_], tree[_], p[_], n, s[_], top;
std::vector<int> v;
struct hhh{
int n, v;
}a[_];
inline bool bbb(hhh x, hhh y){
if(x. v != y. v){
return x. v < y. v;
}
return x. n < y. n;
}
inline void add(int x, int y){
for(; x <= n; x += lowbit(x)){
tree[x] += y;
}
return ;
}
inline int query(int x){
int as = 0;
for(; x; x -= lowbit(x)){
as += tree[x];
}
return as;
}
inline bool kdyi(){//k==1。
v. clear();
top = 0;
for(int i = 1, nw = n; i <= n; i ++){
while((! top || s[top] != a[i]. v) && nw){
s[++ top] = b[nw --];
v. emplace_back(1);
}
if(s[top] == a[i]. v){
v. emplace_back(0);
top --;
}
else{
return 0;
}
}
return 1;
}
inline void kder(){
v. clear();
for(int i = 1; i <= n; i ++){
p[i] = n - a[i]. n + 1;
}
for(int i = 1; i <= n; i ++){
add(i, 1);
}
for(int i = 1, c = n; i <= n; i ++){
int d = query(p[i]) - query(c);
if(d){
v. emplace_back(d);
}
v. emplace_back(0);
add(c = p[i], - 1);
}
printf("2\n%d\n1 1 %d\n", v. size() + 1, n);
for(auto h : v){
if(h > 0){
printf("3 2 1 %d\n", h);
}
if(h < 0){
printf("3 1 2 %d\n", - h);
}
if(! h){
printf("2 1\n");
}
}
return ;
}
int main(){
freopen("sort.in", "r", stdin);
freopen("sort.out", "w", stdout);
scanf("%d", & t);
while(t --){
scanf("%d", & n);
for(int i = 1; i <= n; i ++){
scanf("%d", & b[i]);
a[i]. v = b[i], a[i]. n = i;
}
std::sort(a + 1 , a + n + 1, bbb);
if(kdyi()){
printf("1\n%d\n", v. size());
for(auto h : v){
h ? printf("1 1 1\n") : printf("2 1\n");
}
}
else{
kder();
}
}
return 0;
}
T3 城堡考古
城城堡(\(ccb\))。
不知道我不會我賽時就看出來 \(m=2\) 是斐波那契數列然后矩陣快速冪也不知道寫沒寫真然后不會高級的數學也來不及而且不會神秘的高精度于是遺憾離場咕咕咕。
T4 生命之樹
生命女神!





 依舊赤石。
依舊赤石。

 浙公網安備 33010602011771號
浙公網安備 33010602011771號